Abstract
Accurately predicting the filtration volume (FV) in drilling fluid (DF) is crucial for avoiding drilling problems such as a stuck pipe and minimizing DF impacts on formations during drilling. Traditional FV measurement relies on human-centric experimental evaluation, which is time-consuming. Recently, machine learning (ML) proved itself as a promising approach for FV prediction. However, existing ML methods require time-consuming input variables, hindering the semi-real-time monitoring of the FV. Therefore, employing radial basis function neural network (RBFNN) and multilayer extreme learning machine (MELM) algorithms integrated with the growth optimizer (GO), predictive hybrid ML (HML) models are developed to reliably predict the FV using only two easy-to-measure input variables: drilling fluid density (FD) and Marsh funnel viscosity (MFV). A 1260-record dataset from seventeen wells drilled in two oil and gas fields (Iran) was used to evaluate the models. Results showed the superior performance of the RBFNN-GO model, achieving a root-mean-square error (RMSE) of 0.6396 mL. Overfitting index (OFI), score, dependency, and Shapley additive explanations (SHAP) analysis confirmed the superior FV prediction performance of the RBFNN-GO model. In addition, the low RMSE (0.3227 mL) of the RBFNN-NGO model on unseen data from a different well within the studied fields confirmed the strong generalizability of this rapid and novel FV prediction method.
1. Introduction
Drilling fluids (DFs) perform critical drilling functions like suspending cuttings, balancing formation pressure, cooling tools, and transmitting forces [1,2,3]. DFs can be classified as water-based (WBDF), oil-based (OBDF), or synthetic-based (SBDF) fluids [1,2,4]. WBDFs are often preferred over others due to their cheaper price, lower toxicity, and reduced waste/environmental issues [5,6].
DF characteristics substantially influence drilling performance [7]. Important monitored parameters include gel strength (GL), plastic viscosity (PV), yield point (YP), and filtration properties [2,7,8,9]. GL maintains wellbore stability in certain temperature/pressure conditions. PV measures flow resistance, while YP identifies the pressure needed for the flow [7,10,11]. Among them, the filtration volume (FV) directly impacts borehole stability and lost circulation, as high FV can cause fluid invasion, weaken the borehole wall, and damage formation permeability, impairing well productivity [2,12].
Regulating the FV requires understanding fluid–rock interactions under dynamic downhole conditions, which mud engineers often struggle to predict [13]. Poor FV control can cause drilling problems such as stuck pipes and damaged reservoir formation. Minimizing and controlling FV is critical in complex, extended-reach and HP/HT wells in low permeability reservoirs [3,14]. Reliably predicting the FV is important for wellbore integrity and success [15]. Currently, DF engineers use various FV measurement methods [11]. Methods include low- and high-pressure devices and industry standards 13b-1 and 13b-2 [10]. However, these FV measurement methods are time-consuming and results are only measured once/twice a day. This limitation prevents drilling crews from continuously monitoring for unexpected changes during drilling operations.
Lack of accurate and easy-to-perform semi-real-time FV measurements can result in losses, instability issues, human errors, and poor FV control, especially in complex HP/HT or low permeability wells [16,17]. In attempts to resolve this problem, in recent years there has been a surge in research studies focusing on data-driven methods to predict DF properties, especially the FV. One of the most effective approaches is the use of machine learning (ML) algorithms to predict the FV in DFs [17,18,19].
Historically, Civan F. [20,21] pioneered the development of accurate data-driven techniques for incompressible mud cake filtration. Later, Wu et al. [22] developed an advanced fluid flow simulator, which improved the understanding of DF behavior and interactions with formations. These works advanced predictive analytics using sophisticated methods. However, the complexity of their models and the resources required to execute them limit their use during drilling operations. They also lack information on key properties, particularly fluid density and viscosity. This indicates a need for more practical models to accurately predict the FV.
In the realm of ML models, Jeirani and Mohebbi [18] were the first to use artificial neural networks (ANNs) to predict the FV and the filter cake permeability. Their ANN models accurately simulated multiple datasets for permeability coefficients of determination (R2 = 0.9815) and the FV (R2 = 0.9433) using inputs of time, pressure drop, water content, and salt content. Although their approach demonstrated high accuracy, it relied on laboratory-generated data, which does not represent real-time drilling conditions accurately, necessitating the use of real-time data for improved FV predictions.
Toreifi et al. [23] proposed ANNs with particle swarm optimization (PSO), achieving good prediction accuracy on 1630 combined drilling and DF records (R2 = 0.891). ANNs were also used to predict the FV from 100 laboratory DF samples with very high performance (R2 = 0.99978) [23]. However, these studies relied on data from published studies and laboratory-generated data, which may not accurately represent real-time drilling conditions. Golsefatan and Shahbazi [19] collected over 1000 data records and applied ANN to analyze nanoparticle influence on the FV with less accurate results. Lekomtsev et al. [24] applied extreme learning machine (ELM) and PSO-least square support vector machine (LSSVM) models to that dataset, with PSO-LSSVM achieving the best FV prediction performance (root-mean-square deviation (RMSE) = 0.2459, R2 = 0.999). Ning et al. [17] used a 156-record dataset to predict the nano-FV using ANN and LSSVM models, with ANN demonstrating high prediction performance (R2 > 0.99, MAPE < 7%). Gasser et al. [25] used ANN to predict nano-fluid filtrate invasion with over 2800 data points. Generally, these studies have relied on data obtained from laboratory studies of DF samples with various concentrations and additives of nanoparticles, which may not precisely reflect the actual drilling fluid compositions during the drilling of a specific well.
Gul and van Oort [10] compiled a 1800-point dataset from WBDFs and OBDFs and applied random forest (RF), XGBoost (XGB), support vector machine (SVM), and multilayer perceptron (MLP) models to study correlations between fluid properties and the FV. Their RF model achieved the best prediction performance (R2 = 0.86, mean absolute percentage error (MAPE) = 22.56%). Although their proposed model generated low prediction errors, its applicability is limited as rheological parameters were used as inputs, which are too time-consuming to obtain frequently during drilling operations.
Davoodi et al. [26] applied HML, LSSVM, a multilayer extreme learning machine (MELM) improved by a cuckoo optimization algorithm (COA), and a genetic algorithm (GA) to predict the FV, the PV, and the YP using 1160 records. The inputs used were the fluid density (FD), the solid percentage (S%), and the Marsh funnel viscosity (MFV). The MELM-COA models achieved the best prediction performance with RMSE values of 0.6357, 0.6086, and 0.6796 for the FV, the PV, and the YP, respectively. However, S% is determined daily, and its measurement takes a relatively long time (2–3 h/experiment), limiting that model’s use for frequent FV monitoring in a semi-real-time manner.
Consequently, the existing studies have provided results that demonstrate the capability of using ML, deep learning (DL), and HML models to predict the FV in DFs. However, these previous studies generally rely on published data and/or laboratory-generated fluids, which may not accurately reflect the drilling conditions at a specific time. Moreover, the existing FV prediction models typically have unreliable prediction performance and require new techniques to further leverage comprehensive real-time data. This study aims to address these limitations by utilizing semi-real-time data and advanced HML modeling to improve the FV prediction performance.
The FV can be predicted more frequently by relying on just two input variables, FD and MFV, commonly measured at the well-site every 15–20 min (2 to 3 measurements/h recorded continuously while drilling) [11,27]. These parameters are highly correlated with the FV, as drilling-fluid additives tend to affect DF density and viscosity. ML maps FD-MFV to typical FV outcomes, enabling FV approximation without direct measurement. This information facilitates proactive responses such as adding filtration control additives to modify DF compositions before drilling problems occur. Similarly, MFV provides a practical measure of fluid rheology, indirectly reflecting changes in fluid properties that materialize during drilling [27,28,29]. This novel approach improves upon previous studies, which inadequately predict the FV by relying on measurements taken only about once per day, making them unable to identify rapid downhole changes during drilling operations. The proposed model fulfills the need for a reliable prediction tool that can predict the FV using semi-real-time DF data at short intervals (i.e., several times per hour).
This study, therefore, addresses the research gap by developing a novel HML model to reliably predict the FV based on only the two most readily experimentally measured parameters—FD and MFV. The dataset evaluated includes 1260 records from seventeen wells drilled in two Iranian oil and gas fields using various WBDFs. Two ML models are developed: radial basis function neural network (RBFNN) and multiple extreme learning machine (MELM). These ML models are hybridized with the growth optimizer (GO) to fine-tune the models’ hyperparameters. Combining robust models, short-interval semi-real-time inputs and optimization achieves highly reliable FV predictions that outperform the existing FV prediction models by providing more accurate and faster solutions for assisting drilling crews with monitoring the FV in semi-real-time.
2. Data Collecting and Description
To accurately predict the FV using simple ML and HML models in a frequent manner, it is important to utilize input variables that are routinely measured several times per hour. Therefore, the FD (pounds per cubic foot, pcf) and the MFV (sec/quart) were selected as inputs for the simple ML and HML models based on prior studies showing their significant impact on FV [10,17,18,19,24,26,30,31].
- ❖
- The FD has a direct impact on downhole hydrostatic pressure, which is exerted by the fluid column in the wellbore. The FD influences the FV in several ways. Higher FD increases the FV due to higher hydrostatic pressure, which pushes more fluid through the filter. Additionally, particle–fluid interactions affect cake formation and filtration rate, while changes in temperature and pressure alter the fluid’s properties, affecting its ability to filter [11,12,27,28,32].
- ❖
- The MFV measures the viscosity of DFs under realistic conditions. This test estimates the time it takes for a fixed volume of fluid to flow through a narrow orifice, which is influenced by the Reynolds number, a measure of the drag coefficient. A higher MFV indicates a thicker, more resistant fluid that flows more slowly, resulting in a lower ability to infiltrate pores, thereby resulting in a lower FV [11,28,33,34].
The 17-well compiled dataset (1260 data records) includes FV, FD, and MFV measurements for the WBDFs employed. Table 1 summarizes the dataset statistically. This database is applied for developing HML for accurate semi-real-time FV prediction.

Table 1.
The statistical characterization of the data entries in order to forecast the FV.
3. Methodology
Figure 1 illustrates the methodology applied for establishing and assessing the prediction performance of the FV prediction models proposed.
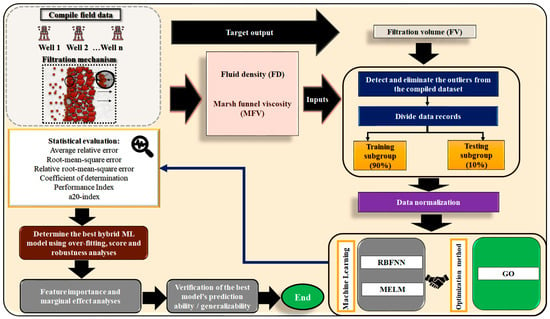
Figure 1.
Flowchart of the procedure applied for developing simple and hybrid ML models to predict FV in DF from two easily measured input variables, FD and MFV.
A preprocessing operation was conducted on the compiled dataset using the Mahalanobis distance (MD) technique to objectively detect and remove outliers (see Section 3.1). The screened and retained data were then divided into two subsets: one for model training (90% of the data) and one for model testing (10% of the data), followed by normalization. Machine learning (ML) algorithms were fine-tuned and applied to the training data. The trained models were tested on unseen data to evaluate their performance and assessed using overfitting analysis, scoring, and robustness analysis to select the best-performing model. Additionally, Shapley additive explanations (SHAP) analysis was used to assess feature importance, while partial dependence plots (PDP) were used to reveal the marginal effects of individual features, providing further insights into the best-performing model. Once the best predictive model was identified, it was applied to unseen data from a different well within one of the studied fields to further evaluate its practical generalizability and reliability. Appendix A.1 provides a detailed description of ML and optimization algorithms used, developed, and evaluated.
3.1. Data Normalization and Outlier Detection
To ensure consistency across the seventeen wells (1260 data records), a normalization step was applied to the variables (FV, FD, and MFV) prior to model development. This step helped eliminate well-specific variations in measurement scales, allowing the ML model to identify consistent patterns across all wells [26]. Crucial steps in the ML model development include data division and selecting an optimal train-to-test ratio. Random division prevents data leakage, and sensitivity analysis determines the ideal ratio for a reliable and generalizable model. Outlying data records were detected and removed to prevent noise and bias, ensuring optimal prediction performance [26]. For this purpose, the Mahalanobis distance (MD) technique is used to identify outliers in the training subset during the ML model configuration [35]. Initially, ML models were established using all available data records to predict the FV. For each data point, a prediction error (Err) was computed (Equation (1)) by comparing measured () and predicted () values. MD values were calculated for each data record (Equation (2)), and outliers were identified based on a predetermined threshold. If the MD value exceeded the threshold, the data point was flagged as a potential outlier and removed from the training dataset unless a valid justification supported its retention [35].
The MD outlier detection analysis was conducted using 10-fold cross-validation to:
- Provide a robust and unbiased estimate of the model’s performance using distinctive groups of data records.
- Minimize overfitting risks by identifying diverse outliers.
3.2. Hybridizing ML and GO Algorithms
In the RBFNN model, the number of clusters in the hidden layer, representing the RBF kernel clusters, is the key hyperparameter. This is determined through trial-and-error analysis to minimize the RMSE of the FV predictions. The chosen number of clusters defines RBFNN decision variables, including output layer weights, kernel center positions, and kernel σ values. Figure 2 illustrates the GO algorithm’s process for identifying the optimal hyperparameter values for the RBFNN predictor.
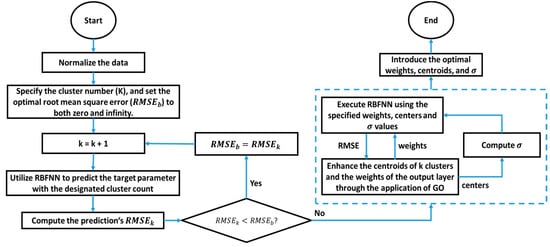
Figure 2.
Applying the GO algorithm to determine optimal hyperparameter values for the RBFNN predictor.
The MELM model’s development often relies on random weight and bias specification, resulting in inconsistent prediction accuracy across multiple runs. To achieve reliable and consistent accuracy, time-consuming and repetitive trials are necessary to determine the optimal configuration. This trial-and-error approach is inefficient. By integrating MELM with optimization algorithms, the model tuning and configuration process can be significantly accelerated. Figure 3 outlines the MELM-GO implementation sequence, which involves a two-stage optimization process.
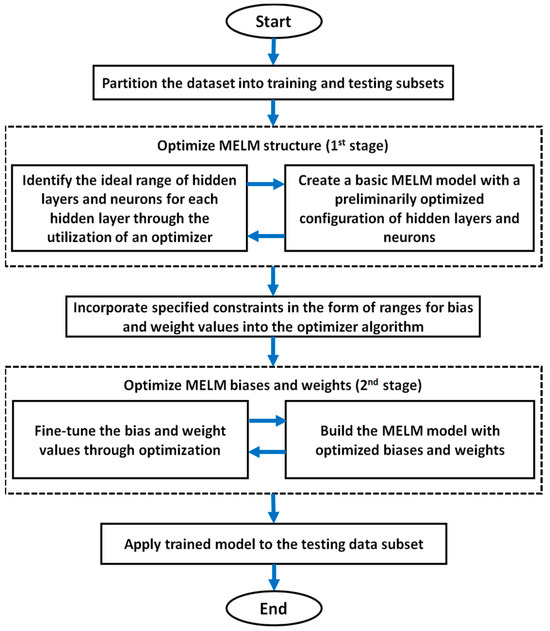
Figure 3.
Flowchart illustrating the implementation of the MELM-GO hybrid ML model designed for predicting the FV properties of DFs.
The GO algorithm (Figure 3) evaluates the optimal MELM structure using estimated ranges, calculating the RMSE for each target hyperparameter. Through iterative adjustments over ten model runs, the algorithm selects the model structure that generates the lowest RMSE. Subsequently, the optimal weights and biases are determined via a second optimization stage, where the number of decision variables corresponds to the total number of weights and biases in the optimal MELM structure. Initial values are assigned to the population, and their RMSE values guide adjustments to weights and biases until the termination condition is reached, yielding the best-performing weights and biases for the optimal MELM model structure. This two-stage optimization strategy replaces random assignment, reducing computational time and significantly enhancing the FV prediction performance of the MELM-GO model. Appendix B explains the primary assessment metrics used to assess the FV prediction performance of the HML models. These are relative error (RE), average relative error (ARE), root-mean-square error (RMSE), relative root-mean-square error (RRMSE), coefficient of determination (R2), performance index (PI), and an index based on the percentage of predictions that fall within the error range of ±20% (a20-index).
4. Results
4.1. Data Exploration
Evaluating the correlation between independent and dependent parameters before developing predictive models is crucial for understanding their relationships and interactions. This evaluation helps in identifying the most significant predictors and eliminating redundant variables, thereby enhancing model accuracy and efficiency. Therefore, the correlation matrix of the collected parameters is presented as a heat map in Figure 4. FD and MFV display direct correlation relationships with FV, indicating that increases in these parameters lead to an increase in the FV. Significantly, the correlation coefficient between FD and MFV is relatively low, suggesting no significant multicollinearity exists between them.
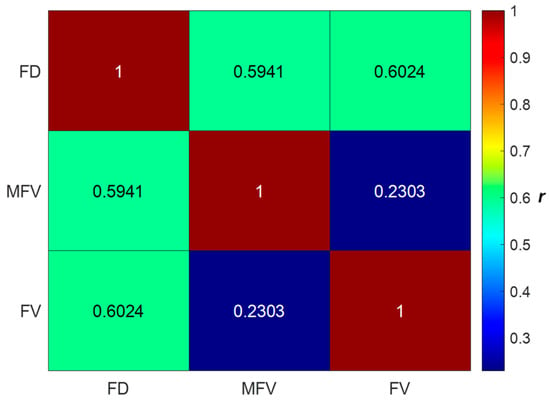
Figure 4.
Heatmap correlation matrix displaying the relationships between independent and dependent parameters for the compiled dataset.
4.2. Data Preprocessing
The training/testing subset separation ratio has a substantial impact on a model’s accuracy and generalizability. The ratio depends on the issue’s features and available data. For complex problems or limited data, a larger portion of the data should be allocated to the training set. Common separation ratios applied are 70/30, 80/20, or 90/10. Figure 5 displays the RMSE sensitivity analysis results of an RBFNN model for various training/testing subset separation ratios. The results show that a 90/10 separation split is most effective, which is applied in this study.
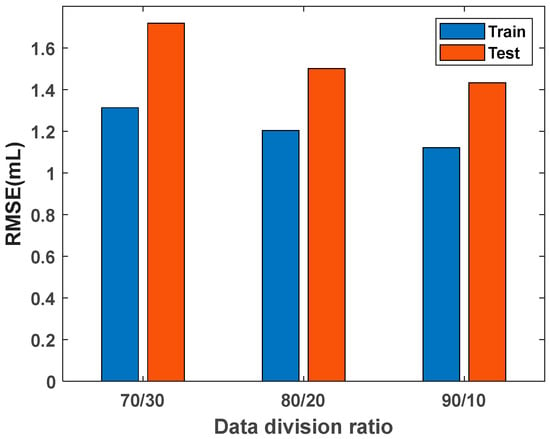
Figure 5.
RMSE results for the FV dataset evaluated with the RBFNN model with three training/testing subset separation ratios.
Figure 6 displays outliers identified applying the MD method with a Gaussian process regression (GPR) model with an automatic relevance determination (ARD) exponential kernel function. In accordance with the problem’s evaluation criteria, this kernel provided the best results. Based on high residual errors [36], a total of 48 outliers (4.2% of the training subset) were identified and eliminated by the MD process, combined with 10-fold cross-validation, before proceeding with the modelling process.
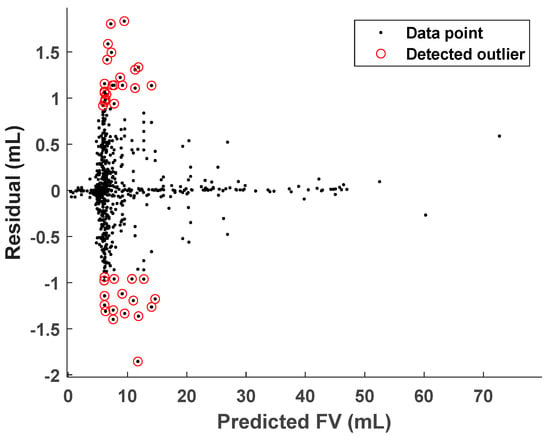
Figure 6.
Identification of outliers in the FV training dataset using GPR–Mahalanobis distance (MD) modeling.
4.3. Tuning the Machine Learning and Optimization Algorithms
The number of decision variables for the RBFNN and MELM models was based on the count of hyperparameters requiring optimization. The RBFNN and MELM models were fine-tuned with the GO algorithm configured with population sizes and number of iterations set at 30 for RBFNN and 50 for MELM. The GO configuration parameters are displayed in Table 2.

Table 2.
Tuning ML algorithm control parameters values via GO optimization.
The GO algorithm was used to fine-tune the RBFNN’s hyperparameters, determining the optimal number of centers to be 28. K-means clustering was then employed to identify these centers, each characterized by unique FD and MFV values. The GO algorithm further optimized the weights associated with each center. This comprehensive approach optimizes the RBFNN’s performance by leveraging clustering and GO techniques. To develop an appropriate FV prediction model using MELM, various MELM models with distinct numbers of hidden layers and neurons were initially generated. Assessing the provisional sensitivity analysis results suggested that a structure with three hidden layers, each with six neurons, resulted in the lowest FV prediction error. To refine this structure, the GO algorithm was employed to optimize the number of hidden layers and neurons. Figure 7 depicts the evolution of RMSE values for forty iterations of the GO algorithm in its MELM optimization process, revealing improvements up to the 35th iteration. The optimal MELM structure identified by GO consisted of three hidden layers with 4, 6, and 4 neurons, respectively. This structure was then used to optimize the weights and the biases for each node.
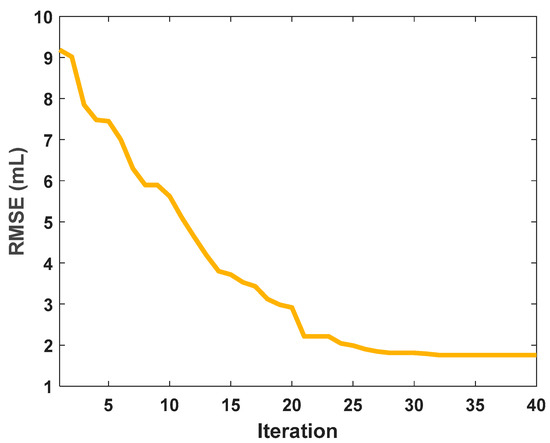
Figure 7.
The iterative reduction of RMSE within various iterations of the GO algorithm is employed to ascertain the optimal structure of the MELM algorithm in the prediction of the FV.
4.4. Developing Predictive Models
Cross-plots comparing the measured and the predicted FV values for the standalone ML (RBFNN, MELM) and optimized HML (MELM-GO, RBFNN-GO) models constructed with training data are illustrated in Figure 8.
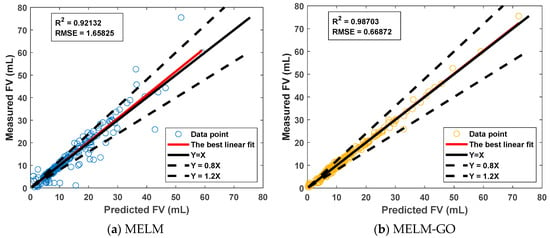
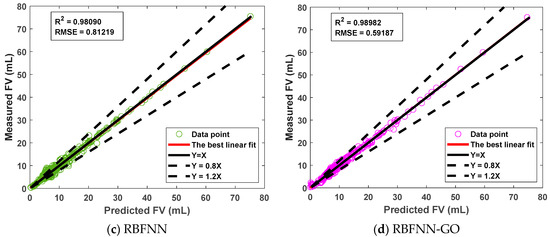
Figure 8.
Comparative cross-plots evaluating accuracy of measured and predicted FV values utilizing (a) MELM, (b) MELM-GO, (c) RBFNN, and (d) RBFNN-GO models on training data.
Predictions generated by the RBFNN-GO model (Figure 8) are in closest proximity to the y = x line, indicating the most accurate trained-model outcomes. RBFNN predictions, on the other hand, exhibit marginally greater variation and deviate more from actual values than RBFNN-GO, indicating less precise estimates. The MELM models generated the most imprecise forecasts, especially the standalone MELM model, which indicates a diminished capacity to accurately quantify the FV.
Figure 9 displays the evolution of the training subset RMSE for sequences of GO iterations. The hybridized RBFNN-GO architecture showed the highest degree of performance consistency, with negligible error fluctuations throughout subsequent optimizations. The RBFNN-GO model converged more slowly than the MELM-GO model but reached an improved solution. The HML models are clearly more effective learners than the standalone models.
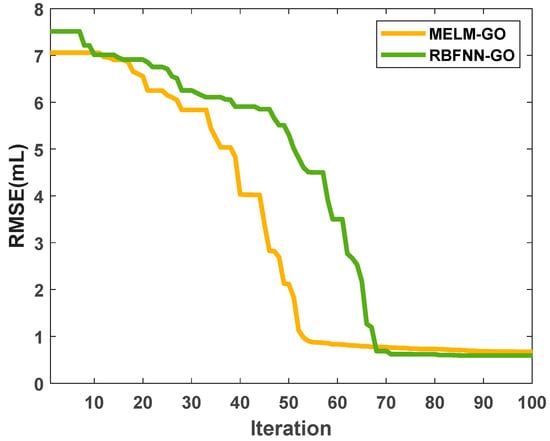
Figure 9.
Assessment of the error convergence of GO algorithm iteration sequences for the two HML models configured to predict the FV.
The prediction performance metrics applied to the training subset (Table 3) rank the models RBFNN-GO (best) > MELM-GO > RBFNN > MELM (worst).

Table 3.
Comparison of prediction performance for standalone and HML models applied to the FV training subset.
Figure 10 presents cross-plots contrasting measured and estimated FV values for the trained standalone ML algorithms (MELM, RBFNN) and optimized HML designs (MELM-GO, RBFNN-GO) applied to the testing data subset. The RBFNN and RBFNN-GO models achieved the most precise FV predictions of the four models evaluated, as seen by the tight alignment with the ideal y = x line. In comparison, the MELM architectures generated more diffuse estimations with numerous points deviating further from the y = x line.
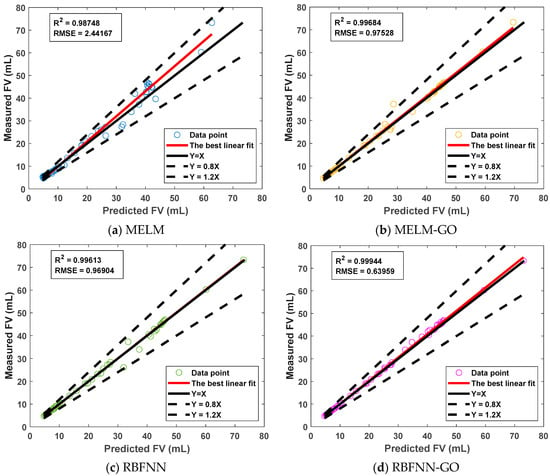
Figure 10.
Comparative cross-plot accuracy evaluations of measured and predicted FV values achieved by the trained (a) MELM, (b) MELM-GO, (c) RBFNN, and (d) RBFNN-GO models applied to the testing data subset.
Table 4 contrasts the statistical accuracy metrics achieved by the ML and the HML trained models applied to forecast FV values for the testing data subset. Collectively, the metrics rank the models RBFNN-GO (best) > RBFNN > MELM-GO > MELM (worst). These results suggest that the trained RBFNN-GO and RBFNN models are more generalizable than either of the MELM models when applied FV dataset studied.

Table 4.
Comparison of prediction performance for standalone and HML models applied to the FV testing subset.
5. Discussion
5.1. Overfitting Index (OFI) Assessment of the Models
Overfitting is a common ML issue where the algorithm prioritizes noise in the dataset, distorting relevant relationships. To address this, an overfitting index (OFI) is used to quantify the models’ ability to generalize. Lower OFI values indicate more generalizable models, while higher values indicate overfitting to the training subsets. The OFI helps assess a model’s ability to identify true underlying trends, and guides optimization efforts to produce trained models that perform well on unseen data [37].
Table 5 lists the calculated OFI values for developed models to predict the FV. Compression of the OFI calculated clearly shows that integration of the ML models, RBFNN and MELM, with GO technique considerably improves the generalizability of the developed models. The hybrid RBFNN-GO model generated the lowest OFI value of 0.0327 when applied to the studied FV datasets (Table 5), reflecting its enhanced generalizability.

Table 5.
Calculated OFI values for developed models applied to the FV datasets.
5.2. Score Analysis of the Models
“Score” analysis was used to evaluate model development and testing for FV prediction effectiveness [38]. Each predictive metric was assigned a numerical value, with the top performing model receiving a score of 4 (because there are four models under consideration). On the other hand, the lowest scoring model received a score of 1. Cumulative scores were used to assess predictive prowess. Scores were derived for both training and testing subsets, and were combined to generate a total score value for each of the four models (Table 6). The score analysis results are illustrated in a radar diagram (Figure 11). The total score values rank the models RBFNN-GO (best) > MELM-GO > RBFNN > MELM (worst), despite the RBFNN model achieving a higher score than the MELM-GO model regarding the testing subset. These results suggest that the OFI model ranking is more meaningful than the total score model ranking in terms of relative model generalizability. The scoring method is assigning too great of a weight to the results of the training subset.

Table 6.
Score analysis results of developed models in relation to individual performance metrics and cumulative scores for training and testing subsets combined to provide an overall total score value for each standalone ML and HML FV prediction model.
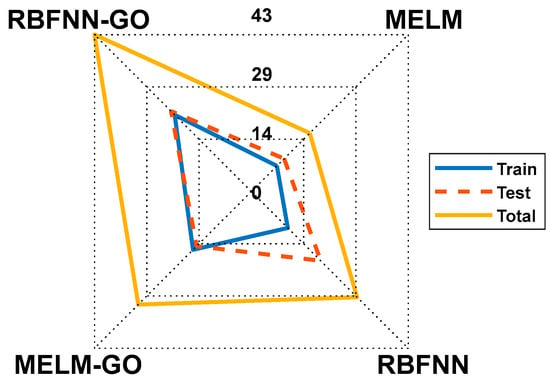
Figure 11.
Radar chart contrasting prediction scores achieved by standalone ML and HML models.
5.3. Robustness Analysis of the ML and the HML Models
To validate the model’s generalizability and real-time applicability, out-of-sample testing and cross-validation techniques were used. Out-of-sample testing assessed performance on excluded data, while cross-validation partitions data into multiple training and validation subsets to estimate the model’s ability to generate reliable predictions when partitioned randomly [39]. Additionally, perturbations were introduced through Gaussian or uniform distributions to evaluate the model’s robustness under changing conditions [40,41]. In this study, a comprehensive robustness evaluation was performed using a Gaussian noise distribution.
Figure 12 displays the noise robustness analysis results in terms of R2 values for the FV predictions of the four models evaluated with various levels of noise added. As to be expected, an elevation in the noise level added results in a decline in the R2 value for the training data for all four models. However, the rate of R2 decline ranks the models as RBFNN-GO (best) > MELM-GO~RBFNN > MELM (worst). These results identify the RBFNN-GO as the most robust of the models evaluated when confronted with noisy data. Notably, the performance of each model declines more rapidly as the added noise increases above ~20–25%.
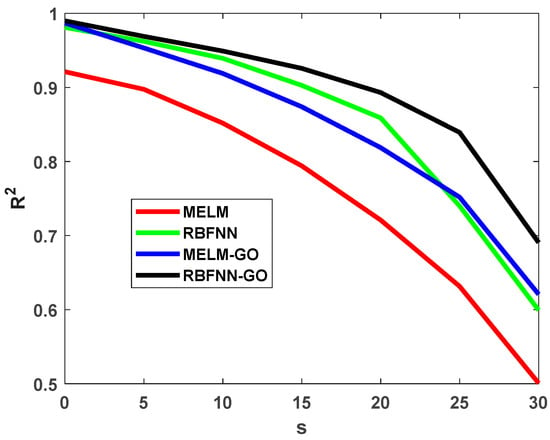
Figure 12.
Relationships between the percentage of added noise to the input variable distributions and R2 values for FV predictions for the ML and HML models.
5.4. Feature Importance Analysis
The FV predictive standalone ML and HML models offer valuable insights into the impact of a DF’s FD and MFV characteristics on the FV. Understanding the degree to which each input variable influences the FV predictions can be provided by the Shapley additive explanations (SHAP) analysis, thereby providing insight into the relative importance of the FD and the MFV in this regard. Such information can assist drilling operations by providing guidance on how best to adjust the DF formulations as the well conditions evolve while drilling. Visualizing the SHAP values improves model interpretability for end-users, building confidence in applying the FV predictions to enhance drilling efficiency and wellbore integrity [26,42]. Figure 13 displays the SHAP analysis applied to the training subset by the best-performing RBFNN-GO model.
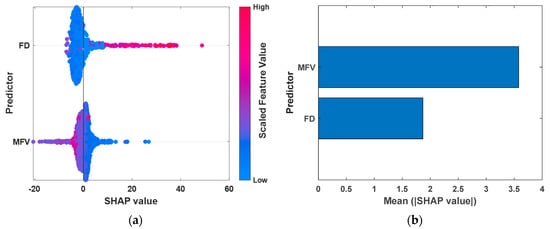
Figure 13.
Visualizing the effect of the two input features on the FV predictions with SHAP values for the RBFNN-GO model applied to the training subset: (a) SHAP detailed feature impact plot and (b) SHAP summary plot of the feature importance.
The mean absolute SHAP values (Figure 13b) are higher for the MFV than the FD, identifying the MFV as the most influential on the FV predictions of the two input variables (Figure 13b). The high values of the MFV variable lead to high SHAP values, which represent predominantly negative impacts on the FV predictions (Figure 13a). On the other hand, the low MFV values generate both positive and negative SHAP values. The high FD values generate predominantly positive SHAP values, whereas the low FD values (the majority of the FD distribution) generate negative SHAP values, representing positive influences on the FV predictions.
5.5. Partial Dependent Plot (PDP) Analysis
PDPs provide a useful tool for analyzing the relationship between input variables and the FV predictions of the ML and the HML models. PDPs can help to identify potential interactions between input and dependent variables and can guide future analysis [43,44]. Figure 14 displays the 3D PDP interrelationships between the two input features involved in the predictions of the FV for the trained RBFNN-GO model.
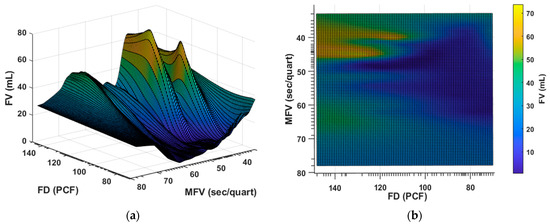
Figure 14.
The (a) 3D and (b) 2D heat map partial dependence plots showcasing the interplay between pairs of input features in the predictions of the FV as generated by the RBFNN-GO model applied to the training subset.
Figure 14 reveals that as the FD values increase the MFV values exert a substantial but highly variable impact on the FV predictions. As the MFV value initially increases from a minimum value of 40 sec/quart, the FV values decline but then progressively rise and fall as the MFV values increase further. The extent of this change in the MFV influence is itself influenced by variations in the FD values. The minimum FV values are generated by the low FD values coupled with the MFV in the range of 40 to 60 sec/quart. Conversely, the maximum FV values are associated with the low values of MFV coupled with the high FD values. The non-linearity of the inter-relationships of the FD and MFV variables (Figure 14) highlight the need for sophisticated ML/HML models to capture their subtleties for accurate semi-real-time prediction purposes.
5.6. Independent Verification of Model Prediction Capability
To rigorously evaluate the best trained and tested model on unseen data, a separate dataset from a well drilled in one of the two studied fields, consisting of ninety-nine data points, was evaluated with the RBFNN-GO model. The statistical characterization of the FD, MFV, and FV variables for the unseen dataset is summarized in Table 7. A comparison of these values with those in Table 1 indicates that the range of changes in the unseen data parameters is entirely covered by the range of changes in the data applied to develop the FV prediction models.

Table 7.
Statistical characterization of ninety-nine data records from a separate well from within the studied fields not involved in the HML model training and testing.
The best-performing model, RBFNN-GO, was applied to predict the FV for the normalized unseen data records. Figure 15 illustrates a comparison between the measured FV values and those predicted by the RBFNN-GO model for the unseen ninety-nine data points. The trained model effectively captures the fluctuations in the FV across the dataset, indicating its strong predictive capability. The RMSE for these FV predictions is 0.3227 mL, reflecting the model’s ability to predict the FV with low errors. The R2 value for these predictions is 0.9624, further confirming the model’s excellent fit to the data and its ability to replicate the observed trends. Considering the model’s reliable FV prediction performance on unseen data from another well, it can be concluded with confidence that the RBFNN-GO model is generalizable and can be applied as a promising predictive tool to provide credible semi-real-time FV predictions for future wells drilled within the studied fields.
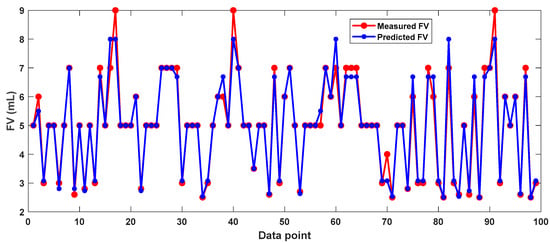
Figure 15.
Comparison of the measured FV values with those predicted by the RBFNN-GO model for the unseen data.
6. The Significance of Frequent and Reliable FV Predictions While Drilling
Accurately predicting FV variations over time is crucial for optimizing the filter cake thickness, the permeability, and the viscosity [10,18,23,26,30,45]. By effectively managing the filter cake area, the differential pressure, and the solids content, drilling operators can minimize fluid incursion and optimize filtration rate, thereby improving the performance of drilling operations [46].
Figure 16 illustrates the workflow for field data to predict the FV with the aid of HML models to enhance drilling performance efficiency. The HML model developed can assist the drilling crew by providing approximately three semi-real-time predictions of the FV per hour during the drilling operation based on just two easily measured parameters, the FD and the MFV, both routinely recorded in the well-site laboratory. The HML model proposed can computationally determine the FV in a much more frequent manner, enabling the crew to monitor this crucial DF property effectively. Such frequent computational monitoring enables the drilling crew to make informed decisions and take effective corrective actions to modify the DF with regard to the FV in case unexpected changes in the FV are detected. Such timely information helps to avoid severe drilling problems such as a stuck pipe. Semi-real-time FV determination offers benefits including managing formation damage, cleaning wellbores, minimizing blockages, and optimizing fluids. These improvements offer the potential to enhance reservoir productivity and wellbore stability once a well is completed.
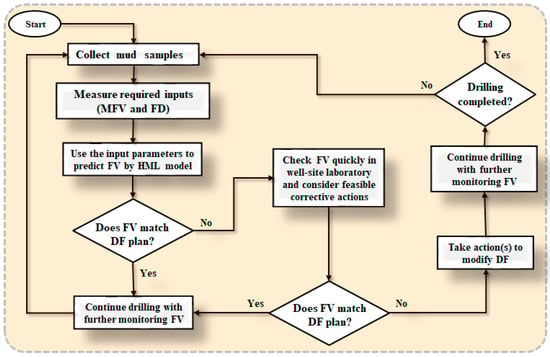
Figure 16.
Workflow diagram demonstrating how the configured HML models can be applied in the DF well-site laboratory to assist the drilling crew with FV semi-real-time monitoring and decision making.
This study addresses knowledge gaps in the semi-real-time FV prediction during drilling using an extensive field database. It demonstrates the feasibility of forecasting short-term FV patterns from the DF density and viscosity inputs using the HML models. Potential applications include semi-automated fluid property monitoring and adjustments and integration into drilling data systems for more responsive drilling optimization. With further refinements, this approach could replace laboratory methods with semi-real-time measurement of FV, revolutionizing proactive DF management. The study establishes a framework for both scientific and practical advancements in drilling efficiency and well construction.
7. Conclusions
The study establishes hybrid machine learning (HML) models to predict the filtration volume (FV) of water-based drilling fluids (WBDF) in semi-real-time, using only two easily and regularly measured parameters, the drilling fluid density (FD) and the Marsh funnel viscosity (MFV), as inputs. Two HML models are developed that are associated with the radial basis function neural network (RBFNN) and multiple extreme learning machine (MELM) algorithms and are optimized with the recently developed growth optimizer (GO). To construct predictive models for the FV, data from seventeen wells drilled in two fields in Iran (1260 data records) were randomly divided into training and testing sets, utilizing a 90/10 training/testing separation ratio determined through sensitivity analysis. Outlying data were detected and eliminated from the process using a Gaussian process regression (GPR)–Mahalanobis distance (MD)-cross-validation technique. The control parameters of the HML model were fine-tuned using the GO algorithm, and these algorithms were then applied to the training data. The testing data subsets were then evaluated with the trained models.
The models’ FV prediction performances were scrutinized with scoring techniques, robustness analysis, and overfitting assessments. The best-performing model, based on these evaluations, was further interpreted using Shapley additive explanations (SHAP) and partial dependency (PDP) analysis. The generalizability and prediction performance of the optimal model was further validated by applying it to predict the FV for unseen data from another well from one of the studied fields. This study’s key findings are:
- ❖
- A two-parameter prediction model is developed, for the first time, to accurately estimate the drilling fluids’ FV in semi-real-time.
- ❖
- A total of forty-eight data records were identified and eliminated as outliers through the GPR-MD-cross-validation technique.
- ❖
- The HML model, RBFNN-GO, exhibited the best FV prediction performance, achieving an RMSE of 0.519 mL (training subset) and 0.6396 mL (testing subset).
- ❖
- The RBFNN-GO model achieved the lowest overfitting index of 0.0327, identifying it as the most generalizable of the four models evaluated.
- ❖
- Score analysis confirmed the superior FV prediction performance of the RBFNN-GO model, and noise robustness testing showed it to be the most robust of the models evaluated.
- ❖
- SHAP analysis of the trained RBFNN-GO model revealed that both the FD and the MFV significantly influenced the FV predictions of DFs, with the MFV exerting somewhat greater influence than the FD.
- ❖
- PDP of the relative influence of the FD and the MFV on the RBFNN-GO model identified that the MFV and the FD exert complex and non-linear inter-relationships that influence the model’s FV predictions. Those relationships show that the model achieves its minimum FV predictions at the low FD values within the MFV range of 40 to 60 and its maximum FV predictions at the low MFV values, especially when the FD value is maximized.
- ❖
- Applying the RBFNN-GO model to ninety-nine unseen data points from another well in the studied fields demonstrated its high predictive accuracy, with an RMSE of 0.3227 mL and an R2 of 0.9624. These results confirm that the model is highly effective at accurately predicting the FV for other wells in the studied fields.
- ❖
- Reliable and regular estimation of the FV offers the potential to avoid formation damage by minimizing the mud filtration invasion and to reduce the risk of differential stuck drill-pipe incidents by minimizing the filter cake thickness.
- ❖
- The developed model improves upon the existing FV prediction models by making it possible to conduct semi-real-time monitoring of the FV during drilling operation with data inputs measured routinely at the well-site.
Author Contributions
Conceptualization, S.D., M.M. and M.A.-S.; data curation, S.D. and M.M.; formal analysis, S.D., M.A.-R., M.A.-S. and M.M.; funding acquisition, V.S.R.; investigation, S.D., M.A.-R. and M.A.-S.; methodology, S.D., M.A.-S. and M.M.; project administration, V.S.R.; resources, S.D. and M.A.-R.; software, S.D. and M.M.; supervision, D.A.W. and V.S.R.; validation, S.D., M.A.-R. and M.M.; visualization, S.D., D.A.W. and M.A.-S.; writing—original draft, S.D., M.A.-S. and M.M.; writing—review and editing, S.D., M.A.-R., M.A.-S., M.M., D.A.W. and V.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The School of Earth Sciences and Engineering at Tomsk Polytechnic University and Saudi Aramco company are acknowledged for their support and permission to publish this work.
Conflicts of Interest
Author Mohammed Al-Rubaii was employed by the company Saudi Aramco, David A. Wood was employed by the company DWA Energy Limited. The remaining authors declare that the re-search was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Acronyms | |
| ANNs | Artificial Neural Networks |
| ARD | Automatic Relevance Determination |
| COA | Cuckoo Optimization Algorithm |
| DF | Drilling Fluids |
| DL | Deep Learning |
| ELM | Extreme Learning Machine |
| GA | Genetic Algorithm |
| GO | Growth Optimizer |
| HML | Hybridized Machine Learning |
| k-NN | k-Nearest Neighbor |
| LSSVM | Least Square Support Vector Machine |
| MELM | Multilayer Extreme Learning Machine |
| MFV | Marsh Funnel Viscosity |
| ML | Machine Learning |
| OBDF | Oil-Based Drilling Fluids |
| PDP | Partial Dependence Plot |
| PSO | Particle Swarm Optimization |
| RBFNN | Radial Basis Function Neural Network |
| RF | Random Forest |
| SBDF | Synthetic-Based Drilling Fluids |
| SHAP | Shapley Additive Explanations |
| SVM | Support Vector Machine |
| WBDF | Water-Based Drilling Fluids |
| XGB | XGBoost |
| Parameters and variables | |
| a20-index | An Index of Predictions within the Error Range of ±20% |
| ARE | Average Relative Error |
| FD | Fluid Density, pcf |
| FV | Filtration Volume, mL |
| HP/HT | High Pressure and High Temperature, °C |
| GL | Gel Strength, lb./100 ft2 |
| MFV | Marsh Funnel Viscosity, sec/quart |
| MAPE | Mean Absolute Percentage Error |
| OFI | Overfitting Index |
| PV | Plastic Viscosity, cP |
| PI | Performance Index |
| R2 | Coefficient of Determination |
| RMSE | Root-Mean-Square Error, mL |
| RRMSE | Relative Root-Mean-Square Error |
| S | Solid Percentage, % |
| YP | Yield Point, lb./100 ft2 |
Appendix A. ML and Optimization Algorithms
Appendix A.1. Radial Basis Function Neural Network (RBFNN)
RBFNNs are a type of artificial neural network designed for approximating scattered multi-dimensional input/output data. Introduced in the 1980s [47], they effectively solve non-linear problems with a single hidden layer, offering computational efficiency over networks with multiple hidden layers. The hidden layer comprises RBF units, which map inputs to a higher dimensional feature space. Advantages include faster training compared to MLPs and strong generalization due to a clear hidden layer [48]. However, limitations include slower control parameter tuning versus MLPs and challenges with large datasets [49]. RBFNN suitability depends on the dataset size and inputs, but their single hidden layer is often beneficial for medium-sized datasets [50]. RBFNNs and k-Nearest Neighbor (k-NN) both employ distance-based approximations but differ in implementation. RBFNNs calculate Euclidean distance between new cases and hidden neuron centers, applying weights to each neuron [48]. Two key parameters must be determined in RBFNNs; in this study, the growth optimizer (GO) was used to find their values, rather than relying on trial-and-error [48].
Appendix A.2. Multilayer Extreme Learning Machine (MELM)
ELM was introduced in 2005 as an efficient single hidden layer neural network [51]. It has been applied to various domains involving regression, classification, and clustering tasks. The architecture resembles conventional backpropagation (BP) artificial neural networks (ANN), but ELM randomly assigns hidden node weights then analytically computes output weights, reducing training time versus conventional ANN methods [52,53]. MELM expands ELM capabilities for intricate non-linear data by incorporating multiple hidden layers [26]. Variables are represented generally as input x (here FD, MFV) and output y (here FV). Weights (w) and biases (β) apply to each hidden node in each hidden layer. Data passes through hidden layers with learned parameters to produce output. Key elements of input, hidden, and output layers are maintained in MELM [54].
Appendix A.3. Growth Optimizer (GO)
Growth optimization (GO) is a recently developed technique to improve problem-solving abilities [55,56]. The GO algorithm employs learning and introspection to generate a list of potential optimization solutions, akin to human knowledge acquisition. It then assesses and adjusts its search method, resembling human knowledge adaptation. The first stage involves generating a population of candidate solutions, X, which are refined throughout the optimization process [56]. The GO algorithm employs indexes “i” and “j” to determine the factors within each solution. The rand (0,1) function generates random solutions within the search space (0 to 1) defined by upper and lower bounds (ub and lb) [55]. The GO algorithm consists of three distinct phases: population segmentation, learning, and reflection. In population segmentation, the algorithm organizes the initial set of possible solutions (X) into a hierarchical structure based on a parameter value of five. The uppermost section contains the current optimal solution, the “leader”, and the two subsequent “elite” candidates. The intermediate section lists solutions in ascending order from P1+1 to the population size N minus P1, while the lower section presents solutions in ascending order from N-P1+1 to the total number of candidates. The algorithm, inspired by leadership characteristics in human society [55,56,57], directs the optimization process. In the learning phase, the GO algorithm facilitates substantial advancements by examining individual variations and investigating their underlying causes [56,57]. The process involves replicating four fundamental variations to understand individual differences and their causes. The reflection phase requires reevaluating early insights and resuming systematic learning when an issue remains unresolved [56,57].
Appendix B. The Evaluation of Forecasting Prediction Performance
The determination of quantitative measures is crucial for assessing the precision and the reliability of the HML and the ML models. These measures provide a precise evaluation of the correlation between the predicted and the actual values, establishing the capabilities of each prediction model. Using distinct data subsets (training, validation, and independent testing datasets), we computed relative error (Equation (A1)), average relative error (ARE, Equation (A2)), root-mean-square error (RMSE, Equation (A3)), and relative root-mean-square error (RRMSE, Equation (A4)). Additionally, we assessed the performance of the FV HML model by computing the coefficient of determination (R2, Equation (A5)), the performance index (PI, Equation (A6)), and the a20-index (Equation (A7)) that indicates the percentage of predicted values within ±20% error range of actual values (m20). These equations compute the prediction performance metrics for the HML models optimized by GO as follows [26,58,59,60]:
Relative error (RE):
Average relative error (ARE):
Root-mean-square error (RMSE):
Relative root-mean-square error (RRMSE):
Coefficient of determination (R2):
Performance Index (PI):
An index represents the percentage of predictions that fall within the error range of ±20% (a20-index):
References
- Deville, J.P. Chapter 4-Drilling Fluids. In Fluid Chemistry, Drilling and Completion; Gulf Professional Publishing: Oxford, UK, 2022; pp. 115–185. ISBN 9780128227213. [Google Scholar]
- Gautam, S.; Guria, C.; Rajak, V.K. A State of the Art Review on the Performance of High-Pressure and High-Temperature Drilling Fluids: Towards Understanding the Structure-Property Relationship of Drilling Fluid Additives. J. Pet. Sci. Eng. 2022, 213, 110318. [Google Scholar] [CrossRef]
- Li, H.; Sun, J.; Xie, S.; Lv, K.; Huang, X.; Zong, J.; Zhang, Y. Controlling Filtration Loss of Water-Based Drilling Fluids by Anionic Copolymers with Cyclic Side Groups: High Temperature and Salt Contamination Conditions. Colloids Surf. A Physicochem. Eng. Asp. 2023, 676, 132089. [Google Scholar] [CrossRef]
- Kariman Moghaddam, A.; Ramazani Saadatabadi, A. Rheological Modeling of Water Based Drilling Fluids Containing Polymer/Bentonite Using Generalized Bracket Formalism. J. Pet. Sci. Eng. 2020, 189, 107028. [Google Scholar] [CrossRef]
- Song, K.; Wu, Q.; Li, M.; Ren, S.; Dong, L.; Zhang, X.; Lei, T.; Kojima, Y. Water-Based Bentonite Drilling Fluids Modified by Novel Biopolymer for Minimizing Fluid Loss and Formation Damage. Colloids Surf. A Physicochem. Eng. Asp. 2016, 507, 58–66. [Google Scholar] [CrossRef]
- Davoodi, S.; Ramazani, A.; Rukavishnikov, V.; Minaev, K. Insights into Application of Acorn Shell Powder in Drilling Fluid as Environmentally Friendly Additive: Filtration and Rheology. Int. J. Environ. Sci. Technol. 2021, 18, 835–848. [Google Scholar] [CrossRef]
- Al-Shargabi, M.; Davoodi, S.; Wood, D.A.; Al-Rubaii, M.; Minaev, K.M.; Rukavishnikov, V.S. Hole-Cleaning Performance in Non-Vertical Wellbores: A Review of Influences, Models, Drilling Fluid Types, and Real-Time Applications. Geoenergy Sci. Eng. 2024, 233, 212551. [Google Scholar] [CrossRef]
- Ghaderi, S.; Ramazani S.A., A.; Haddadi, S.A. Applications of Highly Salt and Highly Temperature Resistance Terpolymer of Acrylamide/Styrene/Maleic Anhydride Monomers as a Rheological Modifier: Rheological and Corrosion Protection Properties Studies. J. Mol. Liq. 2019, 294, 111635. [Google Scholar] [CrossRef]
- Ezell, R.G.; Ezzat, A.M.; Turner, J.K.; Wu, J.J. New Filtration-Control Polymer for Improved Brine-Based Reservoir Drilling-Fluids Performance at Temperatures in Excess of 400°F and High Pressure. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control (SPE-128119-MS), Lafayette, LA, USA, 10–12 February 2010; Volume 1, pp. 25–32. [Google Scholar]
- Gul, S.; van Oort, E. A Machine Learning Approach to Filtrate Loss Determination and Test Automation for Drilling and Completion Fluids. J. Pet. Sci. Eng. 2020, 186, 106727. [Google Scholar] [CrossRef]
- Caenn, R.; Darley, H.C.H.; Gray, G.R. Composition and Properties of Drilling and Completion Fluids, 7th ed.; Gulf Professional Publishing: Oxford, UK, 2016; ISBN 9780128047514. [Google Scholar]
- Davoodi, S.; Al-Shargabi, M.; Wood, D.A.; Rukavishnikov, V.S.; Minaev, K.M. Synthetic Polymers: A Review of Applications in Drilling Fluids. Pet. Sci. 2023, 21, 475–518. [Google Scholar] [CrossRef]
- Movahedi, H.; Jamshidi, S.; Hajipour, M. Hydrodynamic Analysis and Cake Erosion Properties of a Modified Water-Based Drilling Fluid by a Polyacrylamide/Silica Nanocomposite during Rotating-Disk Dynamic Filtration. ACS Omega 2022, 7, 44240. [Google Scholar] [CrossRef]
- Li, H.; Huang, X.; Sun, J.; Lv, K.; Meng, X. Application of Zwitterionic Copolymer as a Filtration Control Agent against High Temperature and High Salinity for Water-Based Drilling Fluids. J. Mol. Liq. 2023, 385, 122419. [Google Scholar] [CrossRef]
- Zhong, H.; Shen, G.; Qiu, Z.; Lin, Y.; Fan, L.; Xing, X.; Li, J. Minimizing the HTHP Filtration Loss of Oil-Based Drilling Fluid with Swellable Polymer Microspheres. J. Pet. Sci. Eng. 2019, 172, 411–424. [Google Scholar] [CrossRef]
- Darley, H.C.H.; Gray, G.R. Chapter 3—Equipment and Procedures for Evaluating Drilling Fluid Performance. In Composition and Properties of Drilling and Completion Fluids, 5th ed.; Gulf Professional Publishing: Oxford, UK, 1988; pp. 91–139. ISBN 978-0-08-050241-0. [Google Scholar]
- Ning, Y.C.; Ridha, S.; Ilyas, S.U.; Krishna, S.; Dzulkarnain, I.; Abdurrahman, M. Application of Machine Learning to Determine the Shear Stress and Filtration Loss Properties of Nano-Based Drilling Fluid. J. Pet. Explor. Prod. Technol. 2023, 13, 1031–1052. [Google Scholar] [CrossRef]
- Jeirani, Z.; Mohebbi, A. Artificial Neural Networks Approach for Estimating Filtration Properties of Drilling Fluids. J. Jpn. Pet. Inst. 2006, 49, 65–70. [Google Scholar] [CrossRef]
- Golsefatan, A.; Shahbazi, K. A Comprehensive Modeling in Predicting the Effect of Various Nanoparticles on Filtration Volume of Water-Based Drilling Fluids. J. Pet. Explor. Prod. Technol. 2020, 10, 859–870. [Google Scholar] [CrossRef]
- Civan, F. Incompressive Cake Filtration: Mechanism, Parameters, and Modeling. AIChE J. 1998, 44, 2379–2387. [Google Scholar] [CrossRef]
- Civan, F. Practical Model for Compressive Cake Filtration Including Fine Particle Invasion. AIChE J. 1998, 44, 2388–2398. [Google Scholar] [CrossRef]
- Wu, J.; Torres-Vendín, C.; Sepehrnoori, K.; Delshad, M. Numerical Simulation of Mud Filtrate Invasion in Deviated Wells. SPE Reserv. Eval. Eng. 2001, 7, 143–154. [Google Scholar] [CrossRef]
- Toreifi, H.; Rostami, H.; Manshad, A.K. New Method for Prediction and Solving the Problem of Drilling Fluid Loss Using Modular Neural Network and Particle Swarm Optimization Algorithm. J. Pet. Explor. Prod. Technol. 2014, 4, 371–379. [Google Scholar] [CrossRef]
- Lekomtsev, A.; Keykhosravi, A.; Moghaddam, M.B.; Daneshfar, R.; Rezvanjou, O. On the Prediction of Filtration Volume of Drilling Fluids Containing Different Types of Nanoparticles by ELM and PSO-LSSVM Based Models. Petroleum 2021, 8, 424–435. [Google Scholar] [CrossRef]
- Gasser, M.; Naguib, A.; Abdelhafiz, M.M.; Elnekhaily, S.A.; Mahmoud, O. Artificial Neural Network Model to Predict Filtrate Invasion of Nanoparticle-Based Drilling Fluids. Trends Sci. 2023, 20, 12–14. [Google Scholar] [CrossRef]
- Davoodi, S.; Mehrad, M.; Wood, D.A.; Ghorbani, H.; Rukavishnikov, V.S. Hybridized Machine-Learning for Prompt Prediction of Rheology and Filtration Properties of Water-Based Drilling Fluids. Eng. Appl. Artif. Intell. 2023, 123, 106459. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, D.; Gao, H.; Hu, Y.; Duan, L. Real-Time Measurement of Drilling Fluid Rheological Properties: A Review. Sensors 2021, 21, 3592. [Google Scholar] [CrossRef]
- Pitt, M.J. The Marsh Funnel and Drilling Fluid Viscosity: A New Equation for Field Use. SPE Drill. Complet. 2000, 15, 3–6. [Google Scholar] [CrossRef]
- Guria, C.; Kumar, R.; Mishra, P. Rheological Analysis of Drilling Fluid Using Marsh Funnel. J. Pet. Sci. Eng. 2013, 105, 62–69. [Google Scholar] [CrossRef]
- Oguntade, T.; Ojo, T.; Efajemue, E.; Oni, B.; Idaka, J. Application of ANN in Predicting Water Based Mud Rheology and Filtration Properties. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition (SPE-203720-MS), Online, 11–13 August 2020. [Google Scholar]
- Davoodi, S.; Al-Shargabi, M.; Wood, D.A.; Minaev, K.M.; Rukavishnikov, V.S. Modified-Starch Applications as Fluid-Loss Reducers in Water-Based Drilling Fluids: A Review of Recent Advances. J. Clean. Prod. 2024, 434, 140430. [Google Scholar] [CrossRef]
- Al-Rubaii; Al-Shargabi, M.; Aldahlawi, B.; Al-Shehri, D.; Minaev, K.M. A Developed Robust Model and Artificial Intelligence Techniques to Predict Drilling Fluid Density and Equivalent Circulation Density in Real Time. Sensors 2023, 23, 6594. [Google Scholar] [CrossRef]
- Chen, H.; Okesanya, T.; Kuru, E.; Heath, G.; Hadley, D. Generalized Models for the Field Assessment of Drilling Fluid Viscoelasticity. SPE Drill. Complet. 2023, 38, 155–169. [Google Scholar] [CrossRef]
- Alizadeh, S.M.; Alruyemi, I.; Daneshfar, R.; Mohammadi-Khanaposhtani, M.; Naseri, M. An Insight into the Estimation of Drilling Fluid Density at HPHT Condition Using PSO-, ICA-, and GA-LSSVM Strategies. Sci. Rep. 2021, 11, 7033. [Google Scholar] [CrossRef]
- Guo, Q.; Ren, H.; Liu, H.; Liu, J.; Chen, N.; Yu, J. A Novel Mahalanobis Distance Method for Predicting Oil and Gas Resource Spatial Distribution. Energy Explor. Exploit. 2023, 41, 481–496. [Google Scholar] [CrossRef]
- Colombo, L.; Oboe, D.; Sbarufatti, C.; Cadini, F.; Russo, S.; Giglio, M. Shape Sensing and Damage Identification with IFEM on a Composite Structure Subjected to Impact Damage and Non-Trivial Boundary Conditions. Mech. Syst. Signal Process. 2021, 148, 107163. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Guan, X.; Liang, B.; Lai, Y.; Luo, X. Research on Overfitting of Deep Learning. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS), Macau, China, 13–16 December 2019; pp. 78–81. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting Concrete Compressive Strength Using Hybrid Ensembling of Surrogate Machine Learning Models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. Robust Robot Localization in a Complex Oil and Gas Industrial Environment. J. Field Robot. 2018, 35, 213–230. [Google Scholar] [CrossRef]
- Poldrack, R.A.; Huckins, G.; Varoquaux, G. Establishment of Best Practices for Evidence for Prediction: A Review. JAMA Psychiatry 2020, 77, 534–540. [Google Scholar] [CrossRef]
- Ribeiro, M.I. Gaussian Probability Density Functions: Properties and Error Characterization; Institute for Systems and Robotics: Lisboa, Portugal, 2004. [Google Scholar]
- Kumar, A.; Arora, H.C.; Kumar, K.; Garg, H. Performance Prognosis of FRCM-to-Concrete Bond Strength Using ANFIS-Based Fuzzy Algorithm. Expert Syst. Appl. 2023, 216, 119497. [Google Scholar] [CrossRef]
- Angelini, M.; Blasilli, G.; Lenti, S.; Santucci, G. A Visual Analytics Conceptual Framework for Explorable and Steerable Partial Dependence Analysis. IEEE Trans. Vis. Comput. Graph. 2023, 30, 4497–4513. [Google Scholar] [CrossRef]
- Danesh, T.; Ouaret, R.; Floquet, P.; Negny, S. Hybridization of Model-Specific and Model-Agnostic Methods for Interpretability of Neural Network Predictions: Application to a Power Plant. Comput. Chem. Eng. 2023, 176, 108306. [Google Scholar] [CrossRef]
- Al-Rubaii; Al-Shargabi, M.; Al-Shehri, D.; Alyami, A.; Minaev, K.M. A Novel Efficient Borehole Cleaning Model for Optimizing Drilling Performance in Real Time. Appl. Sci. 2023, 13, 7751. [Google Scholar] [CrossRef]
- Azar, J.J.; Robello Samuel, G. Drilling Engineering; Quinn, T., Ed.; PennWell Corp.: Essex, UK, 2007; ISBN 9781593700720. [Google Scholar]
- Moody, J.; Darken, C.J. Fast Learning in Networks of Locally-Tuned Processing Units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Rezaei, F.; Jafari, S.; Hemmati-Sarapardeh, A.; Mohammadi, A.H. Modeling of Gas Viscosity at High Pressure-High Temperature Conditions: Integrating Radial Basis Function Neural Network with Evolutionary Algorithms. J. Pet. Sci. Eng. 2022, 208, 109328. [Google Scholar] [CrossRef]
- Xie, T.; Yu, H.; Wilamowski, B. Comparison between Traditional Neural Networks and Radial Basis Function Networks. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1194–1199. [Google Scholar] [CrossRef]
- Chandra, S.; Gaur, P.; Pathak, D. Radial Basis Function Neural Network Based Maximum Power Point Tracking for Photovoltaic Brushless DC Motor Connected Water Pumping System. Comput. Electr. Eng. 2020, 86, 106730. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Jiang, X.W.; Yan, T.H.; Zhu, J.J.; He, B.; Li, W.H.; Du, H.P.; Sun, S.S. Densely Connected Deep Extreme Learning Machine Algorithm. Cognit. Comput. 2020, 12, 979–990. [Google Scholar] [CrossRef]
- Sajjadi, S.; Shamshirband, S.; Alizamir, M.; Yee, P.L.; Mansor, Z.; Manaf, A.A.; Altameem, T.A.; Mostafaeipour, A. Extreme Learning Machine for Prediction of Heat Load in District Heating Systems. Energy Build. 2016, 122, 222–227. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Le, B.T. Rolling Force Prediction of Hot Rolling Based on GA-MELM. Complexity 2019, 2019, 3476521. [Google Scholar] [CrossRef]
- Fatani, A.; Dahou, A.; Abd Elaziz, M.; Al-qaness, M.A.A.; Lu, S.; Alfadhli, S.A.; Alresheedi, S.S. Enhancing Intrusion Detection Systems for IoT and Cloud Environments Using a Growth Optimizer Algorithm and Conventional Neural Networks. Sensors 2023, 23, 4430. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, H.; Zhan, Z.H.; Li, J.; Zhang, H. Growth Optimizer: A Powerful Metaheuristic Algorithm for Solving Continuous and Discrete Global Optimization Problems. Knowl.-Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.; Bu, X.; Zhang, H. Quadruple Parameter Adaptation Growth Optimizer with Integrated Distribution, Confrontation, and Balance Features for Optimization. Expert Syst. Appl. 2024, 235, 121218. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the Evaluation and Comparison of Models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Safaei-Farouji, M.; Wei, N.; Band, S.S.; Mosavi, A. Knowledge-Based Rigorous Machine Learning Techniques to Predict the Deliverability of Underground Natural Gas Storage Sites for Contributing to Sustainable Development Goals. Energy Rep. 2022, 8, 7643–7656. [Google Scholar] [CrossRef]
- Hosseini, S.; Khatti, J.; Taiwo, B.O.; Fissha, Y.; Grover, K.S.; Ikeda, H.; Pushkarna, M.; Berhanu, M.; Ali, M. Assessment of the Ground Vibration during Blasting in Mining Projects Using Different Computational Approaches. Sci. Rep. 2023, 13, 18582. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).