Extreme Value Index Estimation for Pareto-Type Tails under Random Censorship and via Generalized Means

Abstract

The field of statistical extreme value theory (EVT) focuses on estimating parameters associated with extreme events, such as the probability of exceeding a high threshold or determining a high quantile that lies at or beyond the observed data range. Typically, the assumption for univariate data analysis is that the sample is complete, independent, identically distributed, or weakly dependent and stationary, drawn from an unknown distribution F. However, in the context of lifetime data, censoring is a common issue. In this work, we consider the case of random censoring for data with a heavy-tailed, Pareto-type distribution. As is common in applications of EVT, the estimation of the extreme value index (EVI) is critical, as it quantifies the tail heaviness of the distribution. The EVI has been extensively studied in the literature. Here, we discuss several classical EVI-estimators and reduced-bias (RB) EVI-estimators within a semi-parametric framework, with a focus on RB EVI-estimators derived from generalized means, which will be applied to both simulated and real survival data.

1. Introduction and Preliminaries

The primary focus of statistical extreme value theory (EVT) is the estimation of parameters related to extreme events. In EVT, a common assumption for any univariate dataset $(X_1,\dots ,X_n)$ is that the data form a complete sample of size n, which may be independent, identically distributed, or weakly dependent and stationary, drawn from an unknown cumulative distribution function (CDF) $F=F_X$. A key parameter of interest is the unknown extreme value index (EVI), denoted by $\xi \equiv {\xi }_X$, which will be defined later. The estimation of the EVI forms the foundation for estimating all other extreme value parameters. An extended literature review is provided in Appendix A, including a few books on this topic.

When examining extreme events, particularly focusing on large values in the right tail, several key parameters are of interest:

(a)

The probability of exceedance for a high threshold $x_H$, defined as $p_H:=\mathbb{P}(X>x_H)$.

(b)

A high quantile corresponding to a probability $1-q$, where q is small, which is located at or beyond the range of the observed data. It is given by

$${\chi }_{1-q}:=inf\{x:F\left(x\right)\ge 1-q\}=F^{-1}(1-q),\mathrm{where}q<1/n,$$

(1)

with $F^{-1}$ representing the generalized inverse function of F.

(c)

The right endpoint of the underlying distribution F, denoted $x^F:=sup\{x:F\left(x\right)<1\}$.

In the analysis of lifetime or reliability data, observations are often censored, frequently in a random manner. In this context, we will focus specifically on estimating the extreme value index (EVI), ${\xi }_X$, under conditions of random censoring and for a heavy Pareto-type regularly varying right tail function:

$${\overline{F}}_X\left(x\right):=\mathbb{P}(X>x)=1-F_X\left(x\right)=x^{-1/{\xi }_X}{\mathbb{L}}_X\left(x\right),$$

(2)

where $\mathbb{L}(·)$ is a slowly varying function at infinity, i.e., such that $\underset{t\to \infty }{lim}\mathbb{L}\left(tx\right)/\mathbb{L}\left(t\right)=1$, for all $x>0$ (see, among others, Bingham, Goldie and Teugels [1], for details on regular and slow variation). A brief reference to the subject can be found in Reiss and Thomas [2], First Edition (see Section 6.1 of [2]). We further mention a few initial articles on the topic (Beirlant, Guillou, Dierckx and Fils-Viletard [3], Einmahl, Fils-Viletard and Guillou [4], Beirlant, Guillou and Toulemonde [5], and Gomes and Neves [6,7]). Additional references can be found in Appendix A.

In the context of random censoring, we consider a random variable Y such that, instead of observing X directly, we only observe

$$Z=X\wedge Y\mathrm{and}\delta ={\mathbb{I}}_{\{X\le Y\}},$$

(3)

where ${\mathbb{I}}_A$ denotes the indicator function of the set A. The indicator variable $\delta$ indicates whether X has been censored.

Within this framework, semi-parametric EVI-estimators require only minor adjustments to ensure consistency in estimating ${\xi }_X$ across parametric, semi-parametric, or even nonparametric settings.

We shall give special attention to such estimation for heavy tails, i.e., for ${\xi }_X>0$, making use of several generalized means (GM) EVI-estimators (see Gomes and Martins [8], Brilhante, Gomes and Pestana [9] and Penalva, Gomes, Caeiro and Neves [10], among others), which generalize the classical Hill EVI-estimator (Hill [11]), and of one of the most simple minimum-variance reduced-bias (MVRB) estimators—the one in the work of Caeiro, Gomes, and Pestana [12]. We further consider RB-GM EVI-estimators, which will be detailed in Appendix B. For additional GM EVI-estimators, see Paulauskas and Vaičiulis’ study [13] and the recent overview article by Fedotenkov [14].

After a brief introduction in Section 2 regarding the notion of EVI and the most relevant first- and second-order conditions in statistical EVT, under a semi-parametric framework, we advance, in Section 3, with the functional definition of some of the already-mentioned EVI-estimators for complete samples and a heavy right tail, i.e., a positive EVI (see also, Appendix B).

The EVI-estimation under random censoring for the Pareto-type right tails in (2) is the main novelty of this article and will be addressed in Section 4. We shall apply the methodology to simulated data in Section 5, and to a set of survival data related to cancer of the tongue in Section 6, providing some hints for the adequate estimation of the EVI of X, the patient survival lifetime after detection of illness. A few overall comments and intentions of future work are provided in Section 7.

2. The Extreme Value Index (EVI)

The EVI quantifies the heaviness of the right tail $\overline{F}=1-F$ of an underlying distribution F, for large values, and is extensively documented in the literature. Specifically, the EVI corresponds to the parameter $\xi$ in the general extreme value (GEV) cumulative distribution function (CDF), given by

$$G_{\xi }\left(x\right)\equiv {\mathrm{GEV}}_{\xi }\left(x\right):=\left\{\begin{array}{cc}exp\left(-{(1+\xi x)}^{-1/\xi }\right),\hfill & \mathrm{if}\xi \ne 0\mathrm{and}1+\xi x>0,\hfill \\ exp\left(-exp(-x)\right),\hfill & \mathrm{if}\xi =0.\hfill \end{array}\right.$$

(4)

The GEV CDF, in (4), also known as the von Mises–Jenkinson CDF (see von Mises [15] and Jenkinson [16]), represents the limiting distribution of a sequence of linearly normalized maximum values, provided that a non-degenerate limit exists (Fréchet [17], Fisher and Tippett [18], von Mises [15], Gnedenko [19], and de Haan [20]). When this condition holds, we say that the distribution F belongs to the domain of attraction of $G_{\xi }$, denoted by $F\in {\mathcal{D}}_{\mathcal{M}}\left(G_{\xi }\right)$. The EVI, $\xi$, plays a crucial role in determining the behaviour of the right tail $\overline{F}=1-F$: for $\xi <0$; the right tail is light and F has a finite right endpoint ($x^F=sup\{x:F\left(x\right)<1\}<+\infty$). For $\xi >0$, the right tail is heavy with a negative polynomial decay, and F has an infinite right endpoint; when $\xi =0$, the right tail exhibits an exponential decay, and the right endpoint can be either finite or infinite. The literature associated with the maximum likelihood (ML) estimation of $(\lambda ,\delta ,\xi )$ in the GEV model, $G_{\xi }((x-\lambda )/\delta )$, with $G_{\xi }\left(x\right)$ given in (4), and $\lambda \in \mathbb{R}$ and $\delta >0$, respectively location and scale parameters, can be found in the final paragraph of Appendix A.

First- and Second-Order Conditions in EVT

The following extended regular variation property (de Haan [21]) is a well-known necessary and sufficient condition for $F\in {\mathcal{D}}_{\mathcal{M}}\left(G_{\xi }\right)$:

$$\underset{t\to \infty }{lim}{\displaystyle \frac{U\left(tx\right)-U\left(t\right)}{a\left(t\right)}}=\left\{\begin{array}{ccc}{\displaystyle \frac{x^{\xi }-1}{\xi }},& \mathrm{if}\hfill & \xi \ne 0,\hfill \\ lnx,& \mathrm{if}\hfill & \xi =0,\hfill \end{array}\right.$$

(5)

for every $x>0$ and some positive measurable function a, with U standing for a quantile-type function associated with F and defined by

$$U\left(t\right):={\left({\displaystyle \frac{1}{1-F}}\right)}^{\leftarrow }\left(t\right)=inf\left\{x:F\left(x\right)\ge 1-\frac{1}{t}\right\},t\ge 1.$$

(6)

Note that the upper-quantile in (1) can be defined as ${\chi }_{1-q}=U(1/q)$, with $U(·)$ defined in (6). In addition to the first-order condition in (5), a second-order condition is often required to describe the rate of convergence in the first-order condition. A more restrictive assumption than $F\in {\mathcal{D}}_{\mathcal{M}}\left(G_{\xi }\right)$ involves the existence of a function A, which may not change sign and approaches zero as $t\to \infty$, such that

$$\underset{t\to \infty }{lim}{\displaystyle \frac{\frac{U\left(tx\right)-U\left(t\right)}{a\left(t\right)}-\frac{x^{\xi }-1}{\xi }}{A\left(t\right)}}=H_{\xi ,\rho }\left(x\right):={\displaystyle \frac{1}{\rho }}\left({\displaystyle \frac{x^{\xi +\rho }-1}{\xi +\rho }}-{\displaystyle \frac{x^{\xi }-1}{\xi }}\right)$$

(7)

for all $x>0$, where $\rho \le 0$ is a second-order parameter that governs the rate of convergence of the maximum values, normalized linearly, toward the EV limit distribution. In this context, $\left|A\right|$ is regularly varying with a variation index equal to $\rho$ (see Geluk and de Haan [22] and de Haan and Stadtmuller [23]). A slightly more restrictive assumption is that $\xi >0$, $\rho <0$, and that we can select $A\left(t\right)=\xi \beta t^{\rho }$ in the general second-order condition, as described in (7), placing this within Hall and Welsh’s class of models [24].

3. EVI-Estimation for Complete Samples

In all applications of EVT, the EVI-estimation is of primordial importance. For a complete random sample $(Z_1,\dots ,Z_n)$, and heavy Pareto-type right tails, i.e., whenever $\xi >0$, in (4), we first mention the classical Hill (H) estimator in [11], with the functional expression

$$\mathrm{H}\left(k\right)\equiv {\widehat{\xi }}_{k,n}^{\mathrm{H}}:={\displaystyle \frac{1}{k}}\sum _{i=1}^{k}ln{Z}_{n-i+1:n}-ln{Z}_{n-k:n}=:{\displaystyle \frac{1}{k}}\sum _{i=1}^k{V}_{ik},1\le k<n,$$

(8)

where $(Z_{1:n}\le \cdots \le Z_{n:n})$ denotes the ascending-order statistics (OS) associated with the sample $(Z_1,\dots ,Z_n)$. And several generalizations of the Hill EVI-estimator, some of them referred in the following, are now available.

Different GM EVI-estimators were considered around the year 2000 to estimate a positive EVI, also called the tail index, under a semi-parametric framework. Among them, we mention the power mean (PM) of exponent p of the log-excesses, introduced in Gomes and Martins [25], and further studied in [8] and in Segers [26]. Those PM EVI-estimators are valid for a positive EVI, and are defined by

$${\mathrm{PM}}_p\left(k\right)\equiv {\mathrm{PM}}_{k,n,p}\equiv {\widehat{\xi }}_{k,n}^{{\mathrm{PM}}_p}:={\left({\displaystyle \frac{M_n^{\left(p\right)}\left(k\right)}{\Gamma (p+1)}}\right)}^{1/p},\mathrm{for}p>0[{\mathrm{PM}}_1\left(k\right)\equiv H\left(k\right)],$$

(9)

with $\Gamma$ denoting the complete Gamma function, and where

$$M_n^{\left(p\right)}\left(k\right):={\displaystyle \frac{1}{k}}\sum _{i=1}^k{V}_{ik}^p,p\in \mathbb{R},$$

(10)

are the moments of order-p of the log-excesses, $V_{ik},1\le i\le k$, defined in (8). For more recent GM EVI-estimators, also considered in the simulation studies of Section 5, see Appendix B.

3.1. A Few Comments on Reduced-Bias (RB) EVI-Estimation

Besides the GM EVI-estimators discussed previously in (9), and also the ones presented in Appendix B, various classes of RB EVI-estimators are also considered in this article. These classes rely on accurately estimating the second-order parameter vector $(\beta ,\rho )\in (\mathbb{R}\setminus \left\{0\right\},{\mathbb{R}}^{-})$ in the function $A\left(t\right)=\xi \beta t^{\rho }$, in (7). Methods for effectively estimating $(\beta ,\rho )$ are detailed in Gomes and Pestana [27], and more recent classes of $\beta$ and $\rho$ estimators (referenced in Caeiro, Gomes, Beirlant and De Wet [28]) are also promising candidates for estimating $(\beta ,\rho )$. Estimation should be conducted at a high-level $k_1=\lfloor n^{1-ϵ}\rfloor$, with $ϵ\to 0$ and with $\widehat{\rho }-\rho =o_{\mathbb{P}}(1/lnn)$, where $\lfloor x\rfloor$ denotes the integer part of x.

For heavy right tails, we mention one of the most relevant and simple MVRB estimators of $\xi$ (see [12]), given by

$${\overline{\mathrm{H}}}_{k,n,\widehat{\beta },\widehat{\rho }}\equiv {\widehat{\xi }}_{k,n}^{\overline{\mathrm{H}}}:=\mathrm{H}\left(k\right)\left(1-{\displaystyle \frac{\widehat{\beta }{(n/k)}^{\widehat{\rho }}}{1-\widehat{\rho }}}\right),$$

(11)

where $(\widehat{\beta },\widehat{\rho })$ are adequate consistent estimators of the vector $(\beta ,\rho )$ of second-order parameters. For an algorithm related to such estimation and application to the estimation of high quantiles, which was already defined in (1), see [27], and also Caeiro and Gomes [29], among others. Additional RB-GM EVI-estimators, generalizing the MVRB EVI-estimators, in (11), are provided in Appendix B.

3.2. Semi-Parametric Asymptotic Behaviour of EVI-Estimators

For the aforementioned EVI-estimators, as well as for other EVI-estimators, and in the lines of de Haan and Peng [30], we can prove consistency in the whole ${\mathcal{D}}_M\left(G_{\xi >0}\right)$, i.e., whenever (5) holds, with $\xi >0$, provided that k is intermediate, i.e.,

$$k=k_n\to \infty \mathrm{and}{\displaystyle \frac{k}{n}}\to 0,\mathrm{as}n\to \infty .$$

(12)

Under the additional validity of the second-order condition, in (7), and with ^⊙ denoting any of the aforementioned GM EVI-estimators, including the H EVI-estimators, in (8), we can guarantee asymptotic normality of ${\widehat{\xi }}_{k,n}^{\odot }$, i.e., there exists a standard normal RV $P_k^{\odot }$ and real functions ${\sigma }^{\odot }={\sigma }^{\odot }\left(\xi \right)$ and $b^{\odot }=b^{\odot }(\xi ,\rho )$, such that

$${\widehat{\xi }}_{k,n}^{\odot }\stackrel{d}{=}\xi +{\displaystyle \frac{\xi {\sigma }^{\odot }{P}_k^{\odot }}{\sqrt{k}}}+b^{\odot }A(n/k)+o_{\mathbb{P}}\left(A(n/k)\right).$$

With ${\widehat{\xi }}_{k,n}^{•}$ generally denoting any class of RB GM EVI-estimators, including $\overline{\mathrm{H}}$, in (11), and under the validity of the second-order condition, in (7), we obtain

$${\widehat{\xi }}_{k,n}^{•}\stackrel{d}{=}\xi +{\displaystyle \frac{\xi {\sigma }^{•}{P}_k^{•}}{\sqrt{k}}}+o_{\mathbb{P}}\left(A(n/k)\right).$$

4. EVI-Estimation under Random Censorship

In all articles mentioned in Section 3, the available sample is complete. Let us now assume that we are under a framework of random censorship, i.e., we have access to the sample $(Z_i,{\delta }_i)$, $1\le i\le n$, of independent copies of $(Z,\delta )$, in (3), but our goal is to make inference on the right tail of the unknown lifetime distribution $F_X$, i.e., we want to make inference on the right tail,

$${\overline{F}}_X\left(x\right)=\mathbb{P}(X>x)=1-F_X\left(x\right),$$

while $F_Y$, the CDF of Y, is considered to be a nonparametric nuisance parameter. As mentioned in [4], among others, all EVI-estimators need to then be modified in order to be consistent for the estimation of ${\xi }_X$ in the whole domain of attraction, ${\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_X}\right)$. We shall next motivate a possible and simple modification.

A Few Comments on Random Censoring

Let us assume that $F_X\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_1}\right)$, with ${\xi }_1\equiv {\xi }_X$ as the parameter we want to estimate, and that $F_Y\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_2}\right)$, ${\xi }_1,{\xi }_2>0$ (heavy right tails). Also, instead of the potential sample $(X_1,\dots ,X_n)$ (non-observed), and assuming Y is independent of X, we observe

$$\left(\left(\begin{array}{c}{Z}_1\hfill \\ {\delta }_1\hfill \end{array}\right),\dots ,\left(\begin{array}{c}{Z}_n\hfill \\ {\delta }_n\hfill \end{array}\right)\right),Z=min(X,Y),\delta =I_{\{X\le Y\}}.$$

(13)

Example 1. 

To motivate how to estimate ${\xi }_1={\xi }_X$, we shall simplify the problem, assuming that X and Y are indeed Pareto $\left({\xi }_1\right)$ and Pareto $\left({\xi }_2\right)$, respectively, i.e., for all $x\ge 1$, $F_X\left(x\right)=1-x^{-1/{\xi }_1}$ and $F_Y\left(x\right)=1-x^{-1/{\xi }_2}$. Then,

$$F_Z\left(x\right)=\mathbb{P}\left\{min(X,Y)\le x\right\}=1-x^{-1/{\xi }_1}{x}^{-1/{\xi }_2}=1-x^{-{\displaystyle \frac{{\xi }_1+{\xi }_2}{{\xi }_1{\xi }_2}}},$$

i.e., $Z⌢Pareto({\xi }_1{\xi }_2/({\xi }_1+{\xi }_2))$, and we can use the common semi-parametric estimators to estimate ${\xi }_Z={\xi }_1{\xi }_2/({\xi }_1+{\xi }_2)$. On the other hand,

$$\begin{array}{ccc}\hfill c\equiv c_z:=\mathbb{P}(X\le Y|Z=z)& =& \mathbb{P}(\delta =1|Z=z)={\displaystyle \frac{f_X\left(z\right)(1-F_Y\left(z\right))}{f_Z\left(z\right)}}\hfill \\ & =& {\displaystyle \frac{\frac{1}{{\xi }_1}{z}^{-1/{\xi }_1-1}{z}^{-1/{\xi }_2}}{\left(\frac{1}{{\xi }_1}+\frac{1}{{\xi }_2}\right)z^{-1/{\xi }_1-1/{\xi }_2-1}}}={\displaystyle \frac{{\xi }_2}{{\xi }_1+{\xi }_2}}.\hfill \end{array}$$

(14)

Then, the quotient between any estimator of $\xi ={\xi }_Z$ and an estimator of $c=c_Z$ will provide an estimator of ${\xi }_X={\xi }_1$.

Example 2. 

Another key model in EVT is the generalized Pareto (GP) model, associated with excesses over a high threshold (see Balkema and de Haan [31] and Pickands [32]), and given by ${\mathrm{GP}}_{\xi }\left(x\right):=1+ln{\mathrm{GEV}}_{\xi }\left(x\right)$, with ${\mathrm{GEV}}_{\xi }\left(x\right)$ defined in (4). The ML-estimation of $(\xi ,\sigma )$ for a model ${\mathrm{GP}}_{\xi }(x/\sigma )$, $\sigma >0$, is numerically hardly tractable. ML estimates for the regular-case $(\xi >-1/2)$ and $\sigma >0$, in ${\mathrm{GP}}_{\xi }(x/\sigma )$, have been studied in Smith [33], where the POT approach was introduced, with POT standing for peaks-over-threshold. A survey of the POT methodology, together with several applications, can be found in Davison and Smith [34]. Under random censoring, let us assume that for all $x\ge 0$, $F_X\left(x\right)=1-{(1+{\xi }_{1}x)}^{-1/{\xi }_1}$ and $F_Y\left(x\right)=1-{(1+{\xi }_{2}x)}^{-1/{\xi }_2}$. We then obtain

$$F_Z\left(z\right)=1-{(1+{\xi }_{1}z)}^{-1/{\xi }_1}{(1+{\xi }_{2}z)}^{-1/{\xi }_2},$$

$$f_Z\left(z\right)={(1+{\xi }_{1}z)}^{-1/{\xi }_1-1}{(1+{\xi }_{2}z)}^{-1/{\xi }_2}\left(1+{\displaystyle \frac{1+{\xi }_{1}z}{1+{\xi }_{2}z}}\right),$$

and

$$\begin{array}{ccc}\hfill c\equiv c_z:& =& \mathbb{P}(X\le Y|Z=z)\hfill \\ & =& {\displaystyle \frac{{(1+{\xi }_{1}z)}^{-\frac{1}{{\xi }_1}-1}{(1+{\xi }_{2}z)}^{-\frac{1}{{\xi }_2}-1}}{{(1+{\xi }_{1}z)}^{-\frac{1}{{\xi }_1}-1}{(1+{\xi }_{2}z)}^{-\frac{1}{{\xi }_2}-1}\left(1+\frac{1+{\xi }_{1}z}{1+{\xi }_{2}z}\right)}}\hfill \\ & =& {\displaystyle \frac{1}{1+\frac{1+{\xi }_{1}z}{1+{\xi }_{2}z}}}\underset{z\to \infty }{⟶}{\displaystyle \frac{{\xi }_2}{{\xi }_1+{\xi }_2}}.\hfill \end{array}$$

The abovementioned limiting result, at the end of Example 2, holds generally, for any $F_X\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_1}\right)$, $F_Y\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_2}\right)$. Indeed, under the above general setting, in (13), and as can be seen in [4], it is possible to prove that

$$F_X\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_1}\right),F_Y\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_2}\right)⟹F_{Z=min(X,Y)}\in {\mathcal{D}}_{\mathcal{M}}\left(G_{\xi }\right),\mathrm{with}\xi ={\displaystyle \frac{{\xi }_1{\xi }_2}{{\xi }_1+{\xi }_2}}.$$

(15)

Note that

$$\begin{array}{c}{F}_X\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_1}\right),F_Y\in {\mathcal{D}}_{\mathcal{M}}\left(G_{{\xi }_2}\right),{\xi }_1,{\xi }_2>0⟺\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}1-F_X\left(x\right)=x^{-1/{\xi }_1}{\mathbb{L}}_X\left(x\right)and1-F_Y\left(y\right)=y^{-1/{\xi }_2}{\mathbb{L}}_Y\left(x\right)\end{array}$$

are Pareto-type right tails, already mentioned in (2). Since the CDF of $Z=min(X,Y)$ is $F_Z\left(z\right)=1-(1-F_X\left(z\right))(1-F_Y\left(z\right))$, we obtain

$$1-F_Z\left(z\right)=z^{-(1/{\xi }_1+1/{\xi }_2)}{\mathbb{L}}_X\left(z\right){\mathbb{L}}_Y\left(z\right)=:z^{-{\displaystyle \frac{{\xi }_1+{\xi }_2}{{\xi }_1{\xi }_2}}}{L}_Z\left(z\right),$$

i.e., (15) holds.

Consequently, any functional devised for the semi-parametric estimation of the tail index in complete samples associated with the observed sample $(Z_1,Z_2,\dots ,Z_n)$ and based on the $k+1$ upper OS in the sample, generically denoted as ${\widehat{\xi }}_{k,n,Z}^{★}$, will converge towards ${\xi }_Z={\xi }_1{\xi }_2/({\xi }_1+{\xi }_2)$ in (15) for intermediate k, i.e., whenever (12) holds. Moreover, and for the same intermediate sequences k,

$${\displaystyle \frac{{\widehat{\xi }}_{k,n,Z}^{★}}{c}}\underset{n\to \infty }{\overset{p}{⟶}}{\xi }_1\equiv {\xi }_X.$$

Consequently, we only need to find an estimator of $c=c_Z$ in (14) with $1-c$, the percentage of censoring in the right tail of $F_X$. A possible semi-parametric consistent estimator of c (for intermediate k) is

$${\widehat{c}}_{k,n}:={\displaystyle \frac{1}{k}}\sum _{i=1}^k{\delta }_{[n-i+1]},$$

(16)

where ${\delta }_{[n-i+1]},1\le i\le n$ are the induced or concomitant OS associated with the ascending ordering of $(Z_1,Z_2,\dots ,Z_n)$, i.e., ${\delta }_{[n-i+1]}$ is the concomitant value of $\delta$ associated with $Z_{n-i+1:n}$, $1\le i\le n$. An obvious semi-parametric estimator of ${\xi }_X$, based on the observed $(Z,\delta )$, is thus

$${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}={\displaystyle \frac{k{\widehat{\xi }}_{k,n,Z}^{★}}{{\sum }_{i=1}^k{\delta }_{[n-i+1]}}},$$

(17)

an estimator already studied in [6,7], for a few estimation procedures.

The final estimate associated with ${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}$ will be computed using Algorithm 4.5. in [29], which we next summarize:

(i)

Given the observed sample $(Z_1,\dots ,Z_n)$ and $({\delta }_1,\dots ,{\delta }_n)$, compute, for $k=1,\dots ,n-1$, the observed values of ${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}$, in (17).

(ii)

Obtain $j_0$, the minimum value of j, a non-negative integer, such that the rounded values, to j decimal places, of the estimates in (i) are distinct. Define $a_k^{\left(\widehat{\xi }\right)}\left(j\right)=round({\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★},j)$, $k=1,2,...,n-1$, the rounded values of ${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}$ to j decimal places;

(iii)

Consider the sets of k values associated with equal consecutive values of $a_k^{\left(\widehat{\xi }\right)}\left(j\right)$, obtained in (ii). Set $k_{min}^{\left(\widehat{\xi }\right)}$ and $k_{max}^{\left(\widehat{\xi }\right)}$ the minimum and maximum values, respectively, of the set with the largest range. The largest run size is then $l_{\widehat{\xi }}:=k_{max}^{\left(\widehat{\xi }\right)}-k_{min}^{\left(\widehat{\xi }\right)}+1$.

(iv)

Consider all those estimates, ${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}$, $k_{min}^{\left(\widehat{\xi }\right)}\le k\le k_{max}^{\left(\widehat{\xi }\right)}$, now with two extra decimal places, i.e., compute ${\widehat{\widehat{\xi }}}_{k,n,X|Z,\delta }^{★}=a_k^{\left(\widehat{\xi }\right)}(j_0+2)$. Obtain the mode of those estimates and denote by ${\mathcal{K}}^{\widehat{\xi }}$ the set of k-values associated with this mode.

(v)

Take $k^{\widehat{\xi }}$ as the maximum value of ${\mathcal{K}}^{\widehat{\xi }}$.

(vi)

Compute ${\tilde{\xi }}_{n,X|Z,\delta }^{★}={\widehat{\widehat{\xi }}}_{k^{\widehat{\xi }},n,X|Z,\delta }^{★}$.

We have applied this methodology to simulated random censored data in Section 5, as well as real survival data in Section 6, but even before showing the obtained results, we provide some general hints for the adequate EVI-estimation. For heavy right tails, i.e., a positive EVI, we strongly advise the use of any of the MVRB tail index estimators, like the one studied in [12]. GM EVI-estimators can also provide an interesting solution to the problem, and even a better solution can be obtained via RB GM EVI-estimators, the ones considered in this article.

5. Monte-Carlo Simulation

We have considered $X\in {\mathcal{D}}_{\mathcal{M}}\left(E{V}_{{\xi }_1}\right)$, with ${\xi }_1\equiv {\xi }_X=0.25$ censored by $Y\in {\mathcal{D}}_{\mathcal{M}}\left(E{V}_{{\xi }_2}\right)$, with ${\xi }_2={\xi }_{1}p/(1-p)$, $p=0.35\left(0.10\right)0.95$. Then, $Z\in {\mathcal{D}}_{\mathcal{M}}\left(E{V}_{\xi }\right)$, with $\xi \equiv {\xi }_Z={\xi }_1{\xi }_2/({\xi }_1+{\xi }_2)$. Consequently, we allow for a percentage of censoring in the right tail equal to values that change from 65% to 5%.

For heavy right tails, we have performed a large-scale Monte Carlo simulation for different parents. Here, we consider the following:

• X and Y both come from Fréchet models (the CDF of a Fréchet$\left(\xi \right)$ model is $F\left(x\right)=exp(-x^{-1/\xi })$, $x\ge 0$, $\xi >0$ ($\rho =-1$ and $\beta =1/2$)).
• X and Y both come from Burr models (the CDF of a Burr$(\xi ,\rho )$ model is $F\left(x\right)=1-{(1+x^{-\rho /\xi })}^{1/\rho }$, $x\ge 0$, $\xi >0$, $\rho <0$ and $\beta =1$).
• X and Y both come from GP models (the CDF of a GP$\left(\xi \right)$ model is given in Example 2 ($\rho =-\xi$ and $\beta =1$)).

For simplicity, the GM EVI-estimators in (9), (A1) and (A2) will be denoted by PM, MO and L, respectively, and the RB GM EVI-estimators in (A3), (A4) and (A5) by RBPM, RBMO and RBL, respectively.

In Figure 1 and Figure 2, for a sample size $n=1000$, we can see the mean values and the root-mean-squared errors (RMSEs) of some of the estimators under study when we consider

$$X⌢\mathrm{F}\mathrm{r}\mathrm{é}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{t}({\xi }_1\equiv {\xi }_X=0.25)\mathrm{censored} \mathrm{by}Y⌢\mathrm{F}\mathrm{r}\mathrm{é}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{t}({\xi }_2=0.75).$$

We then obtain for the observed Z a tail index $\xi \equiv {\xi }_Z=0.1875$. The censoring in the right tail is thus equal to $25\%$.

Even for sample sizes as small as $n=100$, from the same parents, the results are still interesting, as can be seen in Figure 3 and Figure 4. This generally happens if the censoring in the right tail is not too heavy (smaller than or equal to 25%, for example).

The sample paths and MSE of ${\widehat{c}}_{k,n}$ are presented in Figure 5. From this figure, we can infer that, for both sample sizes, the bias remains very small, up to 70% of the sample size.

Figure 6 and Figure 7 depict, for a sample size of $n=1000$, the mean values and RMSEs of the estimators under study when we consider

$$X⌢\mathrm{Burr}({\xi }_1\equiv {\xi }_X=0.25,\rho =-1)\mathrm{censored} \mathrm{by}Y⌢\mathrm{Burr}({\xi }_2=0.464,\rho =-1),$$

and, in this case, we obtain for the observed Z a tail index $\xi \equiv {\xi }_Z=0.1625$. The censoring in the right tail is thus equal to $35\%$.

For the Burr models, the estimates ${\widehat{c}}_{k,n}$ in (16) exhibit patterns similar to the ones presented in Figure 5 and are presented in Figure 8. As expected, when the censoring in the right tail increases, the k-region where the bias remains very small decreases, and in this case, it is up to 55% of the sample size.

Figure 9 and Figure 10 depict, for a sample size of $n=1000$, the mean values and RMSEs of the estimators under study when we consider

$$X⌢\mathrm{GP}({\xi }_1\equiv {\xi }_X=0.25)\mathrm{censored} \mathrm{by}Y⌢\mathrm{GP}({\xi }_2=0.75),$$

and in this case, we obtain for the observed Z a tail index $\xi \equiv {\xi }_Z=0.1875$. The censoring in the right tail is thus equal to $25\%$. An interesting feature of the GP model is that the use of GM EVI-estimators results in stable sample paths around the true values of ${\xi }_X$ and ${\xi }_Z$, eliminating the need for RB estimation.

The sample paths and MSE of ${\widehat{c}}_{k,n}$ are presented in Figure 11. We can infer from this figure that the bias is practically zero for all k, with $1\le k\le n$.

Based on these figures, we can draw the following conclusions:

• For an appropriate choice of p, the GM estimators of ${\xi }_X$ outperform the Hill EVI-estimator in terms of bias for the Fréchet, Burr and GP models under study.
• Once again, for an adequate choice of p, the GM estimators of ${\xi }_X$ outperform the MVRB EVI-estimator in terms of bias for a wide range of k-values, which depend on both the estimator and the value of the tuning parameter p, for the Fréchet, Burr and GP models under study.
• For the Fréchet and Burr models, all RB GM estimators of ${\xi }_X$ exhibit an even better solution, again for adequate choices of p.
• For the GP models under study, the use of the classic GM estimators is more efficient than the use of its RB versions.
• It is also worth noting that for the GP models under study, all GM estimators exhibit similar behaviour to the Hill estimator.

6. Lifetime Data Analysis (Cancer of the Tongue)

We herein consider data on 80 males diagnosed with cancer of the tongue, with Z denoting time to death or on-study time, in weeks (Section 1.11 in Sickle-Santanello et al. [35], available in Klein and Moeschberger [36] and in the package KMsurv, version 0.1-5, from the software [37]. Data are available through the link, https://www.rdocumentation.org/packages/KMsurv/versions/0.1-5/topics/tongue (accessed on 21 April 2024)).

The estimates of c as a function of k, the number of top OS used in the estimation, with the estimate $\tilde{c}$ marked by the dashed line, computed using an adapted version of Algorithm 4.5 in [29], which was already summarized in Section 4, are shown in Figure 12. On the basis of the stability criteria described above, we obtain the estimate $\tilde{c}=0.4$ for the parameter $c=\mathbb{P}(\delta =1|Z=z)$. We thus have a reasonably high censoring in the right tail, around 60%, and this makes the estimation of parameters of large events slightly problematic.

We shall next provide estimates for ${\xi }_Z$ and estimates for ${\xi }_X$. For ${\xi }_Z$, the use of any of the EVI-estimators under consideration, devised for complete samples, based on the stability criteria above led us to the adaptive estimates presented in

Table 1. Adaptive estimates of the EVI-estimators under study for the tongue cancer data.

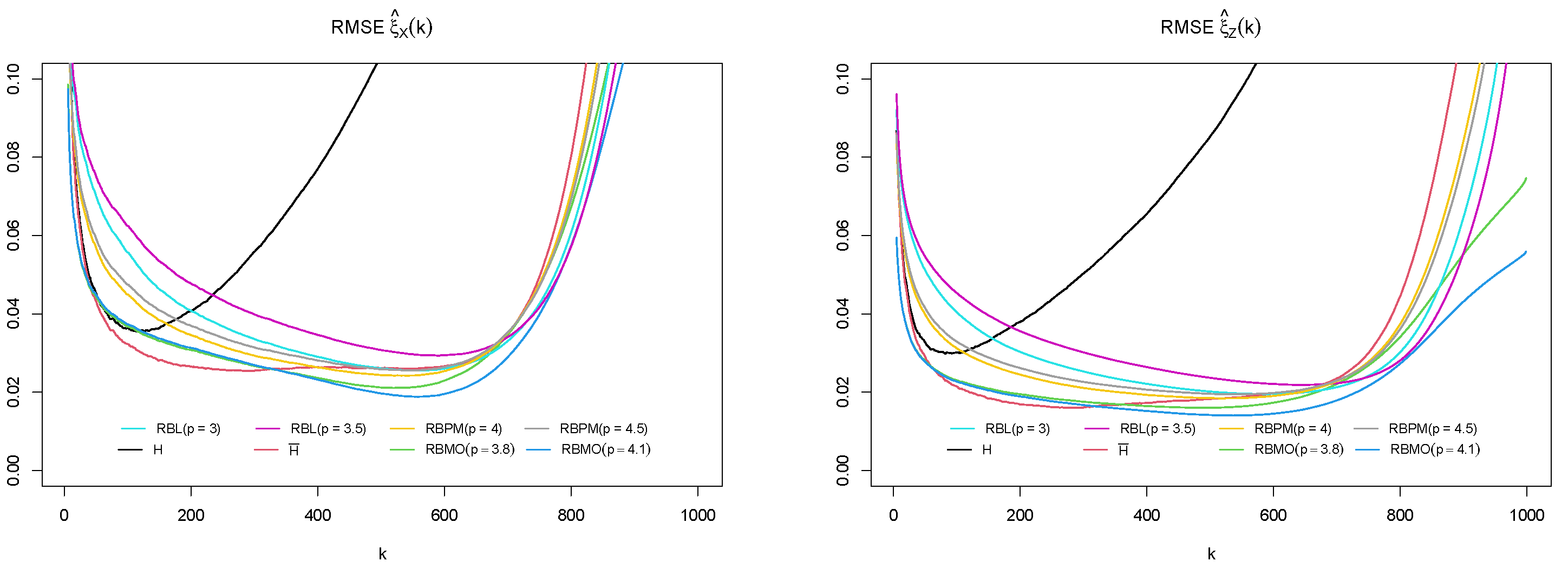
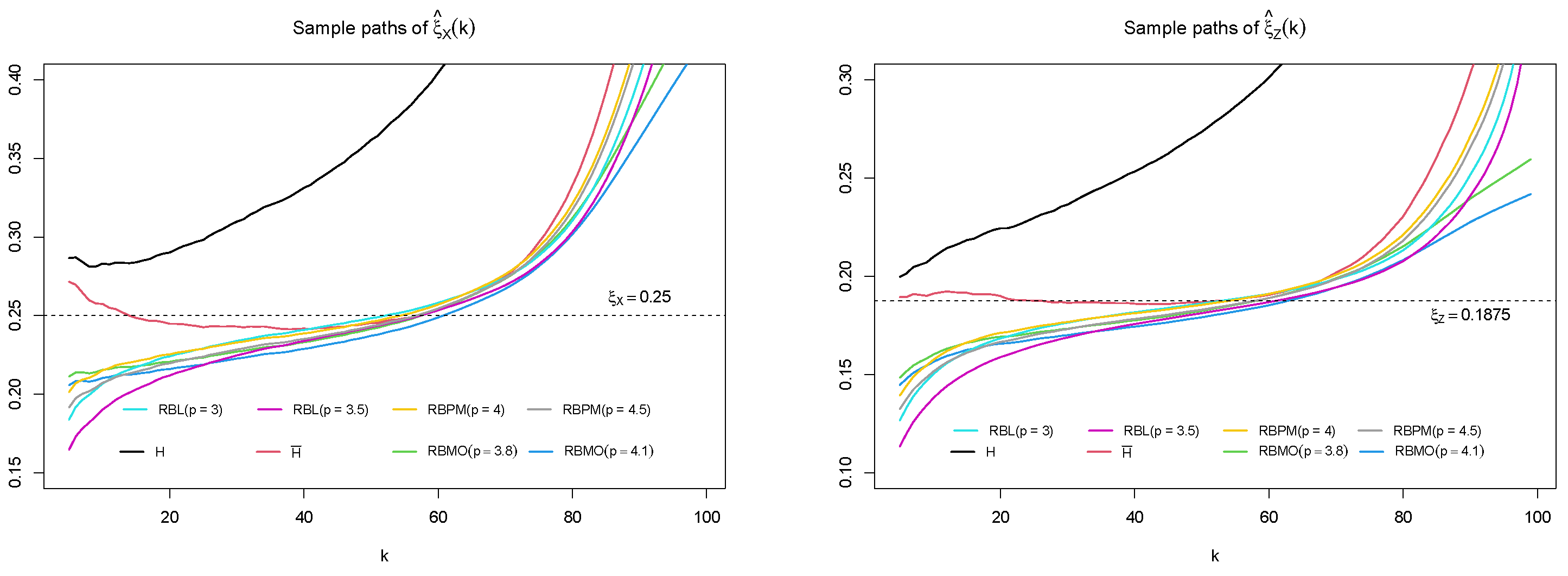
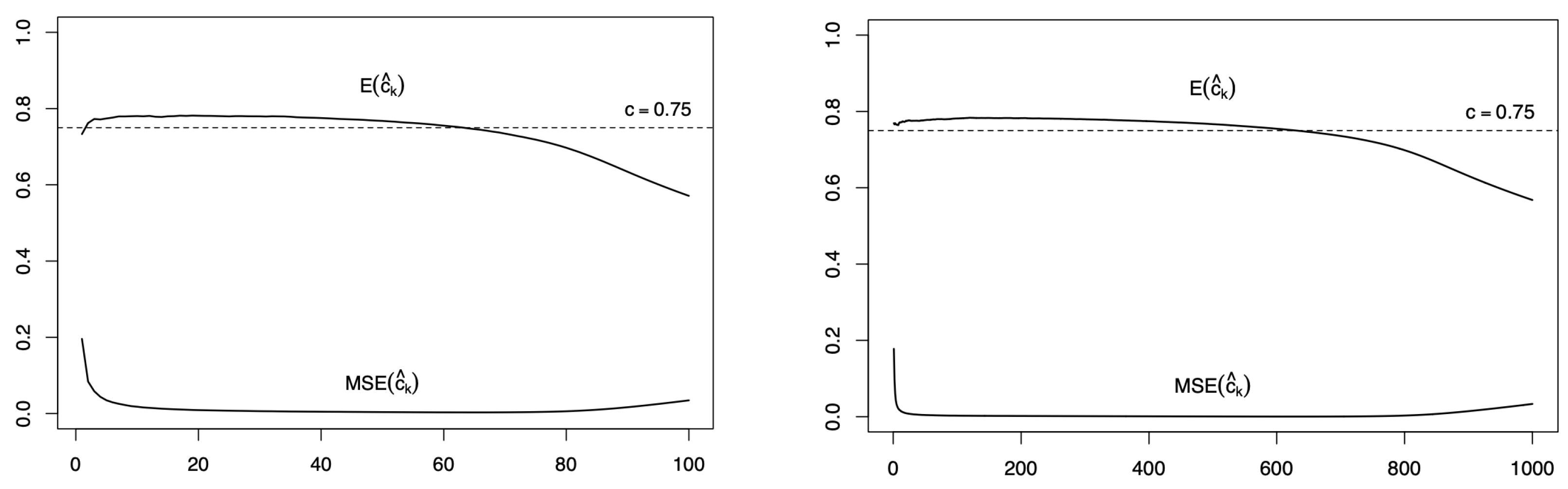
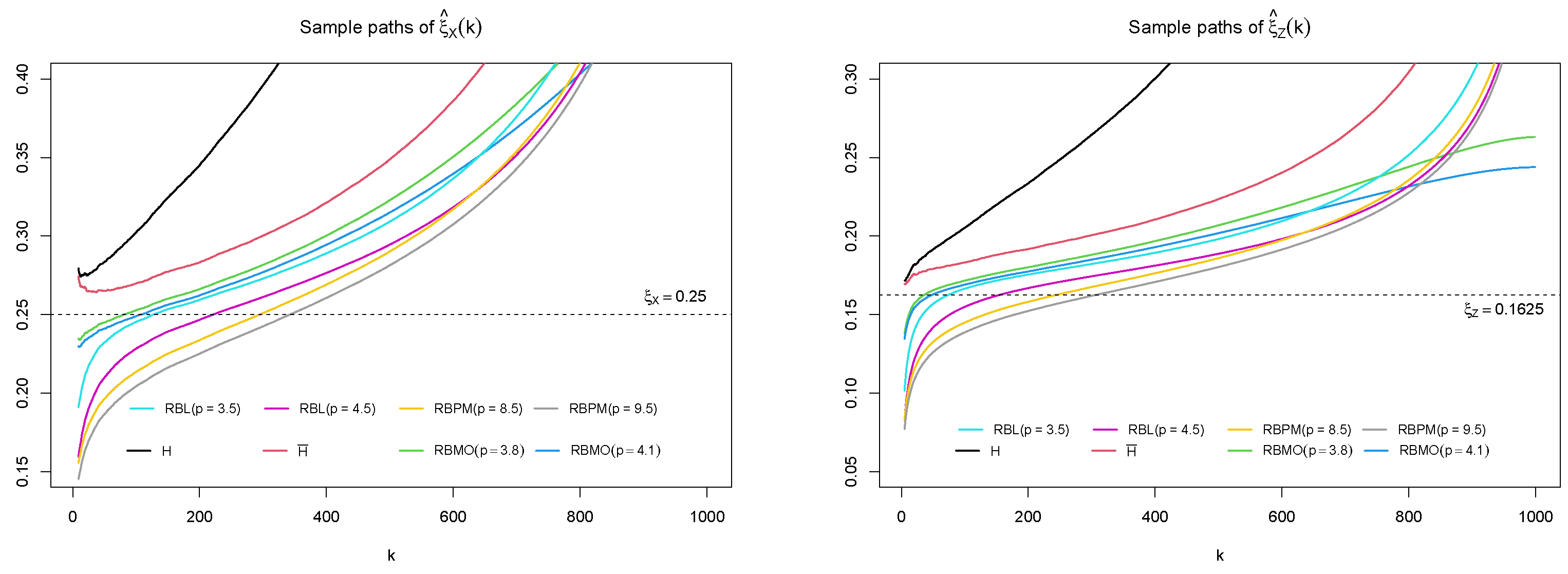
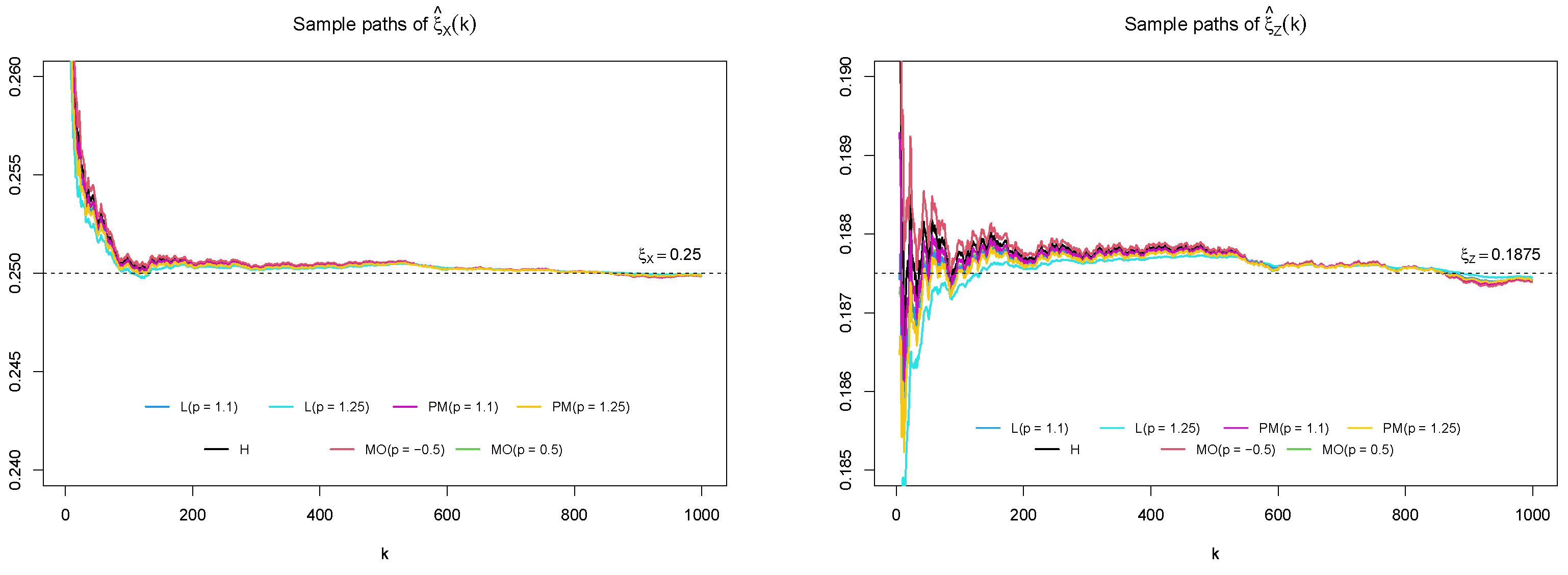
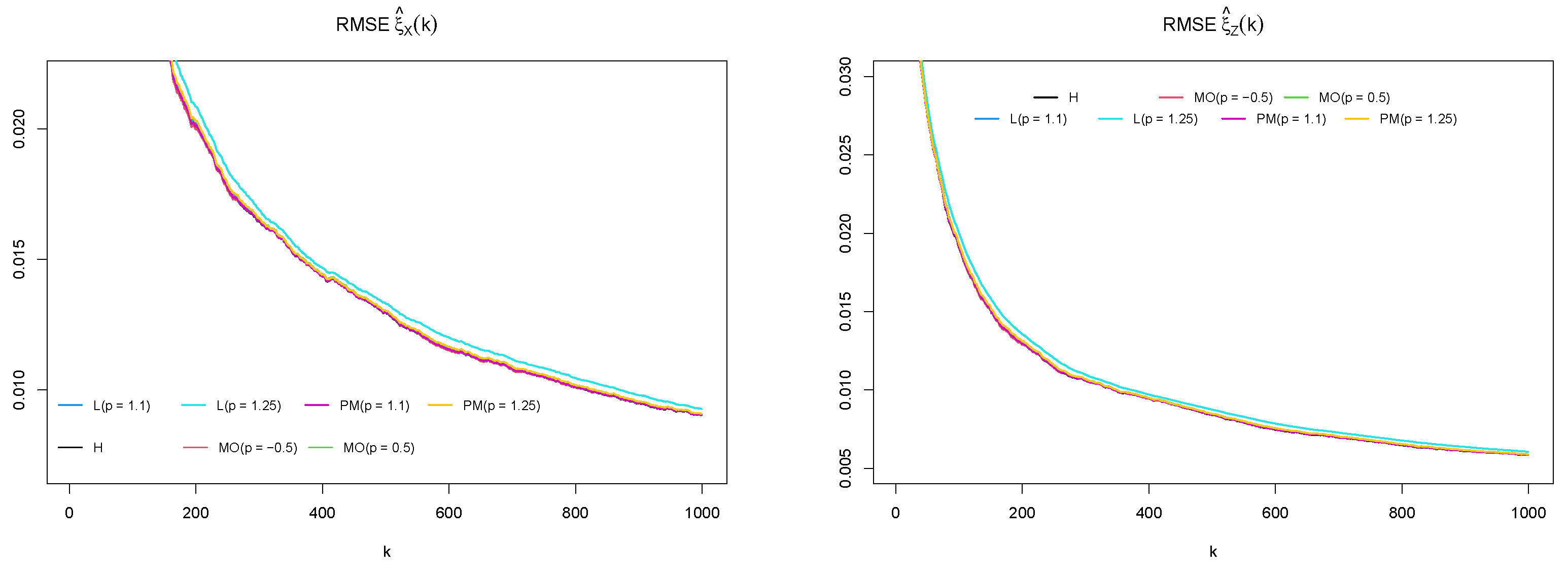
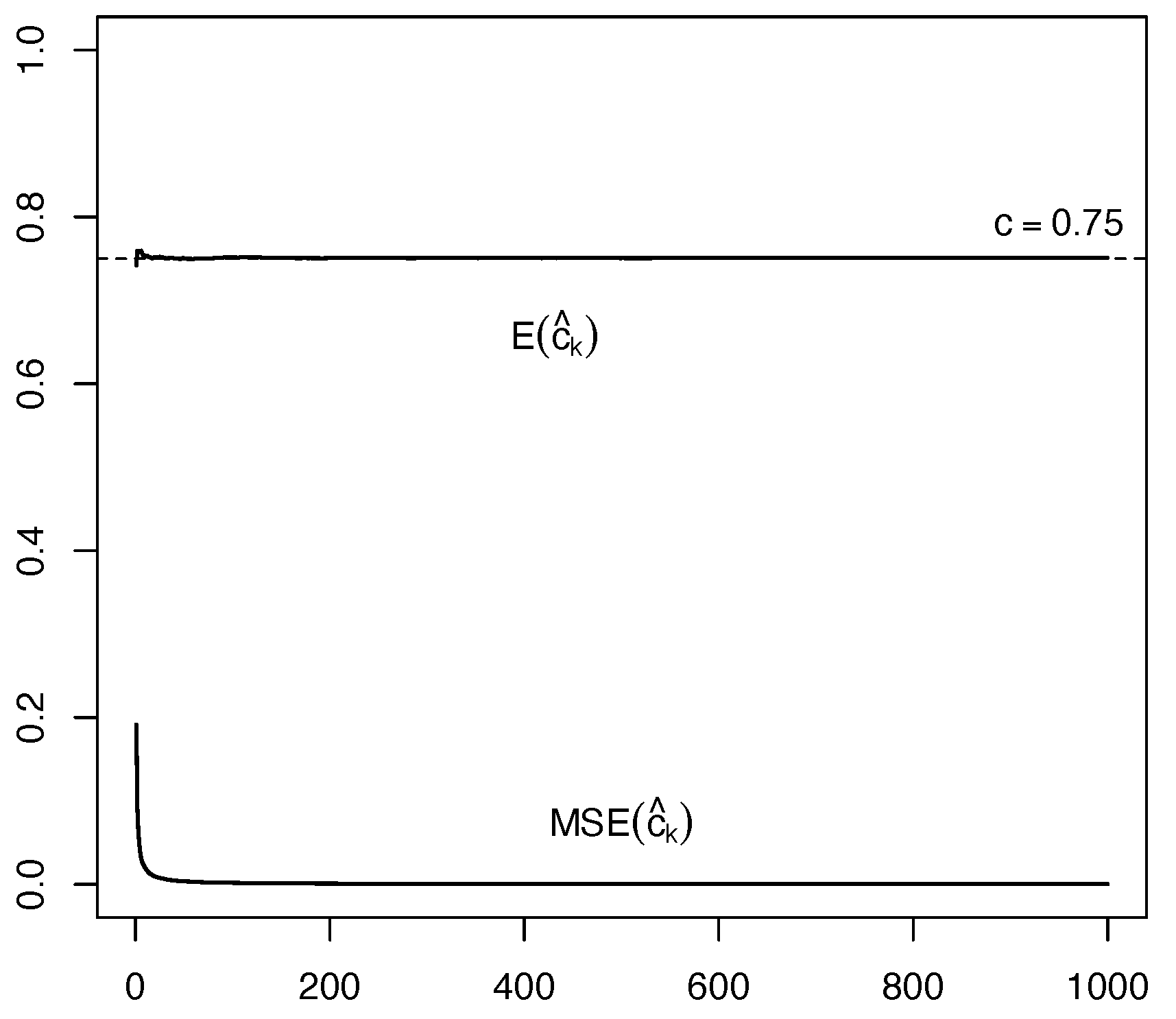
Estimator	H	$\overline{\mathit{H}}$	RBMO	RBMO	RBL	RBL	RBPM	RBPM
p			$p=1.5$	$p=2$	$p=3.5$	$p=4$	$p=6$	$p=7$
$k^c$	33	43	42	28	30	39	32	29
${\widehat{\xi }}_{k^c,n,Z}^{•}$	0.4292	0.2947	0.3061	0.2818	0.2796	0.2865	0.2731	0.2535

. The median of the RB GM EVI-estimators is ${\widehat{\xi }}_Z=0.2807$, and considering the RB EVI-estimators under study, we obtain an overall median estimate of ${\widehat{\xi }}_Z=0.2818$ (depicted by the dashed line in Figure 13 (right)). The corresponding estimate of ${\xi }_X$ is then ${\widehat{\xi }}_X=0.7045$, also depicted by the dashed line in Figure 13 (left). As expected, the use of RB EVI-estimators allows for a significant reduction in bias compared to the classic EVI-estimator.

7. Overall Comments and Future Work

On the basis of the aforementioned results, the estimation of other parameters of extreme events like the probability of exceedance of a high level or a high quantile easily follow, but will be not discussed here. The development of new estimators of $c\equiv c_z:=\mathbb{P}(X\le Y|Z=z)$ is a topic that deserves further study, but is also out of the scope of this paper. The interesting behaviour of the MO_p and RB MO_p estimators for values of p close to $1/\xi$ and its almost non-degenerate and consistent behaviour for $p=1/\xi$ deserves further attention, in the direction of the developments made by Gomes, Henriques-Rodrigues and Pestana [38], among others. Just as with complete samples, RB GM estimation provides a better solution for the estimation of parameters of rare events under random censorship. Apart from the algorithm considered herein for the estimation of the tuning parameter $(k,p)$, several other algorithms (see, among others, Gomes, Caeiro, Henriques-Rodrigues and Manjunath [39], where R-scripts are provided) can be used and compared—a topic also out of the scope of this paper, such as the consideration of this type of RB GM estimation for a general $\xi \in \mathbb{R}$.