MEMS-Based Vibration Acquisition for Modal Parameter Identification of Substation Frame
Abstract
1. Introduction
2. Field Test of Vibration Data Acquisition with Portable Devices
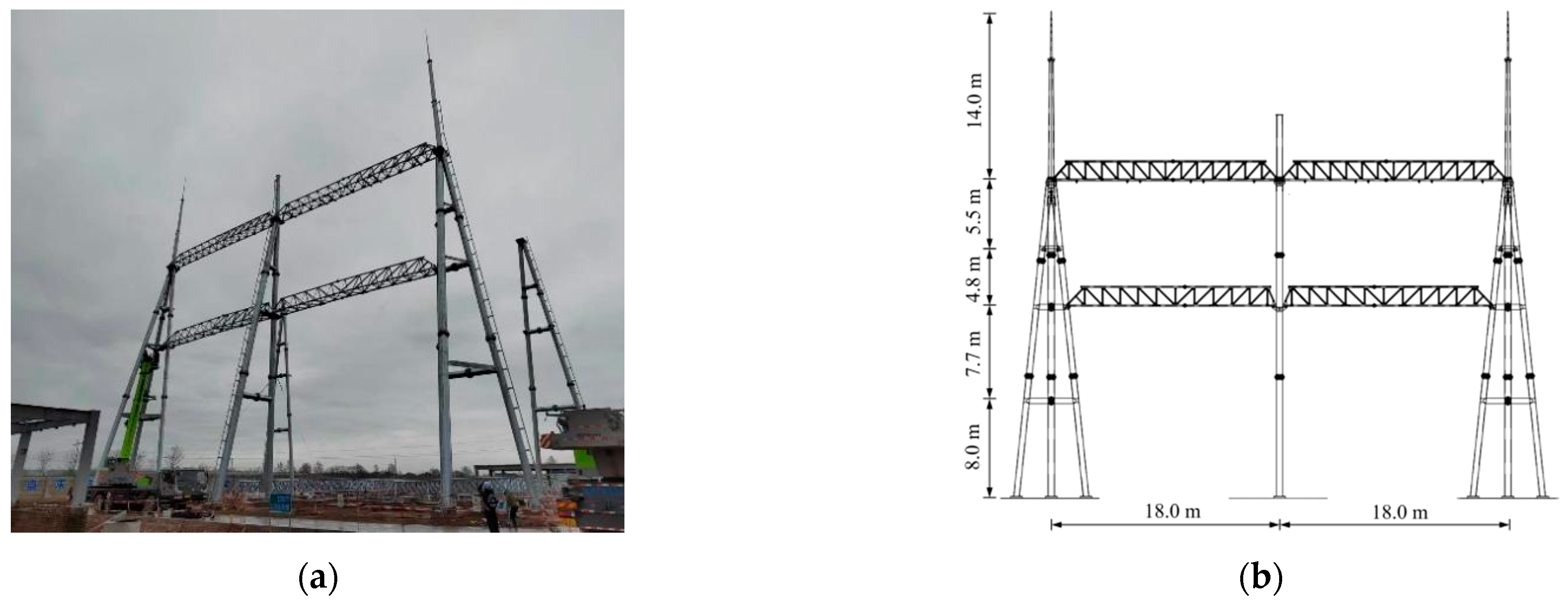
2.1. Overview of the Test Substation Frame
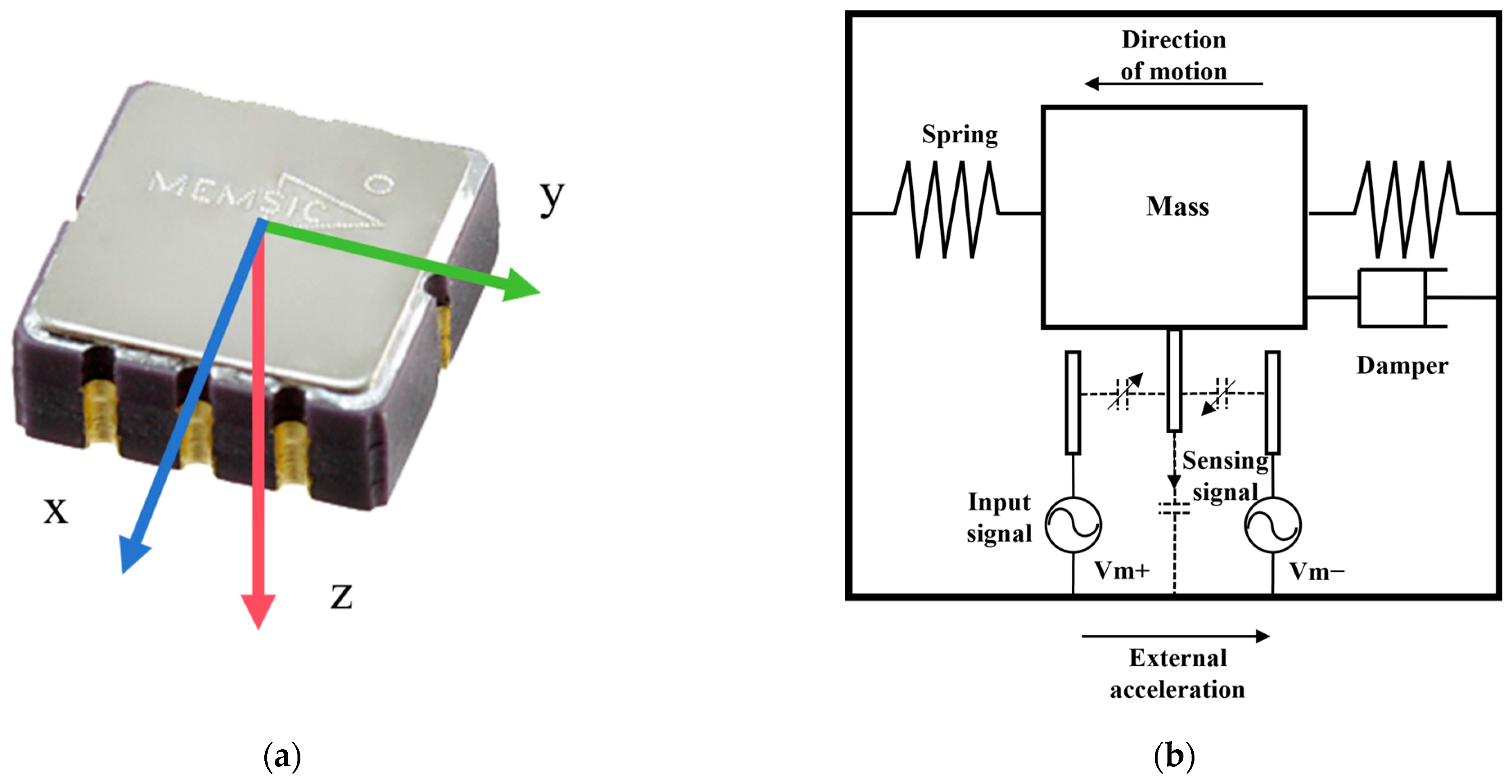
2.2. Working Principle of MEMS Sensors
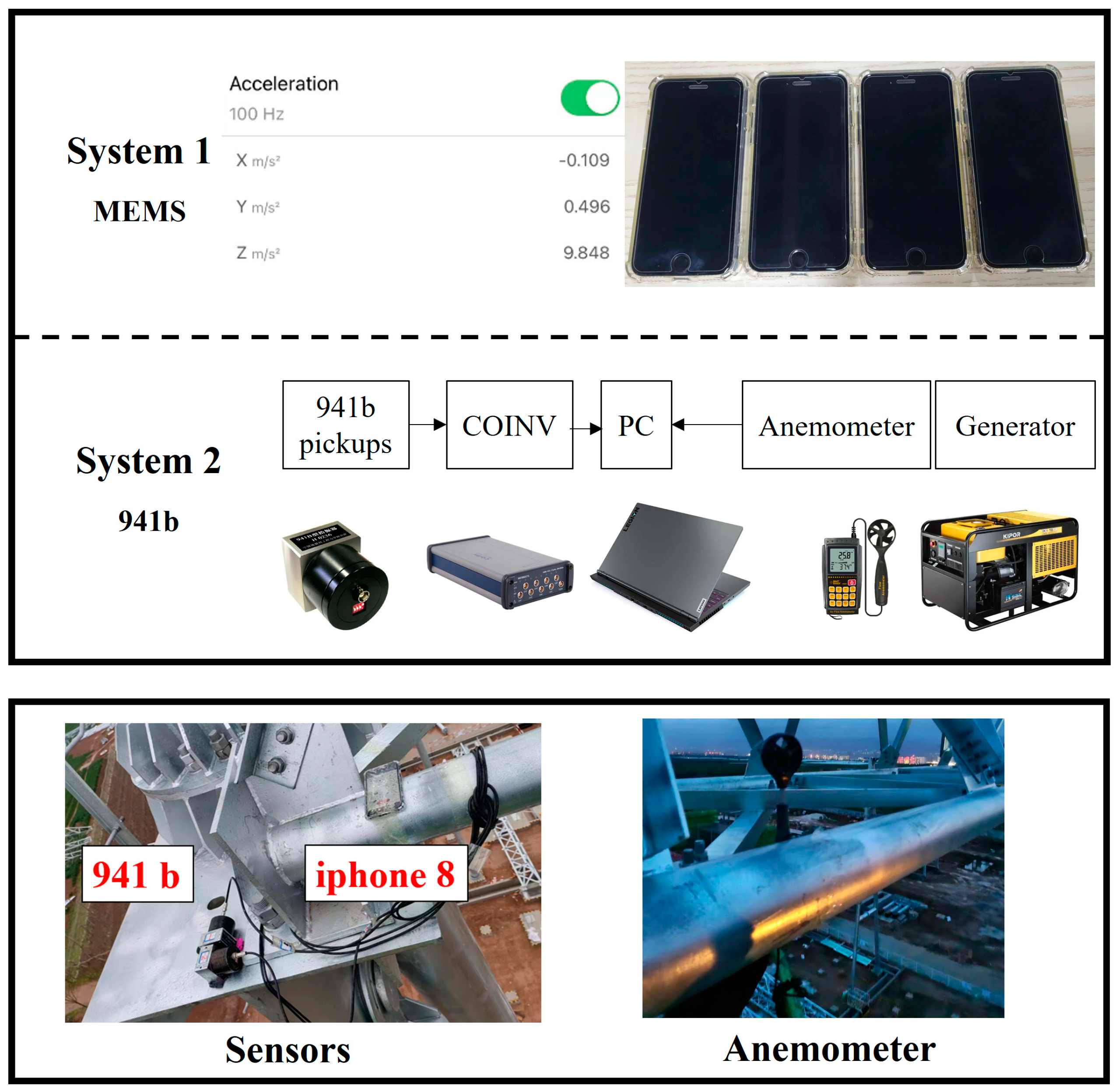
2.3. Field Test
3. Analysis of Experimental Data Characteristics
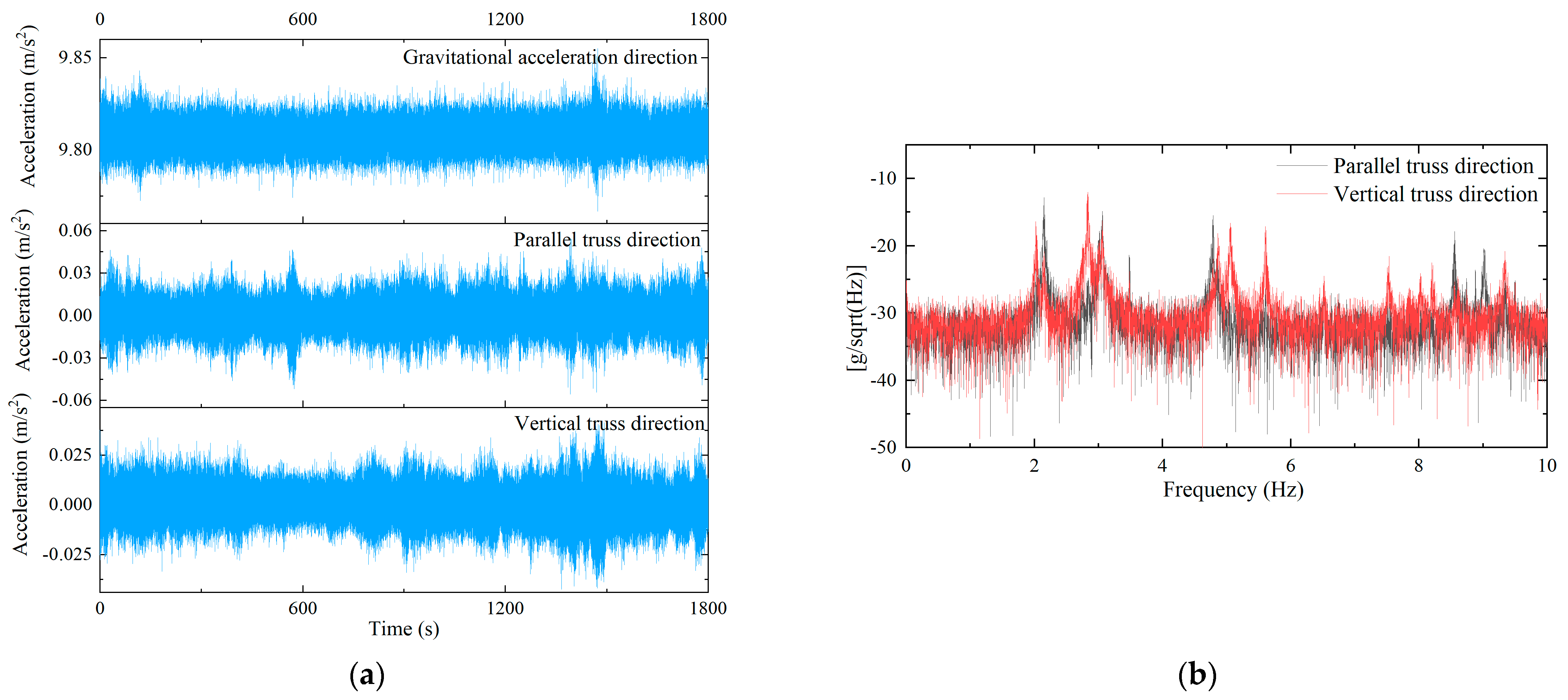
3.1. Time–Frequency Characteristics of MEMS Data
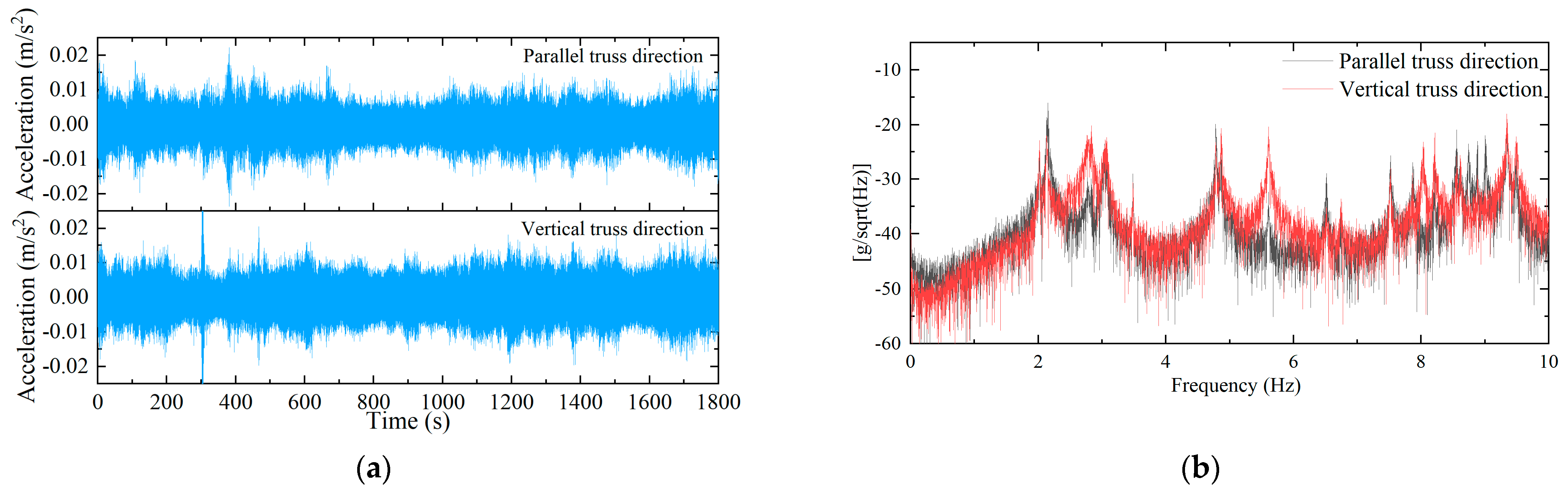
3.2. Time–Frequency Characteristics of Responses Collected by the 941b System
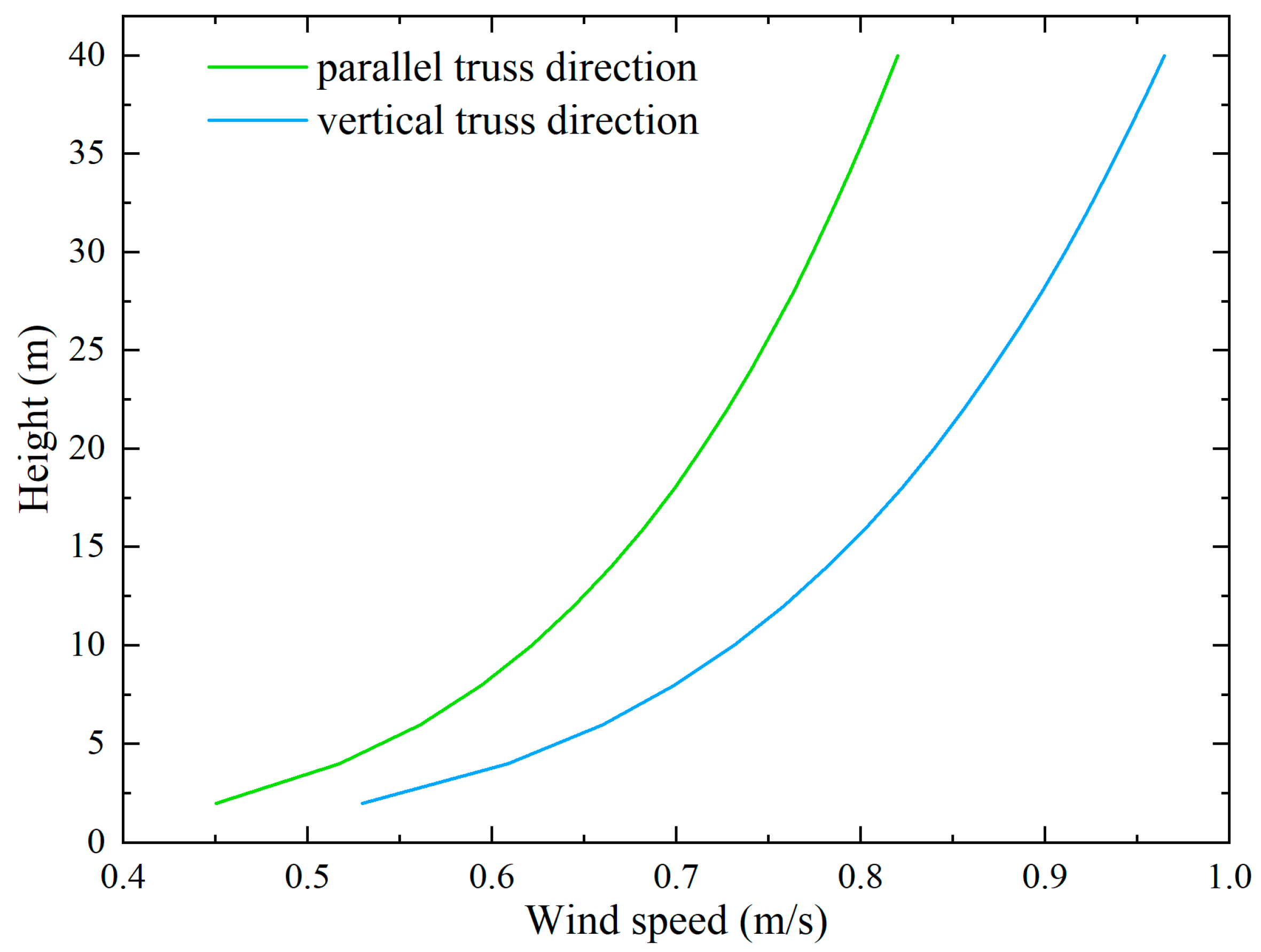
3.3. Wind Speed Time History
4. Modal Analysis of the Substation Frame
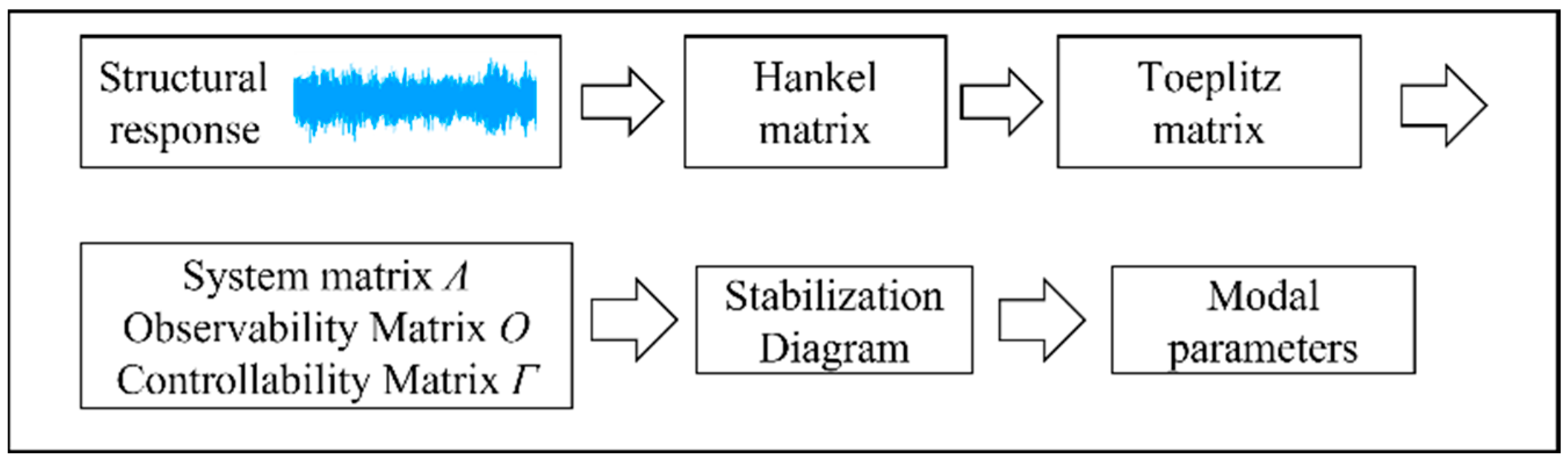
4.1. Covariance-Driven Stochastic Subspace Identification
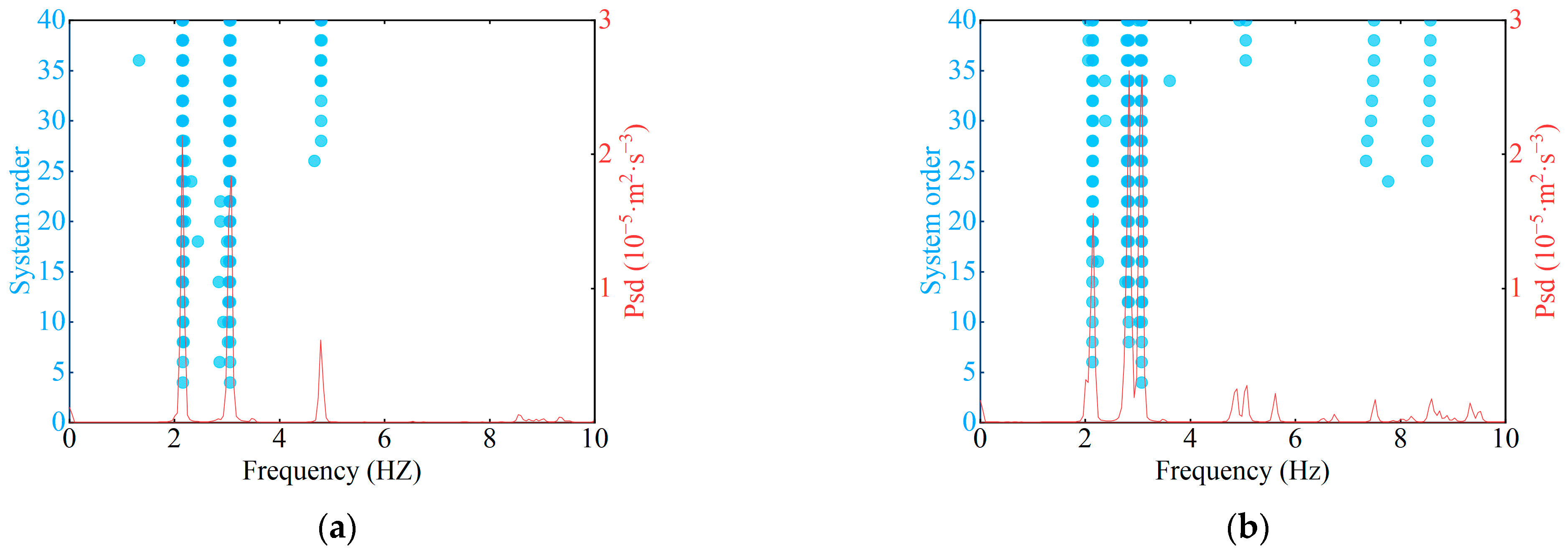
4.2. Modal Parameter Identification of the Substation Frame
4.3. Mode Shapes
5. Conclusions
- (1).
- A method based on MEMS technology for acquiring the dynamic response time histories of structures is proposed, and its feasibility is demonstrated through comparison with traditional vibration monitoring methods. The study found that the vibration response captured by MEMS exhibited slightly higher amplitude compared with results from traditional monitoring methods, primarily due to the MEMS system capturing more environmental noise, which increased the overall variance of the data. However, in terms of frequency-domain analysis, the differences between the two methods at the peak regions were minimal, with the main discrepancies occurring in non-modal, non-resonant regions, corresponding to amplitude differences in the time-domain response.
- (2).
- The primary modes of the new substation frame were identified as follows: the first-order torsional mode at 2.14 Hz, the first-order vertical truss mode at 2.81 Hz, the second-order torsional mode at 3.05 Hz, and the first-order parallel truss mode at 4.78 Hz.
- (3).
- The modal parameter identification results indicate minimal frequency identification differences when using different datasets or identification methods, as the structural frequency is an inherent property of the structure. In contrast, the damping ratio identification results show some variability, which is attributed to differences in the data acquisition systems and the identification theories used. Overall, the identification results are relatively stable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.N.; Wang, J.X.; Fu, X.; Ren, L.; Zhang, Q. Field measurements of typhoon effects on a transmission tower and its modal parameter identification. Adv. Struct. Eng. 2020, 23, 1548–1561. [Google Scholar] [CrossRef]
- Zhu, Y.M.; Sun, Q.; Zhao, C.; Wei, S.T.; Yin, Y.; Su, Y.H. Operational modal analysis of two typical UHV transmission towers: A comparative study by fast Bayesian FFT method. Eng. Struct. 2023, 277, 115425. [Google Scholar] [CrossRef]
- Liu, D.; Bao, Y.; Li, H. Machine learning-based stochastic subspace identification method for structural modal parameters. Eng. Struct. 2023, 274, 115178. [Google Scholar] [CrossRef]
- Lam, H.F.; Fu, Z.Y.; Adeagbo, M.O.; Yang, J.H. Time-domain structural model updating following the Bayesian approach in the absence of system input information. Eng. Struct. 2024, 314, 118321. [Google Scholar] [CrossRef]
- Zhao, C.; Su, Y.; Zhu, Y.; Sun, Q.; Wei, S.; Wang, X. Enhanced semi-automated Bayesian modal identification approach for Ultra-high voltage transmission towers. Structures 2023, 57, 105247. [Google Scholar] [CrossRef]
- Ni, Y.C.; Alamdari, M.M.; Ye, X.W.; Zhang, F.L. Fast operational modal analysis of a single-tower cable-stayed bridge by a Bayesian method. Measurement 2021, 174, 109048. [Google Scholar] [CrossRef]
- Zhang, F.L.; Yang, Y.P.; Ye, X.W.; Yang, J.H.; Han, B.K. Structural modal identification and MCMC-based model updating by a Bayesian approach. Smart Struct. Syst. Int. J. 2019, 24, 631–639. [Google Scholar]
- Zhu, Y.; Sun, Q.; Zhao, C.; Qi, H.; Su, Y. Bayesian operational modal analysis with interactive optimization for model updating of large-size UHV transmission towers. J. Struct. Eng. 2023, 149, 04023184. [Google Scholar] [CrossRef]
- Shao, Y.; Li, L.; Li, J.; An, S.; Hao, H. Computer vision based target-free 3D vibration displacement measurement of structures. Eng. Struct. 2021, 246, 113040. [Google Scholar] [CrossRef]
- Huang, H.; Kono, D.; Toyoura, M. Vision-based vibration measurement of machine tool. J. Adv. Mech. Des. Syst. Manuf. 2022, 16, JAMDSM0014. [Google Scholar] [CrossRef]
- Yang, R.; Singh, S.K.; Tavakkoli, M.; Amiri, N.; Yang, Y.; Karami, M.A.; Rai, R. CNN-LSTM deep learning architecture for computer vision-based modal frequency detection. Mech. Syst. Signal Process. 2020, 144, 106885. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, C.; Jiang, S.; Zhang, J.; Duan, W. Noncontact cable force estimation with unmanned aerial vehicle and computer vision. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 73–88. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, W.; Jin, T.; Chen, B.; Zhang, H.; Zhang, W. A review of computer vision-based structural deformation monitoring in field environments. Sensors 2022, 22, 3789. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Wu, J.; Wang, H.; An, Y.; Tang, G. Computer vision-based illumination-robust and multi-point simultaneous structural displacement measuring method. Mech. Syst. Signal Process. 2022, 170, 108822. [Google Scholar] [CrossRef]
- Khuc, T.; Nguyen, T.A.; Dao, H.; Catbas, F.N. Swaying displacement measurement for structural monitoring using computer vision and an unmanned aerial vehicle. Measurement 2020, 159, 107769. [Google Scholar] [CrossRef]
- Jana, D.; Nagarajaiah, S. Computer vision-based real-time cable tension estimation in Dubrovnik cable-stayed bridge using moving handheld video camera. Struct. Control Health Monit. 2021, 28, e2713. [Google Scholar] [CrossRef]
- Ma, Z.; Choi, J.; Liu, P.; Sohn, H. Structural displacement estimation by fusing vision camera and accelerometer using hybrid computer vision algorithm and adaptive multi-rate Kalman filter. Autom. Constr. 2022, 140, 104338. [Google Scholar] [CrossRef]
- Bogue, R. MEMS sensors: Past, present and future. Sens. Rev. 2007, 27, 7–13. [Google Scholar] [CrossRef]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Ba Hashwan, S.S.; Junaid, M.M. A review of actuation and sensing mechanisms in MEMS-based sensor devices. Nanoscale Res. Lett. 2021, 16, 16. [Google Scholar] [CrossRef]
- Hajare, R.; Reddy, V.; Srikanth, R. MEMS based sensors–A comprehensive review of commonly used fabrication techniques. Mater. Today Proc. 2022, 49, 720–730. [Google Scholar] [CrossRef]
- Hou, Y.; Jiao, R.; Yu, H. MEMS based geophones and seismometers. Sens. Actuators A Phys. 2021, 318, 112498. [Google Scholar] [CrossRef]
- Mustafazade, A.; Pandit, M.; Zhao, C.; Sobreviela, G.; Du, Z.; Steinmann, P.; Zou, X.; Howe, R.T.; Seshia, A.A. A vibrating beam MEMS accelerometer for gravity and seismic measurements. Sci. Rep. 2020, 10, 10415. [Google Scholar] [CrossRef] [PubMed]
- Amami, M.M. The Advantages and Limitations of Low-Cost Single Frequency GPS/MEMS-Based INS Integration. Glob. J. Eng. Technol. Adv. 2022, 10, 018–031. [Google Scholar] [CrossRef]
- Su, Y.H.; Zhu, Y.M.; Zhao, C.; Lam, H.F.; Sun, Q. Bayesian uncertainty quantification of modal parameters and RRF identification of transmission towers with limited measured vibration data. Eng. Struct. 2024, 308, 118019. [Google Scholar] [CrossRef]
- Zhang, F.L.; Au, S.K.; Ni, Y.C. Two-stage Bayesian system identification using Gaussian discrepancy model. Struct. Health Monit. 2021, 20, 580–595. [Google Scholar] [CrossRef]
- Ni, P.H.; Ye, X.W.; Ding, Y. An output-only structural condition assessment method for civil structures by the stochastic gradient descent method. Struct. Control Health Monit. 2022, 29, e3132. [Google Scholar] [CrossRef]
- Feng, Y.; Su, Y.; Zhao, C.; Zhu, Y.; Sun, Q. A two-stage automated OMA framework for transmission towers based on clustering algorithms. Structures 2024, 61, 106023. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Adeagbo, M.O.; Lam, H.F. An efficient dynamic response reconstruction methodology based on model condensation and modal decomposition. Int. J. Struct. Stab. Dyn. 2023, 2450141. [Google Scholar] [CrossRef]
- Diaferio, M.; Foti, D.; Potenza, F. Prediction of the fundamental frequencies and modal shapes of historic masonry towers by empirical equations based on experimental data. Eng. Struct. 2018, 156, 433–442. [Google Scholar] [CrossRef]
- Zhang, F.L.; Gu, D.K.; Li, X.; Ye, X.W.; Peng, H. Structural damage detection based on fundamental Bayesian two-stage model considering the modal parameters uncertainty. Struct. Health Monit. 2023, 22, 2305–2324. [Google Scholar] [CrossRef]
- Ying, Z.G.; Ni, Y.Q. Optimal parameter estimation for uncertain structural systems under unknown random excitations. J. Vib. Control 2024, 10775463241248555. [Google Scholar] [CrossRef]
- Ye, X.W.; Ding, Y.; Ni, P.H. A numerical application of Bayesian optimization to the condition assessment of bridge hangers. Smart Struct. Syst. 2023, 31, 57–68. [Google Scholar]
- Ponzo, F.C.; Auletta, G.; Ielpo, P.; Ditommaso, R. DInSAR–SBAS satellite monitoring of infrastructures: How temperature affects the “Ponte della Musica” case study. J. Civ. Struct. Health Monit. 2024, 14, 745–761. [Google Scholar] [CrossRef]
- Wan, H.P.; Ni, Y.Q. A new approach for interval dynamic analysis of train-bridge system based on Bayesian optimization. J. Eng. Mech. 2020, 146, 04020029. [Google Scholar] [CrossRef]
- Eshkevari, S.S.; Matarazzo, T.J.; Pakzad, S.N. Bridge modal identification using acceleration measurements within moving vehicles. Mech. Syst. Signal Process. 2020, 141, 106733. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Ye, X.W.; Ko, J.M. Monitoring-based fatigue reliability assessment of steel bridges: Analytical model and application. J. Struct. Eng. 2010, 136, 1563–1573. [Google Scholar] [CrossRef]
- Au, S.K. Fast Bayesian ambient modal identification in the frequency domain, Part I: Posterior most probable value. Mech. Syst. Signal Process. 2012, 26, 60–75. [Google Scholar] [CrossRef]
- Bhowmik, B.; Tripura, T.; Hazra, B.; Pakrashi, V. Real time structural modal identification using recursive canonical correlation analysis and application towards online structural damage detection. J. Sound Vib. 2020, 468, 115101. [Google Scholar] [CrossRef]
- Kang, J.; Zeng, S. Uncertainty quantification in operational modal analysis of time-varying structures based on time-dependent autoregressive moving average model. J. Sound Vib. 2023, 548, 117549. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Rahimian Koloor, S.; Petrů, M. Health monitoring of civil infrastructures by subspace system identification method: An overview. Appl. Sci. 2020, 10, 2786. [Google Scholar] [CrossRef]
- Yu, X.; Dan, D.; Ge, L. Time-domain distributed modal parameter identification based on mode decomposition of single-channel vibration response. Eng. Struct. 2023, 289, 116323. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.T.; Jin, A.Y.; Luo, G.H. Parametric analysis of SSI algorithm in modal identification of high arch dams. Soil Dyn. Earthq. Eng. 2020, 129, 105929. [Google Scholar] [CrossRef]
- Li, J.; Bao, T.; Ventura, C.E. A robust methodology for output-only modal identification of civil engineering structures. Eng. Struct. 2022, 270, 114764. [Google Scholar] [CrossRef]
- Zhou, K.; Li, Q.S.; Han, X.L. Modal identification of civil structures via stochastic subspace algorithm with Monte Carlo–based stabilization diagram. J. Struct. Eng. 2022, 148, 04022066. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Zhu, W.; Gu, X. Modal parameter identification of a quayside container crane based on data-driven stochastic subspace identification. J. Vib. Eng. Technol. 2021, 9, 919–938. [Google Scholar] [CrossRef]
- Reynders, E.P.B. Uncertainty quantification in data-driven stochastic subspace identification. Mech. Syst. Signal Process. 2021, 151, 107338. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Rahimian Koloor, S.S.; Petrů, M. A comparative study of the data-driven stochastic subspace methods for health monitoring of structures: A bridge case study. Appl. Sci. 2020, 10, 3132. [Google Scholar] [CrossRef]
- Ren, W.X.; Zong, Z.H. Output-only modal parameter identification of civil engineering structures. Struct. Eng. Mech. 2004, 17, 429–444. [Google Scholar] [CrossRef]
- Tran, T.T.X.; Ozer, E. Synergistic bridge modal analysis using frequency domain decomposition, observer Kalman filter identification, stochastic subspace identification, system realization using information matrix, and autoregressive exogenous model. Mech. Syst. Signal Process. 2021, 160, 107818. [Google Scholar] [CrossRef]
- Qu, C.X.; Yi, T.H.; Yao, X.J.; Li, H.N. Complex frequency identification using real modal shapes for a structure with proportional damping. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1322–1336. [Google Scholar] [CrossRef]
- O’Higgins, C.; Hester, D.; Ao, W.K.; McGetrick, P. A method to maximise the information obtained from low signal-to-noise acceleration data by optimising SSI-COV input parameters. J. Sound Vib. 2024, 571, 118101. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xia, Y. Parameters identification of closely spaced modes with the covariance-drivern stochastic subspace and damping ratio dispersion method. J. Vib. Control 2023, 10775463231197246. [Google Scholar] [CrossRef]
- Zini, G.; Giachetti, A.; Betti, M.; Bartoli, G. Vibration signature effects on damping identification of a RC bridge under ambient vibrations. Eng. Struct. 2024, 298, 116934. [Google Scholar] [CrossRef]
- Fu, S.; Wu, J.; Zhang, Q.; Xie, B. Automated identification and long-term tracking of modal parameters for a super high-rise building. J. Build. Eng. 2024, 95, 110141. [Google Scholar] [CrossRef]
- Zhou, K.; Xie, D.L.; Xu, K.; Zhi, L.-H.; Hu, F.; Shu, Z.-R. A machine learning-based stochastic subspace approach for operational modal analysis of civil structures. J. Build. Eng. 2023, 76, 107187. [Google Scholar] [CrossRef]
- Ditommaso, R.; Ponzo, F.C. Automatic evaluation of the fundamental frequency variations and related damping factor of reinforced concrete framed structures using the Short Time Impulse Response Function (STIRF). Eng. Struct. 2015, 82, 104–112. [Google Scholar] [CrossRef]
- Ditommaso, R.; Iacovino, C.; Auletta, G.; Parolai, S.; Ponzo, F.C. Damage detection and localization on real structures subjected to strong motion earthquakes using the curvature evolution method: The Navelli (Italy) case Study. Appl. Sci. 2021, 11, 6496. [Google Scholar] [CrossRef]
- Ditommaso, R.; Mucciarelli, M.; Ponzo, F.C. Analysis of non-stationary structural systems by using a band-variable filter. Bull. Earthq. Eng. 2012, 10, 895–911. [Google Scholar] [CrossRef]
- Ditommaso, R.; Ponzo, F.C.; Auletta, G. Damage detection on framed structures: Modal curvature evaluation using Stockwell Transform under seismic excitation. Earthq. Eng. Eng. Vib. 2015, 14, 265–274. [Google Scholar] [CrossRef]
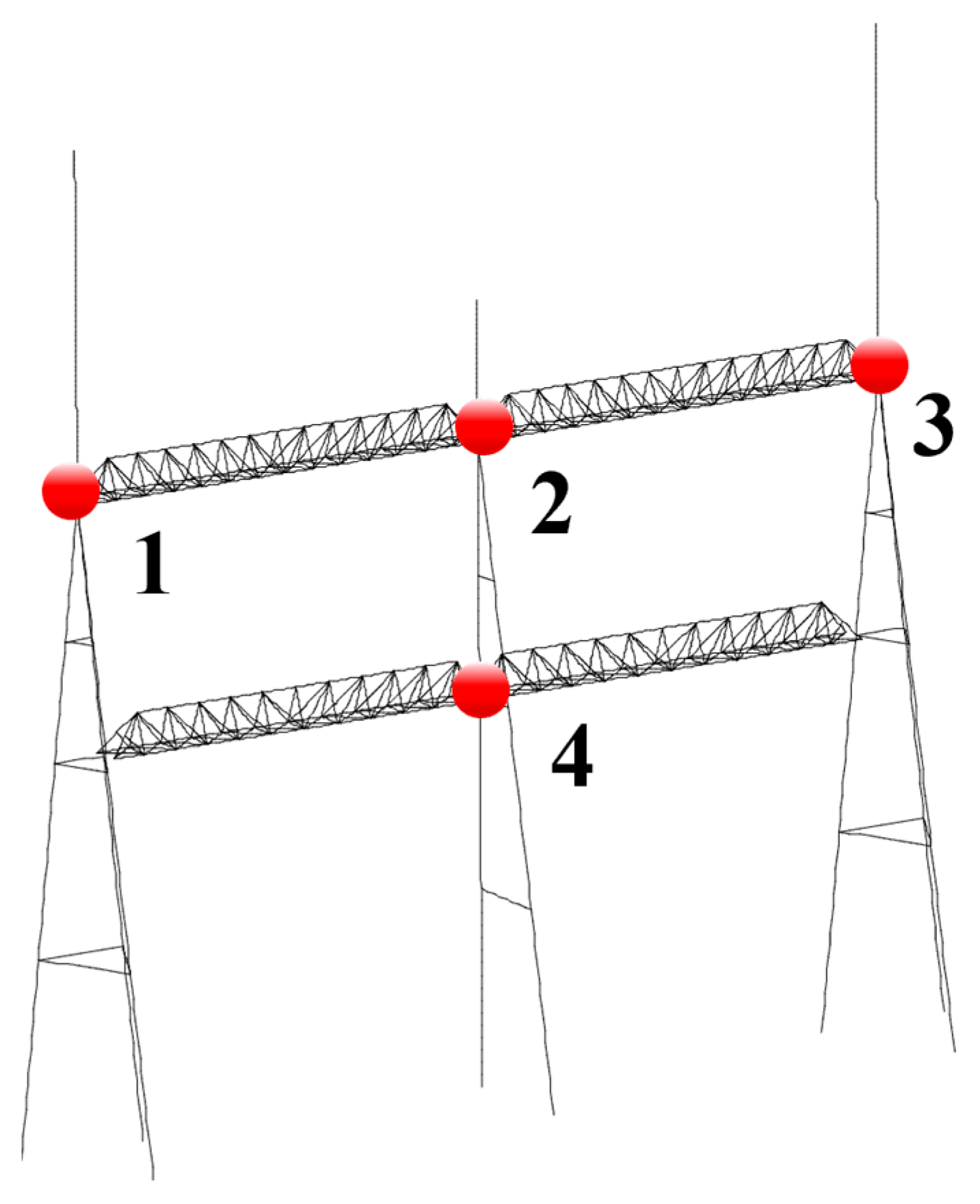


| Mode | Direction | Frequency (Hz) | Damping Ratio (%) | ||||
|---|---|---|---|---|---|---|---|
| MEMS | 941b | Discrepancy | MEMS | 941b | Discrepancy | ||
| 1 | 1st Torsional | 2.14 | 2.15 | 0.01 | 0.31 | 0.23 | 0.08 |
| 2 | 1st Vertical | 2.81 | 2.79 | 0.02 | 1.29 | 1.17 | 0.12 |
| 3 | 2nd Torsional | 3.05 | 3.06 | 0.01 | 0.46 | 0.33 | 0.13 |
| 4 | 1st Parallel | 4.78 | 4.79 | 0.01 | 0.15 | 0.12 | 0.03 |
| Mode | Direction | Frequency (Hz) | Damping Ratio (%) | ||||
|---|---|---|---|---|---|---|---|
| SSI | FDD | Discrepancy | SSI | FDD | Discrepancy | ||
| 1 | 1st Torsional | 2.14 | 2.15 | 0.01 | 0.31 | 0.43 | 0.12 |
| 2 | 1st Vertical | 2.81 | 2.79 | 0.02 | 1.29 | 0.88 | 0.41 |
| 3 | 2nd Torsional | 3.05 | 3.05 | 0 | 0.46 | 0.27 | 0.19 |
| 4 | 1st Parallel | 4.78 | 4.79 | 0.01 | 0.15 | 0.23 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, R.; Sheng, M.; Su, D.; Wang, Y.; Liu, X.; Sun, Q. MEMS-Based Vibration Acquisition for Modal Parameter Identification of Substation Frame. Appl. Sci. 2024, 14, 8190. https://doi.org/10.3390/app14188190
Qiang R, Sheng M, Su D, Wang Y, Liu X, Sun Q. MEMS-Based Vibration Acquisition for Modal Parameter Identification of Substation Frame. Applied Sciences. 2024; 14(18):8190. https://doi.org/10.3390/app14188190
Chicago/Turabian StyleQiang, Ruochen, Ming Sheng, Dongxu Su, Yachen Wang, Xianghong Liu, and Qing Sun. 2024. "MEMS-Based Vibration Acquisition for Modal Parameter Identification of Substation Frame" Applied Sciences 14, no. 18: 8190. https://doi.org/10.3390/app14188190
APA StyleQiang, R., Sheng, M., Su, D., Wang, Y., Liu, X., & Sun, Q. (2024). MEMS-Based Vibration Acquisition for Modal Parameter Identification of Substation Frame. Applied Sciences, 14(18), 8190. https://doi.org/10.3390/app14188190







