A Method to Estimate Dynamic Pore Water Pressure Growth of Saturated Sand-Gravel Materials

Abstract

The liquefaction of saturated sand-gravel material samples from the Xinjiang valley were investigated under cyclic loading. A series of large-scale dynamic triaxial tests were used to determine the dynamic characteristics of the sand-gravel sample under different confining pressures, consolidation stress ratios, and stress levels. A suitable pore water pressure growth model is proposed for the sand-gravel and sand materials. The number of cycles required to cause liquefaction was an important parameter in the dynamic pore water pressure growth model. A method to determine the number of cycles was proposed and verified by a large number of experimental data. The presentation of the pore water pressure simulation results demonstrates that the proposed pore water pressure growth model accurately characterizes the dynamic pore water pressure development in sand-gravel under cyclic loading and is also applicable to sand. The proposed pore water pressure growth model can be used to study the anti-liquefaction characteristics of foundation and dam materials of high earth-rock dams and high sand-gravel dams on deep overburdens.

1. Introduction

Soil liquefaction is a globally significant and typical seismic damage phenomenon that has become a prominent research topic in the field of soil dynamics and geotechnical earthquake engineering [1]. Sand-gravel materials are widely distributed in southwest and northwest China, which are also strong earthquake areas. Some high earth-rock dams are directly built on deep sand-gravel overburdens, and some dams are built with sand-gravel materials. The liquefaction properties of sand-gravel materials in these regions have drawn significant attention from researchers [2,3,4].

The study of sand liquefaction can be traced back to the 1930s, when Casagrand [5] first proposed the concept of critical void ratio and explained the liquefaction behavior of sand at the hand of the relationship between changes in the pore water pressure and the critical void ratio during the shear deformation of saturated loose sand. Seed [6] and Booker et al. [7] used the saturated sand isotropic consolidation cyclic triaxial test to establish the relationship between the dynamic pore water pressure and the number of load cycles. Finn et al. [8] modified Seed and Idriss’s pore water pressure stress model by considering the influence of initial anisotropic consolidation on the dynamic pore water pressure. Xu [9] also proposed an anisotropic consolidation pore water pressure calculation model that considered the effect of the initial shear stress ratio on the liquefaction of saturated sand. Zhang [10] defined three types of pore water pressure growth processes in saturated sand: A (the convex type), B (the concave–convex change microminiature), and C (the concave type). They also proposed corresponding calculation models for different dynamic pore water pressure growth processes. Apart from the above stress models, the pore water pressure model also includes a strain model [11], a transient model [12], an energy model [12,13], an endochronic theory model [14], and an effective stress path model [15].

Table 1. Common pore water pressure growth models.

Pore Water Pressure Model	Equation	Explanation	Reference
Stress model	${\displaystyle \frac{u_{\mathrm{d}}}{{\sigma }_{3\mathrm{c}}}}={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{\mathsf{\pi }}}\arcsin \left[2{\left({\displaystyle \frac{N}{N_{\mathrm{L}}}}\right)}^{{\displaystyle \frac{1}{\theta }}}-1\right]$	$u_{\mathrm{d}}$ is the dynamic pore water pressure; ${\sigma }_{3\mathrm{c}}$ is the initial confining pressure; $N_{\mathrm{L}}$ is the number of cycles required to cause liquefaction; $\theta$ is the experimental constant related to the type of material.	Seed [6]
Strain model	$\left\{\begin{array}{l}\Delta u={\overline{E}}_r\Delta {\epsilon }_{vd}\\ \Delta {\epsilon }_{vd}=c_1\left(\gamma -c_2{\epsilon }_{vd}\right)+{\displaystyle \frac{c_3{\epsilon }_{vd}^2}{\gamma +c_4{\epsilon }_{vd}}}\end{array}\right.$	${\overline{E}}_r$ is the tangent modulus of the one-dimensional unloading curve at a point corresponding to the initial vertical effective stress; $c_1,c_2,c_3,c_4$ are test constants.	Martin et al. [11]
Transient model	$\begin{array}{l}u(t+\Delta t)=u(t)+\Delta u\\ =u(t)+\Delta u_{\sigma }+\Delta u_0+\Delta u_{\mathrm{T}}\\ =u(t+\Delta t)*+\Delta u_{\mathrm{T}}\end{array}$	$\Delta u_{\sigma },\Delta u_0,\Delta u_{\mathrm{T}}$ are increments of the pore water pressure during $\Delta T$; $u{(t+\Delta t)}^{*}$ is the pore water pressure without dissipation at $(t+\Delta t)$; $u(t+\Delta t)$ is the dissipation pore water pressure at $(t+\Delta t)$.	Xie [12]
Energy model	$\left\{\begin{array}{l}{\displaystyle \frac{u}{{\sigma }_0}}=K{W}_R^{\beta }\\ W_R=\left[1-\lg \left(K_c^3\right)\right]W_0\\ W_0={\displaystyle \frac{{\displaystyle \sum W}}{{\sigma }_0}}\end{array}\right.$	${\displaystyle \sum W}$ is the dissipated energy; $K$ and $\beta$ are test constants.	Cao et al. [13]
Endochronic theory	${\displaystyle \frac{u_d}{{\sigma }_v^{\prime }}}={\displaystyle \frac{A}{B}}\ln (1+Bk)$	K is the damage parameter; the variable includes the shear strain amplitude and number of cycles. A and B are test parameters.	Finn [14]
Effective stress path model	$\left\{\begin{array}{l}q/p^{\prime }\ge {\left(q/p^{\prime }\right)}_{\max },\mathrm{loading}\\ q/p^{\prime }<{\left(q/p^{\prime }\right)}_{\max },\mathrm{unloading}\end{array}\right.$	Under loading conditions, additional plastic shear deformation occurs in the soil. The variation of pore water pressure is equal to the variation of the mean effective stress.	Ishihara [15]

lists the commonly used pore water pressure growth models.

Traditional research on soil dynamic liquefaction mainly focused on saturated sand and silt materials [1,16,17,18,19], and less on sand-gravel materials. It is generally believed that sand-gravel materials with coarser grain sizes are less likely to liquefy [20]. Some research [21,22,23,24] has, however, shown that saturated sand-gravel materials will also liquefy under cyclic loading. In 2008, a magnitude 8.0 earthquake caused a large liquefaction area in Wenchuan, Sichuan. The gravel liquefaction area covered as much as 85% of the total liquefaction area [2,3,25]. After the Wenchuan earthquake, some scholars began to research the liquefaction characteristics of sand-gravel materials. Xu [26] used Seed’s pore water pressure model to propose a pore water pressure curve fitting model for sand-gravel materials. This model used the symmetry characteristics of the sand-gravel material relationship curve between the pore pressure ratio and the cyclic number ratio. Zhang [27] found that the normalized pore water pressure growth curve was close to the hyperbolic curve and proposed a hyperbolic pore water pressure growth model. In studying the dynamic pore water pressure model of sand-gravel materials, two problems must still be solved. First, the method for determining liquefaction N_L for most pore water pressure models is not standardized, even though most use the number of cycles required to cause liquefaction N_L to normalize the cyclic loading numbers N. Secondly, compared with sand, there is not sufficient liquefaction test data on sand-gravel materials, and the pore water pressure growth model needs to be further verified. Studying the liquefaction characteristics of sand-gravel materials is, therefore, necessary to provide a basis for the analysis of the liquefaction resistance of dam foundations and dam bodies.

This paper used the GCTS large-scale dynamic triaxial apparatus to carry out a series of undrained cyclic triaxial tests on sand-gravel materials at different initial confining pressures ${\sigma }_{3\mathrm{c}}$ and consolidation stress ratios $K_{\mathrm{c}}$. The paper proposes a method for determining the number of cycles required to cause liquefaction N_L that considers the relative density $D_{\mathrm{r}}$. The pore water pressure growth model of saturated sand-gravel materials was established and its applicability was verified.

The main research objectives of this paper are as follows: (1) To enrich the experimental data on sand-gravel material liquefaction, a series of undrained cyclic triaxial tests were conducted on sand-gravel materials using a GCTS large-scale dynamic triaxial apparatus under varying initial confining pressures and consolidation stress ratios. (2) To propose a method for determining the number of cycles required to cause liquefaction that considers relative density. (3) To establish a pore water pressure growth model for saturated sand-gravel materials and verify its applicability.

The remainder of this paper is organized as follows: Section 2 presents an overview of the test design. Section 3 details the experimental data. Section 4 discusses the estimation model for N_L. Section 5 introduces the pore water pressure growth model for saturated sand-gravel materials. Section 6 provides the conclusions.

2. Test Design

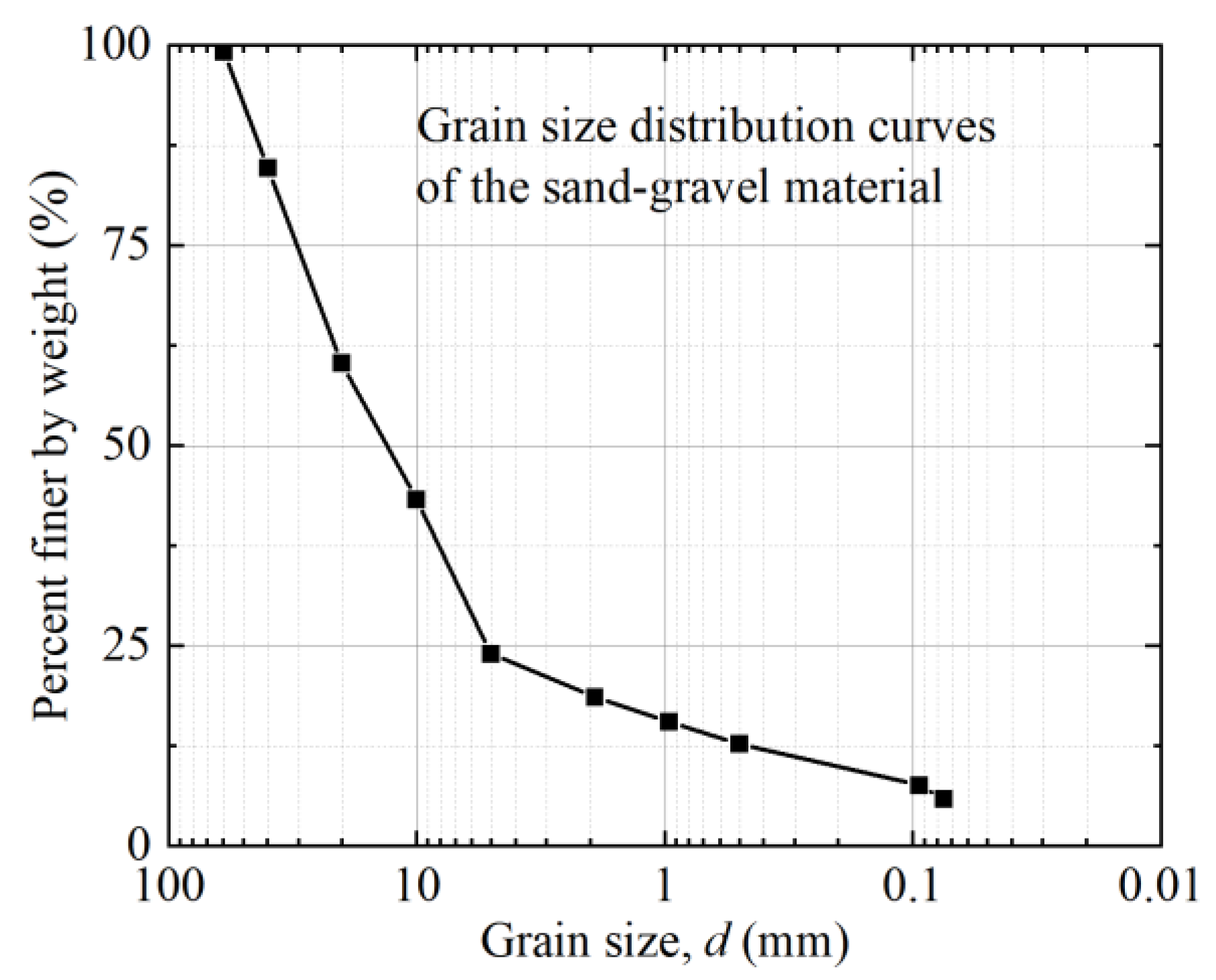
2.1. Test Apparatus and Sample Preparation

The sand-gravel material, which is composed of limestone and was used in the test, originates from a valley in Xinjiang. These materials are rounded and exhibit some degree of cementation, as shown in Figure 1. This study tested a series of sand-gravel materials under undrained conditions through cyclic triaxial tests conducted with the GCTS Instruments large-scale dynamic triaxial apparatus, as illustrated in Figure 2. The test sample diameter D is 300 mm and the height H is 700 mm. For this experiment, the sand-gravel material was prepared using the equivalent substitution method to achieve the desired gradation, with a maximum allowable particle size of 60 mm. The grain size distribution is shown in Figure 3 and the basic physical properties of the prepared material are shown in

Table 2. Physical properties of tested sand-gravel materials.

Sand-Gravel Materials in Xinjiang	Mean Grain Size d50/mm	Specific Gravity Gs	Minimum Dry Density ρmin/g·cm−3	Maximum Dry Density ρmax/g·cm−3	Relative Density Dr	Dry Density ρd/g·cm−3
	14	2.75	1.85	2.34	0.9	2.28

. The sample preparation was divided into five layers and is based on the surface vibration method.

The water head method was used to saturate the specimen. In this method, the water slowly infiltrates from the bottom of the specimen until the water at the top of the specimen seeps out. First, the inlet valve was opened, and 35 kPa lateral pressure was applied to the sample. Thereafter, lateral pressure and axial pressure were applied in a stepwise fashion until the lateral pressure and axial pressure reached the predetermined consolidation stress ratio of each test. The drain valve was then opened to drain and consolidate the sample, after which the drain valve was closed when the sample was consolidated. When the seeped water is stable and no bubbles are generated, the saturation of the specimen is deemed to exceed 95%, which meets the test requirements.

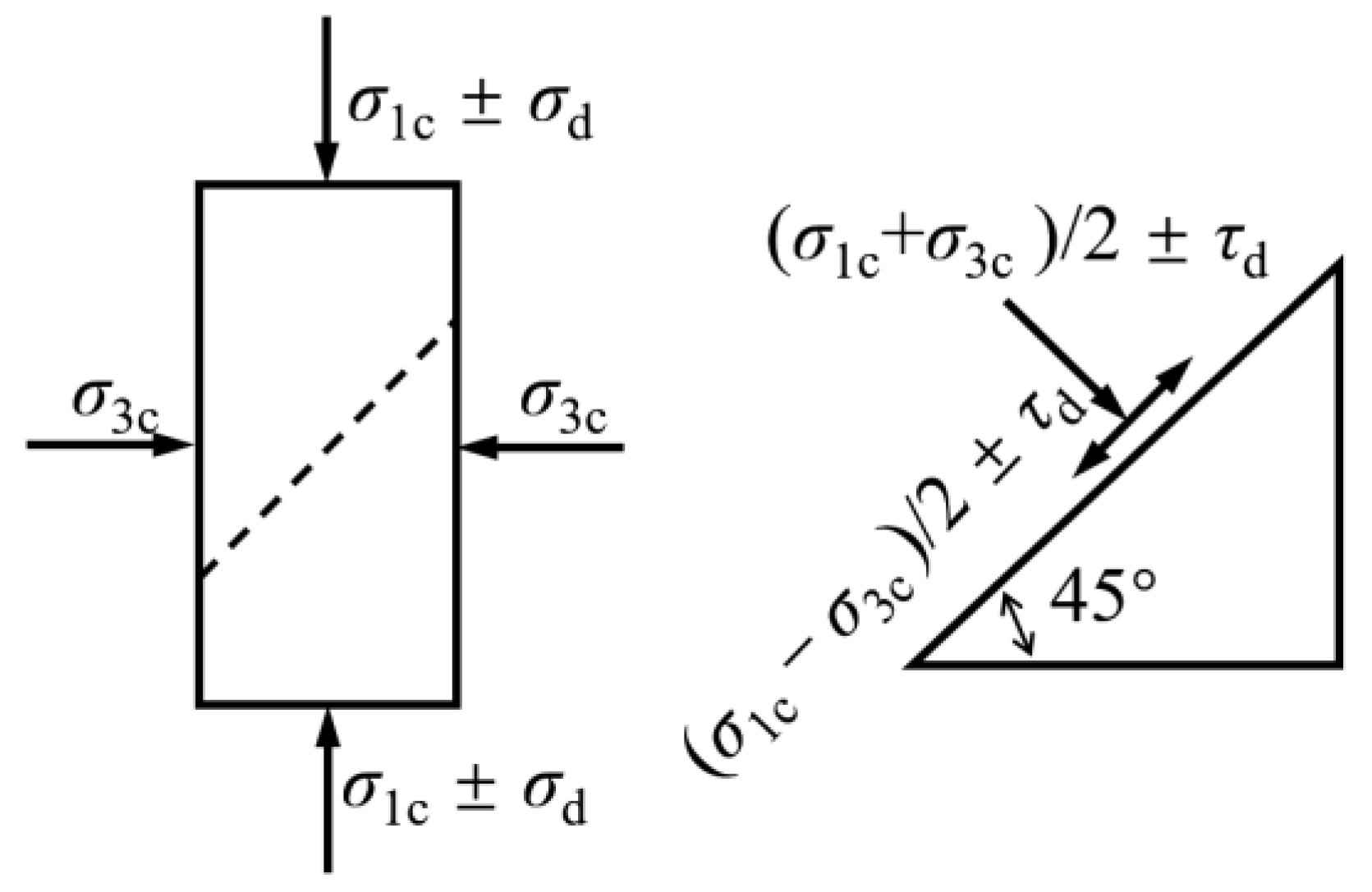
2.2. Test Conditions

For this study, sand-gravel materials with a relative density D_r of 0.9 were consolidated under pressures of 50, 100, 200, and 300 kPa. A sine wave with a loading frequency of 0.33 Hz was employed to apply dynamic stress through vibration until failure occurred. Failure was defined as either an axial strain of 5% or excess pore water pressure reaching the confining pressure. This was performed to study the dynamic characteristics of the sand-gravel materials under different initial effective confining pressures ${\sigma }_{3\mathrm{c}}$, consolidation stress ratios $K_{\mathrm{c}}$, and stress levels.

Table 3. Summary of test schemes.

Test Number	Kc	σ3c (kPa)	σd (kPa)	$\mathbf{C}\mathbf{S}\mathbf{R}$
S1	1.5	50	70.50	0.56
S2		100	142.90	0.57
S3			121.25	0.49
S4		200	291.45	0.58
S5			245.25	0.49
S6			227.65	0.46
S7		300	438.45	0.58
S8			393.15	0.52
S9			346.30	0.46
S10	2.0	50	95.10	0.63
S11		100	190.95	0.64
S12			175.75	0.59
S13		200	387.65	0.65
S14			342.25	0.57
S15			296.75	0.49
S16		300	582.80	0.65
S17			519.35	0.58
S18			447.15	0.50

lists static and dynamic stress control conditions of this test. In dynamic triaxial tests, initial dynamic stress values are determined based on empirical experience. Once the samples meet the failure criteria, ${\sigma }_{\mathrm{d}}$ for each condition is recorded in Table 3. In general engineering practice, the minimum principal stress of dam materials is estimated based on the dam height, and the maximum experimental confining pressure is set to exceed this value. This research aims to investigate the dynamic pore pressure of sand-gravel materials under low confining pressures; therefore, confining pressures ${\sigma }_{3\mathrm{c}}$ are set at 50, 100, 200, and 300 kPa. Most natural soils are in an anisotropic consolidation state; thus, soil strength parameters derived from such conditions are more reflective of real-world scenarios. Accordingly, the consolidation stress ratios, $K_{\mathrm{c}}$, are set at 1.5 and 2.0.

Undrained cyclic triaxial tests were carried out under different cyclic stress ratios (CSRs) after consolidation. The CSR is the ratio of the dynamic shear stress on the 45° slope of the triaxial specimen to its initial normal stress; the formulas are as follows:

$$\left\{\begin{array}{l}{K}_{\mathrm{c}}={\displaystyle \frac{{\sigma }_{1\mathrm{c}}}{{\sigma }_{3\mathrm{c}}}}\begin{array}{l}\\ \end{array}\\ {\sigma }_0^{\prime }={\displaystyle \frac{1+K_{\mathrm{c}}}{2}}{\sigma }_{3\mathrm{c}}\\ {\tau }_{\mathrm{d}}={\displaystyle \frac{{\sigma }_{\mathrm{d}}}{2}}\\ \mathrm{CSR}={\displaystyle \frac{{\tau }_{\mathrm{d}}}{{\sigma }_0^{\prime }}}={\displaystyle \frac{{\sigma }_{\mathrm{d}}}{\left(1+K_{\mathrm{c}}\right){\sigma }_{3\mathrm{c}}}}\end{array}\right.$$

(1)

where ${\sigma }_{1\mathrm{c}}$ is axial stress, ${\sigma }_{3\mathrm{c}}$ is the initial effective confining pressure, $K_{\mathrm{c}}$ is the initial consolidation stress ratio, ${\sigma }_0^{\prime }$ is the initial normal stress, ${\tau }_{\mathrm{d}}$ represents the dynamic shear stress, ${\sigma }_{\mathrm{d}}$ is the axial cyclic stress, and CSR is cyclic stress ratio.

During the test, the sample is consolidated under the stresses ${\sigma }_{1\mathrm{c}}$ and ${\sigma }_{3\mathrm{c}}$. At this point, the initial normal stress, ${\sigma }_0^{\prime }$, on the sample’s 45° slope is $({\sigma }_{1\mathrm{c}}+{\sigma }_{3\mathrm{c}})/2$, and the initial shear stress is $({\sigma }_{1\mathrm{c}}-{\sigma }_{3\mathrm{c}})/2$. Subsequently, under undrained conditions, $\pm {\sigma }_{\mathrm{d}}$ is applied, resulting in an additional dynamic shear stress and normal stress of ${\sigma }_{\mathrm{d}}/2$ on the 45° slope. The stress state of the sample during vibration is illustrated in Figure 4.

3. Analysis of Dynamic Triaxial Test Results of Saturated Sand-Gravel Material

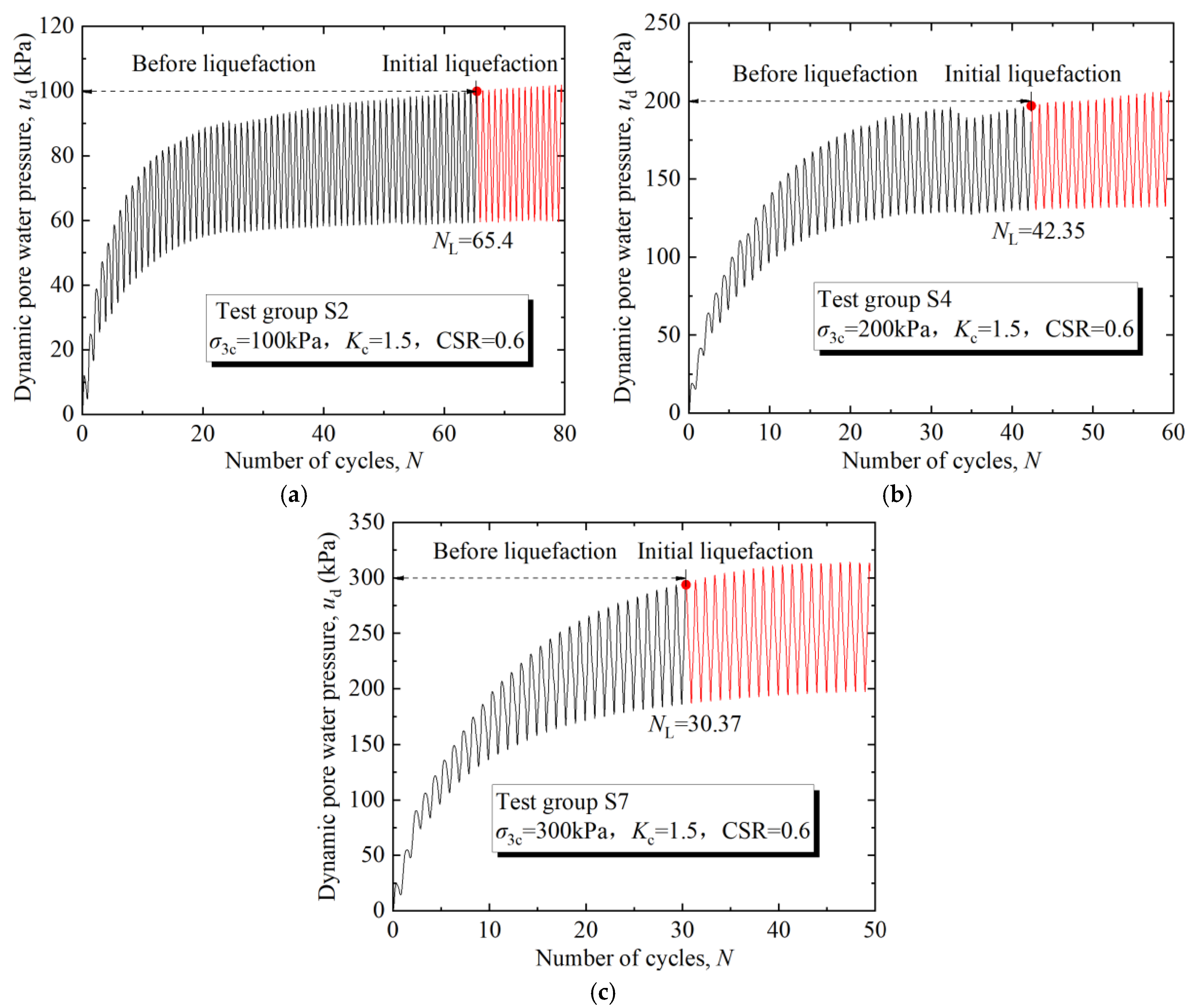
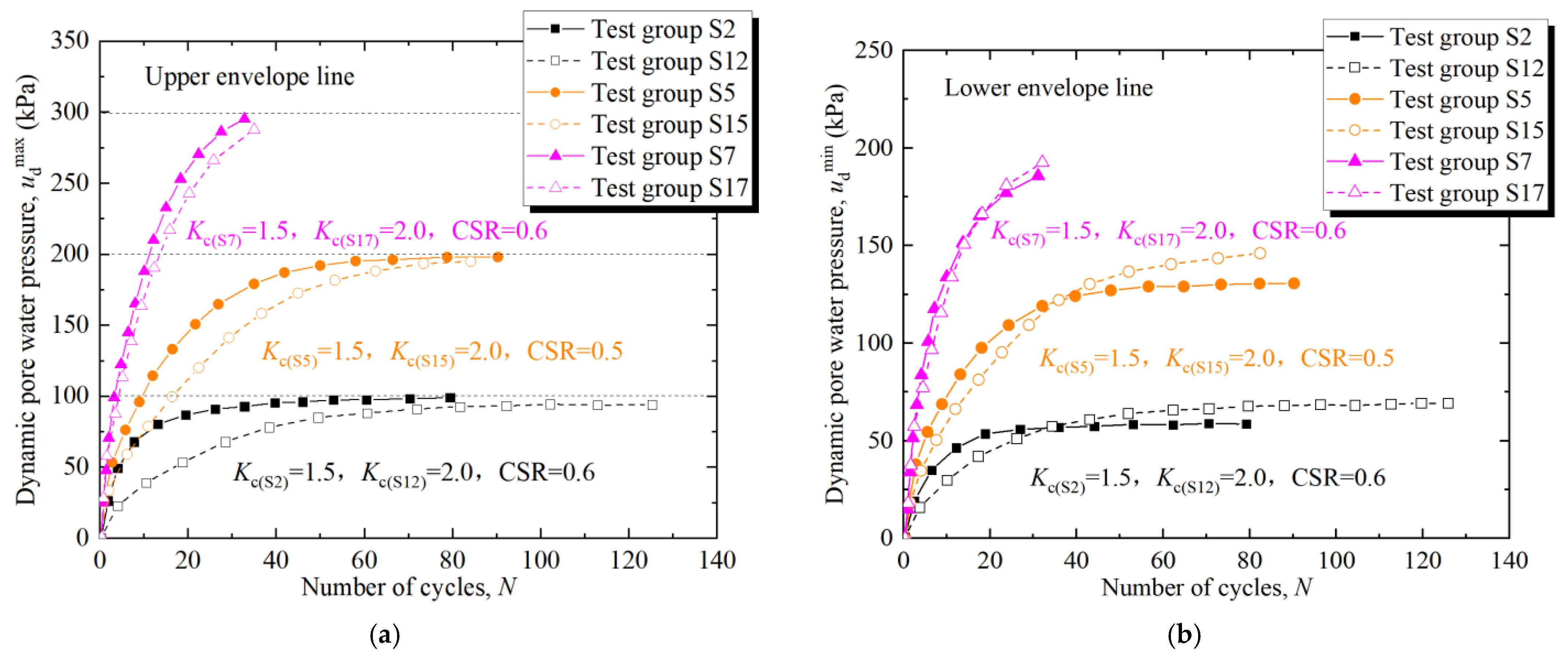
3.1. Dynamic Pore Water Pressure Curve

The dynamic pore water pressure of saturated sand-gravel material increased and periodically fluctuated with periodic increases in the cyclic loading. At the initial stages of increased loading, the dynamic pore water pressure fluctuated slightly but thereafter rose steadily. With an increase in the cyclic numbers, the amplitude of the dynamic pore water pressure increased, but in general, the growth rate of the pore water pressure seemed to decrease. The dynamic pore water pressure of the saturated sand-gravel material was close to the initial effective confining pressure after reaching a certain level of loading. This level of loading was determined by the initial liquefaction of the soil, as illustrated in Figure 5. The black and red lines represent the dynamic pore water pressure of the sand-gravel material prior to and following initial liquefaction, respectively. The number of cycles required for initial liquefaction in each test (S1 to S18) and the excess pore water pressure at 5% axial strain are presented in

Table 4. The results for the $N_{\mathrm{L}}$ and $u_{\mathrm{d}}$ tests on saturated sand-gravel materials.

Test Number	Kc	σ3c (kPa)	ud (kPa)	NL
S1	1.5	50	49.93	174.4
S2		100	99.95	65.4
S3			100.01	147.5
S4		200	197.1	42.35
S5			198.54	74.3
S6			199.79	153.3
S7		300	295.87	30.37
S8			298.07	43.35
S9			299.94	84.3
S10	2.0	50	49.24	145.3
S11		100	95.3	44.3
S12			95.06	105.25
S13		200	187.77	23.3
S14			193.42	35.25
S15			195.93	78.25
S16		300	280.62	18.25
S17			282.71	32.2
S18			281.03	73.2

.

Shamoto Y et al. [28] and Zhang [29] explained pore water pressure growth in saturated sand. The volumetric strain of saturated sand is composed of a volumetric strain ${\epsilon }_{vc}$ due to a change in the mean effective principal stress, and a volumetric strain ${\epsilon }_{vd}$ caused by shear stress. The soil grains are broken during the shearing process so that the mean porosity decreases and the large pores disappear. This changes the soil’s irreversible dilatancy component ${\epsilon }_{vd,ir}$. The slip and dislocation between the soil grains also cause a change in the soil’s reversible dilatancy component ${\epsilon }_{vd,re}$. To meet the volume consistency conditions, ${\epsilon }_{vc}$ must correspondingly change, which causes the effective mean principal stress to change and cause excess pore water pressure. The monotonic increase ${\epsilon }_{vd,ir}$ causes a monotonic increase in the irreversible dynamic pore water pressure and the generation and dissipation of ${\epsilon }_{vd,re}$ causes a fluctuation in the reversible dynamic pore water pressure. The grain size distribution of the sand-gravel material is wider than sand and has larger pores between the soil grains. Slip and dislocation are, therefore, more likely to occur between the gravel and the fine sand materials, causing a monotonic increase in the pore water pressure and larger amplitudinal increases in the dynamic pore water pressure during cyclic loading of the saturated sand-gravel.

Figure 6 shows the upper and lower envelope lines of the pore water pressure growth in the saturated sand-gravel. The sample achieves a smaller maximum pore water pressure at the same number of cycles due to the larger consolidation stress ratio before cyclic loading. This happens because the saturated sand-gravel becomes denser under the larger consolidation stress ratio, and the volume shrinkage of the soil during the shear stress is small while the volume expansion is large, which to a certain extent inhibits the accumulation of pore water pressure.

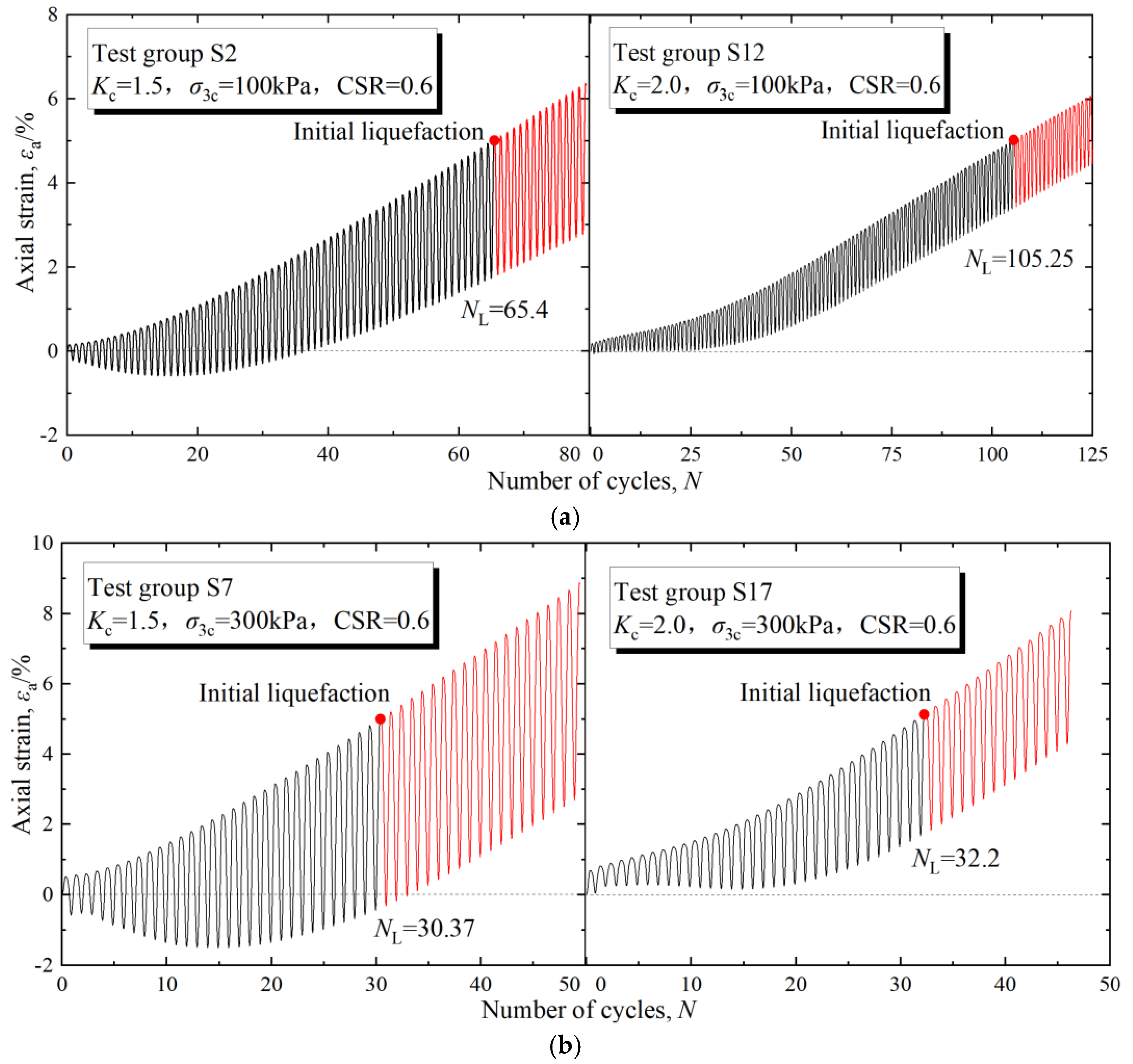
3.2. Relationship between the Strain and the Cyclic Numbers

The dislocation and slip between the saturated grains of sand and gravel generate an axial strain after cyclic loading, which increases and changes with the periodic change in the loading. The amplitude of the axial strain is small during the initial stages of loading but increases gradually with an increase in the number of dynamic cycles. This is because the pore water pressure accumulates during the dynamic loading process, which reduces the mean effective stress of the sample and reduces the dynamic shear modulus of the material. The dynamic strain of the material, therefore, increases accordingly under the same cyclic loading conditions. Under the same confining pressure and cyclic stress conditions, samples with a higher initial consolidation stress ratio and a smaller dynamic strain amplitude experience less pore water pressure growth when the consolidation stress is relatively high. The deviatoric consolidation also causes a significant axial residual deformation of the soil sample, as shown in Figure 7. The black and red lines denote the axial strain of the sand-gravel material before and after reaching initial liquefaction, respectively.

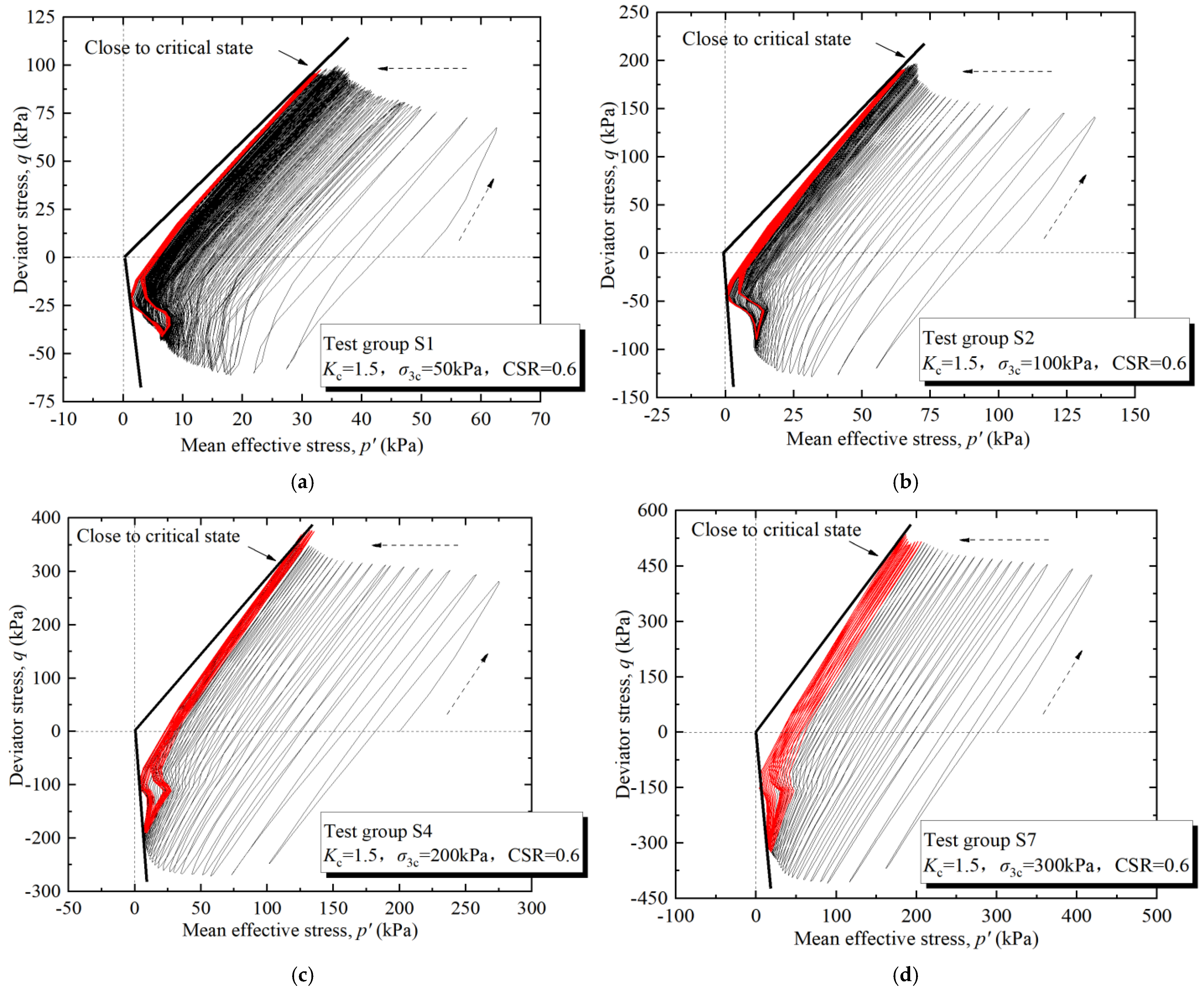
3.3. Effective Stress Path

Studying the stress paths of sand-gravel material liquefaction allows for an understanding of the developmental process of saturated sand-gravel materials. The parameters in Figure 8 are as follows:

$$p^{\prime }=({\sigma }_1^{\prime }+2{\sigma }_{3\mathrm{c}})/3;\hspace{1em}q=({\sigma }_1^{\prime }-{\sigma }_{3\mathrm{c}})/2$$

(2)

where $p^{\prime }$ represents the mean effective stress, $q$ represents the deviator stress, ${\sigma }_1^{\prime }$ is the effective axial stress, and ${\sigma }_{3\mathrm{c}}$ is the initial effective confining pressure.

Figure 8 shows the effective stress path of sand-gravel material as the number of loading cycles increases. The arrows illustrate the direction of development for the mean effective stress path of the sand-gravel materials, while the red line shows the final 10 cycles of the p′-q curve as it approaches the critical state. Cyclic loading causes a dense and undrained soil sample, which in turn causes an increase in the pore water pressure and a decrease in mean effective stress. There is, however, a stage during which the mean effective stress increases during each stress cycle. This is due to the volume shrinkage and expansion of the dense sand-gravel material that occurs during the cyclic loading process. The pore water pressure tends to be stable during the later stages of dynamic loading. The effective stress path of the next loading cycle is close to the previous cycle path, while the effective stress paths tend to overlap.

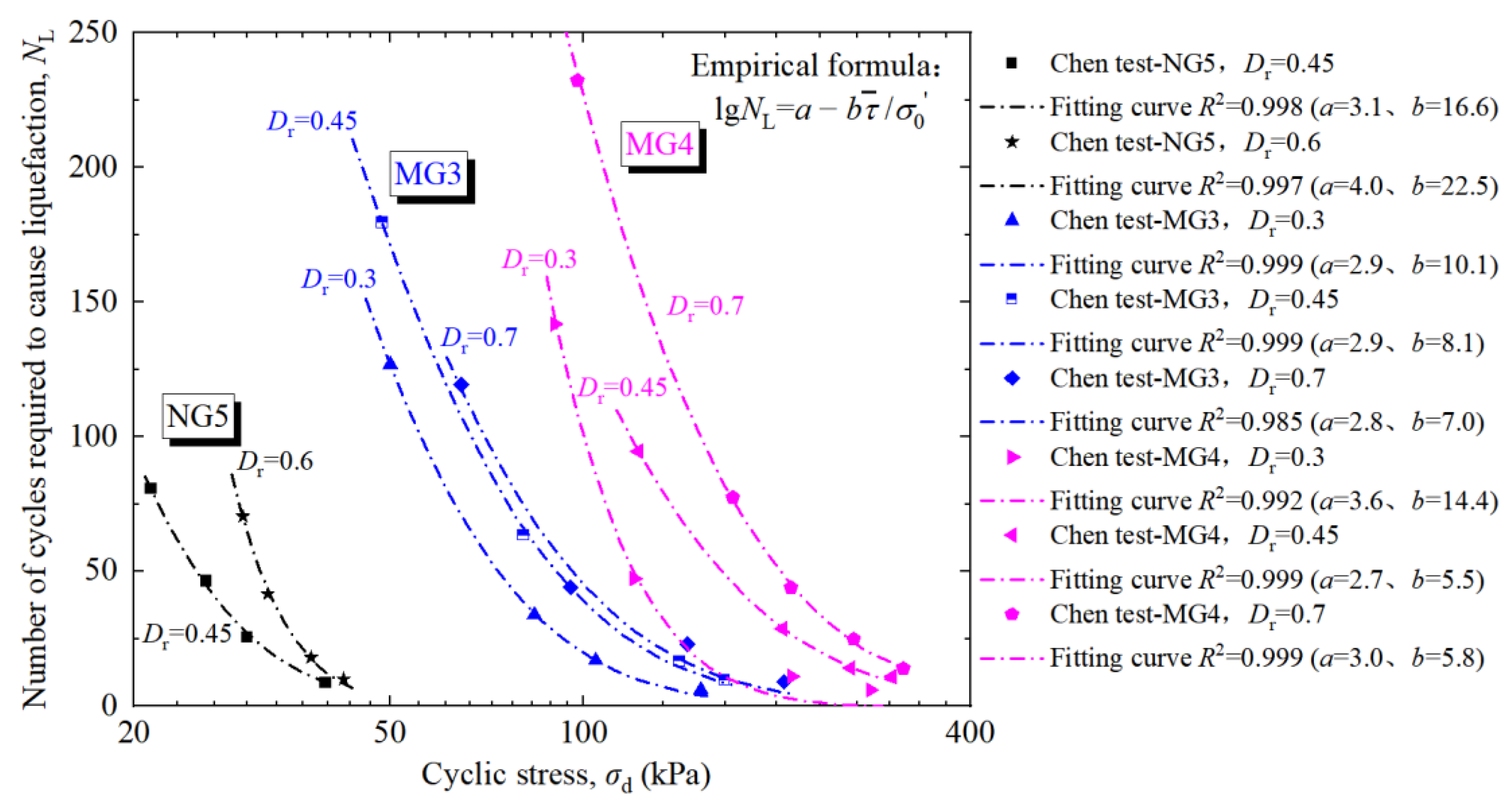
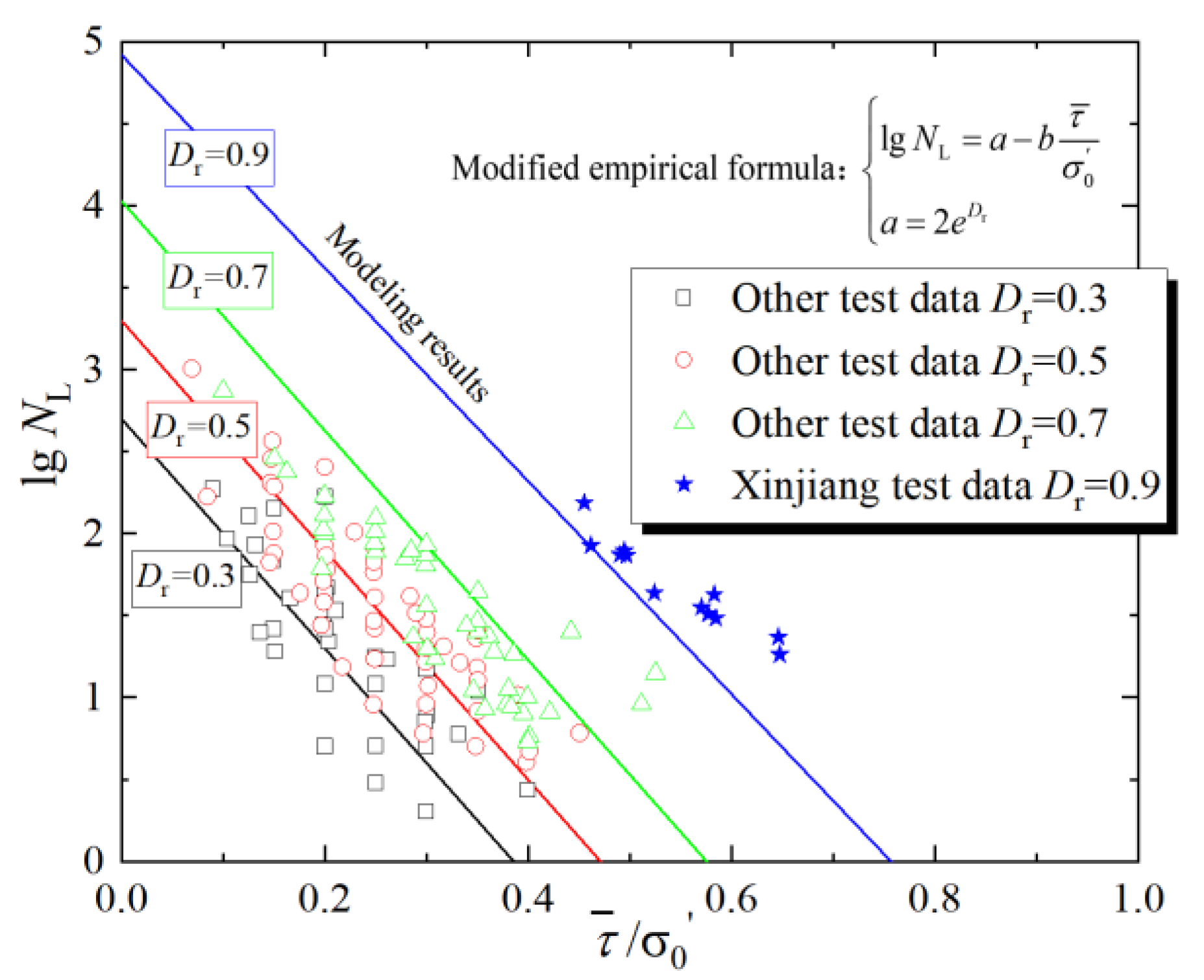
4. The Estimation Model of the Number of Cycles Required to Reach Liquefaction, N_L

4.1. The Verification of N_L

N_L is the number of cycles required to reach liquefaction. N_L is mostly obtained from the liquefaction test curve or empirical formula, such as that proposed by Xu [30]:

$$N_{\mathrm{L}}={10}^{a-b{\displaystyle \frac{{\tau }_{\mathrm{d}}}{{\sigma }_0^{\prime }}}};\hspace{1em}\lg N_{\mathrm{L}}=a-b{\displaystyle \frac{{\tau }_{\mathrm{d}}}{{\sigma }_0^{\prime }}}=a-b{\displaystyle \frac{{\sigma }_{\mathrm{d}}}{\left(1+K_{\mathrm{c}}\right){\sigma }_{3\mathrm{c}}}}$$

(3)

where $a$ and $b$ are constants, ${\tau }_{\mathrm{d}}$ is dynamic shear stress, ${\sigma }_0^{\prime }$ is the initial normal stress on the 45° slope of the sample, ${\sigma }_{3\mathrm{c}}$ is the initial effective confining pressure, ${\sigma }_{\mathrm{d}}$ is the axial cyclic stress, and $K_{\mathrm{c}}$ is the initial consolidation stress ratio. The least squares method was employed to fit the experimental data, resulting in the values of a and b. Under different conditions of $K_{\mathrm{c}}$ and ${\sigma }_{3\mathrm{c}}$, one relationship between N_L and ${\sigma }_{\mathrm{d}}$ can be established. It has been widely used in the field of engineering practice [30,31,32,33]. Figure 9 verifies the accuracy of the empirical formula by using the Chen et al. [34] test data. This empirical formula provides the relationship curves of the different groups of test materials, and the goodness of fit is greater than 0.99. This formula can, however, not consider the influence of other factors, such as relative density, on the cyclic numbers required to reach liquefaction. The number of cycles required to cause liquefaction is often related to various factors such as the soil’s relative density, porosity, consolidation ratio, and initial effective consolidation stress. Therefore, this empirical formula must be corrected to consider these factors.

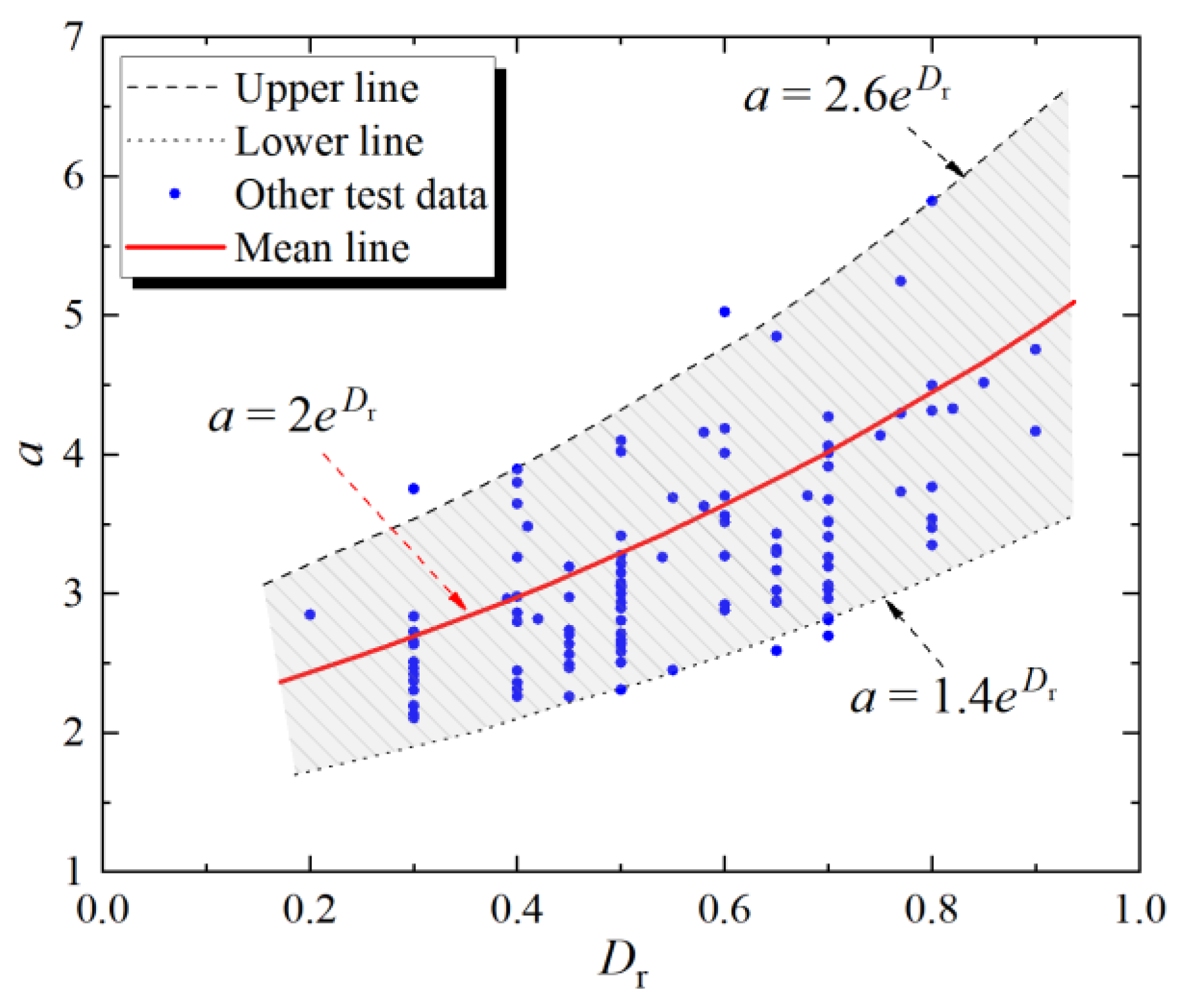
4.2. The Modification of N_L

Factors such as the relative density, porosity, consolidation ratio, and initial effective consolidation stress all affect the N_L. The influence of the relative density on the dynamic strength of soil is clear, in that the dynamic strength of the material increases with an increase in the relative density [35]. The empirical formula proposed by Xu [30] reflects the liquefaction of materials when the dynamic stress is near zero. At extremely small amplitudes, the value of a is associated with the relative density of the material and the number of cycles required to induce liquefaction. The larger the relative density, the larger the a value and the number of cycles required to cause liquefaction. Based on the relationship between a and D_r [19,27,34,36,37,38,39,40,41,42,43,44,45,46,47], the a value is distributed within a curve band. This implies that the mean curve of the relationship between a and D_r can be calculated, as depicted in Figure 10.

The relative density is selected as the parameter of interest in the N_L estimation model so that the empirical formula of Xu [30] can be modified by the relationship between the a value and the D_r mean curve. The expressions are given by the following:

$$\left\{\begin{array}{l}\lg N_{\mathrm{L}}=a-b{\displaystyle \frac{\overline{\tau }}{{\sigma }_0^{\prime }}}\\ a=2e^{D_{\mathrm{r}}}\end{array}\right.$$

(4)

where N_L is the number of cycles required to reach liquefaction, a is related to the relative density of the test material, b is the empirical constant, $\overline{\tau }$ is the mean shear stress, ${\sigma }_0^{\prime }$ is the initial normal stress on the 45° slope of the sample, and D_r is the relative density.

The linear relationship between $\lg N_{\mathrm{L}}$ and $\overline{\tau }/{\sigma }_0^{\prime }$ is established by collecting the test data [27,34,37,38,39,43,48]. Figure 11 shows the dynamic triaxial test results of the Xinjiang sand-gravel material. The test value is slightly higher than the simulation result of the modified empirical formula because the initial consolidation ratio of this test is set to 1.5 or 2.0 and isobaric consolidation is not considered. This difference is, however, still within an acceptable range. The relationship between $\lg N_{\mathrm{L}}$ and $\overline{\tau }/{{\sigma }^{\prime }}_0$ for different relative densities that were obtained by the modified empirical formula shows that the larger the relative density is, the larger the intercept of the function line. This means that small dynamic loading requires more cycles to cause liquefaction of the sample.

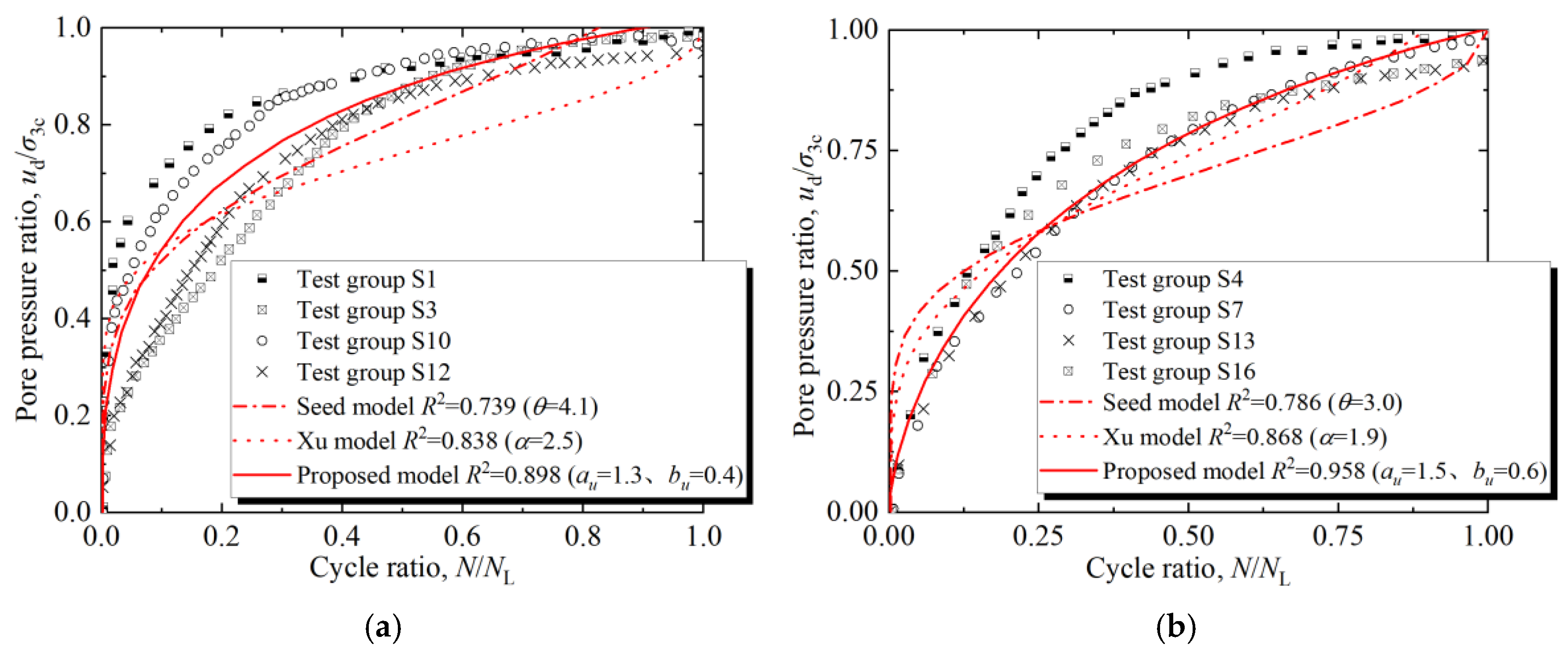
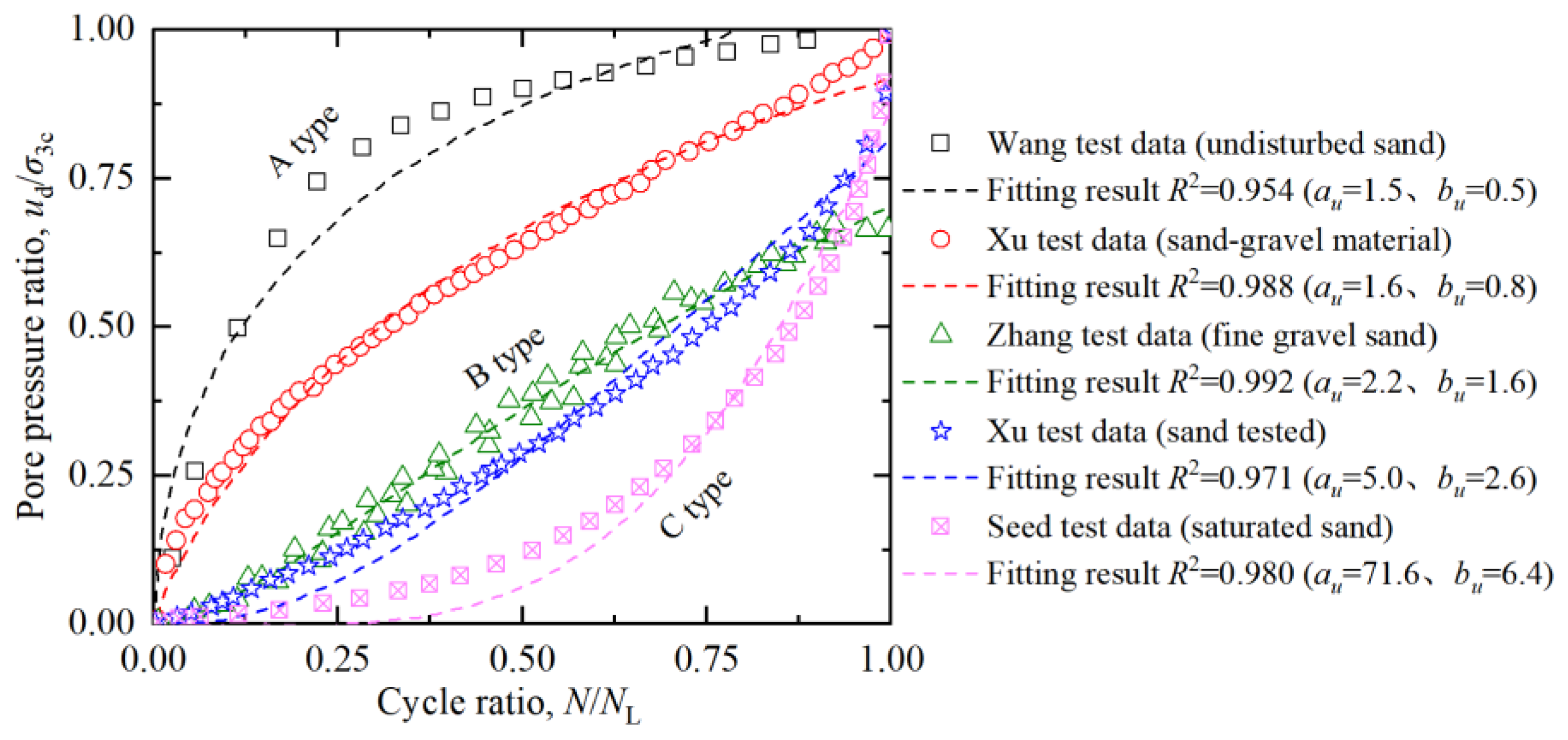
5. Estimation of the Dynamic Pore Water Pressure of the Saturated Sand-Gravel Material

The sand-gravel material dynamic pore pressure growth conforms to the hyperbolic form seen in Figure 5. The modification of the hyperbolic pore pressure model in this paper can be given by the following Equation (5):

$${\displaystyle \frac{u_{\mathrm{d}}}{{\sigma }_{3\mathrm{c}}}}=a_u{\left({\displaystyle \frac{\frac{N}{N_{\mathrm{L}}}}{1+\frac{N}{N_{\mathrm{L}}}}}\right)}^{b_u}$$

(5)

where a_u and b_u are test constants related to the soil properties, $u_{\mathrm{d}}$ refers to excess pore water pressure, ${\sigma }_{3\mathrm{c}}$ is the initial effective confining pressure, N is the number of dynamic cycles, and N_L is the number of cycles required to reach liquefaction. In practical engineering, when the axial strain reaches a certain value, the soil can be judged to be liquefied. Therefore, a_u and b_u are identified as independent parameters in this paper.

The changes in the dynamic pore water pressure and the corresponding fitting curve of Equation (5) for the eight groups of Xinjiang sand-gravel tests are shown in Figure 12. The fitting curves of the Seed [6] pore water pressure model and the Xu [30] pore water pressure model are also shown in Figure 12 for comparison. Under low initial confining pressure conditions, the pore water pressure in the sample increases rapidly during the initial stages of dynamic loading. At lower initial confining pressures, the pore water pressure changes to conform more readily to Equation (5). The initial confining pressure inhibits the accumulation of pore water pressure to a degree. The fitting curves of the Seed and Idriss (1971) [6] and the Xu and Shen (1983) [30] models both overestimate the growth rate of the pore water pressure during the early stages of dynamic loading but underestimate the dynamic pore pressure in the middle and late stages. Therefore, the Seed and Idriss (1971) [6] and the Xu and Shen (1983) [30] pore water pressure models may provide a dangerous pore water pressure prediction result. In contrast, the pore water pressure model proposed in this paper fits most of the test results well.

The results of the sand-gravel and the sand dynamic tests conducted by several researchers [26,27,42,49] and the fitting curves obtained by using the pore water pressure model proposed in this paper are shown in Figure 13. The pore pressure growth model in Figure 13 covers the three forms of pore pressure growth defined by Zhang [10]. The goodness of fit $R^2$ of the pore pressure model proposed in this paper for different test pore pressure ratio curves is greater than 0.95. This means that the pore pressure model proposed in this paper is not only suitable for simulating the dynamic pore pressure growth in sand-gravel materials but is also suitable for sandy materials and that it can simulate three different pore pressure growth modes.

6. Conclusions

This paper investigated the different factors that influence liquefaction using the large-scale dynamic triaxial test on a sand-gravel material from the Xinjiang valley, China. The liquefaction characteristics of saturated sand-gravel materials are similar to those of sand. Our proposed pore water pressure growth model can be universally applied to both sand-gravel materials and sandy materials. We propose an evaluation method for the number of cycles required to reach liquefaction, which is the key parameter in the pore water pressure growth model. The main conclusions of this paper are as follows:

(1)

Dislocation and slip occur between the grains of the saturated sand-gravel material under cyclic loading. This causes both reversible and irreversible two-part volume strains, causing an increase in the periodic fluctuation of the dynamic pore water pressure. The increase in the dynamic pore water pressure is more obvious and the amplitude is larger due to the large pores between the sand-gravel materials. The dense saturated sand-gravel material with its large consolidation stress ratio shows a small volume shrinkage and a large volume expansion, where dilatancy can inhibit the increase in the pore water pressure in the sand-gravel.

(2)

During cyclic loading, volume expansion or shrinkage occurs alternately in the saturated sand-gravel material. The mean effective stress of the sand-gravel material decreases, causing the dynamic shear modulus of the material to decrease and the dynamic strain of the material to increase under the same dynamic stress conditions.

(3)

Even if the relative density of the sand-gravel material reaches 90%, there is still the possibility of liquefaction under dynamic loading. Earth-rock dams that are built on sand-gravel overburdens and earth-rock dams filled with sand-gravel materials in earthquake-prone areas should use our proposed analysis and evaluation method to investigate the possibility of sand-gravel liquefaction. We used test data and considered the influence of relative density to modify the existing empirical formula and provide an evaluation method for the number of cycles required to reach liquefaction. We propose a pore water pressure growth model that is suitable for both sand-gravel and sandy materials. Comparisons and validations demonstrated that the proposed model accurately describes the three types of pore water pressure growth processes during liquefaction. The pore pressure growth model proposed in this paper can be used to analyze the liquefaction resistance of the dam foundations and dam structure of high earth-rock dams and high sand-gravel dams located on deep overburdens.