A Secure Median Implementation for the Federated Secure Computing Architecture

Abstract

In Secure Multiparty Computation (MPC or SMPC), functions are evaluated in encrypted peer-to-peer networks without revealing the private inputs of the participating parties. The median is a non-trivial computation in MPC and is particularly relevant in fields like medicine and economics. Here, we provide an MPC implementation of the median for the Federated Secure Computing (FSC) framework. It is tested on synthetic datasets with varying sizes ($N={10}^2$ to $N={10}^7$) and number of participants ($M=2$ to $M=10$) across different network environments and hardware configurations. Using minimal networking and computational resources on a commercial hyperscaler, we evaluated real-world performance with breast cancer ($N=569$) and heart disease ($N=920$) datasets. Our results showed effective scaling up to $N={10}^6$ entries with runtime between 1 and 4 s, but runtime exceeded 15 s for ${10}^7$ entries. The runtime increased linearly with the number of parties, remaining below one minute for up to $M=10$ parties. Tests with real-world medical data highlight significant network overhead, with runtime increasing from 16 to 17 s locally to over 800 s across hyperscaler regions, emphasizing the need to minimize latency for practical deployment.

1. Introduction

Collaborating on sensitive data is crucial for driving digital transformation, yet it introduces a complex interplay of conflicting interests. On the one hand, there is a clear benefit in driving digital transformation through improved data availability. On the other hand, sharing data openly clashes with various interests in the protection of sensitive information, such as the protection of business secrets in companies or the fundamental right to privacy of individuals. A prime example can be found in biomedical research, where rigorous regulation (e.g., General Data Protection Regulation, GDPR or Health Insurance Portability and Accountability Act, HIPAA) surrounding patient data frequently impedes collaboration among stakeholders. Strict privacy enforcement may hamper progress and endanger the capacity to access sufficiently large datasets essential for accurately addressing clinical inquiries. Fortunately, Privacy-Preserving Computation (PPC) techniques have emerged as promising approaches to data federation that both protect participant interests and stakeholder privacy while still enabling collaboration on federated datasets across institutional borders. These techniques allow insights to be derived from distributed datasets, known as federated analytics, or enable the training of machine learning models without sharing data, as in federated learning, which is increasingly used, for example, in medical research or industrial settings [1,2]. In particular, Secure Multiparty Computation (MPC or SMPC) is a fundamental building block and is considered a gold standard technique in PPC, enabling distributed parties to jointly compute a function without revealing any private data [3]. The use of MPC techniques in real-world applications is growing as complex technology stacks become more manageable and increased computing resources are available. Expertise and cryptography knowledge also play a significant role in the dissemination of the technology [4]. Estimating the costs and benefits of theoretically proven algorithms is often the first step for the application of MPC solutions in fields such as biomedical research.

Our use case is predominantly focused on university medicine applications. Multicentric clinical trials are the gold standard for the development of new diagnostic tools and therapies. The exact understanding of physiological and pathological features on all scales, from epidemiology to personalized medicine, requires the pooling of large patient numbers. Classically, this approach requires data sharing and centralized evaluation. However, in terms of GDPR, health data records are particularly sensitive data, and patient advocates demand better protection of patient privacy. New applications in e-health also require active and dynamic consent by the user as dominion over data shifts from centers to individuals. For these reasons, decentralized approaches to digital health have recently received much interest. COVID proximity warning apps were a recent success on a massive scale. Similarly, e.g., the German Medical Informatics Initiative considers semi-decentralized tools like DataSHIELD as an alternative to open data sharing [5]. We are particularly interested in Federated Secure Computing (FSC), a propaedeutic framework that offers an easy-to-use API to develop distributed applications [6]. In particular, the SIMON (SImple Multiparty ComputatiON) microservice offers pre-made statistical functions to be evaluated by MPC. Among them, the median is one of the most used metrics in any medical descriptive statistics. Patient cohorts are commonly characterized by median age, median tumor size, median therapeutic dose, and so forth. Of course, the median, as one of the most basic statistical functions, also has a wide use outside of medicine in areas as diverse as finance, economy, psychology, media, and IoT applications in automotive and smart home.

In this paper, we describe the implementation of the secure median for FSC/SIMON. We also provide benchmarks for real-world computation of rank-based statistics across a wide range of parameters and situations.

1.1. Related Work

There are several protocols for computing rank-based statistics, which differ in their proposed architecture (clients, server), privacy guarantees (input privacy, output privacy), and core technologies (Homomorphic Encryption, pure MPC, differential privacy; for an introduction to these fundamental building blocks, see [3]). For example, Tueno et al. [7] and Chandran et al. [8] describe solutions for computing rank-based statistics in a star network, i.e., a large number of clients communicating with one or only a few central untrusted servers on which the evaluation is carried out while preserving the privacy of each client using garbled circuits or homomorphic encryption. In addition, Böhler and Kerschbaum [9], proposes a differential privacy approach that involves the use of both garbled circuits and secret-sharing schemes to protect individual privacy, additionally using an exponential mechanism to mask the true output value and thus a security accuracy trade-off. In contrast, Aggarwal et al. [10] aims to determine the exact value of a distributed dataset. For this purpose, the authors designed an efficient algorithm for jointly computing rank-based statistics while keeping individual data inputs private (see Section 2 for details). Although their algorithm is described theoretically, practical implementations and real-world benchmarking are lacking.

The real-world implementation and benchmarking of MPC have become increasingly prominent due to advancements in efficient solutions, better hardware availability, and software improvements that reduce the computational overhead of this technology [11]. This trend is particularly noticeable in biomedical research, including genome-wide association studies, diagnostics [12,13], and drug screening [14]. In 2019, von Maltitz et al. [15] conducted the first MPC with real oncology patient data in Germany, using a Kaplan-Meier estimator. However, such implementations typically require extensive cryptographic knowledge, as most software tools and frameworks like MP-SPDZ [16], FRESCO [17], or ABY [18] require complex technical setups and the manual implementation of MPC functions using specific cryptographic primitives or protocols (see [11] for a detailed overview). More user-friendly solutions are limited, with notable examples being the industry-level platforms, e.g., Sharemind MPC (Cybernetica AS, Tallinn, Estonia) [19] and Carbyne (Robert Bosch GmbH, Stuttgart, Germany) [20], as well as no-code tools like EasySMPC [21]. Recently, Federated Secure Computing [6] introduced an accessible architecture that shifts the burden of complex cryptographic processes to the server and provides a simple API.

1.2. Our Contribution

In this study, we present the implementation and real-world benchmarking of an algorithm for computing rank-based statistics, specifically the median, as outlined by Aggarwal et al. [10]. Our primary motivation was to bridge the gap between theoretical advances in MPC and their practical application and evaluation, focusing on a real-world medical setting. We focused on a concrete statistical function with high demands in biomedicine, i.e., the median, from a protocol for which benchmarking and real-world evaluation was lacking. Implementing and utilizing MPC protocols can be challenging and requires a high level of cryptographic expertise. Our work addresses this by providing a comprehensive guide and evaluation in the context of FSC. By exploring this aspect, we aimed to demonstrate the practical application of MPC in medical research, offering insights into cost-benefit trade-offs and suggesting avenues for future development based on the architecture used.

1.3. Overview

The paper is structured as follows: Section 2 introduces the preliminaries. We provide a brief description of the MPC protocol for rank-based statistics that our implementation is based on, along with the computational framework and topology on which we rely. Section 3 describes the implementation details and the experimental setup we used to benchmark our implementation. The performance evaluation is presented in Section 4. In Section 5, we contextualize our findings within the broader landscape of MPC implementations of rank-based statistics, discussing their implications.

2. Preliminaries

In the following, we provide preliminaries for MPC (for a detailed introduction, see [3]). We consider a scenario where m parties, denoted as $\mathcal{P}=P_1,\dots ,P_m$, each possess a private dataset $D_i\subseteq \mathbb{F}$, with a domain size M. Collectively, these individual datasets $D_i$ merge into a comprehensive dataset $\mathcal{D}$ of size n.

2.1. Secure Multiparty Computation

In MPC, a set of two or more parties participate in an encrypted peer-to-peer network to jointly compute a function $y=f(D_1,\dots ,D_m)$ without revealing each party’s private input. That means that each party only receives the exact result y of that function and nothing more (see Figure 1). The function considered in this work is the identification of the kth-ranked element in a dataset. In other words, in an ordered set $S\subset \mathbb{F}$ the value $x\in S$ which has rank k. Specifically, we are interested in the median value, i.e., finding the value that is ranked $k=\lceil \left|S\right|/2\rceil$. To achieve this goal, MPC relies on protocols defining a set of rules and procedures for the parties involved to follow. These protocols are designed to ensure that the parties can interact with each other securely and reliably, even in the presence of adversaries. By following the protocol, the parties can compute the desired function while preserving the privacy of their inputs and maintaining the security and integrity of the computation.

2.2. Threat Model

The threat model considered here is the semi-honest  adversary also called “honest but curious”. They are meant for generally trustworthy parties who will not maliciously deviate from the protocol but rather cooperate to protect the privacy of their input data. The purpose is to provide some level of data privacy for the parties involved rather than data security against outside attackers or corrupted inside parties.

2.3. Protocol for the kth-Ranked Element

Aggarwal et al. [10] propose a multiparty protocol for computing the exact median that requires only a logarithmic number of secure computations for the size M of the domain $\mathbb{F}$ from which the data set D is drawn. Each party initializes the search range to the range of D and the candidate value to the midpoint of the range. Parties iteratively refine the search range based on securely aggregated counts of elements in their datasets less than or equal to the candidate value. This process continues until the range collapses to the true kth-ranked value. The protocol ensures data confidentiality and scalability in MPC scenarios and is presented in Algorithm 1.

This minimizes the cryptographic overhead to just two comparisons and two secure summations per round. Achieving this is possible through widely applicable protocols, like additive secret sharing. Essentially, additive secret sharing divides shares of a secret among participants, enabling them to calculate sums without disclosing the actual values [22]. Consequently, they can obtain the desired result while safeguarding individual contributions. Algorithm 2 provides a concrete exemplary protocol demonstrating how parties collaboratively compute the sum of their private values while preserving privacy using random numbers.

Algorithm 1 Secure kth-Ranked Element (Aggarwal et al. [10], Protocol 3)

Input: Data $D_1,\dots ,D_m$ held by parties $P_1,\dots ,P_m$, rank k, sizes of each $D_i$, data range $[\alpha ,\beta ]$     Output: kth-ranked element in $D_1\cup \cdots \cup D_m$.   1: Initialize $a\leftarrow \alpha$, $b\leftarrow \beta$, $n\leftarrow \sum |D_i|$   2: repeat              Each $P_i$:   3:     $\mu \leftarrow \lceil {\displaystyle \frac{(a+b)}{2}}\rceil$   4:     $l_i\leftarrow \left|\{x\mid x\in D_i,x<\mu \}\right|$, $g_i\leftarrow \left|\{x\mid x\in D_i,x>\mu \}\right|$             Secure computation between parties:   5:     if ${\sum }_{i=1}^m{l}_i\le k-1$ and $\sum g_i\le n-k$ then   6:         done   7:     end if   8:     if ${\sum }_{i=1}^m{l}_i\ge k$ then   9:         $b\leftarrow \mu -1$ 10:     end if 11:     if ${\sum }_{i=1}^m{g}_i\ge n-k+1$ then 12:         $a\leftarrow \mu +1$ 13:     end if 14: until done

Algorithm 2 Secure summation protocol utilizing additive secret sharing

Input: Values $a_i$ held by parties $P_1,\dots ,P_m$     Output: Sum of the values ${\sum }_{i=1}^m{a}_i$.       Distribute random numbers between parties:   1: for $i=1$ to m do   2:     Party $P_i$ generates a random number $r_i$.   3:     if $i=m$ then   4:         Party $P_i$ sends $r_i$ to $P_1$.   5:     else   6:         Party $P_i$ sends $r_i$ to $P_{i+1}$.   7:     end if   8: end for           Add randomness:   9: for $i=1$ to m do 10:     if $i=1$ then 11:         Party $P_1$ computes adjusted value $a_1^{\prime }\leftarrow a_1-r_1+r_m$. 12:     else 13:         Party $P_i$ computes adjusted value $a_i^{\prime }\leftarrow a_i-r_i+r_{i-1}$. 14:     end if 15: end for     16: Parties share adjusted values $a_i^{\prime }$ and calculate: $sum\leftarrow {\sum }_{i=1}^m{a}_i^{\prime }$ 17: return  $sum$

2.4. Secure Computing Framework

A framework, in this context, refers to the structural foundation or the underlying structure within which a protocol operates. It provides a systematic way to design, analyze, and implement secure multiparty computation protocols. FSC is a recently developed free and open-source framework offloading complex cryptographic tasks to a server while providing an easy-to-use API to develop distributed applications (see Ballhausen and Hinske [6] for a detailed description of the framework). In this architecture, every party runs its own server in a secure peer-to-peer network. By offloading the cryptography server side, the client side is free of dependencies and simple to program. The Framework provides microservices exposed through a RESTful API (The entire codebase is freely available at https://github.com/federatedsecure, last accessed: 20 August 2024).

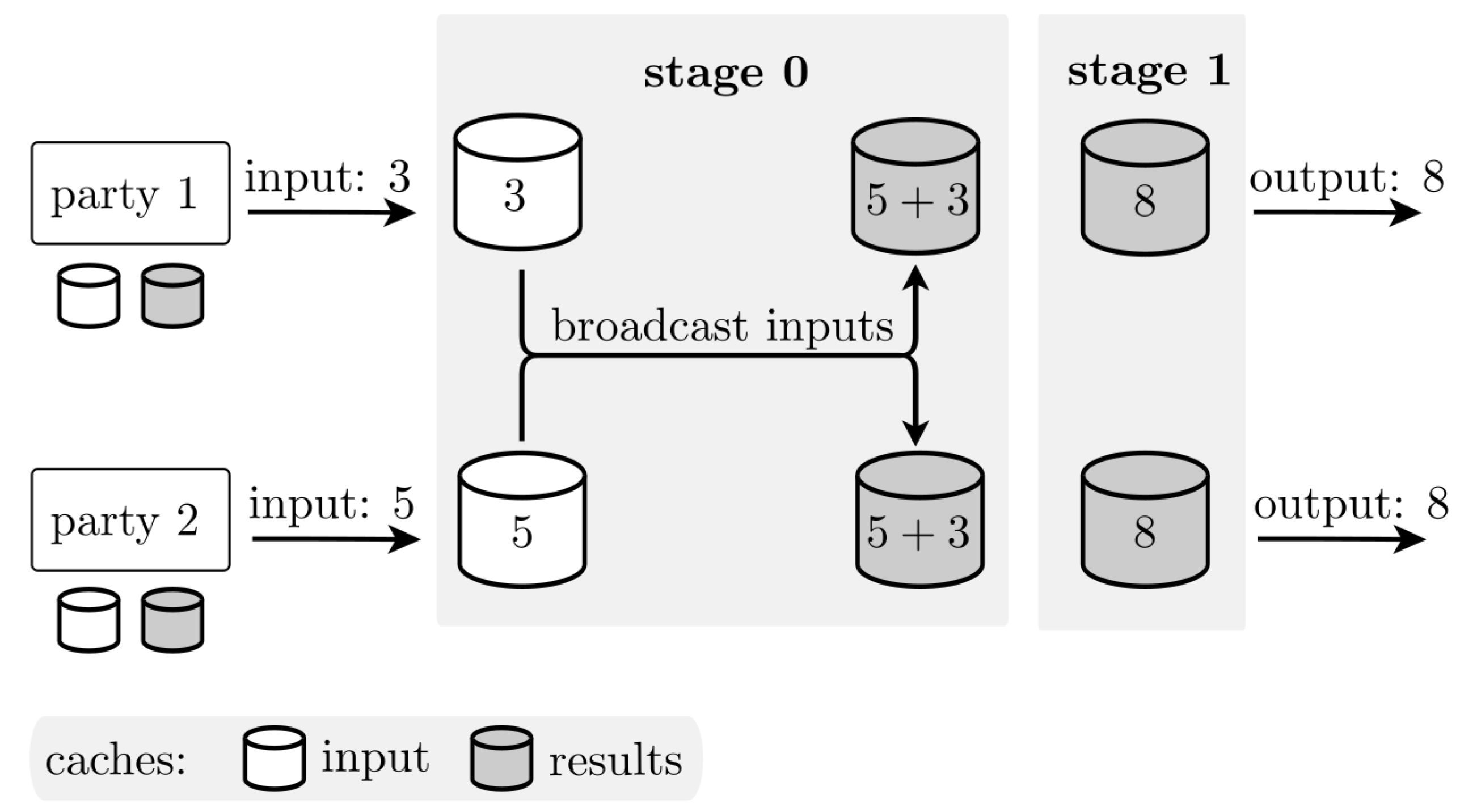
One of these microservices, SIMON, provides MPC functionality. Unlike monolithic MPC frameworks, SIMON does not provide a universal runtime for arbitrary bytecode. Instead, distinct functions must be individually implemented. Typically, these are provided server-side and run ‘stage’ per stage with message passing between parties happening between stages. The messages are stored and aggregated in ‘caches’. The next stage proceeds once all necessary inputs have been received in their respective caches. For example, a (not secure) computation of the sum of the inputs of M parties is displayed in Listing 1.

Listing 1. Examplary (not secure) computation of the sum in SImple Multiparty ComputatiON (SIMON).

Figure 2 illustrates this example for two parties. Each party submits its input to the input cache. In stage 0, these inputs are broadcast and stored in the result cache, where they are automatically aggregated. Once all inputs have been received, the protocol moves to stage 1, where the final aggregated result is retrieved and returned.

Please note that this example demonstrates a non-secure protocol for illustrative purposes. However, this staged approach ensures orderly execution, with each stage depending on the completion of the previous one, allowing the implementation of sequential protocols such as the secure summation protocol (see Algorithm 2), which is the basis for the secure kth-ranked element protocol (see Algorithm 1).

3. Materials and Methods

By abstracting networking for function development and integrating intuitive staging logic, SIMON facilitates function development and provides flexible and core functionality for the implementation of MPC protocols such as the one described in this work. In the following, we describe this implementation as well as the experimental setup for testing.

3.1. Implementation

The original protocol, as detailed in Section 2, has been converted into the staging logic within SIMON, which is described previously (see Listing 2). Specifically, we implemented the Python class MicroprotocolKthElement (Available under https://github.com/federatedsecure/service-simon/blob/main/src/federatedsecure/services/simon/microprotocols/microprotocol_kth_element.py, last accessed: 20 August 2024). After first initialization of the search range and required caches, the main part encapsulates a stage that can be iteratively initialized and called. Similar to the staged approach shown in Figure 2, the stages are iteratively executed, narrowing the search range until the exact kth-ranked value is found (see pseudocode in Listing 2).

Listing 2. Pseudocode for main stage in MicroprotocolKthElement. The variable naming follows the definition in Algorithm 1.

3.2. Experimental Setup

The experimental setup is visualized in Figure 3. In this setup, each party runs its own federated secure compute server instance and provides input data.

3.2.1. Server Setup

To evaluate the implementation, we deployed FSC servers either locally or on AWS EC2 instances across various regions. Local deployment ensures precise execution time measurement, free from network latency interference. Conversely, AWS deployment allows assessing the influence of network overhead on performance. Moreover, leveraging AWS EC2 instances across various regions effectively replicates real-world scenarios, which is particularly beneficial when parties are globally dispersed. There are a few minimum hardware requirements; we were using an office laptop with an Intel Core i5-1235U processor and 8GB RAM for local deployment. AWS EC2 instances were configured using t2.micro or t3.micro tiers, i.e., Intel Xeon processors and 1GB RAM, depending on regional availability. FSC facilitates easy server setup. For example, Listing 3 lists the commands to start two local servers:

Listing 3. Exemplary commands to initiate two local servers.

3.2.2. Client Setup

Client setup is easily implementable in Python and for two parties, a function to compute the median is displayed in Listing 4 (The full client-side code used here is available under https://github.com/federatedsecure/publications/tree/main/secure-median, last accessed: 20 August 2024).

Listing 4. An exemplary client script for computing the secure median. Each party has to call this function, providing their respective data as an array and the corresponding member index.

3.2.3. Test Data

Input data comprised synthetic data of varying sizes as well as two open datasets available in the UC Irvine Machine Learning Repository [23].

Synthetic Data

We generated synthetic data as arrays of varying sizes and data ranges by systematically varying the size from ${10}^2$ to ${10}^7$ and the range from ${10}^1$ to ${10}^3$ using Pythons own random.randint() function while ensuring the inclusion of both the lower and upper bounds of the respective range.

Public Dataset on Breast Cancer

We utilized a publicly available breast cancer dataset obtained from the University of Wisconsin Hospital, Madison, WI, USA. This dataset, comprising 569 samples, includes features related to breast cancer diagnosis, such as radius, texture, perimeter, area, smoothness, compactness, concavity, symmetry, and fractal dimension. Specifically, we focused on the “Radius1” feature for our evaluation. To simulate a dual-centric study, we divided the dataset into two portions, each containing 284 and 285 samples, respectively.

Public Dataset on Heart Disease

Similarly, to simulate a multicentric study, we utilized a public heart disease dataset. This dataset encompasses a total of 920 patients in four databases recorded in four university hospitals: the Cleveland Clinic in Cleveland, OH, USA (303 patients), the Hungarian Institute of Cardiology in Budapest, Hungary (294 patients), the Veterans Administration Medical Center in Long Beach, CA, USA (200 patients) and the University Hospitals in Zurich and Basel, Switzerland (123 patients). The dataset features a variety of attributes, including age, sex, chest pain type, resting blood pressure, serum cholesterol levels, maximum heart rate achieved during exercise, and the presence of specific electrocardiographic abnormalities. We focused our analysis primarily on the “age” column.

4. Results

The following results are based on both local deployment to eliminate networking overhead and AWS EC2 instances deployed in several regions to simulate a real-world scenario.

4.1. Compute Time as a Function of the Size of the Data

The running times as a function of varying dataset sizes and data ranges are illustrated in Figure 4. The setup involved a local deployment on a consumer-grade laptop, with two parties each running a server on localhost. For dataset sizes up to ${10}^6$, the runtimes are consistent, typically between 1 and 4 s, and grow slightly with the data range. However, for datasets larger than ${10}^6$, the runtime grows exponentially. This exponential growth is evident in datasets containing ${10}^7$ entries, where runtimes exceed 15 s.

4.2. Compute Time as a Function of the Number of Parties

The runtime as a function of the number of parties is illustrated in Figure 5. This experiment was also conducted locally on a standard laptop, with each party running a server on localhost. In Figure 5a, the dataset size was fixed at ${10}^2$, while in Figure 5b, the input range was set to ${10}^2$. Notably, the runtime shows a linear growth pattern as the number of parties increases. Additionally, the effect of the data range becomes more significant as the number of parties increases, while there seems to be no systematic increase in running time due to increasing data size up to ${10}^6$, as observed in the previous analysis.

4.3. Networking Overhead

To assess the networking overhead, we conducted a series of experiments utilizing AWS EC2 instances. Specifically, we evaluated the computational performance across six regions covering Europe (Frankfurt: eu-central-1, Zurich: eu-central-2), Asia-Pacific (Tokyo: ap-northeast-1, Mumbai: ap-south-1), and Northamerica (N-California: us-west-1, Ohio: us-east-2). We tested both within each continent and across continents to capture the impact of varying round-trip times (RTT) on runtimes. Here, we set both the data range and dataset size to ${10}^2$. Our measurements revealed an RTT ranging from approximately 7 ms to 200 ms between each pair of AWS regions. Notably, as the RTT increased, so did the runtime. While the runtime remained around 2 s in the local setup, it grew to over 100 s between Frankfurt and Tokyo. See

Table 1. Round trip time (RTT) and duration values between different AWS regions as well as two parties running on localhost. The data size and range were set to ${10}^2$.

Party 1	Party 2	RTT [ms]	Duration [s]
Frankfurt (eu-central-1)	Tokyo (ap-northeast-1)	222.77	128.00
N-California (us-west-1)	Frankfurt (eu-central-1)	149.80	96.69
Tokyo (ap-northeast-1)	N-California (us-west-1)	106.05	61.58
Mumbai(ap-south-1)	Tokyo (ap-northeast-1)	129.33	85.81
Ohio (us-east-2)	N-California (us-west-1)	50.98	34.64
Zurich (eu-central-2)	Frankfurt (eu-central-1)	7.16	6.07
AWS-localhost	AWS-localhost	<0.1	2.04
Localhost	Localhost	<0.1	1.87

.

4.4. Real-World Dataset

For a real-world evaluation, we utilized two datasets. We evaluated the split breast cancer dataset using two AWS EC2 instances located in Frankfurt (eu-central-1) and Tokyo (ap-northeast-1). For the heart disease dataset, we leveraged the inherent grouping and selected AWS regions closest to the original recording sites: Ohio (us-east-1), Northern California (us-west-1), Zurich (eu-central-2), and Frankfurt (eu-central-1). To estimate networking overhead, we also conducted a local setup with two and four parties, respectively. For the breast cancer dataset, the runtime ignoring networking overhead (local deployment) was approximately 4 s. However, networking overhead between Europe and Japan extended the runtime to over 260 s. Similarly, for the heart disease dataset, the runtime on a local deployment was around 16–17 s. With networking, this increased to over 800 s. See

Table 2. Comparison of durations for different datasets and configurations.

Dataset	Duration [s]
	Parties	Localhost	AWS-Localhost	AWS-Regions
breast-cancer	2	3.55	4.12	261.09
heart-disease	4	15.64	16.91	804.81

.

5. Discussion

In our research, we have successfully implemented and performed a real-world benchmarking of a specialized protocol for the computation of rank-based statistics, with a focus on the median, as developed by Aggarwal et al. [10]. We have provided much-needed benchmarking and real-world evaluation of this protocol, demonstrating its viability and effectiveness in practical applications, a prerequisite for real-world settings, including medical research.

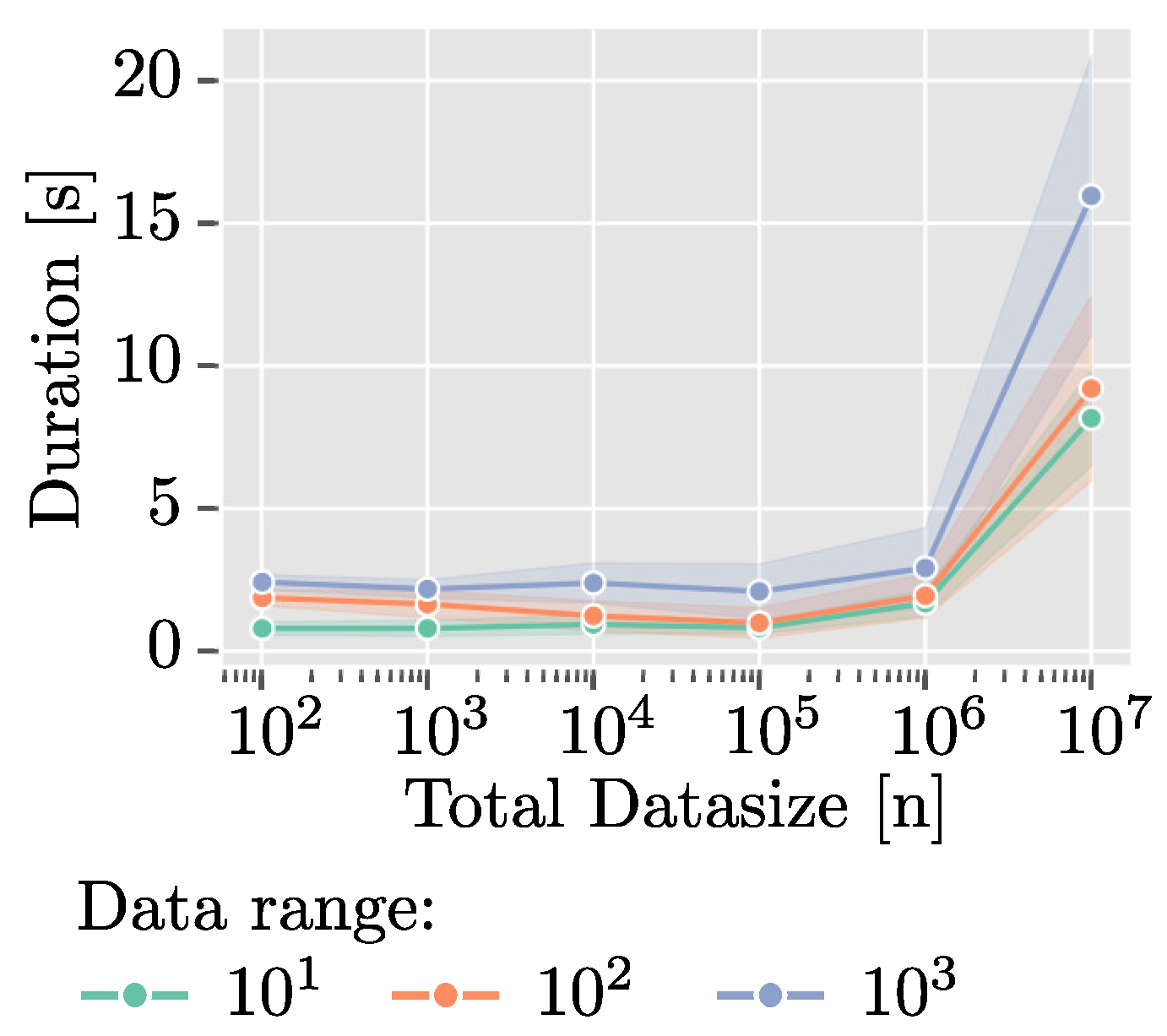
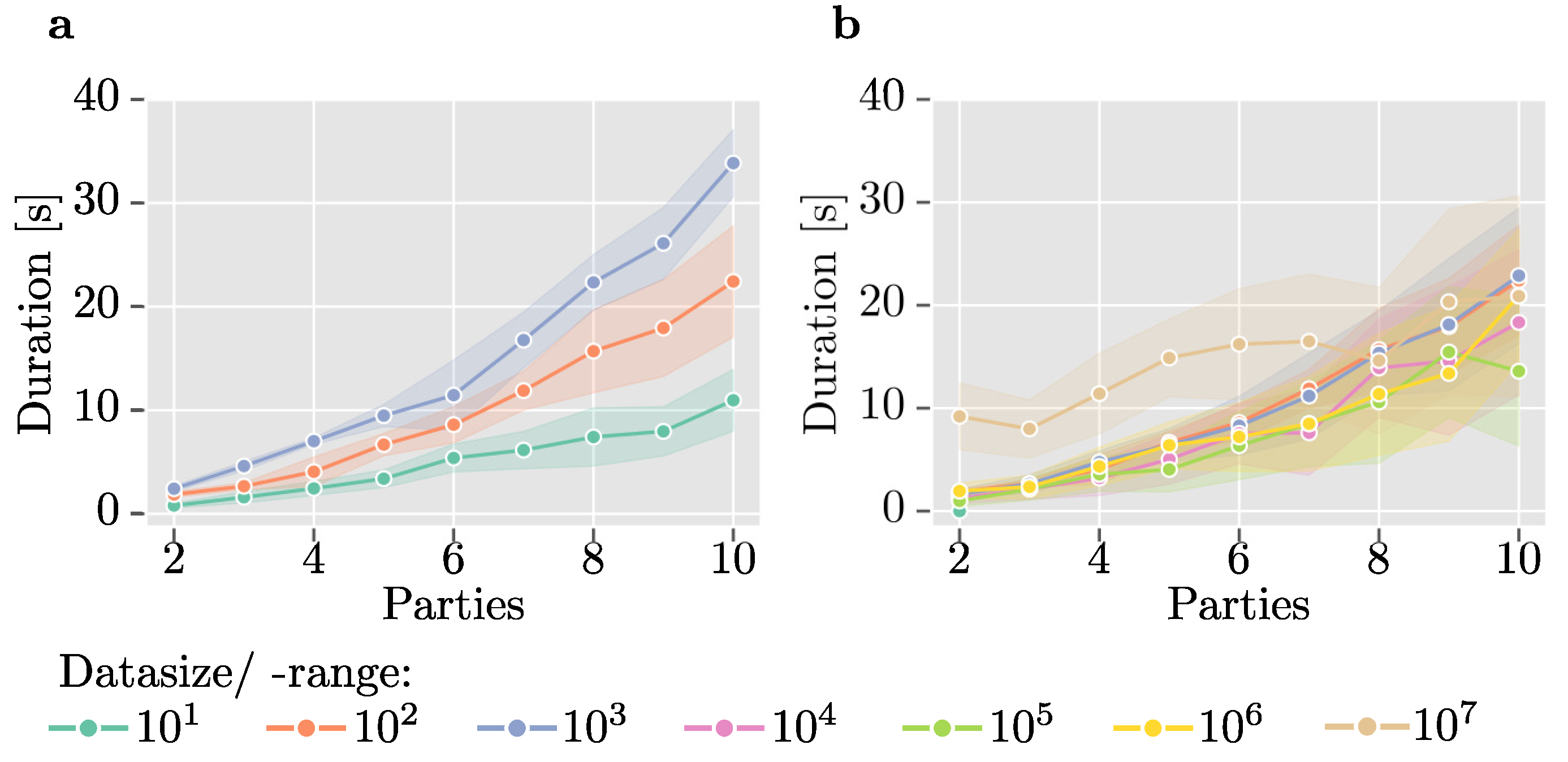
In particular, we show that the protocol scales well with increasing data size up to ${10}^6$ entries, maintaining runtimes between 1 and 4 s, ignoring network overhead. However, for larger datasets (>${10}^7$ entries), the exponential growth in runtime (>15 s) highlights the need for optimization when dealing with very large datasets. Possible solutions include parallelization of processes running locally within each stage on each server or increasing computing resources. Moreover, our analysis indicates a linear growth in runtime as the number of parties increases, evident in both fixed-size and fixed-range experiments. This suggests that the protocol’s efficiency remains manageable even with additional parties, as the runtime consistently remains below one minute for scenarios involving up to ten parties. Such settings are common in fields like biomedical research, e.g., where a few hospitals contribute to a multicentric study and jointly want to compute statistics over their databases without revealing individual inputs. However, for scenarios involving a larger number of parties with only a few data points, a central server model, such as the star network described in [7,8], may be more suitable. This model involves all parties communicating with a central party, reducing communication costs and offloading complex computations to the central untrusted party. Notably, Chandran et al. [8] demonstrated that for 100 parties, each holding one data point, the runtime can be reduced to under a minute, provided the central party has sufficient computing power (32 GB RAM in their example).

Nevertheless, the runtime in our experiments using AWS EC2 instances was dominated by networking overhead. The instances kept minimal and unoptimized were limited to AWS free tier (EC2 t2.micro), classified as “low to moderate” by AWS [24]. This is evident from the measured RTT of up to 222 ms between AWS instances, highlighting the importance of minimizing latency in distributed MPC setups. Böhler and Kerschbaum [9] demonstrated significantly lower runtimes of 1 to 2 s for their differentially private median algorithm with RTTs of 12–25 ms, though comparisons are challenging due to their purpose-optimized implementation.

Additionally, we benchmarked our implementation using real-world datasets to demonstrate its practical applicability in medical research. Networking overhead significantly increases runtime, especially for the heart disease dataset (from 16 to 17 s locally to over 800 s with AWS regions), highlighting the need for strategic resource selection. Despite this, the protocol’s performance on real-world data shows its deployment potential, particularly when network latency is minimized.

5.1. Security Analysis

The security of the underlying secure median algorithm has been demonstrated by Aggarwal et al. [10]. They address both semi-honest parties, who adhere to the protocol but seek to gain additional information and malicious adversaries, who may deviate from the protocol and provide fabricated inputs. While they propose additional steps to extend security to the malicious case, our implementation currently supports only the semi-honest case. A primary weakness in our setting occurs when one of two parties, or all but one of several parties, provides empty input to the computation. Generally, this issue cannot be entirely prevented, as empty or extreme values might be valid inputs. For use cases where such inputs are not expected, parties should impose additional constraints on input data, such as a minimum number of input elements or a specified input range. They should also verify the validity of inputs in the initial stage of the protocol and check their plausibility between stages. Apart from these measures, our implementation does not introduce any additional communication between the parties compared to the original protocol. Consequently, parties do not gain any extra information from each other, and the security analysis of the original algorithm remains valid.

While the datasets remain hidden, in general, revealing the exact kth-ranked value, e.g., the median, reveals one data point and thus the exact value of one individual, which could be used to compromise data of targeted individuals [25]. One solution to additionally protect the output of the computation is to use additional differential privacy techniques, either adding noise to the output or randomly selecting a value from a probabilistic distribution of possible values [9,26,27]. Despite concerns about increased computational overhead, Pettai and Laud [26] argue that this overhead is minimal, while Böhler and Kerschbaum [9] demonstrate the remarkable efficiency of a specific protocol.

5.2. Limitations

This study has several limitations that should be noted. Our benchmarking was conducted in a semi-honest setting, meaning our implementation does not address scenarios involving malicious actors. While Aggarwal et al. [10] describe additional measures for handling malicious settings and commercial solutions like Sharemind MPC [4] as a backend to FSC offer protections against such threats, these models were outside the scope of our baseline implementation.

Additionally, our performance evaluation used synthetic datasets to explore various sizes and participant counts. Although this approach provides insights into computational scaling, it may not fully capture the complexities and variability of real-world data. To address this, we incorporated two medical datasets, which, while limited to the healthcare domain, offer insights into the computational scaling of real-world data irrespective of the domain. The medical context, though, is a particularly interesting application domain due to the sensitivity of patient information, highlighting the need for privacy-preserving techniques in practical applications.

Additionally, we chose not to minimize network latencies in our experiments to demonstrate a range of possible computation times with real datasets. We also conducted experiments using hyperscalers in various regions to cover the spectrum of network latency. In practice, parties could replicate their data privately within the same region, allowing secure peer-to-peer computations to be performed in a low-latency environment, thus achieving computation times closer to the lower end observed in our experiments in local deployment.

6. Conclusions

The application of methods of MPC offers solutions to various challenges of collective research. In our study, we bridge the gap between theoretical advancements in MPC and their practical deployment in medical research, offering the implementation and real-world benchmarking of a theoretical protocol tailored for rank-based statistics within the framework of FSC. By analyzing real-world datasets, we provide a concrete use case demonstrating the applicability of our approach in cloud environments. Our research not only demonstrates the scalability, efficiency, and real-world applicability of the protocol but also identifies key aspects to consider when using MPC solutions in distributed environments. By highlighting the importance of optimizing for a high number of parties as well as reduced networking overhead, we pave the way for more effective and efficient collaborative research endeavors in fields such as biomedical research.