Beyond Traditional Metrics: Exploring the Potential of Hybrid Algorithms for Drought Characterization and Prediction in the Tromso Region, Norway

Abstract

Meteorological drought, defined as a decrease in the average amount of precipitation, is among the most insidious natural disasters. Not knowing when a drought will occur (its onset) makes it difficult to predict and monitor it. Scientists face significant challenges in accurately predicting and monitoring global droughts, despite using various machine learning techniques and drought indices developed in recent years. Optimization methods and hybrid models are being developed to overcome these challenges and create effective drought policies. In this study, drought analysis was conducted using The Standard Precipitation Index (SPI) with monthly precipitation data from 1920 to 2022 in the Tromsø region. Models with different input structures were created using the obtained SPI values. These models were then analyzed with The Adaptive Neuro-Fuzzy Inference System (ANFIS) by means of different optimization methods: The Particle Swarm Optimization (PSO), The Genetic Algorithm (GA), The Grey Wolf Optimization (GWO), and The Artificial Bee Colony (ABC), and PSO optimization of Support Vector Machine (SVM-PSO). Correlation coefficient (r), Root Mean Square Error (RMSE), Nash–Sutcliffe efficiency (NSE), and RMSE-Standard Deviation Ratio (RSR) served as performance evaluation criteria. The results of this study demonstrated that, while successful results were obtained in all commonly used algorithms except for ANFIS-GWO, the best performance values obtained using SPI12 input data were achieved with ANFIS-ABC-M04, exhibiting r: 0.9516, NSE: 0.9054, and RMSE: 0.3108.

1. Introduction

Drought is a complex climate-related event that significantly affects agriculture and water resources, posing increased risks to both the environment and society [1,2]. It is typically characterized by its duration, frequency, and severity [3]. For instance, a meteorological drought refers to decreased average monthly precipitation. As dry conditions persist for several months, they begin to deplete soil moisture and affect plant life, leading to what is known as an agricultural drought [4]. When dryness extends beyond nine months, it can start to impact water bodies and flow patterns, resulting in what is termed as “hydrological drought” [5]. The increased occurrence of these drought types, especially agricultural and hydrological droughts, can disrupt socioeconomic activities and ecosystems [2].

According to the Sustainable Development Goal (SDG) Report [6], around two billion people cannot access clean drinking water, while The Intergovernmental Panel on Climate Change (IPCC) reports that about half of the people in the world experience water scarcity at any time during the year. Moreover, the World Meteorological Organization (WMO) predicts an increase in these numbers due to the impact of climate change and population increase. Rising temperatures, severe droughts and floods, and an increasing number of extreme events can threaten water security in most of the regions around the world.

Future climate projections also suggest that Europe will experience significant drying, even under less aggressive pathway scenarios (SSP126 and SSP245) [7]. With climate projections indicating a long-term slowdown of the Atlantic Meridional Overturning Circulation (AMOC) during this century [8], findings point to an increased drought risk. This risk is in addition to that driven by the global warming signal, particularly affecting the central and southern regions of Europe in the coming decades [1].

Northern Europe, among other regions, is not an exception, and the region also experiences significant changes. Although the anticipated rise in precipitation in Northern Europe is primarily expected during the winter and autumn seasons, whereas a decrease in precipitation is forecasted for the spring and summer months [9]. In 2018, significant areas of Northern Europe experienced a severe drought. Bakke et al. [10] highlighted that gaining a deeper insight into the characteristics and the overarching atmospheric patterns that drive such events is crucial for improving drought prediction and management strategies. Their results, characterized by significant spatial and temporal variability, underscore the complexity of analyzing drought events within various components of the hydrological cycle. It was also demonstrated by Rousi et al. [11] that the summer of 2018 was extreme in the observational record for Europe and that heat anomalies of this magnitude are expected to occur much more frequently in a warmer world, potentially occurring almost every year with a global warming increase of +2 °C. Furthermore, at the start of 2022, numerous regions faced intense drought conditions, further compounding the challenges across Europe [12].

While drought conditions have become less severe in Northern Europe [13,14,15], Wilson et al. [16] found a tendency towards larger water deficits in Southeastern Norway. Additionally, the impacts of changing climatic conditions in the Arctic are occurring at an unprecedented rate and scale, significantly outpacing projections for other global regions. In Sápmi, these changes are expected to have profound effects on nature, ecosystems, and their composition, thereby impacting the entire Sámi cultural landscape [17]. All observed hydroclimatic changes have drawn increasing attention on northern high-latitude research [18,19]. In order to reduce and prevent these negative effects of droughts, scientists have been tracking droughts for a while and trying to convert them into a mathematical form. For this reason, to inform monitoring systems and reveal key drought characteristics, such as duration, frequency, severity, and spatial extent, drought indices have been developed, which vary in the variables used for drought characterization and the level of complexity [20,21]. Some of them include The Palmer Drought Severity Index (PDSI), The Standard Precipitation Index (SPI), The Effective Drought Index (EDI), Z-score, The Streamflow Drought Index (SDI), and The Standardized Precipitation-Evapotranspiration Index (SPEI) [22,23,24,25,26] that have received more attention than the others, owing to their simplicity of implementation and capacity to capture the spatiotemporal variability of droughts. In addition, droughts can also be monitored and detected with some innovative methods, such as The Satellite Gravimetry Technique [27]. Among these, the SPI stands out as a simple, objective, and widely accepted drought index which is used to monitor and assess drought. The SPI estimates the severity and duration of drought based on the deviation of precipitation from the long-term average [23]. The SPI is recommended by the World Meteorological Organization (WMO) as the preferable meteorological drought index. Its uncomplicated calculation, flexibility in terms of timescales, and minimal data requirements (only precipitation) distinguish it from the PDSI and SPEI. The superiority of the SPI in the evaluation of drought has been demonstrated globally, including in South Africa, Finland, Türkiye, Iran, and Italy [28]. Therefore, the SPI is used for drought detection and projection and is part of monitoring systems such as the European Drought Center (EDC), the National Drought Mitigation Center, and the European Drought Observatory (EDO) [21]. In this study, the drought index values were also calculated using the SPI.

Beyond detecting and monitoring drought, forward-looking predictions are significantly important for the sustainability of water resources. Researchers used data-based forecasting models to make future predictions. These models have managed to go beyond physical models, and their reliability has been emphasized by numerous studies [29]. Various researchers in the literature performed drought modeling analyses utilizing machine learning (ML) and deep learning (DL) techniques. The algorithm and model structure used in these studies may vary depending on the specific region being analysed. While Artificial Neural Networks (ANNs) may perform well in one region, Support Vector Machine (SVM) or Adaptive Neuro-Fuzzy Inference System ANFIS may perform effectively in another region. Furthermore, the findings can be altered or impacted by the parameters employed in the model structure or the number of lagged times considered for each parameter. In other words, the performance of the parameters used in model structure and ML algorithms used for one region may exhibit significantly different performance in another region. Nevertheless, the performance of widely used common algorithms does not change. What affects the result is the application of these algorithms with different optimization methods. Thus, by using the most suitable algorithm and optimization technique for a specific location or by employing strategies that enhance the model performance, one might accomplish diverse outcomes and improvements.

These results emphasize the need to enhance our knowledge of droughts and improve prediction methods to develop effective strategies for dealing with the negative impacts of changing conditions. Investigating their emergence and evolution with a combination of conventional and more sophisticated metrics and methods is needed. To do so, ML and deep DL models are recognized as some of the most advanced tools for exploring climate system predictability and making more accurate predictions possible using observed climate data.

ML techniques such as the ANFIS, ANN, Random Forest (RF), and Support Vector Machines (SVM) have been widely used in prediction models [30]. Machine learning methods are well suited for handling large amounts of data and complex analyses because they can efficiently model nonlinear and high-dimensional data that have intricate relationships and missing values. These capabilities make them particularly effective for addressing challenges in complex data-rich environments [31,32,33]. Consequently, ML (machine learning) models have been effectively utilized in environmental and natural hazard research, including tasks like identifying areas prone to land subsidence, landslides, floods, and predicting droughts [30,33].

The ANFIS algorithm, a Neuro-Fuzzy approach that utilizes an adaptive network for learning, has been widely recognized for its effectiveness in forecasting time series within water resources management, dam management, risk assessment, and hydrological modeling. Renowned for its robust capabilities, ANFIS offers significant potential in addressing complex and nonlinear challenges [33,34,35]. The primary strengths of this method include its ability to manage fuzziness, effectively handle data that are insufficient in time or space, and the neural network’s capacity for dissecting complex relationships between dependent and independent variables [33].

Currently, machine learning and deep learning techniques are often combined with optimization techniques to make more robust predictions for various parameters, such as drought, streamflow, energy consumption, etc. Using optimization techniques allows for the more precise calibration of ML models, leading to improved learning and predictions that better match observed values. These techniques are employed worldwide in a variety of fields, including health and the environment (Figure 1).

Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) are frequently preferred optimization techniques [36], as illustrated in Figure 1. To expand the scope of optimization techniques beyond those commonly employed ones in the literature, this study incorporated the Artificial Bee Colony (ABC) and Grey Wolf Optimization (GWO) methods, thereby enabling a more comprehensive comparison [37,38].

Researchers often favor SVM over other machine learning algorithms, such as ANFIS, when estimating hydrological parameters. Numerous modeling studies employing SVM in hydrology have concluded that it is superior compared to other methodologies in terms of effectiveness [39]. Furthermore, some research has unveiled that integrating optimization approaches within hybrid models can yield even better results [40,41].

Apart from ANFIS, SVM is also employed with various optimization methods for drought prediction. Recently, Piri et al. [42] evaluated the effectiveness of four algorithms, SVM with Response Surface Method (SVM-RSM), SVM with PSO (SVM-PSO), standalone SVM, and ANN, using multiple drought indices. They reported that the SVM-PSO model demonstrated superior accuracy and trend detection compared to others, while SVM-RSM exhibited the highest efficiency. Malik et al. [41] developed hybrid models for the prediction of meteorological droughts using the Effective Drought Index (EDI) and compared the results obtained by combining SVM with PSO (SVM-PSO) and Harris Hawks Optimization (SVM-HHO). They found that the SVM-HHO model outperformed the SVM-PSO model in accurately reproducing the median value for Uttarakhand, India. SVM-PSO applications extend beyond drought prediction, as it is also used for estimating hydrological parameters such as precipitation. Du et al. [43] utilized SVM-PSO to predict precipitation in China and proposed it as an efficient method for predicting precipitation.

In this study, we hybridized ANFIS with GA and PSO, which are frequently used optimization algorithms in drought forecasting. We also hybridized ABC and GWO optimizations, which are among the new optimization techniques that have recently started to be used in hydrology with ANFIS. To further expand the methodological repertoire, we also developed a hybrid model by combining SVM, a commonly employed and effective algorithm, with PSO. That is, this study combined the ANFIS model with each of four popular optimization algorithms GA, GWO, ABC, and PSO) to generate hybridized models. In addition, due to its performance and preferability in drought modeling studies, we hybridized SVM and PSO (SVM-PSO) and compared them with other models. The development and comparison of these diverse hybrid models represent a novel contribution to drought forecasting research.

Droughts, characterized by prolonged periods of below-average precipitation, pose significant challenges to water resource management, agriculture, and ecosystems [20]. Accurate and timely drought forecasting is crucial for mitigating these impacts, enabling proactive planning and adaptation measures [44]. This study comprehensively evaluates the drought prediction capabilities of five distinct methods, encompassing both machine learning and optimization techniques. The goal is to determine their strengths, weaknesses, and suitability for different drought forecasting contexts in the Troms region of Norway with a focus on developing a soft computing approach. The five methods under investigation are ANFIS-PSO [33,45], ANFIS-GA [32,33], ANFIS-GWO [37,46], ANFIS-ABC [33,47], and SVM-PSO [42,48].

The aim of this study is to explore the potential of these hybrid architecture for predicting drought on a monthly timescale. The performance of ANFIS models combined with each of four optimization algorithms given above will be compared to that of the SVM-PSO model. Additionally, this study will investigate the influence of data feature selection and the optimization techniques on the accuracy and efficiency of each method. By comparing the performance of these five methods, this research seeks to contribute to the advancement of drought forecasting methodologies and provide valuable insights for selecting the most suitable approach for specific drought prediction contexts. The findings will be relevant for water resource managers, agricultural planners, dam management, risk assessors, and policymakers seeking to enhance drought preparedness and mitigation strategies.

2. Methodology

In this study, we first determined drought events from precipitation data in the region through the SPI. Focusing on key timescales, a set of model structures with the SPI12 and SPI3 values were created, which effectively represent hydrological and meteorological droughts, respectively. We selected Support Vector Machines (SVM) with Adaptive Neuro Fuzzy Inference System (ANFIS) as the ML and DL algorithms to predict droughts and optimized them with ABC, GWO, GA, and PSO. Root Mean Square Error (RMSE), the correlation coefficient (r), and Nash Sutcliffe Efficiency (NSE) utilized to evaluate the model performance statistically while RMSE-Standard Deviation Ratio (RSR) used to interpret model performance both graphically and statistically. MATLAB software was used for all necessary calculations.

2.1. Study Region and Data

The Norwegian climate data were collected at the Tromsø meteorological station (SN90450), which represents maritime climate conditions due to its location on the Norwegian coast (69.6537° N, 18.9368° E), ranging from 1920 to 2022 (Figure 2). A full-scale meteorological observatory is operated by the Norwegian meteorological office in Tromsø [“www.yr.no (accessed on 25 July 2024)” (station ID: SN90450; variables: temperature, precipitation, snow, and wind)] approximately 14 km away from Ramfjorden. Additional information about the station, based on their station ID, can be obtained from the Norwegian Climate Service Center “https://seklima.met.no/ (accessed on 25 July 2024)”.

Tromsø has reported temperature and precipitation changes during the last century, making the meteorological station representative of climate change in the region [49]. A summary of the precipitation data used in this study is shown in

Table 1. Data statistics.

Starting Data	End	Average (mm)	Standard Deviation	Minimum (mm)	Maximum (mm)
08.1920	12.2022	85.49	46.62	0.6	339.8

.

2.2. SPI (Standardized Precipitation Index)

Standardized Precipitation Index (SPI) values can be derived not only from rainfall data collected at various stations but also from gridded precipitation datasets, such as those obtained from satellite or radar through remote sensing or simulated by meteorological models. The World Meteorological Organization (WMO) has endorsed the SPI as a key meteorological drought index for global drought monitoring due to its accessibility and computational simplicity [50]. The efficiency and ease of use in calculating and analyzing drought attributes make the SPI a practical choice, which is why it was also utilized in this study.

The SPI is computed based on long-term precipitation records for a designated region and timescale. These records are then adapted to fit a probability distribution, typically transformed into a normal distribution characterized by the SPI mean of “0” and a standard deviation of “1”. In this study, the gamma distribution was chosen for its suitability with climatic precipitation data and its widespread application in drought studies [23,51]). Positive SPI values indicate above-average precipitation (wet periods), while negative values denote below-average precipitation (dry periods). Because the SPI is normalized, it provides a standardized way to represent both wet and dry conditions.

Table 2. SPI categories [23].

SPI	Category
above and (2.0)	Extremely wet
(1.99)–(1.50)	Severely wet
(1.49)–(1.00)	Moderately wet
(0.99)–(−0.99)	Near normal
(−1.0)–(−1.49)	Moderately dry
(−1.5)–(−1.99)	Severe dry
−2.0 and less	Extremely dry

summarizes commonly used SPI threshold values for defining drought severity.

Equation (1) provides the calculation of gamma probability function of long-term precipitation.

$$g\left(x\right)={\displaystyle \frac{1}{{\beta }^{\alpha }\tau \left(\alpha \right)}}{x}^{\alpha -1}{e}^{{\displaystyle \raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}}\mathrm{f}\mathrm{o}\mathrm{r} x>0$$

(1)

where $\beta$ represents the scale parameter, $\alpha$ represents the shape parameter, and x and $\tau \left(\alpha \right)$ represent rainfall amount and gamma function, respectively. Equation (2) denotes the ranges of $\alpha$ and $\beta$ [52].

$$a={\displaystyle \frac{1}{4A}}\left(1+\sqrt{1+{\displaystyle \frac{4A}{3}}}\right) and \beta ={\displaystyle \frac{\overline{x}}{a}}$$

(2)

where $\overline{x}$ and n defines the average precipitation and number of observations.

$$A=ln\left(\overline{x}\right)-{\displaystyle \frac{\sum ln}{n}}$$

(3)

$$G\left(x\right)={\int }_0^{x}g\left(x\right)dx={\displaystyle \frac{1}{{\beta }^a\tau \left(\alpha \right)}}{\int }_0^x{x}^{\alpha -1}{e}^{{\displaystyle \raisebox{1ex}{$-x$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}}dx$$

(4)

Equation (5) details the parameters essential for calculating the cumulative probability of non-zero rainfall events.

$$G\left(x\right)={\displaystyle \frac{1}{\tau \left(\alpha \right))}}{\int }_0^x{x}^{\alpha -1}{e}^{-t}dt \mathrm{where} t={\displaystyle \frac{x}{\beta }}.$$

(5)

Additionally, the gamma function $\left(G\left(x\right)\right)$ is undefined for 0. In such cases, the cumulative probability of zero and non-zero rainfall is determined using Equation (6), denoted as H(x).

$$H\left(x\right)=q+\left(1-q\right)G\left(x\right)$$

(6)

where q = m/n (zero probability of precipitation), m: number of observations with zero precipitation.

2.3. ANFIS-Adaptive Neuro-Fuzzy Inference System

The Adaptive Neuro-Fuzzy Inference System (ANFIS), introduced by Jang [53], is a sophisticated hybrid model that integrates the principles of both artificial neural networks (ANNs) and fuzzy logic systems. This integration leverages the strengths of both approaches, enabling the emulation of human-like intelligent decision-making processes [30,31,32,33,37,54].

ANFIS is structured as a multi-layer feedforward network that utilizes the learning capabilities of ANNs and Fuzzy Inference Systems (FISs) to create a powerful tool for nonlinear functions [30]. The system is based on the Takagi-Sugeno fuzzy model, which is structured into five distinct layers: the input fuzzification layer, the product layer, the normalized layer, the defuzzification layer, and the output layer [32]. These layers work in concert to process inputs through fuzzy IF-THEN rules and generate outputs by mapping complex nonlinear relationships [55].

$$\mathrm{Rule} 1: if x is X_1 and y is Y_1, then f_1=k_{1}x+l_{1}y+m_1$$

(7)

$$\mathrm{Rule} 2: if x is X_2 and y is Y_2, then f_2=k_{2}x+l_{2}y+m_2$$

(8)

where x and y are inputs; X and Y are fuzzy sets; f is the output; and k, l, and m are the parameters defined by the artificial neural network. The typical architecture of ANFIS consists of five layers. A complete description of ANFIS can be found in Jang [53] and Jang and Sun [56].

The first layer, known as the fuzzification layer, receives inputs and applies a generalized Gaussian membership function to them, determining the degree to which each input belongs to various fuzzy sets. The subsequent layers, including the product and normalization layers, combine these fuzzy inputs using fuzzy logic operators to evaluate the rules of the fuzzy inference system. The defuzzification layer then converts the fuzzy classifications into a crisp output, which is finally aggregated in the output layer.

One of the key advantages of ANFIS is its ability to learn and optimize model parameters through adaptive methods such as back-propagation gradient descent and least squares techniques. This adaptability makes ANFIS particularly effective in handling complex, nonlinear problems where traditional linear models are not sufficient.

However, determining the optimal parameters for the membership functions can be a challenging and time-consuming process. Furthermore, the model can sometimes become trapped at local optimum points. To address these issues, optimization algorithms such as the GWO have been employed to enhance the model’s performance and help it avoid local optima.

Despite its complexity, ANFIS has been widely recognized for its effectiveness across various applications, particularly in areas where modeling nonlinear relationships is crucial. The integration of ANN enhances the model’s learning and optimization capabilities, making ANFIS a robust tool for predictive modeling in uncertain environments.

Overall, ANFIS stands out as a prime example of how combining different computational intelligence techniques can lead to more powerful and versatile modeling approaches, capable of solving a wide range of challenging real-world problems. A comprehensive understanding can be obtained from the foundational works by Jang, [53], as well as further explorations and applications discussed by Takagi and Sugeno [57] and Jang and Sun [56]. Recent optimizations and applications have been explored by researchers such as Keshtegar et al. [35], Zare and Koch [34], and the practical implementations were reviewed by Blyverket et al. [58].

2.4. SVM (Support Vector Machine)

Introduced by Vapnik [59], Support Vector Machine (SVM) is widely applied in classification and regression tasks, significantly benefitting forward-looking forecasts in hydrology, as well as various other fields.

Operating on principles of statistical learning theory, SVM is designed to provide a unique, optimal solution for a dataset, unlike other algorithms that might yield multiple solutions. This characteristic makes it particularly effective in mitigating overfitting scenarios by leveraging a kernel function, which is instrumental in defining decision boundaries within nonlinear contexts.

When utilized specifically in regression tasks, SVM is referred to as Support Vector Regression (SVR) [60]. While ANN primarily aim to minimize the empirical risk, the principal objective of SVR is to facilitate the minimization of statistical learning, enhancing the predictability and robustness of the model [61]. Due to its versatility and efficacy, SVM is popularly adopted not just for regression but also for classification purposes, establishing itself as one of the most prominent and successful algorithms in the machine learning arena, particularly because of its various modifications. These adaptations of SVM have been widely researched and have demonstrated effective outcomes in numerous studies [48,62,63,64,65]. The mathematical formulation of SVM can be seen in Equation (9), which models the relationship between input and output variables:

$$f\left(x\right)=\left(w,\varphi \left(x\right)\right)+b$$

(9)

where f(x) is a high-dimensional feature space, w is a weight of the output variable, and b is the bias term.

The performance of models can vary depending on the choice of kernel functions such as linear, polynomial, radial basis function (RBF), sigmoid, and Gaussian. In this study, the Gaussian kernel was chosen due to its significant impact on model outcomes. When deploying the Gaussian kernel, there are three crucial parameters that influence the performance: the scale parameter of the activation function (γ), the positive constant (C), and epsilon (ε), as discussed by Belayneh et al. [66]. During this research’s computations, these parameters were automatically optimized within the MATLAB program to maximize their efficacy on the model results. For a more comprehensive understanding of the theory and formulation of SVM, interested readers can refer to the detailed literature provided by Panahi et al. [67] and Vapnik [59].

2.5. Optimization Methods for Hybrid Models

In this study, ML and DL algorithms SVM and ANFIS, respectively, were used to predict future droughts. Optimization methods, which are ABC, GWO, GA, and PSO, were used to enhance the model performances. Initially, algorithm learning was performed with 70% of the dataset obtained from the region. Then, the optimization techniques mentioned above were used to further improve the performance of these algorithms. The results obtained from these models were evaluated according to performance evaluation criteria, RMSE, r, and NSE. If the results obtained met satisfactory level, the models were then used for predictions. A summary visual of this process is given in Figure 3.

2.5.1. PSO (Particle Swarm Optimization)

Particle swarm optimization (PSO) is a meta-heuristic algorithm first developed in 1995 by Kennedy and Eberhart [68]. Its advantages such as quick convergence, shorter computation time, and high suitability for optimizing nonlinear problems distinguish PSO from other evolutionary algorithms like GA [48,69]. PSO has gained popularity among researchers for solving optimization problems. Its design is inspired from the shoaling behavior of fish or the flocking behavior of birds searching for food. Each bird or fish is considered a particle that, in fact, represents a solution to the problem [70].

The particle searches in an n-dimensional space, where n denotes the number of parameters of the problem and attempts to find the best solution to the given problem. Upon first implementation of the algorithm, particles are randomly scattered in the problem space. During each iteration, they can update their position through finding the optimal solution [68,71,72,73,74].

The algorithm iterates multiple times until the optimal position discovered for each particle aligns with the overall best position [33,75,76]. Essentially, PSO algorithm concludes when all particles converge at a single point, indicating that the solution to the problem has been optimized.

2.5.2. GA (Genetic Algorithm)

Introduced by Holland in 1960, the development of this algorithm progressed throughout the 1960s and 1970s, the Genetic Algorithm (GA) is a search heuristic inspired by natural selection and Charles Darwin’s theory of evolution. Recognized as a prominent evolutionary algorithm, GA mimics natural processes by favoring the survival of the fittest individuals, as posited by Darwinian principles [32]. The GA optimization technique is one of the most renowned EA-based state-of-the-art algorithms, extensively researched and proven to be very successful in various industrial applications [77,78,79,80]. The considerable interest in GA can also be attributed to its capability as a search-based algorithm to address optimization problems encountered in ML [32]. Bras et al. [81] presented the versatile usage of GA with detailed examples of related studies ranging from obtaining the most useful linguistic summaries to adjusting the parameters in a fuzzy inference network. These engaging techniques involve a population of solutions that evolve and learn through processes similar to biological evolution, including crossover, mutation, and natural selection [81,82]. In GA optimization approaches, the search for the best possible solution is carried out in three stages: population initialization, GA operators, and evaluations using probabilistic transition rules rather than deterministic ones. This process continues until the termination terms and conditions are met [82,83]. As noted by Oladio and Sun [32], a major advantage of GA approaches is that they do not require derivatives of the error function, making them well suited for both continuous and discrete optimization problems. If the criterion is not satisfied, the problem of the generation cycle is done with the aim of improving the answers. Then, the genetic algorithm initiates a sequence of operations divided into three main steps [82,84]. These steps are:

(1)

Crossover (stochastic): part of two solutions “is swapped” to produce new ones.

(2)

Mutation (stochastic): part of a new solution “is flipped” to generate a new one and prevent it from converging into local optima.

(3)

Selection: the new solutions are evaluated according to the objective function, and the best candidates are selected.

In certain instances, such as a high mutation rate that could lead to the loss of good solutions, the elitism operator is employed to guarantee that the optimal solutions are transferred to the next generation without modification, ensuring that the best candidates are maintained within the solution set [81,84].

2.5.3. GWO (Grey Wolf Optimization)

The GWO technique developed by Mirjalili et al. [85] was inspired by the socio-hierarchical behavior and leadership of grey wolves, an algorithm to mimic the social dynamic and intelligence of grey wolves, during hunting [86]. This algorithm excels at handling intricate challenges and has produced successful results in many fields, as mentioned by numerous researchers [87]. It has many advantages in meteorological or hydrological modeling. Some of them: (1) GWO is easy to understand and implement. (2) The understandability of the algorithm minimizes errors in application. (3) Due to the linear structure of the algorithm, a straightforward implementation can be facilitated. The calculation process involves categorizing grey wolves into four types: the alpha wolf (α), beta wolves (β), delta wolves (δ), and omega wolves (ω). In the social hierarchy step (step 1), the best solution is considered as the alpha wolves (α), which are the leaders of the pack [85,86]. The second and third solutions are considered as beta (β) and delta (δ) wolves, respectively. Betas are subservient wolves that assist the alpha in decision-making, and the delta wolves include the sentinels, scouts, elders, caretakers, and hunters in the grey wolves pack. Finally, the remaining solutions are named as omega (ω). Omegas are considered as the scapegoat wolves in the pack and have the lowest rank of grey wolf [88]. The hunting strategy of grey wolves consists of three phases: identifying and approaching the prey, encircling it, and, finally, attacking it as described by Mirbouluki et al. [37], citing Muro et al. [89]. The GWO mathematical model mimics these stages, with the optimal solution referred to as the alpha solution [37]. Beta, delta, and omega solutions are the second, third, and fourth most optimal solutions, respectively. The details of the GWO technique can be found primarily in Mirjalili et al. [85] and the other studies cited in this section.

2.5.4. ABC (Artificial Bee Colony)

The ABC algorithm is a popular swarm-based meta-heuristic optimization algorithm inspired by honey bees’ natural foraging activity, proposed by Karaboga [90], as stated by Reda et al. [91]. The colony of artificial bees in the ABC algorithm consists of three groups of bees: employed bees, onlookers and scouts. Employed bees are responsible for searching for food sources and sharing this information with onlooker bees to recruit them. Onlooker bees tend to select promising food sources based on formation from those employed bees and further search the area around the selected food source, while scout bees are the bees that try to find new food sources independently [31,92,93]. Xu et al. [94] described the process as follows: employed bees initially collect food from familiar locations nearby. Upon discovering nectar, they perform a unique dance known as the waggle dance upon returning to the hive, which informs other bees of the food’s location. Following this, onlooker bees accompany one of these employed bees to further investigate the surrounding area of the food source. Concurrently, scout bees venture independently to randomly search extensive areas. If a food source remains the same for an extended period, the employed bee associated with it transforms into a scout. This bee then independently explores new regions, not relying on the findings from other bees, and returns to report potential new locations to the swarm. A detailed explanation of the standard ABC procedure can be found in Karaboga [90], Li et al. [92], and Vitorino et al. [93].

2.6. Model Performance Assessment

The literature offers a range of statistical performance metrics. In this study, the developed models were evaluated using three distinct statistical methods to assess their prediction accuracy: the Correlation Coefficient (R) (Equation (10)), Root Mean Square Error (RMSE) (Equation (11)), and the Nash–Sutcliffe efficiency (NSE) coefficient (Equation (12)).

In Equations (10)–(13), ${SPI}_{pi}$ = the predicted value, ${SPI}_{oi}$ = the observed value, N = the number of data, $\overline{S{PI}_o}$ = average observed value, and $\overline{S{PI}_p}$ = average predicted value.

The Correlation Coefficient (R) is given in Equation (10) [95]:

$$R={\displaystyle \frac{\sum _{i=1}^N{(SPI}_{pi}-\overline{S{PI}_p})({SPI}_{oi}-\overline{S{PI}_o})}{\sqrt{\sum _{i=1}^N{{(SPI}_{pi}-\overline{S{PI}_p})}^2}\ast \sqrt{\sum _{i=1}^N{({SPI}_{oi}-\overline{S{PI}_o})}^2}}}$$

(10)

RMSE is given in Equation (11) [96]:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=0}^N{\left({SPI}_{oi}-{SPI}_{pi}\right)}^2}$$

(11)

NSE is calculated in Equation (12):

$$NSE=1-\left[{\displaystyle \frac{\sum _{i=1}^N{\left({SPI}_{oi}-{SPI}_{pi}\right)}^2}{\sum _{i=1}^N{\left({SPI}_{oi}-\overline{S{PI}_o}\right)}^2}}\right]$$

(12)

A considerably more significant comparative result was obtained by using an RMSE-Standard Deviation Ratio (RSR), which was derived in Equation (13) [97].

$$RSR={\displaystyle \frac{\sqrt{{\sum }_{i=}^N{\left({SPI}_{oi}-{SPI}_{pi}\right)}^2}}{\sqrt{{\sum }_{i=}^N{\left({SPI}_{oi}-\overline{{SPI}_o}\right)}^2}}}$$

(13)

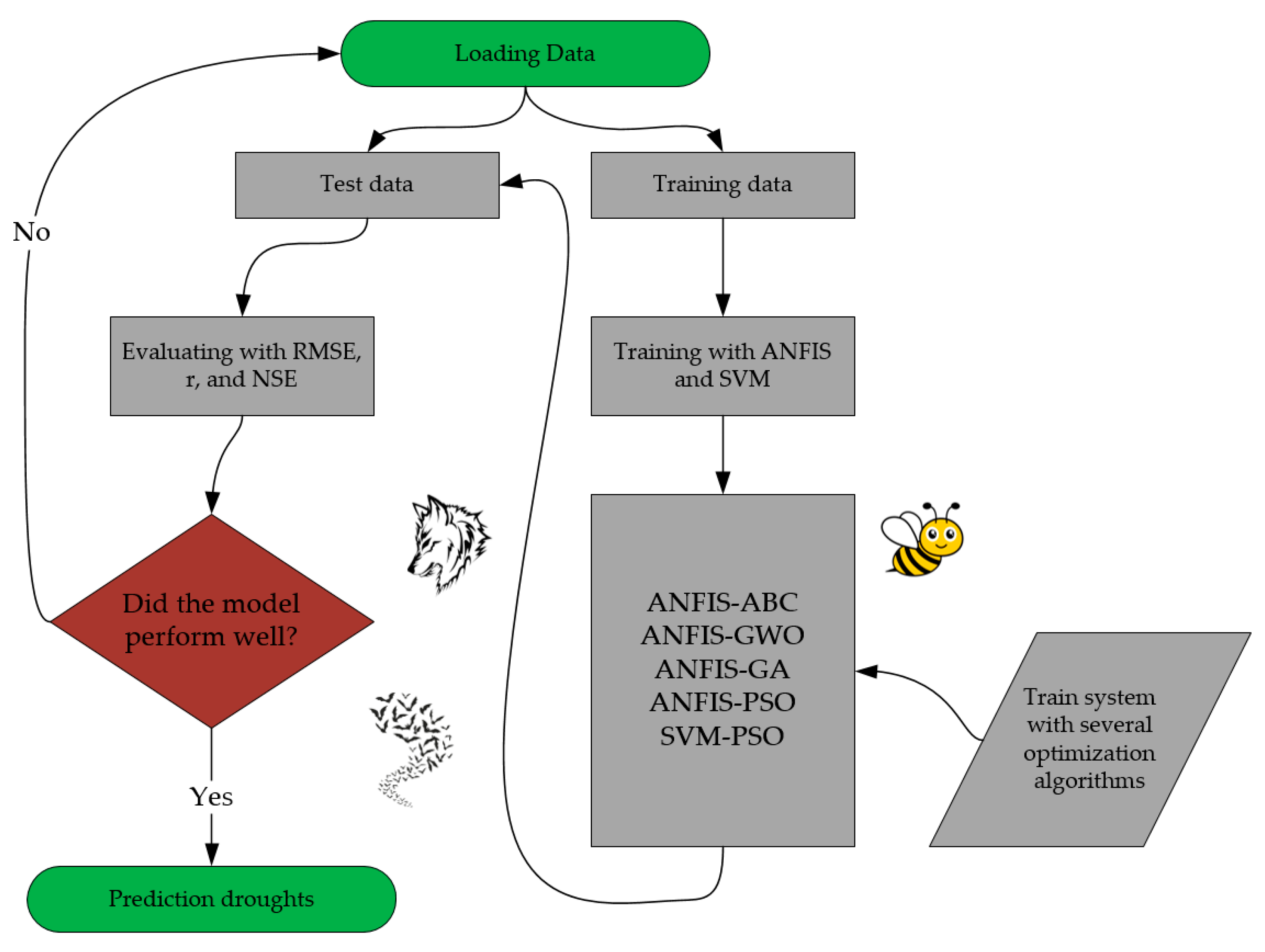
2.7. Model Structure

Research indicates that the 3-month and 12-month durations of the Standardized Precipitation Index (SPI) particularly well represent agricultural and hydrological droughts, respectively [98]. Therefore, this study focused on these specific timescales of the SPI, rather than analyzing all possible time steps. To identify the most informative inputs for the models, cross-correlation was employed when developing the model input structures. The cross-correlation has been a widely used technique by researchers to reveal the relationship between variables such as in [99]. Figure 4 displays the results of the cross-correlation analysis, while

Table 3. Input and output structure of the models.

Model	Inputs							Output
M01						SPI12t−2	SPI12t−1	SPI12t
M02					SPI12t−3	SPI12t−2	SPI12t−1	SPI12t
M03				SPI12t−4	SPI12t−3	SPI12t−2	SPI12t−1	SPI12t
M04			SPI12t−13	SPI12t−12	SPI12t−11	SPI12t−2	SPI12t−1	SPI12t
M05		SPI12t−13	SPI12t−12	SPI12t−11	SPI12t−3	SPI12t−2	SPI12t−1	SPI12t
M06	SPI12t−13	SPI12t−12	SPI12t−11	SPI12t−4	SPI12t−3	SPI12t−2	SPI12t−1	SPI12t
M07						SPI3t−2	SPI3t−1	SPI3t
M08					SPI3t−3	SPI3t−2	SPI3t−1	SPI3t
M09				SPI3t−4	SPI3t−3	SPI3t−2	SPI3t−1	SPI3t
M10			SPI3t−13	SPI3t−12	SPI3t−11	SPI3t−2	SPI3t−1	SPI3t
M11		SPI3t−13	SPI3t−12	SPI3t−11	SPI3t−3	SPI3t−2	SPI3t−1	SPI3t
M12	SPI3t−13	SPI3t−12	SPI3t−11	SPI3t−4	SPI3t−3	SPI3t−2	SPI3t−1	SPI3t

provides information on all the models developed in this study.

Table 3 presents the input and output parameters for the models developed in this study. The input parameters consist of the lagged SPI12 values while output parameters are the SPI12 values at time t, i.e., SPI12_t−1 represents the SPI12 value at time t − 1, SPI12_t−2 represents the SPI12 value at time t − 2, etc.

3. Results and Discussion

In this study, the SPI12 and SPI3 indices, which better represent meteorological and hydrological drought, respectively, were derived using monthly precipitation data from the Tromsø region [98]. The categorization of drought levels based on SPI values was detailed earlier (Table 2). The calculations revealed, as depicted in Figure 5, that both the 12-month and 3-month SPI captured dry and wet periods across all drought classes. According to Figure 5, the most severe drought condition recorded for the SPI12 index occurred in September 1950 (9.1950), while November 1952 (11.1952) marked the most extreme condition for the SPI3 index.

Additionally, further extremely dry periods were observed in September 1935; February, March, April, and June 1950; April 1960; and February 1979, as recorded in the SPI12 index, while the SPI3 index identified significant droughts in September 1957, August 1969, August 1978, June 1987, October 1995, October 1996, August 2015, November 2022, and July 2022. Some of the dry periods are marked as red circles in Figure 5. It was determined that the transitions between dry periods and wet periods were higher in SPI3 due to higher variance values compared to SPI12. Documented in Table 3, the following model input structures were created based on the data derived from SPI12 and SPI3.

The models, constructed with the specified input structure, were evaluated using the optimization techniques outlined earlier, including ANFIS-PSO, ANFIS-GA, ANFIS-GWO, and ANFIS-ABC, as well as SVM-PSO. Consistent with the findings of the existing literature, 70% of the data was employed as learning in the analyses, whereas the remaining 30% was for testing [39,98]. Detailed results from the analysis, applied methodologies for testing data, can be found in

Table 4. Results of the testing data for all models and algorithms.

Models	SVM-PSO			ANFIS-PSO			ANFIS-GA
	r	NSE	RMSE	r	NSE	RMSE	r	NSE	RMSE
M01	0.9172	0.8284	0.4185	0.9343	0.8726	0.3606	0.9352	0.8743	0.3582
M02	0.9258	0.8563	0.3830	0.9348	0.8736	0.3592	0.9338	0.8718	0.3618
M03	0.9270	0.8587	0.3798	0.9352	0.8744	0.3580	0.9330	0.8702	0.3639
M04	0.9494	0.9011	0.3177	0.9511	0.9038	0.3133	0.9388	0.8786	0.3520
M05	0.9483	0.8990	0.3211	0.9500	0.9021	0.3161	0.9484	0.8984	0.3220
M06	0.9514	0.9049	0.3116	0.9496	0.9013	0.3174	0.9429	0.8867	0.3401
M07	0.7665	0.5740	0.6794	0.7850	0.6161	0.6450	0.7886	0.6219	0.6400
M08	0.7806	0.5667	0.6852	0.8019	0.6431	0.6218	0.8031	0.6448	0.6204
M09	0.8043	0.6459	0.6194	0.8015	0.6420	0.6228	0.8092	0.6545	0.6118
M10	0.7823	0.6120	0.6484	0.7854	0.6162	0.6449	0.7857	0.6171	0.6441
M11	0.7980	0.6365	0.6275	0.7960	0.6320	0.6315	0.8022	0.6432	0.6218
M12	0.8085	0.6468	0.6186	0.8206	0.6731	0.5952	0.8140	0.6622	0.6050
	ANFIS-GWO			ANFIS-ABC
	r	NSE	RMSE	r	NSE	RMSE
M01	0.9346	0.4964	0.7170	0.9340	0.8718	0.3617
M02	0.9347	0.4973	0.7164	0.9345	0.8728	0.3604
M03	0.9347	0.4973	0.7163	0.9335	0.8713	0.3625
M04	0.9514	0.4614	0.7415	0.9516	0.9054	0.3108
M05	0.9514	0.4607	0.7420	0.9512	0.9042	0.3127
M06	0.9514	0.4618	0.7412	0.9515	0.9050	0.3114
M07	0.7750	0.5104	0.7283	0.7793	0.6037	0.6552
M08	0.7928	0.5223	0.7194	0.7935	0.6294	0.6337
M09	0.8046	0.5294	0.7141	0.7980	0.6363	0.6278
M10	0.7842	0.5189	0.7220	0.7867	0.6187	0.6428
M11	0.7988	0.5284	0.7148	0.7979	0.6352	0.6287
M12	0.8135	0.5374	0.7079	0.8121	0.6593	0.6075

.

Based on the detailed results in Table 4, where the most successful results are highlighted in bold, M04 operating under the ANFIS-ABC algorithm, achieved r: 0.9516, NSE: 0.9054, and RMSE: 0.3108 and emerged as the best performer among all the algorithms tested. The input for this model was structured using SPI values lagged by 1 and 2 months, as well as by 11, 12, and 13 months. The M06 model with r: 0.9515, NSE: 0.9050, and RMSE: 0.3114 and M05 model with r: 0.9512, NSE: 0.9042, and RMSE: 0.3127 within the ANFIS-ABC category also yield a very similar performance to those achieved by this M04 model. Additionally, in this category, among the models containing SPI3 data in the input structure, the most appropriate result was M12, which is an indication that it is the most suitable model structure. The model, in this category, demonstrated superior performance and predictive capabilities, compared to other model data, including SPI3, combinations evaluated in the study. The results underscore the synergistic relationship between the M12 model’s architecture and the informative content embedded within the SPI3 dataset. This specific combination appears to have effectively captured underlying patterns and trends in the data, leading to enhanced predictive accuracy and overall model efficacy. The convergence in the performance parameters, with slight variations among these models, indicate that they are both leading models such as M04 and suggest that each setup has demonstrated an ability to provide representation of the underlying climate dynamics. The slight underperformance of models M06 and M05 compared to M04 can be attributed to the use of SPI values lagged by 2 and 1 months of those models, respectively. Comparatively, the models utilizing SPI12 data (M01–M06) demonstrated an overall better performance than those configured with SPI3 inputs (M07–M12). This distinction underlines the importance of selecting appropriate SPI indices and their temporal lagged values to optimize model efficiency.

Applying SVM-PSO to M06 generated another successful outcome from the analysis following the M04 model in ANFIS-ABC. M06, which input structure consisted of SPI values lagged by 1, 2, 3, and 4 months, as well as by 11, 12, and 13 months, achieved performance values of r: 0.9514, NSE: 0.9049, and RMSE: 0.3116. Within the scope of this study, the models developed using SPI3 as input data demonstrated lower performance values compared to those utilizing SPI12 data. This suggests that the predictive capabilities and insights derived from SPI12 values were significantly more robust for generating accurate models than those based on SPI3. Potential factors contributing to this disparity could include the higher temporal resolution of SPI12, which may capture longer-term forecasting and the peak points more effectively in time series.

ANFIS-PSO, although demonstrating promising results, delivered a slightly lower performance than that of SVM-PSO. Despite this difference, both methods demonstrated comparable effectiveness. The choice between them may depend on the specific application requirements. Exploring hybrid or ensemble approaches that combine the strengths of both methods could possibly enhance the predictive power. M04, achieving performance values of r: 0.9511, NSE: 0.9038, and RMSE:0.3133, emerged as the top-performing model within ANFIS-PSO. The input structure of this model comprised SPI values that were lagged by 1 and 2 months, as well as by 11, 12, and 13 months. Following the ANFIS-PSO analyses, M05 and M06 produced results very close to those of M04, suggesting similar effectiveness.

ANFIS-GWO exhibited the lowest performance among all the models tested. This suggests a potential misalignment between the ANFIS architecture and the GWO optimization approach. In contrast to the models incorporating SPI12 in their input structures, those created with SPI3 data consistently underperformed. The best-performing model in this class was M12, with performance values of r: 0.8135, NSE: 0.5374, and RMSE: 0.7079.

To enhance a more comprehensive model performance comparison, Figure 6 presents a 3D scatter plot visualization of selected top-performing models. This graphical representation provides a deeper understanding of the relationships between different performance parameters across these models. As shown in Figure 6, the model with the best performance is located at the far right and bottom. Specifically, the ANFIS-ABC-M04 model outperforms all other models evaluated. Its superior performance is likely attributed to the effective combination of ANFIS-ABC and the M04 input structure, which together excel at capturing complex data patterns.

Ridge charts provide an alternative method to visually compare and contrast the model performance. This visualization technique offers a structured overview, facilitating a deeper understanding of the relative strengths and weaknesses of different models (Figure 7). Interestingly, unlike the statistical performance metrics, SVM-PSO-M02 and ANFIS-ABC-M02 appear to most accurately reflect the observed values in the ridge chart (Figure 7). When the other models were examined, it was evident that there were peaks on the graph, especially the initial region, contrary to the observed values. However, subsequent comparative graphs clearly align more closely with the expected outcomes.

The prediction performance across the models can be assessed visually in Figure 8, which displays box plots and normal distributions for both the prediction models and observed values. Considering Figure 8, the ANFIS-ABC-M04 and SVM-PSO-M04 models exhibit the most analogous distributions that align with the normal distribution of observation values. Notably, the range of the predicted values obtained from ANFIS-ABC-M04 are within the same range as the observed values, making it the most successful model among the others. In Figure 8, the excess data in the third quartile of the normal distribution line for the observation values; that is, in the upper range, is aligned in both location and amount with the ANFIS-ABC-M04 model. Additionally, the median and mean values of this model are consistent with the observed values, compared to other methods.

The Taylor diagram is a widely preferred method among scientists working with machine learning for comprehensively comparing the model performance based on multiple criteria. Figure 9 illustrates the findings obtained from the Taylor diagram generated for this study. Upon examining Figure 9, one of the first noticeable results is the significant overlap among the models, which makes it difficult to infer variations among the models in terms of performance alone. On the other hand, it can be depicted from the Taylor diagram that the SVM-PSO-M02 and ANFIS-ABC-M02 models demonstrate relatively lower performance compared to other algorithms. For more nuanced analyses, a violin plot is provided in the following section.

The violin plot is another method for model performance comparison. By displaying the kernel density, average, quartiles, prediction values, and percentages for each predicted model, seen on related observation values, this visualization technique provides a thorough evaluation. Examination of Figure 10 reveals that the ANFIS-ABC-M04 model demonstrates the highest compatibility with the observation and aligned well with the statistical performance values. Moreover, there are discrepancies especially in extreme values and the third quartile between the predicted and observed values for the SVM-PSO-M02 and ANFIS-ABC-M02 models. As a result, these two models lag behind the others in terms of performance.

Figure 11 presents the time series graphs for the two models, ANFIS-ABC-M04 and SVM-PSO-M06, identified as the most successful based on the various comparison methods and statistical evaluations discussed previously. Additionally, Figure 11 also includes scatter plots of these two models. A visual inspection of the scatter diagram indicates a high degree of similarity between the predicted values generated by the ANFIS-ABC-M04 and SVM-PSO-M06 models. Although both models exhibited strong predictive capabilities for the peak values, the ANFIS-ABC-M04 model consistently outperformed the SVM-PSO-M06 model in terms of accuracy.

Figure 11 also displays the time series and scatter plots for the ANFIS-GA-M05 and ANFIS-PSO-M04 models. When looking at the time series, although both models are quite good at capturing peak values, they are behind ANFIS-ABC-M04 and SVM-PSO-M06 in statistical evaluation, except for initial values of observation. This situation does not change in the scatter diagrams. While the time series indicate that both models are relatively effective at capturing peak values, their statistical performance is not as good as ANFIS-ABC-M04 and SVM-PSO-M06, except for the initial observed values. This pattern is consistently also observed in the scatter plots.

Figure 12 presents the results of the RSR analysis. According to the results, the ANFIS-PSO, ANFIS-GA, and ANFIS-ABC algorithms outperformed the other algorithms in terms of the RSR. ANFIS-PSO achieved the best performance according to the RSR metric, while ANFIS-ABC excelled in the statistical analysis. Although ANFIS-PSO emerged as the top performer based on the RSR method, statistical comparisons suggest that the performance of all three algorithms is quite similar. Therefore, this study concludes that all these three algorithms are successful, consistent with what the statistical results suggest.

Overall, while the statistical results were generally comparable among the models, the ANFIS-ABC-M04 model consistently demonstrated superior performance when both the graphical methods and statistical metrics were evaluated. Based on these findings, the ANFIS-ABC-M04 model is identified as the optimal model and algorithm for future drought prediction modeling applications in the region.

Our findings are consistent with those of other studies that have utilized similar algorithms, model input structures, and the SPI for drought prediction modeling. For instance, highlighting the importance of river flows, Turan [100] used Fuzzy Systems, along with a series of optimization algorithms, including ABC, Firefly Algorithm (FA), and Hunter search algorithm (HUS), to predict streamflow in Susurluk Basin. The author reported that the ABC optimization algorithm yielded superior results compared to other methods. Similarly, Karaboga and Kaya [42] investigated the performance of various optimization methods, such as ABC, adaptive ABC (aABC), GA, PSO, and harmony search (HS), combined with ANFIS for identifying nonlinear static systems. They used several performance criteria, including the Wilcoxon test and RMSE, and revealed that ABC with ANFIS was the best-performing method after aABC, while ANFIS-GWO and ANFIS-PSO achieved successful results, according to our findings. Numerous studies in the literature further support the success of these algorithms. For instance, Kikon et al. [36] conducted a study on drought prediction using the Effective Drought Index (EDI) and various machine learning algorithms and optimization techniques. They determined that ANFIS, when combined with PSO, GA, and the Generalized Regression Neural Network (GRNN), produced promising results for estimating the EDI, particularly with the ANFIS-PSO and ANFIS-GA models. In another study on drought prediction modeling in Barrak Valley, Samantaray et al. [101] compared SVM-PSO with a series of hybrid methods, including SVM, back-propagation neural network (BPNN), and an integration of SVM. In their study, SVM-PSO was more effective than other methods. In this study, SVM-PSO was found to be the most successful algorithm after ANFIS-ABC, and it is one of the most effective algorithms in this study. Thereby, the information in the two studies overlaps with each other.

While the findings of many studies align with the results of our study, there are also contrasting results. However, these studies generally focused on estimating different parameters rather than prediction droughts. Moayedi et al. [102], for instance, employed several optimization techniques, such as ABC, GWO, and HHO, for predicting parameters used in groundwater quality assessment. They employed ANN as a tool for simulating groundwater quality characteristics. Their results demonstrated that the GWO-ANN approach effectively simulated and evaluated the groundwater quality with the GWO optimization method outperforming other methods. This is in contrast to our study, where models based on GWO did not exhibit enhanced performance.

This study provides valuable insights into future drought conditions in the Tromsø region and provides guidance to decision-making authorities and institutions for drought prevention, mitigation, and policy development. The findings are particularly relevant for those working in water resources management and related fields.

We recommend the following directions for future research:

• While the SPI is a widely used and well established drought index, exploring other drought indices could provide additional perspectives.
• Expanding the meteorological network in the region by incorporating data from additional stations, if feasible, would enhance the spatial resolution and accuracy of drought modeling.
• Incorporating additional meteorological variables, such as evaporation and temperature, along with data from nearby stations, could improve the model’s predictive capabilities.

Lastly, it is important to acknowledge that the scope of this study was limited by the use of a relatively small set of optimization and learning algorithms as well as the limited number of meteorological stations included in the analysis.

4. Conclusions

This study modeled future droughts in the Tromsø region using a combination of ANFIS with various optimization algorithms and PSO-optimized SVM, based on the monthly precipitation data. Different model input structures employed for incorporating SPI12 and SPI3 data. Additionally, 70% of the data was used for training, and all findings presented in this study are based on the remaining 30% test data. The key findings are summarized below:

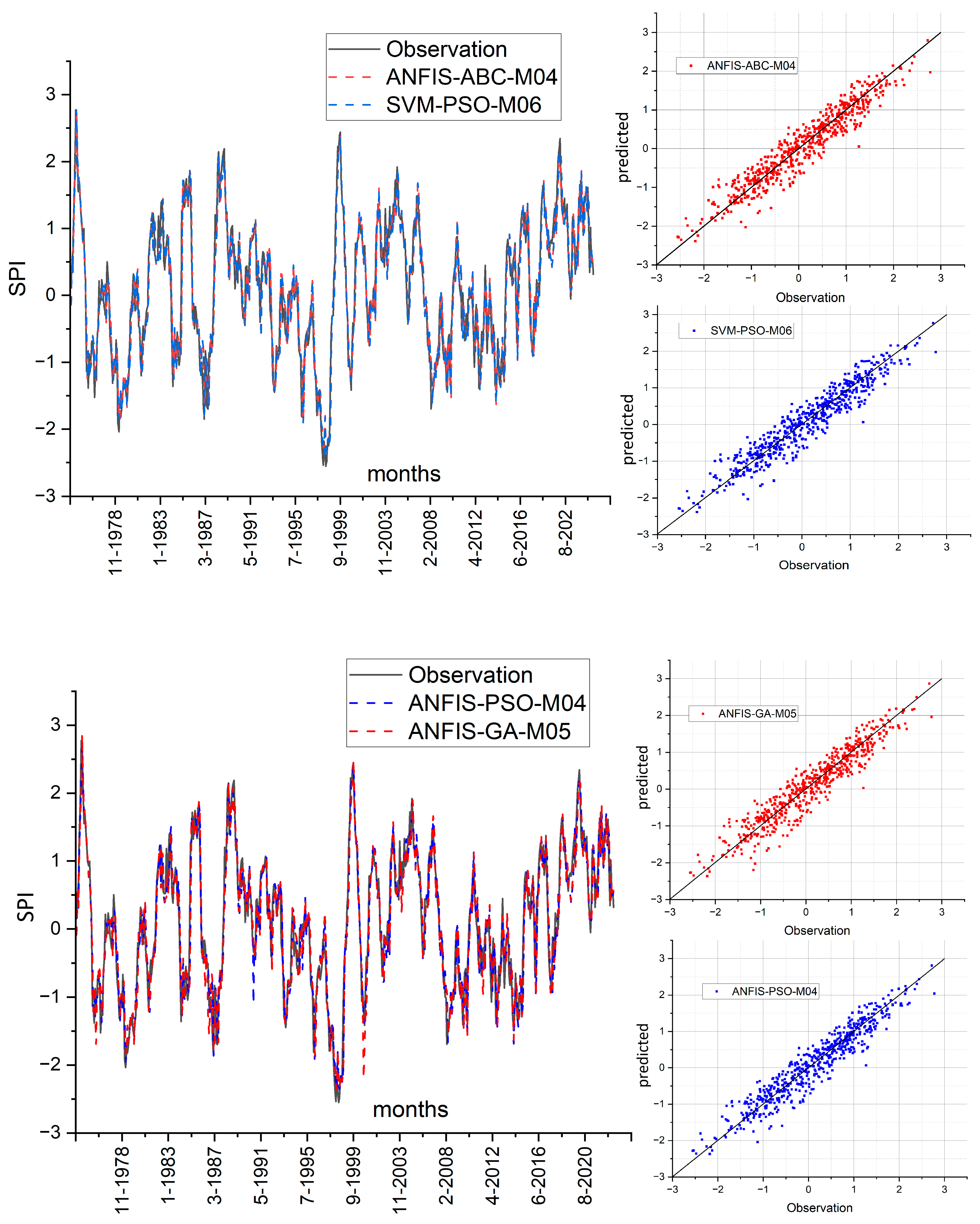
• ANFIS-ABC-M04 emerged as the most successful model in this study. This model and its corresponding input structures are recommended for future drought prediction modeling studies in this region. Given its strong performance, after ANFIS-ABC-M04 model, SVM-PSO-M06 should be another model that can be preferred as a viable alternative.
• Models using SPI12 data in their input structure consistently outperformed those incorporating SPI3 data.
• The input structures of M01, M02, and M03 were created using SPI12 data lagged up to 2, 3, and 4 months, respectively. These models demonstrated a lower performance compared to the M04, M05, and M06 models. As a result, incorporating SPI12 lagged by 11, 12, and 13 months, in addition to those shorter lags, positively impacted the model performance, similar to SPI3 data.
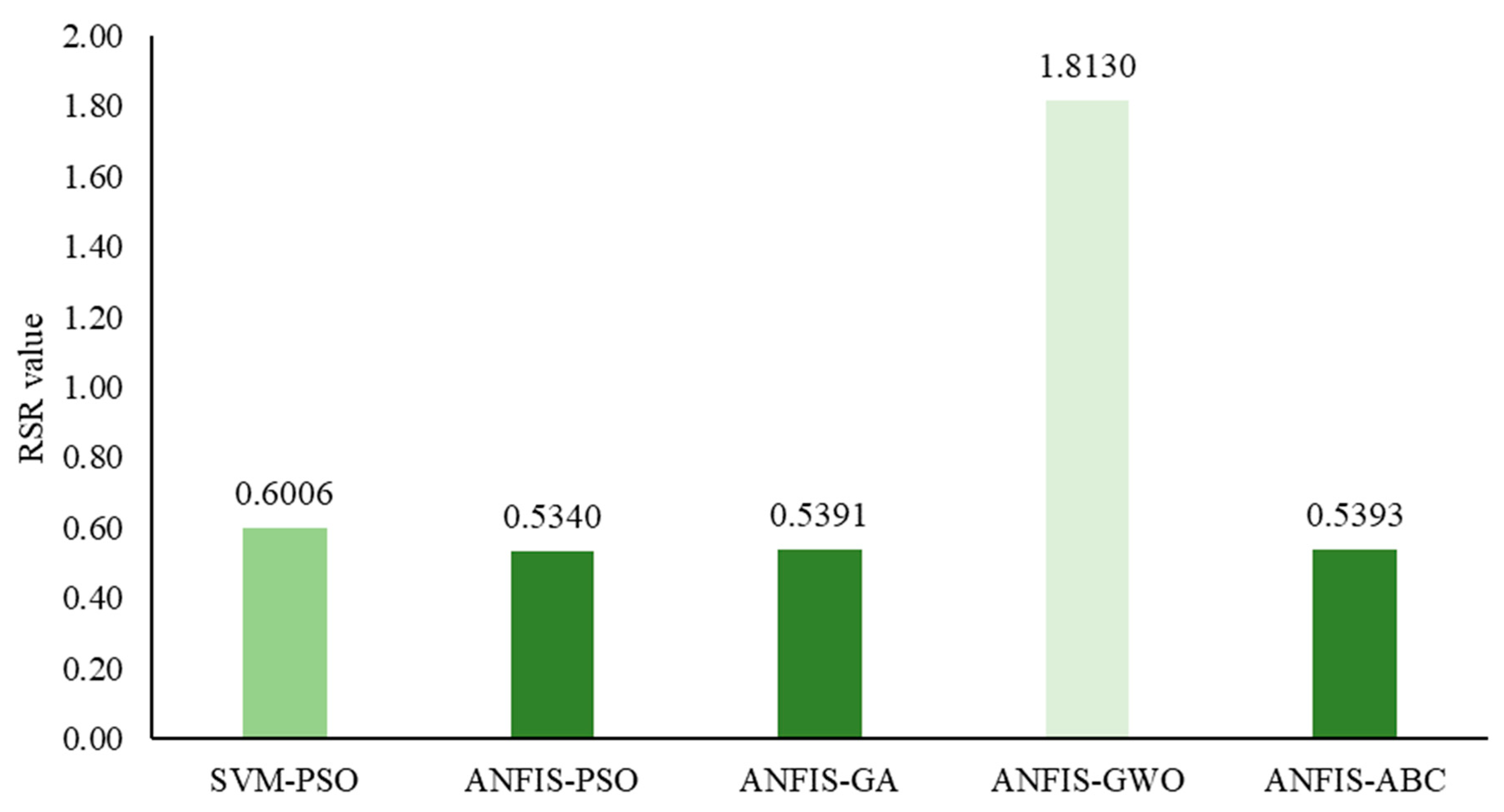
• All algorithms, except for ANFIS-GWO, produced comparable results. The ANFIS-GWO model yielded significantly different outcomes, indicating potential limitations of this algorithm under the specific conditions of the selected region.
• Among the models and algorithms using SPI3 data in their input structure, the ANFIS-GA algorithm with the M09 model/input structure was determined as the most effective.
• Drought analyses displayed higher extremely dry values for SPI3 compared to SPI12.
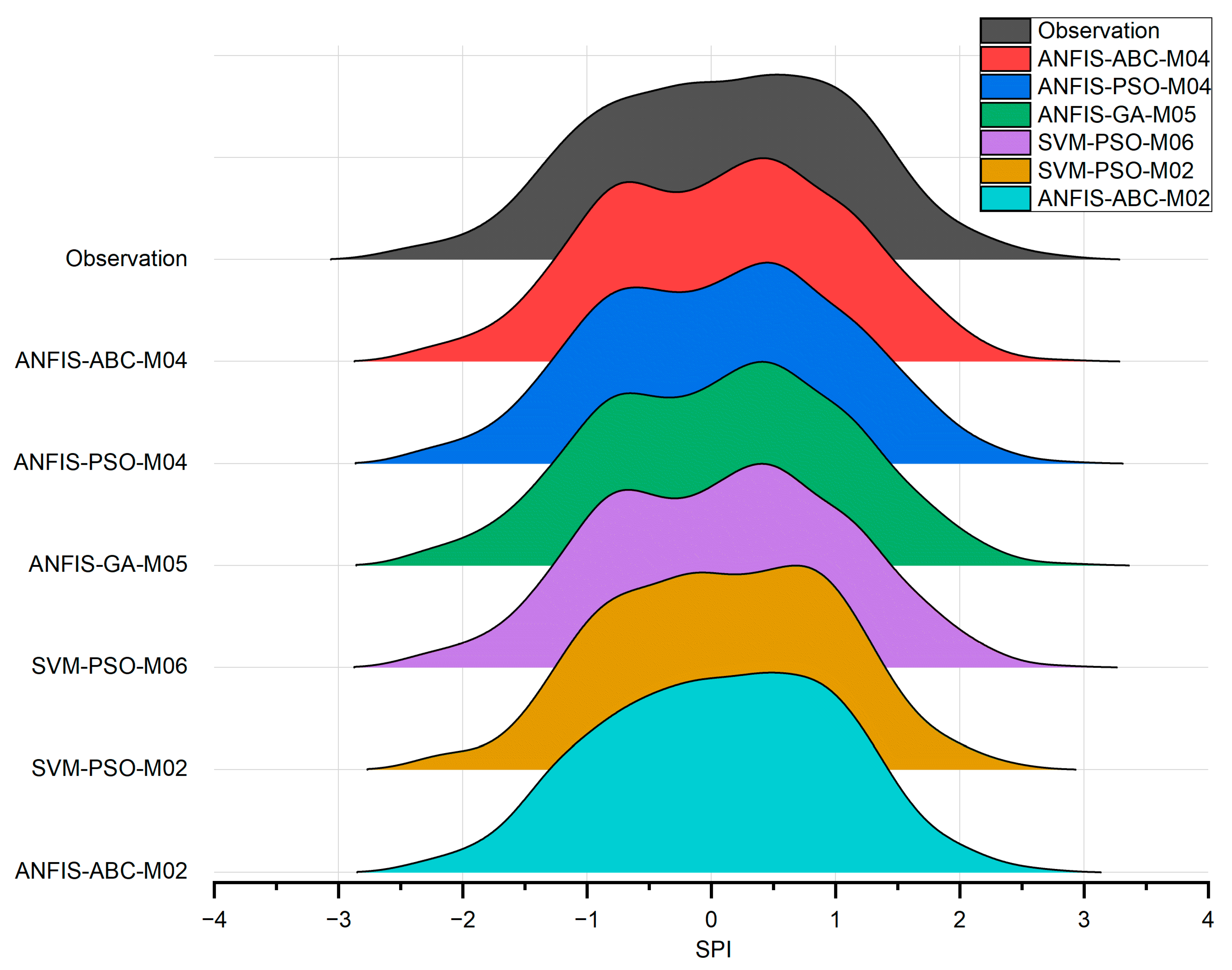
• The ridge chart visualization approach yielded results that did not match the statistical findings for this region.
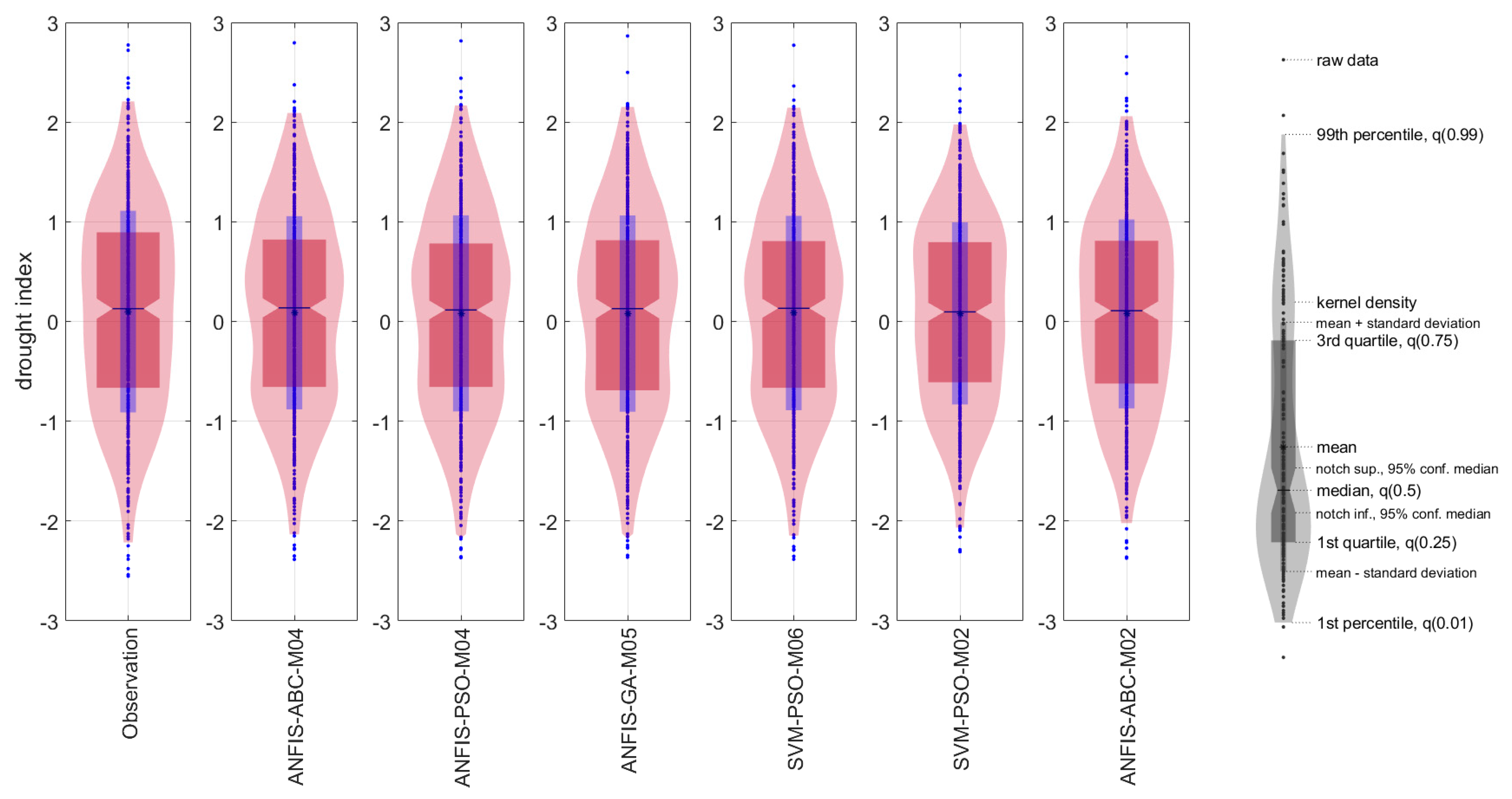
• Graphical evaluation yielded the most effective results, with Taylor and Violin diagrams. These diagrams are recommended for use in future drought modeling studies based on the superior insights they provided compared to the others.
• The basic parameters in creating the Taylor diagram are the RMSE, standard deviation, and correlation coefficient. Accordingly, most of the patterns detected in this diagram overlap. NSE was used in the statistical evaluation in this study. This shows that it is an effective parameter used to distinguish performance between models.
• The utilization of the ABC optimization approach in drought prediction models is recommended due to its superior effectiveness compared to alternative optimization methods. It should be paired with different ML and DL algorithms and employed in future studies.
• Scatter diagrams should be used to evaluate the model performance in prediction models, as they provide precise information into whether the peak values can be predicted accurately or not.