A Methodology for Modeling a Multi-Dimensional Joint Distribution of Parameters Based on Small-Sample Data, and Its Application in High Rockfill Dams
Abstract
1. Introduction
2. Methodology
2.1. Multi-Dimensional Joint Distribution Model
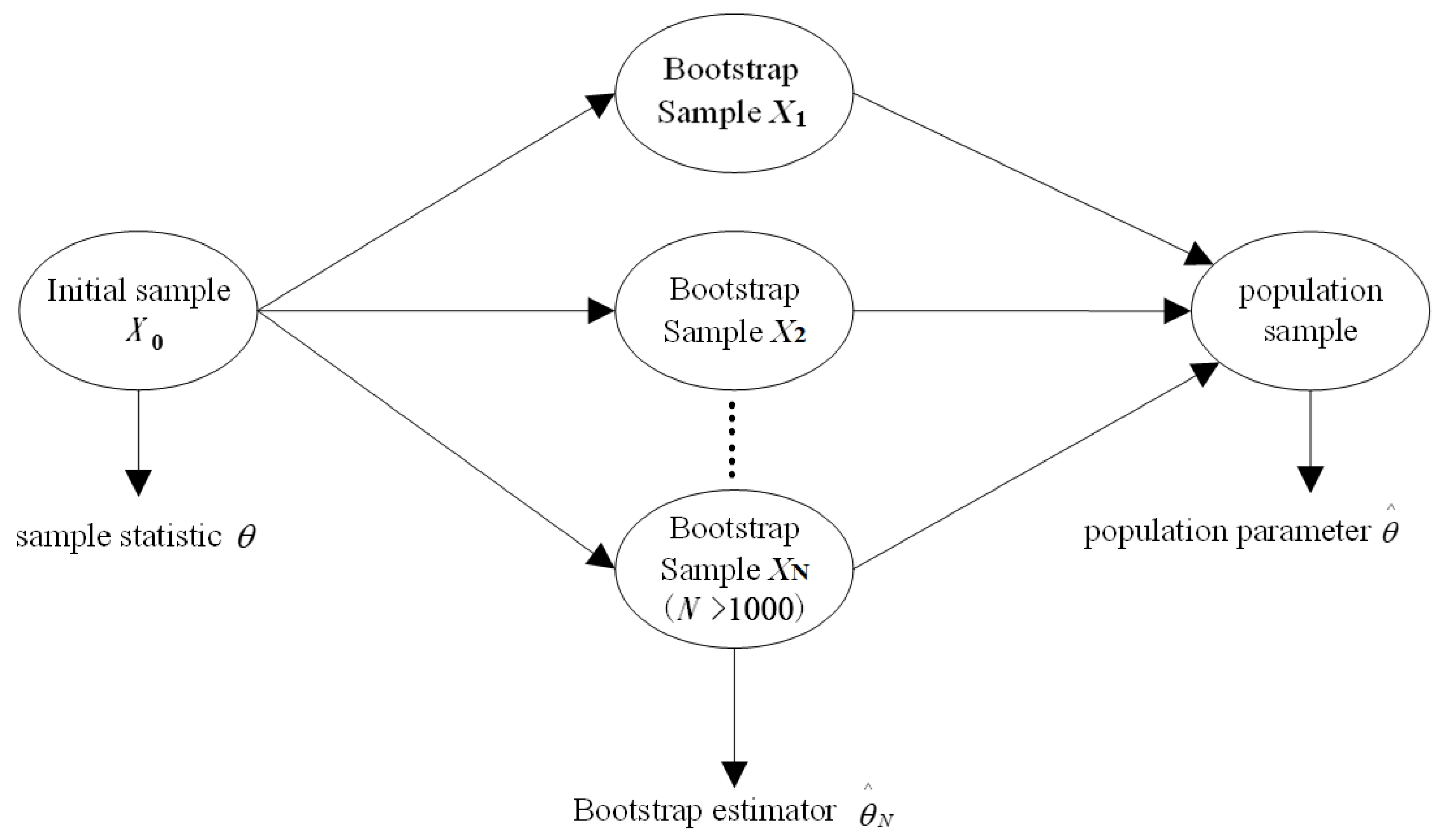
2.1.1. Material Parametric Statistical Method Based on Small-Sample Data
2.1.2. Marginal Distribution Test
2.1.3. The Construction Method of a Multi-Dimensional Joint Distribution Model for Parameters
2.2. Cracking Risk Analysis Method for the Core Wall
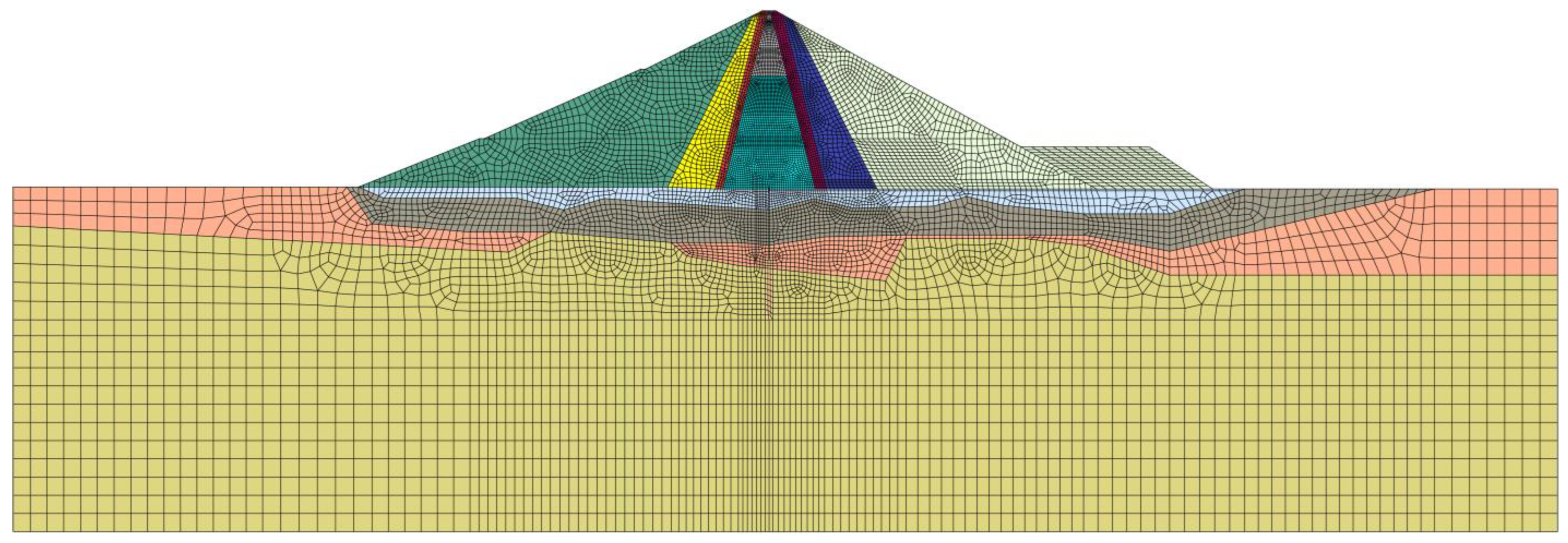
3. Case Study
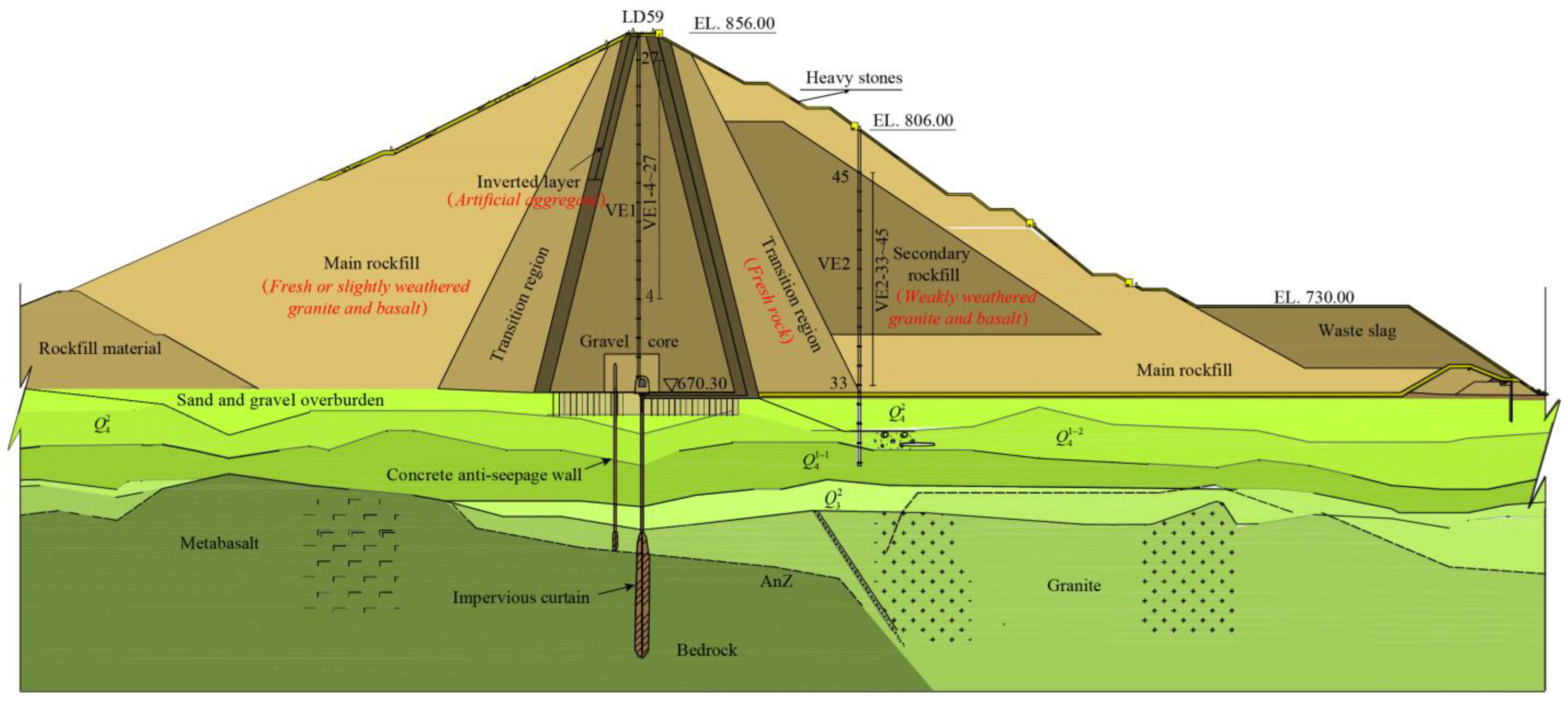
3.1. Project Specification
3.2. Statistical Analysis of the Multi-Dimensional Joint Distribution Model for the Duncan–Chang Model Parameters
3.2.1. Interval Estimation of the Duncan–Chang Model Parameters for High Rockfill Dams
3.2.2. Distribution Types of the Duncan–Chang Model Parameters
3.2.3. The Multi-Dimensional Joint Distribution Model for the Duncan–Chang Model Parameters
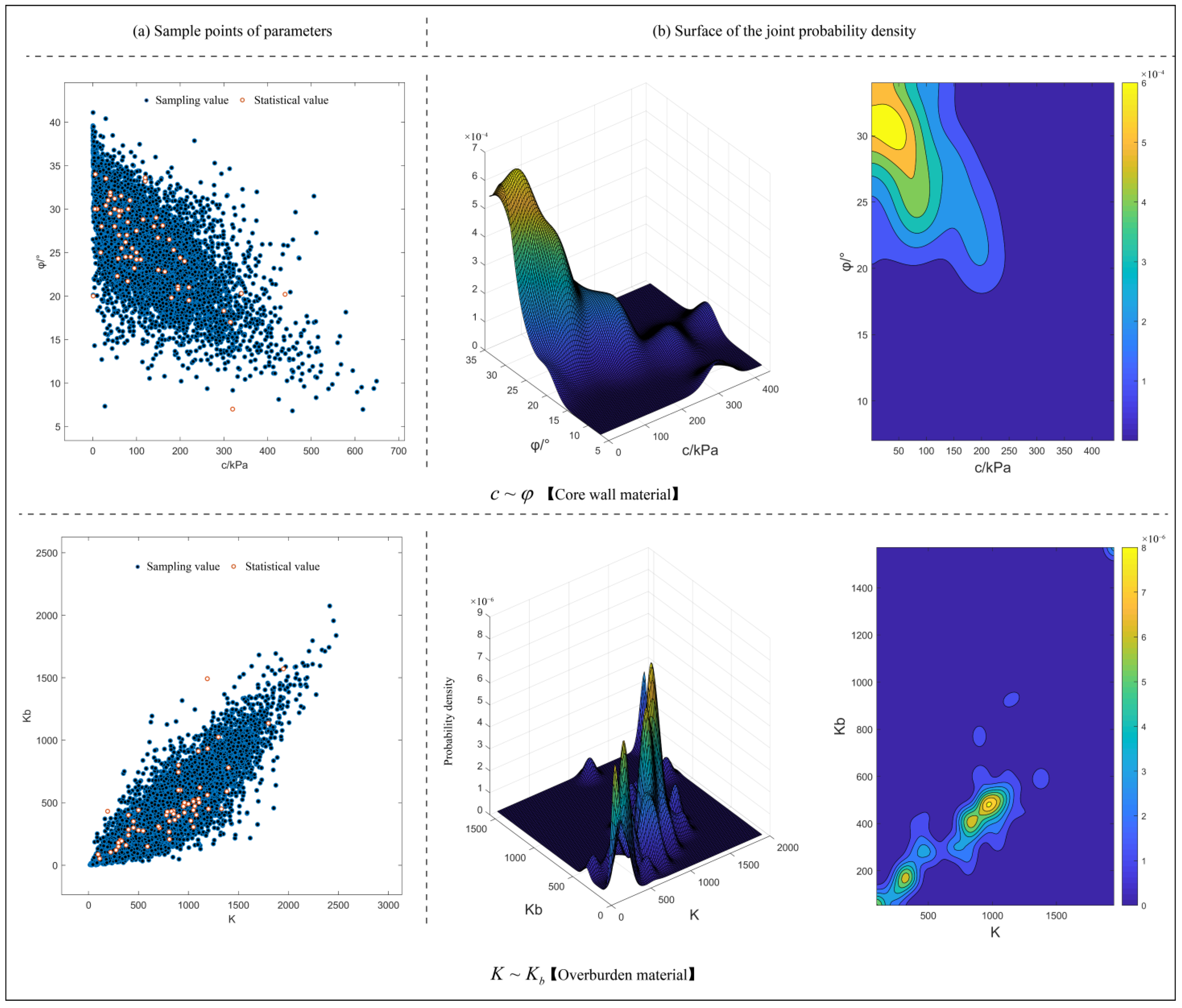
Correlation Analysis of Duncan–Chang Model Parameters
Construction of the Multi-Dimensional Joint Distribution Model for the Duncan–Chang Model Parameters
3.3. Cracking Risk Analysis of the Core Wall
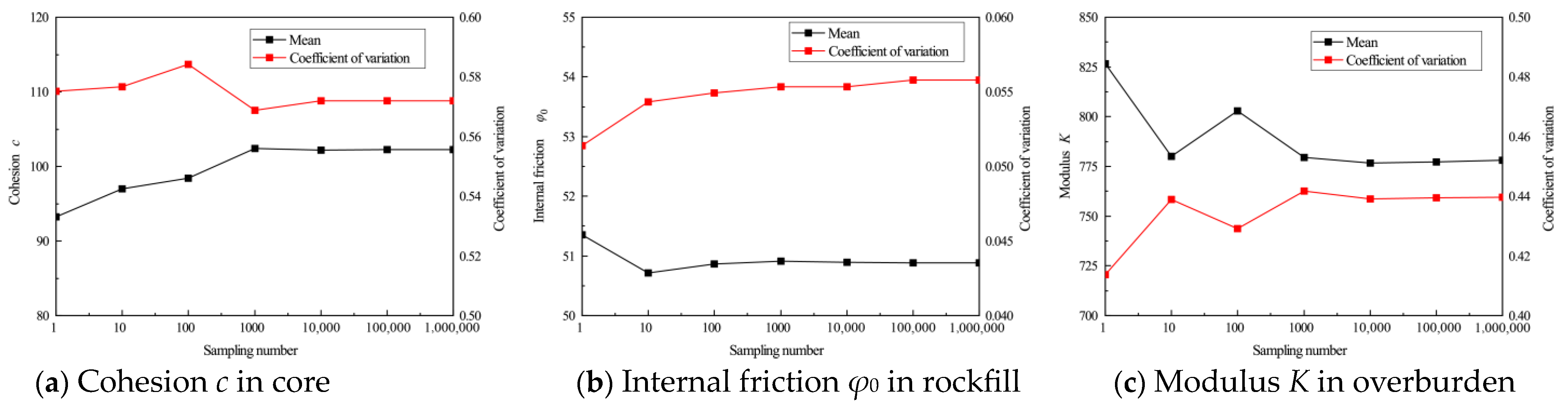
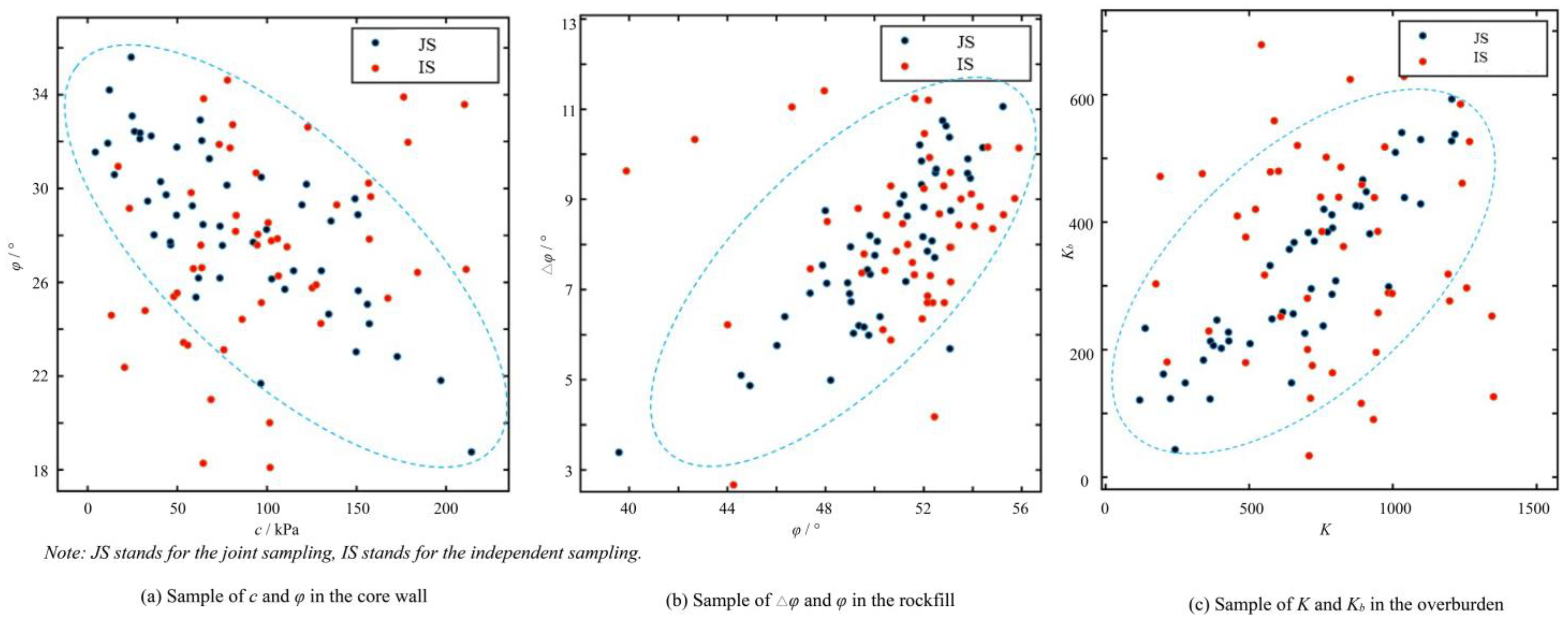
3.3.1. Analysis of the Sample Point Change Law for Independent and Joint Sampling of Parameters
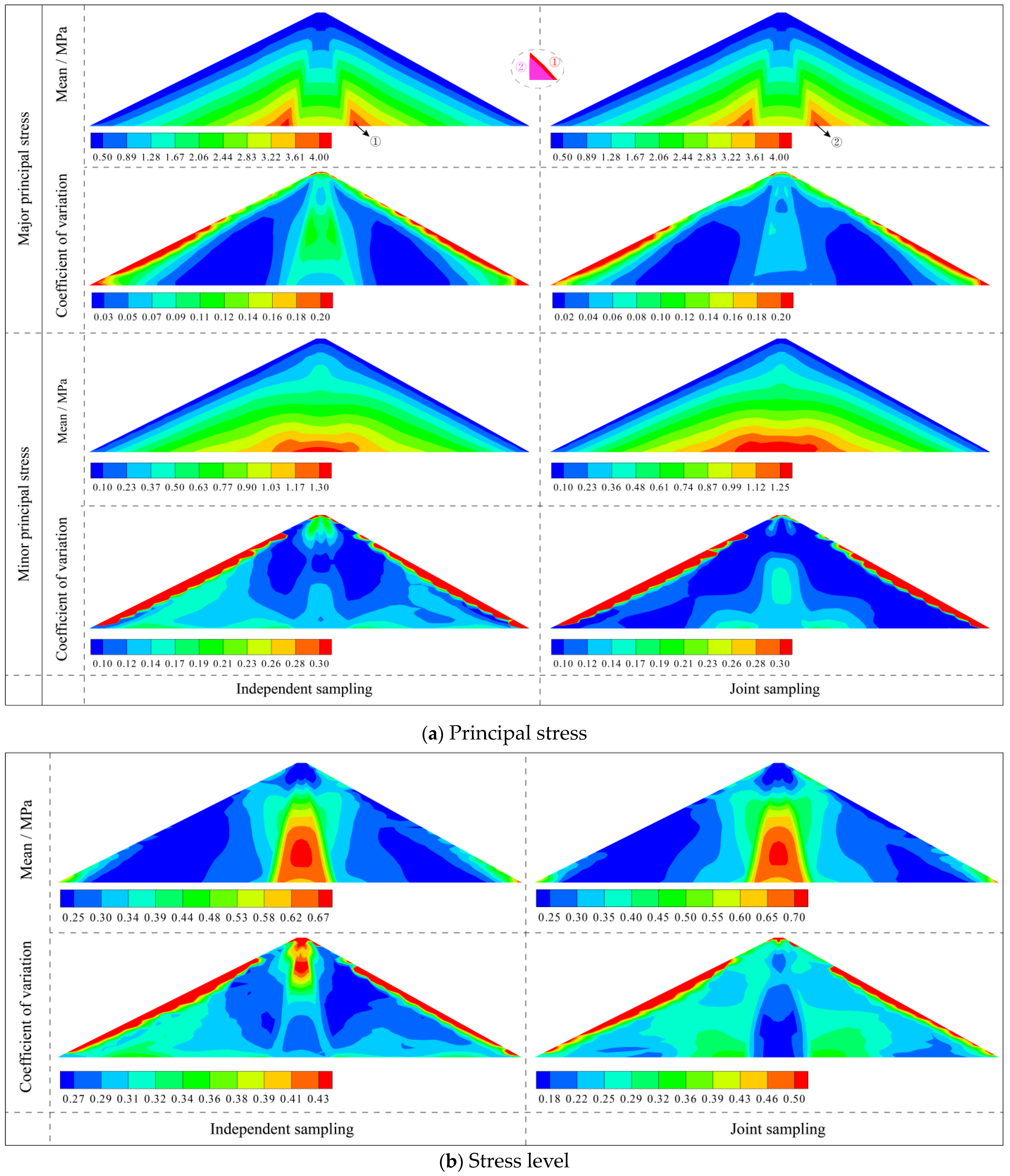
3.3.2. Analysis of the Deformation and Stress of Dams Based on the Independent and Joint Sampling of Parameters
3.3.3. Analysis of the Cracking Risk
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Water Resources of the People’s Republic of China (MWRPRC). 2021 Statistic Bulletin on China Water Activities; China Water Power Press: Beijing, China, 2022. [Google Scholar]
- Guo, X.; Dias, D.; Carvajal, C.; Peyras, L.; Breul, P. A comparative study of different reliability methods for high dimensional stochastic problems related to earth dam stability analyses. Eng. Struct. 2019, 188, 591–602. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, D.; Cao, E.; Wu, X.; Chen, Z. Cracking risk analysis of face slabs in concrete face rockfill dams during the operation period. Structures 2022, 40, 621–632. [Google Scholar] [CrossRef]
- Mouyeaux, A.; Carvajal, C.; Bressolette, P.; Peyras, L.; Breul, P.; Bacconnet, C. Probabilistic analysis of pore water pressures of an earth dam using a random finite element approach based on field data. Eng. Geol. 2019, 259, 105190. [Google Scholar] [CrossRef]
- Chi, F.; Breul, P.; Carvajal, C.; Peyras, L. Stochastic seepage analysis in embankment dams using different types of random fields. Comput. Geotech. 2023, 162, 105689. [Google Scholar] [CrossRef]
- Li, Y.; Min, K.; Zhang, Y.; Wen, L. Prediction of the failure point settlement in rockfill dams based on spatial-temporal data and multiple-monitoring-point models. Eng. Struct. 2021, 243, 112658. [Google Scholar] [CrossRef]
- Pei, L.; Chen, C.; He, K.; Lu, X. System reliability of a gravity dam-foundation system using Bayesian networks. Reliab. Eng. Syst. Saf. 2022, 218, 108178. [Google Scholar] [CrossRef]
- Feng, S.; Hao, P.; Liu, H.; Wang, B.; Wang, B.; Yue, C. A collaborative model calibration framework under uncertainty considering parameter distribution. Comput. Methods Appl. Mech. Eng. 2023, 404, 115841. [Google Scholar] [CrossRef]
- Guan, Z.; Sun, X.; Zhang, G.; Li, G.; Huang, P.; Zhang, B.; Wang, J.; Zhou, X. Deformation and damage behavior of the deep concrete cut-off wall in core earth-rock dam foundation based on plastic damage model—A case study. Structures 2022, 46, 1480–1494. [Google Scholar] [CrossRef]
- Guo, Y.; Cui, Y.; Xie, J.; Luo, Y.; Zhang, P.; Liu, H.; Liu, J. Seepage detection in earth-filled dam from self-potential and electrical resistivity tomography. Eng. Geol. 2022, 306, 106750. [Google Scholar] [CrossRef]
- Phoon, K.; Kulhawy, F. Characterization of model uncertainties for laterally loaded rigid drilled shafts. Geotechnique 2005, 55, 45–54. [Google Scholar] [CrossRef]
- Dithinde, M.; Phoon, K.; De, W.; Retirf, J. Characterization of model uncertainty in the static pile design formula. J. Geotech. Geoenvironmental Eng. 2011, 137, 70–85. [Google Scholar] [CrossRef]
- Zou, Q.; Wen, J. A novel fatigue design modeling method under small-sample test data with generalized fiducial theory. Appl. Math. Model. 2024, 128, 260–271. [Google Scholar] [CrossRef]
- Prakash, A.; Hazra, B.; Sreedeep, S. Probabilistic analysis of soil-water characteristic curve using limited data. Appl. Math. Model. 2021, 89, 752–770. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Chen, J. An advanced Bayesian parameter estimation methodology for concrete dams combining an improved extraction technique of hydrostatic component and hybrid response surface method. Eng. Struct. 2022, 267, 114687. [Google Scholar] [CrossRef]
- Teixeira, J.; Stutz, L.; Knupp, D.; Silva Neto, A. A new adaptive approach of the Metropolis-Hastings algorithm applied to structural damage identification using time domain data. Appl. Math. Model. 2020, 82, 587–606. [Google Scholar] [CrossRef]
- Doan, Q.; Mai, S.; Do, Q.; Thai, D. A cluster-based data splitting method for small sample and class imbalance problems in impact damage classification. Appl. Soft Comput. 2022, 120, 108628. [Google Scholar] [CrossRef]
- Li, D.; Tang, X.; Zhou, C.; Phoon, K. Characterization of uncertainty in probabilistic model using bootstrap method and its application to reliability of piles. Appl. Math. Model. 2015, 39, 5310–5326. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, J.; Luo, Q.; Zhang, W.; Xiong, W.; Kong, D. Conditional probability method for soil slope stability with small sample. J. Eng. Geol. 2021, 29, 205–213. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Chen, Z.; Wang, Y.; Wang, W. Bayesian estimation method for grading characteristic parameters of sand-gravel dam material under small sample condition. Shuili Xuebao 2022, 53, 608–620. [Google Scholar] [CrossRef]
- Wang, B.; Li, D.; Tang, X. Impact of statistical uncertainty in soil parameters on slope stability reliability of rockfill dams. Eng. J. Wuhan Univ. 2019, 59, 758–766. [Google Scholar]
- Kumar, A.; Tiwari, G. An efficient Bayesian multi-model framework to analyze reliability of rock structures with limited investigation data. Acta Geotech. 2024, 19, 3299–3319. [Google Scholar] [CrossRef]
- Liu, P.; Chen, J.; Fan, S.; Xu, Q. Uncertainty quantification of the effect of concrete heterogeneity on nonlinear seismic response of gravity dams including record-to-record variability. Structures 2021, 34, 1785–1797. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Wen, L.; Xu, Z.; Zhang, Y. Reliability analysis of high core rockfill dam against seepage failure considering spatial variability of hydraulic parameters. Acta Geotech. 2024, 19, 4091–4106. [Google Scholar] [CrossRef]
- Yuan, Y.; Guo, Q.; Zhou, Z.; Wu, Z.; Chen, J.; Yao, F. Back analysis of material parameters of high core rockfill dam considering parameters correlation. Rock Soil Mech. 2017, 38 (Suppl. S1), 463–470. [Google Scholar]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Application of the soil parameter random field in the 3D random finite element analysis of Guanyinyan composite dam. Case Stud. Constr. Mater. 2022, 17, e01329. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Method: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Sun, X.; Si, S. Engineering Mathematics Application of MATLAB; National Defence Industry Press: Beijing, China, 2016. [Google Scholar]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, USSR, 2–8 September 1971; Akademia Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Deng, J. Probabilistic characterization of soil properties based on the maximum entropy method from fractional moments: Model development, case study, and application. Reliab. Eng. Syst. Saf. 2022, 219, 108218. [Google Scholar] [CrossRef]
- Dutfoy, A.; Lebrun, R. Practical approach to dependence modeling using copulas. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2009, 223, 347–361. [Google Scholar] [CrossRef]
- Tang, X.; Li, D.; Chen, Y.; Zhou, C.; Zhang, L. Improved knowledge-based clustered partitioning approach and its application to slope reliability analysis. Comput. Geotech. 2012, 45, 34–43. [Google Scholar] [CrossRef]
- Ma, H.; Chi, F. Major technologies for safe construction of high earth-rockfill dams. Engineering 2016, 2, 498–509. [Google Scholar] [CrossRef]
- McFarland, J.; DeCarlo, E. A Monte Carlo framework for probabilistic analysis and variance decomposition with distribution parameter uncertainty. Reliab. Eng. Syst. Saf. 2020, 197, 106807. [Google Scholar] [CrossRef]
- Lu, X.; Chen, C.; Li, Z.; Chen, J.; Pei, L.; Kun, H. Bayesian network safety risk analysis for the dam–foundation system using Monte Carlo simulation. Appl. Soft Comput. 2022, 126, 109229. [Google Scholar] [CrossRef]


| Parameter | c/kPa | φ/° | Rf | K | Kb | m | n | |
|---|---|---|---|---|---|---|---|---|
| Mean | Lower limit | 89.65 | 26.48 | 0.81 | 407.00 | 291.06 | 0.29 | 0.42 |
| Upper limit | 115.92 | 28.20 | 0.83 | 442.02 | 328.05 | 0.35 | 0.47 | |
| SD | Lower limit | 50.62 | 3.43 | 0.05 | 65.18 | 70.67 | 0.11 | 0.10 |
| Upper limit | 64.71 | 4.38 | 0.07 | 98.45 | 94.33 | 0.14 | 0.14 | |
| VC | Lower limit | 0.51 | 0.12 | 0.06 | 0.15 | 0.23 | 0.34 | 0.21 |
| Upper limit | 0.63 | 0.16 | 0.08 | 0.22 | 0.30 | 0.44 | 0.32 | |
| Parameter | Rf | K | Kb | m | n | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Lower limit | 50.31 | 8.18 | 0.74 | 1013.69 | 500.12 | 0.24 | 0.27 |
| Upper limit | 51.47 | 8.97 | 0.77 | 1131.78 | 570.88 | 0.28 | 0.30 | |
| SD | Lower limit | 2.25 | 1.57 | 0.07 | 256.02 | 142.96 | 0.09 | 0.07 |
| Upper limit | 3.39 | 2.25 | 0.08 | 336.70 | 196.82 | 0.13 | 0.10 | |
| VC | Lower limit | 0.04 | 0.18 | 0.09 | 0.22 | 0.26 | 0.35 | 0.25 |
| Upper limit | 0.06 | 0.26 | 0.11 | 0.31 | 0.37 | 0.47 | 0.33 | |
| Parameter | Rf | K | Kb | m | n | ||
|---|---|---|---|---|---|---|---|
| Mean | Lower limit | 38.38 | 0.78 | 699.54 | 332.01 | 0.25 | 0.41 |
| Upper limit | 41.21 | 0.81 | 858.70 | 405.55 | 0.30 | 0.44 | |
| SD | Lower limit | 5.27 | 0.06 | 302.52 | 137.58 | 0.08 | 0.05 |
| Upper limit | 6.99 | 0.08 | 381.92 | 186.23 | 0.12 | 0.08 | |
| VC | Lower limit | 0.13 | 0.07 | 0.37 | 0.36 | 0.31 | 0.13 |
| Upper limit | 0.17 | 0.10 | 0.51 | 0.51 | 0.42 | 0.19 | |
| Parameters | K-S Test | A-D Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | |
| c/kPa | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✓ |
| φ/° | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ |
| Rf | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| Kb | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| m | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| n | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ |
| Rf | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| Parameters | K-S Test | A-D Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | |
| c/kPa | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| φ/° | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ |
| Rf | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| Kb | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✗ |
| m | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ |
| n | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Rf | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| Parameters | K-S Test | A-D Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | |
| ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | |
| ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | |
| ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | |
| ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | |
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
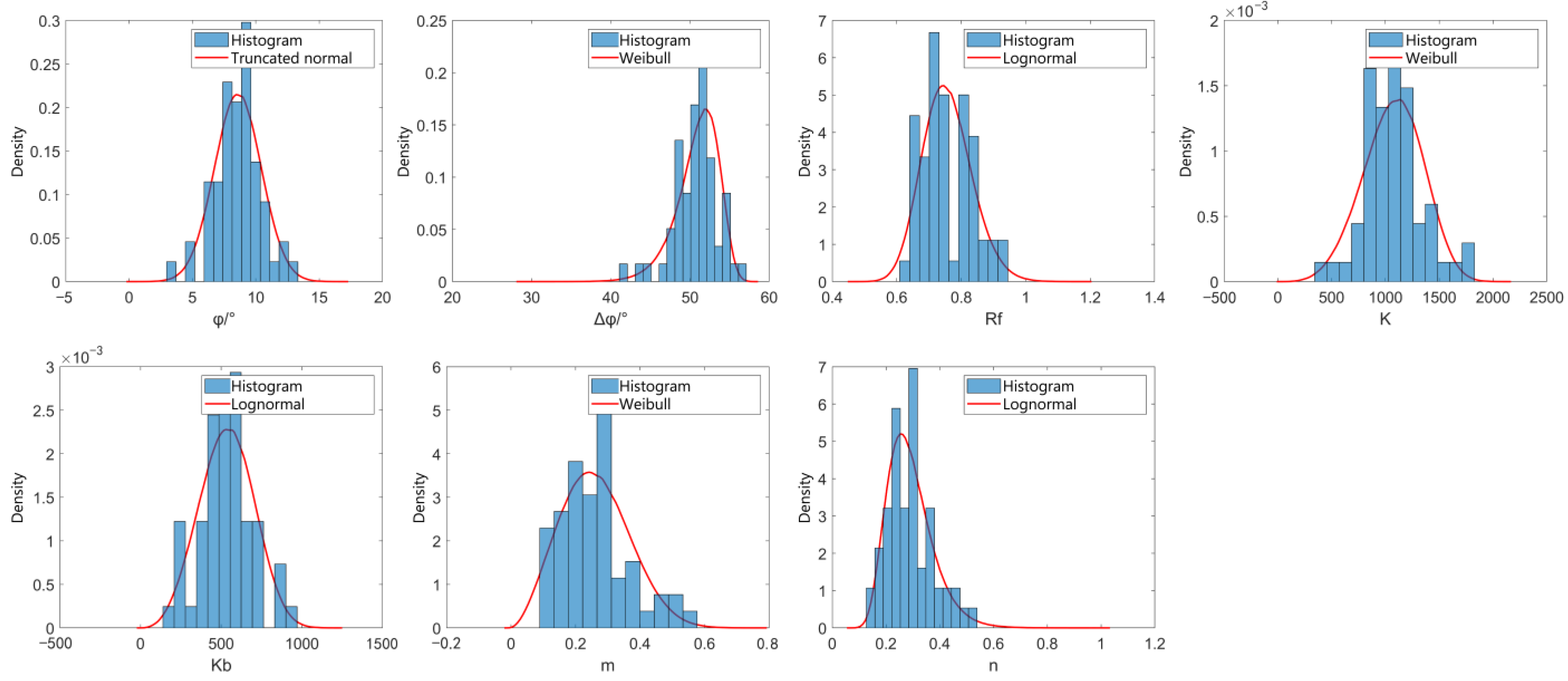
| Parameters | AIC | Optimal Marginal Distribution | |||
|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | ||
| c/kPa | / | 731.14 | / | 709.16 | Weibull distribution |
| φ/° | 376.34 | / | 528.79 | 359.73 | Weibull distribution |
| Rf | / | / | −133.27 | −184.43 | Weibull distribution |
| K | 744.71 | / | / | 730.80 | Weibull distribution |
| Kb | / | / | / | / | Lognormal distribution |
| m | / | / | / | / | Weibull distribution |
| n | −85.36 | / | / | −100.70 | Weibull distribution |
| Parameters | AIC | Optimal Marginal Distribution | |||
|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | ||
| φ0/° | 388.22 | / | / | 490.91 | Truncated normal distribution |
| /° | 478.74 | / | 595.76 | 457.02 | Weibull distribution |
| Rf | −185.30 | −187.36 | / | / | Lognormal distribution |
| K | 1125.10 | 1126.40 | / | 1105.90 | Weibull distribution |
| Kb | 1032.50 | / | / | 1008.60 | Weibull distribution |
| m | −123.15 | −100.23 | / | −159.68 | Weibull distribution |
| n | / | / | / | / | Lognormal distribution |
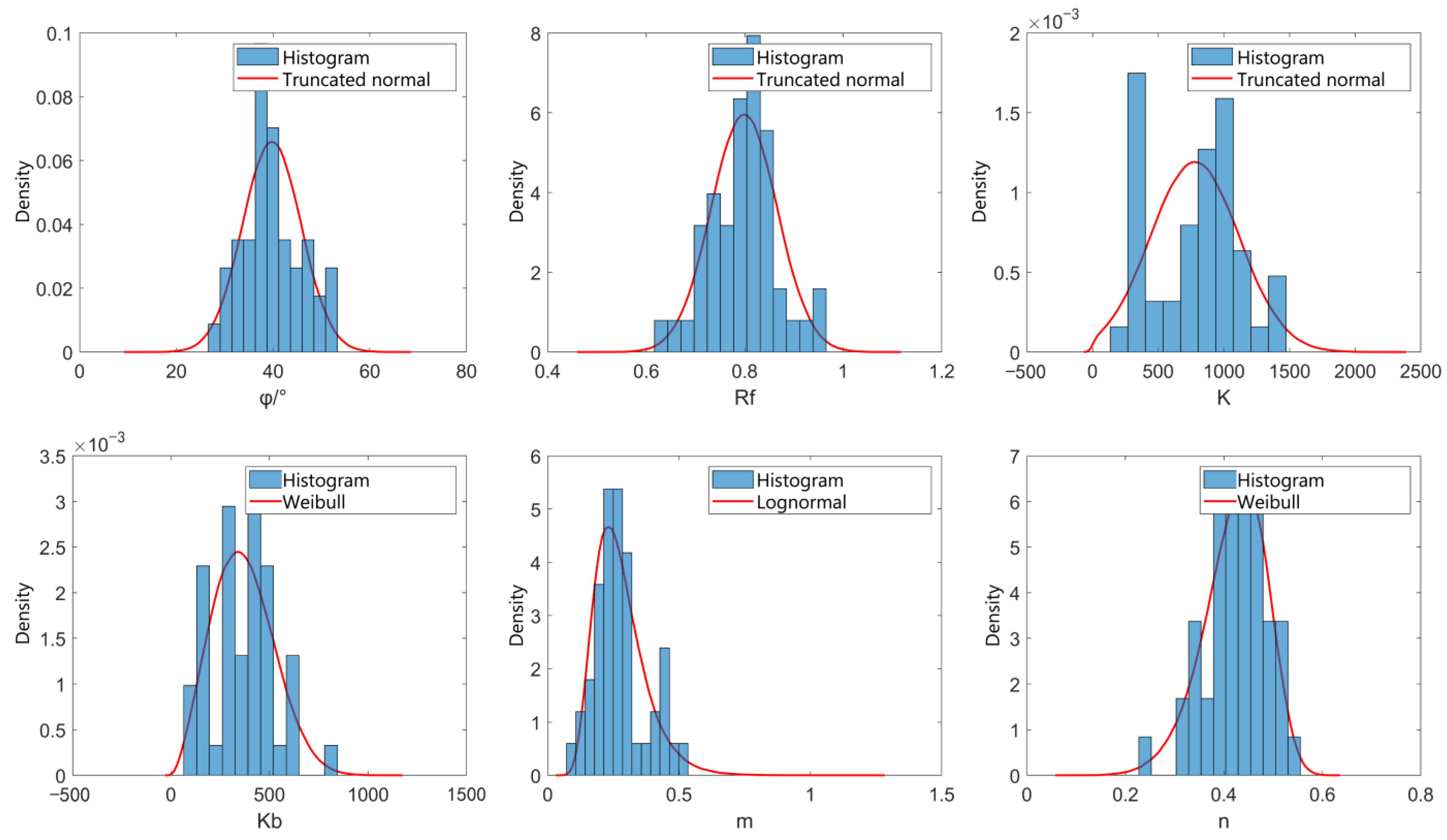
| Parameters | AIC | Optimal Marginal Distribution | |||
|---|---|---|---|---|---|
| Truncated Normal Distribution | Lognormal Distribution | Extremal Distribution | Weibull Distribution | ||
| φ/° | 546.37 | 569.27 | / | / | Truncated normal distribution |
| Rf | −156.37 | −153.66 | / | / | Truncated normal distribution |
| K | 1133.80 | / | 1145.10 | / | Truncated normal distribution |
| Kb | 1065.70 | / | 1049.10 | 1009.90 | Weibull distribution |
| m | / | / | / | / | Lognormal distribution |
| n | −72.56 | −77.49 | −76.99 | −103.41 | Weibull distribution |
| Marginal Distribution | c/kPa | φ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|---|
| Truncated normal distribution | 40 | 0 | 172 | 37 | 0 | 0 | 0 |
| Lognormal distribution | 375 | 5 | 15 | 213 | 9932 | 0 | 61 |
| Extremal distribution | 2016 | 1 | 0 | 116 | 56 | 0 | 2 |
| Weibull distribution | 7569 | 9994 | 9813 | 9634 | 12 | 10,000 | 9937 |
| Marginal Distribution | φ0/° | Δφ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|---|
| Truncated normal distribution | 9711 | 34 | 259 | 0 | 0 | 0 | 0 |
| Lognormal distribution | 0 | 0 | 6777 | 32 | 2 | 0 | 8183 |
| Extremal distribution | 0 | 0 | 2531 | 80 | 6 | 0 | 602 |
| Weibull distribution | 289 | 9966 | 433 | 9888 | 9992 | 10,000 | 1215 |
| Marginal Distribution | φ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|
| Truncated normal distribution | 8298 | 9336 | 10,000 | 0 | 0 | 0 |
| Lognormal distribution | 79 | 419 | 0 | 0 | 9939 | 0 |
| Extremal distribution | 2 | 5 | 0 | 0 | 6 | 0 |
| Weibull distribution | 1621 | 240 | 0 | 10,000 | 55 | 10,000 |
| Parameters | c/kPa | φ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|---|
| 1.00 | −0.68 | 0.31 | 0.15 | 0.17 | −0.31 | 0.06 | |
| 1.00 | 0.12 | 0.34 | 0.22 | −0.35 | 0.28 | ||
| 1.00 | 0.53 | 0.07 | 0.41 | −0.08 | |||
| 1.00 | 0.63 | 0.41 | 0.02 | ||||
| 1.00 | 0.11 | 0.18 | |||||
| 1.00 | 0.40 | ||||||
| 1.00 |
| Parameters | φ0/° | Δφ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|---|
| 1.00 | 0.78 | 0.41 | 0.37 | 0.34 | 0.04 | 0.28 | |
| 1.00 | 0.43 | 0.39 | 0.26 | −0.09 | 0.01 | ||
| 1.00 | 0.25 | 0.15 | 0.28 | 0.05 | |||
| 1.00 | 0.74 | −0.01 | −0.04 | ||||
| 1.00 | −0.17 | 0.23 | |||||
| 1.00 | 0.60 | ||||||
| 1.00 |
| Parameters | φ/° | Rf | K | Kb | m | n |
|---|---|---|---|---|---|---|
| 1.00 | 0.03 | 0.57 | 0.40 | 0.19 | −0.21 | |
| 1.00 | 0.20 | 0.27 | 0.06 | 0.21 | ||
| 1.00 | 0.87 | 0.11 | −0.17 | |||
| 1.00 | 0.08 | 0.06 | ||||
| 1.00 | 0.14 | |||||
| 1.00 |
| Materials | AIC | Number of t Copula < Gaussian Copula | |
|---|---|---|---|
| Gaussian Copula | t Copula | ||
| Core wall | −139.95 | −164.10 | 6720 |
| Rockfill | −251.10 | −264.43 | 8333 |
| Overburden | −137.02 | −171.37 | 6282 |
| c | Internal Friction Angle | Rf | K | Kb | m | n | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| φ | φ0 | Δφ | ||||||||
| Core wall | Mean | 0.06(MPa) | 35° | / | 0.68 | 411.0 | 185.0 | 0.30 | 0.68 | |
| VC | 0.57 | 0.14 | 0.07 | 0.19 | 0.27 | 0.39 | 0.27 | |||
| Type | Weibull | Weibull | Weibull | Weibull | Lognormal | Weibull | Weibull | |||
| Main rockfill | Mean | / | / | 30.76 | 10.0 | 0.63 | 1184.0 | 489.0 | 0.33 | 0.35 |
| VC | / | / | 0.05 | 0.22 | 0.10 | 0.27 | 0.32 | 0.41 | 0.29 | |
| Type | / | / | Truncated normal | Weibull | Lognormal | Weibull | Weibull | Weibull | Lognormal | |
| Secondary rockfill | Mean | / | / | 28.6 | 8.3 | 0.64 | 1027.0 | 380.0 | 0.36 | 0.36 |
| VC | / | / | 0.05 | 0.22 | 0.10 | 0.27 | 0.32 | 0.41 | 0.29 | |
| Type | / | / | Truncated normal | Weibull | Lognormal | Weibull | Weibull | Weibull | Lognormal | |
| Overburden | Mean | / | 38° | / | 0.64 | 780.0 | 400.0 | 0.18 | 0.42 | |
| VC | / | 0.15 | 0.09 | 0.44 | 0.44 | 0.37 | 0.16 | |||
| Type | / | Truncated normal | Truncated normal | Truncated normal | Weibull | Lognormal | Weibull | |||
| Mean | VC | Type | ||
|---|---|---|---|---|
| Cutoff Wall | c (MPa) | 1.13 | 0.25 | Lognormal |
| φ (°) | 42.3 | 0.15 | Normal | |
| E (GPa) | 28.5 | 0.10 | Lognormal | |
| Bedrock | c (MPa) | 1.30 | 0.30 | Lognormal |
| φ (°) | 49.0 | 0.20 | Normal | |
| E (GPa) | 9.0 | 0.15 | Lognormal | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Huang, H.; Lu, X.; Chen, J.; Zhang, X.; Zhao, Z. A Methodology for Modeling a Multi-Dimensional Joint Distribution of Parameters Based on Small-Sample Data, and Its Application in High Rockfill Dams. Appl. Sci. 2024, 14, 7646. https://doi.org/10.3390/app14177646
Guo Q, Huang H, Lu X, Chen J, Zhang X, Zhao Z. A Methodology for Modeling a Multi-Dimensional Joint Distribution of Parameters Based on Small-Sample Data, and Its Application in High Rockfill Dams. Applied Sciences. 2024; 14(17):7646. https://doi.org/10.3390/app14177646
Chicago/Turabian StyleGuo, Qinqin, Huibao Huang, Xiang Lu, Jiankang Chen, Xiaoshuang Zhang, and Zhiyi Zhao. 2024. "A Methodology for Modeling a Multi-Dimensional Joint Distribution of Parameters Based on Small-Sample Data, and Its Application in High Rockfill Dams" Applied Sciences 14, no. 17: 7646. https://doi.org/10.3390/app14177646
APA StyleGuo, Q., Huang, H., Lu, X., Chen, J., Zhang, X., & Zhao, Z. (2024). A Methodology for Modeling a Multi-Dimensional Joint Distribution of Parameters Based on Small-Sample Data, and Its Application in High Rockfill Dams. Applied Sciences, 14(17), 7646. https://doi.org/10.3390/app14177646






