Abstract
This paper focuses on the relationship between decision trees, a typical machine learning method, and data anonymization. It is known that information leaked from trained decision trees can be evaluated using well-studied data anonymization techniques and that decision trees can be strengthened using k-anonymity and ℓ-diversity; unfortunately, however, this does not seem sufficient for differential privacy. In this paper, we show how one might apply k-anonymity to a (random) decision tree, which is a variant of the decision tree. Surprisingly, this results in differential privacy, which means that security is amplified from k-anonymity to differential privacy without the addition of noise.
1. Introduction
Recently, with the rapid evolution of machine learning technology and the expansion of data due to developments in information technology, it has become increasingly important that companies determine how they might utilize big data effectively and efficiently. However, big data often include personal and private information; thus, careless utilization of such sensitive information may lead to unexpected sanctions.
To overcome this problem, many privacy-preserving technologies have been proposed for the utilization of data that nevertheless maintains privacy. Typical privacy-preserving technologies include data anonymization (e.g., [1,2,3]) and secure computation (e.g., [4]). This paper focuses on the relationship between data anonymization and decision trees, a typical machine learning method. Historically, data anonymization research has progressed from pseudonymization to k-anonymity [1], ℓ-diversity [2,5], and t-closeness [3] and is continually growing. Currently, many researchers are focused on membership privacy and differential privacy [6].
In [7,8], the authors pointed out that the decision tree is not robust to homogeneity attacks and background knowledge attacks; they then demonstrated the application of k-anonymity and ℓ-diversity in order to amplify security. However, their proposals could not satisfy the requirements of differential privacy. In this paper, we discuss how we might prevent the leakage of private information via differential privacy provided by a learned decision tree using data anonymization techniques such as k-anonymity and ℓ-diversity.
To prevent leakage of private information, we propose the application of k-anonymity and sampling to a random decision tree, which is a variation of the expanded decision tree proposed by Fan et al. [9]. Interestingly, we show in this paper that this modification results in differential privacy. The essential idea is that instead of adding Laplace noise, as in [10,11] (please see [12] for a survey of a differentially private (random) decision tree), we propose a method of enhancing the security of a random decision tree by sampling and then removing the leaf containing fewer data than some threshold k, which applies to the other leaves of the tree. The basic concept is outlined in [13]. Our proposed model, in which k-anonymity is achieved after sampling, provides differential privacy, as in [13].
As mentioned above, researchers have shifted their attention to differential privacy rather than k-anonymization and ℓ-diversity. In fact, building upon the work outlined in [14], decision trees that satisfy differential privacy use techniques that are typical of differential privacy, such as the exponential, Gaussian, and Laplace mechanisms [10,11,15]. That is, all of these algorithms achieve differential privacy by adding some kind of noise. Our approach is very different from those of others. That said, the basic technique involves applying k-anonymity to each leaf in the random decision tree; this is similar to pruning, which is a widely accepted technique used to avoid overfitting.
The remainder of this paper is organized as follows. Section 2 introduces relevant preliminary information, e.g., anonymization methods and decision trees, and demonstrates how strategies for attacking data anonymization can be converted into attacks targeting decision trees. In Section 3, we demonstrate how much security and accuracy can be achieved in practice when the random decision tree is strengthened using a method that is similar to k-anonymity. In Section 4, the potential advantages of our proposal are discussed. Finally, the paper is concluded in Section 5, which includes a brief discussion of potential future research topics.
2. Preliminaries
2.1. Data Anonymization
When providing personal data to a third party, it is necessary to modify data to preserve user privacy. Here, modifying the user’s data (i.e., a particular record) such that an adversary cannot re-identify a specific individual is referred to as data anonymization. As a basic technique and to prevent re-identification, an identifier, e.g., a person’s name or employee number, is deleted or replaced with a pseudonym ID by the data holder. This process is referred to as pseudonymization. However, simply modifying identifiers does not ensure the preservation of privacy. In some cases, individuals can be re-identified by a combination of features (i.e., a quasi-identifier); thus, it is necessary to modify both the identifier and the quasi-identifier to reduce the risk of re-identification. In most cases, the identifiers themselves are not used for data analysis; thus, removing identifiers does not significantly sacrifice the quality of the dataset. However, if we modify quasi-identifiers in the same manner, although the data may become anonymous, they will also become useless. A typical anonymization technique for quasi-identifiers is “roughening” the numerical values.
2.1.1. Attacks Targeting Pseudonymization
A simple attack is possible against pseudonymized data from which identifiers, e.g., names, have been removed. In this attack, the attacker uses the quasi-identifier of a user u. If this attacker obtains the pseudonymized data, by searching for user u’s quasi-identifier in pseudonymized data, the attacker can obtain sensitive information about u. For example, if the attacker obtains the dataset shown in Table 1 and knows friend u’s zip code is 13068, their age is 29, and their nationality is American, then, by searching the dataset, the attacker can identify that user u is suffering from some heart-related disease. This attack is referred to as the uniqueness attack.

Table 1.
Example of a dataset *.
2.1.2. k-Anonymity
k-anonymity is a countermeasure used to prevent uniqueness attacks.
In k-anonymity, features are divided into quasi-identifiers and sensitive information, and the same quasi-identifier is modified such that it does not become less than k users. Table 2 shows anonymized data that has been k-anonymized () using quasi-identifiers, e.g., zip code, age, and nationality.

Table 2.
k-anonymity () of the dataset shown in Table 1.
2.1.3. Homogeneity Attack
At a cursory glance, k-anonymity appears to be secure; however, even if k-anonymity is employed, a homogeneity attack is still feasible. This attack becomes possible if the sensitive information is the same. Taking the k-anonymized dataset shown on the right side of Figure 1 as an example and assuming the presence of the attacker on the left side of Figure 1, we can make the following statements. Here, the attacker has the necessary information (zip, age) = (13053, 37); all of this sensitive information in the records corresponds with cancer. The attacker can therefore deduce that Bob has cancer.
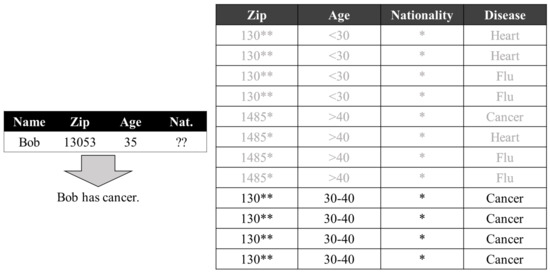
Figure 1.
Homogeneity attack. The * and ** in the Zip column mean that the last one and two digits of the original data are hidden, respectively; while the * in the Nationality column means no partitioned for the corresponding attribute.
2.1.4. Background Knowledge Attack
Homogeneous attacks suggest a problem when records with the same quasi-identifier have the same sensitive information; however, a previous study [3] also argued that there was a problem even in cases in which records were not the same. The k-anonymized dataset on the right side of Figure 2 shows four records with quasi-identifiers (130, <30, *), and two types of sensitive information, i.e., (heart, flu). Here, we can assume that the attacker has background knowledge of the data similar to that shown on the left side of Figure 2. In this case, there are certainly possibilities of heart disease and flu; however, if the probability of Japanese individuals experiencing heart disease is extremely low, Umeko is estimated to instead have the flu. Thus, it must be acknowledged that k-anonymity does not provide a high degree of security.
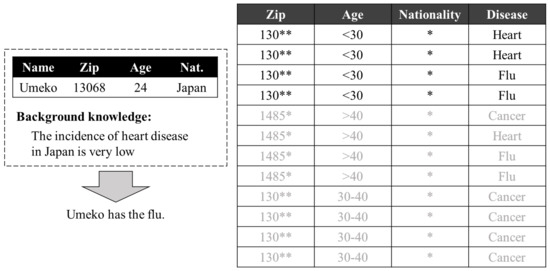
Figure 2.
Background knowledge attack. The * and ** in the Zip column mean that the last one and two digits of the original data are hidden, respectively; while the * in the Nationality column means no partitioned for the corresponding attribute.
ℓ-diversity: ℓ-diversity is a measure used to counteract homogeneity attacks. A k-anonymization table is denoted ℓ-diverse if each similar class of quasi-identifiers has at least ℓ “well-represented” values for sensitive information. There are several different interpretations of the term “well-represented” [2,3]. In this paper, we adopt distinct ℓ-diversity. Distinct ℓ-diversity means that there are at least ℓ distinct values for the sensitive information in each similar class of quasi-identifiers. Table 3 shows anonymized data that are two-diverse ().

2.2. Decision Trees
2.2.1. Basic Decision Trees
Decision trees are supervised learning methods that are primarily used for classification tasks, and a tree structure is created while learning from data (Figure 3). When predicting the label y of , the process begins from the root of the tree, and the corresponding leaf is searched for while referring to each feature of . Finally, through this referral process, y is predicted.
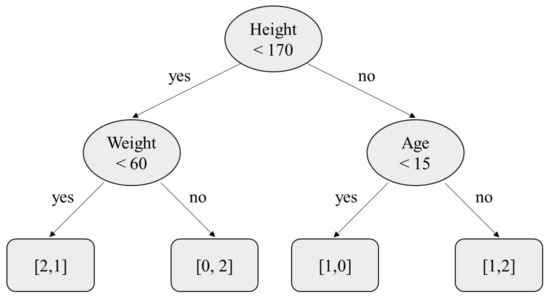
Figure 3.
An example of a decision tree concerning a dataset with two labels, e.g., 1 and 0. The vectors in the leaves show the number of data points being classified, in which the two terms of each vector correspond to the number of data points labeled 1 and 0, respectively.
The label determined by the leaf is derived from the dataset D used to generate the tree structure. In other words, after the tree structure is created, for each element in dataset D, the corresponding leaf is found, and the value of is stored. If , then in each , the number of labeled 0 and the number of labeled 1 are preserved. More precisely, are preserved for each leaf , where and represent the numbers of data points with label y that have values of 0 and 1, respectively. Table 4 shows the notations used in the paper.

Table 4.
The notations used in this paper.
For a given prediction , we first search for the corresponding leaf, and it may be denoted as 1 if , and 0 otherwise. Here, the threshold can be set flexibly depending on where the decision tree is applied, and when providing the learned decision tree to a third party, it is possible to pass and together for each leaf . In this paper, we considered the security of decision trees in such situations.
Generally, the deeper the tree structure, the more likely it is to overfit; thus, we frequently prune the tree, and this technique was employed to preserve data privacy within this paper.
2.2.2. Random Decision Tree
The random decision tree was proposed by Fan et al. [9]. Notably, in their approach, the tree is randomly generated without depending on the data. Furthermore, sufficient performance can be ensured through the appropriate selection of parameters.
The shape of a normal (not random) decision tree depends on the data used; the eventual shape may cause private information to be leaked from the tree. However, the random decision tree avoids this leakage due to its random generation. Therefore, its performance is expected to match the performance of other proposed security methods.
A random decision tree is described in Algorithms 1 and 2. Algorithm 1 shows that the generated tree does not depend on dataset D, except for created by . Here, denotes the 2D array, which represents the number of feature vectors reaching each leaf . However, the preservation of privacy is necessary because depends on D.
In the measurement of each parameter, the depth of the tree being () and the number of trees being 10 are general rules.
2.3. Security Definitions
Part of this work adopts differential privacy to evaluate the security and efficiency of the model.
Definition 1.
A randomized algorithm A satisfies -DP, if for any pair of neighboring datasets, D and , and any :
where is a range of A.
When studying differential privacy, it is assumed that the attacker knows all the elements in D. However, such an assumption may not be realistic. This is taken into consideration, and the following definition is given in [13]:
Definition 2
(DP undersampling, -DPS). An algorithm A satisfies -DPS if and only if the algorithm satisfies -DP, where denotes the algorithm used to initially sample each tuple in the input dataset A with probability β.
In other words, the definition describes the output of A by inputting , which is a result of sampling dataset D. Hence, the attacker may know D but not .
| Algorithm 1 Training the random decision tree [9] |
| Input: Training data , the set of features , number of random decision trees to be generated Output: Random decision trees
|
| Algorithm 2 Classifying the random decision tree [9] |
| Require: 1: return for each , where denotes the leaf corresponding to . |
2.4. Attacks Targeting the Decision Tree
Generally, a decision tree is constructed from a given dataset; however, it is also possible to partially reconstruct the dataset using the decision tree. This kind of attack is considered in [7]. In this section, we explain the workings of such attacks.
Figure 4 shows the reconstruction of a dataset from the decision tree shown in Figure 3. As shown, it is impossible to reconstruct the original data completely from a binary tree model; however, it is possible to extract some of the data. By exploiting this essential property, it is possible to mount some attacks against reconstructed data, as discussed in Section 2.1. In the following, taking Figure 4 as an example, we present a uniqueness attack, a homogeneous attack, and a background knowledge attack.
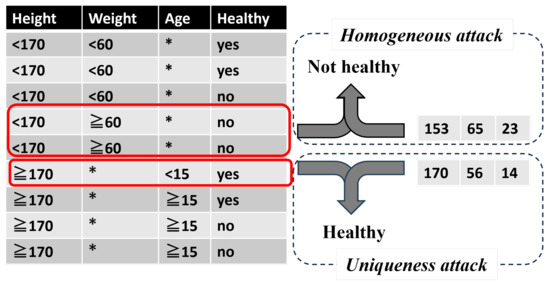
Figure 4.
Example of conversion from decision tree (Figure 3) to anonymized data, where * in Weight and Age columns mean no partitioned for the corresponding attributes, respectively.
- Uniqueness attack: in the dataset (Figure 4) recovered from the model, there is one user whose height is greater than 170 and who is under 15 years of age (as shown in the sixth row (see the 2nd red box shown on the figure), where the relevant leaf is converted via ); thus, it is possible to target this user with a uniqueness attack.
- Homogeneous attack: similarly, in the fourth and fifth rows (see the 1st red box shown on the figure), which are converted from the relevant leaf via , the height , weight , and health status are the same (i.e., “unhealthy”); therefore, a homogeneous attack is possible.
- Background knowledge attack: Similarly, in the seventh, eighth, and ninth rows, there are three users whose data match in both height and age . Among these users, one is healthy (yes) and two are unhealthy (no). As an attacker, we can consider the following:
- (Background knowledge of user A) height: 173, age: 33, healthy;
- (Background knowledge of target user B) height: 171, age: 19.
In this case, if the adversary knows that user A is healthy, he/she can identify that user B is unhealthy.
3. Proposal: Applying -Anonymity to a (Random) Decision Tree
3.1. Construction of
In this section, we demonstrate how one might achieve differential privacy from k-anonymity. More specifically, we present a proposal based on a random decision tree, which is a variant of the decision tree outlined in Section 2.2.2. Said proposal is shown as Algorithm 3. It differs from the original random decision tree in the following ways:
- (Pruning): for some threshold k, if there exists a tree , a leaf , and a label y, satisfying , then let equal 0.
- (Sampling): training using , which is the result obtained after sampling dataset D of each tree with probability .
3.2. Security: Strongly Safe k-Anonymization Ensures Differential Privacy
In the field of data anonymization, in study [13], the authors demonstrated that performing k-anonymity after sampling achieved differential privacy; our proposal is a development upon this core principle. Below, we outline the items necessary to evaluate data security.
Definition 3
(Strongly Safe k-anonymization algorithm [13]). Suppose that a function g has , where and are the domain and range of g, respectively. Suppose that g does not depend on , i.e., g is constant. The strongly safe k-anonymization algorithm A with input is defined as follows:
- Compute .
- .
- For each element in , if , then the element is set to , and the result is set to .
| Algorithm 3 Proposed training process |
| Input: Training data , the set of features , number of random decision trees to be generated Output: Random decision trees
|
Assume that denotes the probability mass function: the probability of succeeding j times after n attempts, where the probability of success after one attempt is . Furthermore, the cumulative distribution function is expressed as follows in Equation (2):
Theorem 1
(Theorem 5 in [13]). Any strongly safe k-anonymization algorithm satisfies -DPS for any , , and
where .
Equation (3) shows the relationship between and in determining the value of when k is fixed.
Let us consider the case where record is applied to a random decision tree , and the leaf reached is denoted by . If a function is defined as
then in Equation (4) is apparently constant, that is, it does not depend on D. Therefore, , which is generated using , can be regarded as an example of strongly safe k-anonymization; consequently, Theorem 1 can be applied.
However, Theorem 1 above can be applied in its original form when there is one , i.e., when the number of trees . Theorem 2 can be applied when .
Theorem 2
(Theorem 3.16 in [17]). Assume is an -DP algorithm for . Then, the algorithm
satisfies -DP.
In Algorithm 3, each is selected randomly, and sampling is performed for each tree. Hence, the following conclusion can be reached.
Corollary 1.
The proposed algorithm satisfies -DPS, for any , , and
where
Table 5 shows the relationship, derived from Equation (6), between and in determining the value of when k and are fixed. The cells in the table represent the approximate value of . For k and , we chose , and , as shown in Table 5.

Table 5.
Approximate value of for and .
3.3. Experiments on k-
The efficiency of the proposal was verified using the Nursery dataset [18], the Adult dataset [19], the Mushroom dataset [20], and the Loan dataset [21]. The characteristics of each dataset are as follows.
- The Nursery dataset contains 12,960 records with eight features, with a maximum of five values for each feature;
- The Adult dataset contains 48,842 records with 14 features. Here, each feature has more possible values and more records than in the Nursery datasets;
- The Mushroom dataset contains 8124 records with 22 features. Compared to the above two datasets, there are more features, but the number of records is small. In general, applying k-anonymity to this kind of dataset is challenging.
- The Loan dataset [21] contains 9578 records with 13 features. We used the “not.fully.paid” feature to label classes. There are four binary attributes and seven numerical attributes in this dataset.
Appendix A contains the evaluation of the basic decision tree with each dataset. Firstly, were set to , , and .
The results from the Nursery dataset obtained via with these parameters are as follows:
- The accuracy of the original decision tree was 0.933, as shown in Table A1.
- As shown in Table 6 (a), for a tree depth equal to four, the accuracy obtained was 0.84, which was inferior to that of the original decision tree.
 Table 6. Accuracy of .
Table 6. Accuracy of . - As shown in Table 6 (a), for a tree depth equal to five, the accuracy decreased drastically as k increased.
The results from the Adult dataset obtained via with the same were as follows: (there were numerical values in this dataset; to handle this, a threshold t was chosen randomly from its domain, and two children for ≤t and >t were produced by the tree)
- The accuracy of the original decision tree was 0.855, as shown in Table A1.
- As shown in Table 6 (b), the achieved accuracy when was 0.817.
The results from the Mushroom dataset obtained via with the same were as follows:
The results from the Loan dataset obtained via with the same were as follows:
- The accuracy of the original decision tree was 0.738 in our experiment.
- As shown in Table 6 (d), the achieved accuracy was around 0.84.
In summary, the accuracy achieved by was slightly inferior to that of the original decision tree.
Changing sampling rate β: To achieve secure differential privacy, the sampling rate should remain small. Maintaining values of , , which were small enough for our practical application, Table 7 shows how the values of changed according to the sampling rate . As shown, for some parameters, the accuracy of the proposed method was relatively good even when and were small.

Table 7.
Accuracy and approximate of when .
4. Discussion
In another highly relevant study [10], Jagannathan et al. proposed a variant of a random decision tree that achieved differential privacy. The accuracy of their proposal is shown in Figures 1 and 2 of [10] for the same datasets with the same class labels; (in [10], instead of five class labels, three were used for the Nursery dataset, i.e., some of the similar labels were merged) their method resulted in similar precision. Because our proposal employs sampling, it is limited by the size of the dataset being utilized; the smaller the dataset (e.g., the Mushroom dataset), the less pronounced the accuracy. However, it must be noted that their approach was very different from ours: Laplace noise was added instead of pruning and sampling. Notably, within their proposal,
for all trees , all leaves , and all labels y. Even in this context, if is small for a certain , , and y, it may be regarded almost as a personal record. A good general approach to handling such cases is to remove the rare records, i.e., to “remove the leaves containing fewer records”. This is a broadly accepted data anonymization technique [22] that is commonly used to avoid legal difficulties. Our proposal shows that pruning and sampling can be combined to ensure differential privacy. If rare sensitive records need to be removed, our method may therefore represent an excellent option.
5. Conclusions
In this paper, we aimed to show the close relationship between the security of data anonymity and decision trees. Specifically, we show how to obtain differentially private (random) decision tree from k-anonymity. Our proposal consists of applying sampling and k-anonymity to the original random decision tree method, which results in differential privacy. Compared to existing schemes, the advantage of our proposal is its ability to implement differential privacy without adding Laplace or Gaussian noise, which provides trained decision trees with a new route to differential privacy. We believe that in addition to random decision trees, other similar algorithms can be augmented to achieve differential privacy for general decision trees. In addition, in future studies, we will explore the differential privacy of federated learning decision trees by extending the proposed method.
Author Contributions
Conceptualization, A.W. and R.N.; methodology, A.W., R.N. and L.W.; software, A.W. and R.N.; formal analysis, A.W., R.N. and L.W.; investigation, A.W., R.N. and L.W.; resources, R.N.; data curation, A.W.; writing—original draft preparation, A.W., R.N. and L.W; writing—review and editing, L.W.; supervision, R.N.; project administration, R.N. and L.W.; funding acquisition, R.N. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JST CREST Grant Number JPMJCR21M1, Japan.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author. The source code used in this study is available on request from the corresponding author since January 2025.
Acknowledgments
We would like to thank Ryousuke Wakabayashi and Yusaku Ito for their technical assistance with the experiments.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Experiments on Attacks against the Decision Tree
We used three datasets to evaluate the vulnerability of decision trees to uniqueness and homogeneous attacks: the Nursery dataset [18], the Adult dataset [19], and the Mushroom dataset [20], In these experiments, we used the and libraries to train the decision trees.
In the experiments, the tree depths were set to four, five, six, seven, and eight. We divided each dataset into a training set and an evaluation set. The training set, which was used to train the decision tree, contained 80% of the records in the dataset. Here, the decision tree was trained 10 times, and averages of the following numbers were computed.
- : the number of leaves that can be identified by a homogeneous attack, that is, the number of leaves for and ;
- : the number of users who can be identified by a homogeneous attack,where leaf denotes the leaves that suffer the homogeneous attack.
Note that in a uniqueness attack, the number of leaves that can be identified is equal to the number of identifiable users. Table A1 shows the experimental results of the homogeneous attack. Regarding the homogeneous attack, even if the tree depth is small, information can be leaked in all datasets. In addition, susceptibility to homogeneous attacks increases as the tree depth increases, as shown in Figure A1.

Table A1.
Number of users () and leaves () that can be identified by homogeneity attacks.
Table A1.
Number of users () and leaves () that can be identified by homogeneity attacks.
| Tree | Nursery | Adult | Mushroom | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth | |||||||||
| 4 | 0.863 | 3965.5 | 2 | 0.843 | 215.2 | 2.4 | 0.979 | 3293.6 | 9 |
| 5 | 0.880 | 5217 | 4.9 | 0.851 | 829.5 | 7.1 | 0.980 | 3568.4 | 12 |
| 6 | 0.888 | 5747.1 | 9.9 | 0.853 | 1621.7 | 18.3 | 0.995 | 6122.6 | 16 |
| 7 | 0.921 | 6837.4 | 19.5 | 0.855 | 1957.4 | 35.2 | 1.000 | 6499 | 20 |
| 8 | 0.933 | 7912.7 | 35.7 | 0.855 | 2316.1 | 60.8 | 1.000 | 6499 | 20 |
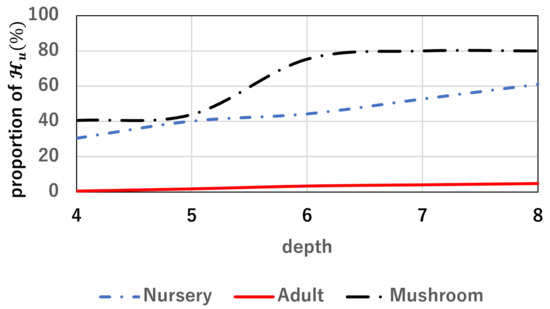
Figure A1.
Tree depth and the proportion of users who can be identified by a homogeneous attack.
References
- Sweeney, L. k-Anonymity: A Model for Protecting Privacy. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Gehrke, J.; Kifer, D.; Venkitasubramaniam, M. ℓ-Diversity: Privacy Beyond k-Anonymity. In Proceedings of the 22nd International Conference on Data Engineering, ICDE 2006, Atlanta, GA, USA, 3–8 April 2006; IEEE Computer Society: Washington, DC, USA, 2006; p. 24. [Google Scholar] [CrossRef]
- Li, N.; Li, T.; Venkatasubramanian, S. t-Closeness: Privacy Beyond k-Anonymity and ℓ-Diversity. In Proceedings of the 23rd International Conference on Data Engineering, ICDE 2007, The Marmara Hotel, Istanbul, Turkey, 15–20 April 2007; IEEE Computer Society: Washington, DC, USA, 2007; pp. 106–115. [Google Scholar] [CrossRef]
- Yao, A.C. How to Generate and Exchange Secrets (Extended Abstract). In Proceedings of the 27th Annual Symposium on Foundations of Computer Science, Toronto, ON, Canada, 27–29 October 1986; IEEE Computer Society: Washington, DC, USA, 1986; pp. 162–167. [Google Scholar] [CrossRef]
- Praveena Priyadarsini, R.; Sivakumari, S.; Amudha, P. Enhanced ℓ– Diversity Algorithm for Privacy Preserving Data Mining. In Digital Connectivity—Social Impact, Proceedings of the 51st Annual Convention of the Computer Society of India, CSI 2016, Coimbatore, India, 8–9 December 2016, Proceedings; Subramanian, S., Nadarajan, R., Rao, S., Sheen, S., Eds.; Springer: Singapore, 2016; pp. 14–23. [Google Scholar] [CrossRef]
- Stadler, T.; Oprisanu, B.; Troncoso, C. Synthetic Data - Anonymisation Groundhog Day. In Proceedings of the 31st USENIX Security Symposium, USENIX Security 2022, Boston, MA, USA, 10–12 August 2022; USENIX Association: Berkeley, CA, USA, 2022; pp. 1451–1468. [Google Scholar]
- Friedman, A.; Wolff, R.; Schuster, A. Providing k-anonymity in data mining. VLDB J. 2008, 17, 789–804. [Google Scholar] [CrossRef]
- Ciriani, V.; di Vimercati, S.D.C.; Foresti, S.; Samarati, P. k -Anonymous Data Mining: A Survey. In Privacy-Preserving Data Mining— Models and Algorithms; Aggarwal, C.C., Yu, P.S., Eds.; Advances in Database Systems; Springer: Berlin/Heidelberg, Germany, 2008; Volume 34, pp. 105–136. [Google Scholar] [CrossRef]
- Fan, W.; Wang, H.; Yu, P.S.; Ma, S. Is random model better? On its accuracy and efficiency. In Proceedings of the 3rd IEEE International Conference on Data Mining (ICDM 2003), Melbourne, FL, USA, 19–22 December 2003; IEEE Computer Society: Washingtom, DC, USA, 2003; pp. 51–58. [Google Scholar] [CrossRef]
- Jagannathan, G.; Pillaipakkamnatt, K.; Wright, R.N. A Practical Differentially Private Random Decision Tree Classifier. Trans. Data Priv. 2012, 5, 273–295. [Google Scholar]
- Fletcher, S.; Islam, M.Z. A Differentially Private Random Decision Forest Using Reliable Signal-to-Noise Ratios. In AI 2015: Advances in Artificial Intelligence, Proceedings of the 28th Australasian Joint Conference, Canberra, ACT, Australia, 30 November–4 December 2015, Proceedings; Pfahringer, B., Renz, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9457, pp. 192–203. [Google Scholar] [CrossRef]
- Fletcher, S.; Islam, M.Z. Decision Tree Classification with Differential Privacy: A Survey. ACM Comput. Surv. 2019, 52, 83:1–83:33. [Google Scholar] [CrossRef]
- Li, N.; Qardaji, W.H.; Su, D. On sampling, anonymization, and differential privacy or, k-anonymization meets differential privacy. In Proceedings of the 7th ACM Symposium on Information, Compuer and Communications Security, ASIACCS ’12, Seoul, Republic of Korea, 2–4 May 2012; ACM: New York, NY, USA, 2012; pp. 32–33. [Google Scholar] [CrossRef]
- Blum, A.; Dwork, C.; McSherry, F.; Nissim, K. Practical privacy: The SuLQ framework. In PODS, Proceedings of the Twenty-Fourth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Baltimore, Maryland, 13–15 June 2005; Li, C., Ed.; ACM: New York, NY, USA, 2005; pp. 128–138. [Google Scholar]
- Friedman, A.; Schuster, A. Data mining with differential privacy. In KDD ’10, Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; Rao, B., Krishnapuram, B., Tomkins, A., Yang, Q., Eds.; ACM: New York, NY, USA, 2010; pp. 493–502. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J.; Venkitasubramaniam, M. L-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data 2007, 1, 3. [Google Scholar] [CrossRef]
- Dwork, C.; Roth, A. The Algorithmic Foundations of Differential Privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Rajkovic, V. Nursery. UCI Machine Learning Repository. 1997. Available online: https://archive.ics.uci.edu/dataset/76/nursery (accessed on 24 August 2024).
- Becker, B.; Kohavi, R. Adult. UCI Machine Learning Repository. 1996. Available online: https://archive.ics.uci.edu/dataset/2/adult (accessed on 24 August 2024).
- Mushroom. UCI Machine Learning Repository. 1987. Available online: https://archive.ics.uci.edu/dataset/73/mushroom (accessed on 24 August 2024).
- Mahdi, N. Bank_Personal_Loan_Modelling. Available online: https://www.kaggle.com/datasets/ngnnguynthkim/bank-personal-loan-modellingcsv (accessed on 24 August 2024).
- Mobile Kukan Toukei (Guidelines). Available online: https://www.intage.co.jp/english/service/platform/mobile-kukan-toukei/ (accessed on 24 August 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).