From Tilings of Orientable Surfaces to Topological Interlocking Assemblies
Abstract
1. Introduction
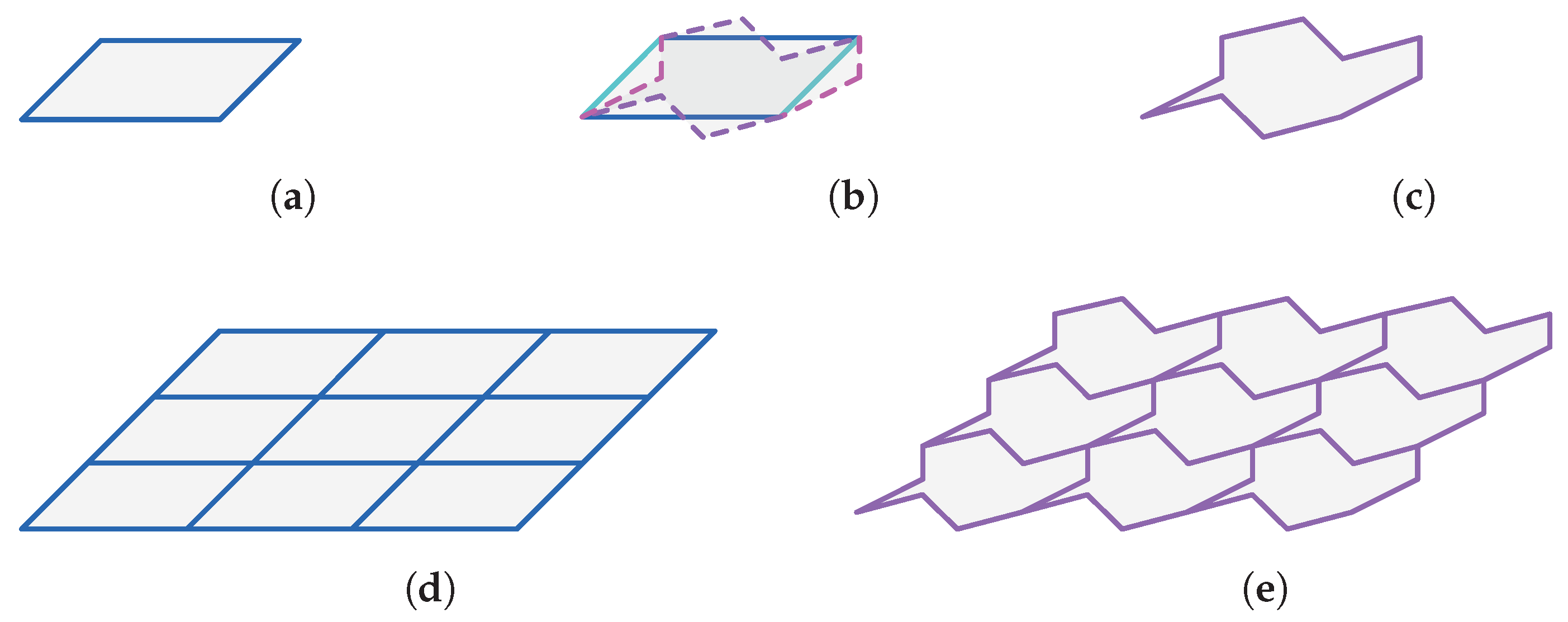
2. Symmetries and the Escher Trick
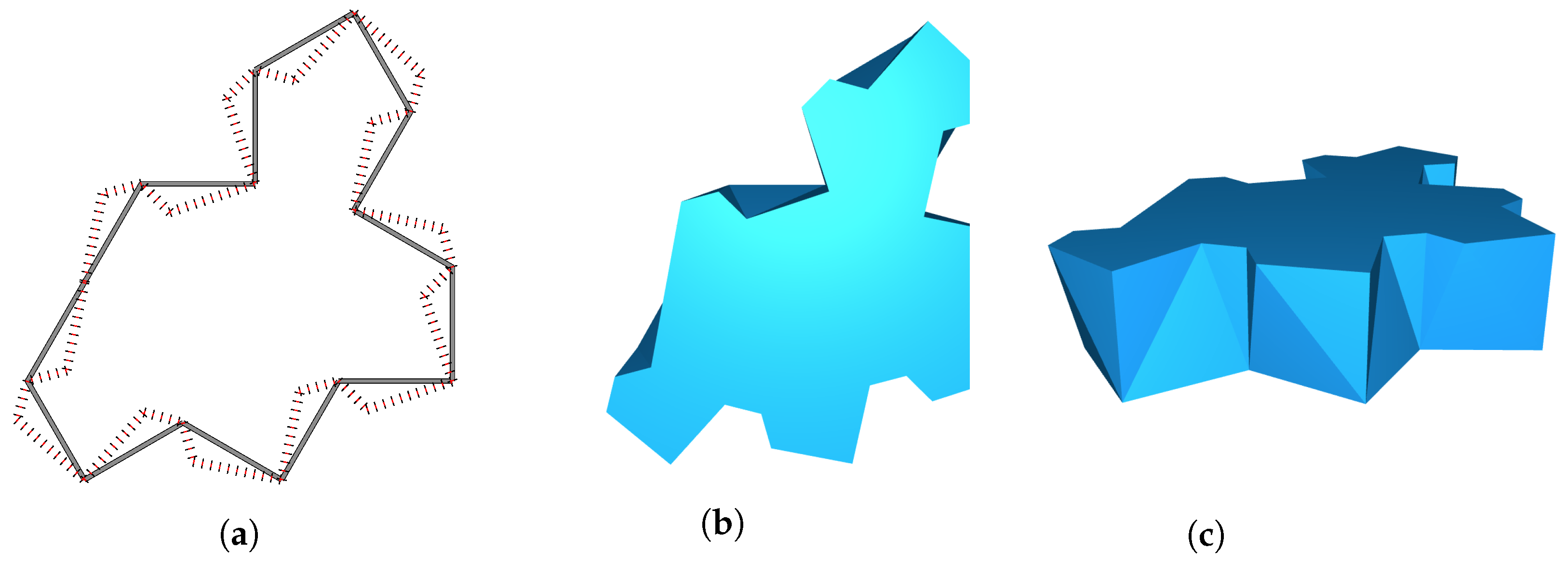
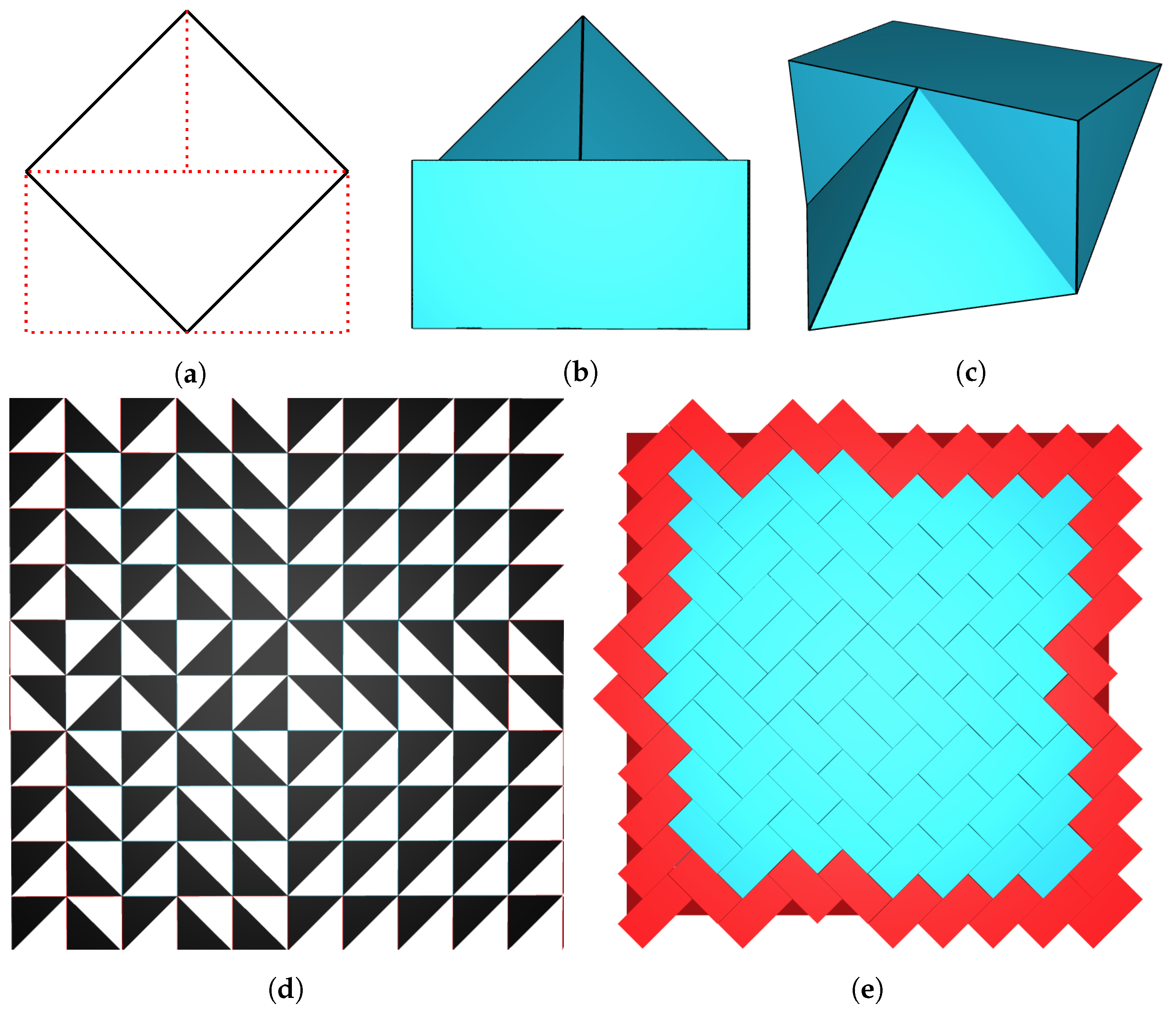
3. Constructing Planar Topological Interlocking Assemblies
4. Constructing Spherical Topological Interlocking Assemblies
4.1. The Modified Escher-like Approach
- for two real numbers the surfaces and are disjoint, i.e., the intersection is empty,
- the set defined as is a connected set in .
4.2. Examples of TIA That Arise from the Modified Escher-like Approach
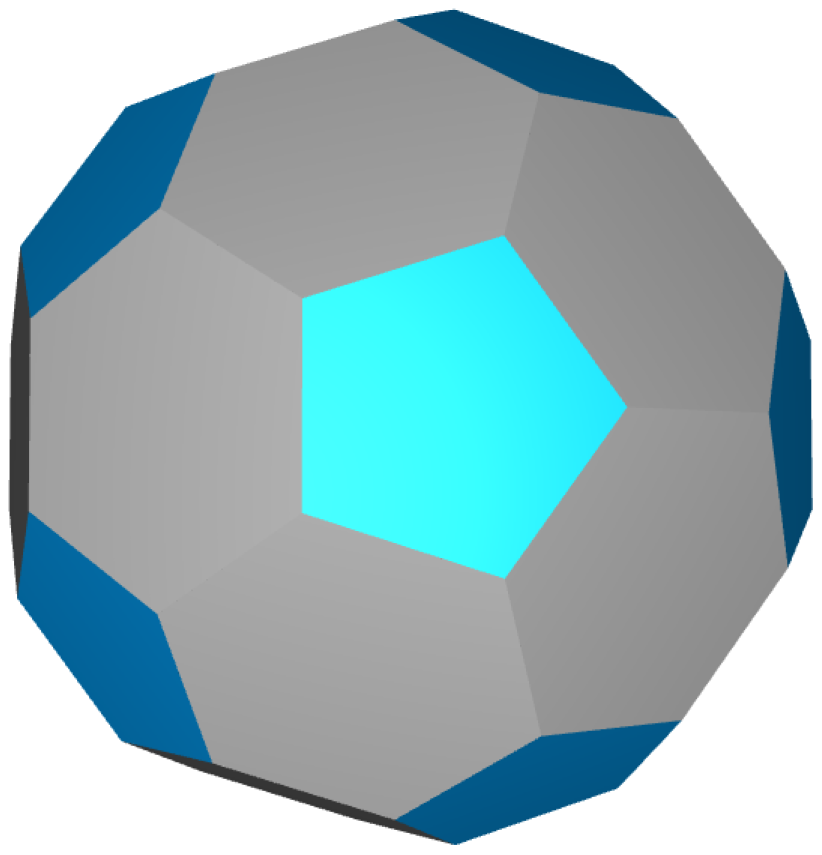
4.2.1. TIA Based on an Archimedean Solid
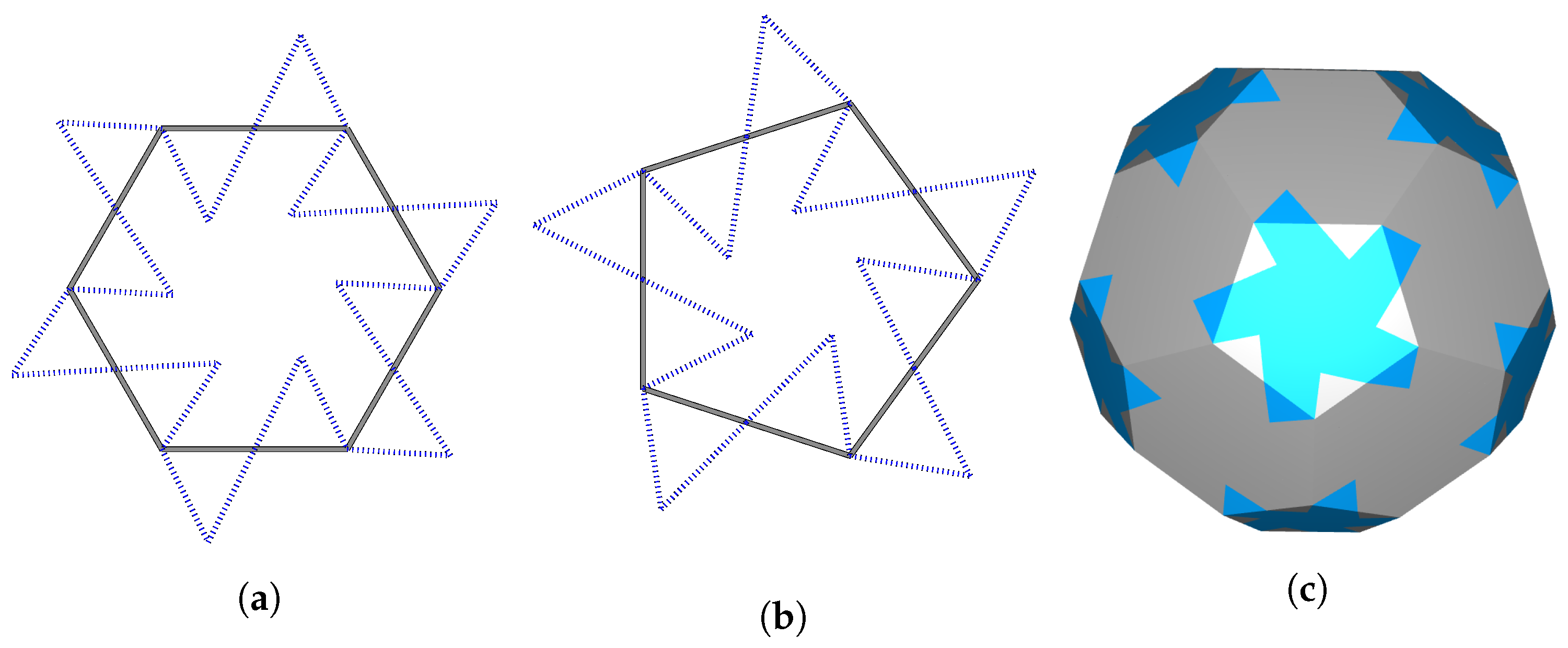
- For , the tile is constructed by deforming the edges of the hexagonal face such that the projection of the tile onto a plane containing the face is the polygon that is indicated by the blue dotted lines in Figure 9a.
- Furthermore, for , the tile is obtained by deforming the edges of the pentagonal face such that the projection of the modified tile onto a plane containing the face is the polygon that is indicated by the blue dotted lines in Figure 9b.
4.2.2. TIA Based on the Unit Sphere
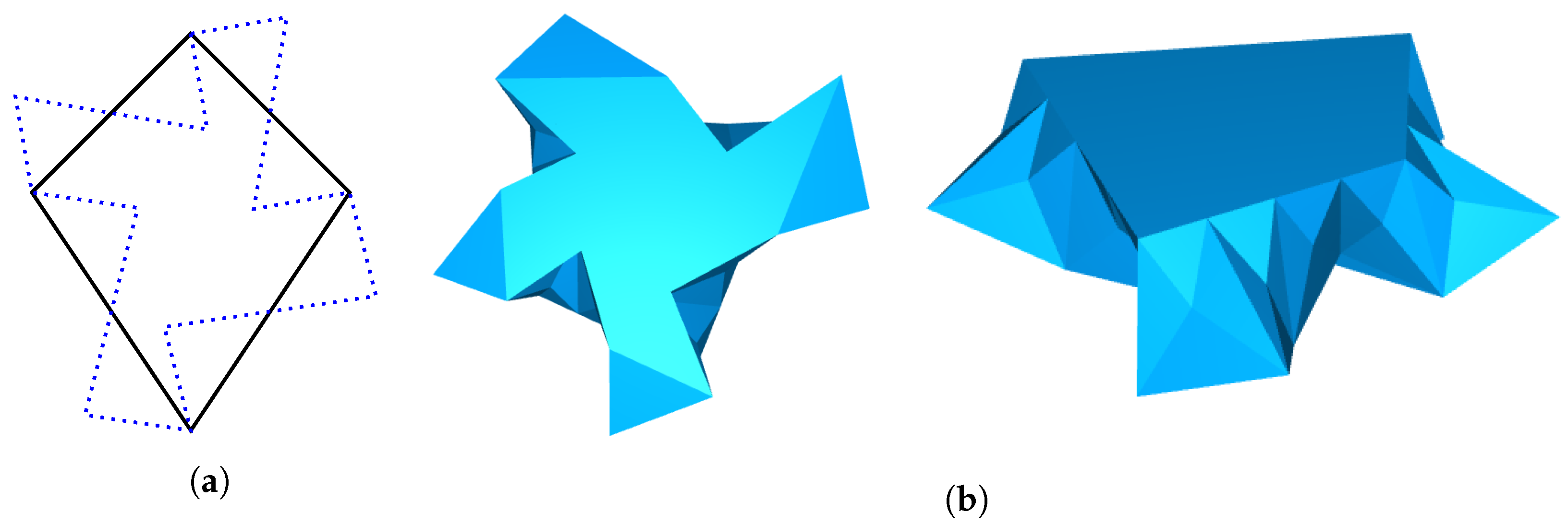
- For , the intersection between the hexagonal face and the spherical hexagon satisfies That means that this intersection contains the vertices of the hexagonal face
- For , the intersection between the pentagonal face and the spherical pentagon satisfy the equality , which means that this intersection contains the vertices of the pentagonal face
4.2.3. TIA Based on a Catalan Solid
5. Conclusions and Outlook
- The successful construction of planar and non-planar TIA using the Escher-like method;
- The exploration of a semi-regular tiling yielding an interlocking structure;
- The extension of the method to non-planar surfaces, such as the unit sphere and various convex polyhedra, demonstrates the feasibility of constructing spherical and polyhedral TIA.
- Practical insights gained from 3D-printed models provides a profound understanding of the assembly and interlocking processes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dyskin, A.V.; Estrin, Y.; Kanel-Belov, A.J.; Pasternak, E. A new concept in design of materials and structures: Assemblies of interlocked tetrahedron-shaped elements. Scr. Mater. 2001, 44, 2689–2694. [Google Scholar] [CrossRef]
- Weizmann, M.; Amir, O.; Grobman, Y.J. Topological interlocking in buildings: A case for the design and construction of floors. Autom. Constr. 2016, 72, 18–25. [Google Scholar] [CrossRef]
- Miodragovic Vella, I.; Kotnik, T. Stereotomy, an Early Example of a Material System. In Proceedings of the 35th eCAADe Conference, Rome, Italy, 20–22 September 2017; pp. 251–258. [Google Scholar] [CrossRef]
- Tessmann, O.; Rossi, A. Geometry as Interface: Parametric and Combinatorial Topological Interlocking Assemblies. J. Appl. Mech. 2019, 86, 111002. [Google Scholar] [CrossRef]
- Harsono, K.; Shih, S.G.; Wagiri, F.; Alfred, W. Integration of Design and Performance Evaluation for Reusable Osteomorphic-Block Masonry. Nexus Netw. J. 2023, 26, 71–94. [Google Scholar] [CrossRef]
- Hua, H. Porous interlocking assembly: Performance-based dry masonry construction with digital stereotomy. Archit. Intell. 2024, 3, 20. [Google Scholar] [CrossRef]
- Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Khor, H.C.; Kanel-Belov, A.J. The principle of topological interlocking in extraterrestrial construction. Acta Astronaut. 2005, 57, 10–21. [Google Scholar] [CrossRef]
- Carlesso, M.; Giacomelli, R.; Krause, T.; Molotnikov, A.; Koch, D.; Kroll, S.; Tushtev, K.; Estrin, Y.; Rezwan, K. Improvement of sound absorption and flexural compliance of porous alumina-mullite ceramics by engineering the microstructure and segmentation into topologically interlocked blocks. J. Eur. Ceram. Soc. 2013, 33, 2549–2558. [Google Scholar] [CrossRef]
- Dyskin, A.; Estrin, Y.; Kanel-Belov, A.; Pasternak, E. Topological interlocking of platonic solids: A way to new materials and structures. Philos. Mag. Lett. 2003, 83, 197–203. [Google Scholar] [CrossRef]
- Kanel-Belov, A.J.; Dyskin, A.V.; Estrin, Y.; Pasternak, E.; Ivanov-Pogodaev, I.A. Interlocking of Convex Polyhedra: Towards a Geometrical Theory of Fragmented Solids. Mosc. Math. J. 2010, 10, 337–342. [Google Scholar] [CrossRef]
- Glickman, M. The G-block system of vertically interlocking paving. In Proceedings of the Second International Conference on Concrete Block Paving, Delft, The Netherlands, 10–12 April 1984; pp. 10–12. [Google Scholar]
- Gallon, J.G. Machines et Inventions Approuvées par l’Académie Royale des Sciences Depuis son Établissement Jusqu’à Present; Avec Leur Description; l’Académie Royale des Sciences: Paris, France, 1735. [Google Scholar]
- Subramanian, S.G.; Eng, M.; Krishnamurthy, V.R.; Akleman, E. Delaunay Lofts: A biologically inspired approach for modeling space filling modular structures. Comput. Graph. 2019, 82, 73–83. [Google Scholar] [CrossRef]
- Akleman, E.; Krishnamurthy, V.R.; Fu, C.A.; Subramanian, S.G.; Ebert, M.; Eng, M.; Starrett, C.; Panchal, H. Generalized abeille tiles: Topologically interlocked space-filling shapes generated based on fabric symmetries. Comput. Graph. 2020, 89, 156–166. [Google Scholar] [CrossRef]
- Mullins, C.; Ebert, M.; Akleman, E.; Krishnamurthy, V. Voronoi Spaghetti & VoroNoodles: Topologically Interlocked, Space-Filling, Corrugated & Congruent Tiles. In Proceedings of the SIGGRAPH Asia 2022 Technical Communications, SA ’22, Daegu, Republic of Korea, 6–9 December 2022. [Google Scholar] [CrossRef]
- Ebert, M.; Akleman, E.; Krishnamurthy, V.; Kulagin, R.; Estrin, Y. VoroNoodles: Topological Interlocking with Helical Layered 2-Honeycombs. Adv. Eng. Mater. 2023, 26, 2300831. [Google Scholar] [CrossRef]
- Goertzen, T.; Niemeyer, A.; Plesken, W. Topological Interlocking via Symmetry. In Proceedings of the 6th FIB International Congress 2022, Oslo, Norway, 12–16 June 2022; Novus Press: Oslo, Norway, 2022. [Google Scholar]
- Goertzen, T. Constructing Interlocking Assemblies with Crystallographic Symmetries. arXiv 2024, arXiv:2405.15080. [Google Scholar]
- Goertzen, T. Mathematical Foundations of Interlocking Assemblies. arXiv 2024, arXiv:2405.17644. [Google Scholar] [CrossRef]
- Wang, Z.; Song, P.; Isvoranu, F.; Pauly, M. Design and Structural Optimization of Topological Interlocking Assemblies. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Bejarano, A.; Hoffmann, C. A generalized framework for designing topological interlocking configurations. Int. J. Archit. Comput. 2019, 17, 53–73. [Google Scholar] [CrossRef]
- Loing, V.; Baverel, O.; Caron, J.F.; Mesnil, R. Free-form structures from topologically interlocking masonries. Autom. Constr. 2020, 113, 103117. [Google Scholar] [CrossRef]
- Kaplan, C.S.; Salesin, D.H. Escherization. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; SIGGRAPH ’00. pp. 499–510. [Google Scholar] [CrossRef]
- Smith, D.; Myers, J.S.; Kaplan, C.S.; Goodman-Strauss, C. An aperiodic monotile. arXiv 2023, arXiv:2303.10798. [Google Scholar] [CrossRef]
- Smith, D.; Myers, J.S.; Kaplan, C.S.; Goodman-Strauss, C. A chiral aperiodic monotile. arXiv 2023, arXiv:2305.17743. [Google Scholar] [CrossRef]
- Akpanya, R.; Goertzen, T.; Liu, Y.; Stüttgen, S.; Robertz, D.; Xie, Y.M.; Niemeyer, A.C. Constructing Topological Interlocking Assemblies Based on an Aperiodic Monotile. In Proceedings of the IASS 2024 Symposium: Redefining the Art of Structural Design, Zurich, Switzerland, 26–30 August 2024; Block, P., Boller, G., DeWolf, C., Pauli, J., Kaufmann, W., Eds.; International Association for Shell and Spatial Structures (IASS): Madrid, Spain, 2024. accepted, not yet published. [Google Scholar]
- Akpanya, R.; Goertzen, T.; Wiesenhuetter, S.; Niemeyer, A.C.; Noennig, J. Topological Interlocking, Truchet Tiles and Self-Assemblies: A Construction-Kit for Civil Engineering Design. In Proceedings of the Bridges 2023: Mathematics, Art, Music, Architecture, Culture, Halifax, NS, Canada, 27–31 July 2023; Holdener, J., Torrence, E., Fong, C., Seaton, K., Eds.; Tessellations Publishing: Phoenix, AZ, USA, 2023; pp. 61–68. [Google Scholar]
- Goertzen, T.; Macek, D.; Schnelle, L.; Weiß, M.; Reese, S.; Holthusen, H.; Niemeyer, A.C. Mechanical Comparison of Arrangement Strategies for Topological Interlocking Assemblies. arXiv 2023, arXiv:2312.01958. [Google Scholar] [CrossRef]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; A K Peters, Ltd.: Wellesley, MA, USA; New York, NY, USA, 2008; pp. xviii+426. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; A Series of Books in the Mathematical Sciences; An introduction; W. H. Freeman and Company: New York, NY, USA, 1989; pp. xii+446. [Google Scholar]
- Dyskin, A.; Estrin, Y.; Pasternak, E.; Khor, H.; Kanel-Belov, A. Fracture Resistant Structures Based on Topological Interlocking with Non-planar Contacts. Adv. Eng. Mater. 2003, 5, 116–119. [Google Scholar] [CrossRef]
- Stüttgen, S.; Akpanya, R.; Beckmann, B.; Chudoba, R.; Robertz, D.; Niemeyer, A.C. Modular Construction of Topological Interlocking Blocks—An Algebraic Approach for Resource-Efficient Carbon-Reinforced Concrete Structures. Buildings 2023, 13, 2565. [Google Scholar] [CrossRef]
- Akpanya, R.; Goertzen, T.; Niemeyer, A.C. A Group-Theoretic Approach for Constructing Spherical-Interlocking Assemblies. In Proceedings of the IASS Annual Symposium 2023: Integration of Design and Fabrication, Melbourne, Australia, 10–14 July 2023; Xie, Y., Burry, J., Lee, T., Ma, J., Eds.; International Association for Shell and Spatial Structures (IASS): Madrid, Spain, 2023; pp. 470–480. [Google Scholar]
- Viana, V. From Solid to Plane Tessellations, and Back. Nexus Netw. J. 2018, 20, 741–768. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akpanya, R.; Goertzen, T.; Niemeyer, A.C. From Tilings of Orientable Surfaces to Topological Interlocking Assemblies. Appl. Sci. 2024, 14, 7276. https://doi.org/10.3390/app14167276
Akpanya R, Goertzen T, Niemeyer AC. From Tilings of Orientable Surfaces to Topological Interlocking Assemblies. Applied Sciences. 2024; 14(16):7276. https://doi.org/10.3390/app14167276
Chicago/Turabian StyleAkpanya, Reymond, Tom Goertzen, and Alice C. Niemeyer. 2024. "From Tilings of Orientable Surfaces to Topological Interlocking Assemblies" Applied Sciences 14, no. 16: 7276. https://doi.org/10.3390/app14167276
APA StyleAkpanya, R., Goertzen, T., & Niemeyer, A. C. (2024). From Tilings of Orientable Surfaces to Topological Interlocking Assemblies. Applied Sciences, 14(16), 7276. https://doi.org/10.3390/app14167276






