Determining the Head Characteristics of Radial Centrifugal Pumps under the Impact of Prewhirl
Abstract
1. Introduction
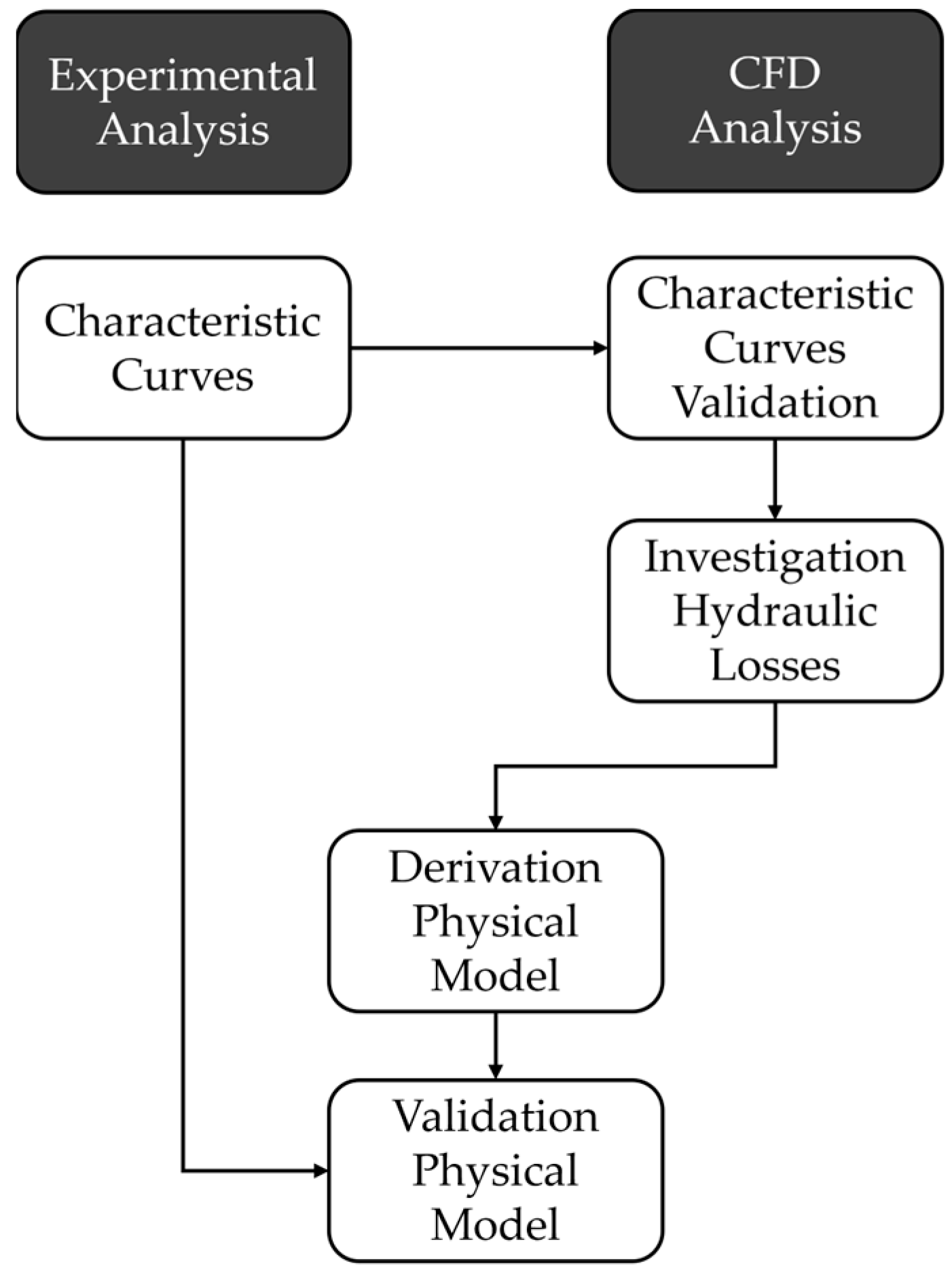
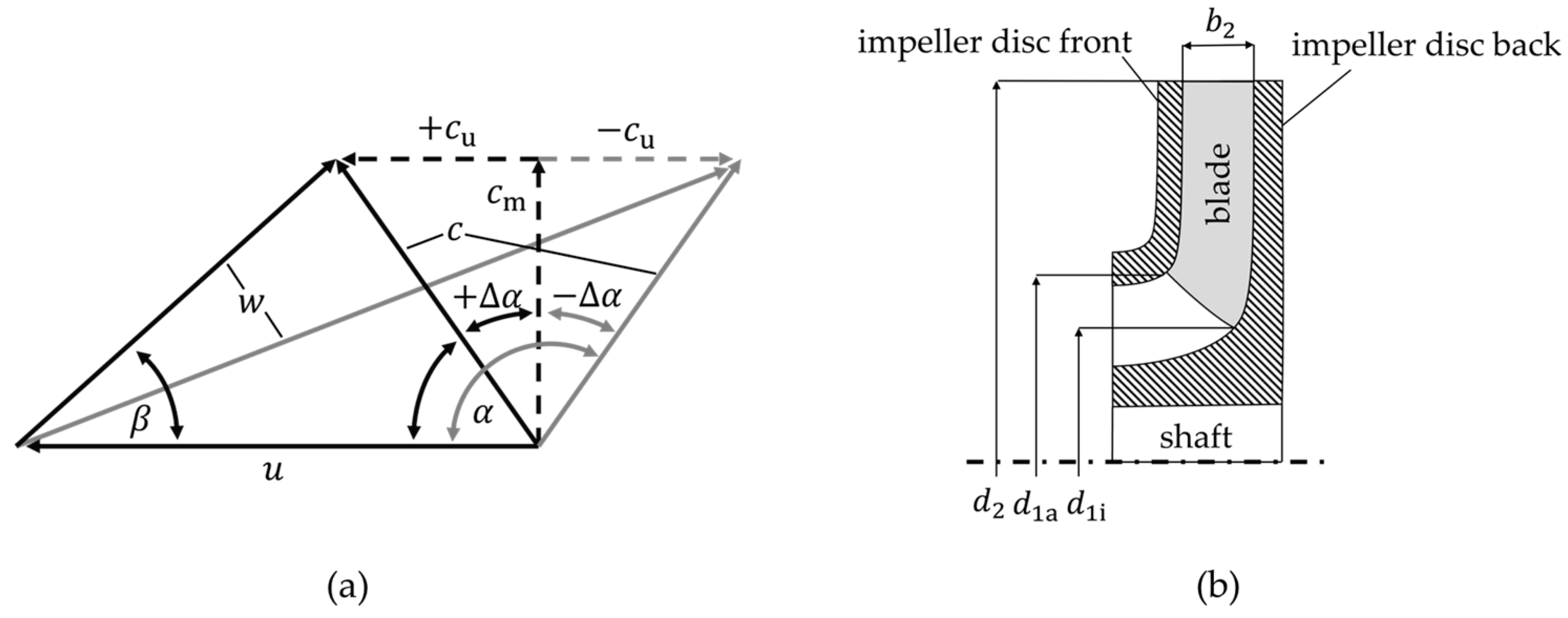
2. Method for Analysing Losses in Centrifugal Pumps with Different Prewhirl Angles
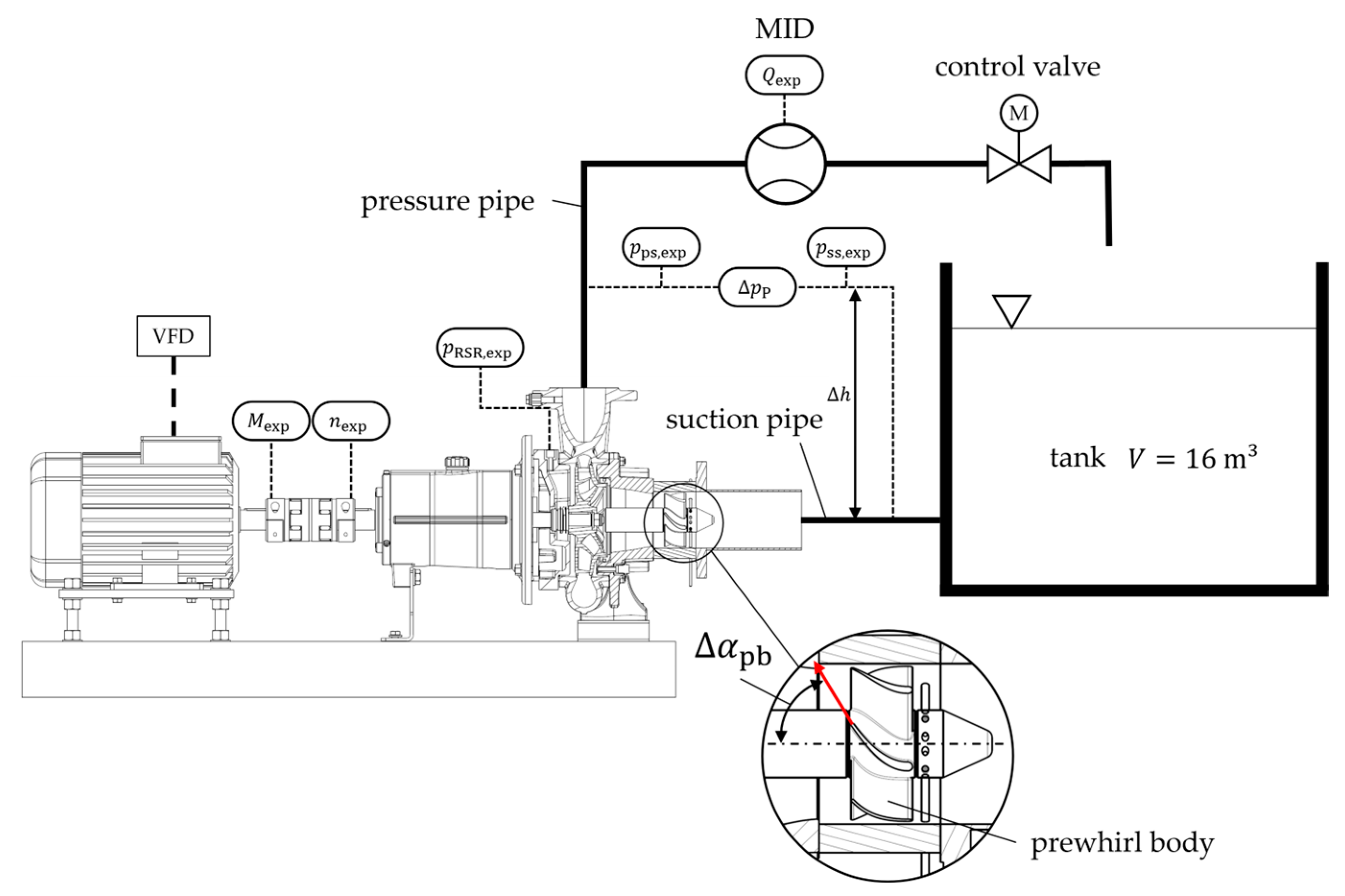
2.1. Experimental Determination of the Head Characteristics with Varying Prewhirl Angles
2.2. 3D Model and Meshes for the Numerical Investigation of Hydraulic Losses
2.3. Setup of the CFD Simulation
3. Analysis and Discussion of the Results
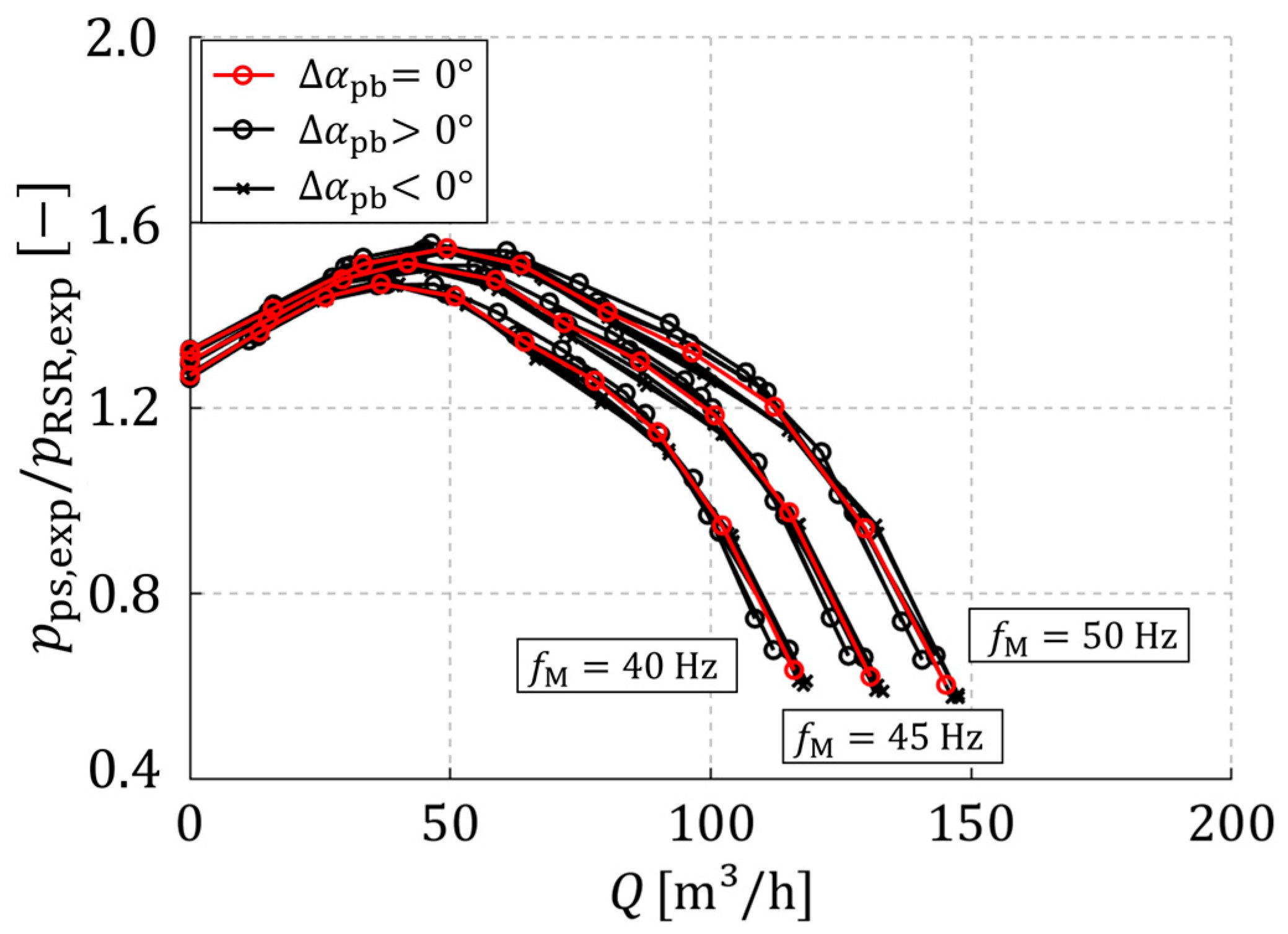
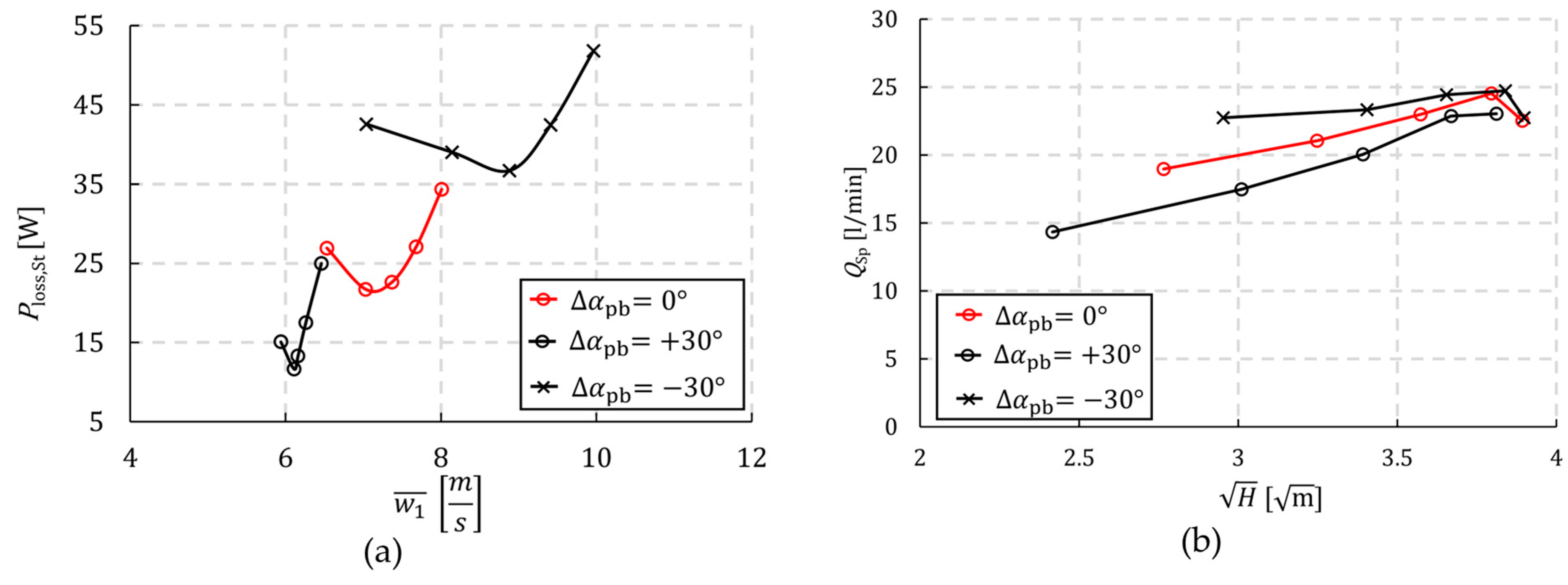
3.1. Analysis and Discussion of the Experimental Results
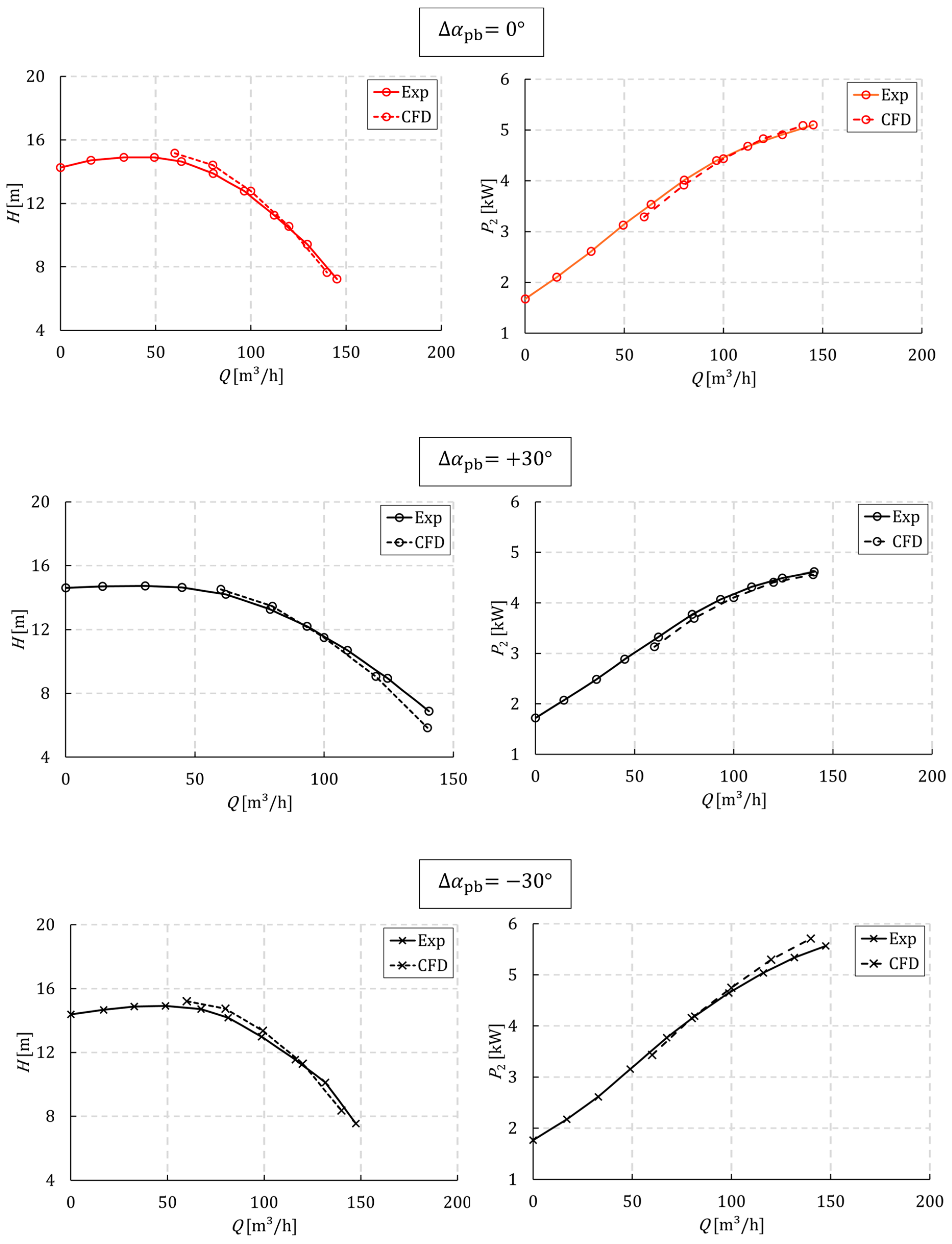
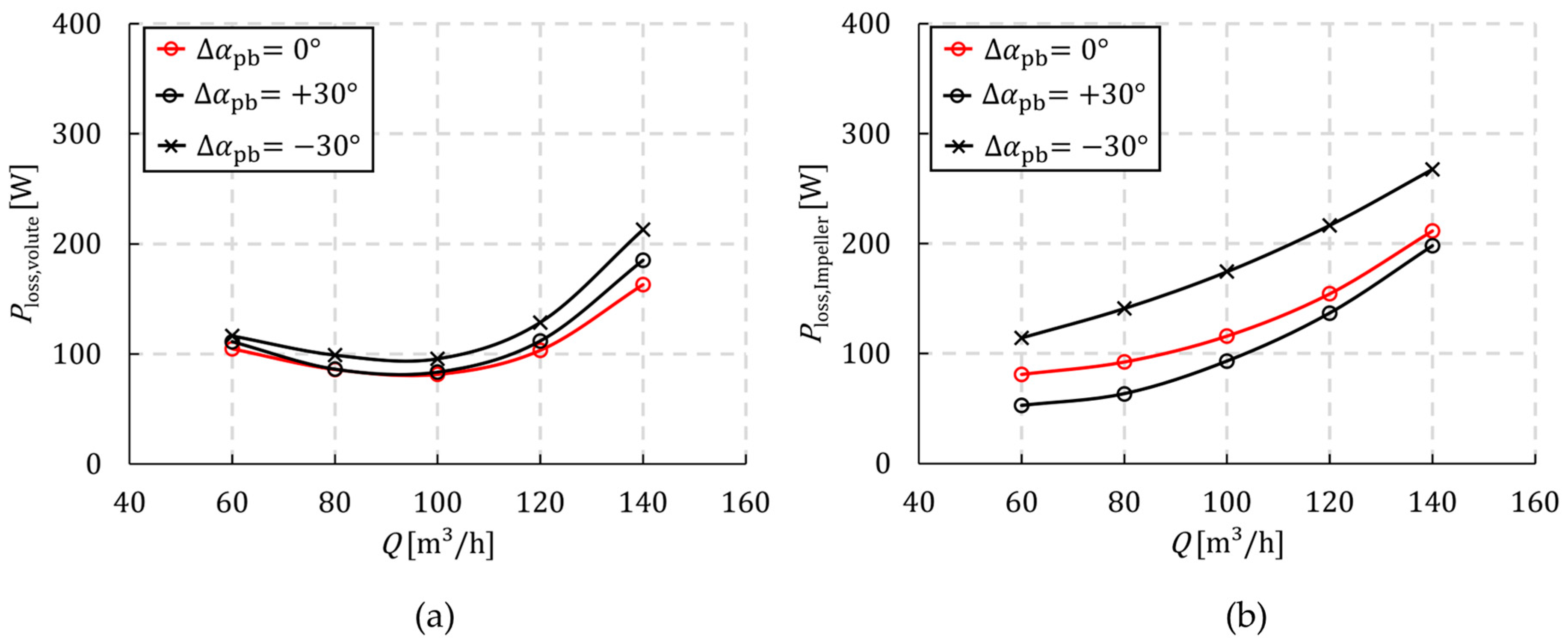
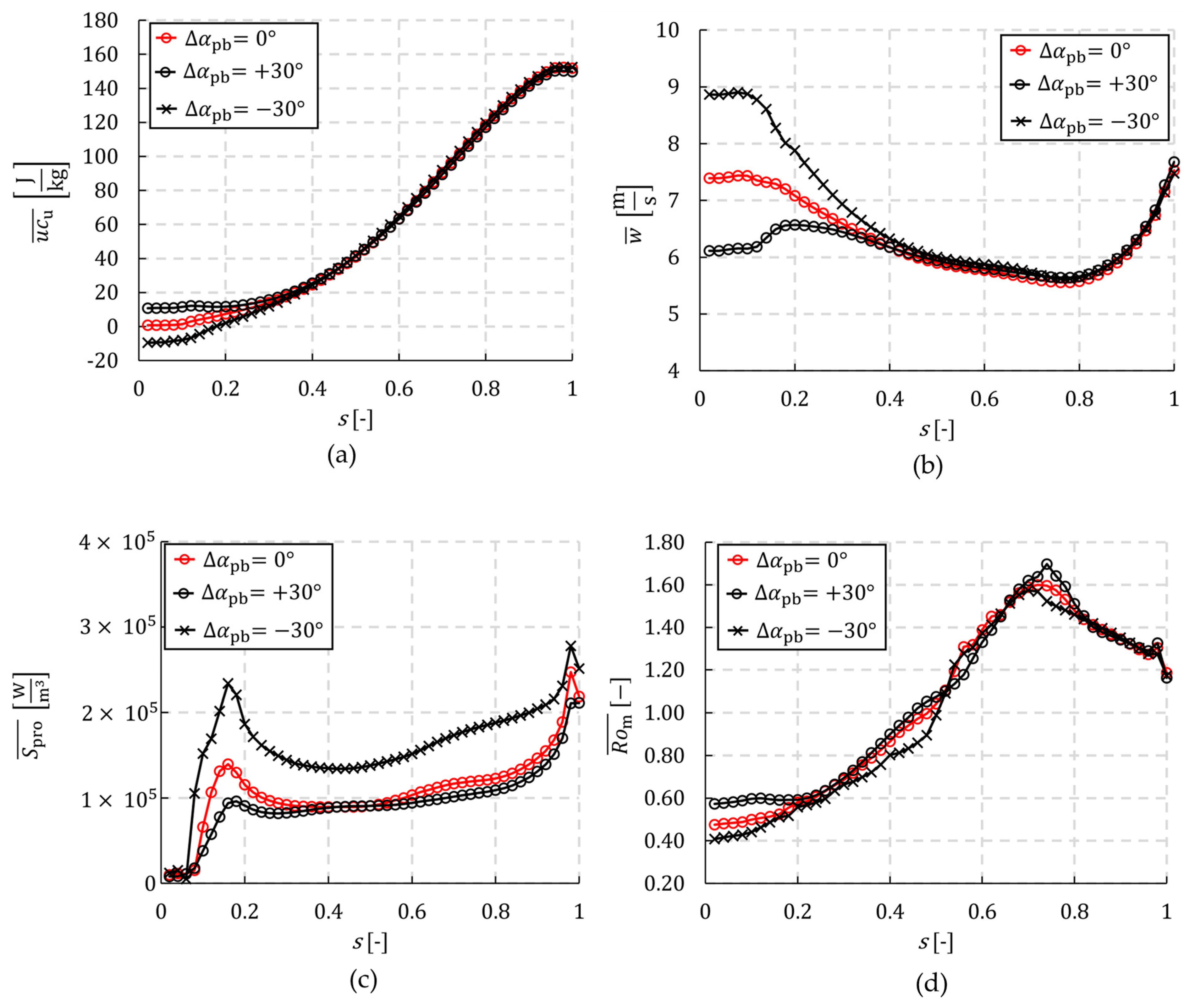
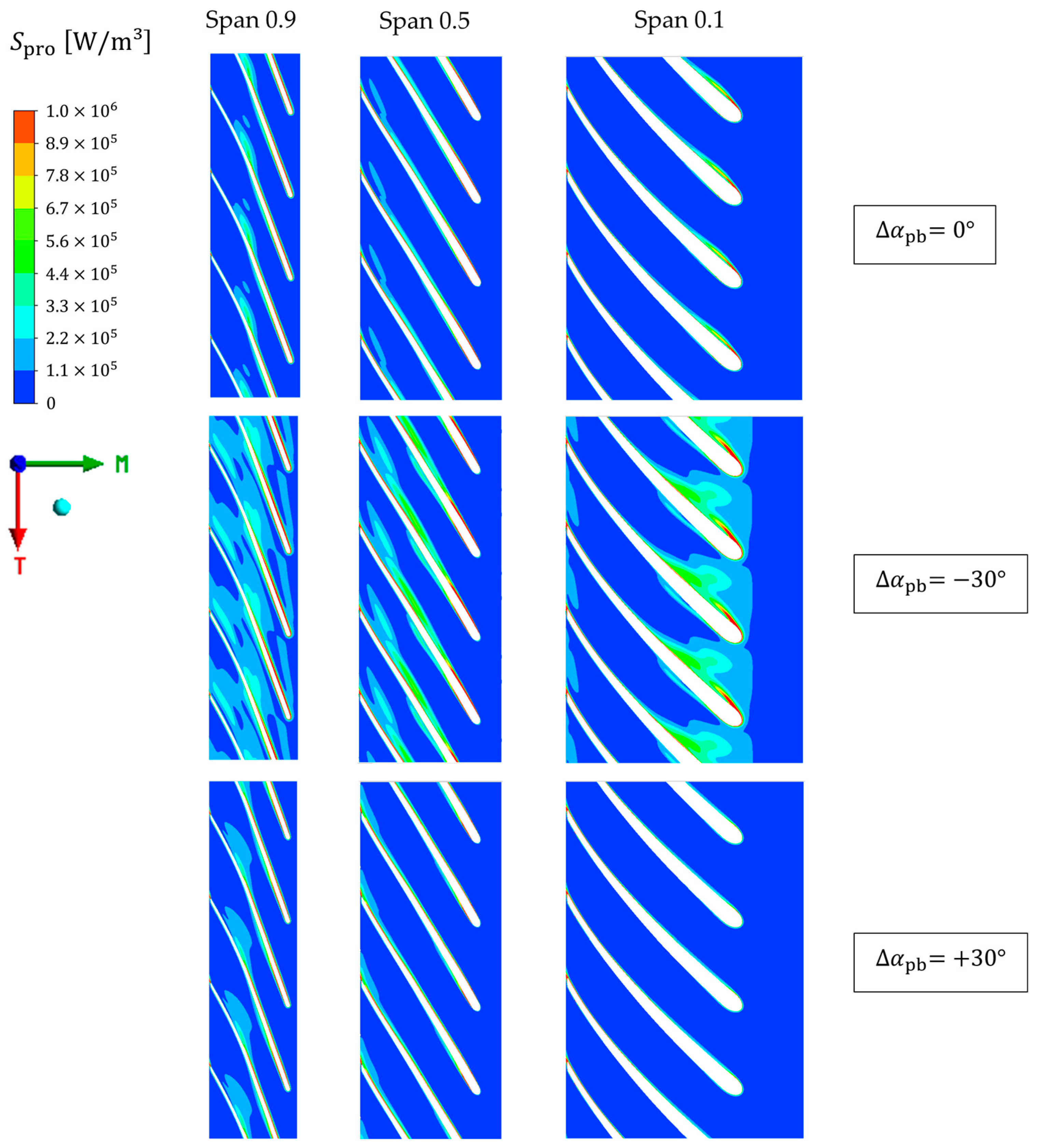
3.2. Validation of the CFD Simulation and Analysis of the Loss Behaviour
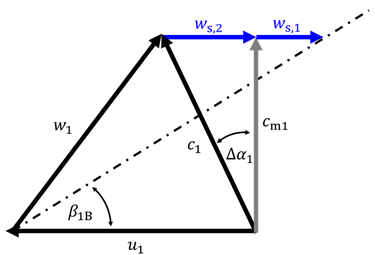
4. Development of a Physical Model for the Head Characteristic Curve
4.1. Derivation of the Model
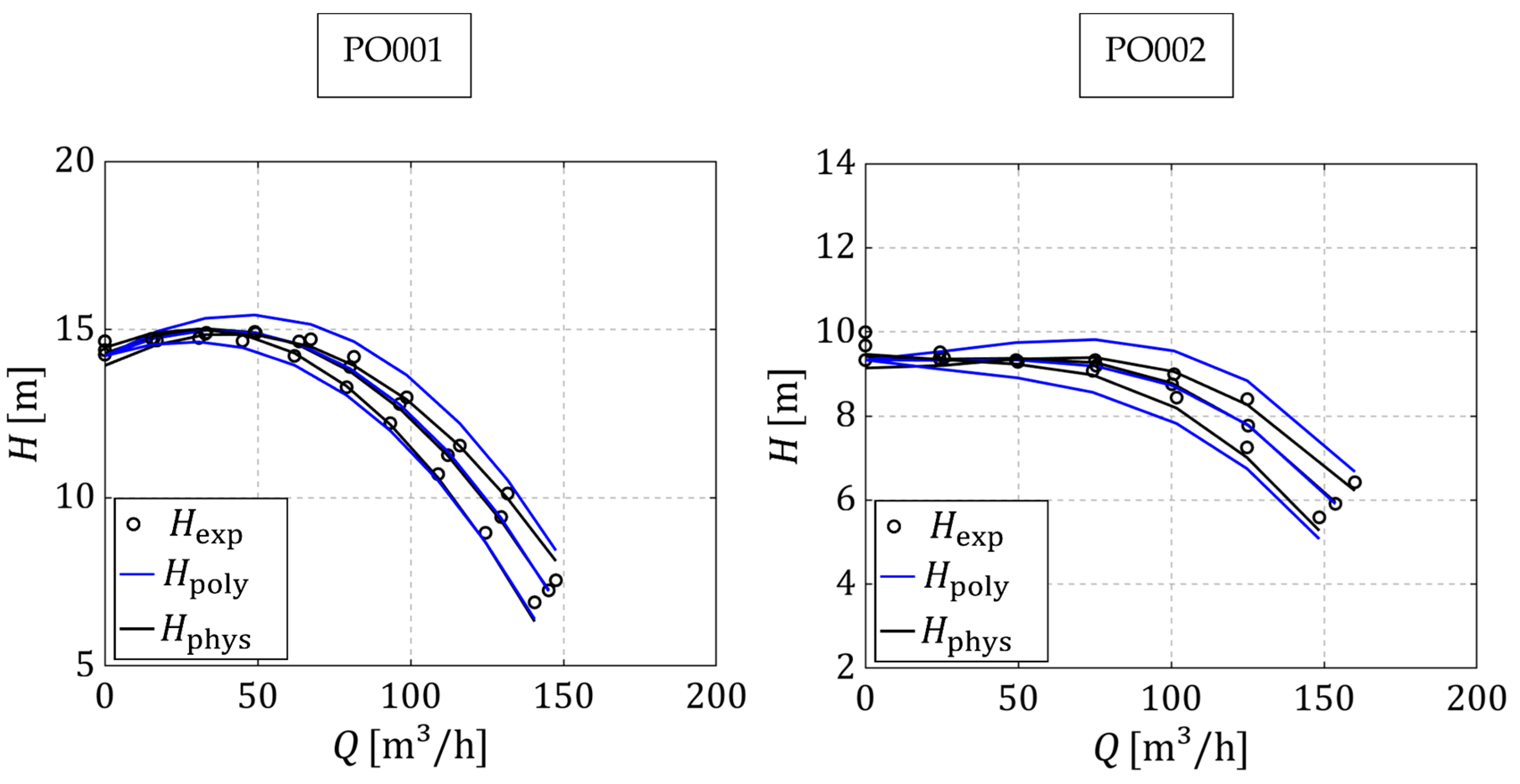
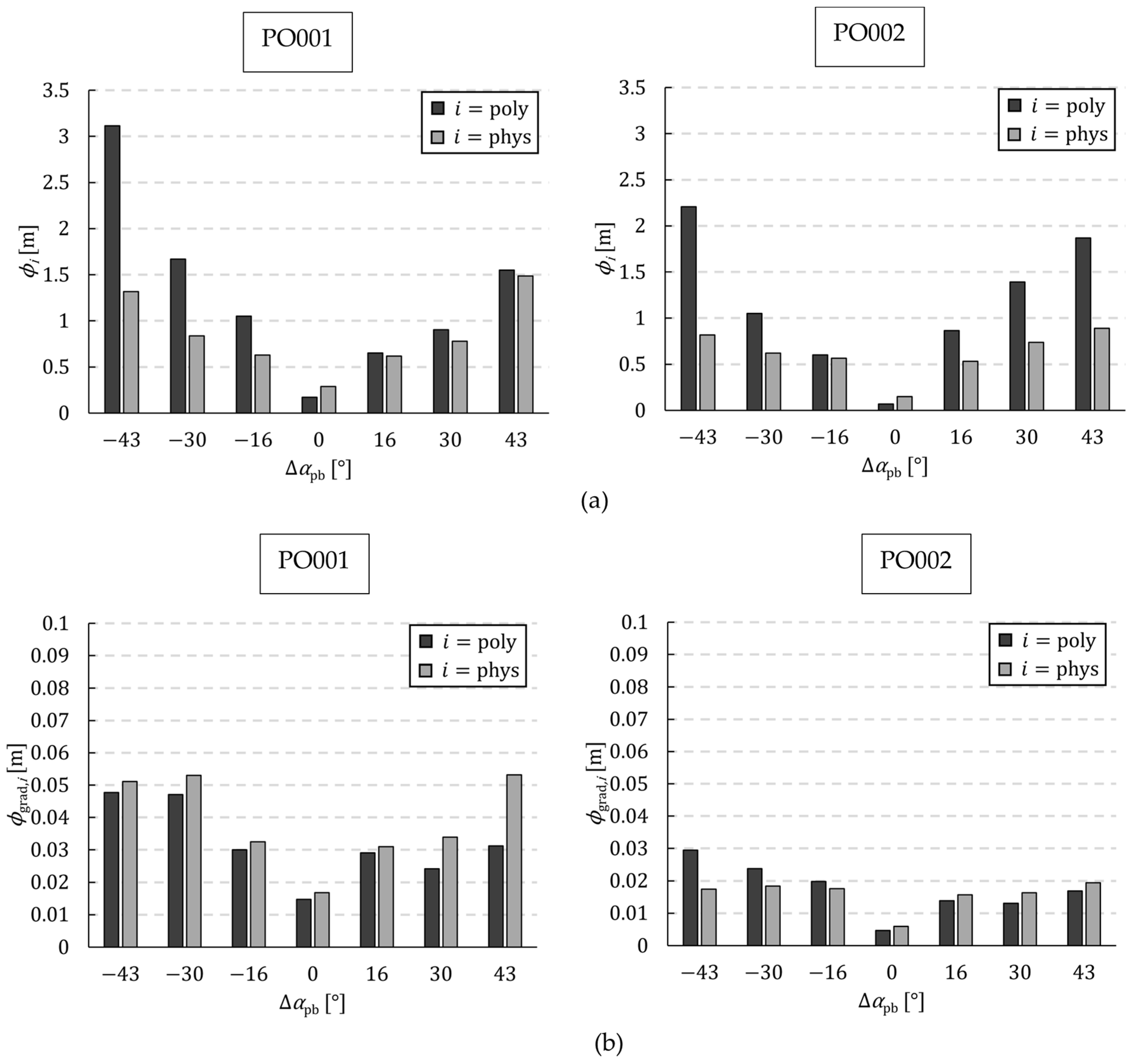
4.2. Comparison between the Models with Different Loss Treatments and the Experimental Results
5. Conclusions
- −
- The hydraulic losses in radial centrifugal pumps are influenced by the prewhirl. The observed changes in losses can be attributed primarily to the pump impeller.
- −
- The extent of the losses depends on the sign of the prewhirl angle. Negative prewhirl angles increase hydraulic losses, while positive prewhirl angles reduce them.
- −
- The majority of the hydraulic losses in the impeller occur at the leading edge of the blades and in the area of the impeller outlet.
- −
- The degree of prewhirl angle has a significant impact on the whirl of the impeller, as well as the relative velocities. The Coriolis force increases in direct proportion to the relative velocity, which can result in the generation of secondary flows. These factors contribute to an increase in the likelihood of loss, particularly at the point of impeller inlet.
- −
- In addition to the secondary flows, the shock losses are also influenced by the prewhirl angles.
- -
- Furthermore, the relative velocities exert an influence on the friction losses in the impeller, whereby these increase with negative prewhirl angles.
- −
- The modelling of impeller losses based on relative velocity allows for the consideration of the differing influences of positive and negative prewhirl angles.
- −
- The model enhances the mapping of the characteristic curves of the head. It can therefore be utilised in the construction of soft sensors for the determination of flow rates in instances of disrupted inflows. This facilitates more accurate flow rate determination.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cross section at the impeller inlet | |
| Coriolis acceleration | |
| absolute velocity | |
| absolute velocity mean meridian streamline impeller inlet | |
| meridional component of absolute velocity | |
| pressure reduction coefficient | |
| circumferential component of absolute velocity | |
| circumferential component of absolute velocity mean meridian streamline impeller inlet | |
| absolute velocity impeller outlet | |
| circumferential component of absolute velocity impeller outlet | |
| circumferential component of absolute velocity impeller outlet blade-congruent flow | |
| outer diameter impeller inlet | |
| mean diameter at impeller inlet | |
| inner diameter impeller inlet | |
| width impeller outlet | |
| diameter impeller outlet | |
| motor frequency | |
| sampling rate | |
| acceleration due to gravity | |
| pump head | |
| experimental measured pump head | |
| pump head determined by physical model | |
| pump head determined by polynomial | |
| head at BEP | |
| head loss prewhirl body | |
| geodetic height between pressure transmitter and suction pipe | |
| turbulent kinetic energy | |
| equivalent sand grain roughness | |
| measured torque | |
| mass flow rate | |
| speed | |
| measured speed | |
| nominal speed | |
| specific speed | |
| pump power consumption | |
| pump power consumption at BEP | |
| measured pump power consumption | |
| power loss | |
| power loss due to shock loss | |
| mechanical power | |
| static pressure | |
| static pressure impeller outlet | |
| measured static pressure at pressure side | |
| static pressure in impeller back side gap | |
| measured static pressure in impeller back side gap | |
| measured static pressure at suction side | |
| static pressure increase in the volute | |
| pressure loss volute | |
| static differential pressure of the pump | |
| flow rate | |
| flow rate of the impeller | |
| flow rate at BEP | |
| measured flow rate | |
| leakage flow | |
| radius | |
| modified Rossby number | |
| dimensionless streamline length | |
| entropy production | |
| averaged entropy production | |
| turbulent part of entropy production | |
| tuning factor | |
| tuning vector | |
| measured period | |
| circumferential velocity | |
| circumferential velocity mean meridian streamline impeller inlet | |
| circumferential velocity impeller outlet | |
| tank volume | |
| flow velocity pressure side | |
| flow velocity suction side | |
| relative velocity | |
| vector relative velocity | |
| relative velocity impeller inlet | |
| relative velocity mean meridian streamline impeller inlet | |
| relative velocity impeller outlet | |
| mean relative velocity | |
| shock velocity | |
| specific hydraulic work | |
| specific impeller work | |
| specific Borda-Carnot shock loss of the impeller | |
| specific friction and turbulence loss of the volute | |
| specific shock loss of the volute | |
| specific friction and turbulence loss of the impeller | |
| specific recirculation loss | |
| specific shock loss of the impeller | |
| objective functional | |
| number of impeller blades | |
| flow angle | |
| whirl angle | |
| prewhirl body angle | |
| blade angle | |
| blade angle impeller outlet | |
| performance factor | |
| hydraulic efficiency of the pump | |
| recirculation efficiency | |
| volumetric efficiency | |
| density of the pumped medium | |
| norm of the objective functional | |
| norm of the objective functional of the gradient | |
| discretisation angle | |
| shock factor | |
| turbulent eddy frequency | |
| vector angular velocity |
Appendix A
| Measured Quantity | Maximum Relative Error |
Appendix B
References
- Sebastian, L. Nutzung des Energiesparpotentials von Kreiselpumpen Durch Szenarienbasierte Regelung; Ruhr-Universi at Bochum: Oberhausen, Germany, 2015. [Google Scholar]
- Desborough, L.; Miller, R. Increasing Customer Value of Industrial Control Performance Monitoring—Honeywell’s Experience. In Chemical Process Control-VI: Assessment and New Directions for Research, Proceedings of the 6th International Conference on Chemical Process Control, Tucson, AZ, USA, 7–12 January 2001; AIChE Symposium Series 326; American Institute of Chemical Engineers (AIChE): New York, NY, USA, 2002; pp. 169–189. [Google Scholar]
- Leonow, S.; Monnigmann, M. Soft Sensor Based Dynamic Flow Rate Estimation in Low Speed Radial Pumps. In Proceedings of the IEEE 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 778–783. [Google Scholar]
- Rakibuzzaman, M.; Suh, S.-H.; Yoon, I.-S.; Jung, S.Y. A Study on the Individual Pump Flow Estimation Processor for Optimal Operation. E3S Web Conf. 2021, 321, 02005. [Google Scholar] [CrossRef]
- Shankar, A.; Subramaniam, U.; Madurai Elavarasan, R.; Raju, K.; Shanmugam, P. Sensorless Parameter Estimation of VFD Based Cascade Centrifugal Pumping System Using Automatic Pump Curve Adaption Method. Energy Rep. 2021, 7, 453–466. [Google Scholar] [CrossRef]
- Roth, M. Experimentelle und numerische Untersuchung zum Einfluss von Einbaubedingungen auf das Betriebs- und Kavitationsverhalten von Kreiselpumpen. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2006. [Google Scholar]
- Fockert, A.; Verhaart, F.; Ferdos, F. Experimentally Determined Effect of Swirl on the Performance of a Rotodynamic Pump. J. Hydraul. Res. 2022, 60, 434–444. [Google Scholar] [CrossRef]
- Siekmann, H. Auswirkung Ungleichmäßiger Zuströmung auf Spezifisch Schnellläufige Kreiselpumpen; TU-Berlin: Berlin, Germany, 1984; p. 250. [Google Scholar]
- Schröder, I.V. Experimentelle Untersuchungen über Vordralleinflüsse auf die Kennlinien von Radialpumpen Verschiedener Schnellläufigkeit; ReportKönigsbrunn, Germany. 2012. Available online: https://docplayer.org/52403643-Experimentelle-untersuchungen-ueber-vordralleinfluesse-auf-die-kennlinien-von-radialpumpen-verschiedener.html (accessed on 11 January 2022).
- Tan, L.; Cao, S.; Gui, S. Hydraulic Design and Pre-Whirl Regulation Law of Inlet Guide Vane for Centrifugal Pump. Sci. China Technol. Sci. 2010, 53, 2142–2151. [Google Scholar] [CrossRef]
- Zhou, C.M.; Wang, H.M.; Huang, X.; Lin, H. Influence of the Positive Prewhirl on the Performance of Centrifugal Pumps with Different Airfoils. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 032020. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Muiz, A.; Mubashir, M.; Ahmed, W. Efficiency Enhancement of Centrifugal Water Pump by Using Inlet Guided Vanes. Eur. J. Adv. Eng. Technol. 2016, 3, 1–4. [Google Scholar]
- Tan, L.; Cao, S.; Wang, Y.; Zhu, B. Influence of Axial Distance on Pre-Whirl Regulation by the Inlet Guide Vanes for a Centrifugal Pump. Sci. China Technol. Sci. 2012, 55, 1037–1043. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L.; Liu, M.; Hao, Y.; Xu, Y. Influence of Prewhirl Angle and Axial Distance on Energy Performance and Pressure Fluctuation for a Centrifugal Pump with Inlet Guide Vanes. Energies 2017, 10, 695. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, B.; Cao, S.; Wang, Y.; Wang, B. Influence of Prewhirl Regulation by Inlet Guide Vanes on Cavitation Performance of a Centrifugal Pump. Energies 2014, 7, 1050–1065. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Y.; Han, Y.W. Impeller Entrance Pre Whirl Characteristics Research. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129, 012026. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Li, Z.; Zhou, X.; Wang, Z. Hydraulic Design of Inlet Guide Vane and Its Full Flow Passage Numerical Simulation on Centrifugal Pump. In Proceedings of the Volume 7: Fluids Engineering Systems and Technologies, American Society of Mechanical Engineers, Montreal, QC, Canada, 14 November 2014; p. V007T09A072. [Google Scholar]
- Zibin, X. Study on the H-Q Characteristic Curves of Centrifugal Pump with Inlet Pre-Whirl. In Proceedings of the IEEE 2015 Sixth International Conference on Intelligent Systems Design and Engineering Applications (ISDEA), Guiyang, China, 18–19 August 2015; pp. 763–766. [Google Scholar]
- Lin, P.; Li, Y.; Xu, W.; Chen, H.; Zhu, Z. Numerical Study on the Influence of Inlet Guide Vanes on the Internal Flow Characteristics of Centrifugal Pump. Processes 2020, 8, 122. [Google Scholar] [CrossRef]
- Song, P.; Wei, Z.; Zhen, H.; Liu, M.; Ren, J. Effects of Pre-Whirl and Blade Profile on the Hydraulic and Cavitation Performance of a Centrifugal Pump. Int. J. Multiph. Flow 2022, 157, 104261. [Google Scholar] [CrossRef]
- Ma, X.; Bian, M.; Yang, Y.; Dai, T.; Tang, L.; Wang, J. Study on the Effect Mechanism of Inlet Pre-Swirl on Pressure Pulsation within a Mixed-Flow Centrifugal Pump. Water 2023, 15, 1223. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Yang, Y.; Wang, S.; Bai, L.; Zhou, L. CFD Simulation of Centrifugal Pump with Different Impeller Blade Trailing Edges. J. Mar. Sci. Eng. 2023, 11, 402. [Google Scholar] [CrossRef]
- Zhang, C.; Pei, J.; Wang, W.; Yuan, S.; Gan, X.; Huang, C.; Chen, J. Unsteady Simulation and Analysis of Energy Loss Mechanism of a Vertical Volute Pump Under Stall Conditions. J. Fluids Eng. 2023; 145, 081201. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Xi, B.; Shi, W.-D.; Wang, C.; Ji, L.-L.; Song, X.-Y.; He, Z.-M. Inter-Stage Performance and Energy Characteristics Analysis of Electric Submersible Pump Based on Entropy Production Theory. Pet. Sci. 2023, 21, 1354–1368. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.; Bai, L.; Wang, H.; Ji, L.; Zhou, L. Energy Performance Prediction Model for Mixed-Flow Pumps by Considering the Effect of Incoming Prerotation. J. Fluids Eng. 2024, 146, 061204. [Google Scholar] [CrossRef]
- Reeh, N.; Manthei, G.; Klar, P.J. Physical Modelling of the Set of Performance Curves for Radial Centrifugal Pumps to Determine the Flow Rate. Appl. Syst. Innov. 2023, 6, 111. [Google Scholar] [CrossRef]
- Gülich, J.F. Kreiselpumpen, Handbuch Für Entwicklung, Anlagenplanung Und Betrieb; 5. Auflage; Springer Vieweg: Villeneuve, Switzerland, 2020; ISBN 978-3-662-59784-2. [Google Scholar]
- Limbach, P.; Müller, T.; Blume, M.; Skoda, R. Numerical and Experimental Investigation of the Cavitating Flow in a Low Specific Speed Centrifugal Pump and Assessment of the Influence of Surface Roughness on Head Prediction. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, NI, USA, 10–15 April 2016. [Google Scholar]
- CFX-Solver Theory Guide. ANSYS, Inc.: Canonsburg, PA, USA, 2022.
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Herwig, H.; Kock, F. Direct and Indirect Methods of Calculating Entropy Generation Rates in Turbulent Convective Heat Transfer Problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Effect of Blade Thickness on Rotating Stall of Mixed-Flow Pump Using Entropy Generation Analysis. Energy 2021, 236, 121381. [Google Scholar] [CrossRef]
- Brun, K.; Kurz, R. Analysis of Secondary Flows in Centrifugal Impellers. Int. J. Rotating Mach. 2005, 2005, 856141. [Google Scholar] [CrossRef]
- Pfleiderer, C. Die Kreiselpumpen für Flüssigkeiten und Gase: Wasserpumpen, Ventilatoren, Turbogebläse, Turbokompressoren, 4th ed.; Springer: Berlin/Heidelberg, Germany, 1955; ISBN 978-3-642-48171-0. [Google Scholar]
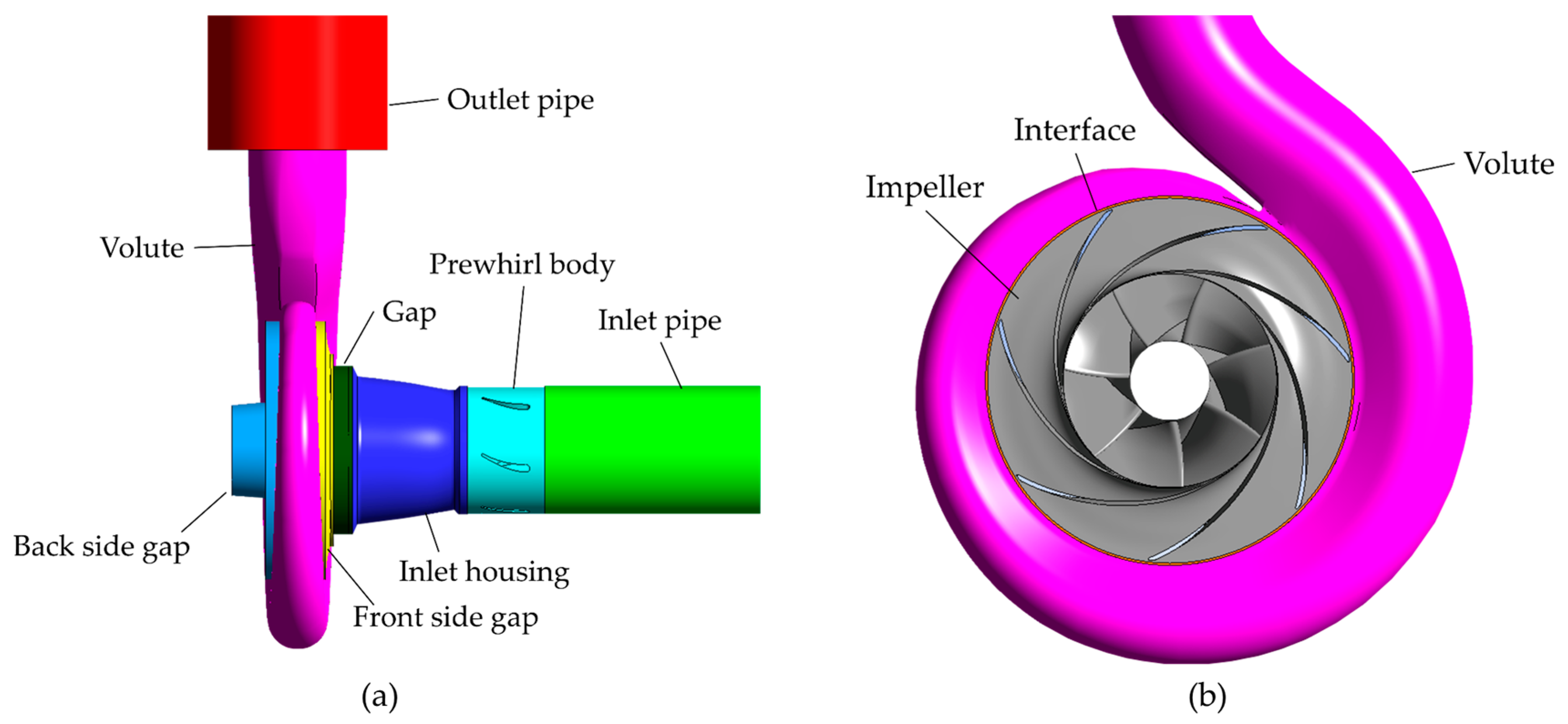
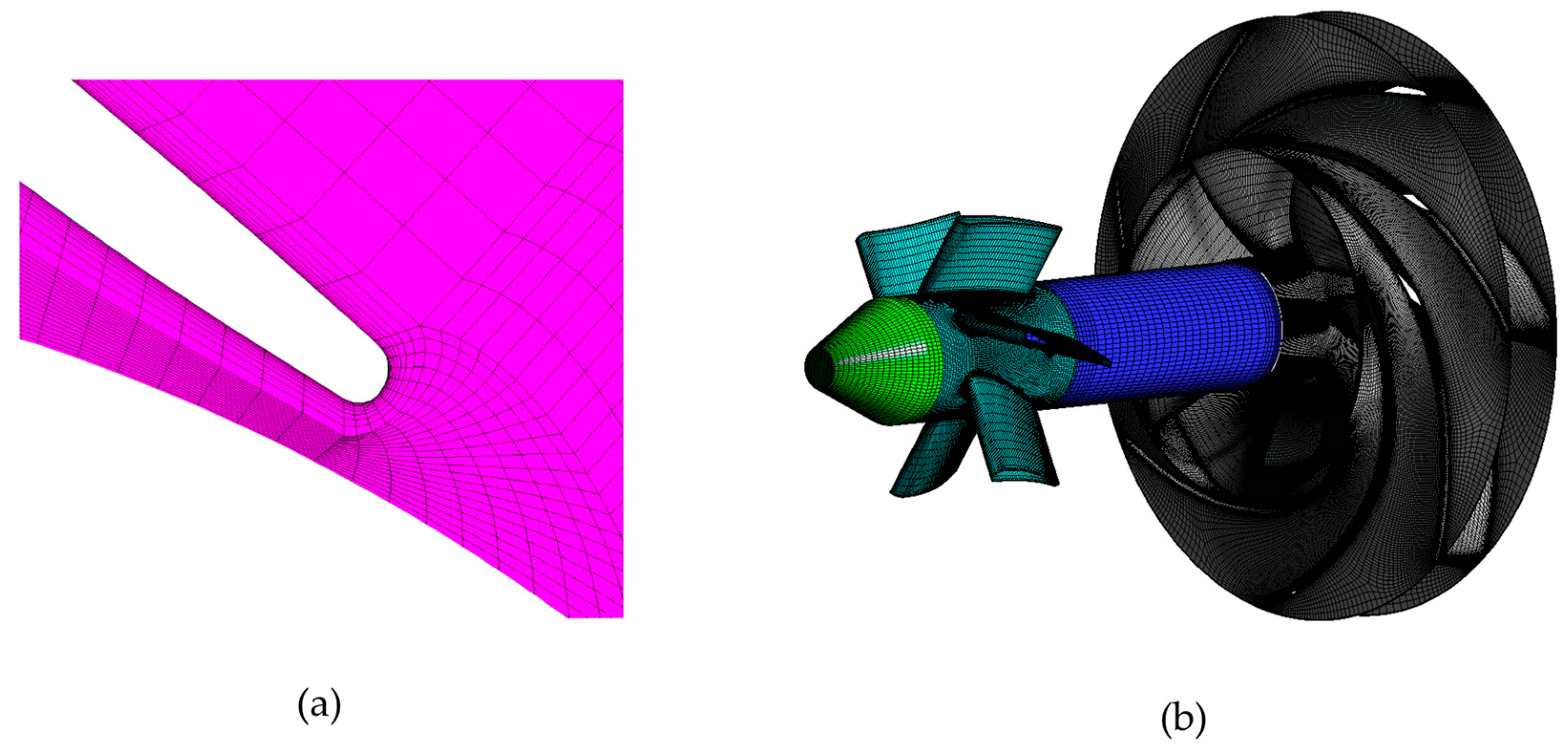
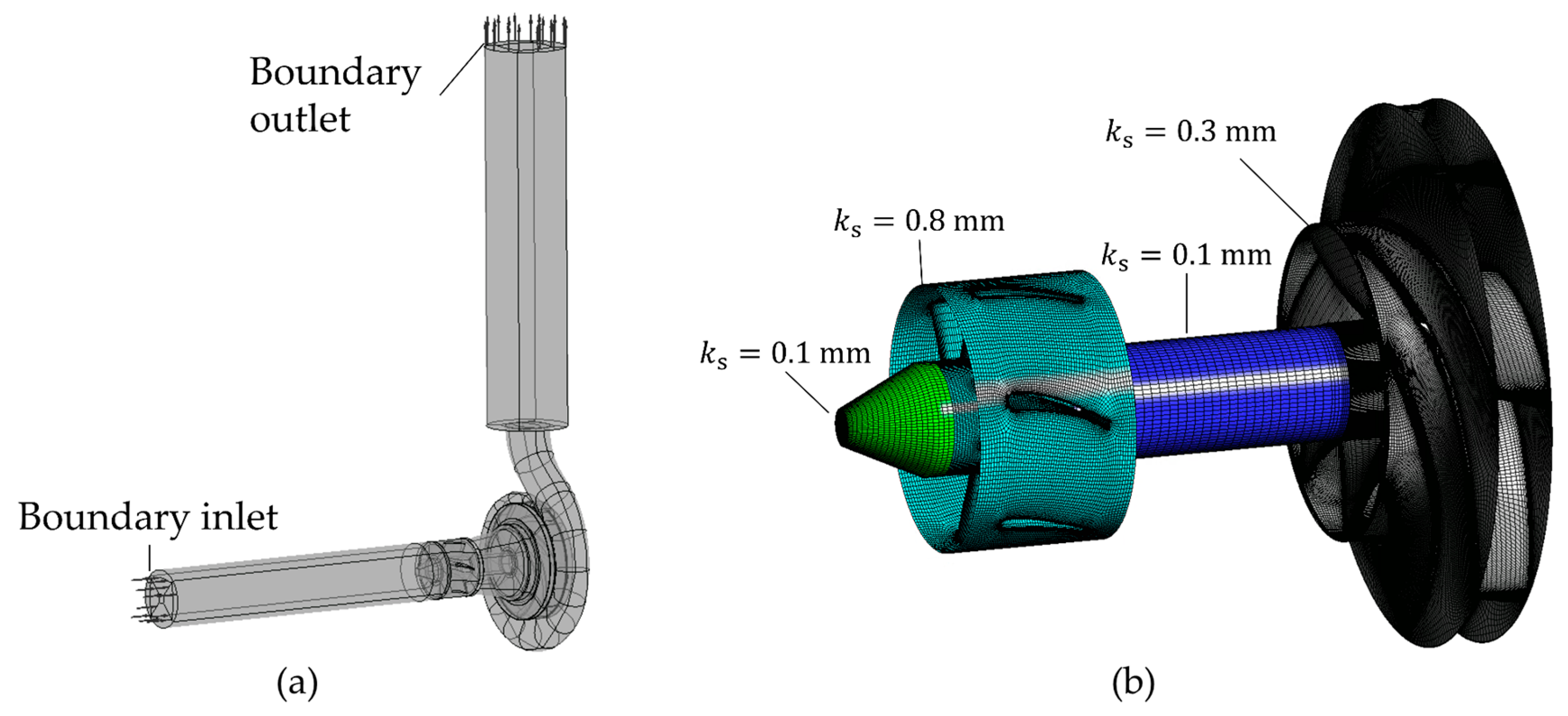
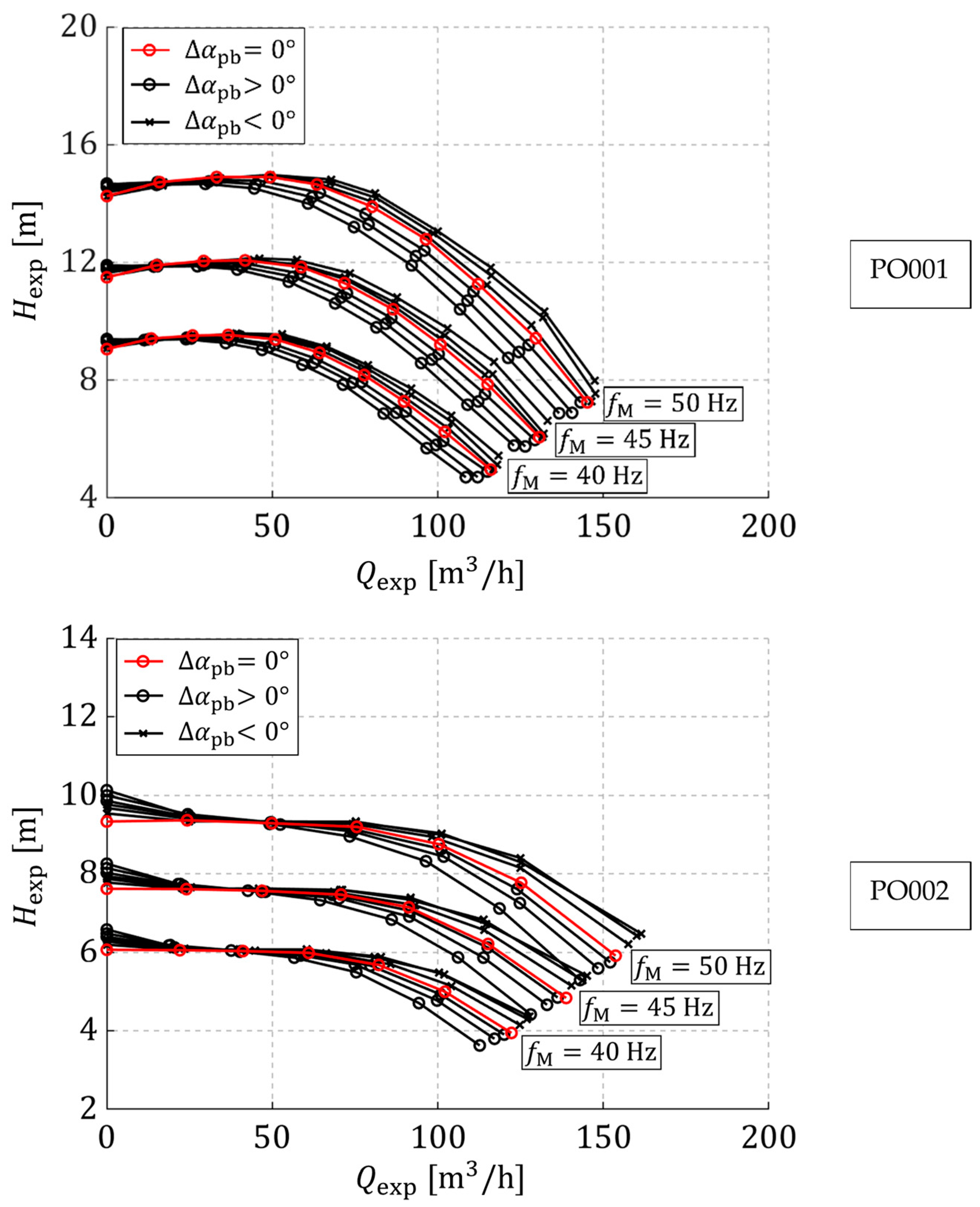
| Parameter | PO001 | PO002 |
|---|---|---|
| Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | |
|---|---|---|---|---|
| Node Number | 1,339,728 | 2,001,547 | 2,376,901 | 4,883,055 |
| 2,744,701 | 2,376,901 | 2,848,057 |
| PO001 | PO002 | ||
|---|---|---|---|
| −43° | −41.73° | −43° | −33.28° |
| −30° | −27.79° | −30° | −21.74° |
| −16° | −14.70° | −16° | −11.01° |
| +16° | +14.22° | +16° | +11.46° |
| +30° | +27.95° | +30° | +22.06° |
| +43° | +41.76° | +43° | +33.95° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reeh, N.; Manthei, G.; Klar, P.J. Determining the Head Characteristics of Radial Centrifugal Pumps under the Impact of Prewhirl. Appl. Sci. 2024, 14, 7224. https://doi.org/10.3390/app14167224
Reeh N, Manthei G, Klar PJ. Determining the Head Characteristics of Radial Centrifugal Pumps under the Impact of Prewhirl. Applied Sciences. 2024; 14(16):7224. https://doi.org/10.3390/app14167224
Chicago/Turabian StyleReeh, Nils, Gerd Manthei, and Peter J. Klar. 2024. "Determining the Head Characteristics of Radial Centrifugal Pumps under the Impact of Prewhirl" Applied Sciences 14, no. 16: 7224. https://doi.org/10.3390/app14167224
APA StyleReeh, N., Manthei, G., & Klar, P. J. (2024). Determining the Head Characteristics of Radial Centrifugal Pumps under the Impact of Prewhirl. Applied Sciences, 14(16), 7224. https://doi.org/10.3390/app14167224







