A Reversible Data-Hiding Method for Encrypted Images Based on Adaptive Quadtree Partitioning and MSB Prediction
Abstract
1. Introduction
- The paper integrates adaptive quadtree partitioning and MSB prediction, to propose an innovative RDH-EI technique that overcomes the KPA vulnerability of the BPCX algorithm in RDH-ED and improves the embedding capacity.
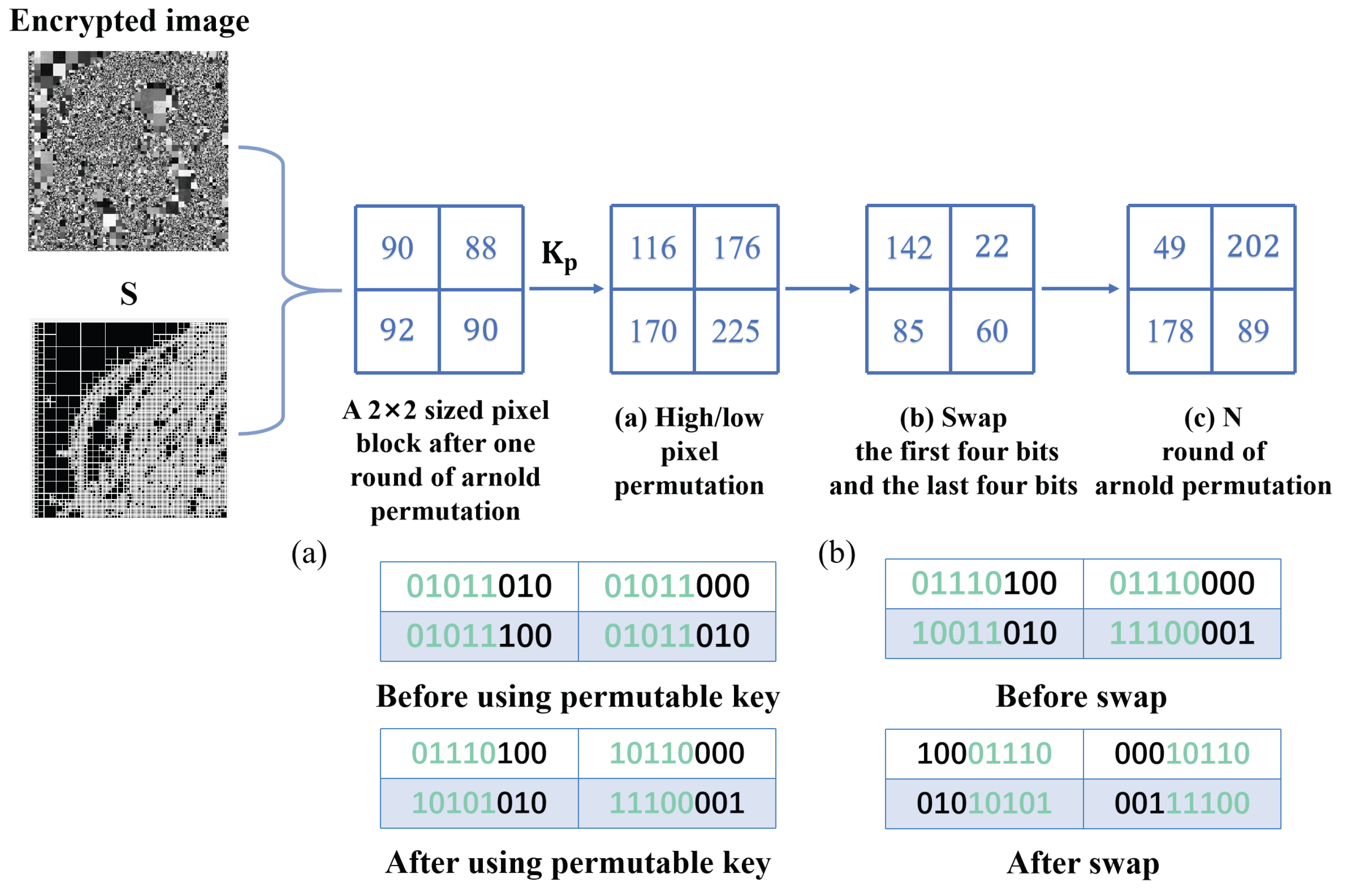
- During the encryption phase, Arnold permutation is introduced for pixel bit modulation, enhancing the security of the BPCX encryption algorithm and defending against KPA attacks.
- Throughout the data embedding process, tagging bits serve to denote the state of the pixel block, optimizing the utilization of inter-pixel redundancy and, thereby, elevating the embedding capacity.
2. Related Works
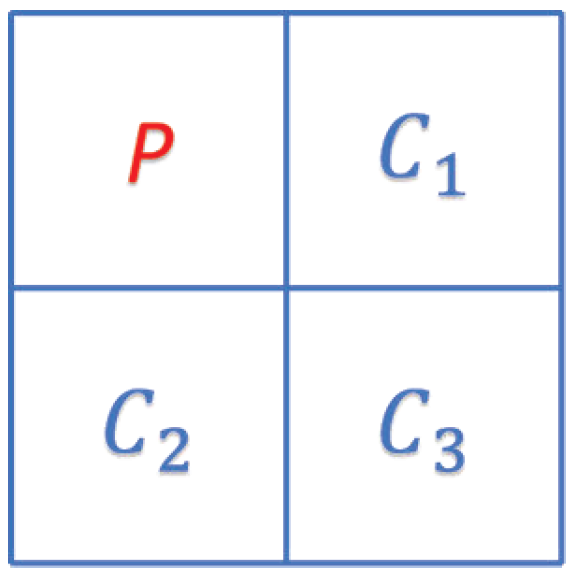
2.1. Adaptive MSB Prediction
- 1.
- Eight bits of the upper-left pixel P and three bits of MD.
- 2.
- Arrange the prediction errors , respectively, where () is the remainder of after removing the shared MSBs.
- 3.
- The remaining three × MD bits are the space available for data-hiding represented by .
- 1.
- Eight bits of the upper-left pixel P, two bits of dim type (the sizes 16 × 16, 8 × 8, 4 × 4, 2 × 2 are denoted by 00, 01, 10, 11, respectively), and three bits of MD.
- 2.
- Arrange the prediction errors (), respectively, where is the remainder of after removing the shared MSBs.
- 3.
- The remaining bits are the space available for data-hiding represented by .
2.2. BPCX Analysis
- 1.
- The maximum number of 0-bit and 1-bit values within an image block remains constant before and after encryption.
- 2.
- The arrangement of pixels within a block does not alter the average value of the block.
- 3.
- The arrangement of pixels within a block does not effectively cover the low frequency information in the image, resulting only in a transformation to a high-definition and fuzzy image.
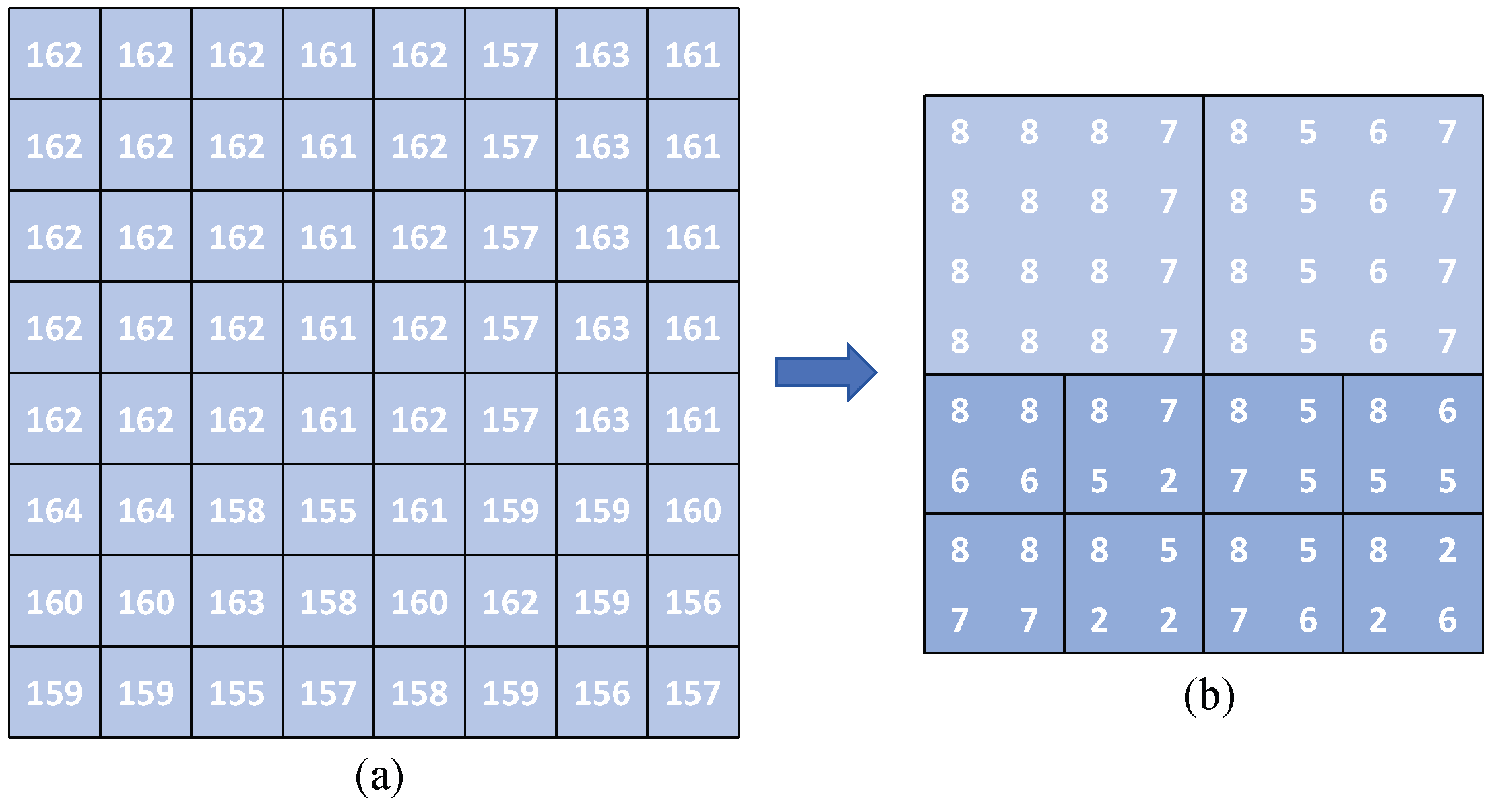
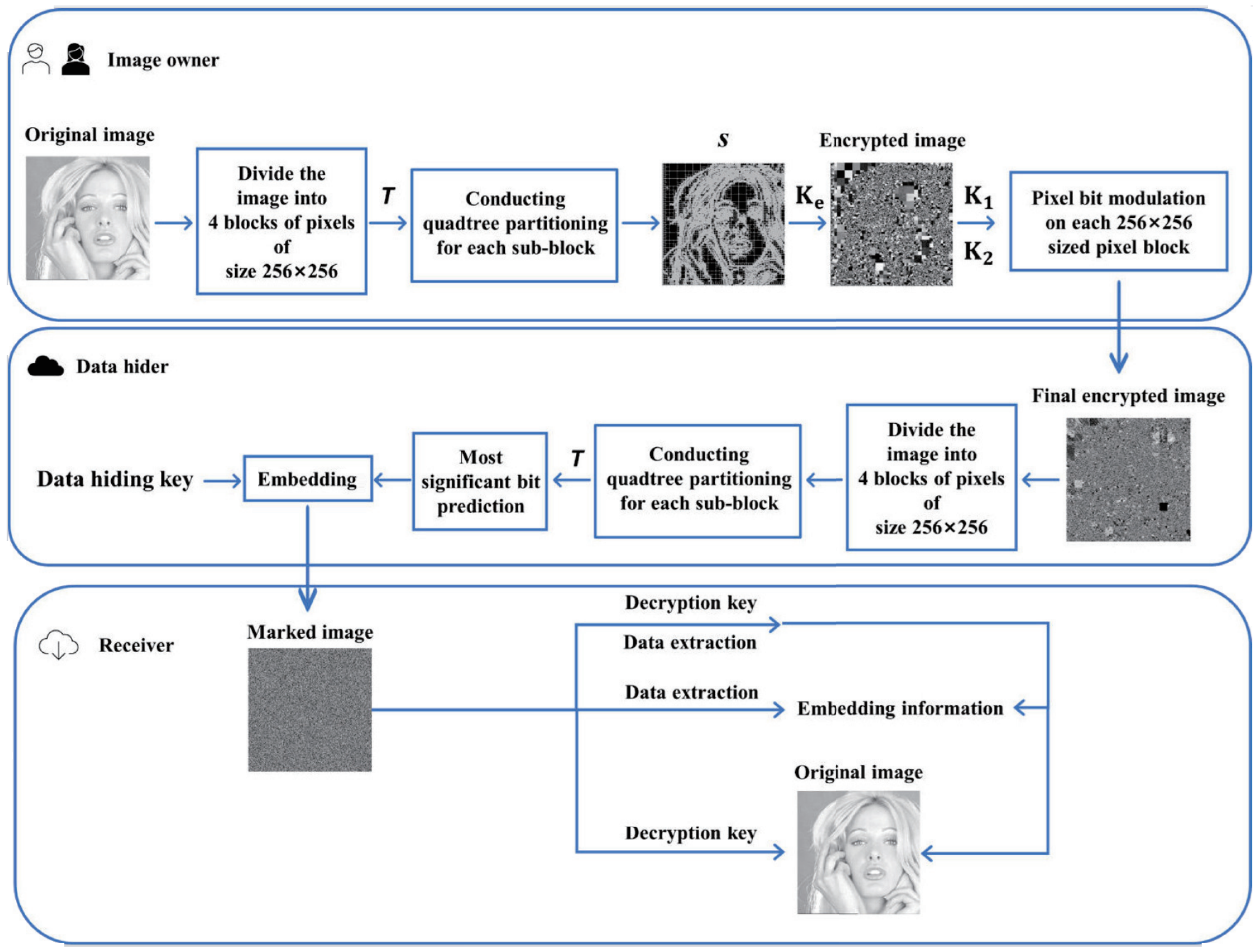
3. Proposed Method
3.1. Image Encryption
| Algorithm 1 Adaptive quadtree partitioning |
|
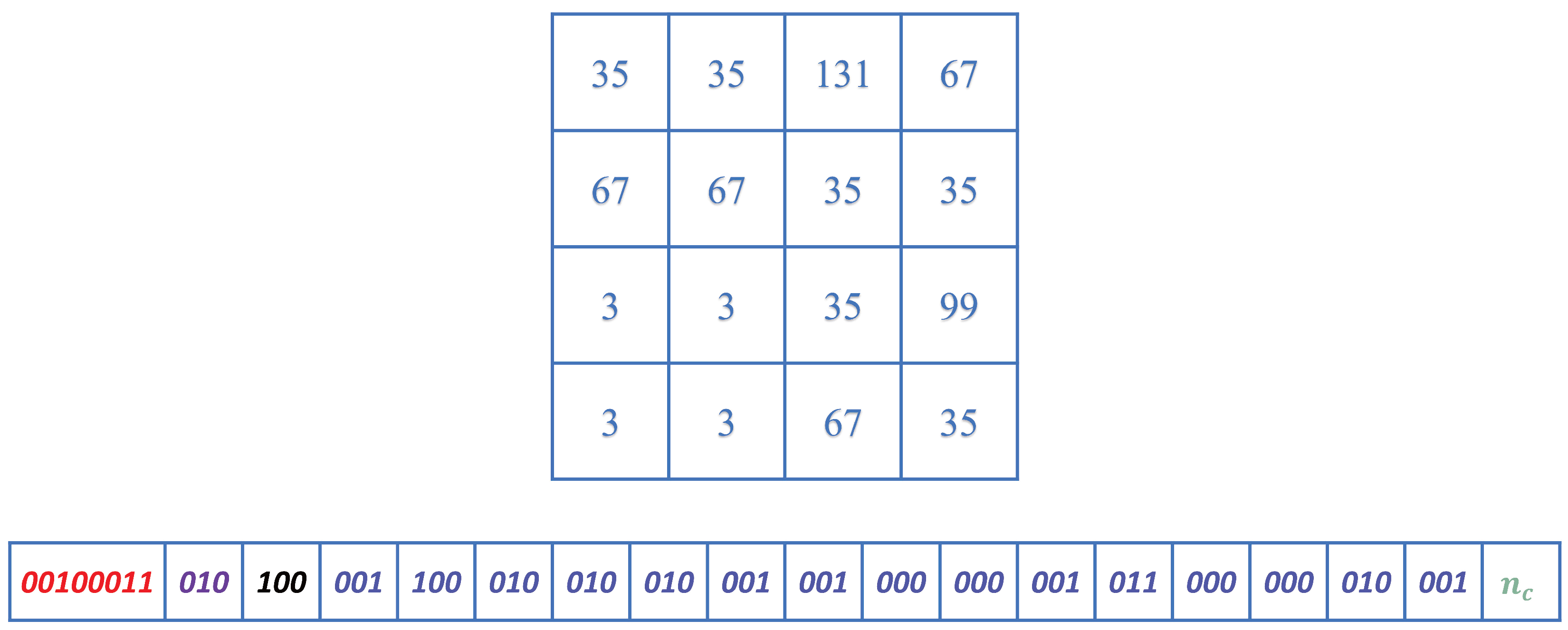
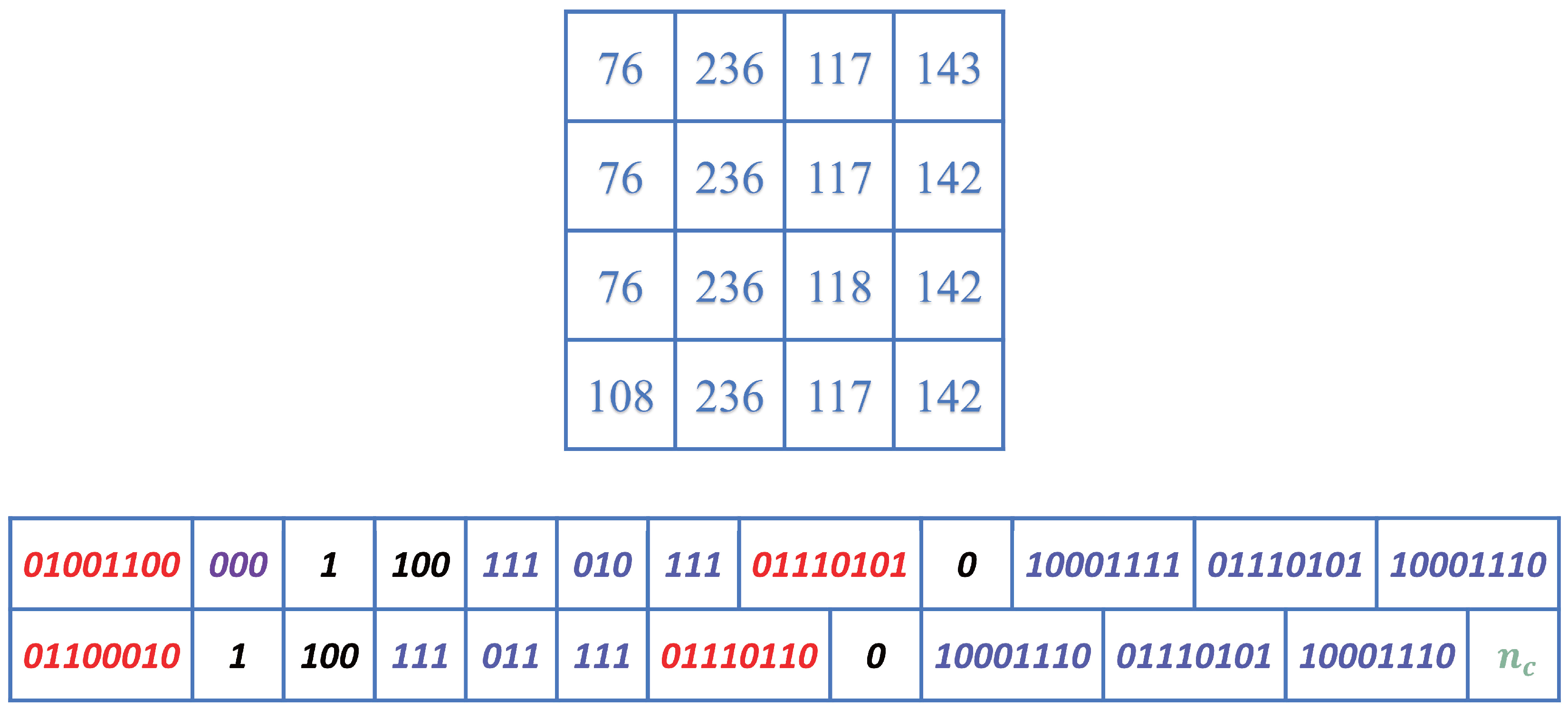
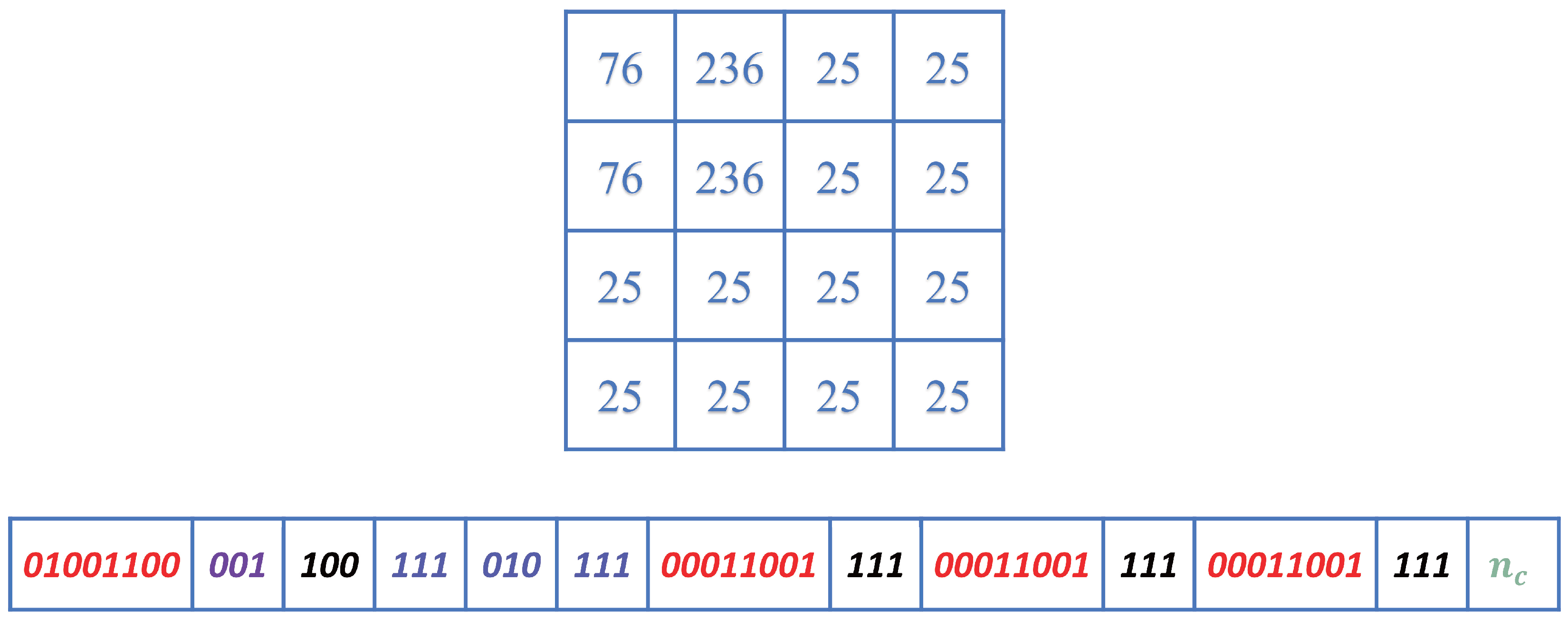
3.2. Data-Hiding
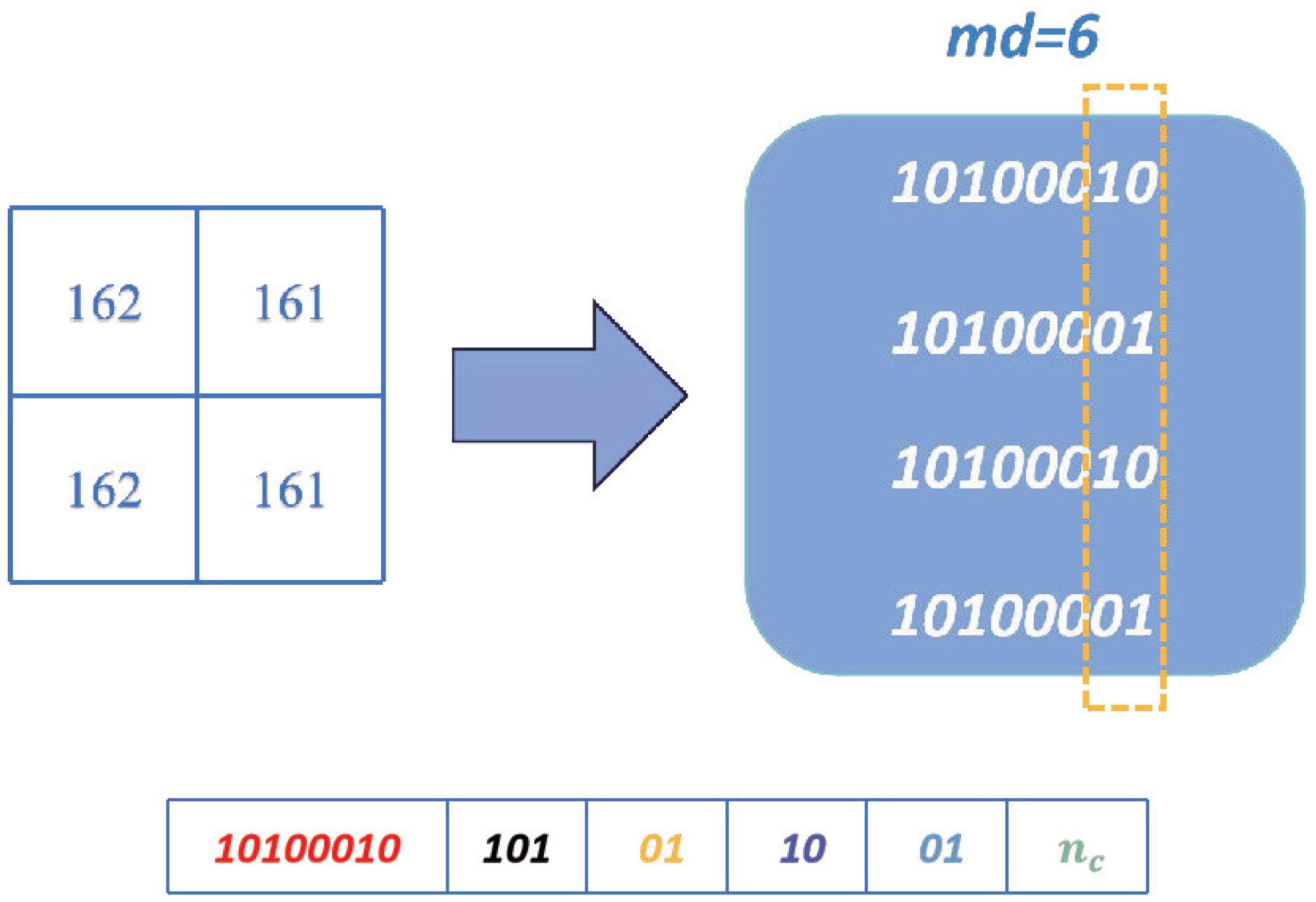
- 1.
- Eight bits of the upper-left pixel P, three bits of Dim (according to the value of dim obtained through (5)), and three bits of MD.
- 2.
- Arrange the prediction errors (), respectively, where is the remainder of after removing the shared LSBs.
- 3.
- The remaining bits are the space available for data-hiding, represented by .
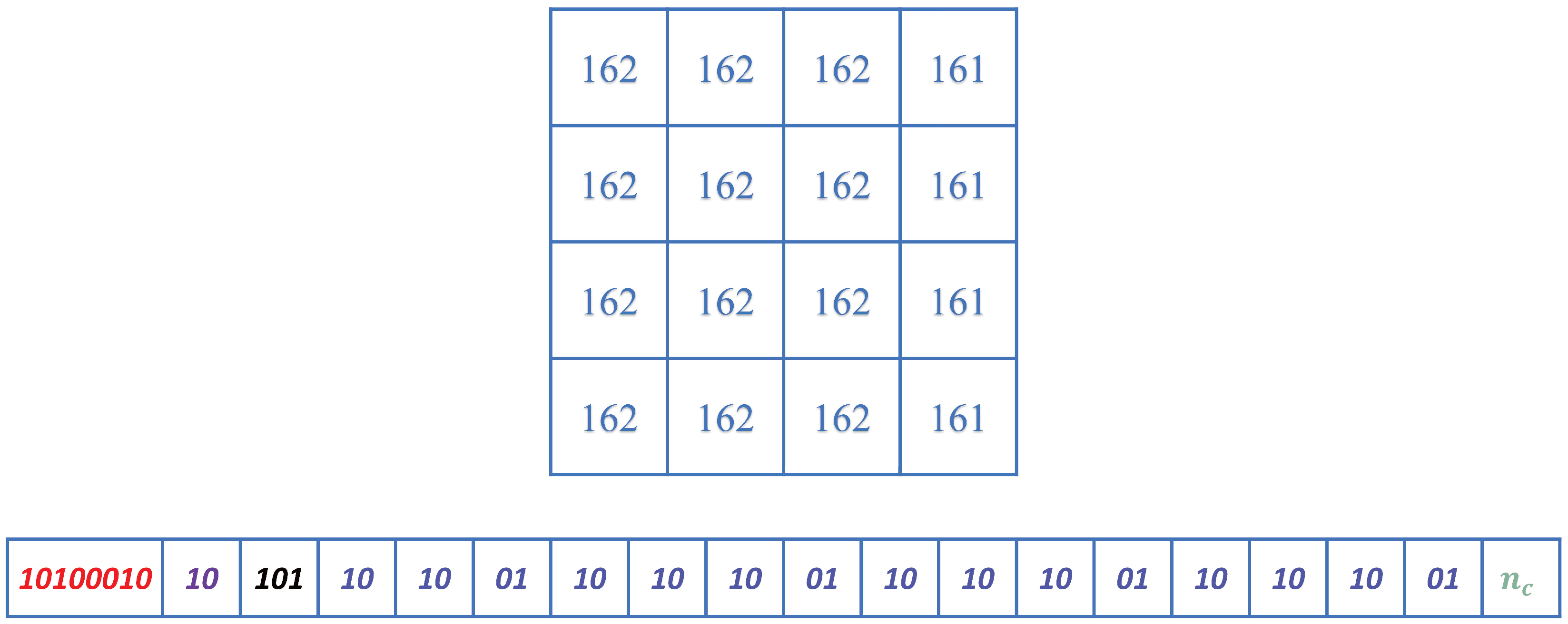
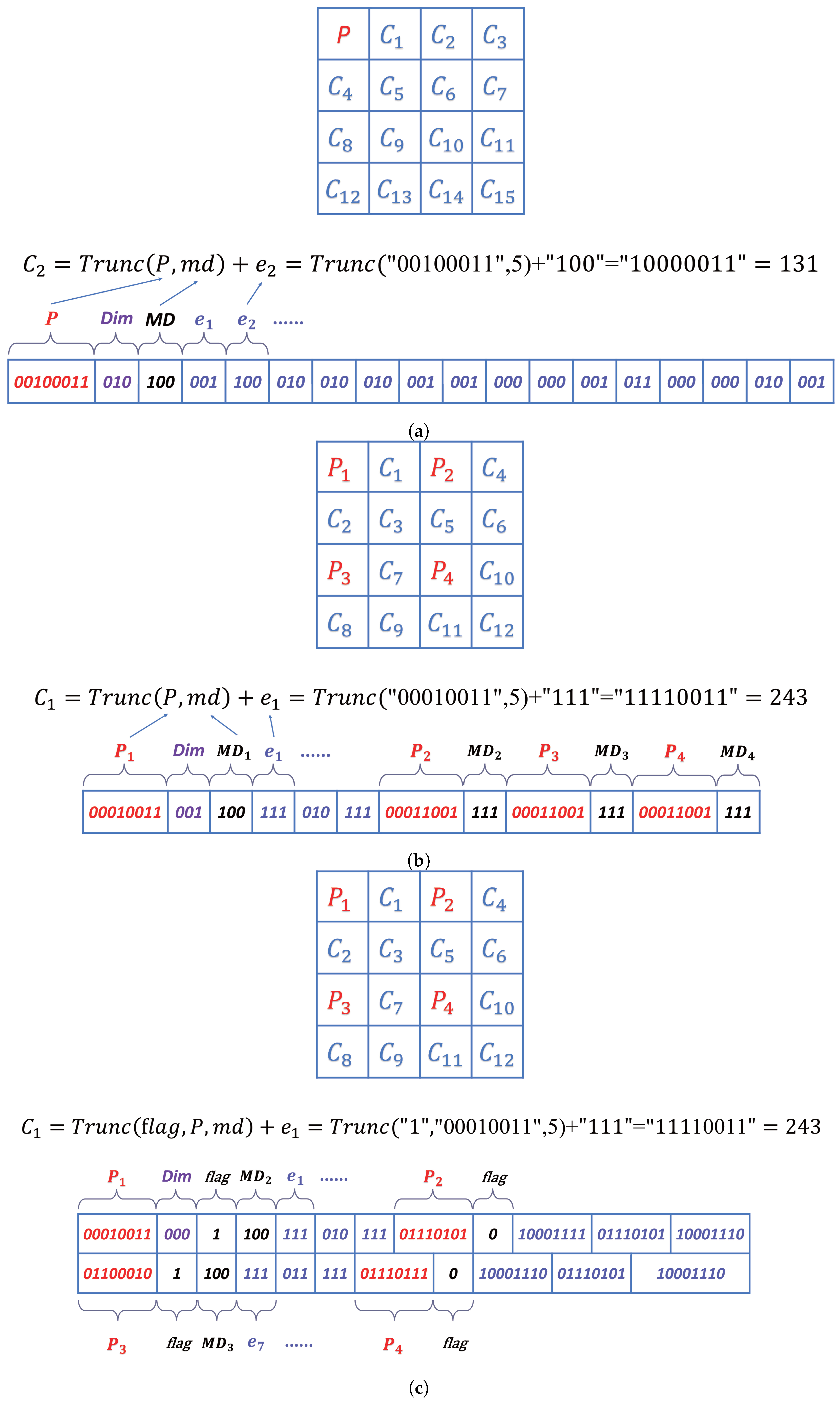
- 1.
- Determine whether it is the first 2 × 2 pixel block to be processed; if so, perform step a; otherwise, perform step b.
- (a)
- Eight bits of the upper-left pixel P, three bits of Dim (for the case where there are unusable blocks, it is encoded as ).
- (b)
- Eight bits of the upper-left pixel P.
- 2.
- Determine whether the current block is a usable block; if yes then perform step c; otherwise, perform step d.
- (c)
- Arrange a tagging bit ‘1’ to represent a usable block, three bits of MD. Next are the prediction errors (), where is the remainder of after removing the shared LSBs.
- (d)
- Arrange a tagging bit ‘0’ to represent an unusable block. Next are the original values of the remaining three pixels.
- 3.
- The remaining bits are the space available for data-hiding, represented by .
- 1.
- Determine whether it is the first 2 × 2 pixel block to be processed; if so, perform step a; otherwise, perform step b.
- (a)
- Eight bits of the upper-left pixel P, three bits of Dim (for this case, it is encoded as D(1)), and three bits of MD.
- (b)
- Eight bits of the upper-left pixel P and three bits of MD.
- 2.
- Arrange the prediction errors (), respectively, where is the remainder of after removing the shared LSBs.
- 3.
- The remaining bits are the space available for data-hiding, represented by .
3.3. Data Extraction and Image Recovery
- 1.
- Retrieve eight bits to obtain P and three bits to obtain Dim, according to the mapping relationship between Dim and dim in (5), which can be derived from the current retrieval of the pixel block size; if dim > 2 then perform the second step; otherwise, perform the third step.
- 2.
- Then, retrieve three bits to obtain MD, which gives md; then, retrieve number of 8-md bits to obtain ( ), and recover the pixel value according to (6).
- 3.
- When dim = 2, four pixel blocks of 2 × 2 size are taken as processing units and for each pixel block of 2 × 2 size, if Dim = D(0) execute step a; otherwise, execute step b.
- (a)
- Next, one bit is retrieved. If it is ‘1’, it means that the current 2 × 2 pixel block is usable, and if it is ‘0’, it is unusable. Then, retrieve three bits to obtain MD, which gives md; next, retrieve three 8-md bits to obtain (), and restore the pixel value according to (7).
- (b)
- Next, retrieve three bits to obtain MD, which gives md, then retrieve three 8-md bits to obtain (), and restore the pixel value according to (7).
4. Experimental Result and Analysis
4.1. Separability and Reversibility
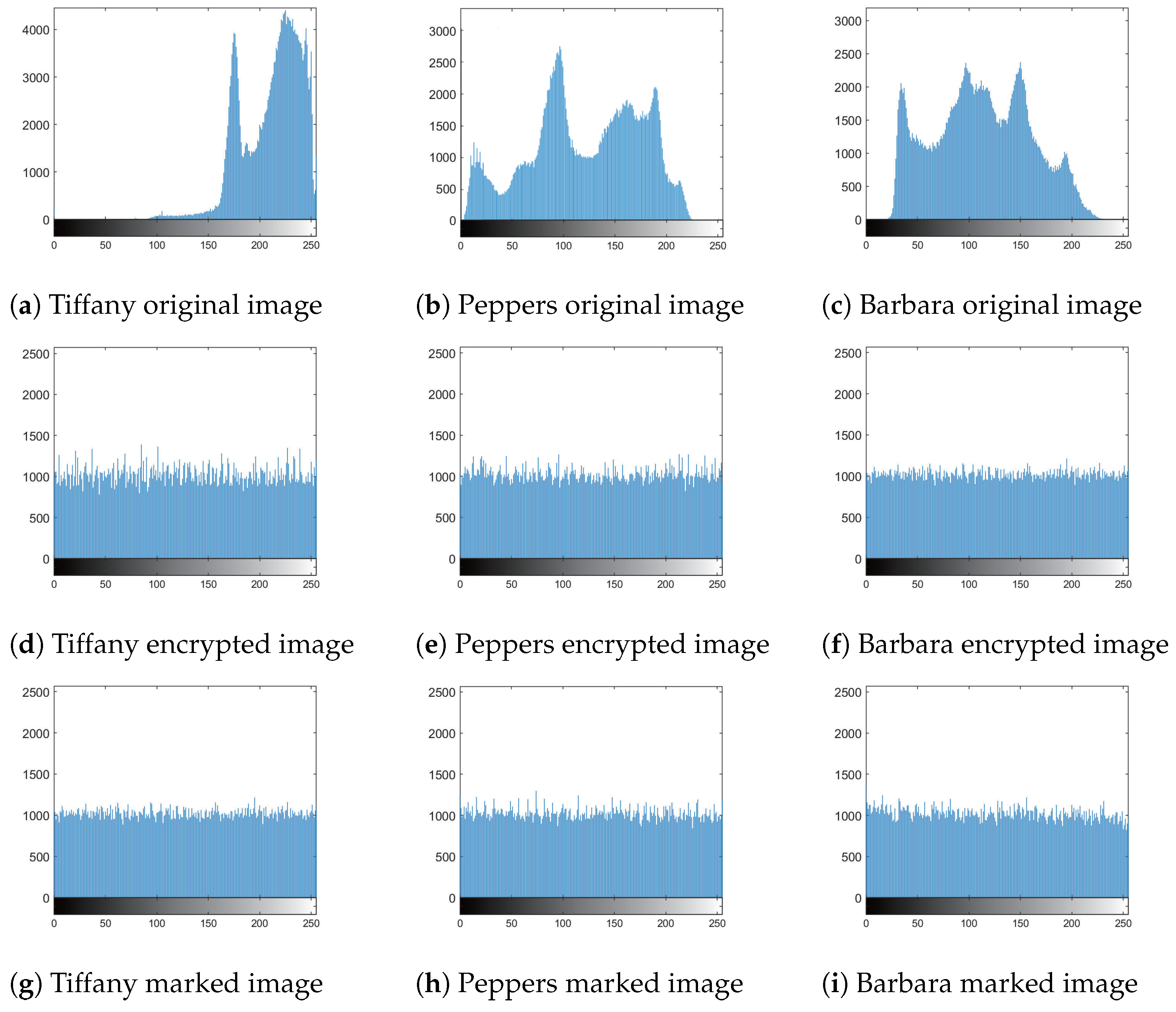
4.2. Security
- 1.
- Shannon entropy
- 2.
- Histogram analysis
- 3.
- KPA attack
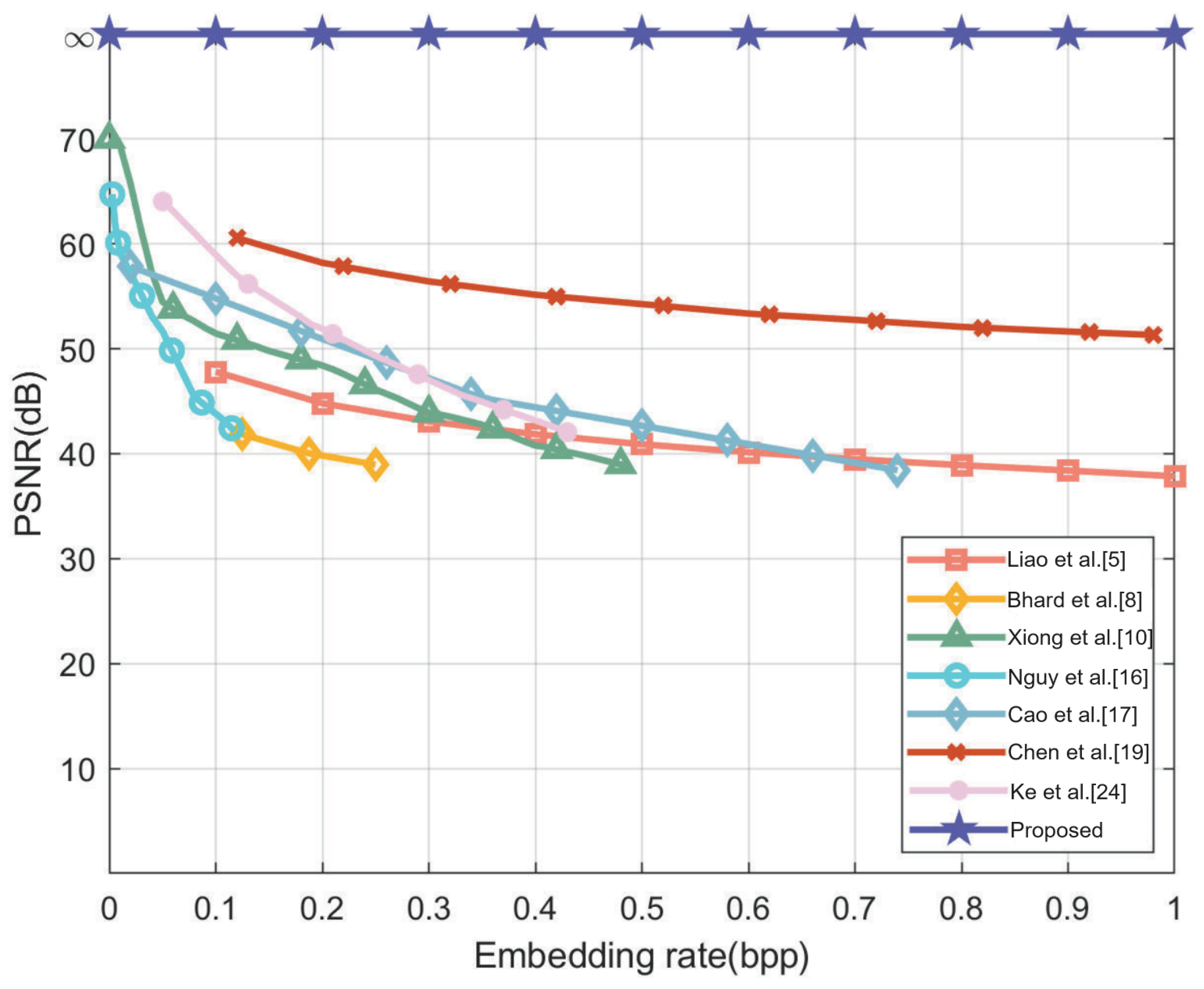
4.3. Embedded Capacity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barton, J.M. Method and Apparatus for Embedding Authentication Information within Digital Data. U.S. Patent, 5 646 997, 1997. [Google Scholar]
- Li, J.; Ma, R.; Guan, H. TEES: An Efficient Search Scheme over Encrypted Data on Mobile Cloud. IEEE Trans. Cloud Comput. 2017, 5, 126–139. [Google Scholar] [CrossRef]
- Puech, W.; Chaumont, M.; Strauss, O. A Reversible Data Hiding Method for Encrypted Images. In Proceedings of the Security, Forensics, Steganography, and Watermarking of Multimedia Contents X, San Johe, CA, USA, 27–31 January 2008; Volume 6819, pp. 534–542. [Google Scholar]
- Zhang, X. Reversible Data Hiding in Encrypted Image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Liao, X.; Shu, C. Reversible data hiding in encrypted images based on absolute mean difference of multiple neighboring pixels. J. Vis. Commun. Image Represent. 2015, 28, 21–27. [Google Scholar] [CrossRef]
- Zhang, X. Separable Reversible Data Hiding in Encrypted Image. IEEE Trans. Inf. Forensics Secur. 2012, 7, 826–832. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X. Reversible Data Hiding in Encrypted Images With Distributed Source Encoding. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 636–646. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Aggarwal, A. An improved block based joint reversible data hiding in encrypted images by symmetric cryptosystem. Pattern Recognit. Lett. 2020, 139, 60–68. [Google Scholar] [CrossRef]
- Di, F.; Huang, F.; Zhang, M.; Liu, J.; Yang, X. Reversible data hiding in encrypted images with high capacity by bitplane operations and adaptive embedding. Multimed. Tools Appl. 2018, 77, 20917–20935. [Google Scholar] [CrossRef]
- Xiong, L.; Dong, D. Reversible data hiding in encrypted images with somewhat homomorphic encryption based on sorting block-level prediction-error expansion. J. Inf. Secur. Appl. 2019, 47, 78–85. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, M.; Zhang, X.; Liu, J.; Su, T.; Yang, X. A Reversible Data Hiding Scheme in Encrypted Domain for Secret Image Sharing Based on Chinese Remainder Theorem. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 2469–2481. [Google Scholar] [CrossRef]
- Chen, B.; Lu, W.; Huang, J.; Weng, J.; Zhou, Y. Secret Sharing Based Reversible Data Hiding in Encrypted Images With Multiple Data-Hiders. IEEE Trans. Dependable Secur. Comput. 2022, 19, 978–991. [Google Scholar] [CrossRef]
- Wang, Y.; He, W. High Capacity Reversible Data Hiding in Encrypted Image Based on Adaptive MSB Prediction. IEEE Trans. Multimed. 2022, 24, 1288–1298. [Google Scholar] [CrossRef]
- Qi, K.; Zhang, M.; Di, F.; Kong, Y. High capacity reversible data hiding in encrypted images based on adaptive quadtree partitioning and MSB prediction. Front. Inf. Technol. Electron. Eng. 2023, 24, 1156–1168. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, W.; Zhao, X.; Yu, N.; Li, F. Reversible Data Hiding in Encrypted Images by Reserving Room Before Encryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 553–562. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Chang, C.C.; Chang, W.C. High capacity reversible data hiding scheme for encrypted images. Signal Process. Image Commun. 2016, 44, 84–91. [Google Scholar] [CrossRef]
- Cao, X.; Du, L.; Wei, X.; Meng, D.; Guo, X. High Capacity Reversible Data Hiding in Encrypted Images by Patch-Level Sparse Representation. IEEE Trans. Cybern. 2016, 46, 1132–1143. [Google Scholar] [CrossRef] [PubMed]
- Puteaux, P.; Puech, W. An Efficient MSB Prediction-Based Method for High-Capacity Reversible Data Hiding in Encrypted Images. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1670–1681. [Google Scholar] [CrossRef]
- Chen, K.; Chang, C.C. High-capacity reversible data hiding in encrypted images based on extended run-length coding and block-based MSB plane rearrangement. J. Vis. Commun. Image Represent. 2019, 58, 334–344. [Google Scholar] [CrossRef]
- Puteaux, P.; Puech, W. EPE-based Huge-Capacity Reversible Data Hiding in Encrypted Images. In Proceedings of the 2018 IEEE International Workshop on Information Forensics and Security (WIFS), Hong Kong, China, 11–13 December 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Yin, Z.; Xiang, Y.; Zhang, X. Reversible Data Hiding in Encrypted Images Based on Multi-MSB Prediction and Huffman Coding. IEEE Trans. Multimed. 2020, 22, 874–884. [Google Scholar] [CrossRef]
- Puteaux, P.; Puech, W. A Recursive Reversible Data Hiding in Encrypted Images Method With a Very High Payload. IEEE Trans. Multimed. 2021, 23, 636–650. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, M.Q.; Liu, J.; Su, T.T.; Yang, X.Y. A multilevel reversible data hiding scheme in encrypted domain based on LWE. J. Vis. Commun. Image Represent. 2018, 54, 133–144. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, M.Q.; Liu, J.; Su, T.T.; Yang, X.Y. Fully Homomorphic Encryption Encapsulated Difference Expansion for Reversible Data Hiding in Encrypted Domain. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2353–2365. [Google Scholar] [CrossRef]
- Di, F.; Zhang, M.; Liao, X.; Liu, J. High-fidelity reversible data hiding by Quadtree-based pixel value ordering. Multimed. Tools Appl. 2019, 78, 7125–7141. [Google Scholar] [CrossRef]
- Qu, L.; He, H.; Chen, F. On The Security of Block Permutation and Co-XOR in Reversible Data Hiding. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 920–932. [Google Scholar] [CrossRef]
- Kocak, O.; Erkan, U.; Toktas, A.; Gao, S. PSO-based image encryption scheme using modular integrated logistic exponential map. Expert Syst. Appl. 2024, 237, 121452. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. Design of two dimensional hyperchaotic system through optimization benchmark function. Chaos Solitons Fractals 2023, 167, 113032. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Image database of BOSSbase 1.01. Available online: http://dde.binghamton.edu/download/ (accessed on 15 July 2024).






| Image | Barbara | Boat | F16 | Goldhill | House | Lake | Peppers | Splash | Tiffany |
|---|---|---|---|---|---|---|---|---|---|
| Original image | 7.4664 | 7.1914 | 6.7140 | 7.4778 | 7.2336 | 7.4845 | 7.5925 | 7.2541 | 6.6009 |
| Method [14] | 7.9965 | 7.9947 | 7.9915 | 7.9977 | 7.9861 | 7.9981 | 7.9914 | 7.9901 | 7.9899 |
| Proposed method | 7.9979 | 7.9956 | 7.9912 | 7.9985 | 7.9869 | 7.9983 | 7.9944 | 7.9924 | 7.9913 |
| EC (bit) | ||||||
|---|---|---|---|---|---|---|
| Image | [13] | [14] | [16] | [20] | [25] | Proposed method |
| Barbara | 327,263 | 349,297 | 34,342 | 253,567 | 25,180 | 347,916 |
| Boat | 334,343 | 386,905 | 27,262 | 259,864 | 29,561 | 376,904 |
| F16 | 492,674 | 534,581 | 73,139 | 260,208 | 48,722 | 551,018 |
| House | 419,121 | 440,927 | 44,009 | 261,024 | 26,058 | 446,916 |
| Lake | 306,395 | 349,582 | 29,750 | 259,896 | 25,137 | 346,679 |
| Peppers | 384,993 | 445,527 | 41,419 | 260,304 | 46,686 | 435,966 |
| Average | Highest | Lowest | ||||
|---|---|---|---|---|---|---|
| (bit) | (bpp) | (bit) | (bpp) | (bit) | (bpp) | |
| Method [13] | 593,090 | 2.2625 | 1,351,139 | 5.1542 | 50,273 | 0.1918 |
| Method [14] | 638,698 | 2.4364 | 2,045,606 | 7.8034 | 15,444 | 0.0589 |
| Proposed method | 648,298 | 2.4731 | 2,045,750 | 7.8039 | 16,150 | 0.0616 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Zhang, M.; Di, F.; Lai, P. A Reversible Data-Hiding Method for Encrypted Images Based on Adaptive Quadtree Partitioning and MSB Prediction. Appl. Sci. 2024, 14, 6376. https://doi.org/10.3390/app14146376
Yue Y, Zhang M, Di F, Lai P. A Reversible Data-Hiding Method for Encrypted Images Based on Adaptive Quadtree Partitioning and MSB Prediction. Applied Sciences. 2024; 14(14):6376. https://doi.org/10.3390/app14146376
Chicago/Turabian StyleYue, Ya, Minqing Zhang, Fuqiang Di, and Peizheng Lai. 2024. "A Reversible Data-Hiding Method for Encrypted Images Based on Adaptive Quadtree Partitioning and MSB Prediction" Applied Sciences 14, no. 14: 6376. https://doi.org/10.3390/app14146376
APA StyleYue, Y., Zhang, M., Di, F., & Lai, P. (2024). A Reversible Data-Hiding Method for Encrypted Images Based on Adaptive Quadtree Partitioning and MSB Prediction. Applied Sciences, 14(14), 6376. https://doi.org/10.3390/app14146376






