Robust Estimation Method against Poisoning Attacks for Key-Value Data with Local Differential Privacy
Abstract
1. Introduction
- Novel LDP Algorithm: We introduce a novel LDP algorithm that is designed to enhance robustness against specific types of poisoning attacks. This newly proposed algorithm leverages an iterative process involving Bayesian posterior probabilities, thereby improving the accuracy of the estimates while maintaining resilience against the impact of poisoning data.
- Experimental Validation: The proposed protocol was empirically validated through a series of experiments employing both synthetic and publicly available open datasets. The experimental results demonstrate the robustness of the proposed algorithm. Comparative analyses reveal superior performance in terms of the estimation accuracy and resistance to poisoning attacks compared with the PrivKV protocol. These findings substantiate the efficacy and practical applicability of the proposed method in the context of privacy-preserving data collection frameworks.
2. Related Works
2.1. Privacy Preservation for Key–Value Data
2.2. Novelty of This Research
3. Local Differential Privacy
3.1. Fundamental Definition
3.2. PrivKV
3.2.1. Sampling
3.2.2. Perturbation
3.2.3. Estimating
3.2.4. PrivKVM
3.3. Poisoning Attack
- Maximum gain attack (M2GA): All fake users generate optimal fake outputs for perturbation messages to maximize the gains of the frequency and mean. That is, they select a targeted key k (selected randomly from r targeted keys) and send to the server.
- Random message attack (RMA): Each fake user uniformly selects a message from the domain and sends , , and with probabilities , , and , respectively.
- Random key–value pair attack (RKVA): Each fake user randomly selects a key k from the target key set with a specified value 1 and perturbs according to the protocol.
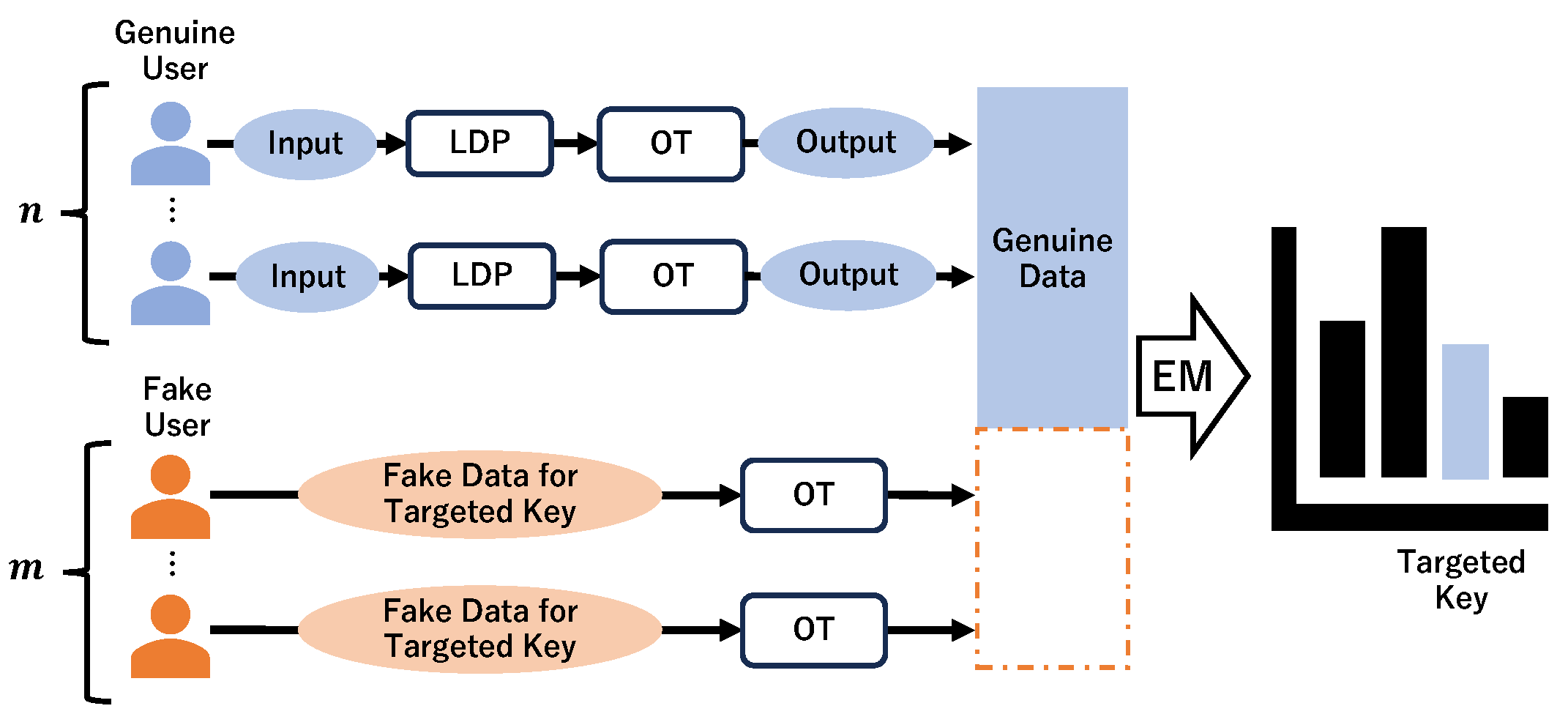
4. Proposed Algorithm
4.1. Concept
4.2. Oblivious Transfer
| Algorithm 1 1-out-of-N OT [7] |
| Suppose A has N messages , where |
|
| Algorithm 2 Perturbation of key–value pairs with OT |
|
4.3. EM Estimation for Key–Value Data
| Algorithm 3 EM algorithm for PrivKV |
|
5. Evaluation
5.1. Data
5.2. Metrics
5.2.1. Accuracy Metrics
5.2.2. Robustness Metrics
5.3. Experimental Results
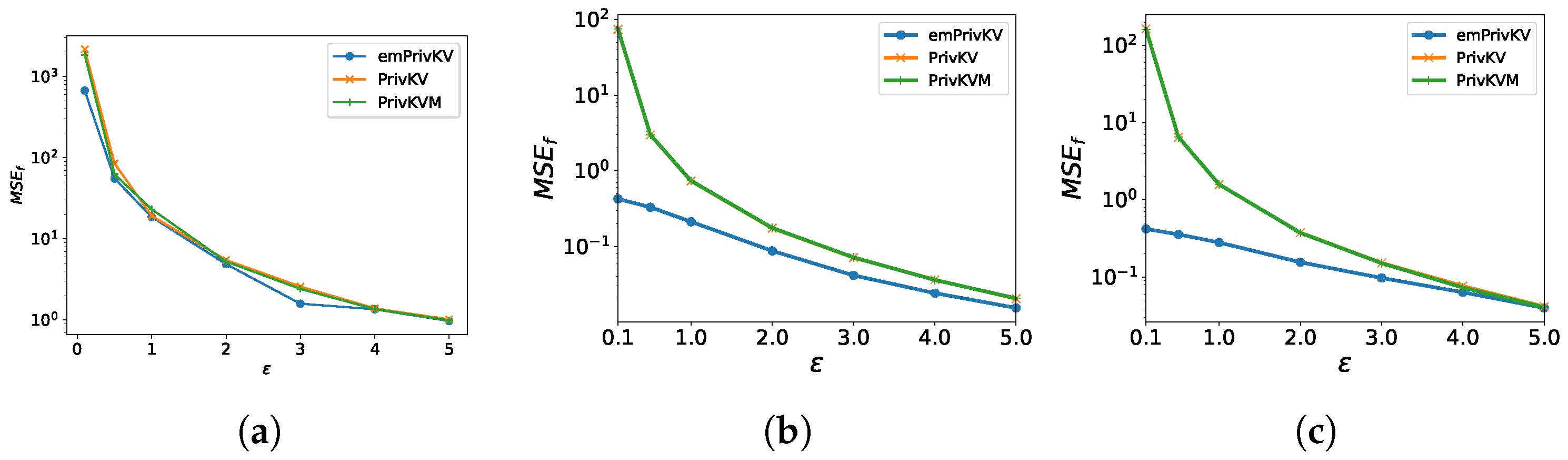
5.3.1. MSE with Respect to
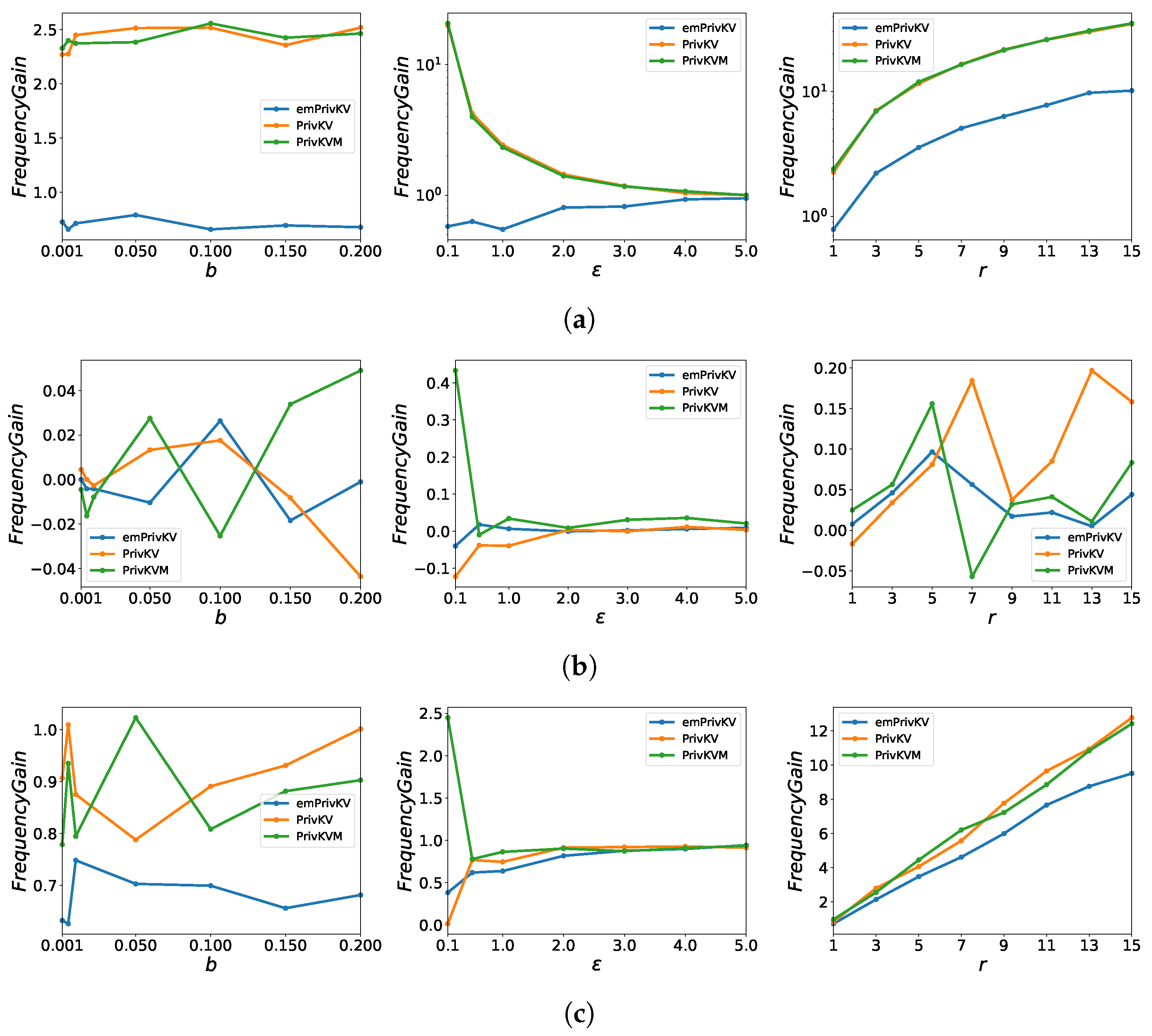
5.3.2. Frequency Gain
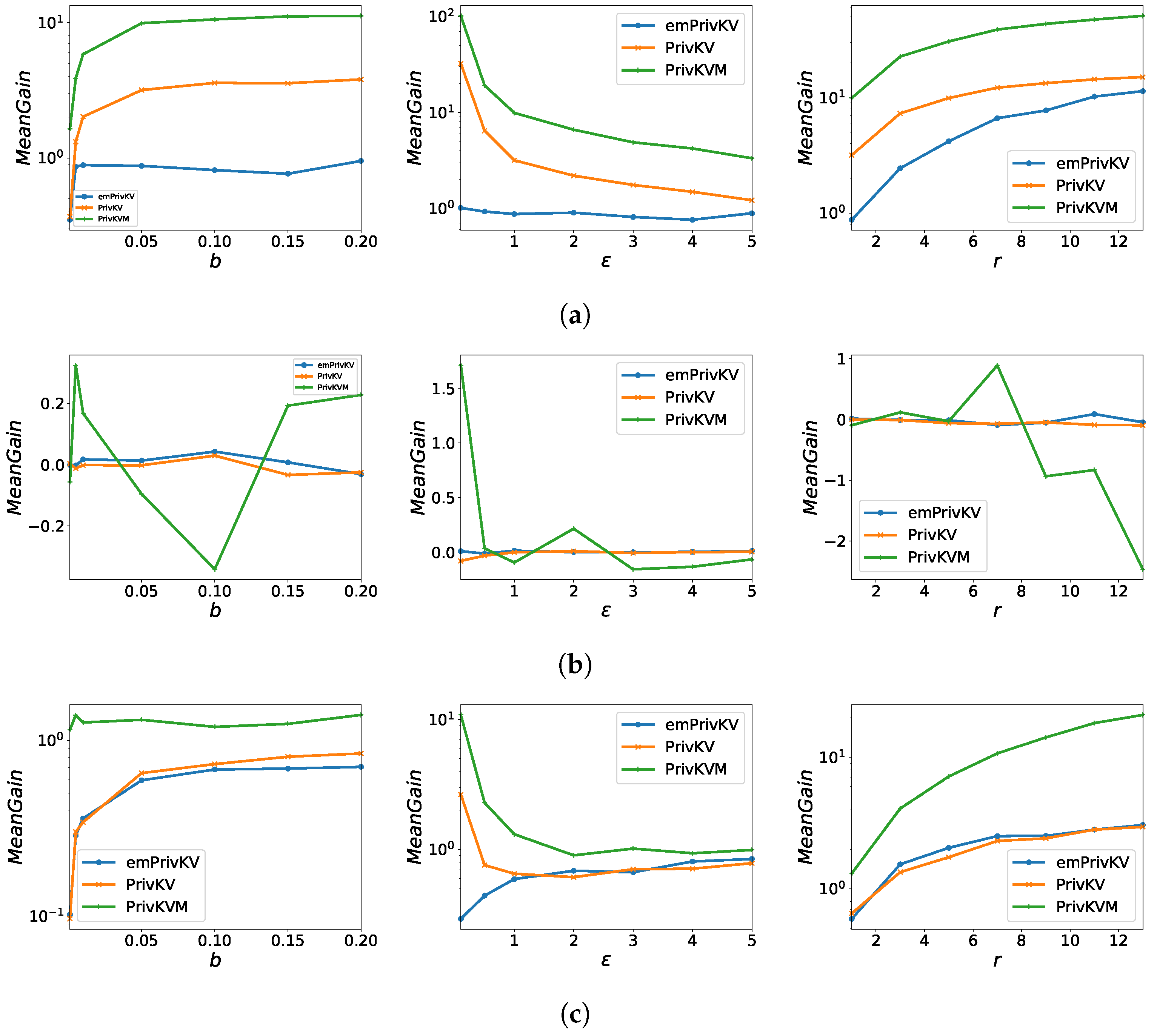
5.3.3. Mean Gain
5.3.4. Gains with OT
5.3.5. The Cost with OT Protocol
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erlingsson, Ú.; Pihur, V.; Korolova, A. RAPPOR: Randomized Aggregatable Privacy-Preserving Ordinal Response. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1054–1067. [Google Scholar]
- Ye, Q.; Hu, H.; Meng, X.; Zheng, H. PrivKV: Key–value Data Collection with Local Differential Privacy. IEEE Secur. Priv. 2019, 5, 294–308. [Google Scholar]
- Gu, X.; Li, M.; Cheng, Y.; Xiong, L.; Cao, Y. PCKV: Locally Differentially Private Correlated key–value Data Collection with Optimized Utility. In Proceedings of the 29th USENIX Security Symposium, Virtual Event, 12–14 August 2020; pp. 967–984. [Google Scholar]
- Ye, Q.; Hu, H.; Meng, X.; Zheng, H.; Huang, K.; Fang, C.; Shi, J. PrivKVM*: Revisiting key–value Statistics Estimation with Local Differential Privacy. IEEE Trans. Dependable Secur. Comput. 2021, 20, 17–35. [Google Scholar] [CrossRef]
- Cao, X.; Jia, J.; Gong, N.Z. Data Poisoning Attacks to Local Differential Privacy Protocols. In Proceedings of the 30th USENIX Security Symposium, Virtual Event, 11–13 August 2021; pp. 947–964. [Google Scholar]
- Wu, Y.; Cao, X.; Jia, J.; Gong, N.Z. Poisoning Attacks to Local Differential Privacy Protocols for key–value Data. In Proceedings of the 31st USENIX Security Symposium, Boston, MA, USA, 10–12 August 2022; pp. 519–536. [Google Scholar]
- Naor, M.; Pinkas, B. Computationally Secure Oblivious Transfer. J. Cryptol. 2005, 18, 1–35. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the em algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Horigome, H.; Hiroaki, K.; Yu, C.M. Local Differential Privacy protocol for making key–value data robust against poisoning attacks. In Proceedings of the 20th International Conference on Modeling Decisions for Artificial Intelligence, Umeå, Sweden, 19–22 June 2023; pp. 241–252. [Google Scholar]
- Dwork, C. Differential privacy. In Proceedings of the 33rd International Colloquium on Automata, Languages and Programming, Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Li, H.; Xiong, L.; Jiang, X.; Liu, J. Differentially private histogram publication for dynamic datasets: An adaptive sampling approach. Inf. Knowl. Manag. 2015, 2015, 1001–1010. [Google Scholar]
- Yang, X.; Wang, T.; Ren, X.; Yu, W. Survey on Improving Data Utility in Differentially Private Sequential Data Publishing. IEEE Trans. Big Data 2021, 7, 729–749. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Sarwate, A.D.; Chaudhuri, K. Signal Processing and Machine Learning with Differential Privacy: Algorithms and Challenges for Continuous Data. IEEE Signal Process. Mag. 2013, 30, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local privacy and statistical minimax rates. In Proceedings of the 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 26–29 October 2013; pp. 429–438. [Google Scholar]
- Kairouz, P.; Oh, S.; Viswanath, P. Extremal mechanisms for Local Differential Privacy. In Proceedings of the Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; pp. 2879–2887. [Google Scholar]
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef]
- Bloom, B.H. Space/time trade-offs in hash coding with allowable errors. Commun. ACM 1970, 13, 422–426. [Google Scholar] [CrossRef]
- Duchi, J.C.; Jordan, M.I.; Wainright, M.J. Minimax optimal procedures for locally private estimation. J. ACM 2014, 61, 1–57. [Google Scholar] [CrossRef]
- Nguyên, T.T.; Xiao, X.; Yang, Y.; Hui, S.C.; Shin, H.; Shin, J. Collecting and analyzing data from smart device users with Local Differential Privacy. arXiv 2016, arXiv:1606.05053. [Google Scholar]
- Wang, N.; Xiao, X.; Yang, Y.; Zhao, J.; Hui, S.C.; Shin, H.; Shin, J.; Yu, G. Collecting and analyzing multidimensional data with Local Differential Privacy. In Proceedings of the 35th IEEE International Conference on Data Engineering, Macau SAR, China, 8–11 April 2019; pp. 638–649. [Google Scholar]
- Ren, X.; Yu, C.M.; Yu, W.; Yang, S.; Yang, X.; McCann, J.A.; Yu, P.S. LoPub: High-Dimensional Crowdsourced Data Publication With Local Differential Privacy. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2151–2166. [Google Scholar] [CrossRef]
- Fanti, G.; Pihur, V.; Erlingsson, Ú. Building a RAPPOR with the unknown: Privacy-preserving learning of associations and data dictionaries. In Proceedings of the Privacy Enhancing Technologies Symposium, Darmstadt, Germany, 19–22 July 2016; pp. 41–61. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Milan, L.Z.; Li, N.; Škoric, B. Estimating Numerical Distributions under Local Differential Privacy. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; pp. 621–635. [Google Scholar]
- Cheu, A.; Smith, A.; Ullman, J. Manipulation Attacks in Local Differential Privacy. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 883–900. [Google Scholar]
- Li, X.; Li, N.; Sun, W.; Gong, N.Z.; Li, H. Fine-grained Poisoning Attack to Local Differential Privacy Protocols for Mean and Variance Estimation. In Proceedings of the USENIX Security Symposium, Anaheim, CA, USA, 9–11 August 2023; pp. 1739–1756. [Google Scholar]
- Wang, S.; Luo, X.; Qian, Y.; Du, J.; Lin, W.; Yang, W. Analyzing Preference Data with Local Privacy: Optimal Utility and Enhanced Robustness. IEEE Trans. Knowl. Data Eng. 2023, 35, 7753–7767. [Google Scholar] [CrossRef]
- Imola, A.; Chowdhury, R.; Chaudhuri, K. Robustness of locally differentially private graph analysis against poisoning. arXiv 2022, arXiv:2210.14376. [Google Scholar]
- Sasada, T.; Taenaka, Y.; Kadobayashi, Y. Oblivious Statistic Collection with Local Differential Privacy in Mutual Distrust. IEEE Access 2023, 11, 21374–21386. [Google Scholar] [CrossRef]
- Borgnia, E.; Geiping, J.; Cherepanova, V.; Fowl, L.; Gupta, A.; Ghiasi, A.; Huang, F.; Goldblum, M.; Goldstein, T. Dp-instahide: Provably defusing poisoning and backdoor attacks with differentially private data augmentations. arXiv 2021, arXiv:2103.02079. [Google Scholar]
- Ma, Y.; Zhu, X.; Hsu, J. Data poisoning against differentially-private learners: Attacks and defenses. arXiv 2019, arXiv:1903.09860. [Google Scholar]
- Naseri, M.; Hayes, J.; Cristofaro, E.D. Local and central differential privacy for robustness and privacy in federated learning. In Proceedings of the Network and Distributed System Security (NDSS) Symposium 2022, San Diego, CA, USA, 24–28 April 2022. [Google Scholar]
- Moya, M.M.; Hush, D.R. Network constraints and multi-objective optimization for one-class classification. Neural Netw. 1996, 9, 463–474. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 IEEE International Conference on Data Mining, NW Washington, DC, USA, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Cao, X.; Jia, J.; Gong, N.Z. Provably secure federated learning against malicious clients. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 6885–6893. [Google Scholar]
- Li, M.; Berrett, T.B.; Yu, Y. On robustness and local differential privacy. Ann. Statist. 2023, 51, 717–737. [Google Scholar] [CrossRef]
- Balle, B.; Wang, Y.X. Improving the gaussian mechanism for differential privacy. In Proceedings of the Machine Learning Research, Stockholm, Sweden, 10–15 July 2018; pp. 394–403. [Google Scholar]
- Acharya, J.; Sun, Z.; Zhang, H. Hadamard Response: Estimating Distributions Privately, Efficiently, and with Little Communication. In Proceedings of the Machine Learning Research, Long Beach, CA, USA, 9–15 June 2019; pp. 1120–1129. [Google Scholar]
- Bassily, R.; Nissim, K.; Stemmer, U.; Thakurta, A. Practical Locally Private Heavy Hitters. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2285–2293. [Google Scholar]
- Wang, T.; Blocki, J.; Li, N.; Jha, S. Locally Differentially Private Protocols for Frequency Estimation. In Proceedings of the USENIX security Symposium, Vancouver, BC, Canada, 16–18 August 2017; pp. 729–745. [Google Scholar]
- MovieLense 10 M Dataset. Available online: https://grouplens.org/datasets/movielens/ (accessed on 1 August 2022).
- Clothing Fit Dataset for Size Recommendation. Available online: https://www.kaggle.com/datasets/rmisra/clothing-fit-dataset-for-size-recommendation/ (accessed on 1 August 2022).
- Phan, T.C.; Tran, H.C. Consideration of Data Security and Privacy Using Machine Learning Techniques. Int. J. Data Inform. Intell. Comput. 2023, 2, 20–32. [Google Scholar]
- Singh, P.; Pandey, A.K. A Review on Cloud Data Security Challenges and existing Countermeasures in Cloud Computing. Int. J. Data Inform. Intell. Comput. 2022, 1, 23–33. [Google Scholar]
- Jones, K.I.; Suchithra, R. Information Security: A Coordinated Strategy to Guarantee Data Security in Cloud Computing. Int. J. Data Inform. Intell. Comput. 2023, 2, 11–31. [Google Scholar]







| Step | PrivKV [2] | Our Work |
|---|---|---|
| 1 Pre-sampling | 1-out-of-d sampling | – |
| 2 Perturbing | Value VPP | |
| Key RR | ||
| 3 Post-sampling | – | 1-out-of-d OT |
| 4 Estimating | MLE | EM |
| Item | Synthetic Data (Gauss) | MoveiLens [42] | Clothing [43] |
|---|---|---|---|
| Ratings | 5,000,000 | 10,000,054 | 192,544 |
| Users (n) | 100,000 | 69,877 | 9657 |
| Items (d) | 100 | 10,677 | 3183 |
| Value range | , | , | , |
| Fraction of malicious users b | 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | 0.15 | 0.2 |
| Frequency gain [%] | 66.7 | 20.8 | 18.6 | 19.3 | 17.1 | 16.7 | 15.8 |
| Mean gain [%] | 18.2 | 20.4 | 24.5 | 30.6 | 25.9 | 21.4 | 27.8 |
| privacy budget | 0.1 | 0.5 | 1 | 2 | 3 | 4 | 5 |
| Frequency gain [%] | 0.6 | 4.8 | 90.0 | 41.7 | 50.0 | 55.6 | 66.7 |
| Mean gain [%] | 1.6 | 14.6 | 15.5 | 36.2 | 40.1 | 41.3 | 44.8 |
| The number of target keys r | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| Frequency gain [%] | 0.7 | 18.8 | 17.8 | 21.2 | 18.2 | 16.3 | 15.8 | 15.2 |
| Mean gain [%] | 20.8 | 13.5 | 21.8 | 30.2 | 25.8 | 27.7 | 25.9 | 25.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horigome, H.; Kikuchi, H.; Fujita, M.; Yu, C.-M. Robust Estimation Method against Poisoning Attacks for Key-Value Data with Local Differential Privacy. Appl. Sci. 2024, 14, 6368. https://doi.org/10.3390/app14146368
Horigome H, Kikuchi H, Fujita M, Yu C-M. Robust Estimation Method against Poisoning Attacks for Key-Value Data with Local Differential Privacy. Applied Sciences. 2024; 14(14):6368. https://doi.org/10.3390/app14146368
Chicago/Turabian StyleHorigome, Hikaru, Hiroaki Kikuchi, Masahiro Fujita, and Chia-Mu Yu. 2024. "Robust Estimation Method against Poisoning Attacks for Key-Value Data with Local Differential Privacy" Applied Sciences 14, no. 14: 6368. https://doi.org/10.3390/app14146368
APA StyleHorigome, H., Kikuchi, H., Fujita, M., & Yu, C.-M. (2024). Robust Estimation Method against Poisoning Attacks for Key-Value Data with Local Differential Privacy. Applied Sciences, 14(14), 6368. https://doi.org/10.3390/app14146368






