Advanced Scale-Propeller Design Using a MATLAB Optimization Code
Abstract
Featured Application
Abstract
1. Introduction
1.1. Rationale
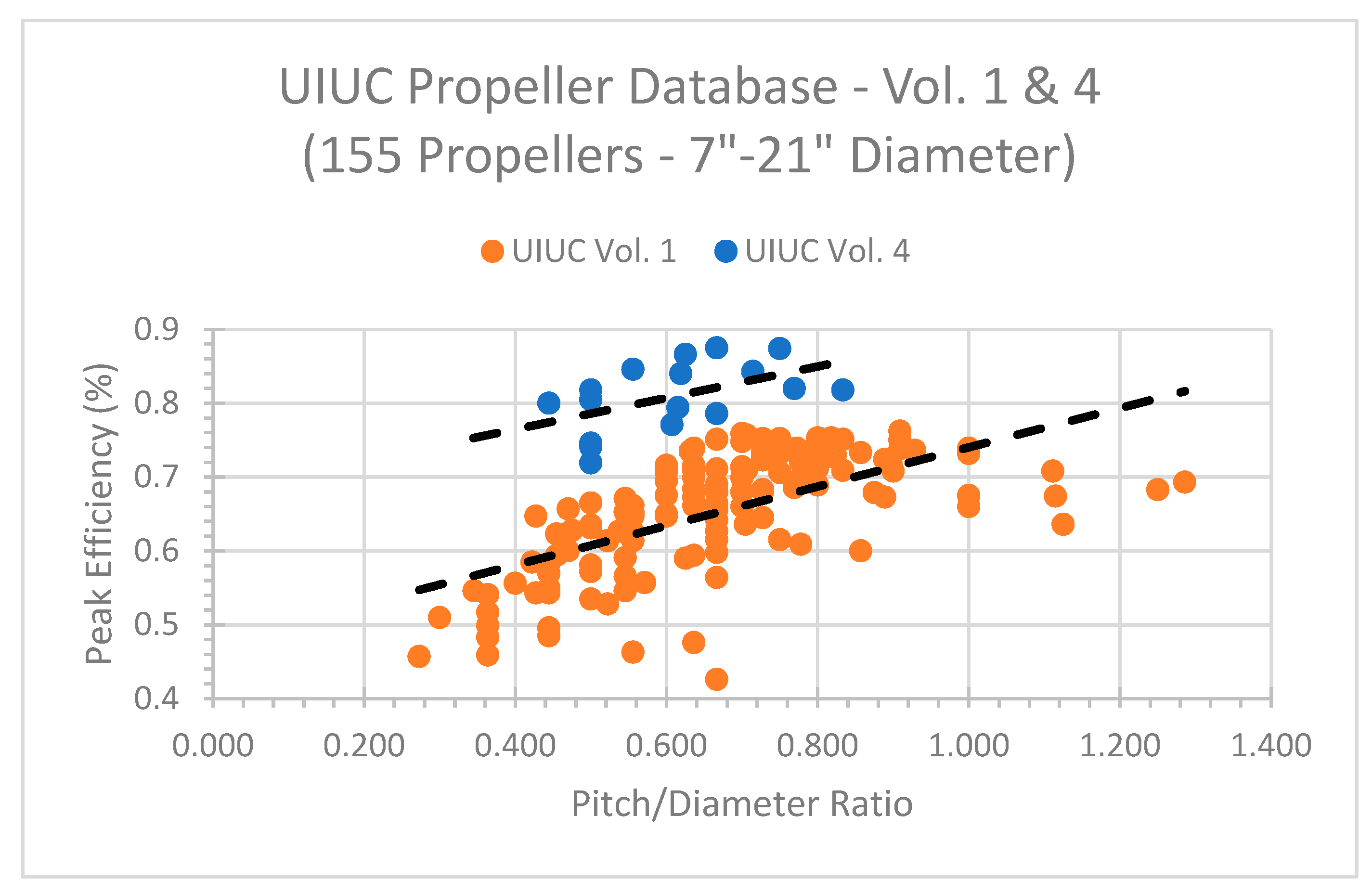
1.2. Propeller Data Analysis
1.3. Aim of the Study
1.4. Literature Review
- The rotor is modelled as an actuator disk, which adds momentum and energy to the air;
- There is no inflow or outflow through the wake boundary;
- The flow is steady, incompressible and inviscid;
- The flow is one dimensional and uniform;
- The flow is uniform through the disk and wake;
- The disc does not impart any swirl to the flow.
1.5. Historical Perspective
1.6. The Optimum Propeller
2. Materials and Methods
2.1. Propeller Theory—Geometry
2.1.1. Airfoil Geometry
2.1.2. Propeller Geometry
2.2. Non-Dimensional Coefficients
2.3. Propeller/Rotor Efficiency
2.3.1. Figure of Merit
2.3.2. Propulsive Efficiency
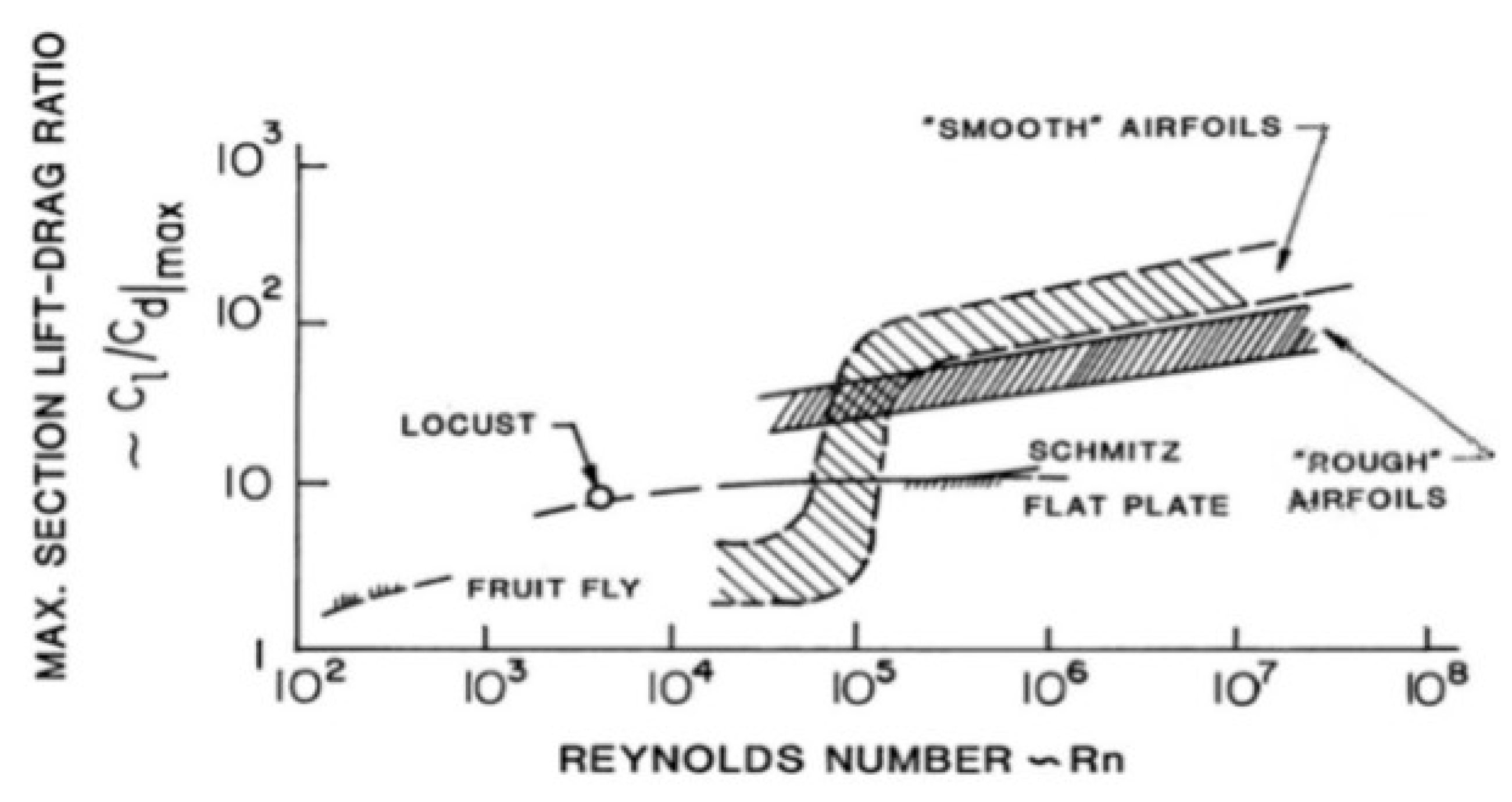
2.4. Reynolds Number
2.5. Propeller Geometry Optimization
2.6. Calculating Propeller Geometry
2.7. Optimising Propeller Geometry
3. Results
3.1. Implementing the Optimization Method Using MATLAB
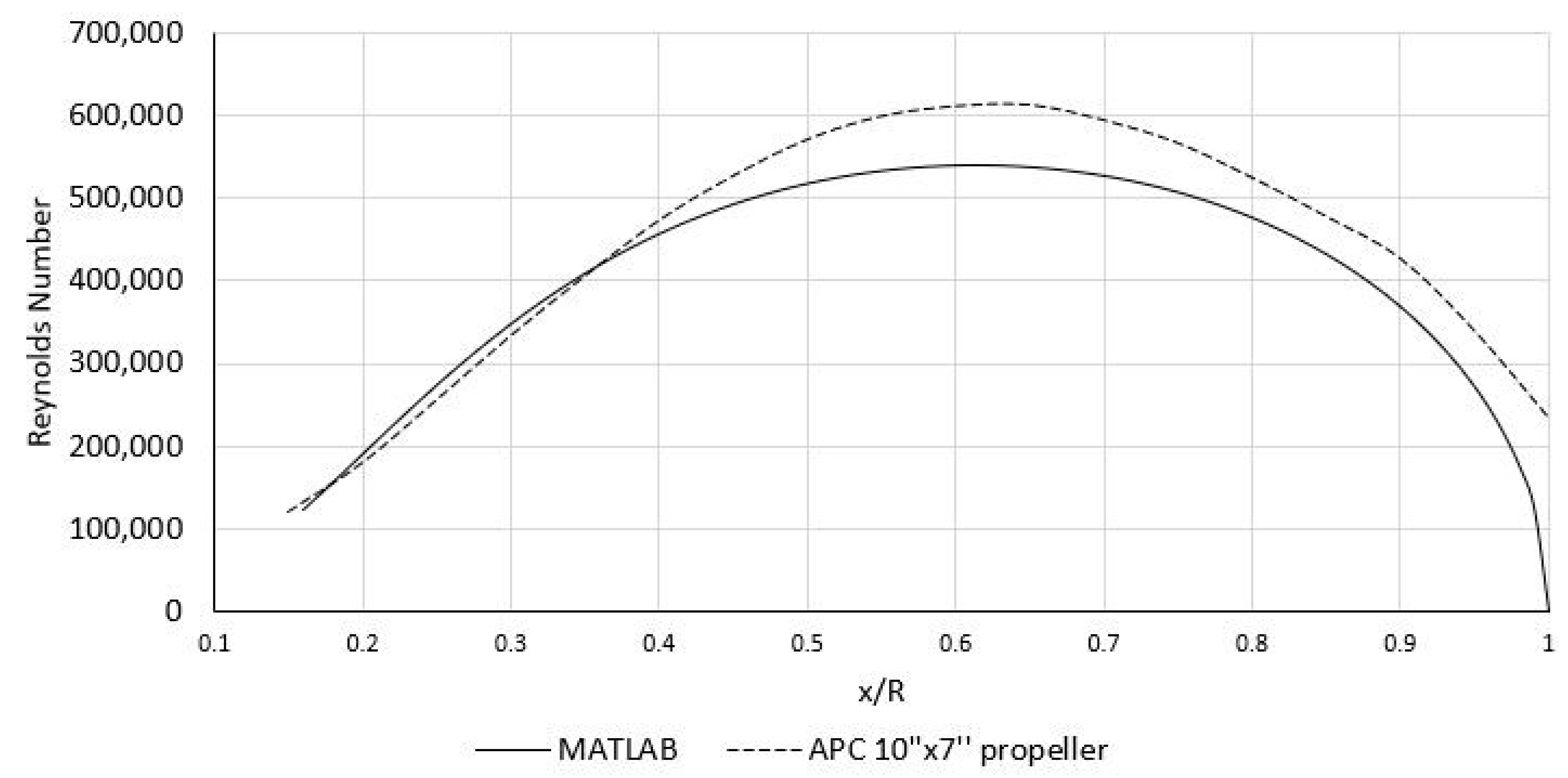
3.2. Reynolds Number Distribution
3.3. Program User Interface Design
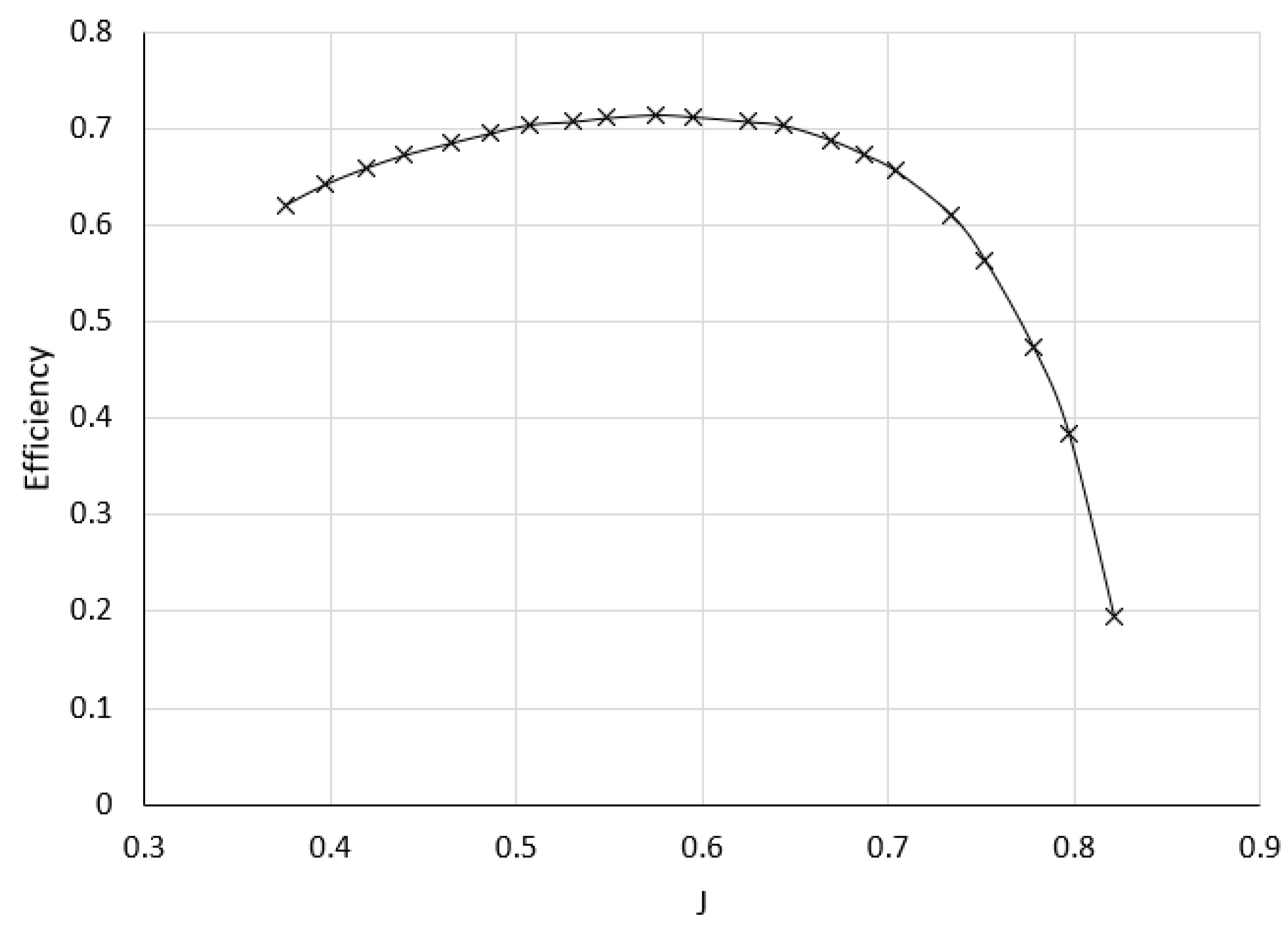
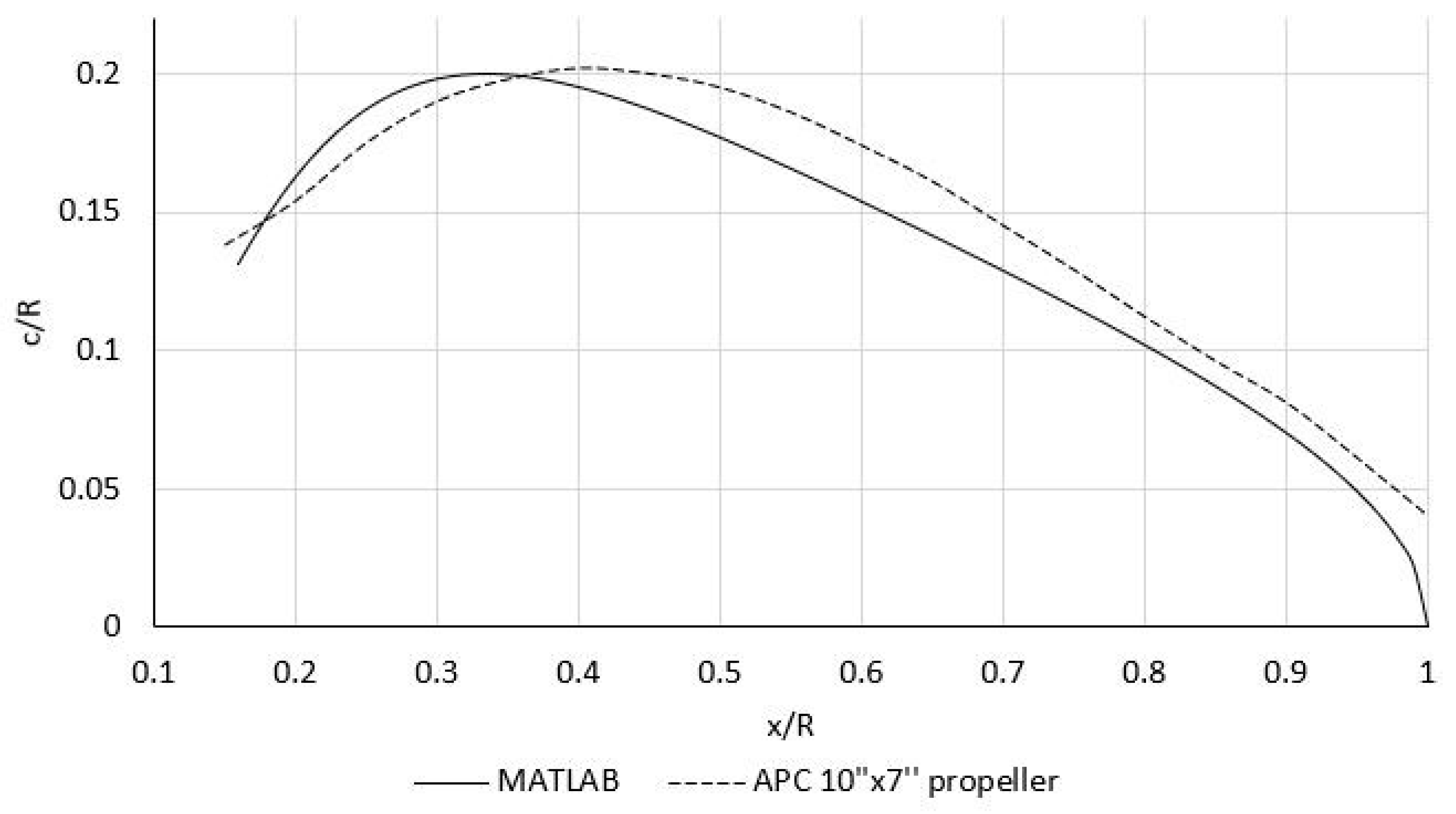
3.4. Validation of the MATLAB Program
4. Discussion
4.1. Summary
4.2. Recommendations for Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Propeller disc area (m2) |
| B | Number of propeller blades |
| c | Blade chord length (m) |
| D | Propeller diameter (inches) |
| F | Prandtl’s momentum loss factor |
| G | Circulation function |
| I1 | Thrust loading integral |
| I2 | Thrust loading integral |
| J | Propeller advance ratio, V/n D |
| J1 | Power Loading integral |
| J2 | Power Loading integral |
| n | Number of complete revolutions per second |
| p | Propeller pitch (inches) |
| P | Shaft power consumed by propeller (W) |
| Q | Propeller shaft torque (Nm) |
| r | Distance along the propeller radius (m) |
| R | Propeller blade radius (m) |
| T | Thrust produced by the propeller (N) |
| V | Freestream velocity (m/s) |
| V1 | Displacement velocity (m/s) |
| W | Total local velocity (m/s) |
| cD | Airfoil section coefficient of drag |
| cL | Airfoil section coefficient of lift |
| CT | Thrust Coefficient |
| CP | Power Coefficient |
| CQ | Torque Coefficient |
| mblade | Mass of a propeller blade (kg) |
| Pc | Design Power Coefficient |
| Tc | Design Thrust Coefficient |
| v, | Displacement velocity (m/s) |
| waxial | Induced axial velocity component (m/s) |
| wswirl | Induced swirl velocity component (m/s) |
| xblade | Extension of a propeller blade (m) |
| xCoG | Distance from centre of rotation to propeller blade centre of gravity (m) |
| Re | Reynolds number |
Greek Symbols
| α | Propeller blade angle of attack (degree) |
| β | Propeller blade angle of twist (degree) |
| ζ | Displacement velocity ratio, v1/V |
| ηp | Propeller efficiency, Tc/Pc ≡ J CT/CP |
| µ | Viscosity of air (kgm−1 s−1) |
| ξ | Non-dimensional radius, r/R |
| Γ | Circulation (m2/s) |
| ρ | Air density (kgm−3) |
| σ | Rotor solidity |
| Ω | Propeller angular speed (rad/s) |
| φ | Flow angle (degree) |
| φs | Wake helix angle (degree) |
| φt | Flow angle at propeller blade tip (degree) |
Appendix A. MATLAB Program Code
References
- Archer, R.D.; Saarlas, M. An Introduction to Aerospace Propulsion, 1st ed.; Prentice Hall: Saddle River, NJ, USA, 1996; pp. 68–121. ISBN 978-0131204966. [Google Scholar]
- Brandt, J.; Deters, R.; Ananda, G.; Selig, M. UIUC Propeller Database. University of Illinois at Urbana-Champaign. October 2019. Available online: https://m-selig.ae.illinois.edu/props/propDB.html (accessed on 10 May 2024).
- Bhagwat, M.J. Optimum Loading and Induced Swirl Effects in Hover. J. Am. Helicopter Soc. 2015, 60, 1–14. [Google Scholar] [CrossRef]
- Sampath, R. An Investigation into UAV Scale Propellers. Master’s Thesis, University of Southampton, Southampton, UK, 2017. [Google Scholar]
- Mejzlik Propellers. Available online: https://www.mejzlik.eu/technical-data/propeller_data (accessed on 28 May 2024).
- Weishaeupl, A. Evaluating the Performance of Scale Propellers Using the Heliciel Software and RCBenchmark Thrust Stands. Master’s Thesis, University of Southampton, Southampton, UK, 2018. [Google Scholar]
- Reynolds, E.; Barnaby, S.; Wingfield, C.; Cowper, W.J.E.; Rigg, A.; Stromeyer, C.E.; Thornycroft, J.T.; Froude, R.E.; Greenhill, A.G. The Screw Propeller. In Minutes of the Proceedings of the Institution of Civil Engineers; ICE: London, UK, 1890; pp. 390–392. [Google Scholar]
- Drzewiecki, S. Méthode pour la Détermination des Éléments Mécaniques des Propulseurs Hélicoïdaux; Imprimerie Gauthier-Villars et Fils: Paris, France, 1892. (In French) [Google Scholar]
- Weick, F. Simplified Propeller Design for Low-Powered Airplanes. No. NACA-TN-212, 1 January 1925. Available online: https://digital.library.unt.edu/ark:/67531/metadc53890/ (accessed on 28 May 2024).
- Glauert, H. Airplane Propellers. In Aerodynamic Theory; Durand, W.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar] [CrossRef]
- Stickle, G.; Crigler, J. Propeller Analysis from Experimental Data. Natl. Advis. Comm. Aeronaut. 1940, 27, 147. [Google Scholar]
- Theodorsen, T. Theory of Propellers, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1948. [Google Scholar]
- McMasters, J.; Henderson, M. Low-Speed Single Element Airfoil Synthesis; Boeing Commercial Airplane Co.: Seattle, DC, USA, 1979. [Google Scholar]
- Gamble, D.E. Automated Dynamic Propeller Testing at Low Reynolds Numbers. Master’s Thesis, Oklahoma State University, Stillwater, OK, USA, 2009. [Google Scholar]
- Koch, L.D. Design and Performance Calculations of a Propeller for Very High-Altitude Flight. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 1998. [Google Scholar]
- Merchant, M.P. Propeller Performance Measurement for Low Reynolds Number Unmanned Aerial Vehicle Applications. Master’s Thesis, Wichita State University, Wichita, KS, USA, 2004. [Google Scholar]
- Carvalho, I.M. Low Reynolds Propellers for Increased Quadcopters Endurance. Master’s Thesis, Universidade da Beira Interior, Covilhã, Portugal, 2013. [Google Scholar]
- Silvestre, M.A.R.; Morgardo, J.; Alves, P.; Santos, P.; Gamboa, P.; Páscoa, J.C. Propeller Performance Measurements at Low Reynolds Numbers. Int. J. Mech. 1998, 9, 932–943. [Google Scholar]
- Kuantama, E.; Craciun, D.; Tarca, I.; Tarca, R. Quadcopter Propeller Design and Performance Analysis. In New Advances in Mechanisms, Mechanical Transmissions and Robotics; Springer International Publishing: Berlin/Heidelberg, Germany, October 2016; pp. 269–277. [Google Scholar] [CrossRef]
- Prior, S.D. Optimizing Small Multi-Rotor Unmanned Aircraft; Taylor & Francis: London, UK, 2018; ISBN 978-1138369887. [Google Scholar]
- Ning, Z.; Hu, H. An Experimental Study on the Aerodynamic and Aeroacoustic Performances of a Bio-inspired UAV Propeller. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, American Institute of Aeronautics and Astronautics, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Larrabee, E.E. Design of Propellers for Motorsoarers; NASA Publication: Washington, DC, USA, 1 January 1979. [Google Scholar]
- Adkins, C.; Liebeck, R. Design of Optimum Propellers. J. Propuls. Power 1994, 10, 676–682. [Google Scholar] [CrossRef]
- Betz, A.; Prandtl, L. Screw Propellers with Minimum Energy Loss. Gott. Rep. 1958, 736, 64. [Google Scholar]
- Goldstein, S. On the Vortex Theory of Screw Propellers. In Proceedings of the Royal Society of London; Series A; Royal Society: London, UK, 1929; Volume 123, pp. 440–465. [Google Scholar]
- Klesa, J. Increasing of Aircraft Propeller Efficiency by Using Variable Twist Propeller Blades. 2008. Available online: https://stc.fs.cvut.cz/history/2008/sbornik/Papers/D2/Klesa_Jan_12122.pdf (accessed on 28 May 2024).
- JavaFoil. Available online: https://www.mh-aerotools.de/airfoils/javafoil.htm (accessed on 10 June 2024).
- Drela, M. QProp. Available online: https://web.mit.edu/drela/Public/web/qprop/ (accessed on 1 June 2024).
- Leishman, G.J. Principles of Helicopter Aerodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-1107013353. [Google Scholar]
- Korkan, K.; Camba, J.; Morris, P. Aerodynamic Databanks for Clark-Y, NACA 4-Digit and NACA 16-Series Airfoil Families; Technical Report; Aerospace Engineering Department, Texas A&M University: College Station, TX, USA, 1986. [Google Scholar]
- Airfoil Tools, Airfoil Database (1638 Airfoils). Available online: http://airfoiltools.com/search/index (accessed on 10 June 2024).
- Advanced Precision Composites. “APC Propeller Performance Data”. Available online: https://www.apcprop.com/technical-information/performance-data/ (accessed on 28 May 2024).









| Propeller | Rotor | ||
|---|---|---|---|
| CTp | Propeller Thrust Coefficient | CT | Rotor Thrust Coefficient |
| CPp | Propeller Power Coefficient | CP | Rotor Power Coefficient |
| CQp | Propeller Torque Coefficient | CQ | Rotor Torque Coefficient |
| Input | Unit |
|---|---|
| Diameter (D) | Inch |
| Velocity (V) | m/s |
| Shaft Power (P) | W |
| Propeller Speed | RPM |
| Air Density (ρ) | kgm−3 |
| Number of Blades (B) | - |
| Airfoil CL | - |
| Airfoil CD | - |
| Non-Dimensional Hub Radius | - |
| Angle of Attack (α) | Degree |
| Displacement velocity ratio convergence level | - |
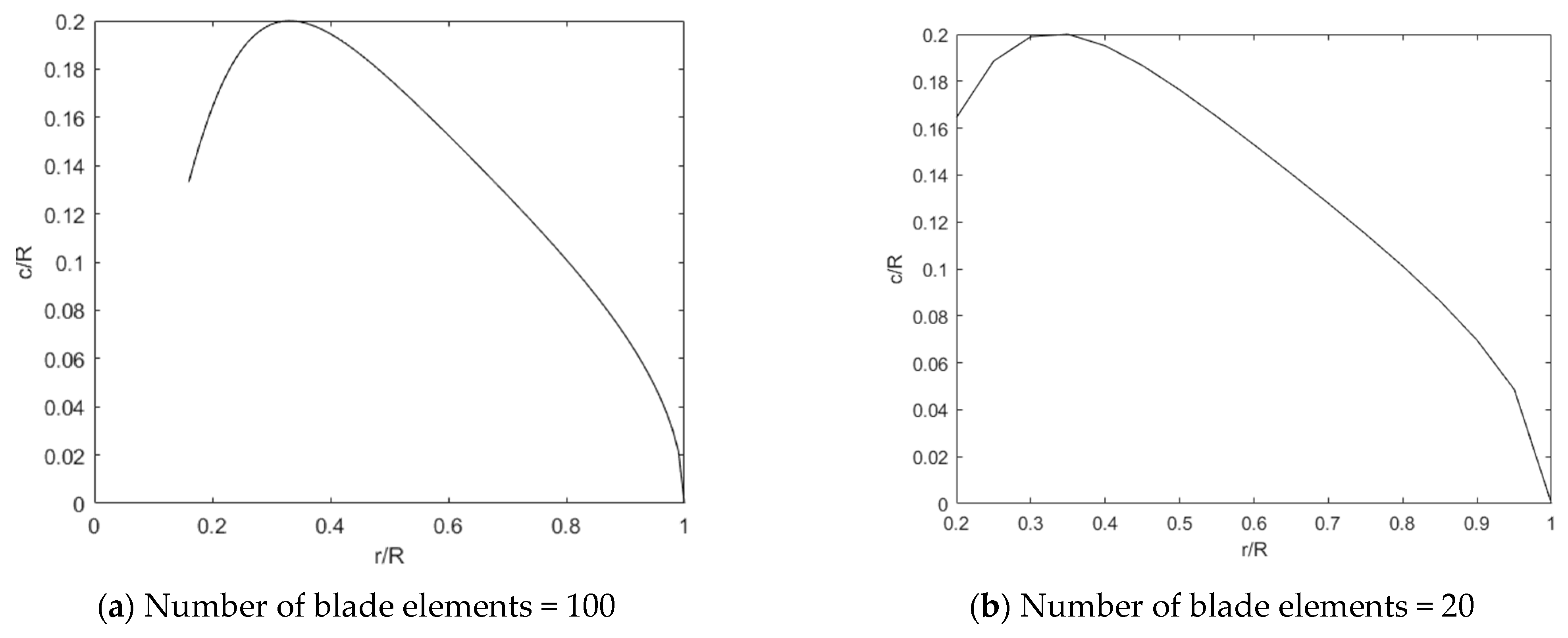
| Number of blade elements | - |
| Input | Input Value |
|---|---|
| Diameter (D) | 10 inch |
| Velocity (V) | 15.87 m/s |
| Shaft Power (P) | 68.77 W |
| Propeller Speed (n × 60) | 6519 RPM |
| Air Density (ρ) | 1.225 kgm−3 |
| Number of Blades (B) | 2 |
| Airfoil CL | 0.4 |
| Airfoil CD | 0.02 |
| Non-Dimensional Hub Radius | 0.15 |
| Angle of Attack (α) | 0◦ |
| Displacement velocity ratio convergence level | 0.1 |
| Number of blade elements | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prior, S.D.; Newman-Sanders, D. Advanced Scale-Propeller Design Using a MATLAB Optimization Code. Appl. Sci. 2024, 14, 6296. https://doi.org/10.3390/app14146296
Prior SD, Newman-Sanders D. Advanced Scale-Propeller Design Using a MATLAB Optimization Code. Applied Sciences. 2024; 14(14):6296. https://doi.org/10.3390/app14146296
Chicago/Turabian StylePrior, Stephen D., and Daniel Newman-Sanders. 2024. "Advanced Scale-Propeller Design Using a MATLAB Optimization Code" Applied Sciences 14, no. 14: 6296. https://doi.org/10.3390/app14146296
APA StylePrior, S. D., & Newman-Sanders, D. (2024). Advanced Scale-Propeller Design Using a MATLAB Optimization Code. Applied Sciences, 14(14), 6296. https://doi.org/10.3390/app14146296







