Study on L-Bending Springback of 45 Steel Leather Cutting Tool Coupled with Local Induction Heating

Abstract

Springback error is a major obstacle in L-bending sheets via cold working. Although thermal processing can effectively reduce the springback phenomenon, it is challenging to heat the sheet globally due to the influence of working conditions. Therefore, this study applied local induction heating to reduce the springback of 45 steel sheets and investigated the effects of bending parameters on springback behavior. Initially, a thermodynamic coupling model and a static model were created utilizing the VOCE hardening model and the von Mises yield criterion in the ANSYS workbench 2022 R2 software. The springback behavior and stress distribution of the sheets were then investigated under different temperatures (room temperature and 800 °C) and bending angles (15°, 30°, 45°, 60°, 75°, and 90°). Simultaneously, the experiments were performed to investigate springback behavior and guarantee the accuracy of the model. The results indicate that the springback reached a minimum value at the 45° bending angle at room temperature while increasing with the increasing bending angle under 800 °C local heating. The springback under local heating can be decreased by 75.2% and the error of the bending angle can improve by 2–7° compared with samples processed in room temperature.

1. Introduction

Leather cutting is an important component of intelligent manufacturing for automobiles, but its inherent properties make it difficult to process [1]. Die cutting enables leather cutting by preparing specially shaped cutters that avoid carbonizing the cut edge of leather caused by the laser cutting and clogging of the leather surface by water jet cutting [2,3]. According to the shape of the bending parts, the bending methods of sheets are divided into V-bending [4], L-bending [5], and so on. The L-bending process is widely employed in the creation of seat cross members for vehicle chassis and the production of leather cutting tools [6]. The 45 steel sheets are often used as leather cutting tools and are formed at different angles through a bending process. These bent sheets are used to form leather cutting molds for cutting leather in one piece. However, this process under cold working has a significant springback error since the elastic deformation region seeks to restore its previous shape after the removal of external force. This phenomenon is inevitable because of the inherent property of the metal deformation process and may result in issues, including production delays and unqualified parts [7].

Springback is influenced by variables, including bending angle, the radius of the bending corner, holding time, temperature, sheet thickness, mold gap, etc. [8]. Extensive research has been conducted to elucidate the mechanism of springback during bending and to minimize the negative effects of springback in the sheet-forming process through prediction or bending compensation [9]. It has been discovered that heating the sheet can effectively reduce the contact pressure and residual stress needed to bend the sheet, increase the formability of sheets, and reduce the risk of the metal sheet rupturing [10]. Global heating and local heating are the two types of heat treatment. The stress change process of the sheet during the bending process is usually obtained using the finite element analysis (FEA) method, which can also make a preliminary prediction of the springback behavior of the sheet. Mohammadi et al. [11] performed shallow-inclined single-point incremental forming of the sheets after global heating and established a finite element model at high temperatures, proving that the redundant deformation zone of the sheet is larger under cold forming. Ozturk et al. [12] conducted the global heating of the sheet and probed into the bending process of V-shaped dies at different temperatures from 50 °C to 300 °C at a bending angle of 60°, indicating that the springback rate decreased as temperature increased, and the minimal value was obtained at 300 °C. In addition, the high temperature can soften the sheet, lessen strain hardening, lower the convex height of the sheet, and enhance the geometric accuracy. Saito et al. [13] developed elastoviscoplastic models of V-bending and U-bending under global heating and discovered that the low flow stress at high temperatures is mostly responsible for the reduction in springback.

Plastic deformation occurs in only a portion of the bent plate; thus, global heating is not necessary. In order to improve the efficiency of thermoforming bending, research on localized heating thermoforming has been carried out [14]. Lee et al. [15] used a heating furnace to globally heat and bend the DP 980 steel sheet and found that when the temperature is higher than 600 °C, the bending angle exceeds the target angle, which is called the bouncing phenomenon. Furthermore, it has been discovered that the plastic deformation brought on by bending under local heating only affects a very small area, and heating the restricted area is sufficient to reduce the flow stress and reduce springback [14]. Finally, experiments and finite element analysis simulations were used to confirm the viability of local heating. Mohammadi et al. [16] regarded AA5182-O as an elastoplastic material and used the Swift hardening law and isotropic von Mises yield criterion for finite element modeling; the simulation results show that laser-local-heating-induced material softening led to a decrease in the forming force and improved the sheet forming accuracy. Duflou et al. [17] used the laser local heating method to dynamically heat the single-point incremental forming of the sheet, which significantly improved the forming limit of the sheet. Göttmann et al. [18] used laser heating to assist the asymmetric incremental forming of titanium alloy sheets. The results showed that the sheet’s forming performance was improved and that the springback increased as the ratio of the elastic modulus to yield stress rose. Despite the fact that numerous local heating techniques, including laser [17], infrared [19], resistance [20], and electric current [21] heating, have been used in the bending process, the application of induction local heating in bending process is rarely reported. Because of its rapid heating and even temperature distribution, induction heating has been widely used in non-isothermal stretching, injection molding, stamping, and other processes [22]. It is worthwhile to investigate the interaction between inductive local heating and L-bending.

In this study, the induction local heating method was introduced to assist in the L-bending of the 45 steel sheet and compared with the cold-working method. The bending behavior under different heating temperatures and bending angles were investigated by both FEA simulation and experiment. Simultaneously, the stress distribution and springback mechanism were further analyzed to explain the bending behavior. Through these efforts, the L-bending process can be optimized to improve the forming accuracy of leather cutting tools.

2. Materials and Methods

2.1. Experimental Scheme

The sheet material employed in this investigation is the Chinese standard 45 steel, which is equivalent to 1045 steel (AISI). The chemical composition of the 45 steel is shown in

Table 1. Chemical composition of 45 steel (wt.%).

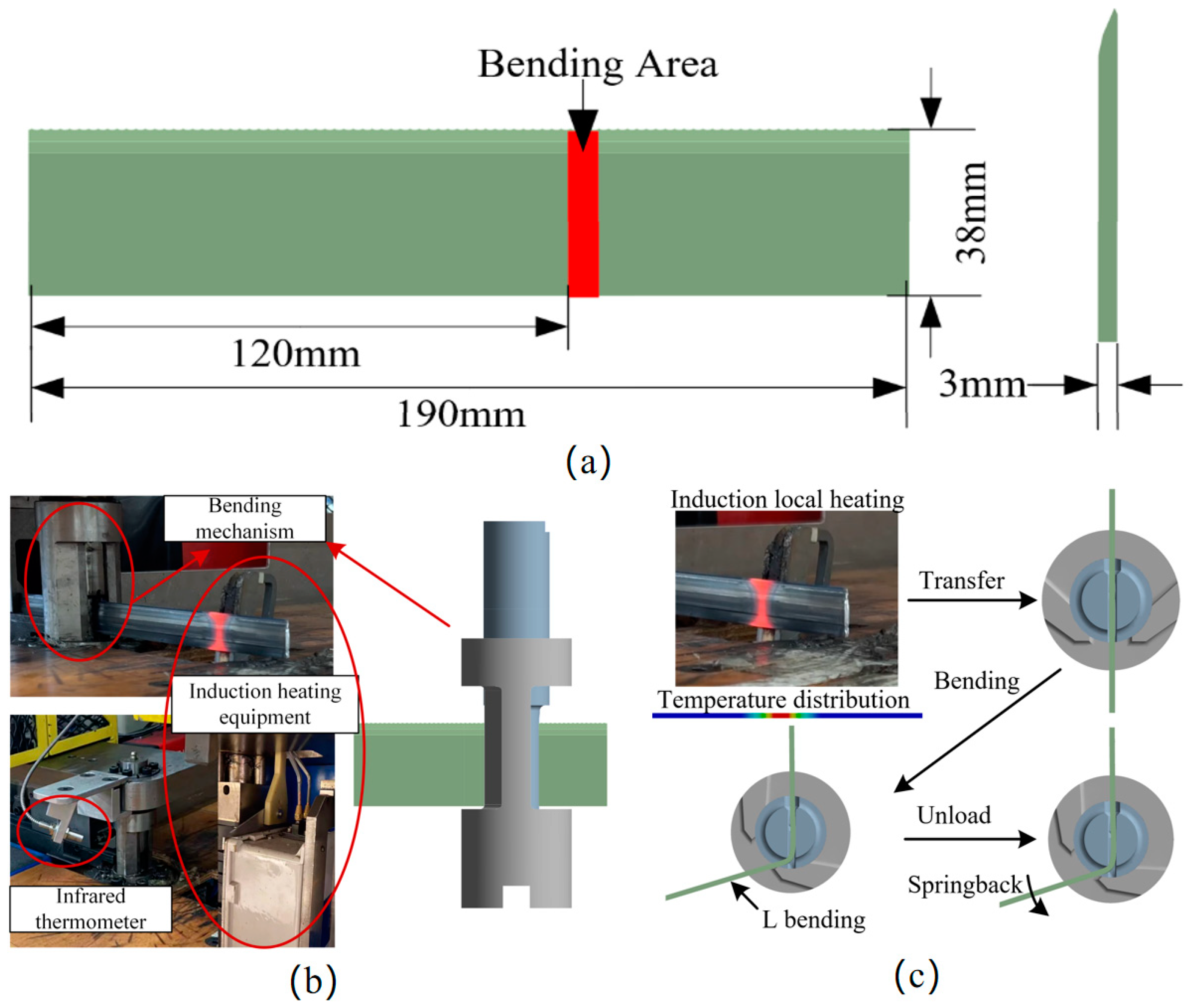
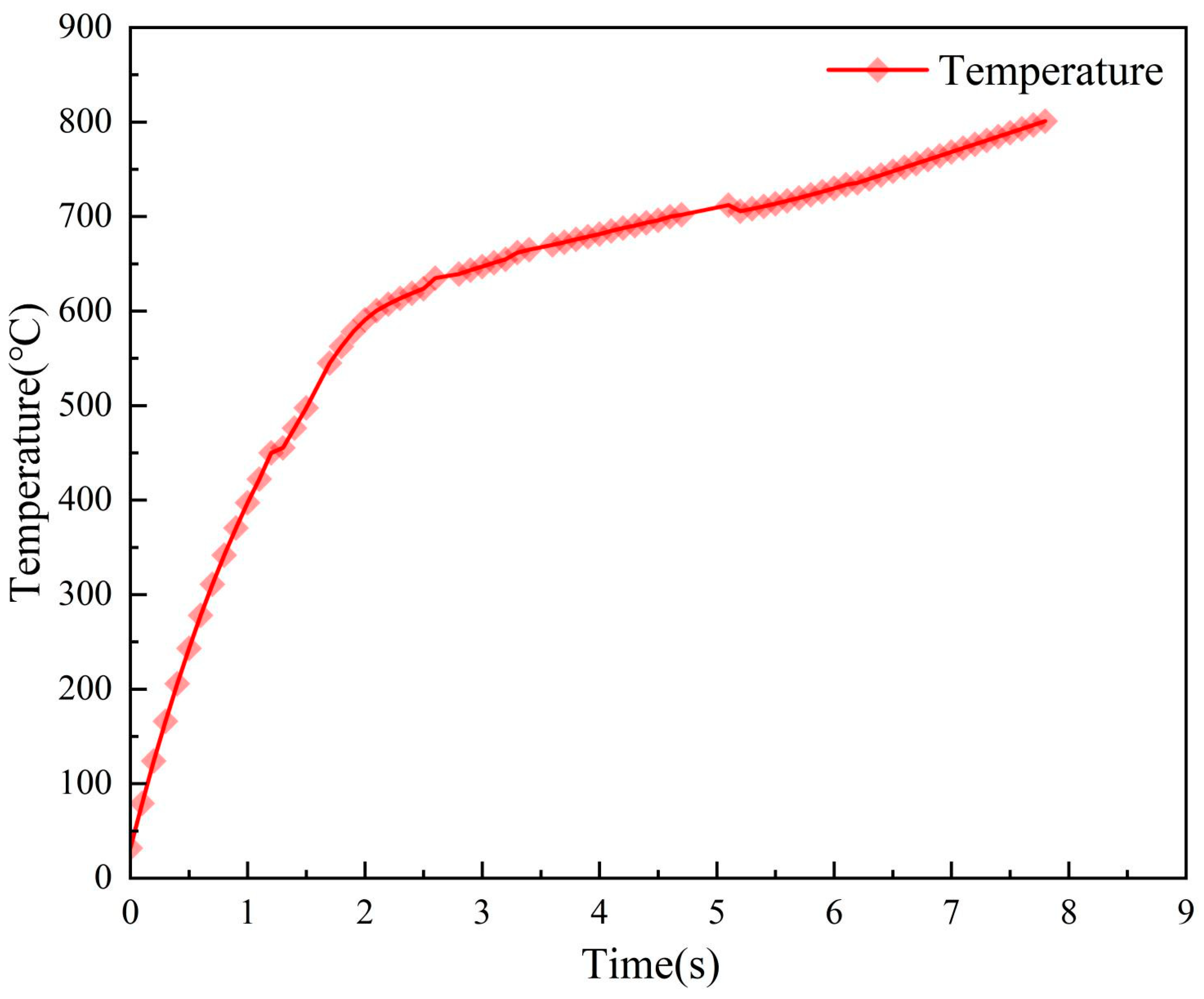
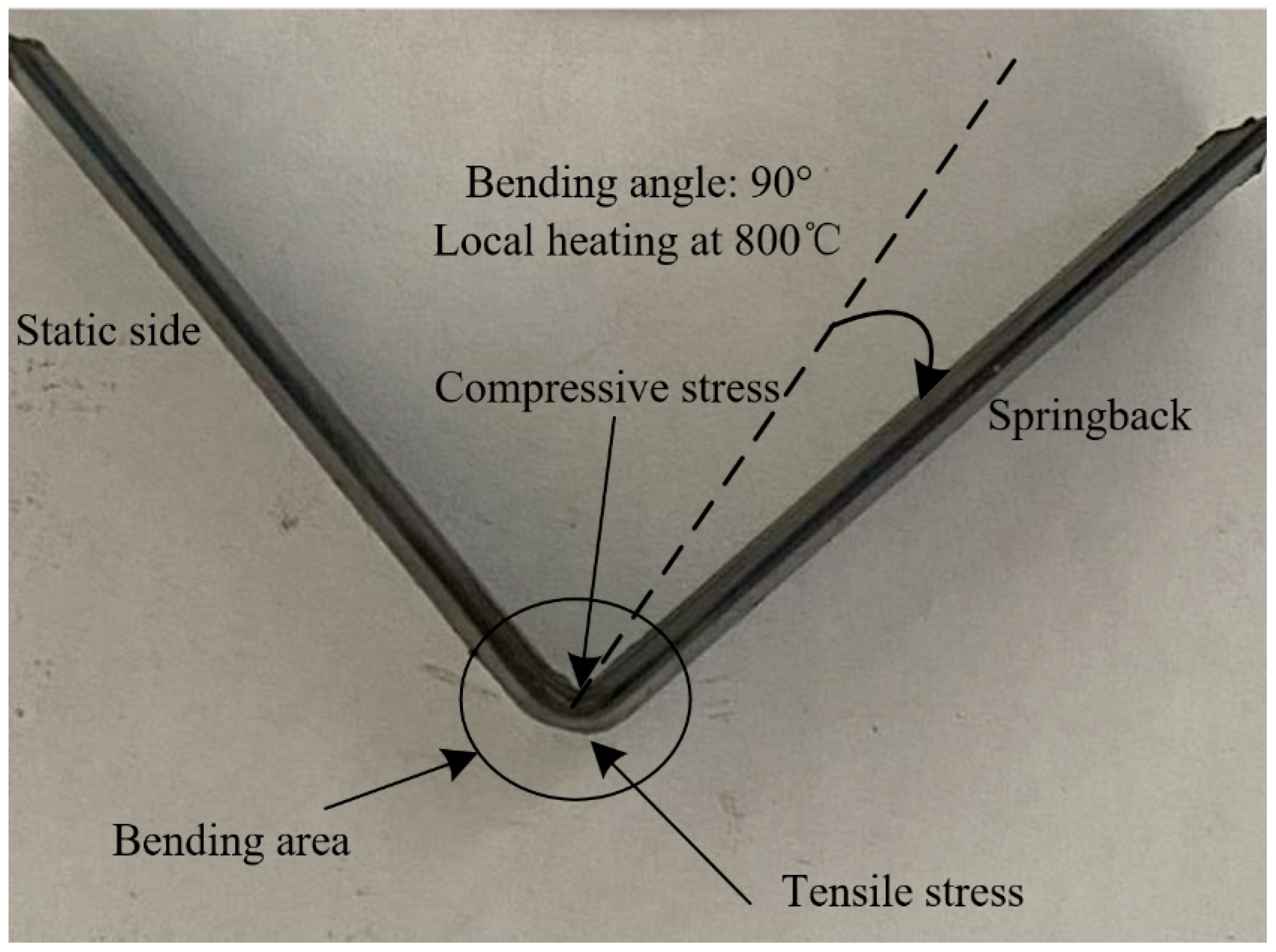
Composition	C	Si	Mn	Cr	Cu	Ni	Fe
Proportion	0.43	0.27	0.60	0.15	0.20	0.22	bal.

, and the dimension of each sheet is 190 × 38 × 3 mm. A high-temperature tensile experiment [23] was used to produce the stress–strain curve of 45 steel at room temperature and 800 °C under the condition of a strain rate of 1 s⁻¹.

Table 2. Thermophysical performance parameters of 45 steel.

Temperature (°C)	100	200	300	400	500	600	700	800
Thermal Conductivity (W·m−1 K−1)	50.72	48.13	45.71	41.74	38.36	33.92	30.15	26.82
Specific Heat Capacity (J·kg−1 K−1)	381.25	404.16	412.52	459.83	509.12	555.14	604.36	659.35
The modulus of Elasticity (MPa)	2.07 × 105	2.02 × 105	1.92 × 105	1.87 × 105	1.69 × 105	1.61 × 105	1.46 × 105	1.32 × 105

displays the thermophysical performance parameters of 45 steel at various temperatures [24]. The trend in the thermophysical performance parameters with temperature is shown in Figure 1a–c. Moreover, the interfacial heat transfer coefficient (IHTC, in W/m² K) is required in the thermodynamic coupling simulation because of the transfer of energy from the heated sheet to the mold and air, as shown in Figure 1d. The IHTC is a value that varies with contact pressure because the pressure between the sheet and the mold affects the transfer of thermal energy.

Figure 2 shows the relevant information on the L-bending process of the sheet. The sheets were machined into a geometric shape with serrations at one end, as shown in Figure 2a, before bending. The bending of the sheets occurs in the local red region of Figure 2a, and the deformation of the sheets is mainly concentrated in this region. The detailed structure of the bending mechanism and the induction heating equipment is shown in Figure 2b. The apparatus is primarily made up of two parts: the outer and the inner molds. The sheet was fixed by the inner mold and bent by the rotation of the outer mold, and different bend angles were achieved by varying the rotation angle of the outer mold. The entire process of the sheet bending during local heating is depicted in Figure 2c.

Through the usage of two infrared thermometers, the retractable induction heating device continuously measured the sheet’s temperature during the induction heating process and the subsequent sheet’s bending process. According to Lee et al. [25], L-bending needed a greater temperature than V-bending in order to considerably reduce springback. This was a result of the differing thermodynamic boundary conditions and forming properties of L-bending and V-bending, causing the higher cooling rate of L-bending. The springback of the sheet under L-bending was only fully decreased when the local heating temperature was not lower than 800 °C [25]. Therefore, 800 °C was chosen as the high-temperature bending temperature in this study, and the room temperature group was set for comparison. The sheet required 7.5 s to heat up, and the width of the heating area was 5 mm. Figure 3 depicts the heating process curve determined using the infrared thermometer. Because the bending process took place only 1.5 s after the sheet had finished heating, the temperature change in the sheet during processing was ignored. The experiment used various bending angles of 15, 30, 45, 60, 75, and 90 degrees with a rotational speed of 60 rad/s for the outer mold.

2.2. Numerical Simulation

The L-bending process of 45 steel sheets was simulated via the finite element model (FEM) in the ANSYS workbench 2022 R2 software to explain the springback mechanism and predict the springback rate. The induction heating process was realized based on the sequential coupling technique, and local heating was realized by importing the results of the transient thermal analysis into the stress analysis [26]. The transient thermal analysis of the sheet is first performed by applying a temperature field of 800 °C. The bending simulation process is then divided into several time steps with corresponding temperature cooling values to ensure the accuracy of the simulation.

The VOCE model is a nonlinear function that fits a plastic strengthening curve of a material based on its properties. The accuracy of the simulation can be improved by VOCE modeling. The nonlinear isotropic hardening model based on the VOCE function was used in the ANSYS software, as shown in Equation (1):

$$\sigma ={\sigma }_0+R_0{\epsilon }_p+R_{\infty }(1-e^{-b{\epsilon }_p})$$

(1)

where ε_p is the plastic true strain, and σ₀, R₀, R_∞, and b are the four material constants of, the initial yield point, linear coefficient, exponential coefficient, and exponential saturation coefficient, respectively. The hardening model is based on the isotropic hardening law, which has the largest springback in comparison to other hardening laws and has high prediction accuracy. The von Mises isotropic yield criterion was used since the anisotropic effect played a minimal role in the bending process and was negligible [27]. The stress–strain relationship of 45 steel at room temperature and 800 °C was obtained in a tensile experiment [23,28]. The parameters of the VOCE model were obtained by fitting the stress–strain curve, as shown in

Table 3. Parameter values of the VOCE model.

σ0	R0	R∞	b
41.26	6.89	162.65	17.49
246.79	−166.72	401.87	28.75

. The stress–strain curve obtained by fitting is shown in Figure 4. The VOCE hardening model accurately predicted the behavior of 45 steel between the yield and tensile strength regions.

The forming mold and sheet were regarded as flexible bodies in the FEM, and due to the complexity of the sheet model, the tetrahedral mesh with a smoother transition was selected. The non-contact and non-heating areas of the mold had a mesh size of 4 mm, which accelerated the speed of the solution. In order to ensure the accuracy of the simulation results, the mesh size of the induction heating area and the contact area were set to 1 mm, and the thickness direction of the sheet was set to at least 3 layers of mesh. The total number of meshes in the model was 55,026, and there were 97,060 nodes. The two stages of the simulated machining process were loading and unloading. The loading phase refers to controlling the angle required for outer tool rotation. The unloading phase refers to the outer tool returning to its original position. The springback was generated after unloading. The bending angle and springback were obtained by solving the element Euler’s angle. The thermal conductivity, specific heat, and other thermophysical characteristics of 45 steel were considered in the finite element model [29].

The friction coefficient in the simulation was set to a fixed value of 0.1 because the bending experiment did not employ lubricating oil, which was similar to the friction coefficient study of many earlier bending investigations. This study would not go into detail about the tiny temperature change that occurs inside the mold during the local heating phase. The VOCE model employed in this study solely took into account the impacts of plastic strain and temperature because the influence of the strain rate was minimal at low mold velocities [27].

The link between the rotation angle of the outer mold and the bending angle of the sheet was established experimentally because the bending mechanism regulated the bending angle of the sheet through the rotation of the outer mold. The sheet’s bending angle was first determined at room temperature and 800 °C when the outer mold rotated by 30, 40, 50, 60, and 70 degrees, as indicated in

Table 4. The bending angle of the sheet corresponds to the rotation angle of the outer mold.

Outer Mold Rotation Angle (°)	30	40	50	60	70
Bending Angle at 800 °C (°)	9.49	45.75	73.83	93.73	105.44
Bending Angle at Room Temperature (°)	7.73	42.01	68.96	88.31	100.17

. The fitting equations for the correspondence between the rotation angle of the outer mold and the bending angle of the sheet at room temperature and 800 ° C are shown in Equations (2) and (3):

$$y_1=-140.4+6.06x-0.038x^2$$

(2)

$$y_2=-148.36+6.49x-0.041x^2$$

(3)

where y₁ is the bending angle at room temperature, y₂ is the bending angle at 800 °C, and x is the rotation angle of the outer mold.

The same outer mold rotation angle was used as an input, and the angle was adjusted to the average of the findings from the two fitting formulas, as shown in

Table 5. The input value for the rotation angle of the outer mold.

Bending Angle (°)	15	30	45	60	75	90
Input (°)	31.58	36.42	40.93	45.83	51.85	59.73

, to more effectively compare the variation in the bending angle of the sheet at various temperatures.

3. Results

3.1. Forming Angle Analysis of the Sheet

It has been proven that process parameters such as temperature and bending angle have considerable impacts on the springback of the sheet. Table 4 illustrates the effects of temperature and the outer mold rotation angle on the bending angle of 45 steel during L-bending. It can be seen that the bending angle of the sheet at room temperature is typically smaller than the bending angle of the sheet at 800 °C, indicating that the sheet’s forming performance has increased at 800 °C when the rotation angle of the outer mold is the same.

Table 6. Simulation and experimental results under room temperature.

Bending angle (°)	15	30	45	60	75	90
Maximum bending angle (°)	16.63	34.75	49.15	64.07	79.65	94.42
Actual bending angle (°)	15.83	33.91	48.23	63.11	78.54	93.13
Springback (°)	0.81	0.84	0.92	0.95	1.11	1.29
Springback rate	5.05%	2.48%	1.91%	1.52%	1.42%	1.39%
Experimental angle (°)	16.68	31.95	49.90	64.01	78.55	91.64
Error	5.39%	5.78%	3.47%	1.43%	0.01%	1.6%

and

Table 7. Simulation and experimental results at local heating under induction local heating.

Bending angle (°)	15	30	45	60	75	90
Maximum bending angle (°)	18.71	33.59	47.27	61.62	75.75	89.83
Actual bending angle (°)	15.48	30.97	45.05	59.31	73.38	87.31
Springback (°)	3.22	2.62	2.22	2.29	2.37	2.53
Springback rate	20.80%	8.46%	4.93%	3.86%	3.23%	2.90%
Experimental angle (°)	15.8	29.82	43.94	56.99	71.21	84.98
Error	2.06%	3.71%	2.47%	3.91%	2.96%	2.65%

show the simulation and experiment results of the bending behavior under different temperatures and bending angles, respectively, where the maximum bending angle and the actual bending angle are the bending angles of the sheets before and after springback under the simulation results, and the springback is the difference between the two. The ratio of the springback to the actual bending angle is known as the springback rate. The inaccuracy in the simulation result is the difference between the real bending angle and the experimental angle. Table 6 and Table 7 demonstrate the extremely small difference in the bending angle between the simulation results and the experimental results. The maximum difference in the actual bending angle between the simulation and the experimental results at 800 °C is just 1.96°, and the corresponding error is 5.78%. The maximum difference in bending angle is 2.32°, and the maximum error between the simulated value and the experimental value at room temperature is 3.91%, indicating that the finite element model has good accuracy.

Figure 5 illustrates the simulation and experimental results of the sheet’s bending angle when the outer mold rotation angle from Table 5 is used as input, confirming the inference that the forming performance of the sheet is enhanced at 800 °C and that the bending sheets at this temperature produce a larger bending angle. This improvement in forming performance is due to the fact that the metallographic structure of 45 steel at room temperature is composed of bulk ferrite and fine lamellar pearlite, and the high temperature of 800 °C expands the pearlite volume and significantly reduces the grain boundary interface, thereby reducing dislocation motion resistance [23].

3.2. Springback and Stress Analysis at Room Temperature

Figure 6 illustrates the springback amount and fluctuation rate with the bending angle at room temperature. When the bending angle is 45 degrees, the springback amount turns, first decreasing and then increasing. In the study of V-bending of MART1400 steel, En et al. [30] also described this phenomenon. The occurrence of this phenomenon is related to the radius of the mold corner and temperature of the mold; only when the temperature is not more than 375 °C and the mold corner radius is not more than 2 mm, the springback amount exhibits a tendency of first reducing and then increasing with an increase in the bending angle. The springback amount tends to rise with the increase in the bending angle when one of these two conditions is not met.

In this study, the corner radius of the mold is almost zero since the bent sheet is being utilized as a leather cutting tool, which also results in the springback behavior previously mentioned at room temperature. Figure 4 shows that the yield strength of 45 steel at room temperature is around 360 MPa, whereas the forming performance of 45 steel has significantly improved under local heating at 800 °C, where the yield strength is only close to 60 MPa. The von Mises yield criterion explains the elastic and plastic deformation in the bending area. At room temperature, when the bending angles are 15° and 30°, the plastic deformation region, as shown in Figure 7, accounts for a relatively small proportion, at which time the elastic deformation area tries to return to its original shape and the springback caused by elastic stress deformation dominates. Figure 8 illustrates how the main influencing element of springback changes from the recovery of the elastic deformation area to the imbalanced compressive and tensile stresses generated by the increasing bending angle when the bending angle is greater than 30° [25]. With a rise in the bending angle, the maximum tensile stress and maximum compressive stress area become increasingly inconsistent and unbalanced.

3.3. Springback and Stress Analysis under Local Heating at 800 °C

As shown in Figure 8, the amount of springback under local heating at 800 °C increases with the increase in the bending angle, which is due to the increase in the bending angle causing a greater amount of deformation around the bending area of 45 steel sheets, leading the two sides of the bending area to produce greater compressive and tensile stresses, respectively. This causes a greater amount of unbalanced stress and springback. Additionally, when the sheet is heated locally to 800 °C, the forming performance of the bending area is improved, and when the 15° and 30° bending is carried out, as shown in Figure 9, the plastic deformation area still takes up a sizable percentage of the sheet. That is to say, after the local heating of the sheet at 800 °C, when the bending angle of the sheet is not lower than 15°, the main influencing factor of springback is always the unbalanced compressive and tensile stresses in the bending area. The springback at various angles at 800 °C decreased by 75.2%, 68%, 58.4%, 58.1%, 53.1%, and 49%, respectively, compared to room temperature, which supports the feasibility of local heating and demonstrates that local heating effectively enhances the forming performance of bent sheets. The main reason for the reduction in springback is that local heating reduces strain hardening around the bending zone and thus the equivalent stress around the bending area.

Figure 9 shows the sheet after bending at 90° under local heating at 800 °C and that only the bending area has plastic deformation. There is no reverse stress distribution and ‘springforward’ phenomenon caused by reverse bending outside the bending area after unloading under global heating, as reported by Lee et al. [15]. The ‘springforward’ phenomenon makes it difficult to ensure the straightness accuracy of the sheet, which is more likely to occur when the sheet is heated globally at high temperatures. This also illustrates why local heating has greater forming accuracy than global heating. Because local heating only affects a tiny portion of the heat-affected zone and heats up quickly, it has less of an impact on how the structure and hardness of the heat-affected zone change. Figure 11 shows that local heating significantly lowers the sheet’s stress level relative to room temperature, which reduces the hardness of the material and increases the likelihood of plastic deformation, which, in turn, enhances the forming performance of the 45 steel material. In addition, during induction local heating, a large amount of energy is transferred from the heat-affected area to the non-heated zone due to heat conduction, which causes the cooling rate during the forming process to be much faster than that of global heating. This aids in the work hardening process in the formed area, where, following induction local heating, a hardness that had been somewhat lowered can be restored to the original hardness or even higher [15].

Figure 10 and Figure 11 depict the equivalent stress of the sheets before unloading, as obtained by the finite element simulation. As can be seen, the sheet’s bending area experiences more stress at room temperature than it does at 800 °C. This difference in stress levels results in a less uneven distribution of stress in the bending area, which, in turn, lowers the springback angle.

According to Figure 8 and Table 7, the springback rate of L-bending at room temperature and 800 °C declined with an increase in bending angle, going from 20.8% and 5% at 15° to 2.9% and 1.4% at 90°, respectively. L-bending also exhibited a lower springback rate at 800 °C than it did at room temperature. Figure 11 further shows that the residual stress level of the sheet is lower under local heating than it is while bending at room temperature, which will extend tool life when the sheet is used as a tool.

4. Discussion and Conclusions

In this study, the induction local heating technique was introduced to assist in manufacturing L-bending leather cutting tools made of 45 steel. The forming angle and springback behavior under different temperatures and bending angles were investigated through both FEA simulation and experiment. The springback mechanism was also investigated by simulation and discussed. The detailed conclusions are as follows:

(1) In order to simulate the bending process of the sheet at room temperature and local heating at 800 °C, an FEA model was developed based on the VOCE hardening model and von Mises yield criterion. The accuracy of the model was verified by experiments, and the maximum errors of the simulated value and experimental value at room temperature and 800 °C local heating were 5.78% and 3.91%, respectively.

(2) The simulation and experimental results show that the forming performance of the sheet under local heating at 800 °C was improved, and under the same outer mold rotation angle, the forming angle of the sheet increased by 2–6° in comparison to room temperature. The local heating also reduces the springback amount of the sheet. The local heating also decreases the sheet’s springback amount, with the maximum springback amount decreasing by 75.2%.

(3) The sheet’s springback amount is affected by two main factors, which are the dominant elastic deformation in the bending areas and the imbalance of the tensile and compressive stresses.

At room temperature, the springback amount of the sheet with the increase in the bending angle shows the law of decreasing first and then increasing. When the bending angle is less than 45 °, the elastic deformation area of the bending area accounts for a larger area; when the bending angle is larger than 45 °, the plastic deformation area tends to stabilize, and the imbalance of tensile and compressive stresses is a major factor affecting the springback. And as the bending angle increases, the tensile and compressive stresses will be more unbalanced, which will lead to an increase in the amount of springback.

The sheet’s ability to be formed has significantly improved under a local heating of 800 °C. The amount of springback brought on by elastic deformation is minimal. The sheet’s unbalanced tensile and compressive stresses are the primary causes of springback. And the amount of springback rises as the bending angle increases.

(4) The sheet’s springback rate declined as the bending angle increased at various temperatures, and it was lower when the sheet was heated locally. The springback rate at room temperature and local heating decreased from 20.8% and 5% at bending 15° to 2.9% and 1.4% at bending 90°, respectively. In addition, local heating significantly lowers the sheet’s residual stress level relative to room temperature.

However, due to various factors, there are some shortcomings in this study that need further improvement and in-depth analysis and research. The next steps of future work can be carried out from the following aspects:

(1)

The FEA carried out in this study adopts a relatively single VOCE hardening model, and the simulation results obtained and the experimental results still have errors. Researchers can try to use other hardening models (e.g., Hollomon, Ghosh, Swift, etc.) to make comparisons to ensure that the highest simulation accuracy is achieved.

(2)

This study only utilizes the finite element simulation of the sheets springback analysis, the analysis method is relatively singular. In the future, the microstructure of the bending place can be studied to further analyze the rebound mechanism.

(3)

The bending angle experiments carried out in this study did not analyze the actual springback angle compared with the simulated springback angle. These experiments can be improved in the future to better study the bending springback.