Development and Application of a Novel Non-Iterative Balancing Method for Hydronic Systems
Abstract
1. Introduction
2. Material and Methods
2.1. Traditional Balancing Methods
2.2. Non-Iterative Methods
2.2.1. Description of the Compensated Method
- -
- CBVs have to be installed on every single terminal;
- -
- The procedure requires flow rate measurements at every terminal, with the re-location of the manometer at every step, which is time consuming;
- -
- The use of CBVs as flow meters requires reaching the minimum pressure at which detection is possible, adding this drop to the drop in every path (the MD path included), thereby increasing the required head pressure of the pump.
- -
- In cases where the most disadvantaged (index) terminal is not also the farthest, an alternative procedure is imposed, the reference terminal has to be properly throttled and the entire branch have to be re-balanced.
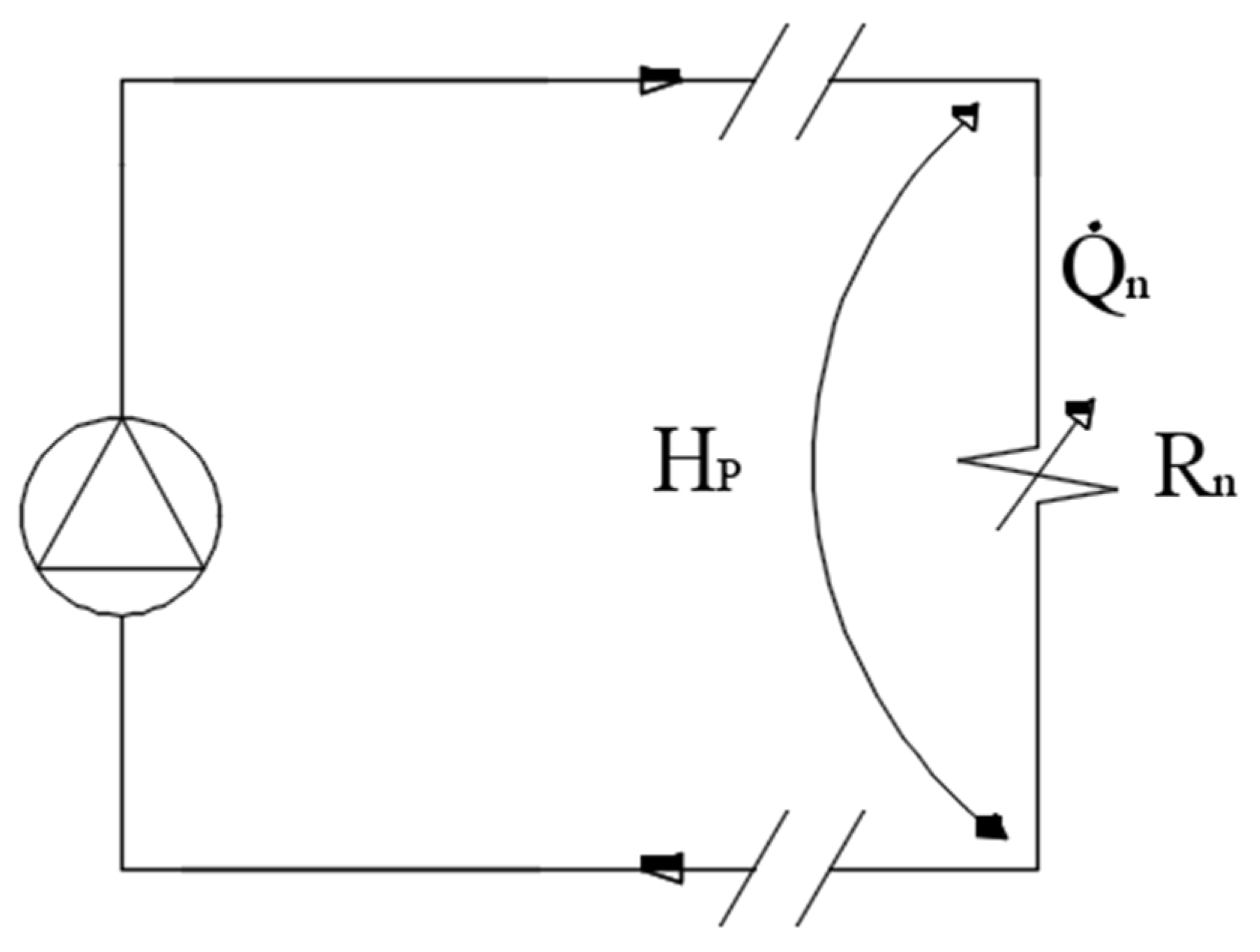
3. Theory and Calculations
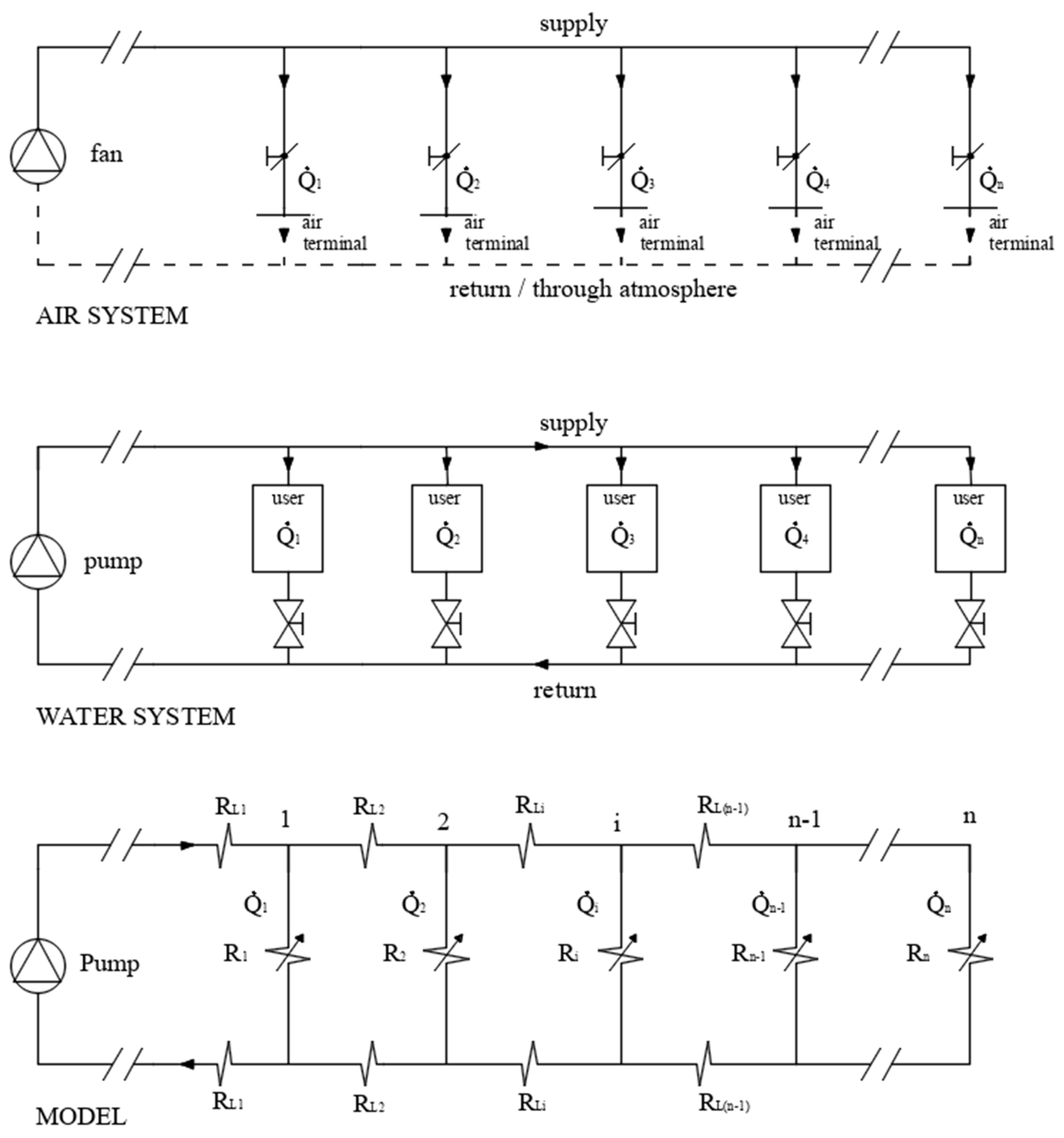
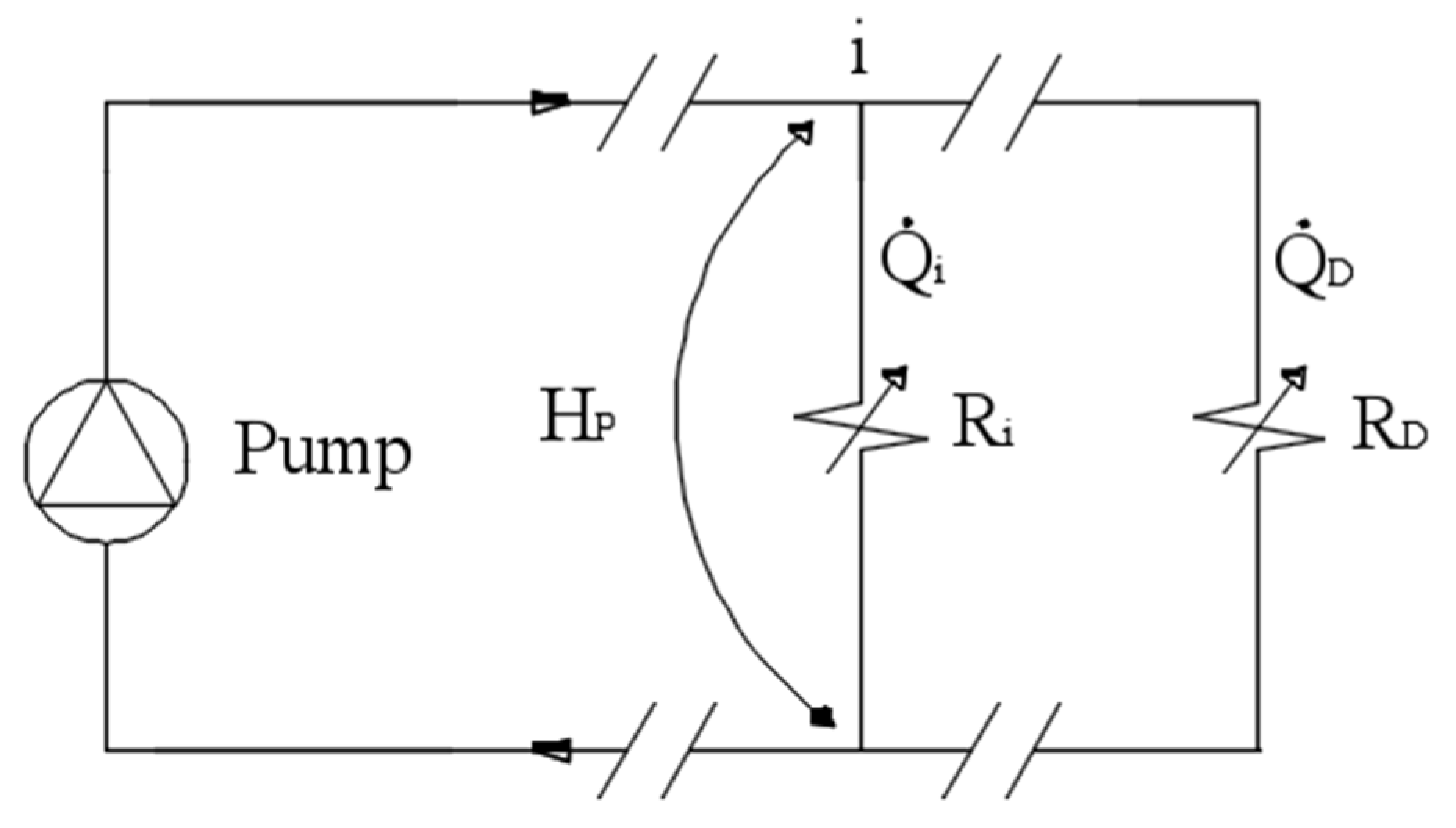
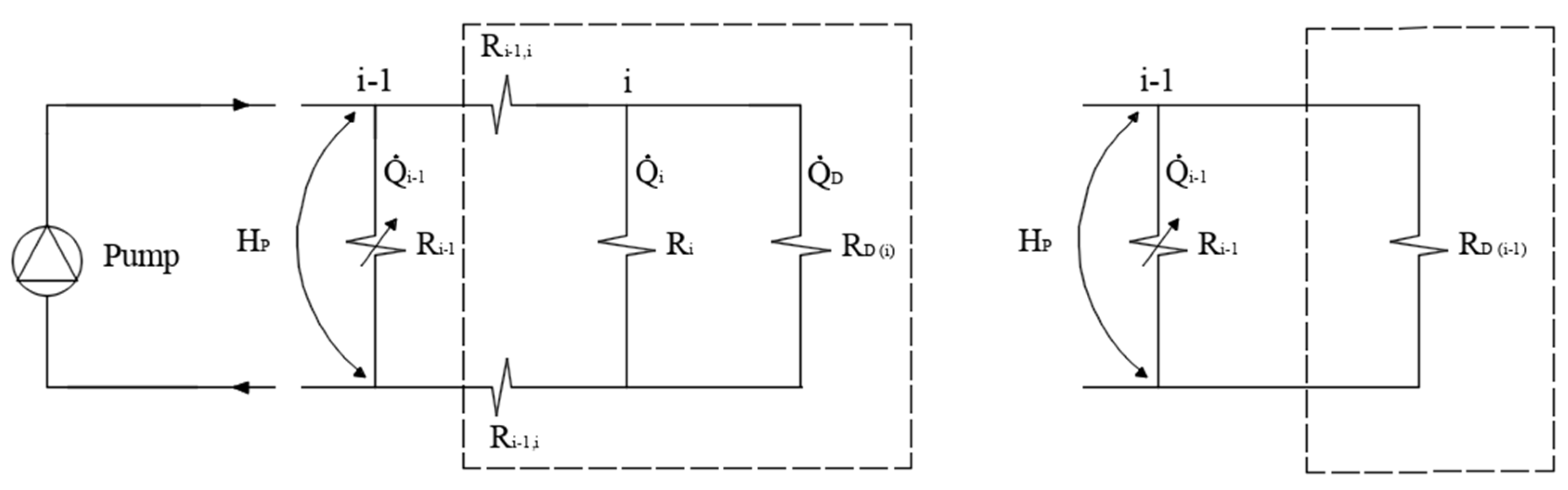
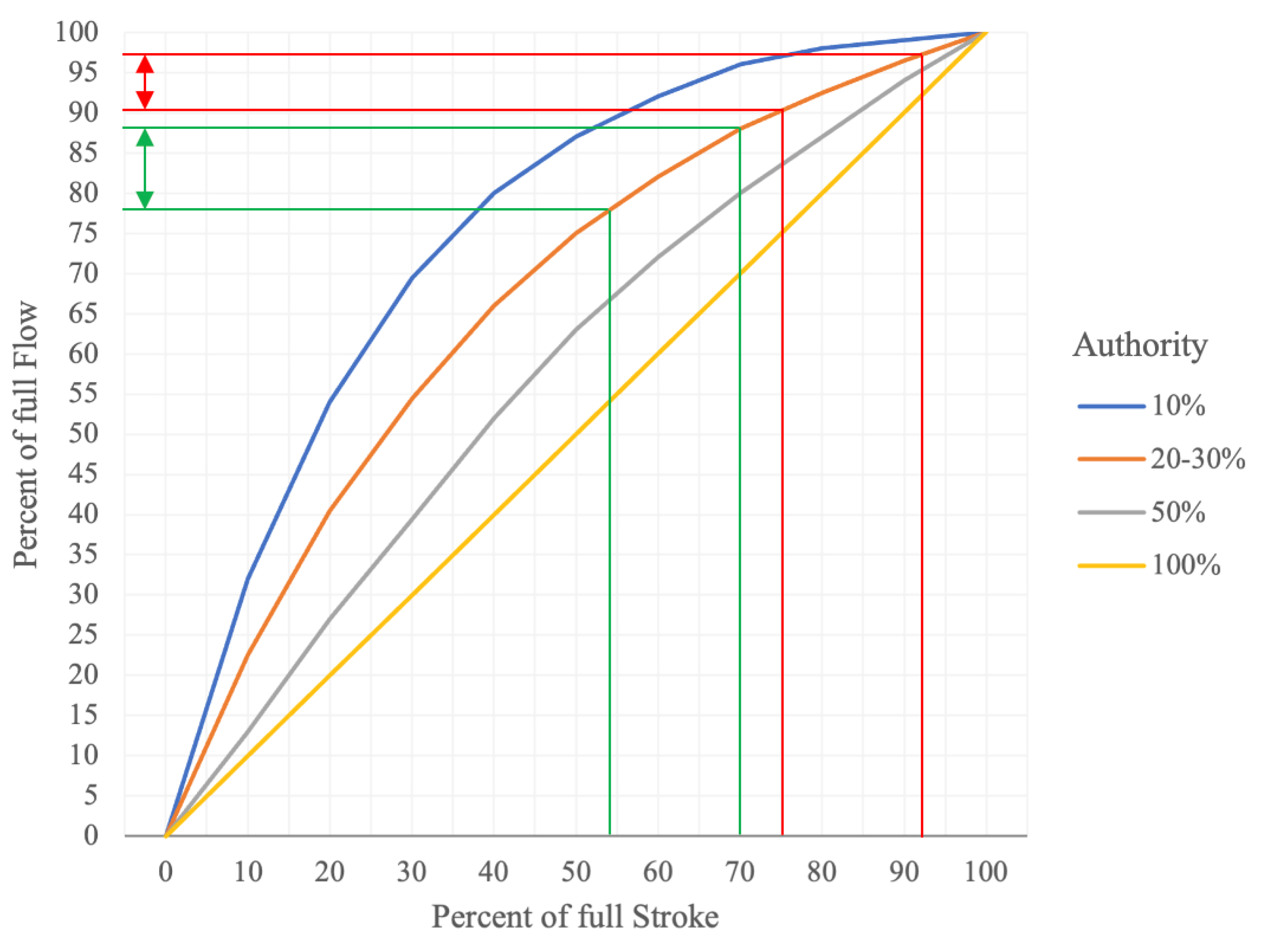
3.1. Progressive Flow Method Theory
- -
- For the series configuration of two components or paths whose loss factors are indicated respectively as Ra and Rb, the following applies:
- -
- For the parallel configuration, the following applies:
- -
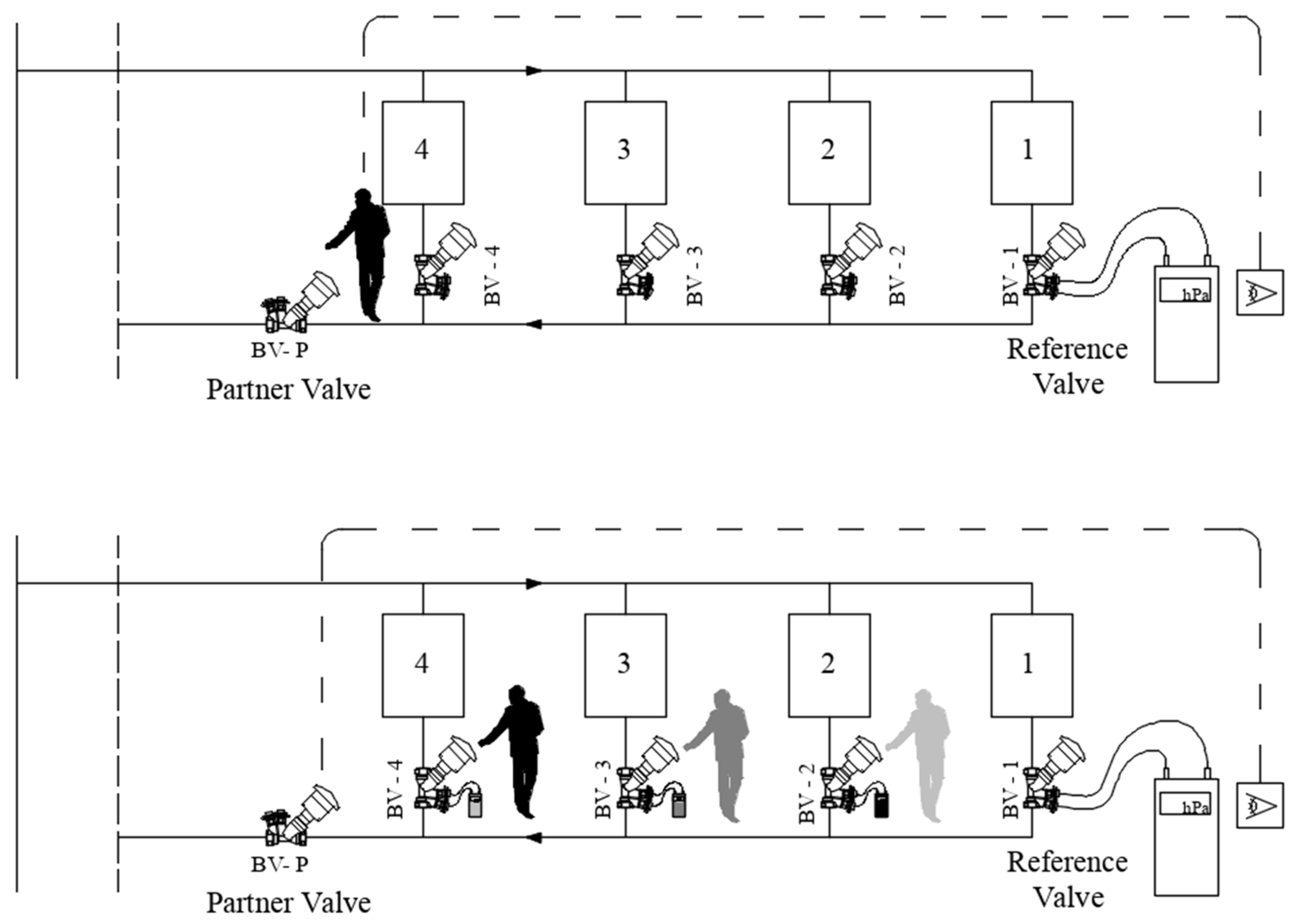
- the procedure starts from the farthest terminal by giving a clear criterion to set the adjustment of its valve position;
- -
- the operator moves backwards and just one terminal at a time is involved;
- -
- a specific control is introduced in order to keep downward (already adjusted) quantities (flow rates and valve positions) unchanged.
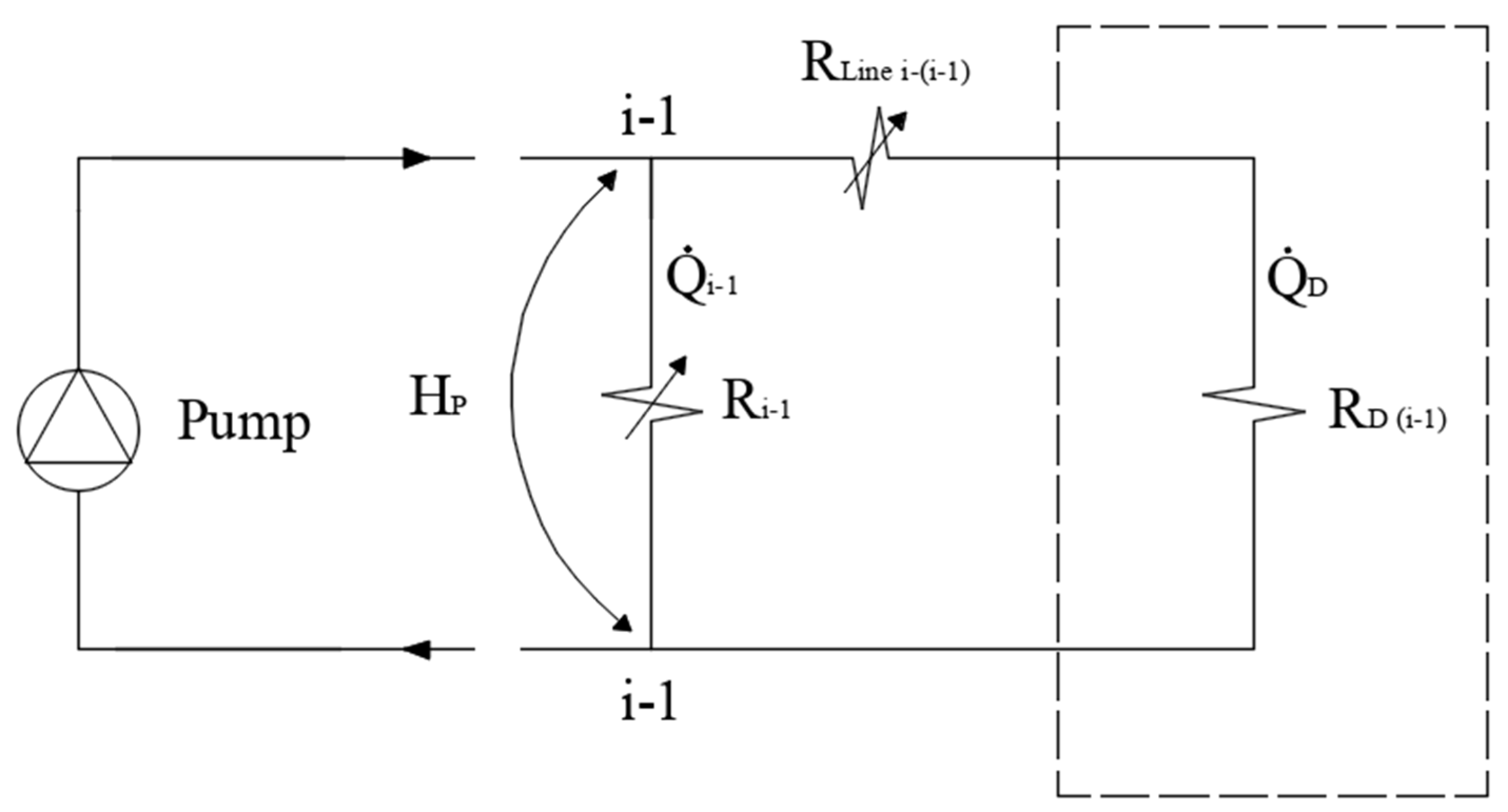
3.2. Management of Cases Where the Farthest Terminal Is Not the Most Disadvantaged
3.3. Optimization of the Number of Flow Meters and Measurements
- -
- on the farthest terminal in direct return configurations (provided that the line valves are installed where needed);
- -
- on the most disadvantaged terminal in reverse return configurations (see Appendix B);
- -
- on the manifold itself in manifold-based configurations (see Appendix B).
- (1)
- Consistency: the variation in flow rate resulting from the activation of any terminal can be detected at the considered measuring point;
- (2)
- Resolution: the range and the resolution of the instrument installed at the control point are suitable for the acquisition of the total flow rate supplied to the portion of the system under balancing and for the correct detection of each increasing step, respectively.
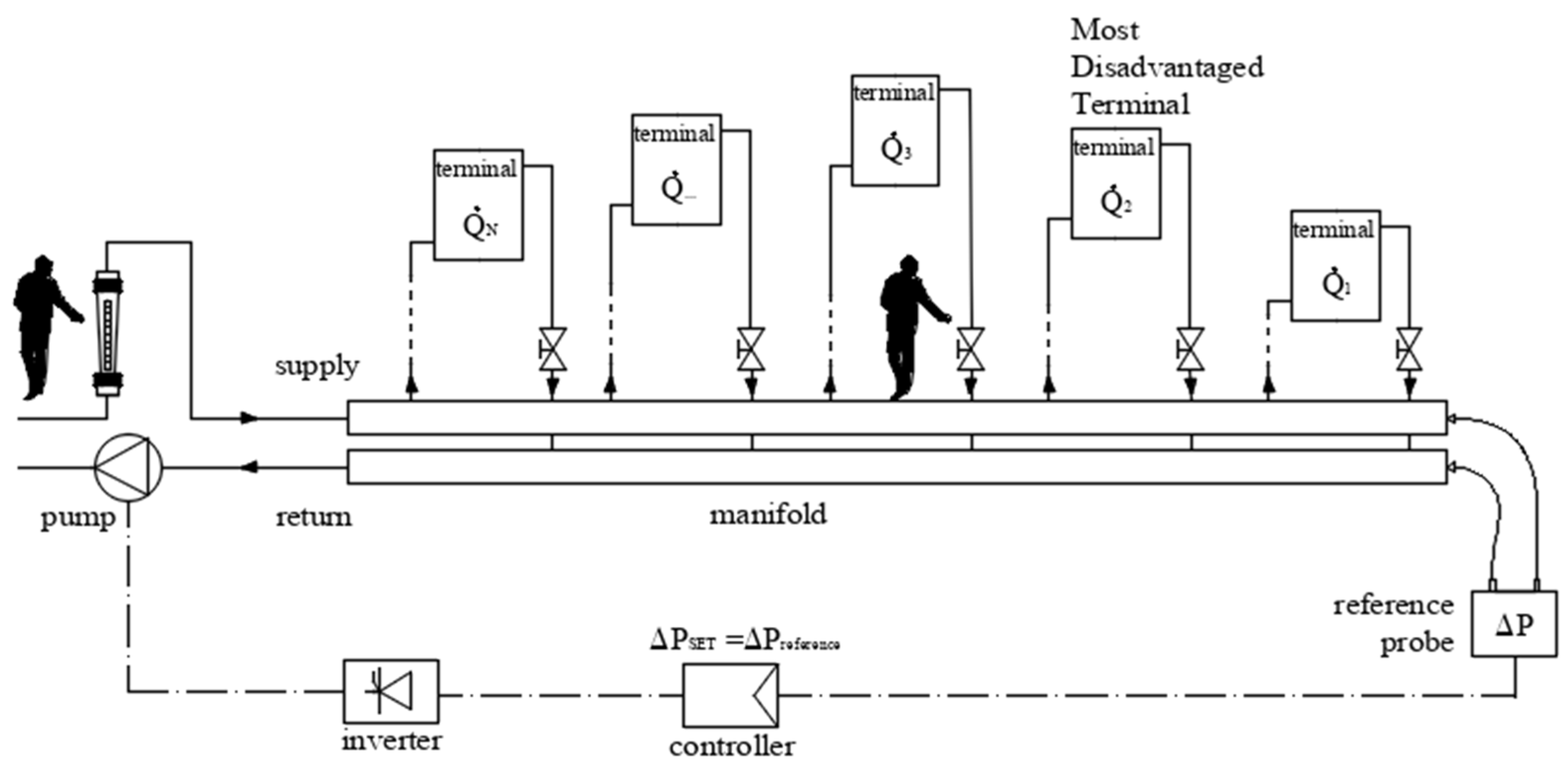
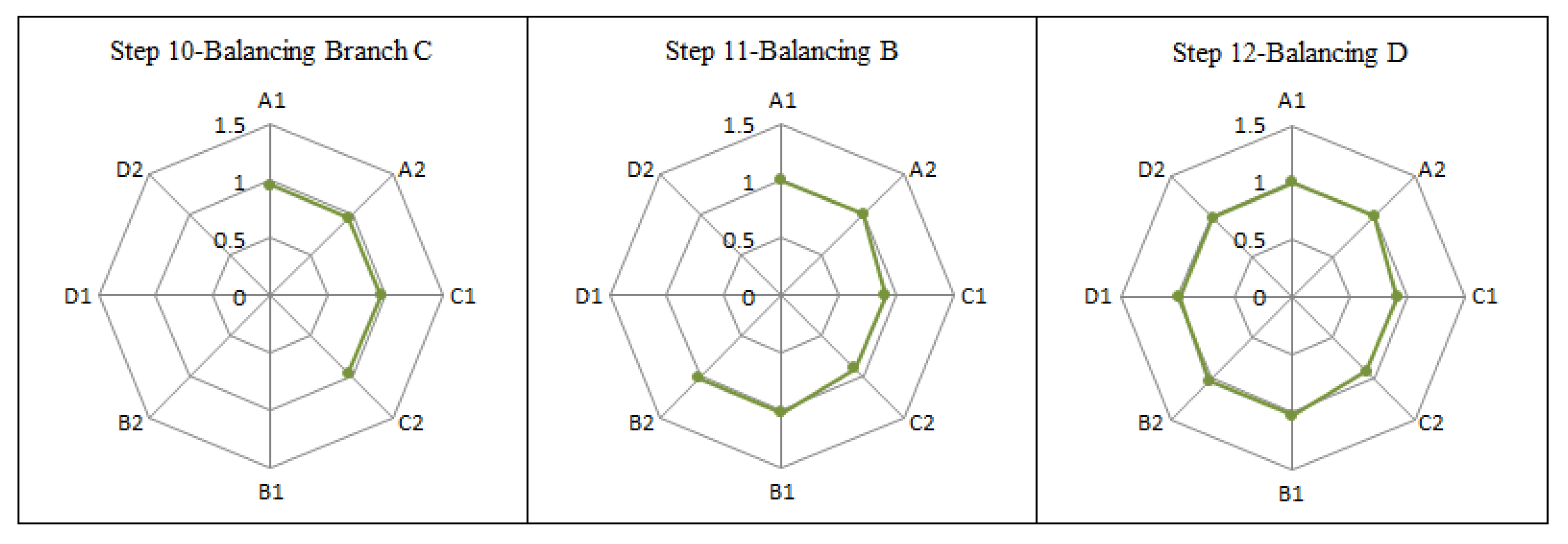
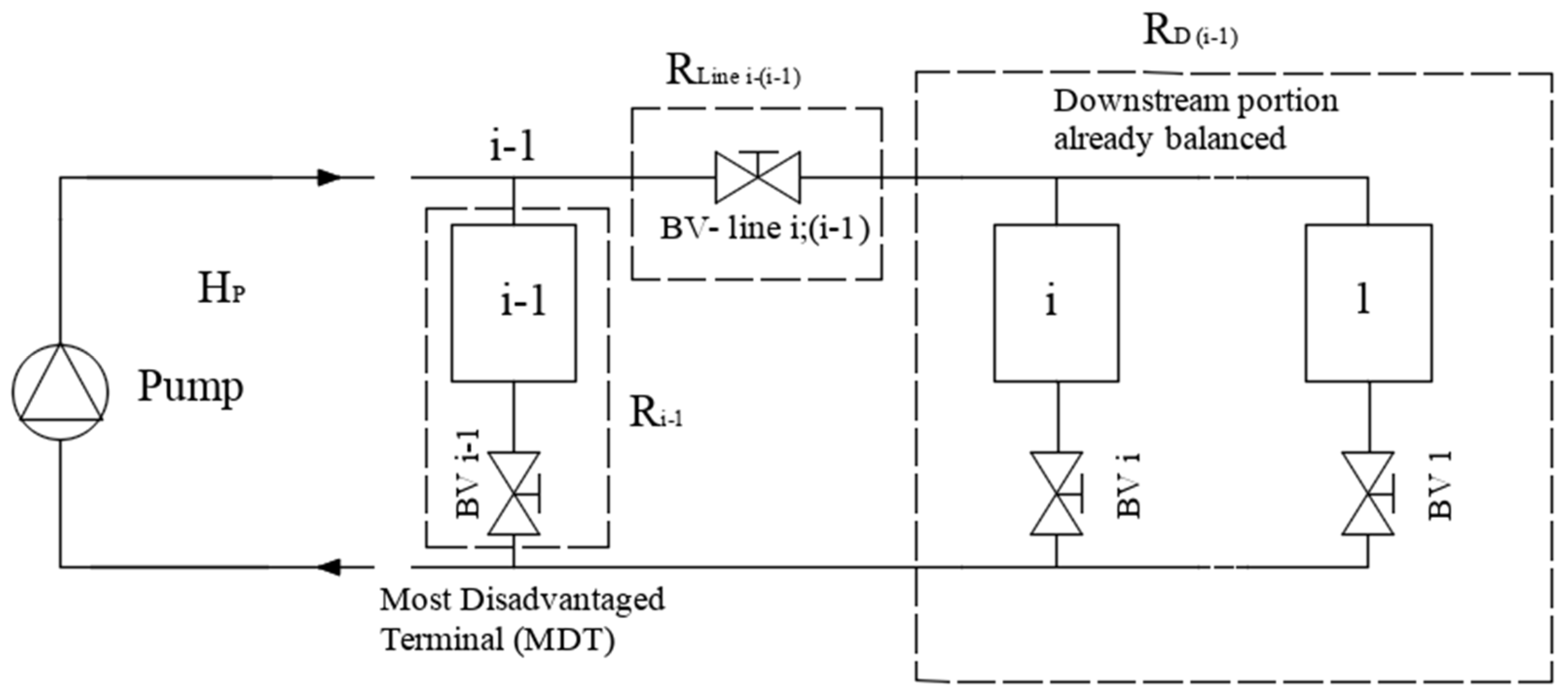
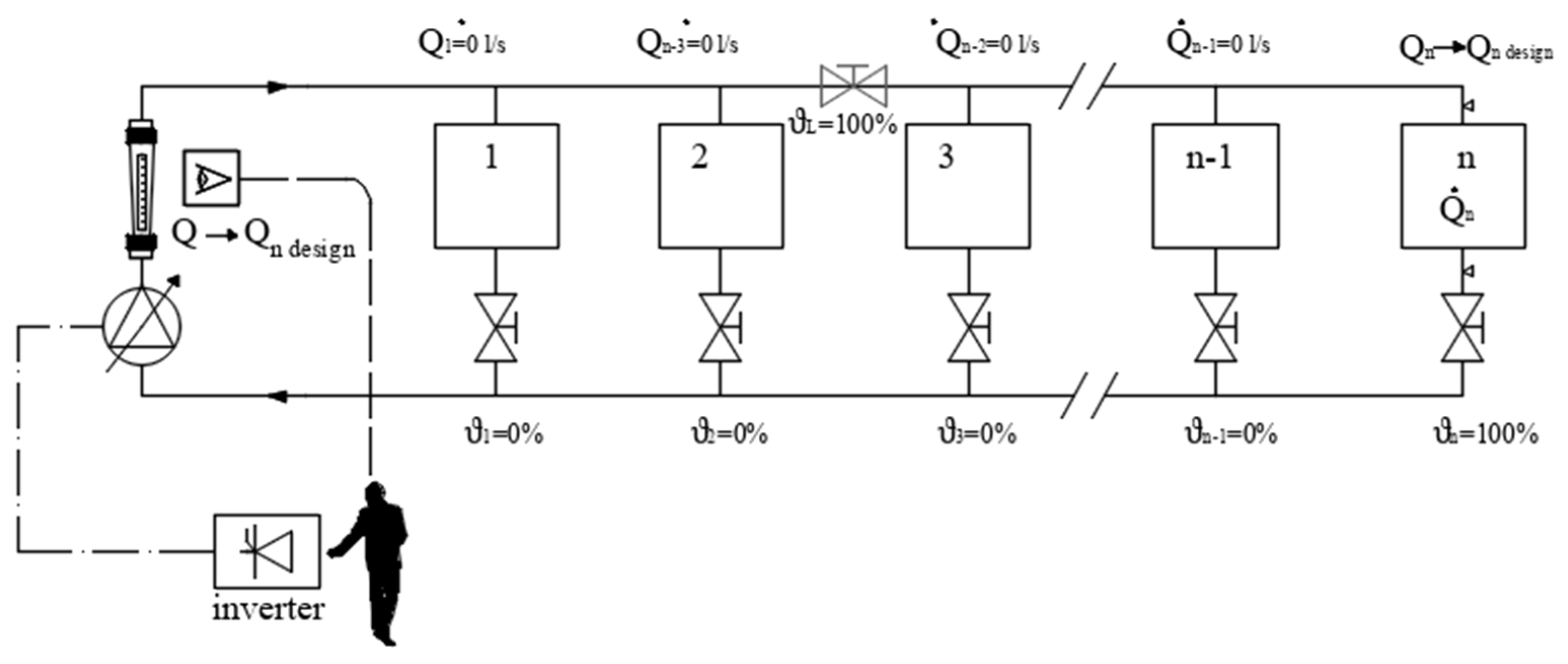
3.4. PFM Balancing Procedure
- -
- take note of the final speed reached with the setting of the last terminal/branch;
- -
- remove the reference pressure control loop;
- -
- set the registered speed as the operating speed of the pump;
- -
- check that the power consumption and the working point are consistent with the pump manufacturer’s specifications.
3.5. Experimental Validation
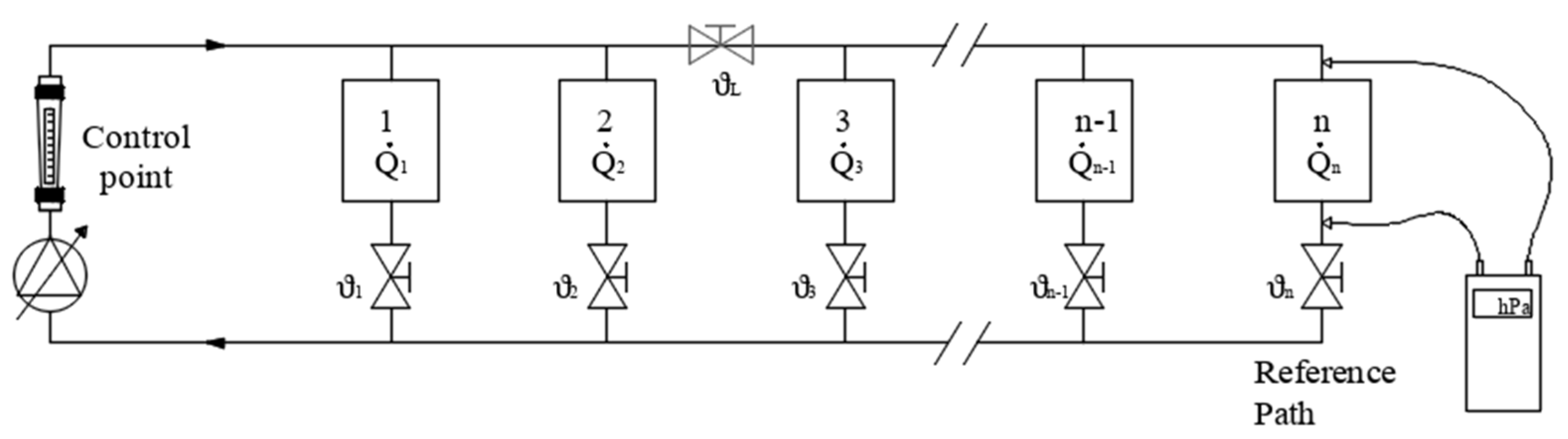
3.5.1. Test Rig Description
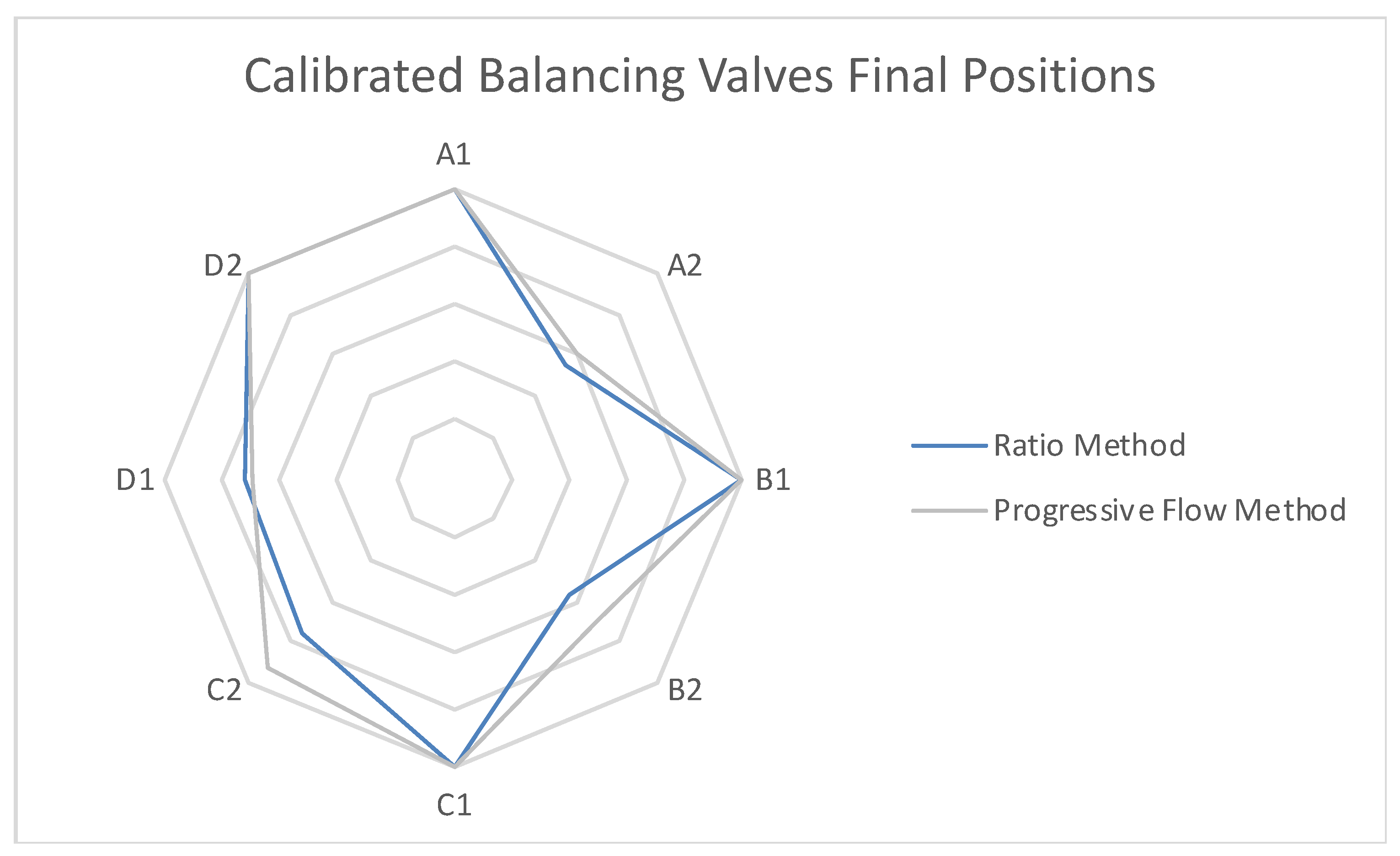
3.5.2. Comparison between Ratio Method and PFM
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |
| CWV | constant water volume system |
| VWV | variable water volume system |
| TAB | testing, adjusting, and balancing procedure |
| CM | compensated method |
| PFM | progressive flow method |
| RM | ratio (or proportional) method |
| SM | stepwise method |
| MD | most disadvantaged (referred to a path or a terminal) |
| CBV | calibrated balancing valve |
| MBV | motorized balancing valve coupled with ultrasonic flow meter |
| Nmeas | overall count of measuring operations (including moving probes, setting up control loop) |
| Nbal | overall count of balancing operations (including adjusting valves and pump speed setting) |
| Nomenclature | |
| flow rate [m−3·s−1] [l·s−1] [l·h−1] | |
| ΔP | pressure drop [Pa] [kPa] |
| ΔT | difference in temperature [K] |
| ΔH, HP | pump head pressure [Pa] [kPa] |
| R | loss factor [Pa·s2·m−6] |
| f | friction factor—dimensionless |
| k | loss coefficient—dimensionless |
| Nmeas | number of measurement readings |
| Nbal | number of balancing operations |
| Subscripts | |
| S | Series |
| P | parallel |
| D | downstream |
| i | refers to the ith component, path, value |
Appendix A. Proportional Method and Step Wise Method Description
Appendix A.1. Traditional Balancing Methods Procedure
Appendix A.2. Proportional Method (Also Referred to as Ratio Method)
Appendix A.3. Stepwise Method
Appendix B. Analysis of Cases Where the Farthest Terminal Is Not the Most Disadvantaged
Appendix B.1. Manifold-Based and Reverse Return Cases
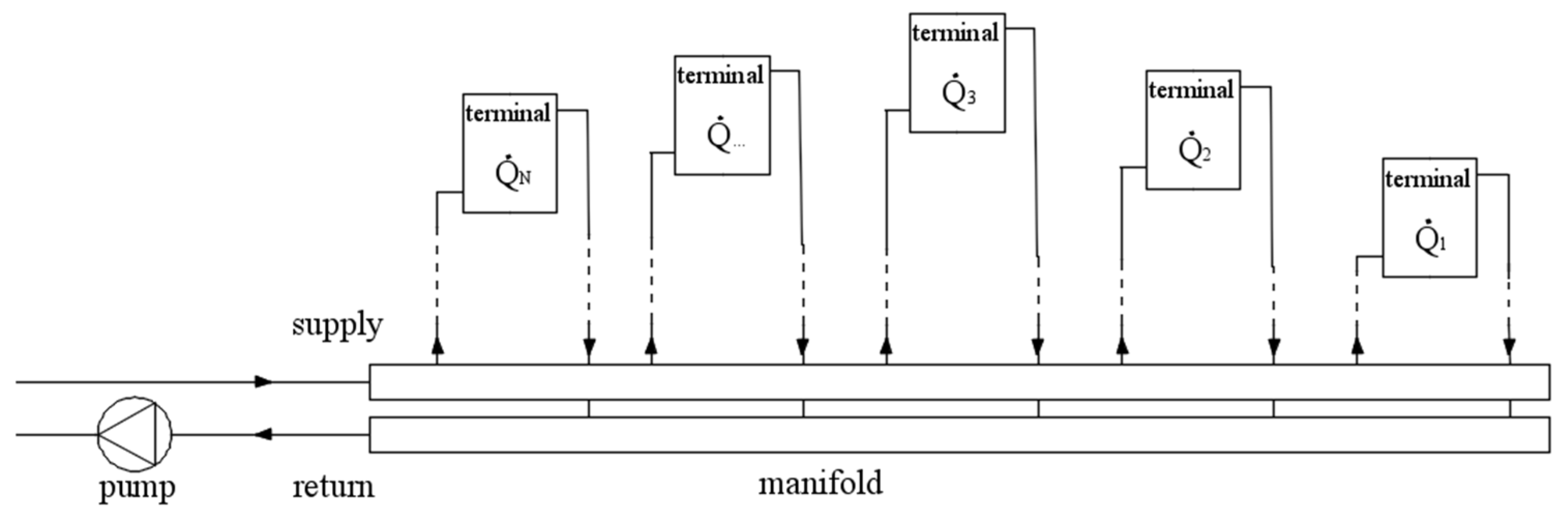
Appendix B.2. Determination of the MD Terminal in Manifold-Based or Reverse Return Configurations
- (1)
- Having individual flow meters available on each terminal user, it is enough to carry out a preliminary measurement with all valves fully open. The most disadvantaged terminal can be found by calculating the characteristic ratio for each path and choosing the one with the lowest value as commonly practiced when using the traditional Ratio Method (see Appendix A.2).
- (2)
- Alternatively, by using a single flow meter at the pump, different sub cases must be considered:
- (i)
- if the terminals are same model and size and connected by piping have similar length, there is no reason why the flow can vary, then the MD terminal is by definition the one with the greatest flow rate value, and there’s actually no need for measurements; this case also arises when terminals of the same size have so significant pressure losses that the path’s differences are negligible.
- (ii)
- if the design flow rate values of the users are the same but path lengths are different, the flow rate of each terminal can be measured by running the pump at a constant speed and fully opening/measuring only one path at a time closing the others. The calculation of the ratio allows the terminals to be sorted and the MD to be identified.
- (iii)
- if both lengths and flow rates of each path/terminal are different, the previous test, to be exhaustive, must be conducted by imposing a constant manifold pressure; this requires a pressure detection across supply and return sections of the manifold. That pressure detection can also be used as pressure reference for control loop in PFM procedure.
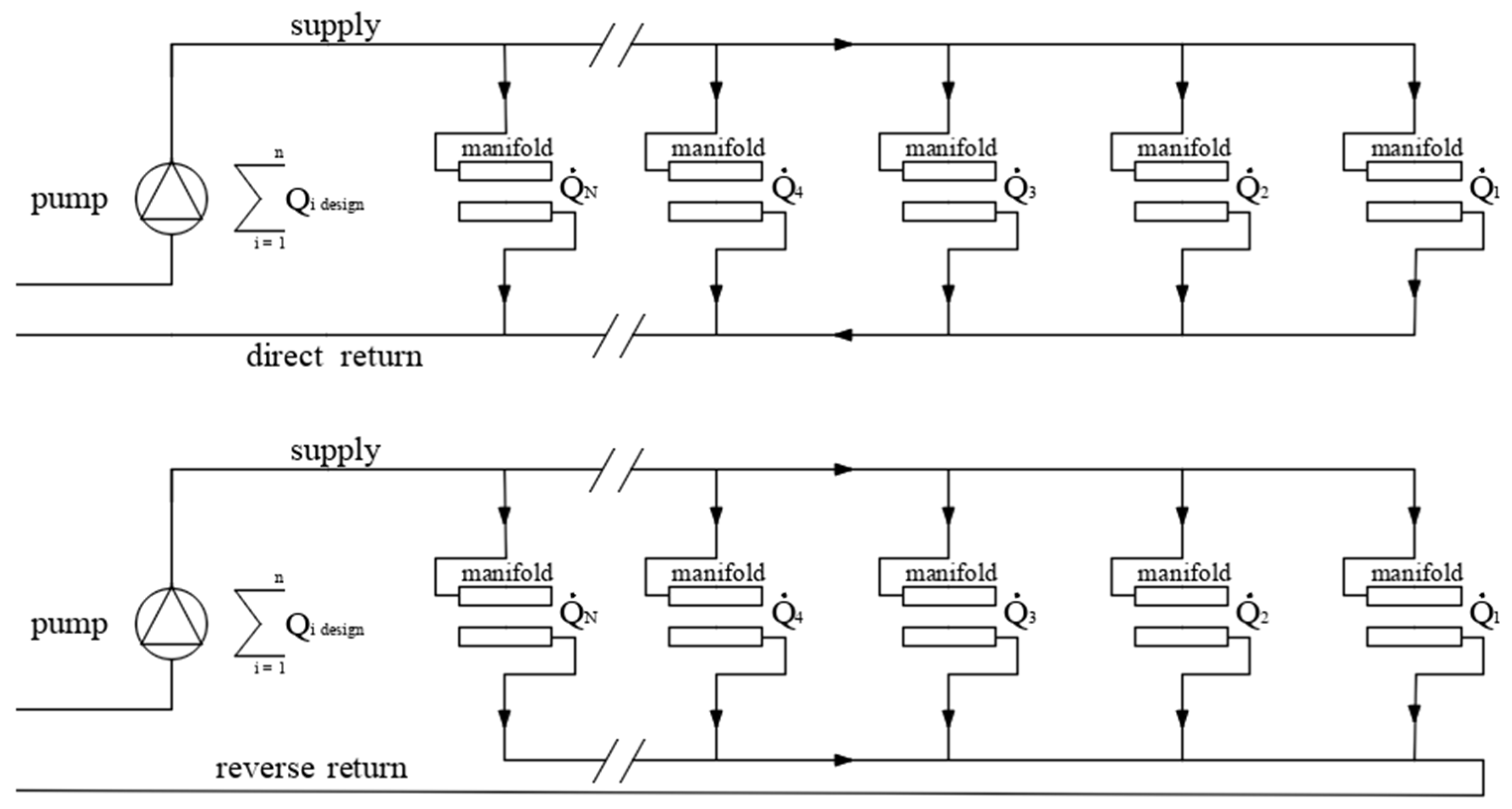
Appendix C. PFM Procedure for Manifold-Based Systems

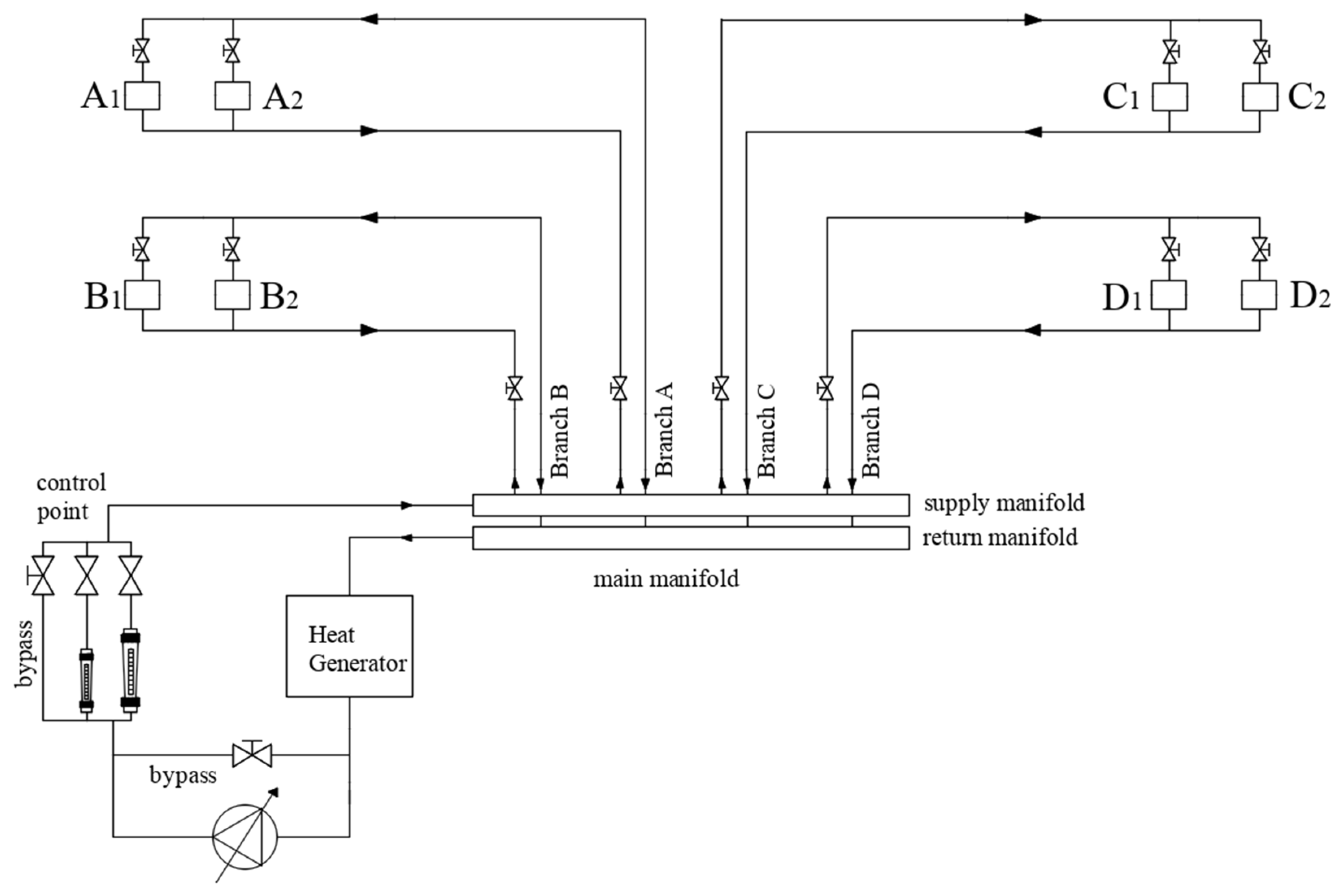
Appendix D. Test Rig Description
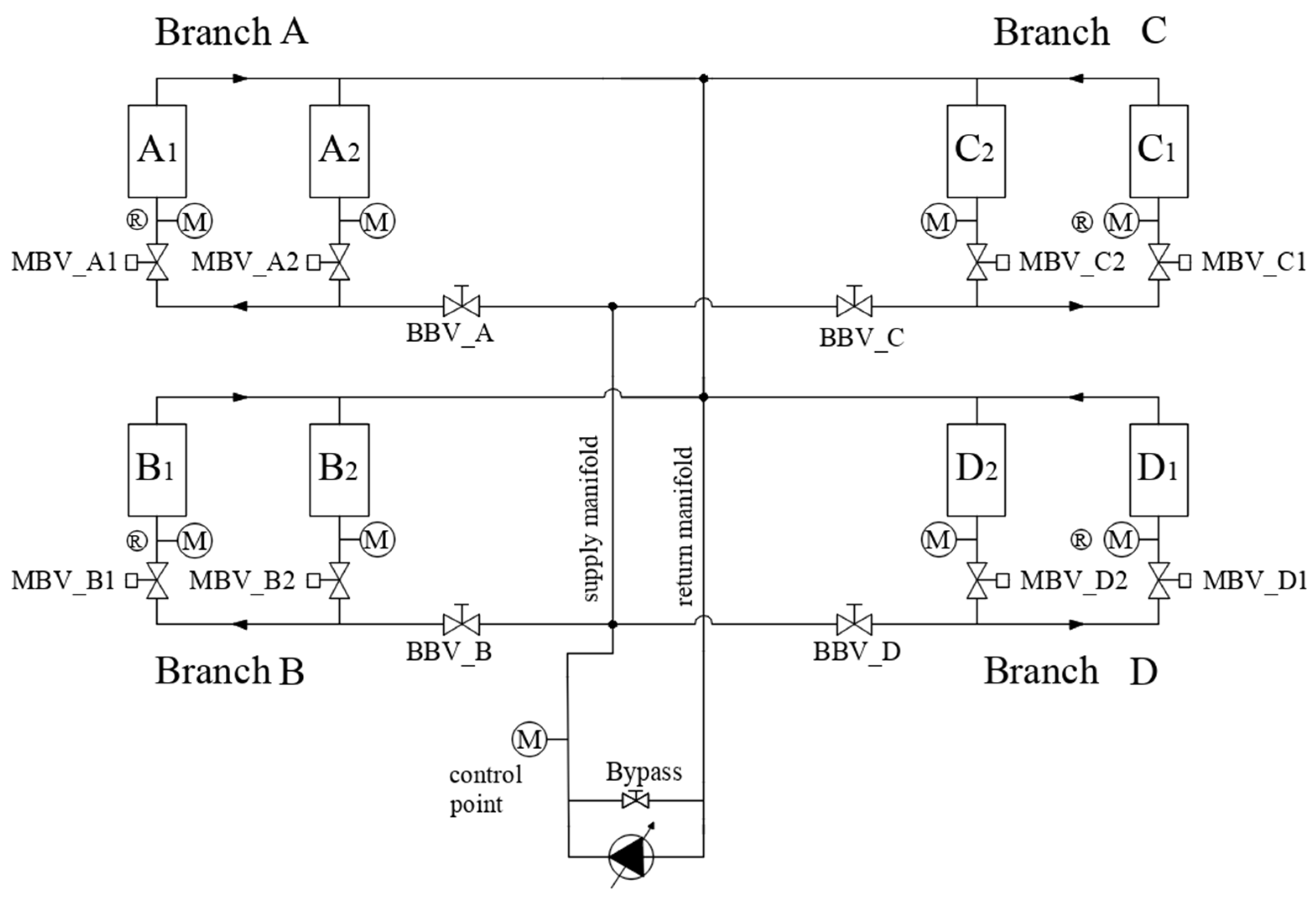
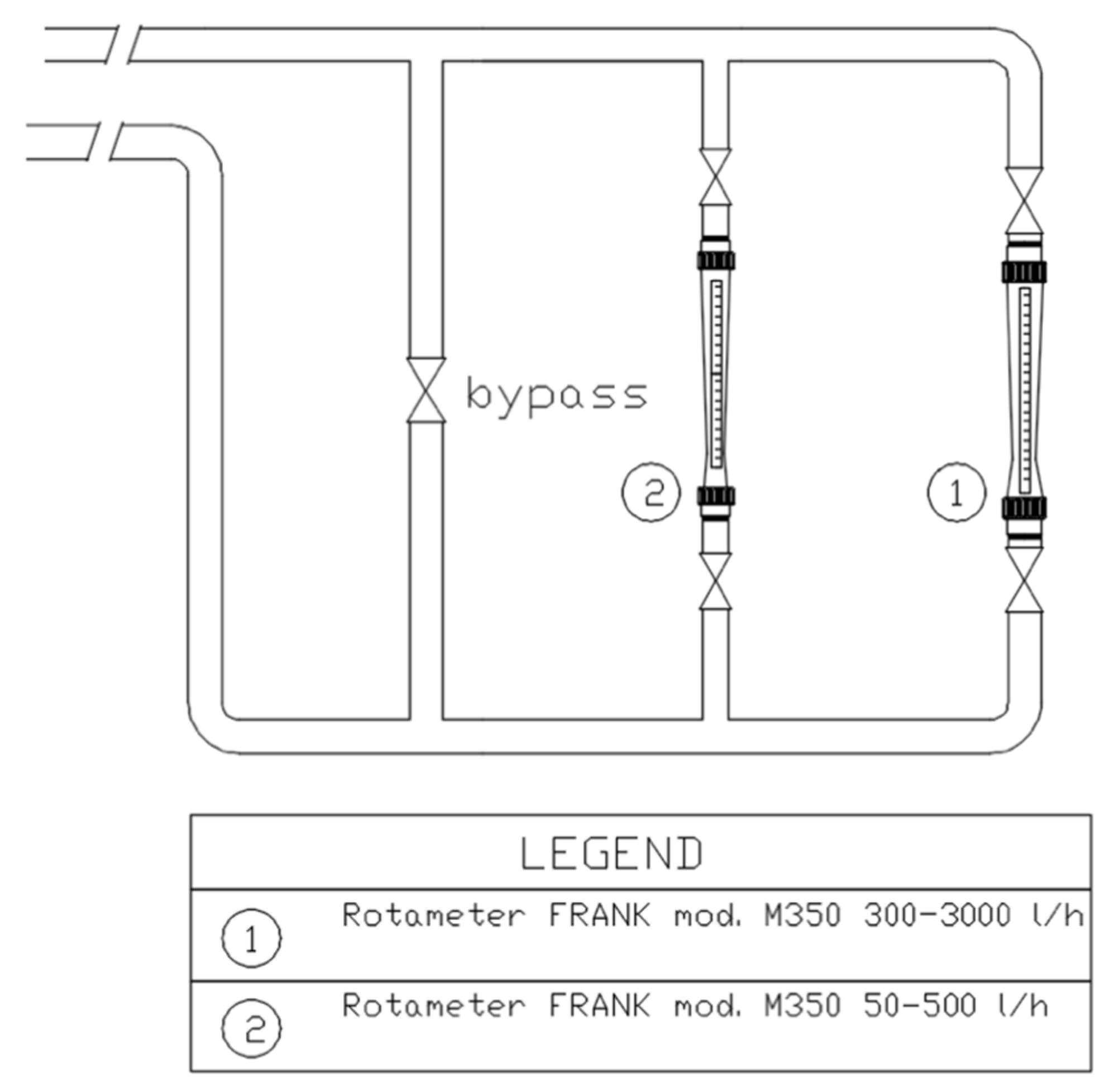
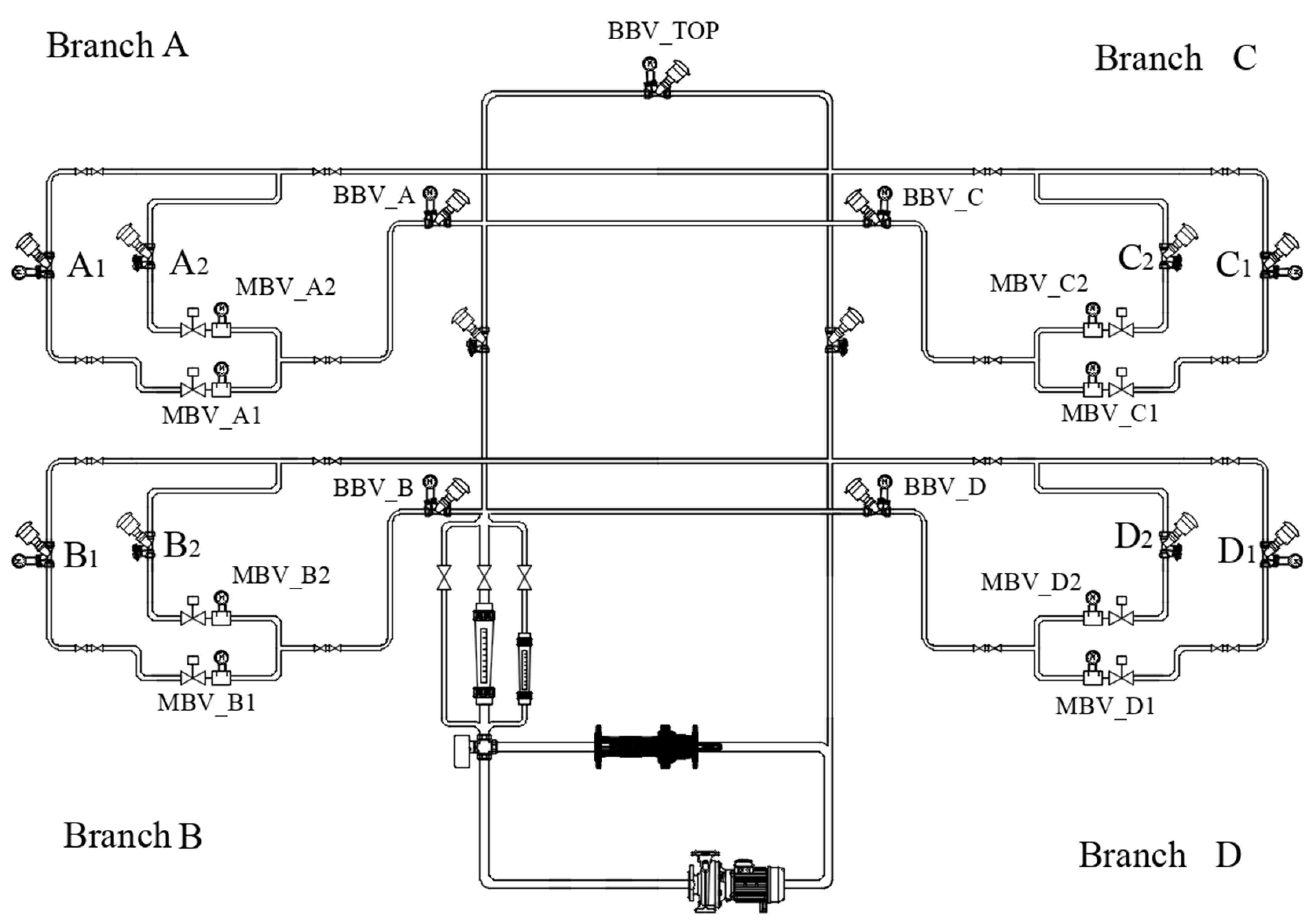
Appendix E. Consistency Check between Rotameters and Ultrasonic Probes
| Branch | Terminal Unit | Flow Rate 33% (400 L/h) | Δ | Flow Rate 66% (800 L/h) | Δ | Flow Rate 100% (1200 L/h) | Δ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rotameter | MBV | [%] | K | Rotameter | MBV | [%} | K | Rotameter | MBV | [%] | K | ||
| A | A1 | 400 | 373 | 6.8 | 0.93 | 800 | 715 | 10.6 | 0.89 | 1200 | 1050 | 12.5 | 0.88 |
| A2 | 400 | 383 | 4.3 | 0.96 | 800 | 730 | 8.8 | 0.91 | 1200 | 1085 | 9.6 | 0.90 | |
| B | B1 | 400 | 377 | 5.8 | 0.94 | 800 | 715 | 10.6 | 0.89 | 1200 | 1085 | 9.6 | 0.90 |
| B2 | 400 | 380 | 5.0 | 0.95 | 800 | 730 | 8.8 | 0.91 | 1200 | 1088 | 9.3 | 0.91 | |
| C | C1 | 400 | 384 | 4.0 | 0.96 | 800 | 728 | 9.0 | 0.91 | 1200 | 1097 | 8.6 | 0.91 |
| C2 | 400 | 382 | 4.5 | 0.96 | 800 | 719 | 10.1 | 0.90 | 1200 | 1071 | 10.8 | 0.89 | |
| D | D1 | 400 | 381 | 4.8 | 0.95 | 800 | 725 | 9.4 | 0.91 | 1200 | 1083 | 9.8 | 0.90 |
| D2 | 400 | 383 | 4.3 | 0.96 | 800 | 732 | 8.5 | 0.92 | 1200 | 1093 | 8.9 | 0.91 | |
| Average | 400 | 380 | 4.9 | 0.95 | 800 | 724.2 | 9.5 | 0.91 | 1200 | 1082 | 9.9 | 0.901 | |
| Asameter: Frank M350 (300–3000 L/h) | |||||||||||||
| MBV: Belimo EPIV DN 15 (300–1200 L/h) | |||||||||||||
Appendix F
Appendix F.1. Application of the Ratio Method (RM) Procedure
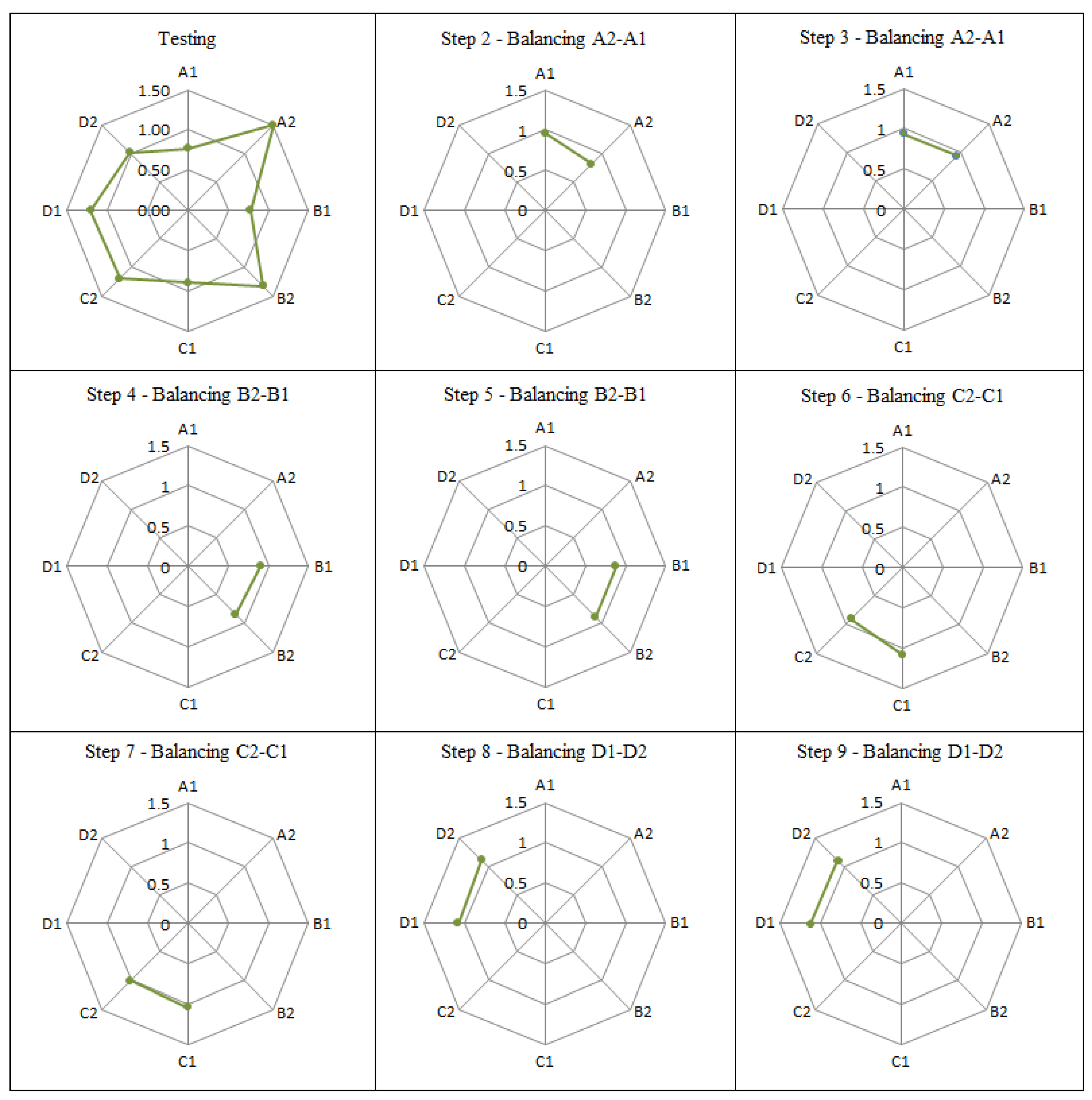

Appendix F.2. Application of the Progressive Flow Method (PFM) Procedure

References
- Directive (EU) 2024/1275 of The European Parliament and of the Council on Energy Performance of Buildings—EPBD; EUR: Rome, Italy, 2024.
- ISO/TC 205, CEN/TC 247, ISO 52120-1:2021; Energy Performance of Buildings—Contribution of Building Automation, Controls and Building Management. Part 1: General Framework and Procedures. ISO: Geneva, Switzerland, 2022.
- Taylor, S.T.; Stein, J. Balancing variable flow hydronic systems. ASHRAE J. 2002, 44, 17–24. [Google Scholar]
- Cholewa, T.; Siuta-Olcha, A.; Balaras, C.A. Actual energy savings from the use of thermostatic radiator valves in residential buildings—Long term field evaluation. Energy Build. 2017, 151, 487–493. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, J.; Thorsen, J.E.; Gudmundsson, O.; Li, H.; Svendsen, S. Method for achieving hydraulic balance in typical Chinese building heating systems by managing differential pressure and flow. Build. Simul. 2017, 10, 51–63. [Google Scholar] [CrossRef]
- Sarran, L.; Smith, K.M.; Hviid, C.A.; Rode, C. Grey-box modelling and virtual sensors enabling continuous commissioning of hydronic floor heating. Energy 2022, 261, 125282. [Google Scholar] [CrossRef]
- Fine, J.P.; Touchie, M.F. A grouped control strategy for the retrofit of post-war multi-unit residential building hydronic space heating systems. Energy Build. 2020, 208, 109604. [Google Scholar] [CrossRef]
- Khamesi, S.S.; Yousefi, H.; Behrouz, B. The Effect of Flow Balance on the Reduction of Life Cycle Cost in Hydronic Networks. J. Energy Manag. Technol. 2024, 8, 93–103. [Google Scholar]
- Henze, G.P.; Floss, A.G. Evaluation of temperature degradation in hydraulic flow networks. Energy Build. 2011, 43, 1820–1828. [Google Scholar] [CrossRef]
- Averfalk, H.; Werner, S. Essential improvements in future district heating systems. Energy Procedia 2017, 116, 217–225. [Google Scholar] [CrossRef]
- Zhang, L.; Gudmundsson, O.; Thorsen, J.E.; Li, H.; Li, X.; Svendsen, S. Method for reducing excess heat supply experienced in typical Chinese district heating systems by achieving hydraulic balance and improving indoor air temperature control at the building level. Energy 2016, 107, 431–442. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Zhu, T. A new hydraulic regulation method on district heating system with distributed variable-speed pumps. Energy Convers. Manag. 2017, 147, 174–189. [Google Scholar] [CrossRef]
- Ashfaq, A.; Ianakiev, A. Investigation of hydraulic imbalance for converting existing boiler based buildings to low temperature district heating. Energy 2018, 160, 200–212. [Google Scholar] [CrossRef]
- Che, Z.; Sun, J.; Na, H.; Yuan, Y.; Qiu, Z.; Du, T. A novel method for intelligent heating: On-demand optimized regulation of hydraulic balance for secondary networks. Energy 2023, 282, 128900. [Google Scholar] [CrossRef]
- Bava, F.; Furbo, S. A numerical model for pressure drop and flow distribution in a solar collector with U-connected absorber pipes. Sol. Energy 2016, 134, 264–272. [Google Scholar] [CrossRef]
- Gomariz, F.P.; López, J.M.C.; Muñoz, F.D. An analysis of low flow for solar thermal system for water heating. Sol. Energy 2019, 179, 67–73. [Google Scholar] [CrossRef]
- De Rosa, R.; Romagnuolo, L.; Frosina, E.; Belli, L.; Senatore, A. Validation of a Lumped Parameter Model of the Battery Thermal Management System of a Hybrid Train by Means of Ultrasonic Clamp-On Flow Sensor Measurements and Hydronic Optimization. Sensors 2023, 23, 390. [Google Scholar] [CrossRef] [PubMed]
- Hámori, S.; Kalmár, F. Hydraulic balancing analysis of a central heating system with constant supply temperature. Environ. Eng. Manag. J. 2014, 13, 2789–2795. [Google Scholar] [CrossRef]
- Ryu, S.-R.; Rhee, K.-N.; Yeo, M.-S.; Kim, K.-W. Strategies for flow rate balancing in radiant floor heating systems. Build. Res. Inf. 2008, 36, 625–637. [Google Scholar] [CrossRef]
- Cho, H.-I.; Cabrera, D.; Patel, M.K. Estimation of energy savings potential through hydraulic balancing of heating systems in buildings. J. Build. Eng. 2020, 28, 101030. [Google Scholar] [CrossRef]
- Cho, H.; Cabrera, D.; Patel, M.K. Identification of criteria for the selection of buildings with elevated energy saving potentials from hydraulic balancing-methodology and case study. Adv. Build. Energy Res. 2022, 16, 427–444. [Google Scholar] [CrossRef]
- Cholewa, T.; Balen, I.; Siuta-Olcha, A. On the influence of local and zonal hydraulic balancing of heating system on energy savings in existing buildings—Long term experimental research. Energy Build. 2018, 179, 156–164. [Google Scholar] [CrossRef]
- Petitjean, R. Total Hydronic Balancing, 3rd ed.; Tour & Andersson AB: Ljung, Sweden, 2012. [Google Scholar]
- Magyar, Z. Hydronic balancing in theory and practice. In Proceedings of the 7th REHVA World Congress, Naples, Italy, 15–18 September 2001; pp. 45–53. [Google Scholar]
- CIBSE Commissioning Code W. Chapter 7—Balancing and regulating water flow rates. In Water Distribution Systems; CIBSE (Chartered Institution of Building Services Engineers): London, UK, 2010. [Google Scholar]
- Pedranzini, F.; Colombo, L.P.M.; Joppolo, C.M. A non-iterative method for Testing, Adjusting and Balancing (TAB) air ducts systems: Theory, practical procedure and validation. Energy Build. 2013, 65, 322–330. [Google Scholar] [CrossRef]
- Tamminen, J.; Ahonen, T.; Ahola, J.; Hammo, S. Fan pressure-based testing, adjusting, and balancing of a ventilation system. Energy Effic. 2016, 9, 425–433. [Google Scholar] [CrossRef]
- Std.111/2008; Measurements, Testing, Adjusting and Balancing of Building HVAC Systems. ANSI/ASHRAE: Peachtree Corners, GA, USA, 2008.
- NEBB. Procedural Standard for Testing, Adjusting and Balancing of Environmental Systems, 8th ed.; NEBB: Gaithersburg, MD, USA, 2015. [Google Scholar]
- American Society of Heating Refrigerating and Air-Conditioning Engineers Inc. (ASHRAE). ASHRAE Handbook—FUNDAMENTALS; ASHRAE: Peachtree Corners, GA, USA, 2021. [Google Scholar]
- Sugarman, S.C. Water Balance Procedures. In Testing and Balancing HVAC Air and Water Systems; The Fairmont Press: Atlanta, GA, USA, 2014; pp. 2023–2024. Available online: http://ebookcentral.proquest.com/lib/polimi/detail.action?docID=3239082.https://ebookcentral.proquest.com/lib/polimi/detail.action?docID=3239082 (accessed on 9 January 2023).
- ASHRAE. Chapter 39—Testing, Adjusting and Balancing. In ASHRAE Handbook—HVAC Applications; American Society of Heating: Atlanta, GA, USA, 2023. [Google Scholar]
- BSRIA. BBG02/10—Commissioning Water Systems; BSRIA: Berkshire, UK, 2010. [Google Scholar]



| Instrument | Model | Measuring Range | Accuracy |
|---|---|---|---|
| Ultrasonic flow meters at terminals | Belimo electronic valves mod. EP015R | 0–1200 L/h | 6% of the reading value ranging from 25% to 100% of the measuring range. |
| Rotameter flow meters at the pump | Frank mod. M350 | 50 ÷ 500 L/h | 8% of measured value for flow rates between 20% and 100% of measuring range according to VDE/DIN 3531. |
| 300 ÷ 3000 L/h | |||
| Pressure probes | Thermokon mod. DPL1V | 0 ÷ 1 Bar | Declared accuracy 1%, resolution 0.2 kPa. |
| Branch | Terminal Unit | H/C Capacity | User ΔP | Flow Rate | TU Valve Position | |
|---|---|---|---|---|---|---|
| [W] | [kPa] | l/h | l/s | Reference | ||
| A | A1 | 1149 | 29.21 | 200 | 0.06 | 0.6 |
| A2 | 1724 | 5.01 | 300 | 0.08 | 3 | |
| B | B1 | 1724 | 5.01 | 300 | 0.08 | 3 |
| B2 | 2011 | 6.82 | 350 | 0.10 | 3 | |
| C | C1 | 1437 | 6.51 | 250 | 0.07 | 2.5 |
| C2 | 2299 | 5.54 | 400 | 0.11 | 3.5 | |
| D | D1 | 1724 | 5.01 | 300 | 0.08 | 3 |
| D2 | 2874 | 5.95 | 500 | 0.14 | 4 | |
| Design Data | Ratio Method | Progressive Flow Method | |||||
|---|---|---|---|---|---|---|---|
| Terminal Unit | Design Flow Rate [l/h] | Valve Opening [%] | Final Pump Speed | Flow Rate Sum of MBV [l/h] | Valve Opening [%] | Final Pump Speed | Flow Rate Rotameter [l/h] |
| A1 | 200 | 100% | 85% | 2622 | 100% | 80% | 2600 |
| A2 | 300 | 55% | 60% | ||||
| B1 | 300 | 100% | 100% | ||||
| B2 | 350 | 56% | 70% | ||||
| C1 | 250 | 100% | 100% | ||||
| C2 | 400 | 75% | 92% | ||||
| D1 | 300 | 73% | 70% | ||||
| D2 | 500 | 100% | 100% | ||||
| Total | 2600 | - | - | ||||
| N | Ratio Method | PFM | Difference |
|---|---|---|---|
| Nmeas | 27 | 14 | −48% |
| Nbal | 22 | 13 | −41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedranzini, F.; Colombo, L.P.M.; Romano, F. Development and Application of a Novel Non-Iterative Balancing Method for Hydronic Systems. Appl. Sci. 2024, 14, 6232. https://doi.org/10.3390/app14146232
Pedranzini F, Colombo LPM, Romano F. Development and Application of a Novel Non-Iterative Balancing Method for Hydronic Systems. Applied Sciences. 2024; 14(14):6232. https://doi.org/10.3390/app14146232
Chicago/Turabian StylePedranzini, Federico, Luigi P. M. Colombo, and Francesco Romano. 2024. "Development and Application of a Novel Non-Iterative Balancing Method for Hydronic Systems" Applied Sciences 14, no. 14: 6232. https://doi.org/10.3390/app14146232
APA StylePedranzini, F., Colombo, L. P. M., & Romano, F. (2024). Development and Application of a Novel Non-Iterative Balancing Method for Hydronic Systems. Applied Sciences, 14(14), 6232. https://doi.org/10.3390/app14146232







