Non-Ideal Push–Pull Converter Model: Trade-Off between Complexity and Practical Feasibility in Terms of Topology, Power and Operating Frequency
Abstract
1. Introduction
- The definition of a methodology based on the development of a sensitivity analysis that allows to identify the impact and the role that each non-ideality of the converter has on the dynamic and steady-state response of its equivalent model;
- The sensitivity analysis performed allows the identification, proposal and validation of non-ideal models oriented to the control of push–pull converters, considering the trade-off between accuracy and practical application;
- The establishment of cause–effect relationships for each of the non-idealities of the converter with respect to their influence on the accuracy of the model, depending on the converter topology and its operating conditions;
- The identification, proposal and validation of non-ideal committed control-oriented circuits and models for the push–pull converter that combine precision and simplicity (reduced order) based on the proposed methodology and sensitivity analysis;
- Both buck and boost topologies have been analysed under real operating conditions of push–pull converters.
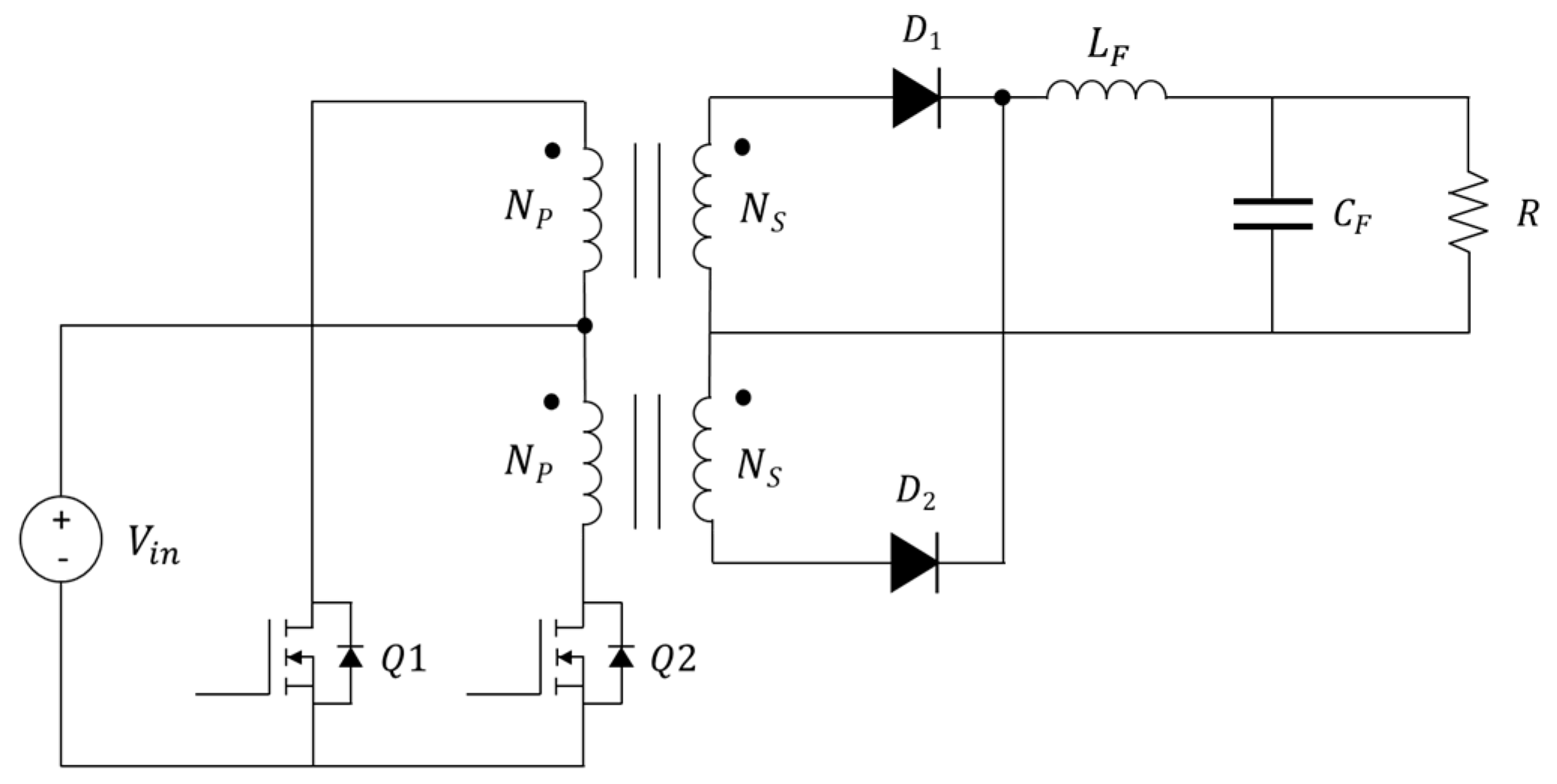
2. Push–Pull Converter: Operating Principle and Non-Ideal Electrical Model
2.1. Push–Pull Converter Operating Principle
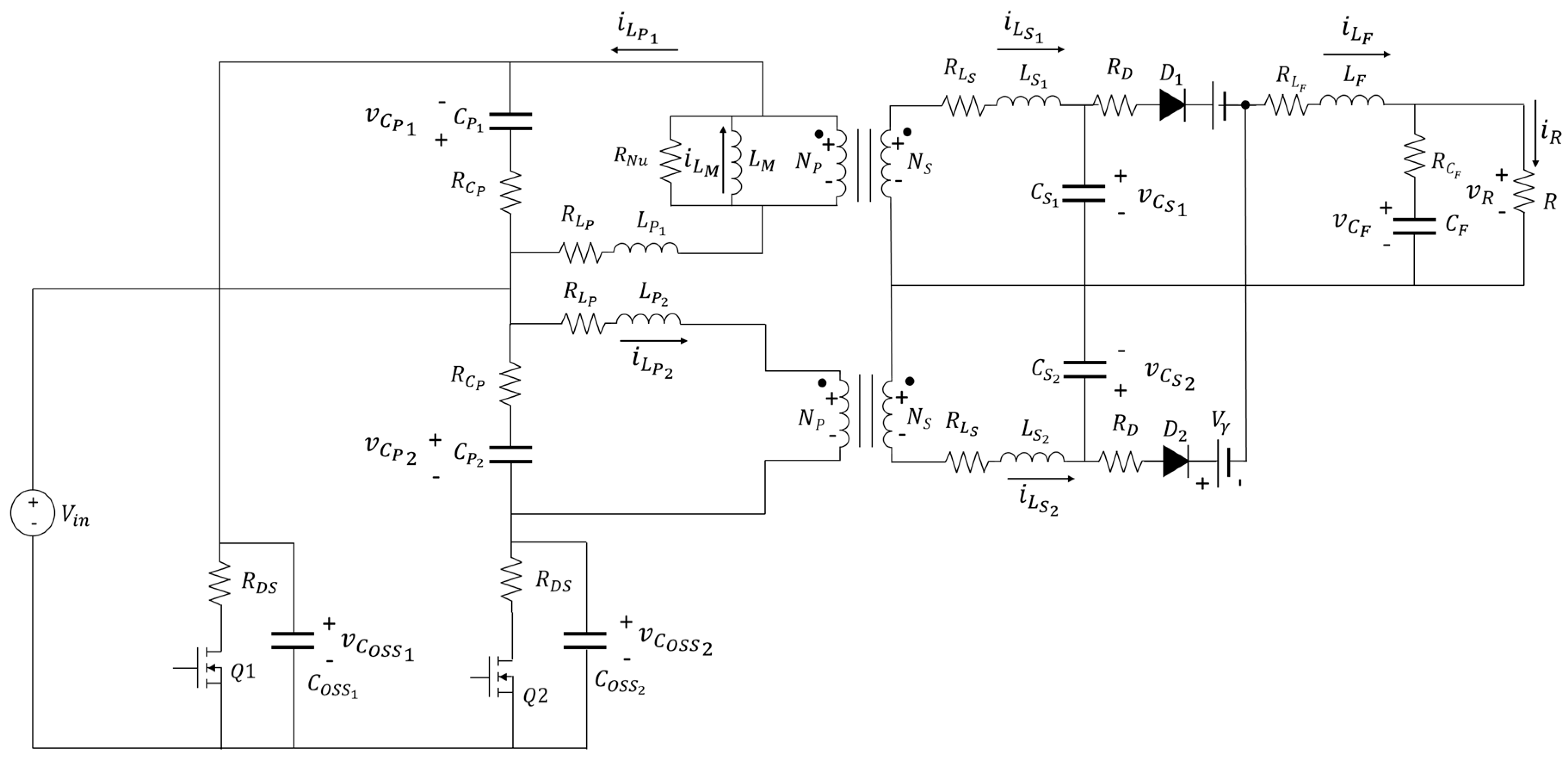
2.2. Non-Ideal Push–Pull Converter Circuit
2.3. Non-Ideal Push–Pull Model
3. Push–Pull Converter Sizing and Parameterisation
3.1. Transformer Sizing and Parametrisation
3.1.1. Transformer Core
3.1.2. Number of Primary and Secondary Winding Turns
3.1.3. Primary and Secondary Windings’ Resistance
3.1.4. Leakage Inductances of Transformer Primary and Secondary Windings
3.1.5. Parasitic Capacitances of Transformer Primary and Secondary Windings
3.1.6. Magnetising Resistance
3.1.7. Magnetising Inductance
3.2. Sizing and Parameterisation of the Output Low-Pass LC Filter
3.2.1. Low-Pass Filter Inductance
3.2.2. Low-Pass Filter Capacitance
3.3. Sizing and Parameterisation of the Switching Devices
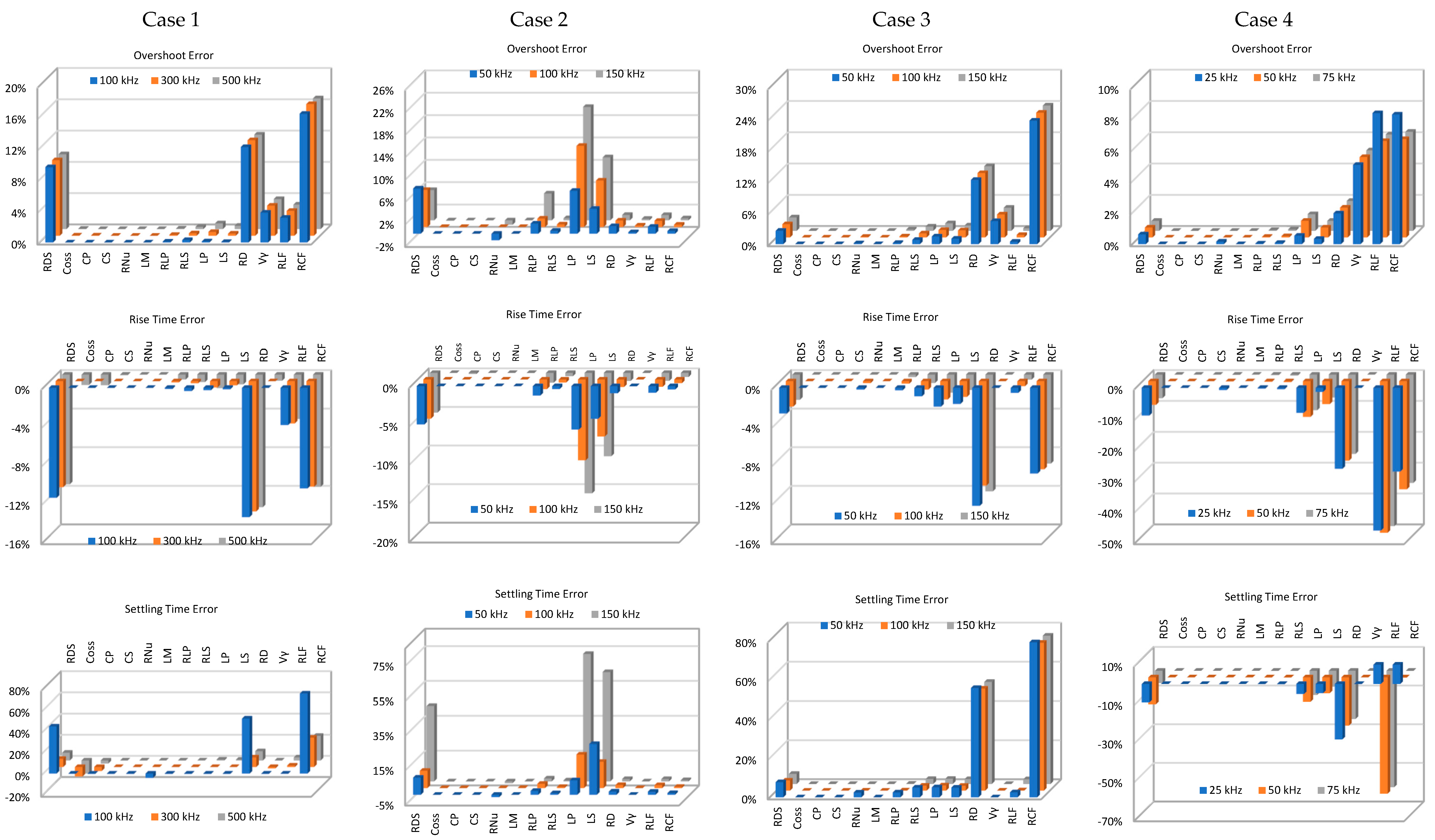
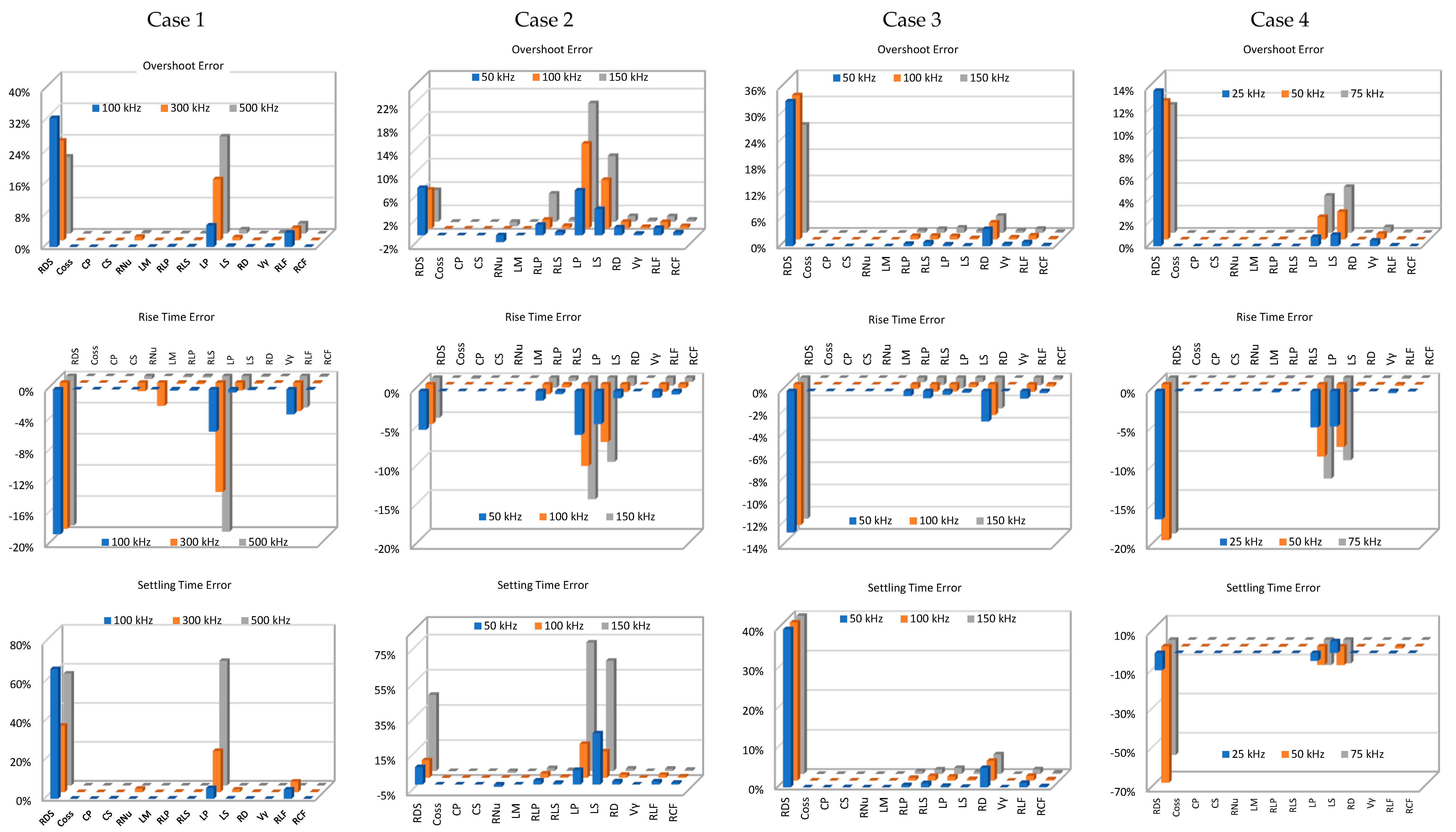
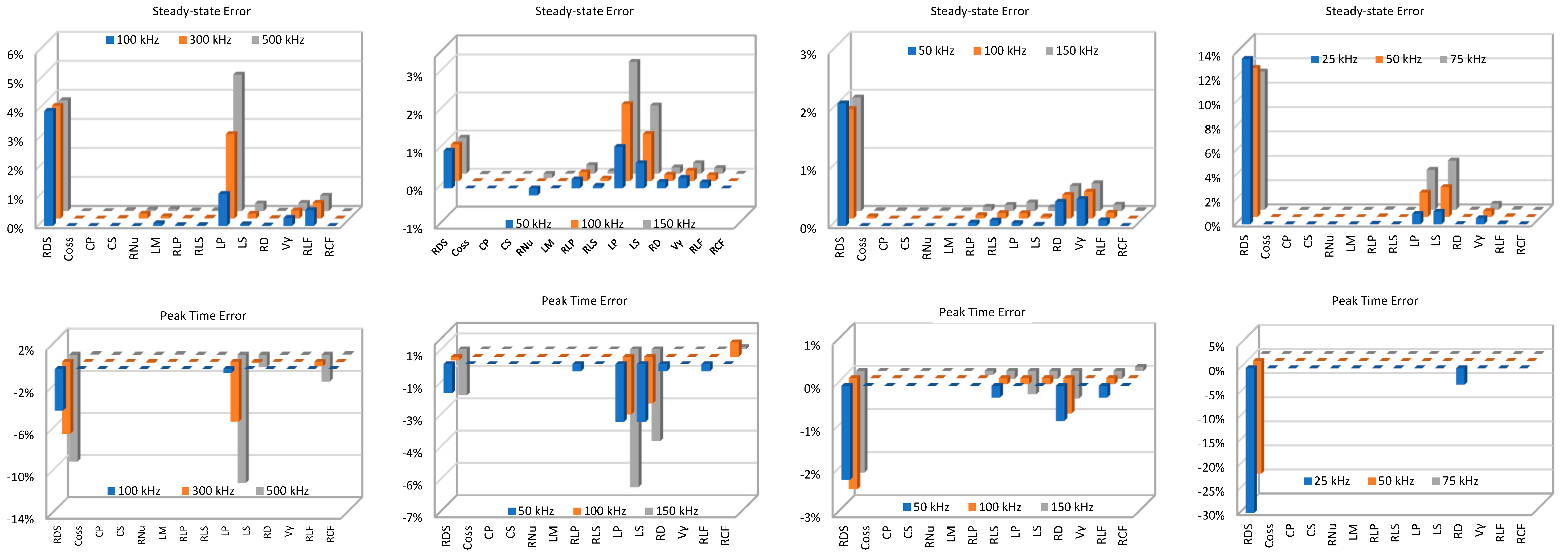
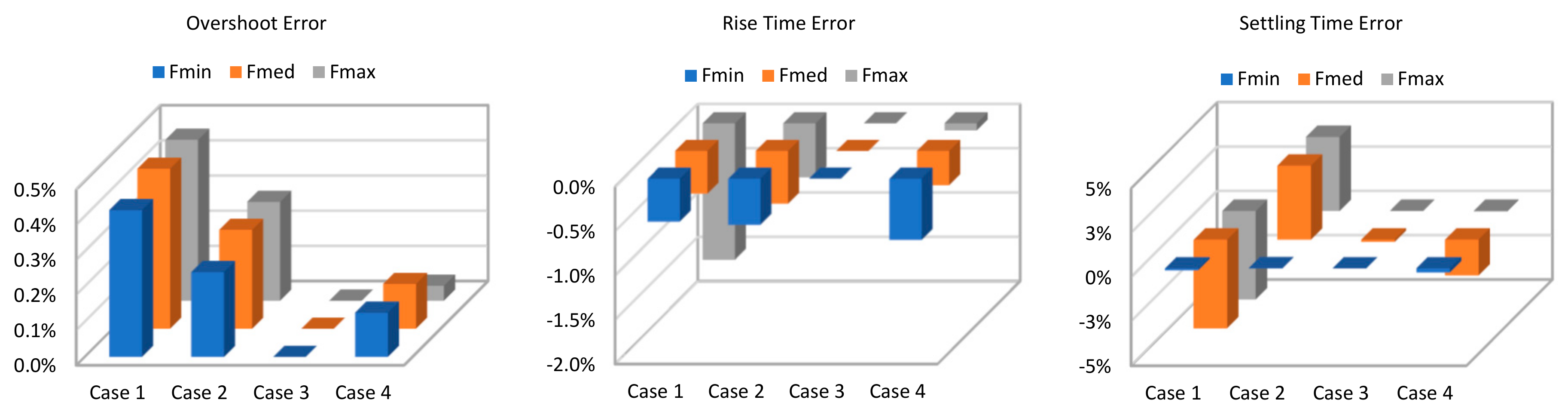
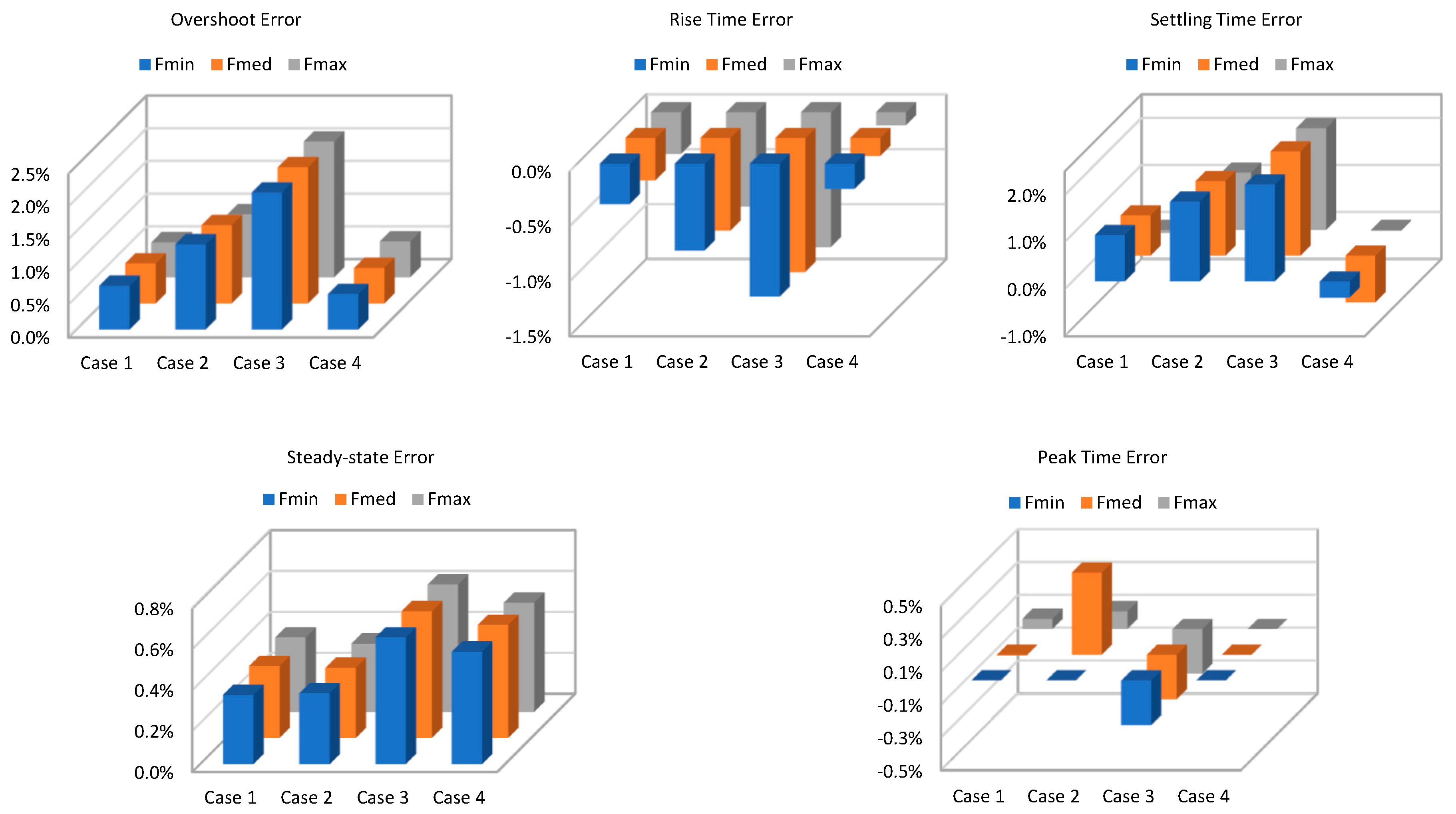
4. Sensitivity Analysis
4.1. Push–Pull Converter Design: Case Studies
- Case 1: Very low power (1 W–10 W) and operating frequencies of 100 kHz, 300 kHz and 500 kHz.
- Case 2: Low power (10 W–100 W) and operating frequencies of 50 kHz, 75 kHz and 150 kHz.
- Case 3: Medium power (100 W–1 kW) and operating frequencies of 50 kHz, 75 kHz and 150 kHz.
- Case 4: High power (1 W–10 kW) and operating frequencies of 25 kHz, 50 kHz and 75 kHz.
4.2. Sensitivity Analysis
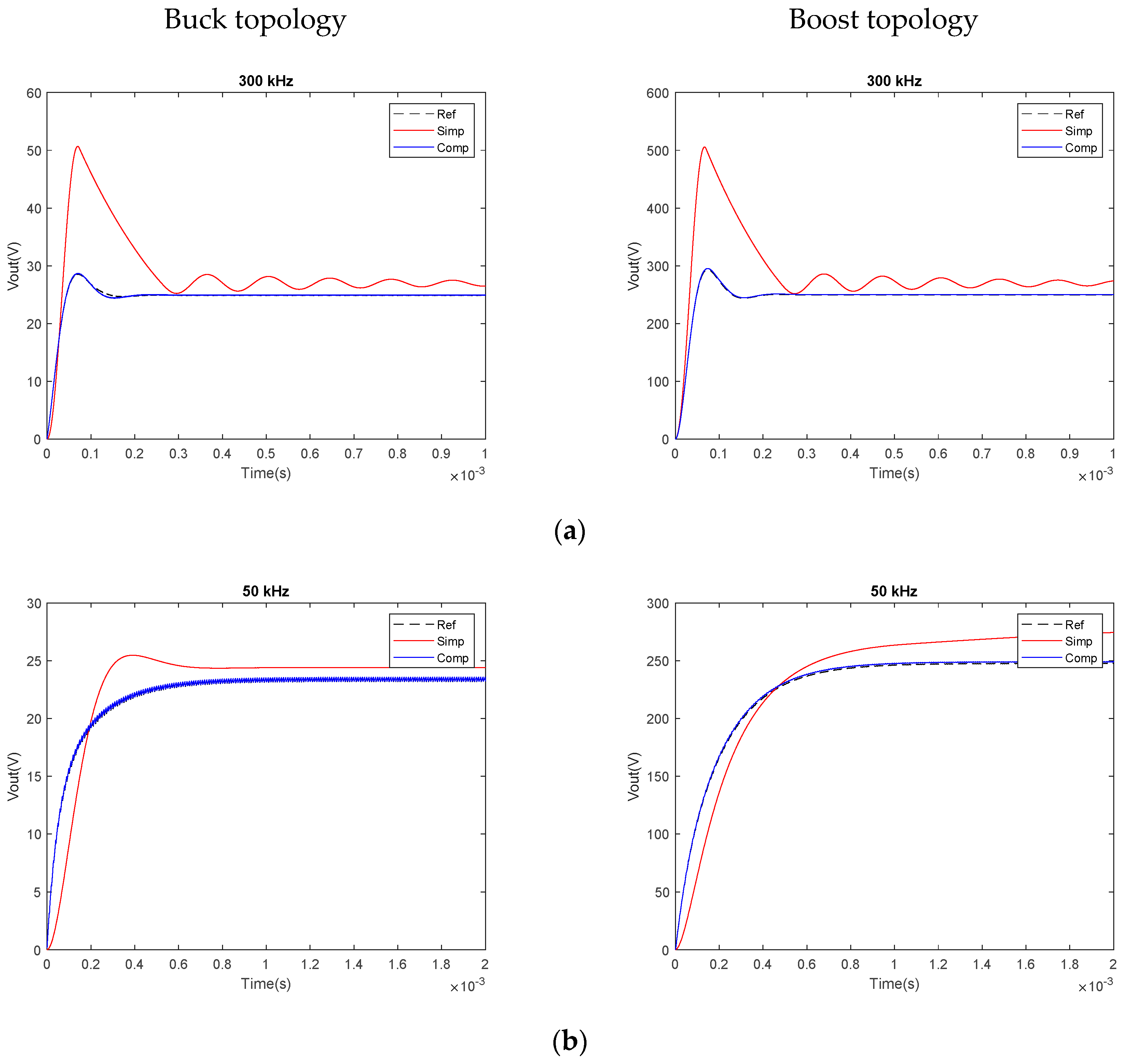
5. Discussion and Derivation of the Models That Meet the Trade-Off between Complexity and Practical Feasibility
5.1. Discussion
5.2. Simplified Models
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Symbols
| Core magnetic cross-section area (cm2) | |
| Temperature coefficient of conductive material (3.9 for copper) | |
| Core area product (cm4) | |
| Window area available for the winding (cm2) | |
| Area of E-type transformer reluctance (m2) | |
| Core window width along x axis (m) | |
| Filter capacitor (F) | |
| Mosfet output capacitance (F); x = 1, 2 | |
| Parasitic primary winding capacitance (F); x = 1, 2 | |
| Parasitic secondary winding capacitance (F); x = 1, 2 | |
| Total parasitic turn-to-turn capacitance of the transformer winding (F) | |
| Duty cycle | |
| Total conductor diameter excluding insulation thickness (mm) | |
| Output branch circulation diodes; x = 1, 2 | |
| Overall conductor diameter including insulation thickness (mm) | |
| Flux density deviation swing (Tesla, T) | |
| Filter inductor ripple current (A) | |
| Filter capacitor ripple voltage (V) | |
| Vacuum electric permittivity (8.854210−15 F/mm) | |
| Relative electrical permittivity of the electrical insulator (3.5) | |
| Switching frequency (Hz) | |
| Core window height (m) | |
| Correction factor for the effective conductor cross-section of the windings | |
| Average operating current of switching devices (A), x = Q (transistor), D (rectifier diode) | |
| Filter capacitor current (A) | |
| Filter inductance current (A) | |
| Parameter associated with the converter topology (0.017 in this case) | |
| Average turn length of secondary windings (m) | |
| Equivalent leakage inductance (F) | |
| Filter inductance (H) | |
| Internal leakage inductance (F) | |
| Leakage inductance of a transformer winding (F) | |
| Leakage inductance due to core magnetising losses (H) | |
| Leakage inductance of the primary winding (H); x = 1, 2 | |
| Leakage inductance of the secondary winding (H); x = 1, 2 | |
| Turn length (mm) | |
| Length of E-type transformer reluctance (m2) | |
| Length of the windings (m) | |
| Yoke leakage inductance (F) | |
| Vacuum magnetic permeability ( H/m) | |
| Relative magnetic permeability of the conductive material | |
| MPPT | Maximum Power Point Tracking |
| Number of turns of the primary winding | |
| Number of turns of the secondary winding | |
| Transformer core power losses density (W/m3) | |
| Output power of the converter (W) | |
| PV | Photovoltaic |
| Mosfet; x = 1, 2 | |
| Wire radius of transformer windings (m) | |
| Load resistor (Ω) | |
| Filter capacitor series resistor (Ω) | |
| Diode series resistor (Ω) | |
| Mosfet drain-sink resistance (Ω) | |
| Equivalent reluctance of transformer sections (A·t/Weber) | |
| Filter inductor series resistor (Ω) | |
| Primary winding resistor (Ω) | |
| Secondary winding resistor (Ω) | |
| Magnetisation resistance related to core losses (Ω) | |
| Resistance of the conductors of the transformer windings (Ω) | |
| Effective resistance of the conductors of the transformer windings (Ω) | |
| Resistivity of the conductive material ( for copper) | |
| Cross-section of the conductive material of transformer windings (m2) | |
| Effective cross-section of the conductive material of transformer windings (m2) | |
| Operating temperature of conductive material (°C) | |
| Activation time of any of the converter electronic switches | |
| Reference temperature of conductive material (°C) | |
| Magnetic flux intensity (Wb) | |
| Blocking voltage of switching devices (V), x = Q (transistor), D (rectifier diode) | |
| Filter capacitor voltage (V) | |
| Transformer core effective volume (m3) | |
| Diode forward voltage (V) | |
| Converter input voltage (V) | |
| Filter inductance voltage (V) | |
| Leakage inductance of the primary winding voltage (V) | |
| Leakage inductance of the secondary winding voltage (V) | |
| Magnetisation resistance voltage (V) | |
| Converter output voltage (V) | |
| Primary winding voltage (V) | |
| Skin depth inside the conductor above which the electron flow rate is reduced to 63% (m) |
References
- Vacheva, G.I.; Genev, K.; Hinov, N.L. Modeling and Simulation of DC-DC Push-Pull Converter. In Proceedings of the 57th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Ohrid, North Macedonia, 16–18 June 2022; pp. 22–25. [Google Scholar]
- Liang, T.J.; Lee, J.H.; Chen, S.M.; Chen, J.F.; Yang, L.S. Novel isolated high-step-Up DC-DC converter with voltage lift. IEEE Trans. Ind. Electron. 2013, 60, 1483–1491. [Google Scholar] [CrossRef]
- Zhang, H.; Quan, L.; Gao, Y. Dynamic modelling and small signal analysis of push-pull bidirectional DC-DC converter. Comput. Model. New Technol. 2014, 18, 14–18. [Google Scholar]
- Ivanovic, Z.; Knezic, M. Modeling Push–Pull Converter for Efficiency Improvement. Electronics 2022, 11, 2713. [Google Scholar] [CrossRef]
- Yisheng, Y. A parallel soft-switching push-pull converter applied in automotive inverters. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, PEDG 2010, Hefei, China, 16–18 June 2010; pp. 423–425. [Google Scholar] [CrossRef]
- Camilo, J.C.; Guedes, T.; Fernandes, D.A.; Melo, J.D.; Costa, F.F.; Sguarezi Filho, A.J. A maximum power point tracking for photovoltaic systems based on Monod equation. Renew. Energy 2019, 130, 428–438. [Google Scholar] [CrossRef]
- Zhang, Z.; Thomsen, O.C.; Andersen, M.A.E. Optimal design of a push-pull-forward half-bridge (PPFHB) bidirectional DC-DC converter with variable input voltage. IEEE Trans. Ind. Electron. 2012, 59, 2761–2771. [Google Scholar] [CrossRef]
- Köse, H.; Aydemir, M.T. Design and implementation of a 22 kW full-bridge push–pull series partial power converter for stationary battery energy storage system with battery charger. Meas. Control 2020, 53, 1454–1464. [Google Scholar] [CrossRef]
- Andújar, J.M.; Vivas, F.J.; Segura, F.; Calderón, A.J. Integration of air-cooled multi-stack polymer electrolyte fuel cell systems into renewable microgrids. Int. J. Electr. Power Energy Syst. 2022, 142, 108305. [Google Scholar] [CrossRef]
- Gómez, J.M.E.; Piña, A.J.B.; Aranda, E.D.; Márquez, J.M.A. Theoretical assessment of DC/DC power converters’ basic topologies. A common static model. Appl. Sci. 2017, 8, 19. [Google Scholar] [CrossRef]
- Chandresh, K.; Makwana, M.V.; Rathod, R.N. Design and Implementation of Soft Switching based Push Pull Converter for LED Application. In Proceedings of the 2019 IEEE International Conference on Innovations in Communication, Computing and Instrumentation, ICCI 2019, Chennai, India, 23 March 2019; pp. 132–135. [Google Scholar] [CrossRef]
- Nugraha, S.D.; Qudsi, O.A.; Yanaratri, D.S.; Sunarno, E.; Sudiharto, I. MPPT-current fed push pull converter for DC bus source on solar home application. In Proceedings of the 2017 2nd International Conferences on Information Technology, Information Systems and Electrical Engineering, ICITISEE, Yogyakarta, Indonesia, 1–2 November 2018; pp. 378–383. [Google Scholar] [CrossRef]
- Meshael, H.; Elkhateb, A.; Best, R. Topologies and Design Characteristics of Isolated High Step-Up DC–DC Converters for Photovoltaic Systems. Electronics 2023, 12, 3913. [Google Scholar] [CrossRef]
- Jayasree, K.S.; Chandrakala, K.R.M.V. Active Cell Balancing Technique for Improved Charge Equalization in Lithium-Ion Battery Stack. In Proceedings of the 4th International Conference on Recent Developments in Control, Automation & Power Engineering, Noida, India, 7–8 October 2021. [Google Scholar]
- Suprabha Padiyar, U.; Kalpana, R. Design & Analysis of Push-pull Converter Fed Battery Charger for Electric Vehicle Application. In Proceedings of the PESGRE 2022—IEEE International Conference on “Power Electronics, Smart Grid, and Renewable Energy”, Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Su, X.; Zeng, N.; Jiang, J. Overview of Isolated Bidirectional DC–DC Converter Topology and Switching Strategies for Electric Vehicle Applications. Energies 2024, 17, 2434. [Google Scholar] [CrossRef]
- Vivas, F.J.; Segura, F.; Andújar, J.M. Generalized, Complete and Accurate Modeling of Non-Ideal Push–Pull Converters for Power System Analysis and Control. Appl. Sci. 2023, 13, 10982. [Google Scholar] [CrossRef]
- Petit, P.; Aillerie, M.; Sawicki, J.P.; Charles, J.P. Push-pull converter for high efficiency photovoltaic conversion. Energy Procedia 2012, 18, 1583–1592. [Google Scholar] [CrossRef]
- Trujillo, C.L.; Velasco, D.; Figueres, E.; Garcerá, G.; Ortega, R. Modeling and control of a push-pull converter for photovoltaic microinverters operating in island mode. Appl. Energy 2011, 88, 2824–2834. [Google Scholar] [CrossRef]
- Vijayan, V.; Sujith, M.; Manjunath, H.V. Analysis and implementation of a high boost DC-DC converter for renewable energy power systems. In Proceedings of the 2014 Annual International Conference on Emerging Research Areas: Magnetics, Machines and Drives, AICERA/ICMMD 2014—Proceedings, Kottayam, India, 24–26 July 2014. [Google Scholar] [CrossRef]
- Xu, G.; Qu, Y.; Li, L.; Xiong, W.; Xia, Z.; Sun, Y.; Su, M. Magnetizing Current Injection Based Push-Pull Dual Active Bridge Converter with Optimized Control to Achieve Full Load Range ZVS for the Distributed Generation System. IEEE Trans. Energy Convers. 2023, 38, 1589–1601. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, C.; Feng, J.; Kan, Z. Analysis of Soft Switching Conditions for Push-Pull Current Type Bidirectional DC/DC Converter. IEEE Access 2024, 12, 59386–59398. [Google Scholar] [CrossRef]
- Jiang, L.; Wan, J.; Li, Y.; Huang, C.; Liu, F.; Wang, H.; Sun, Y.; Cao, Y. A New Push-Pull DC/DC Converter Topology with Complementary Active Clamped. IEEE Trans. Ind. Electron. 2022, 69, 6445–6449. [Google Scholar] [CrossRef]
- Larico, H.R.E.; Greff, D.S.; Heerdt, J.A. Modeling and control of a three-phase push-pull dc-dc converter: Theory and simulation. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference, COBEP/SPEC 2016, Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Delshad, M.; Farzanehfard, H. A new soft switched push pull current fed converter for fuel cell applications. Energy Convers. Manag. 2011, 52, 917–923. [Google Scholar] [CrossRef]
- Zhang, J.; He, Z.; Liu, Y.; Luo, A.; Wang, L.; Wang, H.; Chen, Y.; Pang, Y. High-Efficiency Push-Pull Resonant Converter Solution for Auxiliary Power Supply in 70-kV Isolated Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 632–647. [Google Scholar] [CrossRef]
- Lim, J.W.; Bai, C.; Wagaye, T.A.; Choi, J.H.; Kim, M. Highly Reliable Push-Pull Resonant DC/DC Converter for Medium-Power Applications. IEEE Trans. Ind. Electron. 2023, 70, 1342–1355. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Q.; Xu, J.; Xiao, L. Implementation of an Active-Clamped Current-Fed Push-Pull Converter Employing Parallel-Inductor to Extend ZVS Range for Fuel Cell Application. IEEE Trans. Ind. Electron. 2017, 64, 7919–7929. [Google Scholar] [CrossRef]
- Dixon, L.H. Section 4: Power Transformer Design. In TI Magnetics Design Handbook; Istanbul Technical University: Istanbul, Turkey, 2000; pp. 31–40. [Google Scholar]
- Aldana, A.A.R.; Beltran, O.E.B.; Trujillo, R.C.L. Magnetic design of a push-pull converter. In Proceedings of the 2015 IEEE Workshop on Power Electronics and Power Quality Applications, PEPQA 2015—Proceedings, Bogota, Colombia, 2–4 June 2015. [Google Scholar] [CrossRef]
- Wu, S.; Sun, A.; Xu, W.; Zhang, Q.; Zhai, F.; Logan, P.; Volinsky, A.A. Iron-based soft magnetic composites with Mn-Zn ferrite nanoparticles coating obtained by sol-gel method. J. Magn. Magn. Mater. 2012, 324, 3899–3905. [Google Scholar] [CrossRef]
- Eargle, J.M. Resistance Change with Temperature for Copper. In Electroacoustical Reference Data; Springer: Boston, MA, USA, 2002; pp. 106–107. [Google Scholar] [CrossRef]
- Ida, N.; Bastos, J.P.A. Electromagnetics and Calculation of Fields; Springer: New York, NY, USA, 1997. [Google Scholar]
- Jiashen, T.; Yiming, Z.; Xiguo, R.; Xuhong, W.; Haijun, T. Calculation of leakage inductance of integrated magnetic transformer with separated secondary winding used in ZVS PSFB converter. J. Magn. 2016, 21, 644–651. [Google Scholar] [CrossRef]
- Massarini, A.; Kazimierczuk, M.K. Self-capacitance of inductors. IEEE Trans. Power Electron. 1997, 12, 671–676. [Google Scholar] [CrossRef]
- Dalessandro, L.; Member, S.; Cavalcante, S.; Member, S.; Kolar, J.W.; Member, S. Self-Capacitance of High-Voltage Transformers. IEEE Trans. Power Electron. 2007, 22, 2081–2092. [Google Scholar] [CrossRef]
- Bahmani, A. Core loss evaluation of high-frequency transformers in high-power DC-DC converters. In Proceedings of the 2018 13th International Conference on Ecological Vehicles and Renewable Energies, EVER 2018, Monte Carlo, Monaco, 10–12 April 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.F. A practical transformer core loss measurement scheme for high-frequency power converter. IEEE Trans. Ind. Electron. 2008, 55, 941–948. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Proc. IEEE 1984, 72, 197–221. [Google Scholar] [CrossRef]
- Landgraf, F.J.G.; Emura, M.; de Campos, M.F. On the Steinmetz hysteresis law. J. Magn. Magn. Mater. 2008, 320, 531–534. [Google Scholar] [CrossRef]
- Pleite, J.; Valdivia, V.; Zumel, P.; Gonzalez, C. Transformer and series inductance integration for harmonic filtering in PWM inverters based in a simple design procedure. IEEE Int. Symp. Ind. Electron. 2007, 1201–1206. [Google Scholar] [CrossRef]
- Rashid, M.H. Power electronics and applications. In Proceedings of the 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), Tehran, Iran, 5–6 February 2014. [Google Scholar] [CrossRef]




| Buck Topology | Boost Topology | |||
|---|---|---|---|---|
| Element | Model and Rated Values | Parameters | Model and Rated Values | Parameters |
| Output low-pass filter capacitor | MAL211651338E3, VISHAY® (Malvern, PA, USA) 50 VDC | µF Ω | B32911A3333M000, TDK® (Hutchinson, MN, USA) 50 VDC | nF Ω |
| Output low-pass filter inductance | SRR1005-151K, Bourns® (Riverside, CA, USA) | µH mΩ | 22R156C, Murata Power Solutions® (Westborough, MA, USA) | mH Ω |
| Transformer | EFD15/8/5, TDK® Ferrite material: N87 Turn ratio: 180:20 | EFD15/8/5, TDK® Ferrite material: N87 Turn ratio: 18:200 | ||
| 13.5 µH 166 nH | µH 52 µH | |||
| 1.882 Ω mΩ | 26 mΩ 2.606 Ω | |||
| 0.67 pF pF | pF 0.36 pF | |||
| 260 mH MΩ | 2.5 mH MΩ | |||
| Output resistance | - | 90 Ω | - | 9000 Ω |
| Mosfet | BSS127SSN-7, DiodesZetex® (Plano, TX, USA) 600 VDC, 0.07 A | 2 pF Ω | IXTP8N65X2M, IXYS® (Milpitas, CA, USA) 60 VDC, 0.5 A | 0 pF Ω |
| Diode | LL4148, Onsemi® (Scottsdale, AZ, USA) 100 VDC, 0.2 A | VDC Ω | US1M-E3/61T, VISHAY® 1000 VDC, 1 A | .75 VDC Ω |
| Buck Topology | Boost Topology | |||
|---|---|---|---|---|
| Element | Model and Rated Values | Parameters | Model and Rated Values | Parameters |
| Output low-pass filter capacitor | EEEFN1H680XP, Panasonic® (Osaka, Japan) 50 VDC | µF mΩ | EEEHB1HR68AR, Panasonic® 50 VDC | nF mΩ |
| Output low-pass filter inductance | PM127SH-330M-RC, Bourns® | µH mΩ | 1433507C, Murata Power Solutions® | mH mΩ |
| Transformer | E25.4/10/7, TDK® Ferrite material: N87 Turn ratio: 140:16 | E25.4/10/7, TDK® Ferrite material: N87 Turn ratio: 14:156 | ||
| µH 1.12 µH | 850 nH 106 µH | |||
| 300 mΩ mΩ | 24 mΩ mΩ | |||
| pF pF | pF pF | |||
| mH MΩ | mH MΩ | |||
| Output resistance | - | 9 Ω | - | 900 Ω |
| Mosfet | STN1HNK60, STMicroelectronics® (Geneva, Switzerland) 600 VDC, 0.4 A | 20 pF Ω | NDT3055L, Onsemi® 100 VDC, 4 A | 0 pF, mΩ |
| Diode | BYG22D-E3/TR3, VISHAY® 200 VDC, 2 A | VDC mΩ | US1M-E3/61T, VISHAY® 1000 VDC, 1 A | .75 VDC Ω |
| Buck Topology | Boost Topology | |||
|---|---|---|---|---|
| Element | Model and Rated Values | Parameters | Model and Rated Values | Parameters |
| Output low-pass filter capacitor | UBT1J221MHD8, Nichicon® (Kyoto, Japan) 35 VDC, 1S3P | µF mΩ | EZPE50106LTA, Panasonic® 500 VDC | 10 µF 22 mΩ |
| Output low-pass filter inductance | IHDM1008BCEV4R7M30, VISHAY® | µH mΩ | 1433445C, Murata Power Solutions® | µH mΩ |
| Transformer | E42/21/20, TDK® Ferrite material: N87 Turn ratio: 24:3 | E42/21/20, TDK® Ferrite material: N87 Turn ratio: 3:26 | ||
| 3 µH 46 nH | 4 nH, 309 nH | |||
| 53 mΩ 1.7 mΩ | 0.6 mΩ mΩ | |||
| 0.6 pF pF | pF 9.5 pF | |||
| mH 19.8 MΩ | µH kΩ | |||
| Output resistance | - | 0.9 Ω | - | 90 Ω |
| Mosfet | IXTP8N65X2M, IXYS® 650 VDC, 4 A | 0 mΩ 20 pF | RFP50N06, Onsemi® 60 VDC, 50 A | 0 pF mΩ |
| Diode | BYV32E-200,127, WeEn Semiconductors Co., Ltd.® (Shanghai, China) 200 VDC, 20 A | VDC mΩ | UF5408-E3/54, VISHAY® 1000 VDC, 3 A | VDC mΩ |
| Buck Topology | Boost Topology | |||
|---|---|---|---|---|
| Element | Model and Rated Values | Parameters | Model and Rated Values | Parameters |
| Output low-pass filter capacitor | B43464A9688M000, TDK® 400 VDC, 1S2P | mF 9 mΩ | C4AQLBW6130A3NK, KEMET® (Fort Lauderdale, FL, USA) 500 VDC | 130 µF 2.4 mΩ |
| Output low-pass filter inductance | CS-631M-450ª, CoilsWS® | nH mΩ | EES55244-131M-45A, CoilsWS® (Orange, CA, USA) | 130 µH 6.6 mΩ |
| Transformer | 2xE100/60/28, TDK® Ferrite material: N87 Turn ratio: 1:9 | 2xE100/60/28, TDK® Ferrite material: N87 Turn ratio: 1:9 | ||
| 1 µH 12.4 nH | 12 nH 1.5 µH | |||
| 6.2 mΩ µΩ | 43 µΩ 29 µΩ | |||
| 45 pF pF | pF 46 pF | |||
| mH MΩ | 130 µH kΩ | |||
| Output resistance | - | 0.09 Ω | - | 9 Ω |
| Mosfet | SPW47N60C3FKSA1, INFINEON® (Allentown, PA, USA) 650 VDC, 47 A | 2200 pF 0 mΩ | IXFN420N10T, IXYS® 100 VDC, 420 A | 0 pF mΩ |
| Diode | STTH20004TV1, STMicroelectronics® 400 VDC, 240 A | VDC mΩ | DSEI30-10A, IXYS® 1000 VDC, 30 A | VDC mΩ |
| Buck Topology | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | |||||||||||||
| 100 kHz |  | ||||||||||||
| 300 kHz |  | ||||||||||||
| 500 kHz |  | ||||||||||||
| Case 2 | |||||||||||||
| 50 kHz |  | ||||||||||||
| 100 kHz |  | ||||||||||||
| 150 kHz |  | ||||||||||||
| Case 3 | |||||||||||||
| 50 kHz |  | ||||||||||||
| 100 kHz |  | ||||||||||||
| 150 kHz |  | ||||||||||||
| Case 4 | |||||||||||||
| 25 kHz |  | ||||||||||||
| 50 kHz |  | ||||||||||||
| 75 kHz |  | ||||||||||||
| Legend for colour intensity | |||||||||||||
| High | Moderate | Reduced | Negligible | ||||||||||
| Boost Topology | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | ||||||||||||||
| 100 kHz |  | |||||||||||||
| 300 kHz |  | |||||||||||||
| 500 kHz |  | |||||||||||||
| Case 2 | ||||||||||||||
| 50 kHz |  | |||||||||||||
| 100 kHz |  | |||||||||||||
| 150 kHz |  | |||||||||||||
| Case 3 | ||||||||||||||
| 50 kHz |  | |||||||||||||
| 100 kHz |  | |||||||||||||
| 150 kHz |  | |||||||||||||
| Case4 | ||||||||||||||
| 25 kHz |  | |||||||||||||
| 50 kHz |  | |||||||||||||
| 75 kHz |  | |||||||||||||
| Legend for colour intensity | ||||||||||||||
| High | Moderate | Reduced | Negligible | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas, F.J.; Andújar, J.M.; Segura, F. Non-Ideal Push–Pull Converter Model: Trade-Off between Complexity and Practical Feasibility in Terms of Topology, Power and Operating Frequency. Appl. Sci. 2024, 14, 6224. https://doi.org/10.3390/app14146224
Vivas FJ, Andújar JM, Segura F. Non-Ideal Push–Pull Converter Model: Trade-Off between Complexity and Practical Feasibility in Terms of Topology, Power and Operating Frequency. Applied Sciences. 2024; 14(14):6224. https://doi.org/10.3390/app14146224
Chicago/Turabian StyleVivas, Francisco José, José Manuel Andújar, and Francisca Segura. 2024. "Non-Ideal Push–Pull Converter Model: Trade-Off between Complexity and Practical Feasibility in Terms of Topology, Power and Operating Frequency" Applied Sciences 14, no. 14: 6224. https://doi.org/10.3390/app14146224
APA StyleVivas, F. J., Andújar, J. M., & Segura, F. (2024). Non-Ideal Push–Pull Converter Model: Trade-Off between Complexity and Practical Feasibility in Terms of Topology, Power and Operating Frequency. Applied Sciences, 14(14), 6224. https://doi.org/10.3390/app14146224










