1. Introduction
The eye is one of the most important organs of the human body, and the fundus, as an important part of the eye, has a large number of capillaries distributed on it, which are the only capillaries that can be directly observed non-invasively in the human body [
1]. There is a close relationship between fundus health status and systemic diseases [
2]. The fundus refers to the posterior tissues inside the eyeball, including structures such as the retina, macula, blood vessels, choroid, and optic nerve [
3]. Medical research has shown that these structures are not only responsible for the formation and conduction of vision but also reflect the overall health of the body. For example, diabetes is a common systemic disease that causes retinal vasculopathy, which, in turn, leads to diabetic retinopathy [
4]. High blood pressure can also cause changes in the blood vessels in the fundus, causing, for example, arteriosclerosis and retinal edema [
4]. In addition, systemic diseases such as kidney disease, anemia, and leukemia can also be manifested through fundus lesions [
5]. Many diseases in the human body will produce corresponding pathological changes to the retina of the fundus, and most patients have lesions in the fundus when the body has no obvious perception [
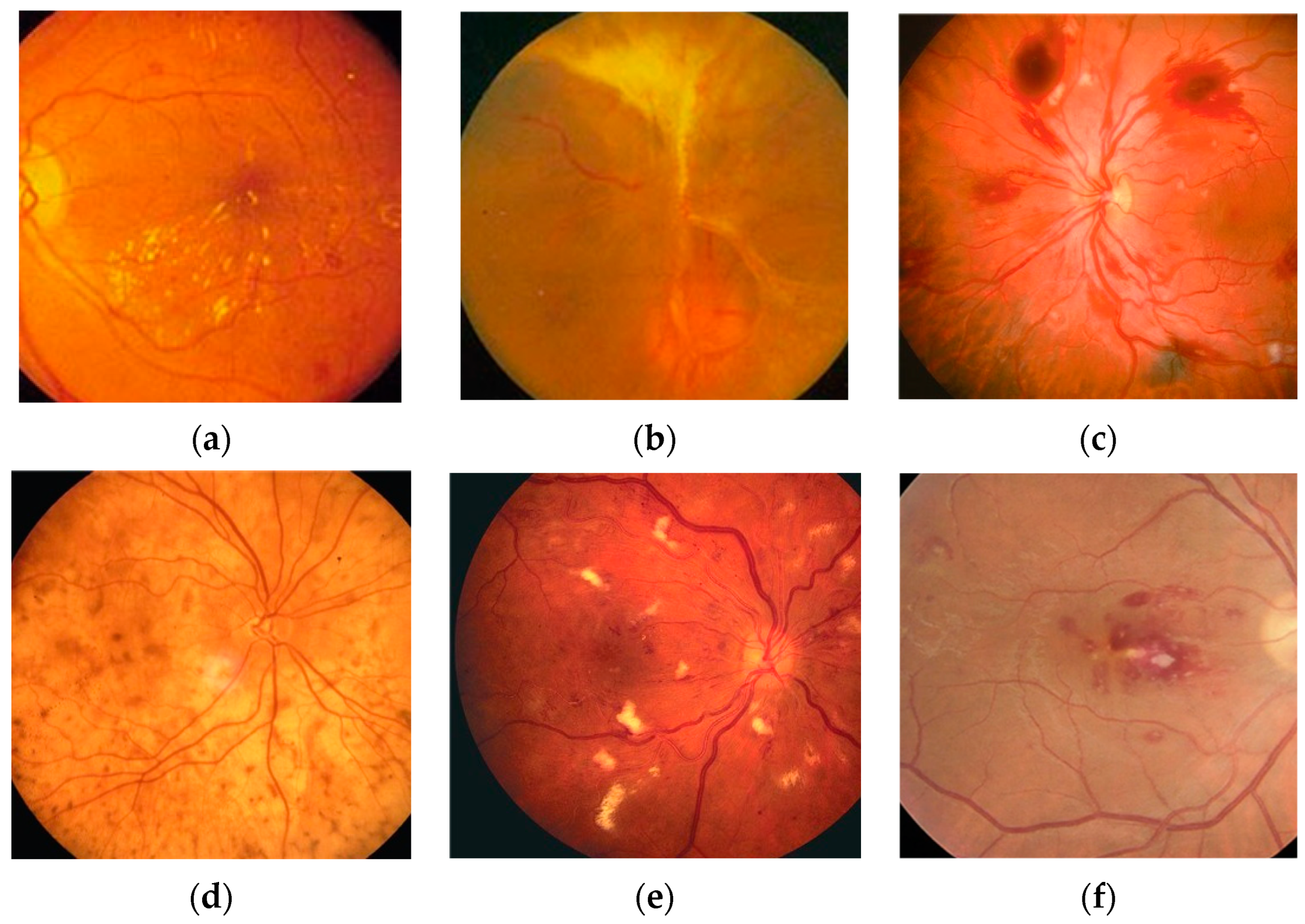
6]. Some typical fundus lesion features are shown in
Figure 1. The World Health Organization predicts that by 2030, the number of people with diabetic retinopathy will increase to 180.6 million, the number of people with age-related eye disease glaucoma will increase to 95.4 million, and the number of people with age-related macular degeneration will increase to 243.3 million [
7]. Therefore, it is of great significance to make an early diagnosis of human health through fundus examination for the prevention and timely treatment of diseases.
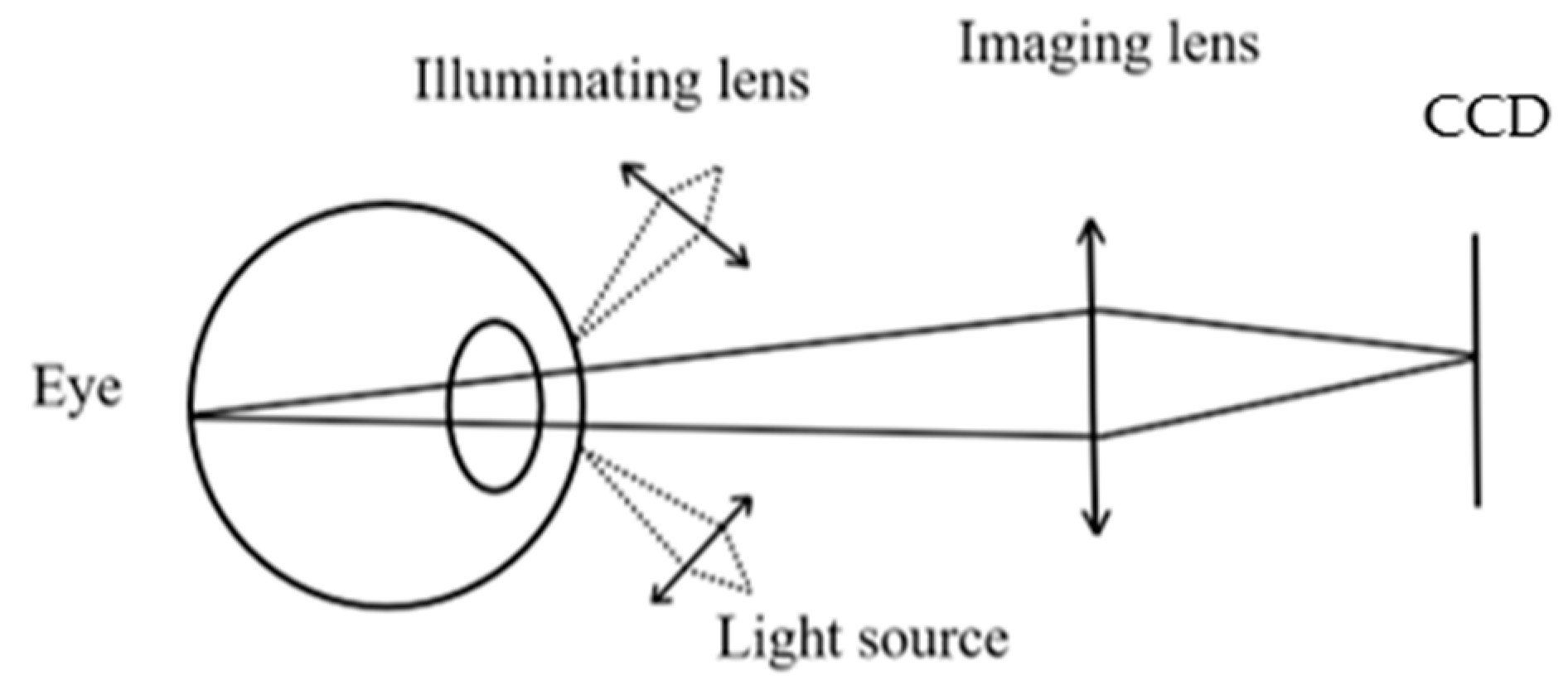
With the continuous development of technology, innovation, and upgrades, ophthalmic medical devices are also being updated, in which fundus cameras are specially used to capture fundus images, gradually replacing traditional ophthalmoscopy methods. Fundus cameras use a special imaging and illumination system to clearly capture the structures behind the eyeball, including the vitreous, retina, choroid, and optic nerve [
8], providing objective fundus images, helping doctors observe changes in fundus lesions, and providing ophthalmologists with a more accurate and comprehensive diagnosis basis. Secondly, fundus cameras can also be used to compare the effects of treatments, evaluating the effectiveness of treatments by observing changes in fundus images. At present, desktop fundus cameras can obtain good quality fundus images and shorten the time of consultation, but there are also some disadvantages that cannot be ignored, such as the high price of equipment, high acquisition and maintenance costs, the need for them to be operated by doctors, and the requirement of extra training and guidancefor initial purchase. In addition, due to the complexity of the optical system and the large and heavy equipment, the camera is not suitable for mobile examination and follow-up use. It has not yet been widely used in all medical institutions, and only some large hospitals or specialized ophthalmic medical institutions can introduce and use such systems, which has high limitations.
So, the main challenges in fundus camera design include the following:
(1) Optical design: The optical design of the fundus camera is key, and needs to ensure that the camera can capture high-quality, high-resolution fundus images. Factors to consider when designing include the wavelength, intensity, and optimization of the optical path of the light source. At the same time, due to the physiological structure and optical properties of the human eye, it is also necessary to ensure that the optical system is safe for the human eye.
(2) Image processing: The processing of fundus images is another important challenge in fundus camera design. Fundus images are often affected by various factors, so advanced image processing technology is required to improve image quality and the visibility and identification accuracy of lesion areas.
(3) System integration and miniaturization: With the development of technology, people have put forward higher requirements for the portability and ease of use of fundus cameras. Integrating high-precision optics, image acquisition and processing systems, light source systems, and other auxiliary functions into a small, lightweight device is a challenging task.
(4) Cost control: Cost control also needs to be considered while ensuring the performance of the equipment. Core components such as high-precision optical components and image processing chips are often costly, and how to reduce costs while ensuring performance is a practical challenge in fundus camera design.
Jiang Jian-yu et al. designed a 39° field of view of visible light non-mydriasis fundus camera optical system, which resolved the 10 μm structure of the fundus [
7] and eliminated the stray light caused by the surface reflection of the omental objective lens group by polarization. The fundus retina illumination was uniform [
7] but the imaging system was too long, reaching 265 mm. WANG Xiao-heng et al. designed a 40° field of view dual-light source fundus camera optical system [
9], where visible light was used to shoot retinal images, near-infrared light was used for observation, the beamsplitter of visible light transmission and infrared light reflection were used to realize the dual-light source common beam path design, and corneal stray light was suppressed through the ring light source. The imaging system was 228 mm, so the length was still long, and the final design result was still relatively complex. In 2019, Diego Palacions et al. from the University of Miami in the United States [
9] developed a handheld fundus camera based on Shumei Pai and implanted the Linux operating system and OpenCV library into the system. Four fundus images with a field of view angle of 10° were stitched together to obtain images with a field of view of 16° [
10]. However, it was easy to lose the details of the fundus in the stitching of the image, the composite image could be distorted, and the proportion of each tissue could not be truly reflected.
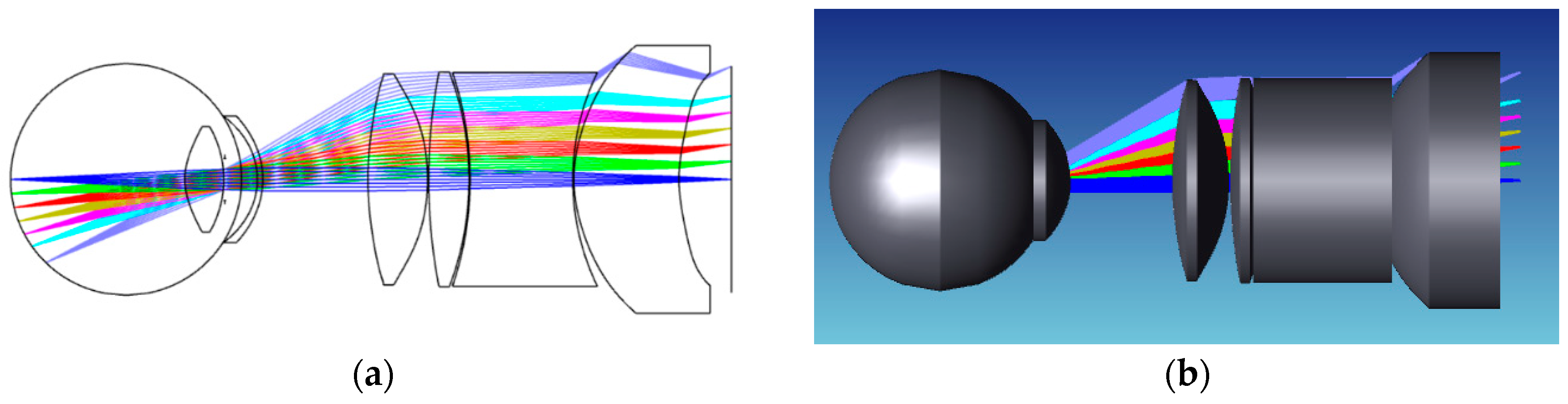
In this context, our research presents a non-coaxial annular array illumination structure using aspherical lenses to reduce the total length of the system. This pioneering approach was designed to make the optical system compact. Our study was dedicated to facilitating the miniaturization of fundus cameras to match with components with different functions to realize the integration of functions and solve the problem of difficult and large volumes of stray light suppression in the traditional fundus optical system. We firmly anticipate that our contributions will propel advancements in the field, providing more detailed and accurate images tailored to practical applications.
The main contributions of this work are summarized as follows:
(1) Based on the actual light source size, diaphragm size, image quality requirements, and object resolution accuracy [
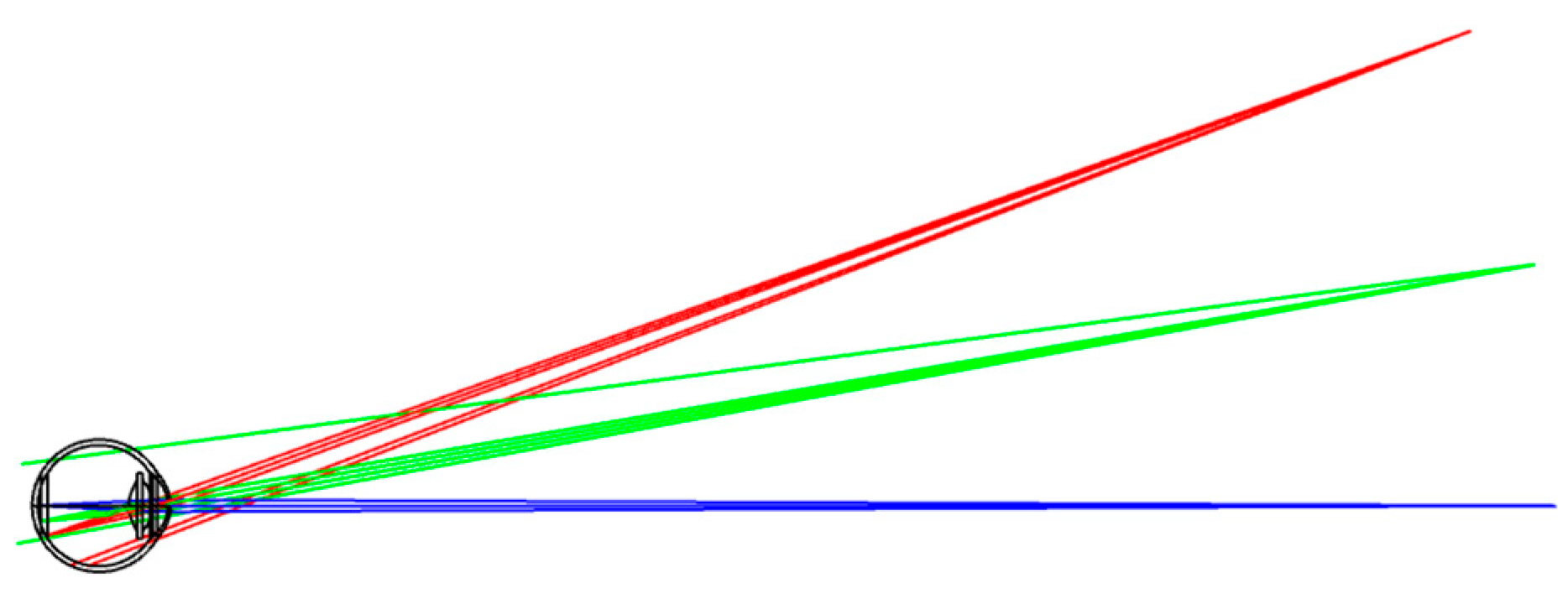
11], we present a lens combination of aspheric and spherical lenses to image the human eye that has a field of view angle of 50° and a total imaging length of 34.6 mm, realizing miniaturization and a large field of view. The miniaturized design is easy to use in many settings, the large field of view effectively avoids the shadow caused by image stitching, and the high resolution means that the physiological features of the fundus can be clearly displayed, meeting the need for high accuracy in lesion identification and classification.
(2) In order to achieve the acquisition of high-resolution clear images, the fundus illumination system was designed to assist in the design. Point light sources and four illumination arrays were used to meet the fundus illumination height and the working distance of the illumination system, achieving a uniform illumination of the fundus so that the fundus blood vessels, optic disc, and lesions could be accurately displayed.
(3) To approach the practical application more accurately, our light resources employed the solar spectrum LED with low blue light, high green light, and high CRI, which reduced blue light damage to the human eye, improved the contrast of the fundus image, and restored the true color of the object more accurately, thus being more suitable for fundus lighting.
5. Limitations
Although this study achieved some results in miniaturized large-field imaging, there are still some limitations, which may have a certain impact on the interpretation and generalization of the research results.
The eye model we considered was based on the standard human eye, but we needed to take into account that the visual acuity of different people is different, so this design is not suitable for a human eye with different refractions. In addition, we only acquired images and did not carry out subsequent image processing and analysis, which did not make the system more automated. In order for everyone to obtain a clear image with the camera and obtain the results of lesion analysis directly, here are some key design considerations for the future:
(1) Adjustable eyepiece: The camera’s eyepiece should have diopter adjustment, similar to the power adjustment of glasses. This can be achieved by setting a diopter dial or knob on the eyepiece, which the user can adjust according to their visual condition.
(2) Autofocus system: In addition to manually adjusting the diopter, the camera should also be equipped with an advanced autofocus system. The system quickly and accurately identifies the subject and automatically adjusts the focus as needed to ensure crisp images [
31].
(3) Software design: In terms of software, the clarity of the image can be further improved through algorithm optimization. For example, image processing techniques can be utilized to correct image blurring due to diopter differences. After the image is collected, the image processing and analysis are automatically carried out, and the result is displayed to the user.
(4) Compatibility considerations: The camera may also consider compatibility with glasses or other vision aids. For example, special interfaces or accessories can be designed so that the user can wear glasses while using the camera.