Vibration Characteristics and Structural Optimization of Pipeline Intelligent Plugging Robot under Turbulent Flow Field Excitation

Abstract

Pipeline maintenance technology based on pipeline intelligent plugging robot (PIPR) has become an effective method for failure accident prevention of high-pressure subsea oil and gas pipelines. However, during the plugging operation, the vortexes and pressure fluctuation are presented under turbulent flow field excitation, which may lead to vortex-induced vibration and failure of the plugging operation. Therefore, in order to ensure the reliability of pipeline plugging, the vibration characteristics are analyzed using numerical simulation, providing guidance on the structural optimization of PIPR’s end face. Firstly, the flow field characteristics under different PIPR’s end faces are investigated. Secondly, an experimental scheme is designed based on Latin Hypercube Sampling Design (LHSD) optimized by greedy strategy. A mathematical model of the end face’s parameters and pressure gradient is established using a back propagation (BP) neural network. Then, an improved whale optimization algorithm (IWOA) is proposed to optimize the end face’s parameters to minimize the pressure gradient of the flow field. Finally, the experimental study is performed to observe the turbulent flow field and pressure fluctuation to validate the optimization results. The results demonstrate that the PIPR’s end face has a great influence on the vortex-induced vibration response. After structural optimization, the average pressure gradient of the optimal PIPR’s end face has decreased by 84.69% and 54.55% before and after the plugging process, compared to the original end face. This study can provide a reference for pipeline plugging operations, which is significant for preventing pipeline failure accidents.

1. Introduction

High-pressure subsea pipelines are crucial for oil and gas transportation. With the increase in service time, pipeline failure accidents have frequently occurred due to corrosion [1,2]. At present, the plugging technology of opening holes is relatively mature for pipeline maintenance. However, this technology requires making holes and much operation time [3], which can cause secondary damage to the pipeline and reduce the pipeline life. The location of opening holes is easily affected by the terrain, and the plugging distance and oil discharge can increase. Moreover, the opening holes method consumes a huge amount of human resources, and the high cost is beneficial for large-scale pipeline maintenance operations.

In recent years, subsea pipeline maintenance technology based on pipeline intelligent plugging robots (PIPR) has become an effective way for high-pressure intelligent plugging. The PIPR does not require reducing pipeline pressure and opening holes, which can ensure pipeline reliability and transportation efficiency. During the high-pressure plugging operation, the coupling vibration between the flow field and PIPR aggravates the deterioration damage of PIPR [4]. Therefore, it is of great significance to study the vibration characteristics and vortex-induced vibration suppression methods of PIPR under turbulent flow field excitation, thereby improving the plugging stability and preventing pipeline failure accidents.

Pipeline intelligent isolation plugging technology is widely used for the maintenance operation of high-pressure subsea pipelines. PIPR is a core part of the pipeline plugging operation. Plugging Specialists International (PSI) designed a high-pressure PIPR; the maximum plugging pressure can reach 25 MPa. The fixed-point plugging technology under the remote control of the pressure pipeline was developed by American T. D. Williamson (TDW) company, and the high-pressure plugging operation was completed under 35 MPa [5]. Oil States Hydro Tech is a company specializing in plugging and repairing subsea oil and gas pipelines [6]. This company can perform plugging operations at 1651 m below sea level. Zhu et al. [7] proposed a spherical PIPR with trajectory control algorithms for adjusting the rotation angle and vertical displacement. Yan et al. [8] designed a novel PIPR with airbag plugging, which consisted of a drive unit, a connection unit, and a blocking unit. Wu et al. [9] developed an energy-saving PIPR, where an impeller was introduced for energy conservation, and the fuzzy proportional integral derivative (PID) controller was used for velocity-tracking control. Tang et al. [10] innovatively designed a PIPR with an autonomous plugging hydraulic control system, and the changes in hydraulic cylinder parameters and axial displacement of rubber cylinders were studied. Miao et al. [11] proposed a modular composite-driven PIPR; the dynamic model and nonlinear controller were established for motion adjustment under deformation excitation. Gen et al. [12] used neural network methods to establish the relationship between PIPR’s slip parameters, and the functional relationship was optimized to obtain the optimal structural parameters for the maximum slip anchoring force. Mirshamsi et al. [13] developed two differential equations to obtain in-pipe transient compressible fluid properties. The differential motion equation of the PIPR’s speed regulation module was solved to obtain the speed and position. Liang et al. [14] designed a speed control system with a brake unit for PIPR, which could achieve active speed control for PIPR. Liu et al. [15] established a dynamic analytical model to describe the mechanical behaviors of PIPR’s speed regulation module and proposed a quantitative assessment method.

The plugging-induced vibration of the PIPR is the result of a multi-physics field. The vibration produced by external fluid pulsation is called external-induced excitation [16]. The common external-induced excitation is the problem of cylindrical disturbance, and the pressure pulsation of the in-pipe flow field is only related to the size of the turbulence, so this phenomenon is also called turbulent vibration [17,18]. In addition, alternatively, shedding the vortex near the cylindrical wake can occur due to the unstable motion of fluid, which also produces the vortex-induced vibration [19].

During the plugging process, due to the obstruction of PIPR, the in-pipe flow field can change violently, which causes turbulent vibration and instability of the plugging operation. In the past few years, research on the flow field characteristics and evolution law has been performed. Zhang et al. [20] investigated the pressure fluctuation characteristics using dynamic mesh simulation; the influence of deceleration time, flow velocity, and PIPR’s aspect ratio was analyzed, and the optimal parameters were obtained for reducing the pressure fluctuation. Tang et al. [21] analyzed the throttling pressure control flow field of the traction speed regulation and braking mechanism, and the influence of the speed control valve was studied. Miao et al. [22] designed a spoiler device for reducing the pressure difference of the flow field during the plugging process, and different plugging velocities were experimentally investigated to compare the pressure pulsation. Zhang et al. [23] simulated the transient pressure behaviors of PIPR in natural gas pipelines, and the implicit and explicit coupled method was developed for the simulation of moving interfaces.

In summary, the present relevant research has mainly focused on the mechanical structure and control system. Meanwhile, the turbulent flow field characteristics have been considered to ensure the plugging stability and the structure of PIPR has been optimized to reduce the turbulent vibration [24]. However, the limitations of the investigations reviewed above can be concluded as follows: (1) There are few reports on the influence of the end face’s structure on the vibration characteristics of PIPR. (2) Although the size of PIPR’s structure is optimized for vibration reduction, such as diameter and length, the size of the end face has not been considered for optimization. (3) The response surface method has been widely used for the structural optimization of PIPR, but this method is limited to nonlinear relationships. In addition, traditional optimization methods are prone to falling into local optimum, such as GA and PSO, which makes it difficult to achieve the global optimum.

In this paper, the vibration characteristics and structural optimization are investigated for PIPR under turbulent flow field excitation. The flow field characteristics of the plugging process under different PIPR’s end faces are analyzed. An experimental scheme for different end face parameters is designed based on LHSD optimized by greedy strategy. The nonlinear relationship between the end face’s parameters and the pressure gradient is established using the BP neural network. In order to minimize the pressure gradient of the flow field, an improved whale optimization algorithm (IWOA) is proposed to determine the optimal parameters of the end face. Finally, an experimental setup is established to verify the superiority of the optimized end face, and the turbulent flow field fluctuation is observed using particle image velocimetry (PIV) technology. This study can provide guidance for ensuring the reliability of plugging operation and provide a reference for the engineering design of PIPR.

2. Numerical Study

2.1. Physical Model

The PIPR in the high-pressure pipeline is mainly driven by the pressure difference between the front and rear liquid media. After reaching the designated operating position, the PIPR is remotely controlled by the control center to perform the plugging operation. The mechanical structure of PIPR mainly consists of a pressure-bearing platform, a pressure-bearing head, a sealing ring, a wedge-shaped cylinder, sliders, and a driving system, as shown in Figure 1. The wheel group distributed around the central axis of the PIPR can support the pipeline wall, which can ensure the stable movement of the PIPR. And the traditional PIPR’s end face is the footstep-shaped end face.

The schematic diagram of the plugging process is shown in Figure 2. During the plugging operation, the axial length of the PIPR is shortened from the original state to the completion, and the sliders distributed in the circumferential direction expand radially, which are stuck on the pipeline’s inner wall. The sealing ring deforms under axial compression, and it forms a high-pressure interference fit with the pipeline wall to achieve intelligent plugging.

2.2. Flow Field Model

The plugging-induced vibration of the PIPR is the result of multi-physics. During the plugging operation, in-pipe fluid decreases rapidly with the increase in the plugging process. The sudden contraction of the in-pipe flow field induces intermittent de-flow of the fluid near the plugging area. It can cause resonance damage and wake vortex of PIPR, resulting in a large vibration phenomenon [17,18]. The in-pipe fluid makes the pipeline structure vibrate, and the moving pipeline structure interacts with the PIPR, which in turn affects the vibration form of the in-pipe fluid. Therefore, a complex fluid–structure coupling phenomenon is formed.

The flow field model around the PIPR is shown in Figure 3. The length of the pipeline model is 10 m. The in-pipe medium is single-phase incompressible liquid gasoline, and the centerlines of the pipeline and PIPR are coincident. Numerical simulation of the plugging process is performed using ANSYS 18.1. The main parameters of the flow field model are shown in

Table 1. The main parameters of flow field model.

Parameter	Symbol	Value
The diameter of the pipeline	D	0.8 m
Flow density	ρ	830 kg/m3
Operating pressure	P0	5 MPa
Dynamic viscosity	µ	0.000332 kg/(m·s)
The length of PIPR	L	1110 mm
The length of upstream	L1	4445 mm
The length of downstream	L2	4445 mm
The diameter of PIPR	d	720 mm
The diameter of sliders	d1	640 mm

.

The boundary condition of the pipeline entrance is the velocity entrance, and the flow velocity is 3 m/s. The boundary condition of the pipeline outlet is the fully developed flow. The walls of the pipeline and PIPR are non-slip walls. The grids of the flow field model are divided using tetrahedral meshes, as shown in Figure 4.

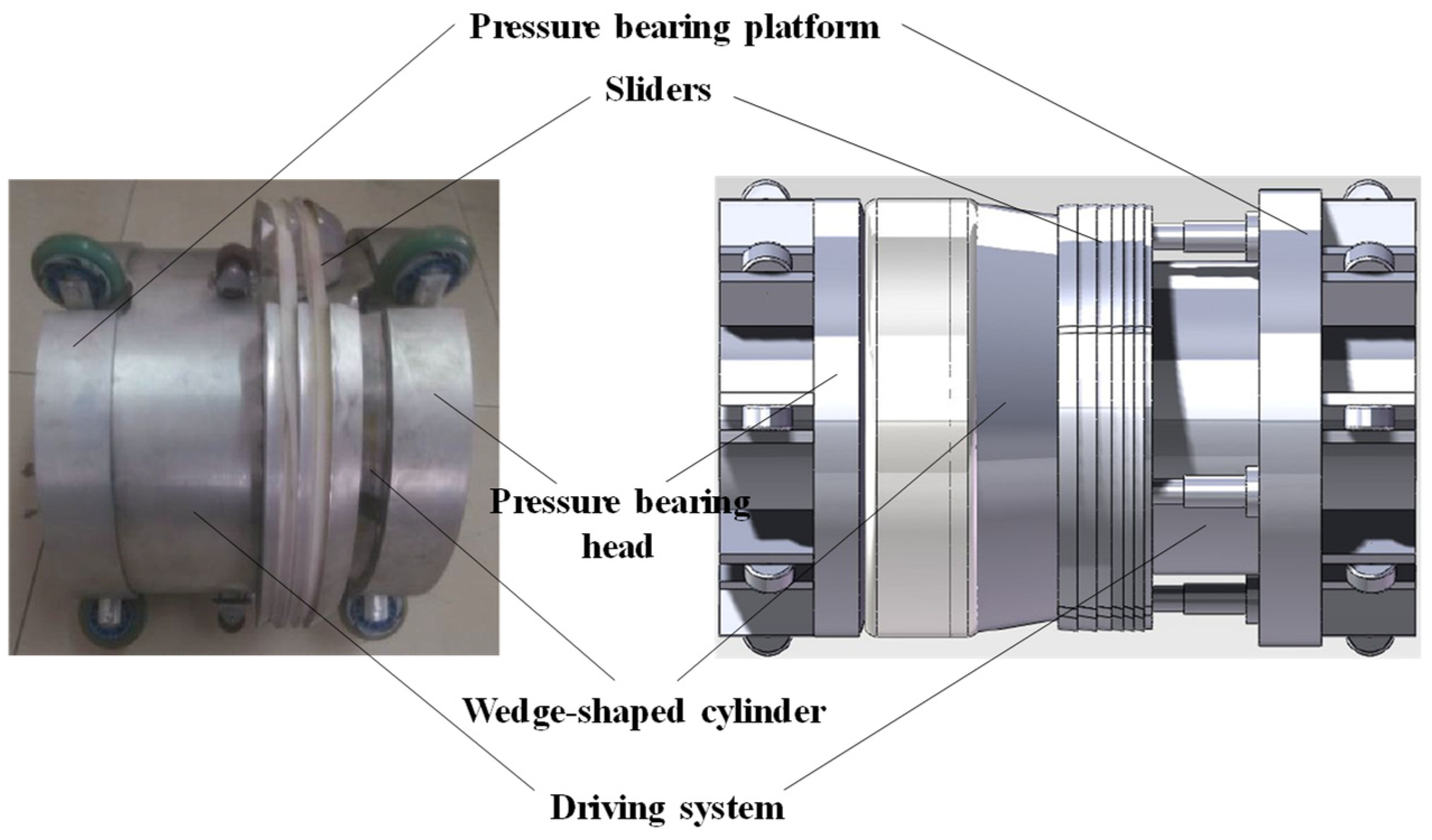
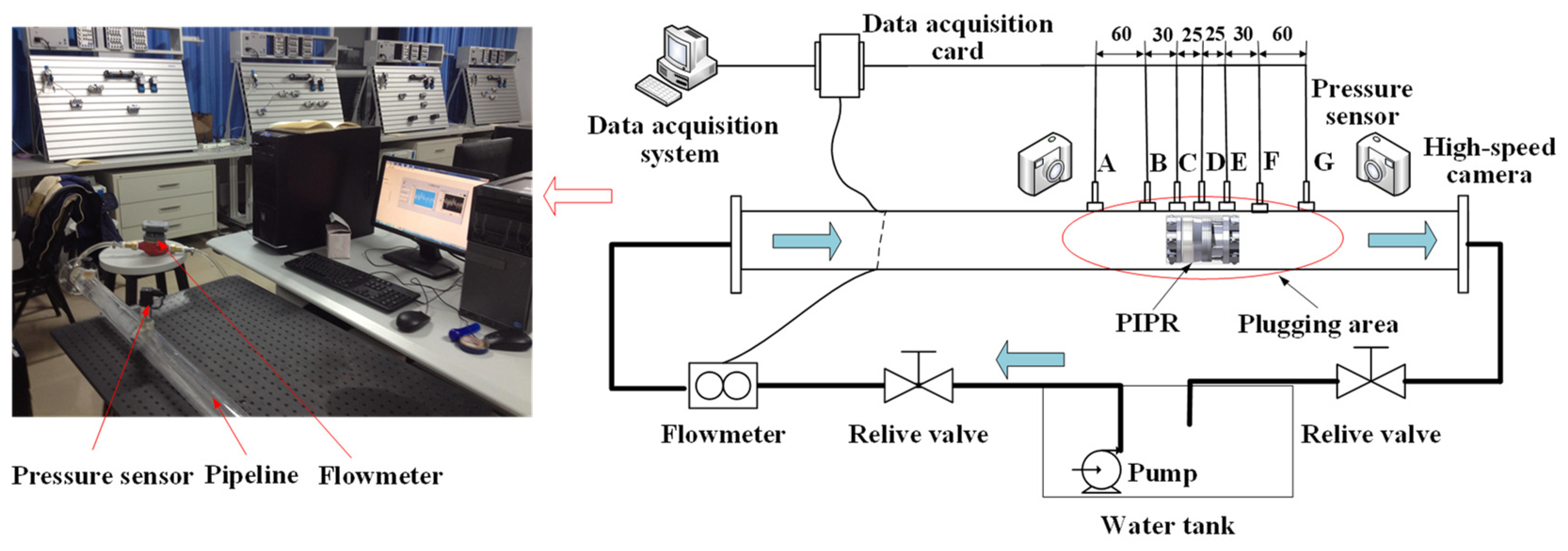
2.3. Numerical Simulation Results of Pipeline Plugging Process

During the plugging process, the motion of the in-pipe medium belongs to the problems of high Reynolds number. Assuming that the fluid in the pipeline is incompressible and no heat transfer occurs, the mass conservation equation and momentum conservation equation of the PIPR can be expressed as follows:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial (\rho V_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho V_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho V_z)}{\partial z}}=0$$

(1)

$$\{\begin{array}{c}\begin{array}{l}{\displaystyle \frac{\partial (\rho V_x)}{\partial t}}+{\displaystyle \frac{\partial (\rho V_x{V}_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho V_x{V}_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho V_x{V}_z)}{\partial z}}\\ ={\displaystyle \frac{\partial }{\partial x}}(\mu {\displaystyle \frac{\partial V_x}{\partial x}})+{\displaystyle \frac{\partial }{\partial y}}(\mu {\displaystyle \frac{\partial V_x}{\partial y}})+{\displaystyle \frac{\partial }{\partial z}}(\mu {\displaystyle \frac{\partial V_x}{\partial z}})+[-{\displaystyle \frac{\partial (\rho V_x^{\prime 2})}{\partial x}}-{\displaystyle \frac{\partial (\rho V_x^{\prime }{V}_y^{\prime })}{\partial y}}-{\displaystyle \frac{\partial (\rho V_x^{\prime }{V}_z^{\prime })}{\partial z}}]-{\displaystyle \frac{\partial p}{\partial x}}\end{array}\\ \begin{array}{l}{\displaystyle \frac{\partial (\rho V_x)}{\partial t}}+{\displaystyle \frac{\partial (\rho V_y{V}_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho V_y{V}_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho V_y{V}_z)}{\partial z}}\\ ={\displaystyle \frac{\partial }{\partial x}}(\mu {\displaystyle \frac{\partial V_y}{\partial x}})+{\displaystyle \frac{\partial }{\partial y}}(\mu {\displaystyle \frac{\partial V_y}{\partial y}})+{\displaystyle \frac{\partial }{\partial z}}(\mu {\displaystyle \frac{\partial V_y}{\partial z}})+[-{\displaystyle \frac{\partial (\rho V_x^{\prime }{V}_y^{\prime })}{\partial x}}-{\displaystyle \frac{\partial (\rho V_y^{\prime 2})}{\partial y}}-{\displaystyle \frac{\partial (\rho V_y^{\prime }{V}_z^{\prime })}{\partial z}}]-{\displaystyle \frac{\partial p}{\partial y}}\end{array}\\ \begin{array}{l}{\displaystyle \frac{\partial (\rho V_z)}{\partial t}}+{\displaystyle \frac{\partial (\rho V_z{V}_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho V_z{V}_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho V_z{V}_z)}{\partial z}}\\ ={\displaystyle \frac{\partial }{\partial x}}(\mu {\displaystyle \frac{\partial V_z}{\partial x}})+{\displaystyle \frac{\partial }{\partial y}}(\mu {\displaystyle \frac{\partial V_z}{\partial y}})+{\displaystyle \frac{\partial }{\partial z}}(\mu {\displaystyle \frac{\partial V_z}{\partial z}})+[-{\displaystyle \frac{\partial (\rho V_x^{\prime }{V}_z^{\prime })}{\partial x}}-{\displaystyle \frac{\partial (\rho V_y^{\prime }{V}_z^{\prime })}{\partial y}}-{\displaystyle \frac{\partial (\rho V_z^{\prime 2})}{\partial z}}]-{\displaystyle \frac{\partial p}{\partial z}}\end{array}\end{array}$$

(2)

Therefore, the simple algorithm was chosen for calculation. At the same time, due to the high Reynolds number in the flow field, large vorticity vibration is generated during the plugging process, so the model is set as the standard k-ε model, whose turbulent kinetic energy (k) equation (shown in Equation (3)) and turbulent dissipation rate (ε) equation (shown in Equation (4)) can be expressed as follows:

$$\begin{array}{l}{\displaystyle \frac{\partial (\rho k)}{\partial t}}+{\displaystyle \frac{\partial (\rho k{V}_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho k{V}_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho k{V}_z)}{\partial z}}\\ ={\displaystyle \frac{\partial }{\partial x}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x}}\right]+{\displaystyle \frac{\partial }{\partial y}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial y}}\right]+{\displaystyle \frac{\partial }{\partial z}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial z}}\right]+G_k+G_b-\rho \epsilon \end{array}$$

(3)

$$\begin{array}{l}{\displaystyle \frac{\partial (\rho \epsilon )}{\partial t}}+{\displaystyle \frac{\partial (\rho \epsilon V_x)}{\partial x}}+{\displaystyle \frac{\partial (\rho \epsilon V_y)}{\partial y}}+{\displaystyle \frac{\partial (\rho \epsilon V_z)}{\partial z}}\\ ={\displaystyle \frac{\partial }{\partial x}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial \epsilon }{\partial x}}\right]+{\displaystyle \frac{\partial }{\partial y}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial \epsilon }{\partial y}}\right]+{\displaystyle \frac{\partial }{\partial z}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial \epsilon }{\partial z}}\right]+C_{1\epsilon }{\displaystyle \frac{\epsilon }{k}}(G_k+C_{3\epsilon }{G}_b)-C_{2\epsilon }\rho {\displaystyle \frac{{\epsilon }^2}{k}}\end{array}$$

(4)

Among them, ${\mu }_t=c_{\mu }\rho {\displaystyle \frac{k^2}{\epsilon }}$, $C_{\mu }=0.09$, $C_{1\epsilon }=1.44$, $C_{2\epsilon }=1.92$, ${\sigma }_k=1$, ${\sigma }_{\epsilon }=1.3$.

Pipeline inner wall has a great influence on the turbulence model, while the standard k-ε model is mainly suitable for the calculation of turbulent flow field, where there may be a large velocity gradient, turbulent kinetic energy transfer, energy consumption, etc. Therefore, the near-wall method is selected, and enhanced wall processing is applied to improve the calculation accuracy.

Because the PIPR is operated under the action of in-pipe pressure difference, its motion law conforms to Newton’s second law.

$$m{\displaystyle \frac{dv}{dt}}=(P_1-P_2)A_d-F_g-F_f$$

(5)

Among them, v is the motion speed of PIPR, P₁ is the upstream pressure of PIPR, P₂ is the downstream pressure of PIPR, A_d is the equivalent cross-sectional area of PIPR, F_g is the component of the self-weight of the PIPR in the velocity direction, F_f is the friction force between the PIPR and the pipeline inner wall.

The component of the self-weight of the PIPR in the velocity direction is:

$$F_g=mg\sin \gamma$$

(6)

Among them, m is the mass of PIPR, g is the gravity acceleration, γ is the angle between the pipeline and the horizontal line.

The friction force F_f is caused by the interaction between the cup and the pipeline inner wall, which is an elastic deformation force. The friction force F_f of the PIPR is obtained according to the matching relationship between the cup and pipeline inner wall.

$$\{\begin{array}{l}{F}_f=2\pi r_p{L}_{pw}{\mu }_f{N}_f\hfill \\ N_f={\displaystyle \frac{E_i{\delta }_p}{r_p\left(1-v_i\right)}}\hfill \end{array}$$

(7)

Among them, $r_p$ is the radius of PIPR, $L_{pw}$ is the contact length between the PIPR and pipeline wall, ${\mu }_f$ is the friction coefficient between the PIPR and pipeline wall, $N_f$ is the pressure of the contact surface, $E_i$ is the elastic modulus of the cupola material, ${\delta }_p$ is the change value of the cupola in the direction of the radius, and ${\epsilon }_i$ is the Poisson ratio of the cupola material.

By substituting Equations (6) and (7) into Equation (5), the force model of the PIPR during the plugging process can be expressed as:

$$m{\displaystyle \frac{dv}{dt}}=(P_1-P_2)A-mg\sin \gamma -2\pi r_p{L}_{pw}{\mu }_f{\displaystyle \frac{E_i{\delta }_p}{r_p\left(1-{\epsilon }_i\right)}}$$

(8)

Without considering the energy input outside the PIPR, the axial motion model of the PIPR can be expressed as follows:

$${\rho }_p{\displaystyle \frac{\partial v_z}{\partial t}}+{\rho }_p{v}_z{\displaystyle \frac{\partial v_z}{\partial z}}+{\rho }_p{v}_r{\displaystyle \frac{\partial v_z}{\partial r}}=f_{pz}+{\displaystyle \frac{\partial {\sigma }_z}{\partial z}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \left(r{\tau }_{rz}\right)}{\partial r}}$$

(9)

The radial motion model of the PIPR is as follows:

$${\rho }_p{\displaystyle \frac{\partial v_r}{\partial t}}+{\rho }_p{v}_z{\displaystyle \frac{\partial v_z}{\partial z}}+{\rho }_p{v}_r{\displaystyle \frac{\partial v_r}{\partial r}}=f_{pr}+{\displaystyle \frac{\partial {\tau }_{rz}}{\partial z}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \left(r{\sigma }_r\right)}{\partial r}}-{\displaystyle \frac{{\sigma }_{\theta }}{r}}$$

(10)

Among them, $\rho$_p is the density of the PIPR, v_z is the axial velocity of the PIPR, v_r is the radial velocity of the PIPR, f_pz is the axial component of the volume force of the PIPR, f_pr is the radial component of the volume force of the PIPR, $\sigma$_r is the radial stress of the PIPR, ${\sigma }_{\theta }$ is the circumferential stress of the PIPR, and $\tau$_rz is the shear stress of the PIPR.

The numerical simulation of the traditional PIPR with the footstep-shaped end face is performed. In order to observe the simulation results of the in-pipe obstructed flow field more intuitively, the center surface of the pipeline is taken as the observation surface. Figure 5a shows the fluid pressure on the center surface of the pipeline before the plugging operation. It can be seen that the pressure downstream of the flow field shows a clear regional distribution and a decreasing trend along the flow direction. This pressure distribution is mainly caused by the external structure of the PIPR. Figure 5b shows the distribution of fluid pressure on the center surface of the pipeline when the plugging process reaches 99%. It can be seen that a significant pressure difference has occurred between the upstream and downstream. The continuous accumulation of high-pressure fluid in the upstream leads to an increase in in-pipe pressure, which can cause large shock vibrations on the PIPR.

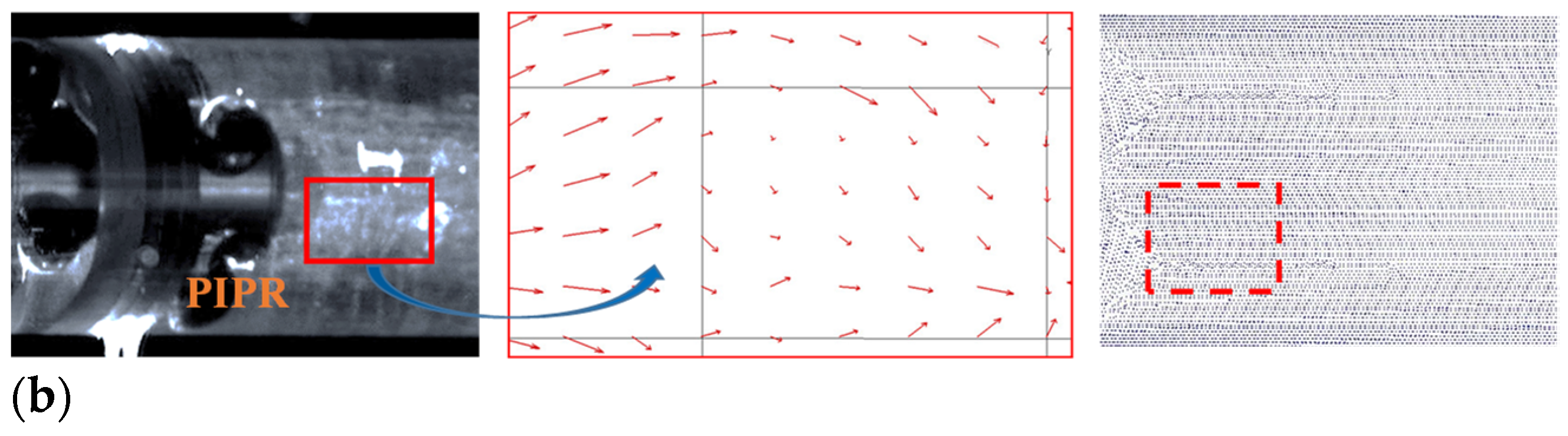
The velocity distribution of the flow field around the PIPR is shown in Figure 6. Through the plugging operation, the velocity values of in-pipe fluid particles vary significantly. As shown in Figure 6a, before the plugging process starts, there is a local area on the front-end face of the PIPR with a flow velocity close to zero, called the stagnation zone. The blockage of the PIPR can lead to the dissipation of fluid kinetic energy. At the same time, the fluid also causes a certain impact on the PIPR. Boundary layer separation and vortex have occurred at the edge of the PIPR’s tail, which can form a clear reflux zone with a certain fluctuation in the flow direction. Due to severe energy loss in the reflux zone, the flow velocity significantly decreases. The flow velocity distribution after the plugging process is shown in Figure 6b. The fluid inside the entire pipeline is almost stagnant, indicating that the upstream and downstream of the PIPR are isolated. At this time, the plugging operation is completed.

Figure 7 shows the velocity distribution of fluid particles on the central surface of the pipeline. It is clearly shown that the highest velocity of in-pipe fluid particles exists in the gap between the PIPR and pipeline wall. Comparing Figure 7a,b shows that with the increase in plugging progress, the velocity of fluid particles in the gap becomes higher. The velocity value after the plugging process is much higher than that before the plugging process. As the plugging operation progresses, the pressure difference before and after the PIPR continues to increase, and the fluid passing through the slit also gains more kinetic energy.

The force acting on the PIPR is particularly important for the structural design and control of the PIPR, which directly determines the movement status of the PIPR. Therefore, the relationship between the force of the PIPR, plugging process, and pipeline operating parameters is analyzed, as shown in Figure 8. Figure 8a shows the relationship between the force of the PIPR and the plugging process and inlet pressure. From the initial state to the plugging state of 80%, the in-pipe upstream pressure increases, which can increase the force on the PIPR continuously. Until the plugging process reaches 80%, the force of PIPR begins to decrease due to the in-pipe pressure distribution. The pressure difference between the upstream and downstream is relatively large, and negative pressure may occur in some areas. Therefore, the pressure generated on the PIPR can be partially offset. Figure 8b shows the relationship between inlet velocity and the plugging process, as well as the force of the PIPR. It can be seen that the plugging process and inlet velocity have a significant impact on the force fluctuation of the PIPR. The smaller the inlet velocity, the smaller the impact force on the PIPR. When the plugging process reaches 50%, the flow velocity directly affects the in-pipe pressure distribution.

In summary, all three variables involved have a significant influence on the force of the PIPR, and the effects of the plugging process and inlet velocity are more pronounced. The PIPR with the original stepped end face bears a high level of stress during the later stage of the plugging process. In addition, significant pressure fluctuations and vortex-induced vibration occur, mainly caused by the increased turbulent flow field excitation, and the plugging operation is not stable. Therefore, the PIPR’s end face with a certain degree of radian is proposed to reduce the disturbance and pressure gradient of the in-pipe flow field.

2.4. Numerical Simulation Results of PIPR with Different End Faces

According to the evolution law of the in-pipe flow field during the plugging process, the PIPR’s end face has a great influence on vibration characteristics. In this section, two types of PIPR end faces are used for comparison with the traditional footstep-shaped end face, namely hemispherical-shaped end face and parabolic-shaped end face, as shown in Figure 9. The parameter settings of the grid model and boundary condition remain unchanged.

2.4.1. Numerical Simulation Results of PIPR with Hemispherical-Shaped End Face

The pressure distribution of the PIPR with a hemispherical-shaped end face is shown in Figure 10. It can be seen that the upstream fluid pressure after the plugging process is smaller than that of PIPR with the original footstep-shaped end face. Therefore, the hemispherical structure of the PIPR plays a significant role in the redistribution of pressure during the plugging operation. During the plugging operation, although the pressure distribution trend on the hemispherical surface is roughly the same as that of the footstep-shaped end face, the pressure distribution near the downstream low-pressure area is different before the plugging process. The pressure gradient area is relatively small. From the perspective of the PIPR’s force, the PIPR with a hemispherical end face is not greatly influenced by the low-pressure area.

The velocity distribution of the flow field around the PIPR with a hemispherical-shaped end face is shown in Figure 11. Compared with the PIPR with a footstep-shaped end face, the velocity of the flow field around the PIPR with a hemispherical-shaped end face is not uniformly distributed before plugging. A thicker boundary layer area appears upstream of the PIPR, and the stagnation area near the front-end face of the PIPR is smaller. The distribution of fluid particles with high velocity is roughly the same as that of the PIPR with a footstep-shaped end face. Two stagnation regions extend on the rear end face, and the downstream flow field is not symmetrically distributed.

It can be seen from Figure 12 that the distribution of fluid particles on the entire center plane was relatively stable before the plugging process, and the overall level of in-pipe flow velocity is lower than that of the original model. In the later stage of the plugging process, the flow velocity is almost zero, and only fluid particles that pass through the narrow gap between the PIPR and pipeline inner wall have high velocity. There is a significant difference in the flow field of the downstream compared to the footstep-shaped end face. The separation points of the boundary layer move backward due to the hemispherical surface, which can result in weaker separation intensity and a reduction in the area affected by downstream vortices. The stable flow field only exerts force on the PIPR from the static pressure, and it does not generate fluctuations to interfere with the plugging operation.

2.4.2. Numerical Simulation Results of PIPR with Parabolic-Shaped End Face

The pressure distribution of the PIPR with a parabolic-shaped end face is shown in Figure 13. Figure 13a shows the three pressure distribution areas near the rear end facing downstream, and the pressure values increase in sequence along the flow direction. The pressure near the rear end face is the smallest, which is similar to the pressure distribution trend of the PIPR with a footstep-shaped end face. Figure 13b shows the pressure distribution in the later stage of the plugging process, which includes the upstream high-pressure zone and downstream low-pressure zone. The in-pipe pressure distribution trend of different end faces is basically the same at the end of the plugging process, but the pressure values are different. After comparison, the in-pipe pressure of the PIPR with a parabolic-shaped end face is the highest. High pressure generates static pressure directly acting on the body of the PIPR, which can cause compression on the overall structure of the PIPR.

The velocity distribution of the flow field around the PIPR with a parabolic-shaped end face is shown in Figure 14. Figure 15 shows the distribution of fluid particles on the entire center plane. Similar to the footstep-shaped end face, the thickness of the boundary layer area is relatively thin, and there are gradient zones with different velocity values in the downstream area. The higher the flow velocity, the greater the kinetic energy of the fluid particles and the greater the impact on the PIPR, which is not conducive to the stability of the plugging operation.

3. Structural Optimization of PIPR’s End Face

3.1. The Improved Model of PIPR

Based on the numerical simulation in Section 2, the PIPR’s end face has a great influence on the vibration characteristics during the plugging process. Therefore, an improved model of PIPR is proposed for structural optimization of PIPR’s end face. The schematic diagram of the improved model is shown in Figure 16. For practical engineering, PIPR usually works together with other functional modules [25], such as pipeline inspection gauge (PIG), anchoring module, etc. They are connected to each other by connecting rods and ball bearings, resulting in a connection groove in the center of PIPR’s end face, as shown in Figure 16. The shape parameter S_p is proposed for measuring the type and curvature of curved surfaces, and its value is related to the eccentricity e of the conic curve. The shape of the end face is elliptical when 0.01 ≤ S_p < 0.5. If S_p = 0.5, it is a parabolic-shaped end face. When 0.5 < S_p ≤ 0.99, it is an end face with the shape of a double-leaf hyperbolic.

The parameters and boundary conditions of the flow field model remain unchanged. The pressure and velocity distribution of the original plugging state are analyzed. Figure 17 shows the cloud map of fluid pressure distribution. It can be seen that the pressure of the improved model has decreased due to the improved end face. Local high pressure has occurred at the connection groove position, and the fluid pressure changes violently in the narrow gap between the PIPR and pipeline inner wall, which causes an impact on the pipeline wall. Overall, the pressure distribution of the flow field around the PIPR from upstream to downstream is clearly localized and radially symmetrical. The low-pressure area is mainly concentrated in the flow field near the tail of the PIPR, and the generation of backflow and vortices results in a large amount of energy loss.

Figure 18 shows the cloud map of in-pipe flow velocity distribution. It can be seen that the upstream flow field of the PIPR is stable, and the flow velocity is obviously low with the improved model. The flow velocity near the connection groove of the front end face is almost zero due to the obstruction of the connection groove on the fluid in this area, which results in a large amount of kinetic energy loss. Similar to the original structure, when the fluid passes through the narrow gap between the PIPR and pipeline inner wall, the flow velocity significantly increases due to the small area and high pressure. After passing through the narrow gap due to the opening of the flow channel, the flow velocity shows a deceleration trend. In addition, there is a clear reflux phenomenon at the tail of the PIPR, resulting in a lower velocity and a stagnation point area. And it can cause resistance to the forward movement of the PIPR. At the same time, the flow velocity contour at the tail of the PIPR is conical, which is similar to the contour of the rear-end face.

3.2. Experimental Scheme Based on LHSD Optimized by Greedy Strategy

Although the improved model of PIPR can reduce the pressure impact compared to the original model, turbulent vibration caused by pressure fluctuation has also influenced the stability of the plugging process. Therefore, the end face of PIPR is optimized to reduce the pressure fluctuation. The response surface method is widely used for structural optimization, but the experimental schemes designed by this method are limited, and the polynomial fitting is not suitable for complex nonlinear relationships. For these problems, LHSD is proposed for the design of the experimental scheme. In order to make the sample distribution more uniform, the greedy strategy is introduced for global optimization, which can ensure the space-filling properties and equilibrium properties [26]. Aiming at the structure of PIPR’s end face, the thickness of the surface (s), bottom height (h), the radius of the connection groove (r), and shape parameter (S_p) are selected as optimization variables. The ranges of each optimization variable are shown in

Table 2. The ranges of each optimization variable.

Optimization Variable	Range
s	14–24 cm
h	2–12 cm
r	2–8 cm
Sp	0.01–0.99

.

The pressure gradient of the flow field is an index for measuring the pressure fluctuation [27]. The average absolute pressure values of 12 planes at different positions are extracted; the coordinates are shown in

Table 3. The coordinates of 12 planes at different positions.

Number	1	2	3	4	5	6	7	8	9	10	11	12
Z/cm	−110	−90	−70	−50	−30	−10	10	30	50	70	90	110

. Pressure gradient values between adjacent points can be obtained, as shown in Equation (11). The average pressure gradient ($\overline{{\displaystyle \frac{\Delta P}{\Delta L}}}$) of all positions is the optimization objective, which is related to the stability of the flow field.

$${\displaystyle \frac{\Delta P}{\Delta L}}=\left|{\displaystyle \frac{P_2-P_1}{L_2-L_1}}\right|$$

(11)

where P₁ and P₂ are the pressure values of different positions; L₁ and L₂ are the coordinates of different positions.

Within the range of optimization variables, 300 sets of experiments are designed using the LHSD optimized by greedy strategy. According to the experimental schemes, the average pressure gradient of each group is calculated through numerical simulation. Partial results are shown in

Table 4. The simulation results of different parameters of the end face.

Number	s/cm	h/cm	r/cm	Sp	$\overline{\frac{\mathbf{\Delta }\mathit{P}}{\mathbf{\Delta }\mathit{L}}}$/Pa/m
1	22.45	10.73	4.99	0.66	31,254.11
2	14.60	11.93	3.76	0.10	28,827.85
3	16.97	5.22	7.29	0.78	30,020.79
4	18.40	8.04	6.28	0.99	32,902.59
5	20.27	9.39	5.58	0.47	29,739.70

.

3.3. Pressure Gradient Model Based on BP Neural Network

In order to analyze the influence of four optimization variables on the average pressure gradient, the significance test is performed, as shown in

Table 5. The results of the significance test.

Variable	F Value	p Value Prob > F
s	1.59	0.2268
h	5.38	0.0348
r	2.17	0.1615
Sp	11.84	0.0036

. The p value of less than 0.05 indicates that the variables are significant. It can be seen that the influence of h and S_p is greater than that of the other two variables. The significance of the four variables is ranked as S_p > h > r > s.

The interactive influence of optimization variables is shown in Figure 19. It can be seen that the curved surfaces are a downward depression. The influencing trend of the four optimization variables is different, and the influence of S_p is the most obvious. With the increase in S_p, the average pressure gradient first decreases and then increases. When S_p is small, with the increase in h, the average pressure gradient gradually increases; when S_p is large, with the increase in h, the average pressure gradient first increases and then decreases. For s, when S_p is small, with the increase in s, the average pressure gradient gradually increases, but the trend is contrary when S_p is large. For r, when S_p is small, with the increase in r, the average pressure gradient gradually decreases, but the trend is contrary when S_p is large.

BP neural network is a multi-layer feed-forward network trained by the error inverse propagation algorithm. It uses the gradient descent method to continuously adjust the weights and thresholds so that the error is minimized. Then, the nonlinear mapping relationship between the input data and output data is established. Due to the advantages of nonlinear fitting of the BP neural network, the BP model for PIPR’s end face parameters and average pressure gradient is constructed, as shown in Figure 20. The BP model includes one input layer, one hidden layer, and one output layer. The neuro number of the hidden layer is 5. The maximum number of training epochs and learning rate of the gradient descent algorithm is set to 100 and 0.1, respectively. Eighty percent of experimental samples are selected as a training set, and twenty percent of experimental samples are selected as a test set.

The prediction results of the average pressure gradient based on the BP neural network are shown in Figure 21. It can be noticed that the prediction results are roughly all distributed around a curve with a slope of 1, which indicates that the BP model has a good prediction performance. To verify the advantages of the established BP neural network model, the support vector machine (SVM), generalized regression neural network (GRNN), random forest (RF), and response surface method are used for comparison. Three evaluation metrics are selected to measure the regression effect, namely the mean average error (MAE), mean absolute percentage error (MAPE), and coefficient of determination (R²).

Table 6. The evaluation metrics of different methods.

Method	MAE	MAPE	R2
BP	23.514	0.001	0.999
SVM	1405.042	0.044	0.222
GRNN	331.243	0.011	0.932
RF	2049.021	0.064	1.737
Response surface method	800.429	0.025	0.376

shows the evaluation metrics of different methods. Compared with other methods, the MAE and MAPE of the BP neural network are smaller, and the R² of the BP neural network is closer to 1, which indicates that the prediction capability of the BP model is more precise and reliable. Meanwhile, the differences in MAE, MAPE, and R² of different methods are large. The comparison results demonstrate that the BP model can achieve accurate prediction for the average pressure gradient.

3.4. The Optimization Results of PIPR’s End Face

Based on the established pressure gradient model, the parameters of PIPR’s end face are optimized to minimize the average pressure gradient of the flow field. The fitness function is shown in Equation (12). WOA is a biological heuristic algorithm developed based on the hunting behavior of humpback whales [28]. It updates the position by simulating the way humpback whales search, surround, and capture food to realize the optimization process. Compared to traditional optimization algorithms, WOA has good optimization performance and convergence stability. The search space of WOA is constructed by the four parameters of PIPR’s end face, and the optimal parameter combination is the optimal location of the whale population. The search process for the optimal parameter combination can be transformed into a swarm search process for the whales’ optimal location.

$$\begin{gathered} F\left(X\right)=\min f\left(s,h,r,S_p\right)=\min {\displaystyle \frac{\overline{\Delta P}}{\Delta L}} \\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}14\le s\le 24\\ 2\le h\le 12\\ 2\le r\le 8\\ 0.01\le S_p\le 0.99\end{array} \end{gathered}$$

(12)

However, for the spiral-hunting mechanism of WOA, the convergence speed in the later stage can be improved, but this method can also cause the population to rapidly gather in the solution space, which leads to a decrease in population diversity and increases the possibility of local optimum. Therefore, the golden sine algorithm (GSA) is introduced to improve the WOA. For this algorithm, the whales capture their prey using a gold sinusoidal spiral motion. At each iteration, the whales communicate information with the optimal individual, and they learn the position difference between themselves and the optimal individual. Meanwhile, the coefficient obtained by the golden section is used to gradually reduce the search space, and the distance and orientation of position updating can be controlled. The optimization method of basic WOA has been improved, which can coordinate global exploration and local development so as to improve the optimization accuracy and convergence speed. The position updating based on GSA can be expressed as follows:

$$X\left(t+1\right)=X\left(t\right)\times \left|\sin \left(R_1\right)\right|+R_2\times \sin \left(R_1\right)\times \left|x_1\times X^{*}\left(t\right)-x_2\times X\left(t\right)\right|$$

(13)

where R₁ is a random number of [0, 2π], which determines the moving distance of the individuals in the next iteration; R₂ is a random number of [0, π], which determines the location updating direction of the individuals in the next iteration; x₁ and x₂ are the coefficients by introducing the golden section, they are expressed as follows [29,30]:

$$\begin{array}{l}{x}_1=-\pi +\left(1-\tau \right)\times 2\pi \\ x_2=-\pi +\tau \times 2\pi \\ \tau ={\displaystyle \frac{\sqrt{5}-1}{2}}\end{array}$$

(14)

The population size of IWOA is 30, and the maximum number of iterations is 200. The values of the fitness function of IWOA and WOA are shown in Figure 22. It can be seen that the original WOA and IWOA both have faster convergence speeds, but the final results of IWOA are smaller than that of WOA, which indicates the advantages of the WOA algorithm improved by GSA.

In order to verify the superiority of IWOA for the optimization of PIPR’s end face, the optimization results of WOA, GA, PSO, and response surface method are compared, as shown in

Table 7. The optimization results of different methods.

Method	s/cm	h/cm	r/cm	Sp	$\overline{\frac{\mathbf{\Delta }\mathit{P}}{\mathbf{\Delta }\mathit{L}}}$/Pa/m
IWOA	18.76	4.25	7.17	0.27	25,135.38
WOA	14	2	8	0.33	27,164.62
PSO	24	2	8	0.59	26,144.70
GA	14.08	2.02	7.83	0.33	27,221.86
Response surface method	14.09	2.02	7.19	0.32	27,391.37
Before optimization	24	12	8	0.01	33,565.43

. It can be seen that the average pressure gradient obtained by IWOA is the smallest. Compared with the improved PIPR model before optimization, the average pressure gradient has decreased by 25.11%. The optimization results of the WOA, GA, and response surface methods are similar, and PSO has better optimization performance compared to these three methods. Therefore, the end face optimized by IWOA can effectively reduce the pressure fluctuation, which is significant for turbulent vibration suppression of the flow field.

4. Experimental Study

4.1. Experimental Setup

In order to verify the optimization results of PIPR’s end face, an experimental setup was designed, as shown in Figure 23. The experimental system includes a hydraulic pump, relive valve, flowmeter, pressure sensor, and data acquisition system. During the experiment, the hydraulic pump was first opened to inject the water into the pipeline, and the pressure data were collected when the pipeline was filled with a smoothly flowing medium. Due to the limited space, a similarity experiment was performed on the pipeline with a 50 mm diameter, and the structural parameters of PIPR were proportionally reduced. To study the flow field characteristics at different locations, seven observation points were set on the pipeline, namely A–G in Figure 23. With the increase in the plugging process, the in-pipe flow field changes more dramatically. Therefore, the observation points are not evenly distributed, and they are more concentrated at the position of complete plugging. To observe the in-pipe flow field more clearly, a transparent pipeline of organic glass was used to capture the motion trajectory of the particles through PIV technology. The PIV system included high-speed cameras, a telocentric lens, and a laser generator. A detailed description of experimental equipment is shown in

Table 8. A detailed description of the experimental equipment.

Experimental Equipment	Type	Measurement Range	Accuracy
Flowmeter	LDG-MIK-DN 50	0–10,000 m3/h	0.3%
Pressure sensor	MIK-P300	0–1 MPa	0.1%
Data acquisition system	NI-PXI-6236	-	16 bit
High-speed camera	Hi-Sense 600	-	-
Laser generator	Dual-Power	0–400 mJ	-

.

To validate the advantages of PIPR’s end face optimized by IWOA, the improved PIPR model before optimization and the original PIPR model were used for comparison. Based on the numerical simulation and optimization results in Section 3, the end face optimized by IWOA is elliptical. Before optimization, the improved PIPR model had a parabolic-shaped end face, and the original PIPR model had a footstep-shaped end face, as shown in Figure 1. The PIPRs with three different end faces were used in the plugging experiment, respectively. The vibration characteristics and pressure fluctuation of the flow field were compared for three PIPR’s end faces.

4.2. Experimental Results of PIPRs with Three Different End Faces

The results of the PIV experiment for PIPRs with three different end faces are shown in Figure 24, Figure 25 and Figure 26. It can be seen from Figure 24 that the surrounding flow field is relatively stable, benefiting from the end face optimized by IWOA. Before the plugging process, there are no vortices of varying sizes in the flow field. At the end of the plugging operation, there is no vortex or backflow phenomenon in the experiment. From the velocity vector distribution of numerical simulation, a symmetrical vortex appears at the tail of PIPR. And fluid particles still smoothly transition along the surface of the elliptical end face. Figure 25 shows the unstable flow field and vortex structure for the improved PIPR model before optimization. When fluid particles pass through a narrow pipeline wall, there is no smooth transition, which is caused by fluid backflow. For the original PIPR model with a footstep-shaped end face in Figure 26, the vortex structure is more obvious, and fluid particles are more densely distributed. When the plugging operation is nearly completed, most of the in-pipe fluid particles are basically in a static state, and the original vortex structure and flow field characteristics at the tail of PIPR gradually disappear, which is consistent with the numerical simulation results.

The tail flow field of the PIPR with a curved end face is stable, and the vortex evolution has finished before the plugging operation is completed. Because the curved structure can make fluid particles flow more smoothly compared to a footstep-shaped structure, there are no obvious flow field characteristics like the tail of PIPR with a footstep-shaped end face. For the flow field characteristics at the tail of PIPR, the tail flow field of improved PIPR’s end face optimized by IWOA is more stable than the other two models, which can ensure the stable development of in-pipe flow field and the thorough evolution of vortex structure. In summary, the optimization of PIPR’s end face can reduce the impact caused by turbulent flow field excitation.

To verify the similarity between experimental and simulation results, the pressure values of monitoring point A during the plugging process are obtained and compared for the original footstep-shaped PIPR’s end face, as shown in Figure 27. For the leakage that exists in the experimental setup, the experimental results are slightly smaller than the simulation results, but the maximum relative errors are only 10.33%. Therefore, the plugging experiment and numerical simulation are consistent.

In order to observe the pressure fluctuation of the flow field for the above three PIPR’s end faces, namely the improved PIPR’s end face optimized by IWOA (Model 1), improved PIPR’s end face before optimization (Model 2), and original footstep-shaped PIPR’s end face (Model 3), the pressure values of seven observation points (A–G) are compared, as shown in Figure 28. Due to the similarity experiment, the pressure of the flow field is smaller than that of the experiment. Before the plugging operation, the pressure values of Model 1 were stable and smaller than that of Model 2. The upstream pressure and downstream pressure of Model 3 are larger, and the pressure variation is more drastic. After the plugging operation, the pressure values of the plugging area and downstream of Model 1 are smaller in general. The pressure oscillation of Model 2 and Model 3 is larger than that of Model 1.

Table 9. The average pressure gradient of different PIPR end faces.

PIPR’s End Face	Before the Plugging Process	After the Plugging Process
Model 1	0.15 Pa/m	0.30 Pa/m
Model 2	0.80 Pa/m	0.94 Pa/m
Model 3	0.98 Pa/m	0.66 Pa/m

shows the average pressure gradient of seven observation points of different PIPR’s end faces. Before and after the plugging operation, the average pressure gradient of Model 1 decreased by 84.69% and 54.55% compared with that of Model 3. After comparison, the values of the average pressure gradient of Model 1 are the smallest. Therefore, the pressure fluctuation of the turbulent flow field can be greatly reduced through the structural optimization of PIPR’s end faces.

5. Conclusions

In this study, the vibration characteristics and structural optimization of PIPR under turbulent flow field excitation are investigated. The flow field characteristics of different PIPR’s end faces before and after the plugging process are analyzed using numerical simulation. In order to reduce the pressure fluctuation of the flow field, an experimental scheme for optimization of PIPR’s end face is designed based on LHSD optimized by greedy strategy. According to the simulation results under different end face parameters, the BP neural network is used to construct the nonlinear model between the end face’s parameters and pressure gradient. The WOA improved by GSA is proposed to minimize the average pressure gradient by optimizing the end face’s parameters. Finally, an experimental setup is established to observe the turbulent flow field fluctuation and pressure fluctuation. The main conclusions can be summarized as follows:

(1)

In-pipe flow field characteristics are different under different PIPR’s end faces, and the curved end faces can reduce the vortex-induced vibration and pressure shock on the PIPR.

(2)

The end face’s parameters have different influences on the pressure gradient. The prediction errors of the BP neural network are smaller than those of other methods; the values of MAE, MAPE, and R2 are 23.514, 0.001, and 0.999, respectively.

(3)

The optimization results of PIPR’s end faces optimized by IWOA are the best. Compared with the improved PIPR model before optimization, the average pressure gradient has decreased by 25.11%.

(4)

The results of the PIV experiment show that the tail flow field of the optimal PIPR’s end face is more stable, and the average pressure gradient has decreased by 84.69% and 54.55% before and after the plugging process.

This study is significant for the structural design of PIPR and ensuring the plugging stability, which can provide guidance for pipeline failure prevention. However, during the plugging operation, in-pipe multiphase flow may influence the flow field characteristics. Consequently, further study will focus on the interaction of transient multiphase flow and PIPR in numerical and experimental tests.