Enhancing Precision in SQUID Sensors: Analyzing Washer Geometry Dependence at the Microscale

Abstract

In the field of high-precision physical field detection, measurements based on magnetic signals are crucial due to their exceptional accuracy, sensitivity, and stability. Superconducting Quantum Interference Devices (SQUIDs), with their ultra-high sensitivity, have become key in detecting minute changes in magnetic flux. However, with increasing demands for higher precision, further enhancing device performance under quantum constraints remains a significant challenge. This study improved the precision of SQUID sensors by optimizing the geometry of microscale washers using the physical response of superconducting films under micromachining technologies and quantum constraints. Our research extensively examined the effects of square, octagonal, and circular washers on the magnetic field response, shielding currents, and inductance. Experimental results showed that, compared to traditional square washers, octagonal washers significantly enhanced sensor sensitivity and efficiency by minimizing edge magnetic flux and optimizing current distribution. Notably, all observed inductance values exceeded predictions based on traditional empirical formulas, with square washers showing the highest average relative error of 80.8%, while circular and octagonal washers had errors of 65.31% and 66.43%, respectively. This breakthrough not only lays a new theoretical foundation for the design of SQUID sensors but also provides robust evidence for enhancing magnetic field detection through microscale technological innovation.

1. Introduction

Low-frequency magnetic fields are omnipresent and offer crucial insights across a broad spectrum of applications. The multitude of sensing scenarios and the prevalence of numerous physical systems demonstrating significant magnetic responses have catalyzed the development of diverse magnetometer technologies [1].

Ultrasensitive magnetic sensors [2,3,4] play a vital role in various technical fields [3]. The non-contact measurement characteristics of magnetic sensors enable them to work without disturbing the observation system [2,3]. This characteristic inspires an increasing number of scientists to dedicate themselves to magnetic sensing research [4] and thus develop various precision measurement instruments, including Superconducting Quantum Interference Devices (SQUIDs), Giant Magnetoresistance (GMR), Tunneling Magnetoresistance (TMR), Hall Effect Sensors [4], Diamond Magnetometers based on Nitrogen Void (NV) Centers [5], and Atomic Magnetometers [6]. Among them, due to their ultra-high sensitivity, wide dynamic range, frequency response, minimal measurement disturbance, and broad application areas, SQUIDs have emerged as one of the most popular choices for ultrasensitive magnetic sensors [3,7,8,9,10]. The current research focuses on the further miniaturization of SQUIDs and efforts to enhance their sensitivity and field resolution. Researchers are actively pursuing strategies to increase the accessibility of SQUIDs for various applications by reducing their design and manufacturing costs.

DC Superconducting Quantum Interference Devices (DC SQUIDs) [11] are the world’s best-performing magnetic flux detectors [9,10]. These magnetic sensors utilize flux quantization [12] and Josephson tunneling effects [13,14].

Specifically, flux quantization dictates that, in a superconducting loop, the magnetic flux enclosed by the loop must be quantized in terms of the flux quantum ${\varphi }_0={\displaystyle \frac{h}{2e}}$. Conversely, the Josephson effect [15] refers to the quantum tunneling phenomenon of a Cooper pair across a thin potential barrier between two superconductors linked by a non-superconducting electric layer. SQUID devices, constructed utilizing the aforementioned physical phenomena, are inductively [16] coupled to suitable input circuits to measure a range of physical quantities [17], encompassing magnetic fields, magnetic field gradients, voltages, and magnetization. They serve as pivotal tools in diverse fields such as medicine, geology [18], materials testing [19], magnetic induction communication [7], cosmology and astrophysics [20], condensed matter physics [21], and quantum computing [1,22,23,24].

SQUIDs are classified into two categories, depending on the bias mode: Direct Current (DC) SQUIDs and Radio Frequency (RF) SQUIDs.

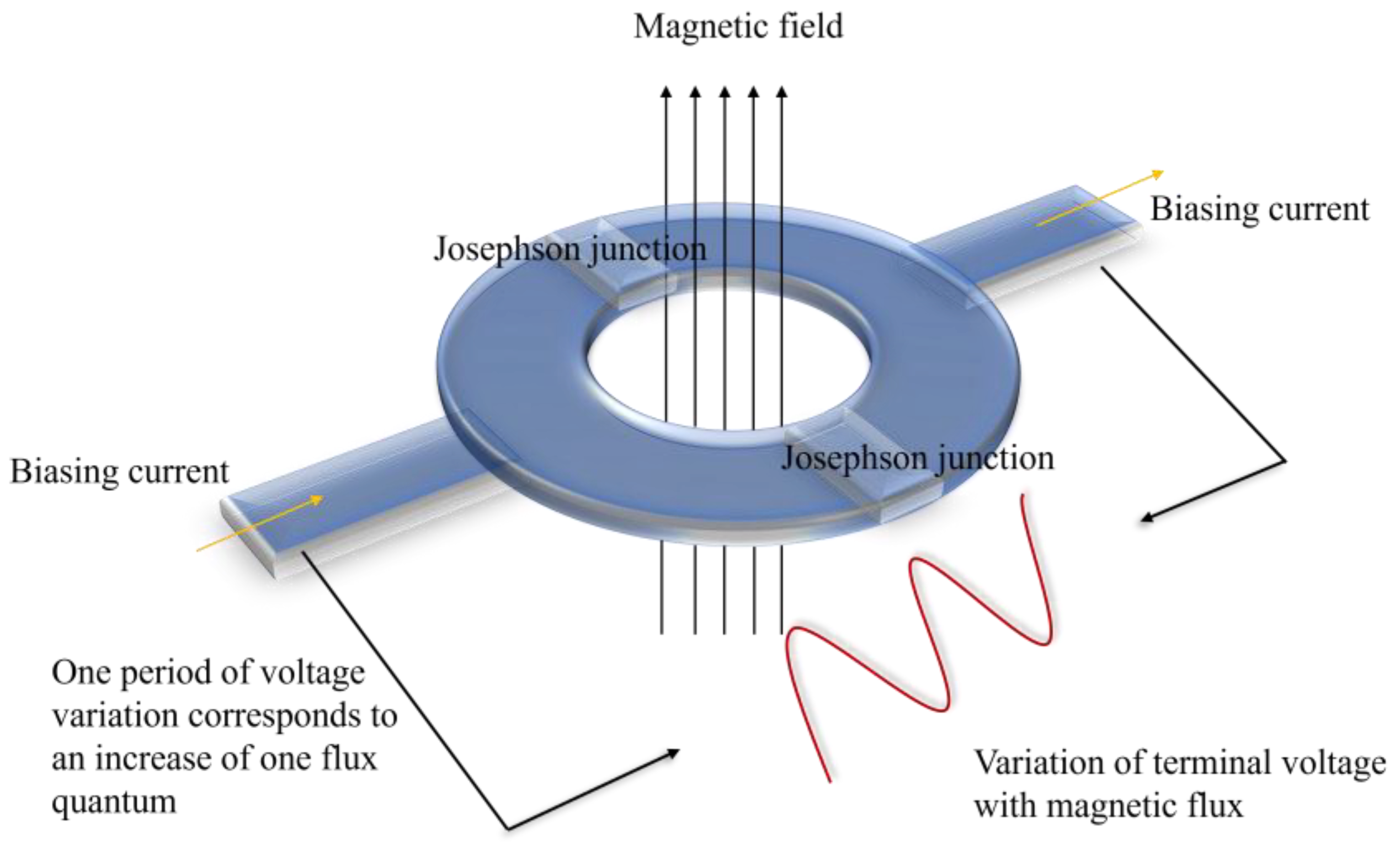
The first type is a DC SQUID, comprising two Josephson junctions connected in parallel on a superconducting loop. When a constant bias current slightly exceeding the critical current flows through the device, the Josephson junctions become resistive. Consequently, there exists a periodic relationship between the voltage across the device and the applied magnetic flux, with a period of one flux quantum ${\Phi }_0$. This configuration enables the detection of magnetic flux changes as small as ${10}^{-6}{\Phi }_0$ [25]. Figure 1 shows the schematic diagram of the DC SQUID.

The second type is the RF SQUID, featuring a sensitive element comprising a single Josephson junction incorporated within a superconducting loop [25,26], This junction is inductively coupled to a LC resonant circuit. The device is driven by a high-frequency signal [27], typically ranging from tens to hundreds of megahertz, which is applied to an energy storage circuit magnetically coupled to the SQUID [28].

The discovery of the DC SQUID by Jaklevic et al. occurred only a few years after Josephson predicted superconducting tunneling [15]. Subsequently, the RF SQUID was introduced shortly thereafter [25]. However, due to the technical limitations of the time, it was significantly more challenging to achieve two-point contacts with similar parameters compared to a RF SQUID with only one point contact. Consequently, RF SQUIDs became the standard device in the ensuing years. As thin-film fabrication processes advanced, DC SQUIDs began to supplant RF SQUIDs from the 1970s and 1980s onward. DC SQUIDs typically offer higher sensitivity, lower noise, greater versatility, and improved stability compared to RF SQUIDs [9]. These characteristics render the DC SQUID ideal for high-resolution measurements across a wide array of fields.

A typical DC SQUID device comprises four main components: two Josephson junctions, consisting of two thin potential barriers connected to a superconducting loop; a superconducting loop, often made of the underlying superconducting material Nb in niobium-based SQUIDs, commonly referred to as the “washer”; a superconducting ring, serving as the primary component of the SQUID; an input coil, utilized to convert the measured magnetic field into a flux detectable by the SQUID; and a feedback coil, employed to provide feedback magnetic fields during operation, thereby linearizing the SQUID’s response. Washer coils in SQUIDs play a crucial role in their functionality and performance [29]. Their shape and size significantly impact the overall performance and sensitivity of the device. Primarily, washer coils amplify the magnetic field within the SQUID loop. By increasing the area that captures magnetic field lines, these coils markedly enhance the device sensitivity. Additionally, they serve to shield against external electromagnetic interference, with well-designed washer coils effectively reducing noise [30]. Washer coils also influence various SQUID parameters, including inductance and critical current. Through optimization of the shape and size, washer coils can amplify the magnetic field inside the ring, enhance the magnetic flux collection, and effectively suppress the external magnetic flux and potential resonance to minimize external noise [31]. Therefore, optimizing washer design is pivotal for enhancing the performance of SQUID devices.

This study aims to investigate methods for enhancing SQUID performance by optimizing the shape and size of the washer coil through simulations. By leveraging advanced computational tools and optimization algorithms, we seek design solutions to improve the sensitivity and efficiency of the device. Our simulation findings will contribute to extending the application of SQUIDs across various environments.

2. Numerical Calculations

The optimization parameters inherent to DC SQUID device design typically encompass factors such as device noise and energy resolution. In this section, we will derive expressions specifically pertaining to these design parameters. Furthermore, our study confines its scope to uncoupled SQUIDs, specifically focusing on the fundamental “bare” DC SQUID device model solely comprising washers.

2.1. DC SQUID Noise

2.1.1. 1/f Noise

1/f noise, also known as flicker noise, can significantly limit the performance of practical devices at low frequencies. In SQUID devices, 1/f noise primarily arises from two sources: fluctuations of the critical current $I_0$ in the Josephson junctions and the motion of flux lines (vortices) trapped in the body of the SQUID or in the superconducting input circuit. The SQUID directly induces changes in the stray magnetic flux coupled to the SQUID magnetic ring, which is generated by vortices moving with a radial motion spectral density $S_{\mathrm{r}}\left(f\right)$, and this generates flux noise, expressed as $S_{\mathsf{\Phi }}=S_{\mathrm{r}}(\partial {\mathsf{\Phi }}_{\mathrm{a}}/\partial r{)}^2$, where $r$ is the radial distance of the vortex from the SQUID hole. The surface spin fluctuation is a dominant source of 1/f noise in superconducting devices. This fluctuation is influenced by the physical dimensions and layout of the washer geometry.

While 1/f noise in low Tc SQUIDs generally does not pose a serious issue, the increasing demand for higher measurement accuracy in the field of magnetometry drives researchers to pursue designs that minimize this noise even further.

2.1.2. Noise Voltage Model

In the absence of excess noise due to resonances, the voltage noise in a SQUID can be modeled as arising from two nearly uncorrelated noise currents: one circulating within the SQUID loop and the other passing through the SQUID device. Therefore, under ideal conditions [16], the spectral density of the voltage noise on the SQUID can be expressed as

$$S_V={\left({\displaystyle \frac{\partial V}{\partial \mathsf{\Phi }}}\right)}^2{\displaystyle \frac{4k_{B}T{L}^2}{2R}}+4k_{B}T{R}_{\mathrm{d}\mathrm{y}\mathrm{n}}$$

(1)

where $R_{\mathrm{d}\mathrm{y}\mathrm{n}}={\displaystyle \frac{\partial V}{\partial I}}$ is the dynamic resistance of the SQUID, ${\displaystyle \frac{\partial V}{\partial \mathsf{\Phi }}}$ is the derivative of the voltage with respect to the magnetic flux, $k_B$ is the Boltzmann constant, $T$ is the absolute temperature of the device, $L$ is the loop inductance, and $R$ is the resistance of the external shunt resistor parallel to the junction quasiparticle resistance.

If the noise voltage across the SQUID is $V_N\left(t\right)$, two independent Nyquist noise currents on the SQUID produce white current noise around the SQUID and the SQUID loop with spectral densities of $S_V\left(f\right)$ and $S_J\left(f\right)$. The corresponding flux noise can be given by the following equation:

$$S_{\mathsf{\Phi }}\left(f\right)={\displaystyle \frac{S_V\left(f\right)}{V_{\mathsf{\Phi }}^2}}$$

(2)

where $V_{\mathsf{\Phi }}=R/L$ is the flux-to-voltage transfer coefficient.

2.1.3. Noise and Inductance Limit

Due to the balance between quantum systems and noise, an upper limit is imposed on the superconducting loop inductance:

$${\displaystyle \frac{{\mathsf{\Phi }}_0^2}{2L}}\gg 2\pi k_{B}T$$

(3)

${\mathsf{\Phi }}_0$ is the magnetic flux quantum, and $L_{th}$ is introduced to represent the thermal noise inductance, which is a theoretically defined inductance value used to quantify the noise level of SQUID. According to the above formula, it can be recorded as

$$L_{th}={\displaystyle \frac{{\varphi }_0^2}{4\pi k_{B}T}}$$

(4)

In the low-temperature SQUID system, and at 4.2 K, the text states $L_{th}$ is approximately $5.9 \mathrm{nH},$ which is $5900 \mathrm{pH}$, which places an upper limit on the value of $\mathrm{L}$.

2.2. The Energy Resolution

Another crucial parameter of DC SQUIDs is the noise energy per unit bandwidth, commonly known as energy resolution. This metric directly influences the SQUID’s capability to detect weak signals. A higher energy resolution enables the SQUID to operate effectively even in environments with elevated noise levels. Essentially, enhancing the energy resolution enables the SQUID to more accurately differentiate genuine signals from background noise, thus enhancing measurement precision and reliability. Moreover, a higher energy resolution directly enhances the SQUID’s sensitivity to changes in the magnetic fields, making it more adept at detecting subtle variations. Therefore, energy resolution is one of the core indicators of SQUID system performance, which has a direct impact on its signal detection capability, noise limit, measurement sensitivity, and application range [32].

Presenting as noise energy per unit bandwidth offers a simplified characterization of flux noise, using Equations (1) and (2), which can be reformulated as the following equation:

$$\epsilon ={\displaystyle \frac{S_{\mathsf{\Phi }}\left(f\right)}{2L}}$$

(5)

The energy resolution may then be written as

$$\epsilon ={\displaystyle \frac{k_{B}T}{L}}\left\{{\displaystyle \frac{L^2}{R}}+{\displaystyle \frac{2R_{\mathrm{d}\mathrm{y}\mathrm{n}}}{{\left(\partial \mathrm{V}/\partial \mathsf{\Phi }\right)}^2}}\right\}$$

(6)

Disregarding the self-screening effects, the total flux passing through the SQUID can be approximated as essentially equivalent to the externally applied flux. To optimize the SQUID’s energy resolution, it is crucial to establish correlations between the noise equation and the SQUID’s design parameters, simplifying the design process. Here, we introduce the parameter $\beta ={\displaystyle \frac{2L{I}_c}{{\Phi }_0}}$, where L represents the superconducting loop inductance, and $I_c$ is the critical current of each junction. From the previous researcher’s simulation [33], the above equation has the best value at $\beta \approx 1$. $R_{\mathrm{d}\mathrm{y}\mathrm{n}}$ and ${\displaystyle \frac{\partial \mathrm{V}}{\partial \mathsf{\Phi }}}$ are taken as approximations, and the energy resolution can be written at a low temperature of $4.2\mathrm{K}$:

$$\epsilon =k_{B}T{\displaystyle \frac{L}{R}}\left\{1+{\displaystyle \frac{\sqrt{2}(1+\beta {)}^2}{{\beta }^2}}\right\}$$

(7)

Defining the Stewart–McCumber parameters as ${\beta }_c=(2\pi /{\mathsf{\Phi }}_0)I_c{R}^{2}C$, where $C$ is the junction capacitance, the above equation can be rewritten as

$$\epsilon =k_{B}T\sqrt{LC}\sqrt{{\displaystyle \frac{\pi \beta }{{\beta }_c}}}\left\{1+{\displaystyle \frac{\sqrt{2}(1+\beta {)}^2}{{\beta }^2}}\right\}\equiv \gamma k_{B}T\sqrt{LC}$$

(8)

Therefore, in this case, the superconducting tunneling effect can be expressed by the equivalent inductance $L_{\mathrm{J}}={\displaystyle \frac{{\mathsf{\Phi }}_0}{2\pi I_{\mathrm{c}}}}$.

The quality factor $Q_{\mathrm{J}}$ in the context of magnetic sensors, such as SQUIDs, is a measure of the sensor’s performance and efficiency in capturing and processing the magnetic flux, which is influenced by several factors. Under the RCSJ model, the quality factor can be written as $Q_{\mathrm{J}}=R(C/L_{\mathrm{J}}{)}^{1/2}$. In order to minimize the mixing effect in nonlinear systems, the quality factor of the resonant circuit should be kept below 1. Therefore, in practice, the best energy resolution results are obtained when ${\beta }_c\approx 0.7$ and $\beta =1$; at this point, the energy resolution can be rewritten as

$$\epsilon \approx 16k_{\mathrm{B}}T{\left(\mathrm{L}\mathrm{C}\right)}^{1/2}$$

(9)

2.3. Other Considerations

Based on the application requirements, the design should aim to ensure that the effective area is sufficiently large while keeping the magnetic field noise at a relatively low level. The effective area is determined by the following equation [30]:

$$A_{\mathrm{e}\mathrm{f}\mathrm{f}}={\displaystyle \frac{{\mathsf{\Phi }}_{\mathrm{s}}}{B_{\mathrm{a}}}},$$

(10)

${\mathsf{\Phi }}_{\mathrm{s}}$ is the flux coupled into the SQUID by the applied magnetic field $B_{\mathrm{a}}$, and too small an effective area of the washer leads to the following results: the magnetic flux noise ${\varphi }_{\mathrm{N}}\left(f\right)$ may be very low, and the corresponding areas $A_s$ of the planar devices are also small (typically, ${10}^{-4}$ to ${10}^{-2} \mathrm{m}{\mathrm{m}}^2$). We then define the magnetic field noise equation:

$$B_{\mathit{N}}\left(f\right)={\displaystyle \frac{{\Phi }_{\mathit{N}}\left(f\right)}{{\overline{A}}_{\mathit{s}}}}$$

(11)

Consequently, $B_{\mathit{N}}\left(f\right)$ is often too high for many applications, too small a washer will not couple quite as effectively to most real input circuits, and the magnitude of the captured flux will be too small to fulfill its function; due to this, the larger the washer size, the more appropriate it will be.

Considering the resonance frequency-related issues, a new requirement for the design of the SQUID washer is introduced: the optimal operating frequency can be given by the following equation:

$$f_{\mathrm{o}\mathrm{p}}={\displaystyle \frac{0.3I_{0}R}{{\mathsf{\Phi }}_0}}$$

(12)

The long lead of the input coil in the coupled SQUID makes the stripline resonance $f_s$ much lower than $f_{\mathrm{o}\mathrm{p}}$, and larger-size washers also cause the washer resonance $f_w$ to approach $f_{\mathrm{o}\mathrm{p}}$ ($f_{\mathbf{w}}={\displaystyle \frac{c}{2{\mathcal{l}}_{\mathrm{c}\mathrm{f}\mathrm{f}}\sqrt{{\epsilon }_r\left(1+\frac{{\lambda }_{L,w}+{\lambda }_{L,i}}{h}\right)}}}$); often, people make compromises when designing: $4f_s<f_{\mathrm{o}\mathrm{p}}<{\displaystyle \frac{f_w}{4}}$.

In summary, the SQUID washer design process should balance all aspects of the parameter requirements to achieve the most appropriate design.

3. Methodology

In this research, we employed the Python library SuperScreen [34] to conduct simulations of the magnetic response of 2D superconductors. SuperScreen 0.10.4 is a finite element method (FEM) software specifically tailored for simulating superconducting circuits and devices. It is capable of simulating the magnetic response of a superconducting film or a multi-layered structure composed of superconducting films subjected to an applied inhomogeneous out-of-plane magnetic field. Additionally, the software package is proficient in simulating screening effects and computing inductance in superconducting circuits, facilitating the interpretation and analysis of measurements about superconducting thin films and devices. Moreover, it provides visualization functionalities for simulation results, making the SQUID design process more intuitive compared to previous research methodologies.

3.1. Effective Area

In this section, we present formulas for calculating the inductance and the effective field-sensitive area of the three washers, Figure 2 shows the uncoupled SQUID washer. The geometry and size of the washer, along with the distribution of the magnetic field it captures, collectively determine the effective field-sensitive area of the washer coil within SQUID devices. Due to flux compression caused by the superconducting structures, $A_{\mathrm{e}\mathrm{f}\mathrm{f}}$ is usually quite different from the geometric dimensions of the SQUID hole [16], and the effective area determines the amount of magnetic flux that the SQUID loop can capture. Furthermore, the magnitude of the effective area directly influences the total flux traversing the SQUID loop and affects both the device noise and the quality factor.

The relevant figure of merit for a magnetometer is the rms magnetic field noise:

$$S_B^{1/2}\left(f\right)={\displaystyle \frac{S_{\mathsf{\Phi }}^{1/2}\left(f\right)}{A_{\mathrm{e}\mathrm{f}\mathrm{f}}}}$$

(13)

The magnetic field noise can be optimized by enhancing these parameters to achieve better alignment for an improved sensor quality factor. The washer interrupts the inductive loop via the slit below to establish connections with the two Josephson junctions, which serve as sensitive structures. In accordance with the empirical formula for slit inductance,

$$L_{sl}\approx {\displaystyle \frac{0.3pH}{\mu m}}$$

(14)

This value is significantly smaller than the total washer inductance. For simplicity, we initially disregard the contribution of the slit to the washer inductance and effective area. Consequently, our optimization efforts are directed towards the design of other washer parameters to attain high field sensitivity and minimize device noise. Due to flux compression caused by superconducting structures, the effective area often significantly deviates from the geometrical dimensions of the SQUID hole, $A_{\mathrm{e}\mathrm{f}\mathrm{f}}$ is not proportional to the geometrical area of the structure, as the size and shape of the effective area directly influence the noise characteristics and sensitivity of SQUIDs. Under the assumption that, in idealized superconducting structures, the film thickness and the London penetration depth are markedly less than the linewidth and spacing, analytical equations for the effective area of regular polygons with N edges have been derived through numerical analysis. The formula for the perimeter of a regular polygon is $c=N\tan \left({\displaystyle \frac{\pi }{N}}\right)d$. When a uniform magnetic flux density $\mathrm{B}$ is applied to a superconducting loop, and the magnetic flux is concentrated into a hole within the loop, the effective area is [35]

$$A_{\mathrm{e}\mathrm{f}\mathrm{f}}={\gamma }_A(A_{\mathrm{h}}{A}_{\mathrm{t}}{)}^{{\displaystyle \frac{1}{2}}},$$

(15)

The geometric factor is denoted by ${\gamma }_A$, and takes the value ${\gamma }_A=1-0.68/(d/w+2.07{)}^{1.75}$, $A_{\mathrm{h}}$ and $A_{\mathrm{t}}$ are the area of the internal holes of the washer ring and the total area of the loop, respectively, and the values are given by the following equation:

$${\left(A_{\mathrm{h}}{A}_{\mathrm{t}}\right)}^{{\displaystyle \frac{1}{2}}}=\left({\displaystyle \frac{N}{4}}\right)\tan \left({\displaystyle \frac{\pi }{N}}\right)d\left(d+2w\right)$$

(16)

If the shape of the washer is square—that is, $N=4$—the above formula can be simplified to

$$(A_{\mathrm{h}}{A}_{\mathrm{t}}{)}^{{\displaystyle \frac{1}{2}}}=d\left(d+2w\right)$$

(17)

The shape of the octagonal washer $N=8$ can be given by the following equation:

$$(A_{\mathrm{h}}{A}_{\mathrm{t}}{)}^{{\displaystyle \frac{1}{2}}}=0.83d\left(d+2w\right)$$

(18)

When the washer shape is circular, $N\to \mathrm{\infty }$, the above equation is rewritten as

$$(A_{\mathrm{h}}{A}_{\mathrm{t}}{)}^{{\displaystyle \frac{1}{2}}}=\pi /4d\left(d+2w\right)$$

(19)

We utilize the Matplotlib library in Python to visualize the effective area formulas of various washer types, the results of which are shown in Figure 3, enabling a visual comparison of changes in the effective area with parameters d and w. From the figure, it is evident that, under identical parameters, the square washer exhibits the largest effective area, which can lead to a superior quality factor. However, an excessively large loop area may introduce excessive inductance. Balancing various parameters by refining the shape to ultimately achieve the optimal device design will be addressed in our subsequent work.

3.2. Washer Modeling

To precisely simulate and analyze the physical characteristics of the washer shape, we leveraged the NumPy library in Python for mathematical modeling. We defined the essential dimensional parameters of the washer, particularly its inner and outer diameters, serving as the foundation for constructing the model. Utilizing the built-in code provided by the SuperScreen 0.10.4 software package, we seamlessly generated the model of the washer shape.

Simulating Complex Washer

However, the function of this software package is limited, and it is difficult to model complex patterns. In order to simulate and analyze the performance of complex washer shapes, we adopted a method that combines layout GDS files and the NumPy library.

This method involves two primary steps: Firstly, develop a program to convert the GDS file of the layout into a two-dimensional array format compatible with NumPy. This initial step enables the extraction of detailed geometric information from complex shapes. Subsequently, these shapes are accurately modeled using NumPy. Figure 4 illustrates the successful modeling of complex washer shapes achieved through this method. The graphic displays two octagonal washers connected in series, demonstrating the method’s capability to precisely reconstruct complex washers.

This approach not only simplifies the modeling process of complex shapes but also provides an accurate graphical foundation for our subsequent simulation analysis. Additionally, it offers reliable model support for optimized design and performance evaluation.

3.3. Other Parameter Settings

3.3.1. Film Thickness and Penetration Depth

In superconductors, the Meissner effect causes them to repel an external magnetic field. However, magnetic fields can partially penetrate a very small area near the surface of a superconductor. To preserve the superconducting properties and ensure the stability and reliability of the Josephson junction, it is essential to maintain the thickness of a superconducting film as much greater than the penetration depth of the material. For instance, in this experiment, the penetration depth of Nb, denoted as λ, is approximately 80 nm. Hence, the thickness of all superconducting films used in the experiment is set to 250 nm to guarantee robust superconducting behavior.

3.3.2. Magnetic Field Source Setup and Simulation

When conducting simulation studies, selecting an appropriate magnetic field source is critical to ensure the accuracy of the calculation results. In this study, we specifically selected magnetic dipoles as the magnetic field source.

The value of the magnetic field at distance $\overrightarrow{r}$ for a magnetic dipole with magnetic moment $\overrightarrow{m}$ can be given by the Biot–Savart law:

$$\overrightarrow{B}={\displaystyle \frac{{\mu }_0}{4\pi r^3}}\left[{\displaystyle \frac{3\left(\overrightarrow{m}\cdot \overrightarrow{r}\right)\cdot \overrightarrow{r}}{r^2}}-\overrightarrow{m}\right]$$

(20)

Consider the magnetic moment of the rotating magnetic dipole as

$$\overrightarrow{m}=100A\cdot m^2$$

(21)

The numerical selection of this magnetic moment reflects the specific requirements for magnetic field strength and direction for simulation purposes, ensuring that the simulation results can match the actual use, and the distance between the point magnetic dipoles in the simulation is set to 100 m, pointing in the direction of the z-axis. We evaluated the magnetic field generated by the magnetic dipole on a planar grid covering the area from −250 µm to 250 µm, and the position of the evaluated magnetic field was 1 µm forward along the z-axis. Figure 5 is a magnetic dipole simulation result.

3.3.3. Simulation Target

To explore the interaction between superconducting washer rings and magnetic fields, we first simulate the Meissner effect to predict the microscale behavior of superconductors under applied magnetic fields, analyzing how washer geometry influences device performance. Additionally, in the operation of DC SQUID devices, the shielding current is crucial. This current circulates within the superconducting loop of the SQUID to maintain the quantization of magnetic flux within the loop. This process is closely related to the Meissner effect, where surface currents automatically counteract the external flux to stabilize the internal flux, thereby effectively shielding against variations in the external magnetic fields. The strength of the shielding current directly impacts the sensitivity and precision of the SQUID. The design of washer inductance directly affects multiple performance metrics of DC SQUID devices, making it crucial for device optimization. Well-designed inductance balances the dynamics of quantum systems and noise.

• Meissner Screening.

In our simulation model of the superconducting ring, we emulate the influence of an external magnetic field by introducing a circulating current through the central aperture of the ring. Specifically, we designate a circulating current of 1 mA to mimic the effect of an external magnetic field, thus ensnaring an equivalent magnetic flux within the apertures of the superconducting ring. However, it is pertinent to acknowledge that, within these apertures, the boundary effect of the superconductor may induce a stable magnetic flux, consequently fostering the generation of a circulating current in response to this external magnetic field. This methodological approach affords us the opportunity to scrutinize the efficacy of various washer designs in repulsing magnetic fields, thereby facilitating the identification of designs that optimize Meissner screening.

• Current distribution.

Our analytical endeavor primarily revolves around scrutinizing the distribution of the current and integrated current density across the washer structure to corroborate the presence of circulating currents. Our overarching objective is to delineate the spatial distribution of supercurrents and compute the aggregate circulating current within the washer, thereby furnishing insights into how design modifications engender alterations in current confinement efficiency and overall sensor efficacy. The sheet current, serving as a proxy for thickness-integrated current density, emerges as a pivotal physical quantity indispensable for scrutinizing both the static and dynamic responses to applied magnetic fields and currents, as well as for comprehending the nuances of eddy currents within the film. Concurrently, the stream function, denoted as g, assumes the role of delineating the local magnetization of the film or the area density of magnetic dipole sources.

$$\overrightarrow{J}\left(x,y\right)=-\widehat{z}\times \overrightarrow{\nabla }g=\overrightarrow{\nabla }\times \left(g\widehat{z}\right)=\left({\displaystyle \frac{\partial g}{\partial y}},-{\displaystyle \frac{\partial g}{\partial x}}\right)$$

(22)

• Magnetic flux and self-inductance.

The process of computing the magnetic flux and self-inductance of a ring is pivotal for comprehending the behavior of superconductivity in a non-zero magnetic flux state. These parameters serve as cornerstones for quantifying the sensor’s response to an external magnetic field and its self-resonant properties. Following the calculations in Section 2, aimed at providing a preliminary assessment of the varying impacts of different ring designs on the final device, our overarching objective is to pinpoint configurations that maximize the sensitivity and dynamic range of the sensor. These objectives serve as guiding principles throughout the simulation process, ensuring that we undertake a thorough analysis of the washer loop to optimize the performance of the SQUID sensor.

4. Results

In this investigation, we utilized the SuperScreen 0.10.4 software software package to systematically explore the spatial distribution of magnetic fields and current densities within superconducting washer loops of various geometries, including square, circular, and octagonal shapes.

To ensure a comprehensive evaluation of the impact of washer ring geometry on device performance, we controlled two design parameters of the washer model. In Section 2.2 of this study, we introduce the parameter $\beta ={\displaystyle \frac{2L{I}_c}{{\Phi }_0}}$, a formula that approximately determines the inductance of the device’s loop, where $L$ denotes the loop inductance and $I_c$ the critical current. Drawing on previously reported data, with the critical current density set at $80 {\mathsf{A}/\mathsf{c}\mathsf{m}}^2$ and considering a square junction of 2 μm in side length [36], allows for the calculation of the loop inductance to be approximately $322.97 \mathrm{p}\mathrm{H}$. These considerations have guided the initial parameter settings for the SQUID washer design as follows: D = 200 μm, W = 75 μm. This configuration facilitated a comparison of all three washers under identical effective area parameters.

Within our simulation framework, we replicated the influence of external magnetic fields by defining a circulating current passing through the central hole of the superconducting ring. Specifically, a circulating current of 1 mA was specified to mimic an external magnetic field. However, within the aperture, the boundary effect of the superconductor allowed the formation of a stable magnetic flux under the influence of an external magnetic field, thereby generating a circulating current.

The Figure 6 illustrates a modeling comparison of three distinct washer geometries:

4.1. Meissner Effect

To effectively elucidate how superconducting washer loops interact with magnetic fields, it is first necessary to explore the Meissner effect. This work could model the behavior of superconductors in the presence of external magnetic fields.

The x-axis and y-axis in each plot represent the spatial dimensions of the washer loops in micrometers. These axes define the plane in which the washer loop lies and, consequently, where the magnetic field distribution is being observed.

Figure 7 is the results of the Meissner effect simulations, the analysis of magnetic field distribution within washers of varying geometrical shapes reveals a consistently uniform low magnetic field area across all three configurations, characterized by the prevalence of deep blue hues in the visualizations. This uniformity suggests an effective repulsion of magnetic fields within the interiors of washers of all shapes under the predefined conditions of film thickness and penetration depth. The alignment of the orange curves with the baseline in subsequent graphs further substantiates this effective exclusion of magnetic fields. Upon examining the symmetry of magnetic field distribution across different washer geometries, it becomes evident that circular washers exhibit a higher degree of symmetry compared to square washers, while octagonal washers demonstrate an intermediate level of symmetry. Quantitative simulations of magnetic fields at the boundaries of these washers reveal values of 0.23 mT for square washers, 0.20 mT for circular washers, and 0.18 mT for octagonal washers. This underscores the superior efficacy of octagonal washers in minimizing the boundary effects, aligning with the stringent design standards crucial for optimal SQUID functionality.

Furthermore, considering the manufacturing complexity and uniformity aspects, the octagonal washer loop presents a more practical manufacturing solution than the circular counterpart. The octagonal geometry strikes a balance between minimizing undesirable boundary effects and maintaining symmetry, making it the optimal configuration. It offers a simplified manufacturing approach without compromising device functionality, thus addressing the practical implications of washer shape on SQUID device design.

4.2. Screening Currents

Screening currents, also known as supercurrents, circulate within the superconducting loop of the SQUID to uphold the quantization of magnetic flux inside the loop. When an external magnetic field is applied, these currents adapt to counteract the external flux within the superconductor, effectively shielding the superconducting loop from alterations in the external magnetic fields.

The functionality of a SQUID hinges on the interference pattern generated by two superconducting paths containing Josephson junctions. These screening currents influence the phase difference between the superconducting wave functions along these paths, which, in turn, is highly sensitive to the magnetic flux. This sensitivity enables the SQUID to discern incredibly minute changes in magnetic flux, thereby translating them into measurable voltage changes across the Josephson junctions.

Our examination of the current density distributions across three unique washer loop configurations unveils a prominent concentration of current density at the peripheries of the devices, while the inner regions exhibit negligible to zero current density, as evidenced by the coloration in the loop diagrams provided earlier. The subsequent graphs, depicting current density ($\left|J\right|$) in units of [$\mathrm{m}\mathrm{A}/\mathsf{\mu }\mathrm{m}$] plotted against distance along the cut (μm), further validate this observation. Notably, this distribution pattern is confined within the London penetration depth of the superconductor surface, with the Meissner effect fosters a high-density current near the boundary.

Our simulations on the circulation of currents within SQUID washer loops (Figure 8) unveil an intriguing observation: the current magnitude across circular, octagonal, and square washers remains largely equivalent. However, upon comparative analysis at y = −150 μm, it becomes evident that the square washer loop manifests the lowest current density, particularly at its corners, indicating a significantly lower stability in current density compared to the circular washer loop. Conversely, the performance of the octagonal washer loop closely mirrors that of the circular one, displaying comparable efficacy and stability. Nonetheless, this inconsistency marks a slight dip in current density stability compared to their circular counterparts.

The simulation results of the applied circulating currents indicate that the magnitude of currents generated by the three types of washer loops is approximately equivalent. However, the comparative analysis at y = −150 μm highlights that the square washer loop displays the lowest current density, especially at its corners, indicating significantly lower stability in the current density compared to the circular washer loop. Conversely, the performance of the octagonal washer loop closely mirrors that of the circular one, exhibiting comparable efficacy and stability.

The study on magnetic dipole simulation (Figure 9) further elucidates this point, demonstrating a clear tendency for vortex formation along the inner edges of the square washer. The magnetic fields emanated by magnetic dipoles culminate in the generation of flux vortices at the periphery of square washers. The dynamics and redistribution of these vortices instigate alterations in the local magnetic fields, necessitating the redistribution of superconducting currents within the vortices to uphold the conservation of the magnetic flux. This readjustment of the current, in tight coupling with the washer, engenders flux noise, significantly undermining the device’s sensitivity and its capacity to discern weak signals. Evidently, the emergence of vortices in practical washer design applications is deemed detrimental.

One significant source of 1/f noise is the motion of flux lines (vortices) trapped in the body of the SQUID or in the superconducting input circuit. To model this dependency, we consider the noise power spectral density $S_{\mathsf{\Phi }}\left(f\right)$, which is given by

$$S_{\mathsf{\Phi }}(f)={\displaystyle \frac{A}{f^{\alpha }}}$$

(23)

where $A$ is a parameter that depends on the geometry of the washer, and $\alpha$ is close to 1.

Simulation results of magnetic dipole fields clearly indicate that 1/f noise in SQUIDs is significantly influenced by the geometry of the washer. Different geometries, such as square, circular, and octagonal washers, impact the distribution of the current density and the pinning sites for vortices, which, in turn, affect the 1/f noise characteristics. For instance, the octagonal washer geometry tends to distribute the current more evenly compared to the square washer, thereby reducing the concentration of high-current density regions that contribute to vortex movement and, consequently, 1/f noise.

Through comprehensive analysis, we have discerned that, in real-world SQUID applications, circular and octagonal washer loops offer distinct advantages over traditional square loops. The configuration of octagonal washers not only significantly reduces detrimental edge effects but also markedly alleviates current crowding at corners and the formation of eddies along the straight edges of the washer. These phenomena can lead to distortions in the magnetic field measurements. Therefore, SQUIDs equipped with circular and octagonal washers demonstrate superior performance, rendering them the optimal choice for optimizing the SQUID sensor design.

4.3. Coupling Energy of Two Parallel JJs

The Josephson energy of a single Josephson junction is defined as $E_{\mathrm{J}}\equiv I_0{\mathsf{\Phi }}_0/2\pi$, where $I_0$ is the critical current. For two parallel Josephson junctions, the total energy can be considered as the algebraic sum of the individual Josephson energies. Assuming the critical currents of both junctions are the same, the energy of each junction can be expressed as $E_{\mathrm{J}1}\equiv I_1{\mathsf{\Phi }}_0/2\pi$ and $E_{\mathrm{J}2}\equiv I_2{\mathsf{\Phi }}_0/2\pi$. For two parallel Josephson junctions, assuming they have identical critical currents, when considering the phase differences across the two junctions, the total Josephson energy is influenced by these phase differences:

$$E_{J_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}=E_{J_1}\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_1\right)+E_{J_2}\mathrm{c}\mathrm{o}\mathrm{s}\left({\delta }_2\right)$$

(24)

Furthermore, if there is coupling between the two Josephson junctions, such as in a SQUID loop, the coupling energy must also be considered. The coupled energy can be expressed as:

$$E_{J_{\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}}}=E_{J_1}\mathrm{c}\mathrm{o}\mathrm{s}({\delta }_1)+E_{J_2}\mathrm{c}\mathrm{o}\mathrm{s}({\delta }_2)-{\displaystyle \frac{M{I}_1{I}_2}{2}}$$

(25)

where $M$ is the mutual inductance between the two junctions.

The geometry of the washer significantly affects the magnetic field and current distribution, which, in turn, influences the coupling energy between Josephson junctions (JJs). For instance, in our simulations, device edges lead to significant changes in the magnetic field and current distribution, and the stability of the current distribution, in turn, affects the coupling between the two Josephson junctions. We observed that the current distribution in octagonal washers is more uniform. This design minimizes regions of high current density that can lead to vortex motion and reduce 1/f noise. Such a uniform current distribution results in a more stable coupling energy between the JJs.

4.4. Self-Inductance

In the preceding theoretical sections, we explored the influence of washer inductance on different device parameters, emphasizing the delicate balance between quantum system dynamics and noise considerations. This equilibrium sets a maximum limit for the inductance in superconducting loops, capped at 5900 pH for devices operating at low temperatures. The optimal performance demands lower inductance values to ensure sensitivity. Figure 10 shows that, under the same inner diameter conditions, the inductance values of octagonal and circular washers are smaller than the traditional square washer design.

The self-inductance of a washer is given by

$$L={\displaystyle \frac{{\mathsf{\Phi }}_h^f}{I_h}},$$

(26)

where $I_h$ is the current that circulates around the hole, and ${\mathsf{\Phi }}_h^f$ is the fluxoid for a path enclosing the hole [37], assuming a total current of 1 mA circulates in a clockwise direction within the ring, the simulation results are shown in Figure 10.

Linear regression analysis of the inductance variation with the washer diameter (D) yields different slopes for each washer shape: for circular washers, the slope is 2.0829; for octagonal washers, it is 2.1969; and notably higher for square washers, with a slope of 2.8391. The analysis results indicate that the inductance of square washers significantly increases with the diameter enlargement, compared to circular and octagonal washers. This heightened sensitivity to size variations could potentially impact the sensor’s sensitivity and noise levels adversely. Conversely, circular and octagonal washers exhibit a more controlled and less pronounced increase in inductance with size, indicating their superior ability to maintain stable inductance across different sizes. This characteristic enables them to strike an optimal balance between enhancing the device sensitivity and minimizing device noise.

Figure 11 depicts a comparative study between inductance values calculated using conventional empirical formulas and those derived from incorporating an externally applied circulating current for washers of square, circular, and octagonal shapes. The slopes of inductance versus washer diameter (D), obtained from empirical formulas for square, circular, and octagonal washers, are, respectively, 1.57, 1.32, and 1.26. In contrast, the inductance slopes derived in this study for washers of all shapes markedly exceed the predictions of traditional empirical formulas.

To assess the deviation of inductance values between various washer shapes and those predicted by empirical formulas, we calculated the average relative error between the simulated inductance and the empirical inductance for each shape. The results revealed that square washers exhibited an average relative error of 80.8%, circular washers showed a deviation of 65.31%, and octagonal washers presented an error of 66.43%. Notably, the discrepancy is most pronounced for square washers, with circular and octagonal washers also showing variations, albeit to a lesser extent, yet still surpassing conventional estimates. This discrepancy is attributed to significant edge effects induced by the acute angles of polygonal washers, which substantially impact inductance. Additionally, the washer shape influences the distribution of superconducting currents within the loop. The observed higher inductance values across the board are speculated to arise from the inability of traditional formulas to fully account for external interferences, suggesting that these conventional approaches may not accurately capture the intricate magnetic response processes of the washers.

4.5. Other Parameters

To more comprehensively evaluate the device performance under different washer shapes, this article also simulates the signal-to-noise ratio, total current (x cut), x cut error, total current (y cut), y cut error, the total fluxoid 1, and the total fluxoid, where the total fluxoid 1 is the applied field flux and the total fluxoid is the response flux.

The simulation results of the signal-to-noise ratio (SNR, Figure 12) show that, in most diameter ranges, the octagonal washer has a clear advantage, with an average SNR of about 12.5% higher than that of washers of other shapes. This may be due to the advantages of the octagon in signal capture and noise suppression. In addition, as the diameter of the washer increases, the SNR of all shapes increases; among which, the SNR of washers with larger diameters increases most significantly.

Here is the correlation matrix visualization for the washer parameters (Figure 13). The analysis revealed a substantial positive correlation between the inner diameter (D) of the washer and both its self-inductance and total magnetic flux. This correlation implies that, as the inner diameter of the washer increases, both the self-inductance and total magnetic flux experience a pronounced increase. In our design criteria, a lower self-inductance is preferred, and for the purpose of achieving optimal inductive coupling with the input coil, a smaller inner diameter is also desirable. However, considering the field noise ${\mathrm{S}}_{\mathrm{B}}^{{\displaystyle \frac{1}{2}}}\left(\mathrm{f}\right)$ related to magnetic sensors, a larger diameter is favored. This necessitates the pursuit of a new equilibrium in subsequent design iterations.

Furthermore, the analysis has revealed a significant negative correlation between the diameter of the washer (D) and the total current. This negative correlation underscores that, as the washer’s diameter increases, there is a discernible decrease in the total current measured on the x and y planes. Such reduced currents are less effective in inducing response voltages across Josephson junctions, leading to a notable reduction in the sensor’s sensitivity—a scenario clearly undesirable in our design considerations.

5. Discussion

In this study, we have endeavored to establish a methodology that integrates numerical computations with the SuperScreen library to simulate and optimize washer coils within SQUIDs. Our analysis encompasses simulations of various washer coil shapes, with a specific focus on their magnetic field response, screening current behavior, and self-inductance. In traditional SQUID design practices [36], the exploration of washer geometric parameters has often been limited to rudimentary numerical calculations of inductance, relying on rough empirical formulas. However, this approach lacks the depth required to comprehensively understand how various physical effects influence device performance. Such limitations hinder the precise determination of subsequent design parameters, as inaccuracies in washer inductance can significantly impact the selection of shunt resistors and the fabrication process of Josephson junctions, ultimately affecting the sensitivity and noise levels of the final device.

To address these shortcomings, our study introduces an innovative approach that utilizes a Python package for the first time to model, simulate, and visualize the electromagnetic responses, screening currents, inductance coefficients, and other critical parameters of different washer geometries. Using the research methods outlined above, we have drawn conclusions regarding the geometric dependence of washers, highlighting the advantages of octagonal and circular washers over traditional square washers in device applications. The simulation results reveal that the magnetic field at the boundary of the square washer is 0.23 mT, compared to 0.20 mT for the circular washer and 0.18 mT for the octagonal washer, indicating that the optimized octagonal washer significantly reduces boundary effects. These findings demonstrate that octagonal washers not only mitigate boundary effects more effectively but also exhibit greater stability throughout the manufacturing process.

In contrast, square washers, under magnetic dipole field conditions simulating real-world applications, exhibit vortex formation at their edges, diminishing screening currents and impacting the conversion efficiency from captured magnetic flux to output voltage. Additionally, our analysis reveals that the significantly higher slope of the inner diameter versus inductance curve for the square washer at 2.8391, compared to octagonal and circular washers, is detrimental to device design. Our analysis highlights significant deviations between the simulated inductance values and those predicted by empirical formulas, most notably in square washers with an 80.8% error, followed by circular and octagonal washers. The differences we noted stem primarily from the pronounced edge effects introduced by the acute angles in polygonal washers, markedly influencing their inductance.

Furthermore, our research indicates that excessively enlarging the washer’s inner diameter not only increases device noise but also leads to problematic coupling with subsequent superconducting electronic circuits. This effectively undermines the advantages of an increased effective area, resulting in diminished magnetic flux-to-voltage conversion coefficients. These issues manifest as low sensitivity and high device noise within the SQUID system.

In summary, the high boundary effects of square washers, vortex formation at their edges in real-world applications, and the sensitivity of inductance to changes in the inner diameter highlight that traditional square washers no longer meet the requirements for high sensitivity and low noise compared to the newer octagonal washers.

While this research has made significant strides in optimizing the SQUID washer design and providing new perspectives for enhancing device performance through improved washer geometries, it primarily focuses on the core component of the DC-SQUID—the washer. The intricate coupling relationships among various coils have historically been overlooked in computational and simulation studies, indicating the need for further in-depth exploration in this area. This limitation could potentially constrain our conclusions, as the ultimate performance of SQUID devices is not solely dependent on washer design but also on the cumulative effects of other components, such as Josephson junctions and superconducting circuit layouts. Therefore, while our research underscores the effectiveness of washer geometry optimization for enhancing device performance, a holistic optimization of the entire system is essential for practical applications. Moving forward, our research will focus on two key areas to achieve groundbreaking advancements in SQUID design and application:

• System-level simulation and optimization: We plan to develop more comprehensive simulation models that consider the interactions among all critical components within the SQUID system. By integrating various elements such as Josephson junctions, superconducting loops, and coupling circuits, we aim to optimize the overall performance of SQUIDs for diverse applications.
• In-depth study of coupling effects: Through experimental and theoretical analysis, we intend to thoroughly investigate the coupling mechanisms between different components in SQUID systems. By understanding how these interactions collectively impact the sensitivity and noise characteristics of SQUIDs, we can develop strategies to minimize unwanted coupling and enhance device performance.

Through these forthcoming research endeavors, we anticipate overcoming the limitations identified in this study and making significant contributions to the advancement of superconducting quantum sensing technology.

6. Conclusions

This study uses the Python package for modeling and optimizing SQUID devices, streamlining design processes. We investigated how washer geometries (circular, octagonal, and square) affect SQUID performance, focusing on washer inductance, shielding currents, and the noise spectrum. Shielding current simulations indicated that the octagonal geometry distributes the current more evenly, minimizing high-current density regions that contribute to vortex movement and 1/f noise; this uniform current distribution leads to a reduction in 1/f noise. The noise spectrum analysis showed that circular and octagonal washers produce lower noise levels across a range of frequencies. The results show circular and octagonal washers enhance sensitivity and reduce noise better than traditional square washers. These discoveries hold great potential for breakthroughs in a number of fields, such as increased sensitivity to tiny magnetic fields that can speed up data processing and, in the case of medical instrumentation applications, significantly improve the spatial resolution of devices. With the growing demand for detecting extremely weak magnetic fields, SQUIDs, with a sensitivity at the $fT/\sqrt{\mathrm{H}\mathrm{z}}$ level and noise at the $\mu {\mathsf{\Phi }}_0/\sqrt{\mathrm{H}\mathrm{z}}$ level, play a crucial role in enabling high-resolution magnetic field sensing [37]. Our research lays the groundwork for achieving femtotesla sensitivity and beyond in SQUID sensors through meticulous optimization, representing a significant leap in weak magnetic field detection. However, integrating these optimized washer designs into diverse SQUID applications and scaling up for mass production while maintaining precision remain the primary challenges for future endeavors.