Correction Compensation and Adaptive Cost Aggregation for Deep Laparoscopic Stereo Matching
Abstract
:Featured Application
Abstract
1. Introduction
- A correction compensation module is proposed to overcome correction errors. Unlike previous work, we learn about correction error information from a real laparoscopic dataset and compensate for errors in both the horizontal and vertical directions.
- An adaptive cost aggregation module is proposed to improve prediction performance in ill-posed regions. We skillfully quantify the value of cost volume elements based on their distribution and theoretically link high-value elements to those in ill-posed regions. By emphasizing high-value elements during the cost aggregation process, we improve the regularization effect on elements in ill-posed areas.
- Without ground truth labels, we propose an unsupervised depth estimation method for stereo laparoscopic images based on the proposed modules. Our model outperforms the state-of-the-art unsupervised methods and well-generalized models.
2. Related Work
2.1. Learning-Based Stereo Matching
2.2. Stereo Matching for Laparoscopic Images
3. Materials and Methods
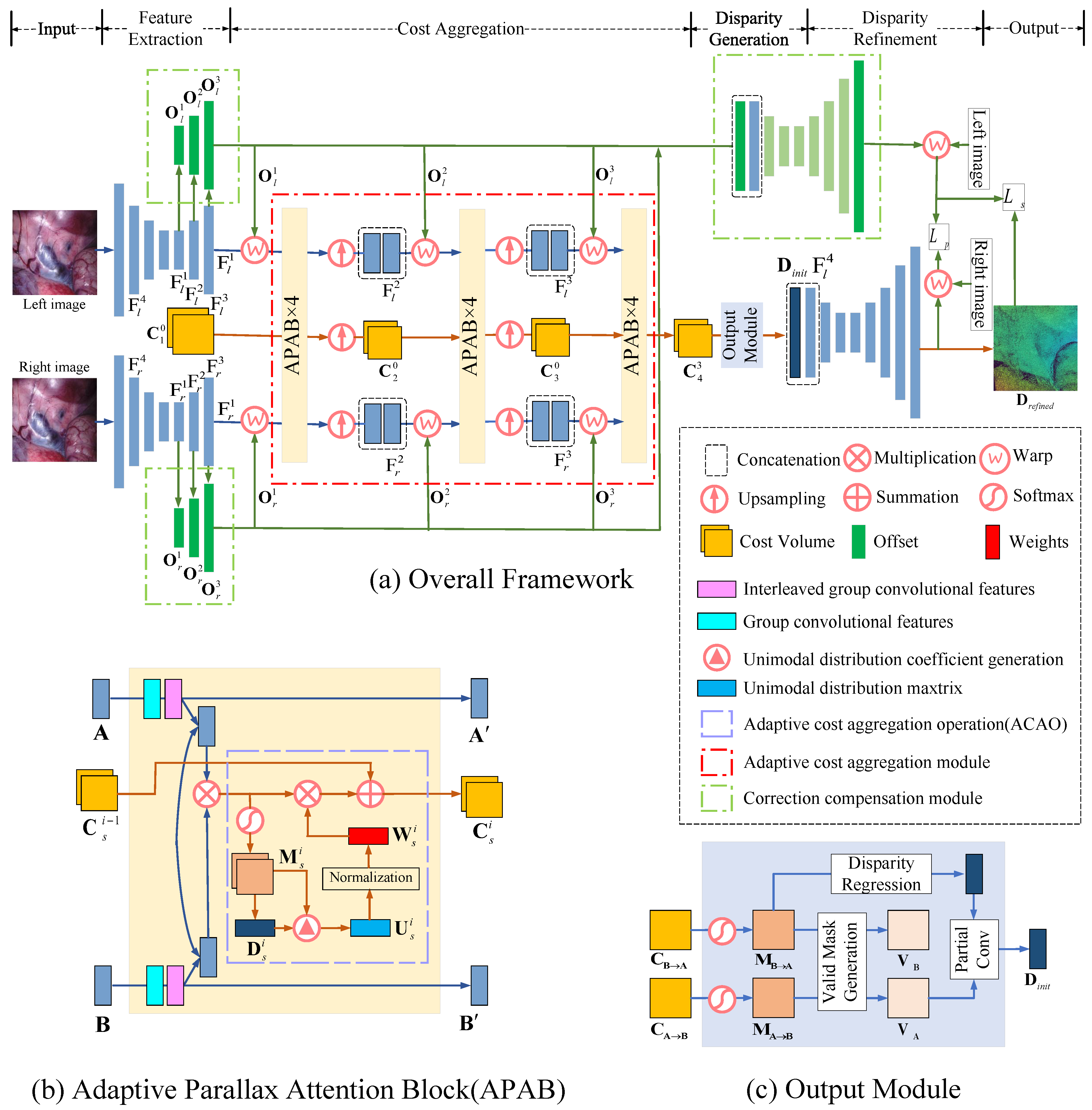
3.1. Network Architecture
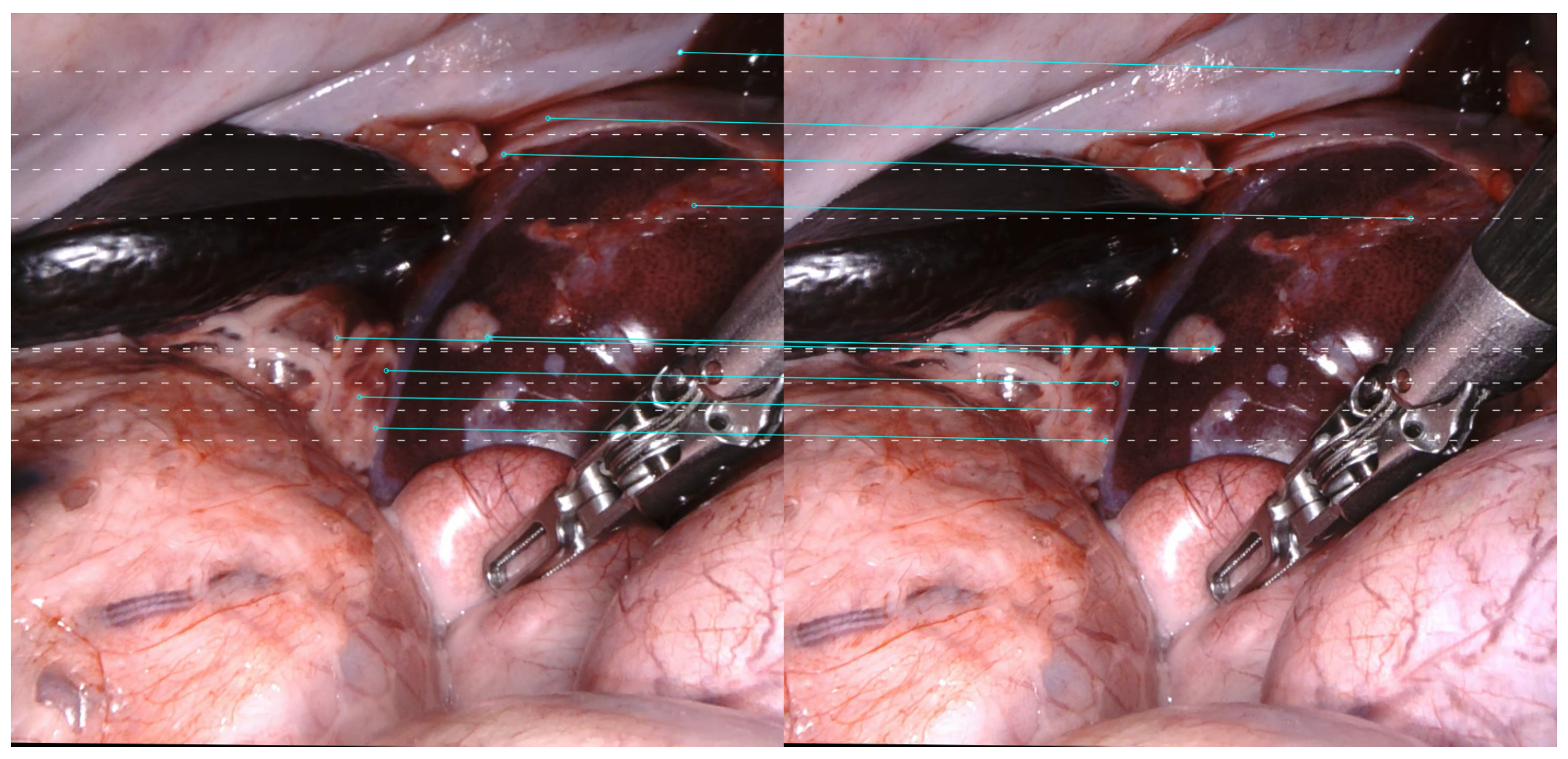
3.2. Correction Compensation Module
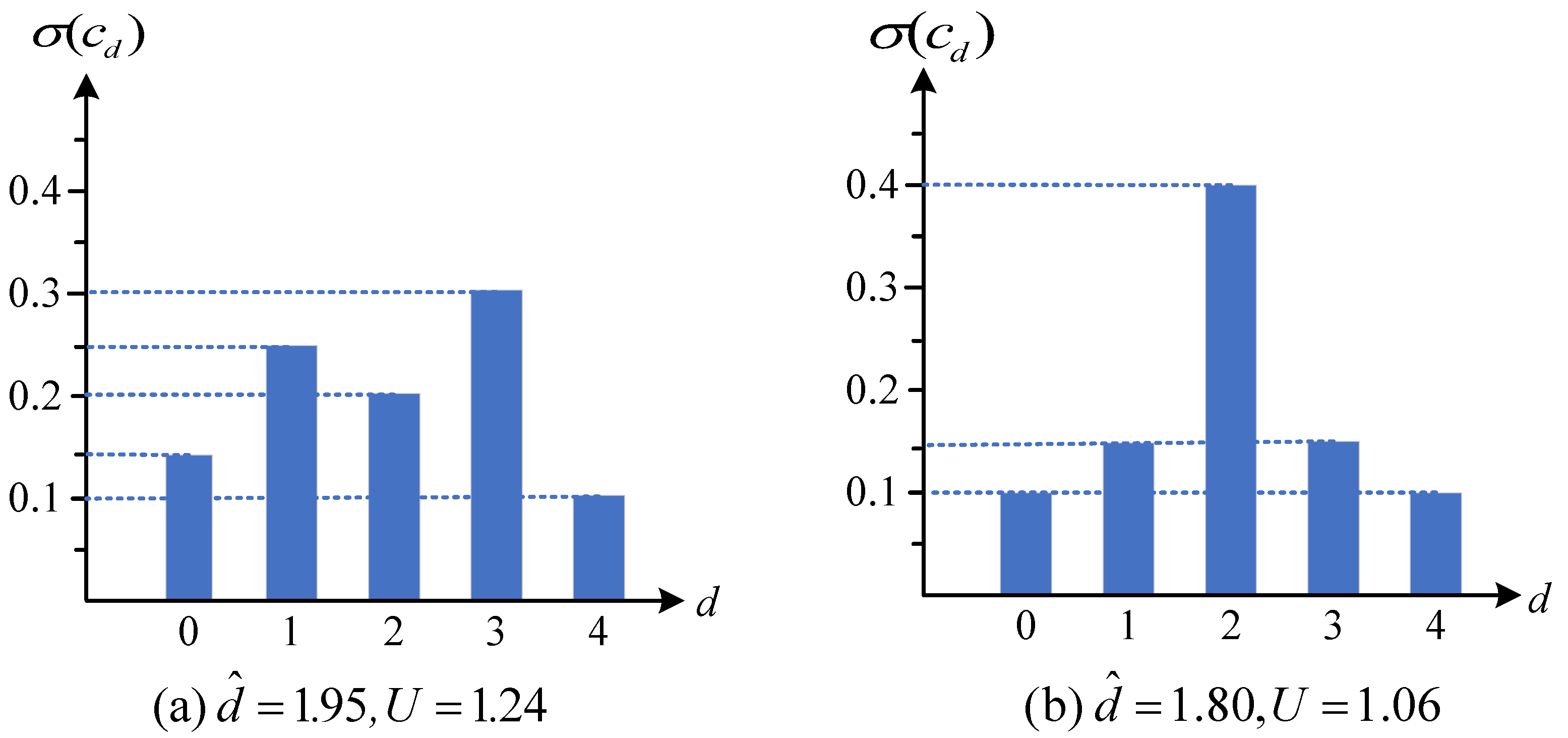
3.3. Adaptive Cost Aggregation Module
3.3.1. Adaptive Cost Aggregation Operation
3.3.2. Interleaved Group Convolution Structure
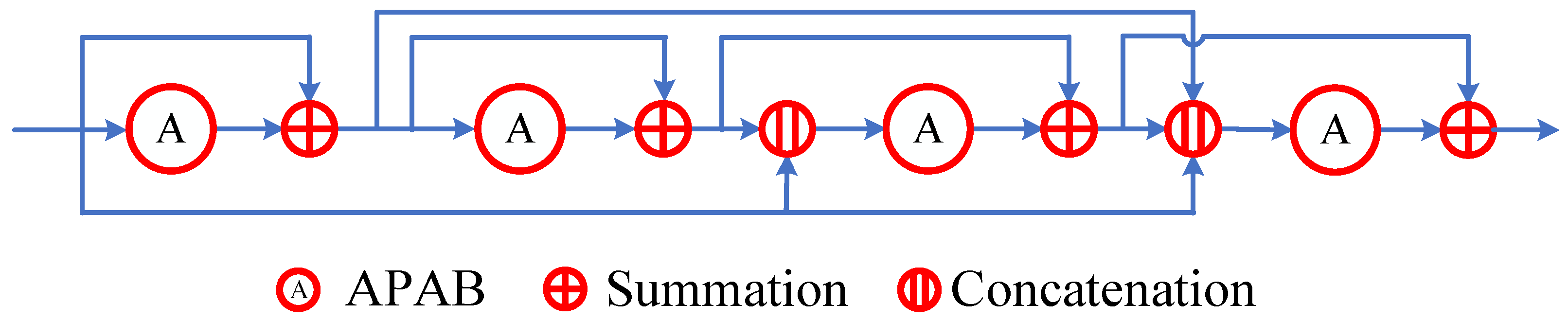
3.3.3. Dense Connection Structure
3.4. Loss
4. Experiments and Results
4.1. Datasets and Metrics
4.2. Implementation Details
4.3. Ablation Study
4.3.1. Correction Compensation Module
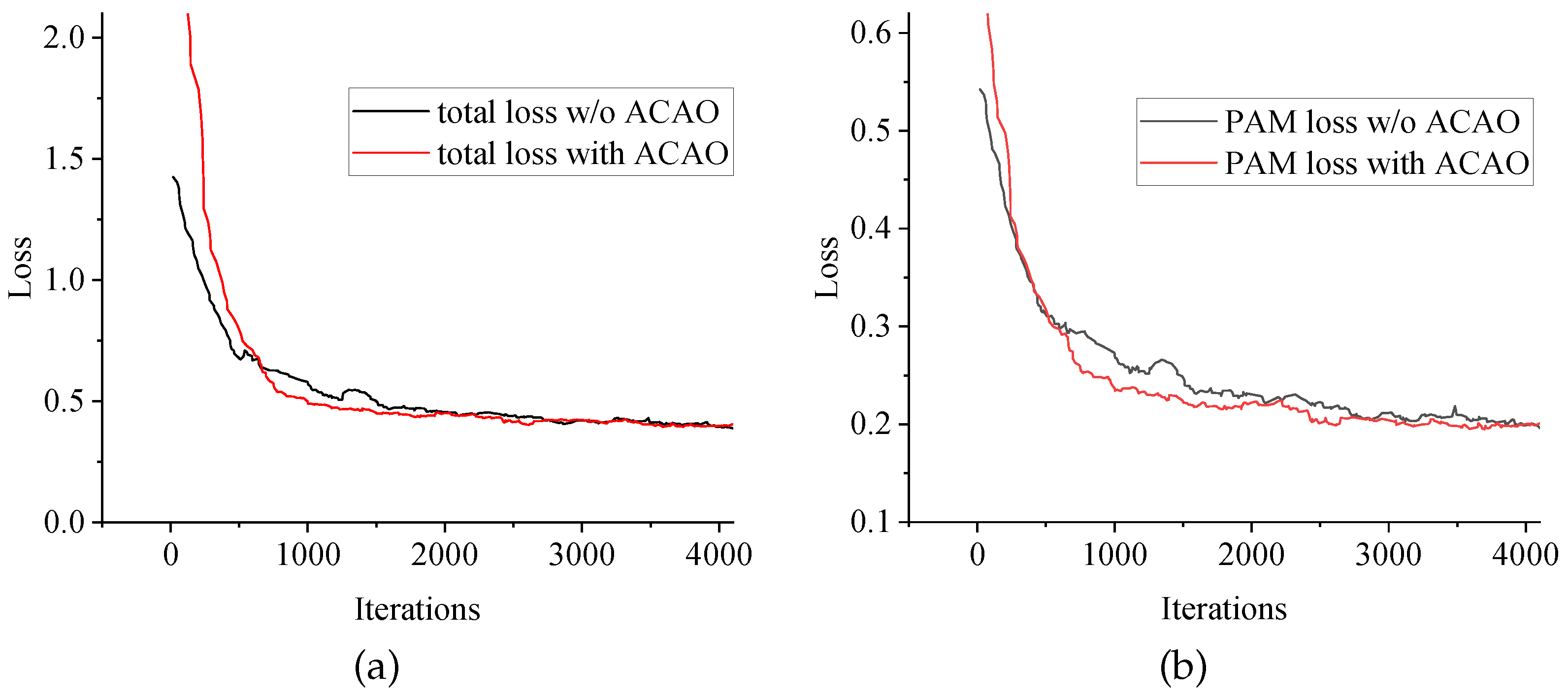
4.3.2. Adaptive Cost Aggregation Module
4.4. Comparison Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APAB | Adaptive parallax attention block |
| ACAO | Adaptive cost aggregation operation |
| IGCS | Interleaved group convolution structure |
| GCS | Group convolution structure |
| DCS | Dense connection structure |
| SSIM | Structural similarity |
| PAM | Parallax attention mechanism |
| 3D | Three-dimensional |
| CNN | Convolutional neural network |
References
- Arezzo, A.; Vettoretto, N.; Francis, N.K.; Bonino, M.A.; Curtis, N.J.; Amparore, D.; Arolfo, S.; Barberio, M.; Boni, L.; Brodie, R.; et al. The use of 3D laparoscopic imaging systems in surgery: EAES consensus development conference 2018. Surg. Endosc. 2019, 33, 3251–3274. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Chen, E.C.S.; Pautler, S.; Peters, T.M. A Robust Edge-Preserving Stereo Matching Method for Laparoscopic Images. IEEE Trans. Med. Imaging 2022, 41, 1651–1664. [Google Scholar] [CrossRef] [PubMed]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar] [CrossRef]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-resolution stereo datasets with subpixel-accurate ground truth. Lect. Notes Comput. Sci. 2014, 8753, 31–42. [Google Scholar] [CrossRef]
- Chang, J.R.; Chen, Y.S. Pyramid Stereo Matching Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5410–5418. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, J. AANet: Adaptive Aggregation Network for Efficient Stereo Matching. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1956–1965. [Google Scholar] [CrossRef]
- Cheng, X.; Zhong, Y.; Harandi, M.; Dai, Y.; Chang, X.; Li, H.; Drummond, T.; Ge, Z. Hierarchical Neural Architecture Search for Deep Stereo Matching. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Volume 33, pp. 22158–22169. [Google Scholar]
- Tankovich, V.; Häne, C.; Zhang, Y.; Kowdle, A.; Fanello, S.; Bouaziz, S. HITNet: Hierarchical Iterative Tile Refinement Network for Real-time Stereo Matching. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14357–14367. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, J.; Guo, P.; Yang, X. Attention Concatenation Volume for Accurate and Efficient Stereo Matching. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12971–12980. [Google Scholar] [CrossRef]
- Cheng, X.; Zhong, Y.; Harandi, M.; Drummond, T.; Wang, Z.; Ge, Z. Deep Laparoscopic Stereo Matching with Transformers. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2022, Singapore, 18–22 September 2022; pp. 464–474. [Google Scholar] [CrossRef]
- Huang, B.; Zheng, J.Q.; Nguyen, A.; Xu, C.; Gkouzionis, I.; Vyas, K.; Tuch, D.; Giannarou, S.; Elson, D.S. Self-supervised Depth Estimation in Laparoscopic Image Using 3D Geometric Consistency. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2022, Singapore, 18–22 September 2022; pp. 13–22. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Xiong, P.; Cai, T.; Yan, Z.; Yang, L.; Liu, J.; Fan, H.; Liu, S. Practical Stereo Matching via Cascaded Recurrent Network with Adaptive Correlation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 16242–16251. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Allan, M.; Mcleod, J.; Wang, C.; Rosenthal, J.C.; Hu, Z.; Gard, N.; Eisert, P.; Fu, K.X.; Zeffiro, T.; Xia, W.; et al. Stereo correspondence and reconstruction of endoscopic data challenge. arXiv 2021, arXiv:2101.01133. [Google Scholar]
- Luo, H.; Wang, C.; Duan, X.; Liu, H.; Wang, P.; Hu, Q.; Jia, F. Unsupervised learning of depth estimation from imperfect rectified stereo laparoscopic images. Comput. Biol. Med. 2022, 140, 105–109. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Zhu, C.; Meurer, M. Camera Calibration Error Modeling and Its Impact on Visual Positioning. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; pp. 1394–1399. [Google Scholar] [CrossRef]
- Yang, Z.; Simon, R.; Li, Y.; Linte, C.A. Dense Depth Estimation from Stereo Endoscopy Videos Using Unsupervised Optical Flow Methods. In Proceedings of the Medical Image Understanding and Analysis, Oxford, UK, 12–14 July 2021; pp. 337–349. [Google Scholar]
- Pratt, P.; Bergeles, C.; Darzi, A.; Yang, G.Z. Practical Intraoperative Stereo Camera Calibration. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014, Boston, MA, USA, 14–18 September 2014; Golland, P., Hata, N., Barillot, C., Hornegger, J., Howe, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 667–675. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. In International Journal of Computer Vision; Springer: Berlin/Heidelberg, Germany, 2004; Volume 60, pp. 91–110. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, H.; Shen, X.; Jia, J. Unsupervised Learning of Stereo Matching. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1576–1584. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Wang, Y.; Liang, Z.; Lin, Z.; Yang, J.; An, W. Parallax Attention for Unsupervised Stereo Correspondence Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2108–2125. [Google Scholar] [CrossRef] [PubMed]
- Mayer, N.; Ilg, E.; Häusser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar] [CrossRef]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-End Learning of Geometry and Context for Deep Stereo Regression. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar] [CrossRef]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H. GA-Net: Guided Aggregation Net for End-To-End Stereo Matching. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 185–194. [Google Scholar] [CrossRef]
- Liu, B.; Yu, H.; Long, Y. Local Similarity Pattern and Cost Self-Reassembling for Deep Stereo Matching Networks. In Proceedings of the The Thirty-Sixth AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2022; Volume 36, pp. 1647–1655. [Google Scholar] [CrossRef]
- Yang, G.; Zhao, H.; Shi, J.; Deng, Z.; Jia, J. SegStereo: Exploiting Semantic Information for Disparity Estimation. In Proceedings of the Computer Vision–ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 660–676. [Google Scholar] [CrossRef]
- Li, A.; Yuan, Z.; Ling, Y.; Chi, W.; Zhang, S.; Zhang, C. Unsupervised Occlusion-Aware Stereo Matching With Directed Disparity Smoothing. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7457–7468. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Drenkow, N.; Ding, A.; Creighton, F.X.; Taylor, R.H.; Unberath, M. Revisiting Stereo Depth Estimation From a Sequence-to-Sequence Perspective with Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 6177–6186. [Google Scholar] [CrossRef]
- Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical Deep Stereo Matching on High-Resolution Images. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5510–5519. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]


| Hyperparameter | Value | Description |
|---|---|---|
| m | 4 | Maximum pixel offset for features of 1/16 scale |
| 0.1 | Weight coefficients for the magnitude loss | |
| 0.1 | ||
| 0.1 | ||
| 0.5 | ||
| 1 | Weight coefficients for the scale loss | |
| 1 | ||
| 1 | ||
| 0.05 | Weight coefficients for the left–right consistency loss | |
| 0.1 | ||
| 0.15 | ||
| 0.2 | ||
| 0.1 | Weight coefficients for the total loss of the network L | |
| 1 | ||
| 0.5 |
| dim | EPE↓ | D1↓ | D3↓ | MAE↓ | |||
|---|---|---|---|---|---|---|---|
| 2.616 | 20.104 | 17.407 | 2.767 | ||||
| 71.431 | 90.505 | 90.116 | 26.557 | ||||
| ✓ | 2.641 | 20.690 | 17.887 | 2.765 | |||
| ✓ | ✓ | 2.244 | 14.338 | 11.986 | 2.475 | ||
| ✓ | ✓ | ✓ | |||||
| y | ✓ | ✓ | ✓ | 2.163 | 14.879 | 12.271 | 2.142 |
| ACAO | IGCS | DCS | GCS | Params (G)↓ | Flops (M)↓ | EPE↓ | D1↓ | D3↓ | MAE↓ |
|---|---|---|---|---|---|---|---|---|---|
| 7.82 | 75.46 | 1.951 | 12.073 | 9.557 | 1.897 | ||||
| ✓ | 7.82 | 75.46 | 1.873 | 10.367 | 8.314 | 1.799 | |||
| ✓ | ✓ | 6.22 | 52.83 | 1.877 | 10.767 | 8.540 | 1.904 | ||
| ✓ | ✓ | ✓ | 6.42 | 55.66 | |||||
| ✓ | ✓ | ✓ | 6.42 | 55.66 | 1.952 | 12.035 | 9.566 | 1.897 |
| Method | Test Set I | Test Set II | Avg. (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| kf1 | kf2 | kf3 | kf4 | kf5 | kf1 | kf2 | kf3 | kf4 | kf5 | ||
| W. Xia [14] | 5.70 | 7.18 | 6.98 | 8.66 | 5.13 | 13.8 | 6.85 | 13.1 | 5.70 | 7.73 | 8.08 |
| T. Zeffiro [14] | 7.91 | 2.97 | 1.71 | 2.52 | 2.91 | 5.39 | 1.67 | 4.34 | 3.18 | 2.79 | 3.54 |
| C. Wang [14] | 6.30 | 2.15 | 3.41 | 3.86 | 4.80 | 6.57 | 2.56 | 6.72 | 4.34 | 1.19 | 4.19 |
| J.C. Rosenthal [14] | 8.25 | 3.36 | 2.21 | 2.03 | 1.33 | 8.26 | 2.29 | 7.04 | 2.22 | 0.42 | 3.74 |
| D.P.1 [14] | 7.73 | 2.07 | 1.94 | 2.63 | 0.62 | 4.85 | 0.65 | 1.62 | 0.77 | 0.41 | 2.33 |
| D.P.2 [14] | 7.41 | 2.03 | 1.92 | 2.75 | 0.65 | 4.78 | 1.19 | 3.34 | 1.82 | 0.36 | 2.63 |
| S. Schmid [14] | 7.61 | 2.41 | 1.84 | 2.48 | 0.99 | 4.33 | 1.10 | 3.65 | 1.69 | 0.48 | 2.66 |
| STTR [28] | 9.24 | 4.42 | 2.67 | 2.03 | 2.36 | 7.42 | 7.40 | 3.95 | 7.83 | 2.93 | 5.03 |
| HybridStereoNet [10] | 7.96 | 2.31 | 2.23 | 3.03 | 1.01 | 4.57 | 1.39 | 3.06 | 2.21 | 0.52 | 2.83 |
| H. Luo [15] | 8.62 | 2.69 | 2.36 | 2.29 | 2.51 | 6.06 | 0.95 | 2.97 | 0.86 | 1.23 | 3.05 |
| PASMnet [21] | 8.99 | 2.53 | 1.93 | 2.93 | 1.31 | 5.11 | 1.52 | 3.71 | 2.04 | 0.83 | 3.09 |
| Ours | 8.80 | 2.55 | 1.65 | 2.21 | 1.11 | 4.23 | 1.13 | 3.06 | 1.61 | 0.62 | 2.70 |
| Method | EPE↓ | D1↓ | D3↓ | MAE↓ |
|---|---|---|---|---|
| HybridStereoNet [10] | 1.569 | 6.273 | 4.750 | 1.438 |
| PASMnet [21] | 2.279 | 14.640 | 12.779 | 2.242 |
| Ours |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yang, B.; Zhao, X.; Shi, Y. Correction Compensation and Adaptive Cost Aggregation for Deep Laparoscopic Stereo Matching. Appl. Sci. 2024, 14, 6176. https://doi.org/10.3390/app14146176
Zhang J, Yang B, Zhao X, Shi Y. Correction Compensation and Adaptive Cost Aggregation for Deep Laparoscopic Stereo Matching. Applied Sciences. 2024; 14(14):6176. https://doi.org/10.3390/app14146176
Chicago/Turabian StyleZhang, Jian, Bo Yang, Xuanchi Zhao, and Yi Shi. 2024. "Correction Compensation and Adaptive Cost Aggregation for Deep Laparoscopic Stereo Matching" Applied Sciences 14, no. 14: 6176. https://doi.org/10.3390/app14146176
APA StyleZhang, J., Yang, B., Zhao, X., & Shi, Y. (2024). Correction Compensation and Adaptive Cost Aggregation for Deep Laparoscopic Stereo Matching. Applied Sciences, 14(14), 6176. https://doi.org/10.3390/app14146176





