Entity-Alignment Interaction Model Based on Chinese RoBERTa

Abstract

Entity alignment aims to match entities with the same semantics from different knowledge graphs. Most existing studies use neural networks to combine graph-structure information and additional entity information (such as names, descriptions, images, and attributes) to achieve entity alignment. However, due to the heterogeneity of knowledge graphs, aligned entities often do not have the same neighbors, which makes it difficult to utilize the structural information from knowledge graphs and results in a decrease in alignment accuracy. Therefore, in this paper, we propose an interaction model that exploits only the additional information on entities. Our model utilizes names, attributes, and neighbors of entities for interaction and introduces attention interaction to extract features to further evaluate the matching scores between entities. Our model is applicable to Chinese datasets, and experimental results show that it has achieved good results on the Chinese medical datasets denoted MED-BBK-9K.

1. Introduction

A knowledge graph (KG) is an important tool for efficiently using visualization technology to describe knowledge resources that constructs a relational network that can be understood by both computers and humans. It is a structured data model that stores and represents knowledge in the form of a graph. It represents entities in the real world and the relationships between them in the form of nodes and edges, thereby organizing and connecting information. It is composed of many triples consisting of entities, relationships, and attributes. For example, the sentence “Einstein was born in Germany, and his profession was physicist” can be decomposed into two triples: Einstein-birthplace-Germany and Einstein-profession-physicist. Although knowledge graphs and semantic networks have similarities in knowledge representation, they have their own focuses and characteristics in terms of structure, application, and implementation. Knowledge graphs focus more on data integration and query. They contain rich entity attributes and specific fact triples and have a higher degree of structure. Semantic networks focus more on the representation and reasoning of knowledge. They mainly focus on concepts and relationships, focus less on the representation of attributes and specific facts, and are more used for association and reasoning between concepts.

With the rapid development of artificial intelligence and big-data technology, knowledge graphs are gradually penetrating into various fields, such as knowledge reasoning [1], recommendation systems [2], and question-answering systems [3]. The graphs are often incomplete, as they are built using different data sources for different purposes. As the amount of data continues to grow, a single graph often cannot meet the needs of downstream tasks, and the problem of how to find equivalent entities in the knowledge graphs constructed from different data sources is the challenge answered by knowledge fusion.

Entity alignment (EA) is a basic task in knowledge fusion. It is the process of identifying and connecting the same real-world entities represented in different data sources or knowledge graphs. Its purpose is to eliminate redundancy, integrate scattered information, and use complementary information between different knowledge graphs to improve data consistency and accuracy and achieve a unified large-scale knowledge graph so as to better support downstream applications driven by knowledge graphs. Figure 1 shows an example of entity alignment. The first step is to find two aligned entities and further screen their neighbors. The neighbor nodes connected by dotted lines represent aligned entities, and they point to the same thing in the real world. Graph structure, as a powerful data representation, is widely used in entity-alignment tasks to effectively capture rich relationships and semantic information between entities, thereby enabling entity matching and alignment across data sources. Specific techniques have evolved, from traditional knowledge graph embedding (KGE) models such as MTransE [4] and IPTransE [5] to later neural networks (NNs) such as the attention-based graph convolutional network (GCN) [6], HGCN [7], RDGCN [8], and VR-GCN [9]. However, despite the significant progress made by graph-structure approaches in entity-alignment tasks, a number of challenges and constraints remain. In particular, when dealing with large-scale knowledge graphs, graph-structure methods often face problems such as low computational efficiency, high data sparsity, and high semantic ambiguity. In order to enhance the precision and efficacy of entity alignment, researchers have begun to explore how to utilize additional information associated with entities to enhance the performance of entity alignment. Existing work has demonstrated the impact of additional information on multiple tasks. For example, Yang et al. [10] proposed that in the entity-alignment task, Hit Ratio@1 would drop by at least 30% if entity descriptions were ignored.

In order to align the graphs using additional information, the most prevalent method is to initialize the embedding of each node with additional information and apply a variant GCN model to update the node embeddings by aggregating the embeddings of all neighbors [11]. However, different knowledge graphs are often highly heterogeneous, resulting in equivalent entities not always having similar neighbors. In this case, propagating different neighbors may introduce noise and thus impair performance. Although some studies have attempted to distinguish the effects of different neighbors, GCN-like models continue to integrate the additional information from all neighbor entities in order to represent a given entity. Yang et al. [10] were aware of this problem and addressed it through a modeling process that thoroughly separates the additional information from the graph structure. Nevertheless, this approach neglects to consider the additional information pertaining to the neighbor entities. Furthermore, in a manner analogous to the aggregation of neighbors, all attributes are aggregated together in order to represent an entity, which also leads to noisy matching between entities.

In order to address the aforementioned issues, we propose RoBERTa-INT, a RoBERTa-based interaction model. BERT is a pre-trained language model that encodes the context of all words in a sentence through a bidirectional Transformer architecture. RoBERTa is an optimized BERT model. By increasing the amount of training data, extending the training time, increasing the batch size, adopting a dynamic masking strategy, and removing the Next Sentence Prediction task, RoBERTa significantly improves the model’s performance in various natural-language-processing tasks. We mimic the cognitive process of humans comparing two entities, typically starting with comparing the current entities and then checking for similar neighbors. Subsequently, based on the embedding of the name and attributes, each pair of neighbors or attributes is compared, and the relationship between them is thereafter referred to as an interaction, rather than simply being aggregated. In this way, RoBERTa-INT is able to effectively handle the noise-matching problem caused by aggregated neighbors or attributes, which improves the effect of entity alignment.

The principal contributions of this study are as follows:

• This paper puts forward a novel entity-alignment model, RoBERTa-INT, which enhances the accuracy and robustness of entity alignment through the utilization of the additional information associated with entities.
• Traditional entity-alignment models combine the graph-structure information, which often suffers from unreasonable aggregation of neighbor information, leading to the problem of noise matching. This paper presents a solution to the aforementioned problem through the introduction of an interaction model, which utilizes names, attributes, neighbors, and attentions of entities for interaction and captures the matching relationships between neighbors from a fine-grained and semantic perspective.
• We evaluate the model in detail on the Chinese datasets MED-BBK-9K [12], and the results demonstrate that the efficacy of the method proposed in this paper is significantly better than that of baseline models.

2. Related Works

Entity alignment represents a crucial undertaking within the domain of knowledge graphs. Its objective is to establish correspondences and alignments between entities with analogous semantics across disparate knowledge graphs, thereby facilitating the integration and consolidation of knowledge across diverse data sources. In the related work of entity alignment, researchers mainly improve the alignment effect by utilizing graph-structure information and additional information associated with entities.

2.1. Methods Based on Graph-Structure Information

In the area of entity alignment using graph-structure information, researchers have worked on mining the relationships, paths, and subgraph structures among entities in the knowledge graph for accurate entity alignment.

TransE-based methods. Bordes et al. [13] proposed the TransE model, which models entities by interpreting triples as translations of entities over low-dimensional embeddings and maps entities into low-dimensional vector spaces using graph-structure information. Although TransE is capable of achieving good results, it is unable to handle complex relationships, such as those involving one-to-many, many-to-one, and many-to-many cases. Chen et al. [4] proposed the MTransE model, an extension of TransE, which maps the representation of entities in different knowledge graphs to a unified embedding space by modeling the translation of relationships across knowledge graphs. Zhuang et al. [5] proposed the IPTransE model, an iterative path-based transformational embedding approach that aims to optimize the entity-alignment task by exploiting the path information between entities in the knowledge graph.

GCN-based methods. Wang et al. [14] proposed the GCN-Align model, which represents the knowledge graph as a graph structure and uses GCN to learn the representation of entities, where the node representations are continuously updated by aggregating the information on neighbor nodes. However, GCN-Align also suffers from the disadvantages of high requirements with regard to the quality of graph structure and high computational complexity.

GNN-based methods. Cao et al. [15] proposed the MuGNN model, which uses GNN to encode structural features from different perspectives to learn alignment-oriented embeddings. This approach can explicitly complete the knowledge graph and also prune exclusive entities, in turn utilizing the heterogeneous structural information from the knowledge graph to effectively improve the quality of the alignment. Sun et al. [16] proposed the AliNet model, which aggregates the information associated with multi-hop neighbors of entities at each layer through a gating mechanism and uses an attention mechanism to reduce noise. However, the model relies on high-quality graph-structure data and requires a certain number of high-quality pre-aligned entities as training data.

Other methods. Zhang et al. [17] proposed the RALG model, constructed a heterogeneous linear graph that clearly captures the correlation between relationships and designed a new aggregation method in the form of triples to enhance the correlation between entities and their correspondences. Luo et al. [18] proposed a framework called ASGEA, which connects entities in different knowledge graphs through anchor links, extends along these paths to construct alignment subgraphs containing all potential alignment paths, and designs interpretable path-based GNNs to improve alignment performance and interpretability. ASGEA performs well in entity alignment and cross-modal entity-alignment tasks. However, it also suffers from drawbacks such as high computational complexity and poor results in cases of sparse anchor links.

2.2. Methods Based on Additional Information

In addition to graph-structure information, many existing approaches facilitate entity-alignment performance by employing additional information from the graph, including entity names, descriptions, images, attributes, etc.

Entity-name-based methods. Azzalini et al. [19] utilized word-embedding and sentence-embedding models trained on an external corpus to convert entity names and attributes into vector representations, which are blocked by locally sensitive hashing and clustering algorithms to identify semantically similar entity records. On the test datasets, this approach proved to be effective in exploiting the semantic information of entity names. Ge et al. [20] proposed an effective end-to-end entity alignment framework, EASY, which can eliminate labor-intensive preprocessing by fully discovering the name information provided by the entities themselves and jointly fuse the features captured by entity names to improve alignment results. Zhang et al. [21] proposed the MultiKE model, a framework for unifying multiple views of entities, which embeds entities using various combination strategies based on the views of entity names, relationships, and attributes. In addition, several cross-graph inference methods were designed to enhance the alignment between two graphs. Zhao et al. [22] proposed the UEA model, an unsupervised framework for performing entity alignment in the open world, which generates structural representations and integrates them with additional information to provide a more comprehensive view of the alignment to enhance alignment performance.

Image-based methods. Liu et al. [23] investigated the use of visual semantic representations to align entities in heterogeneous knowledge graphs. The proposed new method, EVA, combines visual knowledge with other auxiliary information to create an overall representation of entities, providing strong signals for cross-graph entity alignment.

Entity-attribute-based methods. Liu et al. [24] believed that attribute triplets can also provide key alignment signals, but this concept has not been well explored. They proposed to use attribute value encoders and divide KG into subgraphs to effectively model various types of attribute triplets, achieving remarkable results on the baselines of cross-lingual and monolingual datasets. Wang et al. [25] proposed a new method for directly learning entity-pair embeddings for entity alignment. The pairwise connected graphs of two graphs are first generated, and then the entity-pair embeddings of the pairwise connected graphs are learned for predicting the equivalence of entities. In this process, similar features are generated through the attributes of the entity pairs and the similar features are propagated using GNN to obtain the final embeddings of the entity pairs. Different graphs may have many different attribute types, and even the same attributes may have different data structures and value granularities. To solve this problem, Yang et al. [26] proposed the COTSAE model, which combines structural and attribute information associated with entities by co-training the two embedding learning components separately, and proposed a joint-attention approach to collaboratively learn attribute type and value attention in the model.

3. Methodology

3.1. Problem Definition

Knowledge Graph: We defined the knowledge graph $G=(E,R,A,V)$, where $e\in E$, $r\in R$, $a\in A$, and $v\in V$ denote entities, relationships, attributes and corresponding attribute values, respectively. For example, the author of the book How the Steel Was Tempered is Nikolai Ostrovsky, and its publication year is 1932. This can form a relational triple How the Steel Was Tempered-Author-Nikolai Ostrovsky and an attribute triple How the Steel Was Tempered-Publishing Year-1932. The entities contained in it are How the Steel Was Tempered and Nikolai Ostrovsky, the relationship is the author, the attribute is the publishing year, and the attribute value is 1932. The number of hops in the knowledge graph refers to the number of relationships (edges) from one entity to another in the knowledge graph. Each relationship (edge) represents a “hop”, so the number of hops is a way to describe the distance between two entities. For example, the number of hops from an entity to its nearest neighbor is 1. $N^h\left(e\right)={\left\{\left(r_i,e_i\right)\right\}}_{i=1}^{\left|N^h\left(e\right)\right|}$ denotes the set of all h-hop neighbors of entity $e$, where $h$ is the number of hops, and the i-th neighbor contains a neighbor relationship $r_i$ and the corresponding entity $e_i$, where $\left|N^h\left(e\right)\right|$ denotes the number of $N^h\left(e\right)$. $N\left(e\right)$ denotes the set of all neighbors of entity $e$. $A\left(e\right)={\left\{\left(a_i,v_i\right)\right\}}_{i=1}^{\left|A\left(e\right)\right|}$ denotes the set of attributes of entity $e$, and the i-th attribute contains a name $a_i$ and the corresponding attribute value $v_i$, where $\left|A\left(e\right)\right|$ denotes the number of $A\left(e\right)$.

Entity Alignment: Given two knowledge graphs $G$ and $G^{\prime }$ and a set of already aligned entity pairs $\mathrm{P}=\left\{\right(\mathrm{e}~{\mathrm{e}}^{\prime }\left)\right\}$, we aimed to derive a ranking function $\mathrm{f}:\mathrm{E}\times {\mathrm{E}}^{\prime }\to \mathbb{R}$ to compute the similarity scores between the two entities, based on which we ranked the correctly aligned entity $e^{\prime }$ to any queried entity $e$ as high as possible among all the entities in $E^{\prime }$. A ranking function makes it possible to score entity pairs. Such a function needs to accept input features, calculate similarity scores, and output similarity scores. The term “ranking” refers to the use of this score to find the best matching entity. The method used to derive the ranking function is very important because it directly affects the accuracy and effect of the entity-alignment task.

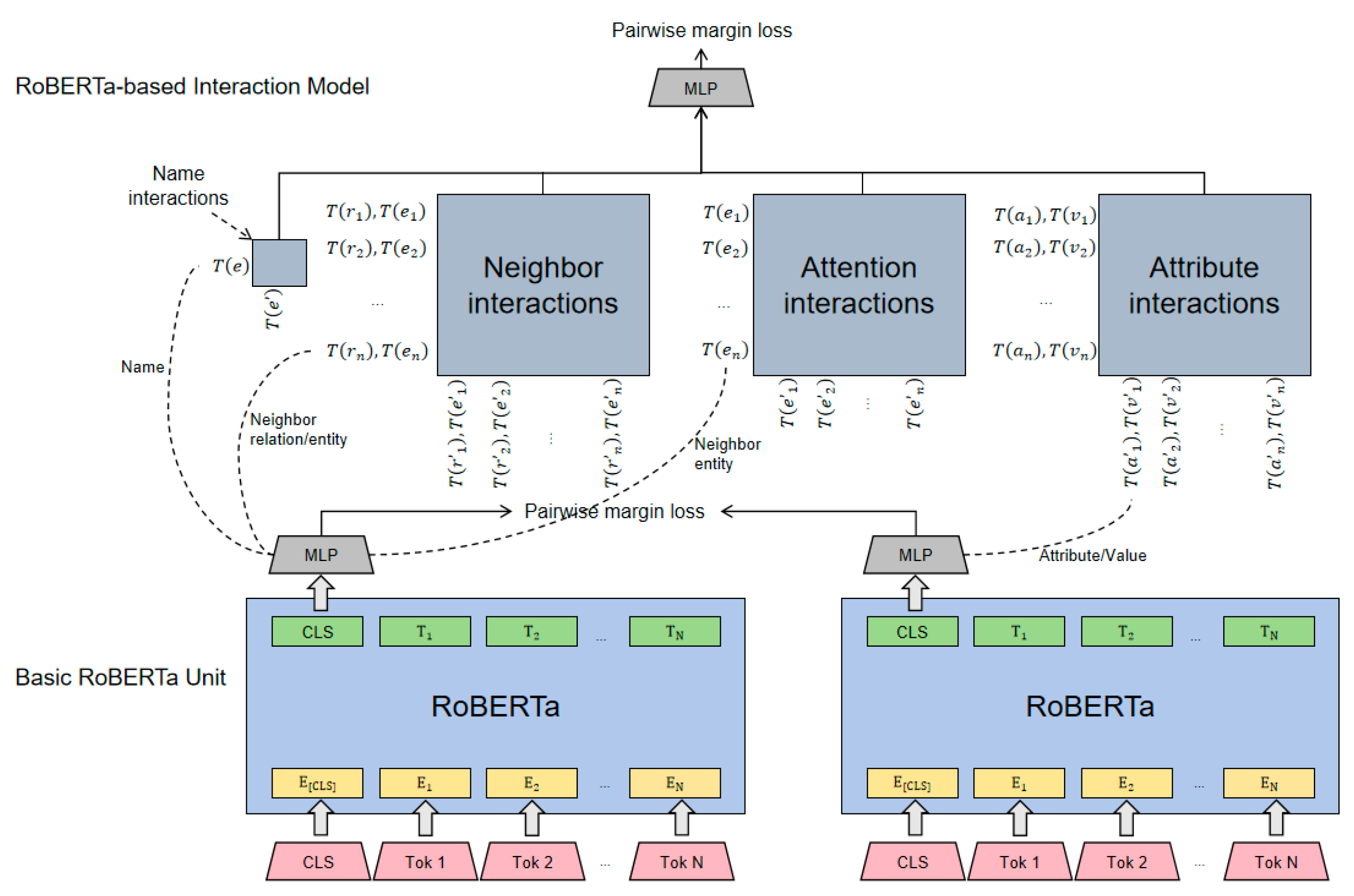
3.2. The Model Framework

The RoBERTa-INT model proposed in this paper consists of the Basic RoBERTa Unit and the RoBERTa-based Interaction Model. Figure 2 shows the whole model framework. We will explain the Basic RoBERTa Unit and the RoBERTa-based Interaction Model in detail in Section 3.2.1 and Section 3.2.2.

3.2.1. Basic RoBERTa Unit

We used entity alignment as a downstream task to fine-tune RoBERTa. First, we constructed the training data $D=\left\{\left(e,e_0^{\prime },e_1^{\prime }\right)\right\}$, where each triple $\left(e,e_0^{\prime },e_1^{\prime }\right)\in D$ contains a query entity $e\in E$, correctly aligned samples $e_0^{\prime }\in E^{\prime }$ and negative samples $e_1^{\prime }$ randomly sampled from $E^{\prime }$. For example, for a constructed training data (Einstein, Albert Einstein, Newton), “Einstein” is the query entity from $E$; “Albert Einstein” is its correctly aligned entity in $E^{\prime }$, which means that they point to the same person or thing in the real world; “Newton” is a negative sample entity randomly sampled from $E^{\prime }$. For each entity $e$ in the datasets, we applied a pre-trained Chinese RoBERTa to accept its name as input, take the corresponding value of the CLS label, and then map it using MLP, and the result obtained was used as the vector representation of that entity.

$$T\left(e\right)=MLP\left(CLS\left(e\right)\right)$$

(1)

the RoBERTa model parameters are fine-tuned based on this vector representation and margin loss with the following equation:

$$L=\sum _{\left(e,e_0^{\prime },e_1^{\prime }\right)\in D}\mathit{max}\left\{0,d\left(e,e_0^{\prime }\right)-d\left(e,e_1^{\prime }\right)+\alpha \right\}$$

(2)

where $d(.)$ denotes the Manhattan distance function of vectors $T\left(e\right)$ and $T\left(e^{\prime }\right)$ and $\alpha$ denotes the marginal loss. The negative sample-sampling method was derived from the BootEA model proposed by Sun et al. [27]. The following interaction model uses these embeddings as the basic units. Due to the lack of computational resources, the RoBERTa units was fine-tuned using the above method, and the model parameters were fixed during the subsequent interactions.

3.2.2. RoBERTa-Based Interaction Model

Based on the Basic RoBERTa Unit, we constructed an interaction model consisting of Name Interaction, Neighbor Interaction, Attention Interaction and Attribute Interaction. The main components are as follows:

Name Interaction. Given two entities $e$ and $e^{\prime }$ in the graphs $G$ and $G^{\prime }$, the name vector representations $T\left(e\right)$ and $T\left(e^{\prime }\right)$ of entities $e$ and $e^{\prime }$ are computed using the RoBERTa unit described above, and then the cosine similarity of $T\left(e\right)$ and $T\left(e^{\prime }\right)$ is computed, and the result of the computation is the name interaction.

Neighbor Interaction. In this section, we established the interaction between neighbors $N\left(e\right)$ and $N\left(e^{\prime }\right)$. The idea was to compare the names of each neighbor pair, rather than learning the global representation of entities $e$ and $e^{\prime }$ by aggregating the names of all neighbors as in existing work. We applied the basic RoBERTa unit to obtain ${\left\{T\left(e_i\right)\right\}}_{i=1}^{\left|N\left(e\right)\right|}$ and ${\left\{T\left(e_i^{\prime }\right)\right\}}_{i=1}^{\left|N\left(e^{\prime }\right)\right|}$, and, for the neighbor entities of entities $e$ and $e^{\prime }$, to compute the similarity matrix between the two embedding sets based on their names, and then to apply a dual aggregation function to extract similarity features from the matrix. We denote by $B$ the interaction between the neighbors of entities $e$ and $e^{\prime }$, and each element $b_{ij}$ represents the interaction, i.e., the cosine similarity between $T\left(e_i\right)$ and $T\left(e_j^{\prime }\right)$:

$$b_{ij}=\frac{T\left(e_i\right)\cdot T\left(e_j^{\prime }\right)}{‖T\left(e_i\right)‖\cdot ‖T\left(e_j^{\prime }\right)‖}$$

(3)

where $T\left(e_i\right)$ and $T\left(e_j^{\prime }\right)$ are obtained by Formula (1) for the i-th neighbor of $e$ and the j-th neighbor of $e^{\prime }$, respectively.

We applied the dual aggregation function to extract the similarity features of rows and columns of $B$. Neighbors are unordered and independent of each other. Therefore, we used the RBF kernel-aggregation function [28] to extract the cumulative similarity features. The RBF kernel-aggregation function calculates the similarities between the input feature vectors and uses these similarities as weights to perform weighted summation on the input feature vectors to obtain an aggregated feature vector. This method can effectively capture the complex relationship between the input features.

Before extracting the similarity cumulative features, we performed a maximum-pooling operation on each row $B_i=\left\{b_{i0},...,b_{ij},...,b_{in}\right\}$ to obtain the maximum similarity $b_i^{max}$, i.e., we select the most likely aligned sample for the i-th neighbor of entity $e$ from the neighbors of entity $e^{\prime }$. The reason for this is that due to the heterogeneous nature of the knowledge graph, the neighbor entities of two aligned entities are not identical, and we need to care only about the similarity between the neighbor entity of entity $e$ and the one that is most similar to the one in the neighbors of entity $e^{\prime }$. Next, the maximum similarity $b_i^{max}$ is converted into a row-based feature vector $X^r\left(B_i\right)$, where the k-th element $X_k\left(b_i^{max}\right)$ is converted by the k-th RBF kernel into the mean ${\mu }_k$ and variance ${\sigma }_k$. $X^r\left(B_i\right)$ for all rows is then averaged into a row-based similarity embedding ${\upsilon }^r\left(N\left(e\right),N\left(e^{\prime }\right)\right)$, as follows:

$$\begin{gathered} b_i^{max}={max}_{j=0}^n\left\{b_{i0},\dots ,b_{ij},\dots ,b_{in}\right\} \\ {X}_k\left(b_i^{max}\right)=exp\left[-\frac{{\left(b_i^{max}-{\mu }_k\right)}^2}{2{\sigma }_k^2}\right] \\ {X}^r\left(B_i\right)=\left[X_1\left(b_i^{max}\right),\dots ,X_k\left(b_i^{max}\right),\dots ,X_K\left(b_i^{max}\right)\right] \\ {\upsilon }^r\left(N\left(e\right),N\left(e^{\prime }\right)\right)=\frac{1}{\left|N\left(e\right)\right|}\sum _{i=1}^{\left|N\left(e\right)\right|}\mathit{log}{X}^r\left(B_i\right) \end{gathered}$$

(4)

where $n$ is the maximum number of neighbors, $K$ denotes the number of RBF kernels, and $r$ denotes row aggregation. If the number of $\left|N\left(e\right)\right|$ is less than $n$, $B$ will be filled with values of 0. The kernel function is used to convert one-dimensional similarity to k-dimensional similarity for enhanced differentiation, where the kernel function with $\mu =1$ and $\sigma \to 0$ only considers exact matching between neighbors, while the other kernel functions capture semantic matching between neighbors.

Features are aggregated along rows in the above process to reflect the degree of similarity of each neighbor $e_i\in N\left(e\right)$ with the neighbors $N\left(e^{\prime }\right)$ of $e^{\prime }$. Similarly, we also aggregated features along the columns to obtain the degree of similarity of each neighbor $e_j^{\prime }\in N\left(e^{\prime }\right)$ with the neighbors $N\left(e\right)$ of $e$. Finally, the row-aggregation vector ${\upsilon }^r$ is spliced with the column aggregation vector ${\upsilon }^c$ as the final similarity embedding, as follows:

$$\upsilon \left(N\left(e\right),N\left(e^{\prime }\right)\right)={\upsilon }^r\left(N\left(e\right),N\left(e^{\prime }\right)\right)\oplus {\upsilon }^c\left(N\left(e\right),N\left(e^{\prime }\right)\right)$$

(5)

where $\oplus$ denotes the splice operation and $c$ denotes column aggregation, the neighbor interaction is shown in Figure 3. First, we computed the similarity matrix between neighbors $N\left(e\right)$ and $N\left(e^{\prime }\right)$, and then applied the maximum pooling operation to each row to obtain the maximum similarity $b_i^{max}$ between each neighbor and the most similar neighbor. Then $b_i^{max}$ is converted into a row-based feature vector $X^r\left(B_i\right)$, and the RBF kernel function is used to enhance the distinguishing ability of the features. Different kernel functions are used here to capture the exact match and semantic similarity between neighbors. Finally, the row aggregate feature vector ${\upsilon }^r\left(N\left(e\right),N\left(e^{\prime }\right)\right)$ and the column aggregate feature vector ${\upsilon }^c\left(N\left(e\right),N\left(e^{\prime }\right)\right)$ are concatenated as the final neighbor similarity representation. In addition, in order to consider the influence of neighbor relationships, the similarity matrix $M$ between neighbor relationships is also calculated, and it is element-wise multiplied with the entity similarity matrix to enhance the support of similar neighbor relationships for entity alignment. We explain the similarity matrix $M$ between neighbor relationships below.

Neighboring Relationship Mask Matrix. For entities $e$ and $e^{\prime }$, their neighbor triples are $\left(e,r_i,e_i\right)$ and $\left(e^{\prime },r_j^{\prime },e_j^{\prime }\right)$, respectively, entities $e$ and $e^{\prime }$ are more likely to be aligned if the neighbor entities $e_i$ and $e_j^{\prime }$ are similar and the relationships $r_i$ and $r_j^{\prime }$ are also similar. Based on the above assumptions, we computed not only the similarity matrix between neighbor entities $B$, but also the similarity matrix between neighbor relationships $M$. $M$ was regarded as a mask matrix and was multiplied by $B$, i.e., $B=B\otimes M$, where $\otimes$ denotes the product of elements. To compute $M$, we needed to embed each neighbor relationship. We averaged $T\left(e\right)$ over all associated head and tail entities and joined them to represent the relationship.

Interactions Between Multi-hop Neighbors. One-hop neighbor interaction may miss some important information because it is limited to a single path of information transfer. In contrast, multi-hop neighbor interaction is able to capture the relationship between entities more comprehensively. For one-hop neighbors $N^1\left(e\right)$ and $N^1\left(e^{\prime }\right)$ and multi-hop neighbors $N^t\left(e\right)$ and $N^t\left(e^{\prime }\right)$, we constructed the interaction matrices between $N^1\left(e\right)$ and $N^1\left(e^{\prime }\right)$, $N^1\left(e\right)$ and $N^t\left(e^{\prime }\right)$, $N^t\left(e\right)$ and $N^1\left(e^{\prime }\right)$, $N^t\left(e\right)$ and $N^t\left(e^{\prime }\right)$, respectively, extracted the similarity vectors using the aggregation function of Formulas (4) and (5), respectively, and connected them as the final neighbor-similarity embedding.

Attention Interaction. In order to further enhance the expressiveness of the model, we incorporated attention interaction into the interaction model to capture finer-grained feature matching and improve the accuracy of entity alignment. We applied the multi-head attention mechanism to compute the similarity between entities and their neighbors. Specifically, we first linearly transformed the embeddings of entities and their neighbors to generate query vectors, key vectors, and value vectors. These vectors are divided into multiple heads, and each head independently performs the scaled dot-product attention computation with the following equation:

$$Attention\left(Q,K,V\right)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(6)

where $Q$ is the query vector, from the neighbor embedding of entity $e$; $K$ and $V$ are the key vector and value vector, respectively, both from the neighbor embedding of entity $e^{\prime }$; $d_k$ is the dimension of each head.

All the outputs of the heads are concatenated together and transformed through linear layers to obtain the final interactive feature representation, as follows:

$$Featur{e}_{Multi-head}\left(e,e^{\prime }\right)=Linear\left(concat\left(Attentio{n}_1,...,Attentio{n}_i,...,Attentio{n}_n\right)\right)$$

(7)

where $n$ denotes the number of attention heads and ${\mathit{Attention}}_i$ denotes the attention output of the i-th head.

Attribute Interaction. The attribute triples of entities $e$ and $e^{\prime }$ are $\left(e,a_i,v_i\right)$ and $\left(e^{\prime },a_j^{\prime },v_j^{\prime }\right)$, respectively, which are similar to the entity neighbor triples, so attribute interaction can be analogous to neighbor interaction. We converted the similarity matrix between neighbor entities to the similarity matrix between $T{\left(v_i\right)}_{i=1}^{\left|A\left(e\right)\right|}$ and $T{\left(v_i^{\prime }\right)}_{i=1}^{\left|A\left(e^{\prime }\right)\right|}$ and changed the mask matrix between neighbor relationships to the mask matrix between $T{\left(a_i\right)}_{i=1}^{\left|A\left(e\right)\right|}$ and $T{\left(a_i^{\prime }\right)}_{i=1}^{\left|A\left(e^{\prime }\right)\right|}$. The aggregation function of Formulas (4) and (5) was next used to generate the attribute similarity vector $\upsilon \left(A\left(e\right),A\left(e^{\prime }\right)\right)$. To avoid nested interaction, we ignored the attributes of neighbors.

The Final Combination. Given the cosine similarity $\cos \left(T\left(e\right),T\left(e^{\prime }\right)\right)$ between the names of entities $e$ and $e^{\prime }$, the neighbor-similarity vector $\upsilon \left(N\left(e\right),N\left(e^{\prime }\right)\right)$, the attention-interaction feature $Featur{e}_{Multi-head}\left(e,e^{\prime }\right)$ and the attribute-similarity vector $\upsilon \left(A\left(e\right),A\left(e^{\prime }\right)\right)$, we joined them together and applied the MLP layer to obtain the final similarity score between entities $e$ and $e^{\prime }$, as follows:

$$\begin{gathered} \upsilon \left(e,e^{\prime }\right)=\left[\mathit{cos}\left(T\left(e\right),T\left(e^{\prime }\right)\right)\oplus \upsilon \left(N\left(e\right),N\left(e^{\prime }\right)\right)\oplus Featur{e}_{Multi-head}\left(e,e^{\prime }\right)\oplus \upsilon \left(A\left(e\right),A\left(e^{\prime }\right)\right)\right] \\ d\left(e,e^{\prime }\right)=MLP\left(\upsilon \left(e,e^{\prime }\right)\right) \end{gathered}$$

(8)

finally, $d\left(e,e^{\prime }\right)$ was brought into the Formula (2) marginal-loss equation, and the MLP parameters in Formula (8) were fine-tuned according to the loss.

3.3. Entity Alignment

In the process of entity alignment, we first applied the basic RoBERTa unit to obtain the embedding of each entity through Formula (1), calculate the cosine similarity between the embedding of entity $e$ in graph $G$ and the embedding of each entity in graph $G^{\prime }$, and return top-k similar entities as candidate entities for entity $e$. Next, for entity $e$ and each candidate entity, we applied the RoBERTa-based interaction model to infer the matching scores between them and rank all candidate entities for evaluation.

4. Experiments

First, we describe the datasets, parameter settings, and evaluation metrics used for the experiment. Next, we conduct a comparative analysis to compare our proposed method with existing methods to demonstrate its superior validity. Finally, we explore the impact of the model components on the model results.

4.1. Datasets

We conducted experiments on the MED-BBK-9K datasets. This dataset was first proposed in 2020 as a new benchmark for entity-alignment evaluation and was extracted from two actual medical-domain knowledge graphs. Specifically, the MED subgraph was constructed from a medical resource that covers fine-grained knowledge such as diseases, symptoms, and drugs, supporting applications such as question-answering systems and medical assistants. The BBK subgraph was extracted from the information boxes of Baidu Baike through natural-language-processing technology. A total of 9162 one-to-one entity mapping connections were annotated between these two subgraphs through manual and heuristic rules. More details of the MED-BBK-9K datasets are shown in

Table 1. Statistics of the datasets.

Dataset	KGs	Entities	Relation		Attribute
			Relationships	Triples	Attributes	Triples
MED-BBK-9K	MED	9162	32	158,357	19	11,467
	BBK	9162	20	50,307	21	44,987

.

Generally speaking, the more data are used for training, the better the model performs. However, in the entity-alignment task, it was necessary to use a smaller proportion of total data for the training set to verify the model performance on unknown entity pairs; the model showed maximal efficiency of data utilization with 30% of the data used for training, and most existing entity-alignment models have a training-to-testing ratio of 3:7. Therefore, in order to make a fair comparison with other existing models, we also set 30% of pre-aligned entity pairs to be used for training, and the rest were used for testing.

4.2. Parameter Settings and Evaluation Metrics

Our model was implemented in PyTorch (https://pytorch.org/) and was run on an NVIDIA GeForce RTX 4090 (24 GB) GPU (Santa Clara, CA, USA). The specific model-parameter settings are shown in

Table 2. Experimental parameters of the entity-alignment model.

Parameter Name	Parameter Information
The embedding dimension of CLS	768
MLP dimension in Formula (1)	300
MLP dimension in Formula (8)	11 → 1
The number of candidates returned $k$ in Basic RoBERTa Unit	50
The maximum value of neighbors and attributes $n$	250
Margin $\alpha$ (Fine-tuning RoBERTa)	3
Margin $\alpha$ (Fine-tune MLP in Formula (8))	1
The number of RBF kernels $K$	20
Mean $\mu$	The range of values is from 0.025 to 0.975, with an interval of 0.05, and the total number is 20
Variance $\sigma$	0.1
Initial learning rates (Fine-tuning RoBERTa)	0.00001
Initial learning rates (Interaction model)	0.0005

, and we used AdamW for parameter optimization.

The evaluation metrics we used were Hit Ratio (Hits)@k (k = 1, 5) and Mean Reciprocal Rank (MRR). Hits@k denotes the proportion of valid entity pairs that have correctly aligned entities among the first k alternatives corresponding to them for all target entities. $N$ is the set of triples; $\left|N\right|$ is the number of ternary sets; $\coprod \left(.\right)$ is the indicator function: if the condition is true, the value of the function is 1, and if the condition is false, the value of the function is 0. The calculation formula is as follows:

$$H\mathrm{it}s@k=\frac{1}{\left|N\right|}\sum _{i=1}^{\left|N\right|}\coprod$$

(9)

MRR is the average of the inverse of the rankings of matches to the correct entity, calculated as follows:

$$MRR=\frac{1}{\left|N\right|}\sum _{i=1}^{\left|N\right|}\frac{1}{ran{k}_i}$$

(10)

where ${\mathit{rank}}_i$ denotes the ranking of alignment to the correct entity and $N$ is the number of aligned entity pairs.

4.3. Experimental Results

We summarize the results of our model with other baseline models on the MED-BBK-9K datasets in

Table 3. Experimental results from different entity-alignment models applied to the MED-BBK-9K datasets. The best is bold.

Model		MED-BBK-9K
		Hits@1	Hits@5	MRR
Only graph-structure information.	BootEA	30.7	49.5	0.399
	RDGCN	30.6	42.5	0.365
Graph-structure information and additional information.	GCN-Align	6.5	15.3	0.117
	OntoEA	51.7	70.3	0.604
Only additional information.	BERT-INT	53.8	60.2	0.567
	RoBERTa-INT	59.2	66.8	0.625

, where the experimental results of BootEA, RDGCN, GCN-Align and OntoEA are from Xiang et al. [29]. We classified these models into three categories: utilizing only graph-structure information, combining graph-structure information and additional information, and utilizing only additional information.

Only graph-structure information. BootEA [27] uses TransE to represent the semantics of entities and relationships in the knowledge graph, and this approach captures the diverse relational information between entities in a knowledge graph well. In order to better capture the common semantics among different knowledge graphs, the model also proposes a new objective function that requires absolutely low scores for the positive-example triples, which helps to reduce the embedding bias in the uniform space.

RDGCN [8] constructs a dual graph structure, including entity and relationship graphs, to better capture relational information by allowing interaction between the two graphs, effectively integrating complex relational information into the entity representation. This model applies a GCN layer with highway gates on the entity graph to better integrate neighboring structural information.

Graph-structure information and additional information. GCN-Align [14] uses GCN to embed entities from different graphs into a unified vector space with the expectation that equivalent entities are close to each other. The method utilizes structural information (entity relationships) and attribute information associated with entities to improve the alignment performance. Compared with other embedding-based methods, this method does not require relationships or attributes to be aligned between atlases, and the model complexity is lower.

OntoEA [29] is an ontology-guided knowledge-graph-alignment technique that explicitly models category conflict relationships to enrich the embedded semantic representation and avoid incorrect mappings. To model category-conflict relationships, it generates a category-conflict matrix to represent different types of category conflicts. In this process, it employs a simple method to introduce entity name information, using pre-trained word embeddings to initialize the vector representation of entities or ontologies.

Only additional information. BERT-INT [11] uses a pre-trained BERT model to encode the name/description of entities, obtains representation vectors of the entities, and aggregates features from different views in an interaction model in order to estimate the matching scores of the entities. The model benefits from the powerful semantic modeling capability of BERT and the effectiveness of the interaction mechanism to achieve better performance on the entity-alignment task.

The experimental results show that our model achieves the best Hits@1 and MRR on the Chinese medical datasets MED-BBK-9K. According to the Hits@1 metric, its performance is 5.4% higher than that of the second-highest performer, BERT-INT, which can be attributed to the fact that (1) as a pre-trained language model, the Chinese RoBERTa that we used is better than the BERT in terms of semantic modeling on the processing datasets; (2) in terms of model input, we used entity name information as input to RoBERTa, while BERT-INT prioritizes entity description information. The MED-BBK-9K datasets used in the experiments was constructed from medical resources and Baidu Encyclopedia, which may not have good descriptive information, while entity name information is something that all entities must have; (3) in a difference from BERT-INT, we introduced the Attention Interaction Module, which captures complex contextual relationships and augmented feature representations and thus improves the performance of entity alignment, as is verified in Section 4.4.

Compared with the previous optimal model OntoEA, our model is 3.5% lower in the Hits@5 metrics but 0.021 higher in MRR metrics. We believe the possible reasons are as follows: (1) OntoEA utilizes the ontology information from the knowledge graph, enhances the semantics of the entity representations by jointly learning the entity embedding and the ontology embedding, and introduces the class-conflict-loss module and iterative collaborative-training strategy, which effectively avoids incorrect entity alignment and improves the quality of entity alignment; (2) OntoEA ignores the attribute information associated with entities. In this regard, our model includes the Attribute Interaction Module, which rationally utilizes attribute information; (3) OntoEA relies on manual annotation or automatic alignment systems for ontology part. It relies on high-quality ontologies for datasets, and for datasets with fewer entity categories, the ontology information is less useful and cannot fully utilize the model’s advantages. Our model needs only to utilize the existing additional information associated with entities without additional processing in the alignment and does not rely too much on the datasets.

4.4. Ablation Experiment

In order to investigate the effectiveness of the modules in our proposed method, we conducted ablation experiments on the MED-BBK-9K datasets, and the results are shown in

Table 4. Ablation-experiment results for the application of our model to the MED-BBK-9K datasets, where w/o means removing the module and BERT means replacing the RoBERTa module with the BERT module. The best result is in bold.

Model	MED-BBK-9K
	Hits@1	Hits@5	MRR
RoBERTa-INT	59.2	66.8	0.625
w/o name interaction	44.9	59.5	0.515
w/o neighbor interaction	55.8	64.5	0.596
w/o attribute interaction	56.8	66.5	0.610
w/o attention interaction	55.5	64.0	0.588
BERT	56.5	65.9	0.606

.

We conducted five sets of experiments. The first set tested the complete model. In the second set of experiments, we removed the module of name interaction. Compared with the complete model in the first set, the Hits@1 metrics decreased by 14.3%. It can be seen that the name information associated with entities plays a dominant role in the entity-alignment task, and the experimental results of Xiang et al. [29] verify this fact. In the second and third set of experiments, where neighbor interaction and attribute interaction were removed, respectively, all three metrics were reduced to different degrees, which shows that modeling the interaction of neighbors and attributes is effective. In the fourth set of experiments, we removed the module of attention interaction, and the overall performance of the model decreased. Compared to simple similarity computation, the multi-attention mechanism can fully capture the complex semantic relationships between entities, resulting in more comprehensive and accurate matching results. In the fifth set of experiments, we replaced the basic RoBERTa unit with Chinese BERT, and we found that Chinese RoBERTa combines better with the interaction model and performs better.

5. Conclusions

We propose an entity-alignment method based on RoBERTa interaction in this paper. The model fully utilizes the additional information associated with the entity such as name, neighbors and attributes by designing a multi-view interaction module, and uses the pre-trained Chinese RoBERTa model, the dual aggregation function, pairwise margin loss function and other techniques. Finally, it achieves good results on the Chinese medical datasets MED-BBK-9K. However, the model has some limitations. The model introduces the relationship mask matrix and multi-hop neighbor information in the interaction module, but it does not bring much improvement in performance, as was verified in the ablation experiment that involved removing neighbor interaction module. We believe that this is because the representation of relationships and attributes is not perfect enough to fully reflect their semantic information. In the future, we plan to try to introduce more additional information to improve the semantics of entities, such as images [23] and ontologies [29], so as to further improve the effect of entity alignment.