Study of Slope Stability of the Mining Wall in an Open-Pit Coal Mine by the Paste Cut-and-Backfill Method

Abstract

According to this study’s findings, slope stability problems in open-pit coal mines can be avoided, and mine wall collapse can be effectively mitigated by the use of cut-and-backfill mining techniques. The main research results are as follows: (1) The stope and waste rock’s geotechnical, physical, and mechanical characteristics were gathered and examined; the geotechnical and mechanical characteristics found in this study largely satisfy the criteria for slope stability analysis. (2) Cemented paste backfill (CPB) materials were made of mine waste rock and fly ash at a desired ratio, mixed with cement as a bond material, and were tested in the laboratory, using a combination of cement percentages of 6%, 8%, and 10% for the cement content and 25%, 30%, 35%, and 40% for the fly ash content, to determine the ideal mix for artificial ground support in underground mines, taking into account both economic and performance factors. (3) By using this model, the changes in CPB strength were investigated under various factors influencing the cement ratio, and limit equilibrium modeling was used with the FLAC-Slope 8.1 program with different cement paste backfill ratio to calculate the factor of safety for each cement percentage after 1 day, 3 days, 7 days, and 28 days of curing time (CT) to obtain the optimum compressive strength and shear straight of cemented paste backfill with high paste fill shear strength on the slope. (4) The research results are of great significance for the safety of important facilities in open-pit mines and provide a basis for the design and safety implementation of open-pit slope engineering.

1. Introduction

Within the field of geotechnical engineering, slope stability analysis assesses the stability of excavations, embankments, and slopes. It entails determining how likely it is for a slope to break or deform excessively when subjected to different loads, such as those caused by gravity, water, and seismic forces. On slopes, a number of mining techniques are frequently employed, including contour mining, highwall mining, and surface auger mining [1,2,3].

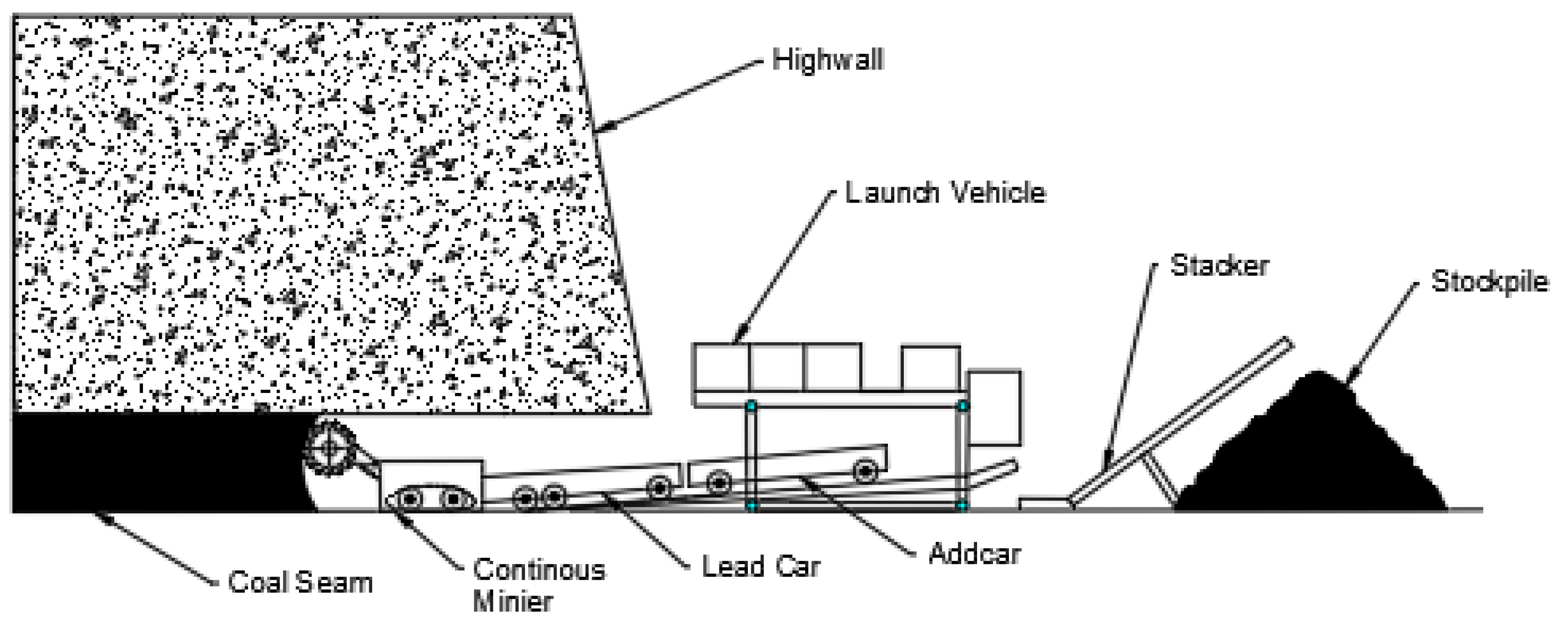
Highwall mining is a type of mining where a continuous miner or another type of machinery is used to remove coal or other minerals from a slope.

The highwall is the face of the slope, and the machine is operated from the top of the slope.

The stability of the slope of the mining walls in open-pit coal mines is a major problem since slope collapses can result in severe repercussions such as fatalities, destruction of infrastructure and equipment, and large financial losses [4]. In order to preserve slope stability and prevent surface subsidence, the paste cut-and-backfill method of mining entails removing coal seams beneath the mine wall and backfilling the empty spaces with paste. Nonetheless, nothing is known about how effectively this technique works to guarantee slope stability, especially when it comes to open-pit coal mines [5].

This study uses the paste cut-and-backfill method to examine the slope stability of mining walls in open-pit coal mines. This study will simulate the excavation of a coal seam beneath the mine wall, examine how coal mining affects the stability of the slope, and assess how well paste backfilling works to stop slope failure. Backfilling is a technique that includes utilizing a mixture of cement, water, and tailings to fill subterranean spaces and support the surrounding rock mass [6]. This study will also look at the characteristics of the reclamation materials used for backfilling and their appropriateness for supporting the mine wall [7]. Through the use of the paste cut-and-backfill method, the results of this study will shed important light on the slope stability of mining walls in open-pit coal mines and help develop solutions that effectively reduce the danger of slope failure in these types of settings [7].

2. Case Study Site

Engineering Geological Conditions

The Vulcan open-pit coal mine is situated in the Tete province in the heart of Mozambique [8]. The deposit has a large number of bands of sandstone and siltstone in addition to Gondwana-variety allochthonous coal [9]. Excessive quantities of phosphorus in coal can affect how well the coal is used while making steel, since phosphorus is considered a pollutant. Significant diversity is observed in the Chipanga deposit, both laterally across the Moatize deposit and vertically inside the Chipanga seam. Due to its position and mining activities, the area is vulnerable to geological disturbances and natural hazards. These factors are especially important to take into account when working with shift lengths and cemented paste backfill. The Vulcan open-pit coal mine is linked to a number of geological disturbances and natural hazards, including water pollution, land-grabbing and displacement, violence and fatalities, heavy metal contamination, and soil and sediment pollution.

According to the actual drilling histogram of the Vulcan open-pit coal mine [8,9], the distribution of rock layers is shown in

Table 1. Rock mechanics parameters and distribution of rock layers.

Number	Lithology	Thickness (m)	Density (kg·m−3)	Cohesion (MPa)	Internal Friction Angle (°)
1	Siltstone Sandstone	50.71	2460	2.45	40
2	Coal1	1.32	1675	3.5	24
3	Siltstone1	3.57	2010	3.75	38
4	Coal2	0.41	1500	3.5	24
5	Siltstone2	2.08	2400	3.75	38
6	Coal3	1.36	1670	3.5	24
7	Siltstone3	3.06	2290	3.75	38
8	Coal4	1.82	1730	3.5	24
9	Siltstone4	3.44	2280	3.75	38
10	Coal–Siltstone1	5.80	2010	2.45	40
11	Siltstone5	1.07	2220	3.75	38
12	Coal–Siltstone2	1.23	1890	2.45	40
13	Siltstone6	1.16	2390	3.75	38
14	Coal5	2.32	1710	3.5	24
15	Siltstone7	0.68	2500	3.75	38
14	Coal–Siltstone3	0.78	2020	2.45	40
17	Siltstone8	0.71	2420	3.75	38
18	Coal–Siltstone4	1.24	2050	2.45	40
19	Thin Variable Siltstone	0.97	2470	2.45	40
20	Coal6	0.90	2050	2.45	40
21	Siltstone/Tillite	0.97	2590	2.45	40

and the case study area can be seen in Figure 1.

3. Backfilling and Mining Methods

3.1. Principles of Paste Cut-and-Backfill Mining

Slope stability in open-pit operations is largely controlled by backfill techniques, which include a variety of approaches such as hydraulic fill, paste fill, and cemented rock fill. By adding materials to mined-out areas, these techniques help to stabilize the surrounding rock mass and increase overall stability. Furthermore, by occupying the spaces left by the mining process, they can assist in mitigating environmental issues like water intrusion and sedimentation [10,11].

But there are several drawbacks to the paste cut-and-backfill technique as well. In order to guarantee that the cement paste backfill has the required strength and rheological qualities, thorough design and management are required [12,13]. The process can also be expensive and time-consuming because it calls for the high wall to be excavated as well as the shipping and installation of the cement paste backfill [14].

Overall, managing the high walls of open-pit coal mines can be accomplished with the paste cut-and-backfill approach, but success depends on careful planning and execution.

In order to mitigate the increased stress on the soil layers, coal pillars will be left in place to accept pressure from the rock layer above throughout the excavation process. This will allow the cement paste backfill method to be employed in this phase of the research and examine the safety factor induced by this method [15]. See Figure 2 and Figure 3 for the highwall mining layout.

The compressibility of uncemented or lightly cemented backfill with small cohesions under external compressions related to rock wall closure can be accurately described by the soft soil model. Increasing the cement content in the backfill material can increase its compressibility, which can be taken into consideration when attempting to improve the backfill compressibility value. On the other hand, this can also make the backfilling procedure more expensive and environmentally harmful [16].

A typical work shift in the mining industry lasts eight to twelve hours.

3.2. Procedure for Preparing and Transporting Materials for Backfilling with Cement Paste

Cement paste backfill materials are prepared and transported in four steps: namely waste rock, fly ash, and cement preparation; raw material weighing; raw material mixing with water; and pumping and backfilling. The entire deposit is mined in a single strip using the strip-mining method, and the strip is then backfilled all at once [17,18]. See Figure 4 for the procedure for backfill materials made of cement paste.

(1)

Preparing the raw materials (cement, fly ash, and waste rock): Cement and fly ash are delivered to silos for reserve, and waste rock is crushed using a crusher system.

(2)

Weighing of raw materials: Using weighing equipment, each raw material is weighed proportionately based on the intended content (waste rock, fly ash, and cement).

(3)

Water-based mixing: To ensure that the mixture of various ingredients is balanced, weighed raw materials are given to the mixer, and water is added to stir in line with the planned paste density.

(4)

Pumping and backfilling: The thoroughly blended slurry is put into the pumping bucket and pumped to the subsurface backfilling working face with the backfilling pump.

3.3. The Mining and Backfilling Sequence Design

The mining and backfill procedures of short-side coal paste cut-and-backfill mining in open-pit coal mines are divided into two steps based on simulation experiments of similar materials [19]. Six hours are needed for the excavation process, and three hours are needed for the filling process. The pillars, which measure two meters in width, three meters in height, and five meters in length, are intended to support the roof structurally.

The first step is to divide the coal seam into several narrow strip coal pillars according to a certain width, numbered 1 to 17. The process involves excavating the odd coal pillar first, filling it after excavation, and then excavating the next coal pillar at the same time. Ultimately, the even narrow coal pillar and the backfill body support the upper rock stratum [20]. The second step involves extracting the coal pillars of an even number and filling them gradually, until all pillars are excavated and the backfill body fully supports them [21,22]. See Figure 5 for the operation diagram of the end shearer.

Paste cut-and-backfill mining, with a maximum backfill body force of 13.48 MPa, was shown in simulation results for comparable materials to efficiently regulate the stability of short-side slopes in open-pit coal mines.

The excavation process upsets the initial stress equilibrium in the rock and causes the redistribution of stress; hence, the area surrounding the coal pillar will experience an increase in stress. It is therefore advisable to avoid excavating the former coal pillar’s stress-rise area when excavating the subsequent coal pillar [23]. Consequently, after one coal pillar has been excavated, a specific distance must be covered in order to guarantee the safety of the subsequent coal pillar excavation according to the Vulcan open-pit coal mine’s geological conditions [24].

The slope is stable according to limit equilibrium analysis [25,26], with the best compressive strength of the cemented paste backfill occurring at 12% cement content, 40% fly ash content, and 72% paste density. However, in order to obtain the best mix at a fair cost, it was decided to cut the cement percentage to 8%. The associated strain was found to be 0.022, and the unconfined compressive strength (UCS) was determined to be 12.22 MPa.

(1)

The excavation and paste cut-and-backfill mining:

The initial stage replicates the mining process of the working face and the abandonment of coal pillars to support the work site’s roof as numbers 1–9. This will highlight the need to leave the coal pillars in their intended position after the coal has been excavated and to paste backfill right away, as illustrated in Figure 6 for the first step of excavated and past backfill replacement.

(2)

Digging coal pillars and paste backfill:

The coal pillars that were left 5 cm after the first phase, as seen in Figure 7 for the step of excavation and paste backfill replacement, will be dug out again in the second step and positioned for paste cut-and-backfill mining as numbers 10–17. After the model is observed, the data are read from the record. After secondary mining, the law governing the movement and deformation of the slope mine wall during the entire excavation and paste cut-and-backfill mining operation is finally determined. See Figure 7 for the step of excavation and paste backfill replacement 10 to 17.

4. Mechanical Properties of Paste Backfill Materials Made of Cement

4.1. Materials and Preparation of Samples

4.1.1. Materials

The materials used for cemented paste backfill were fly ash and mine waste rock mixed in a desired ratio with cement to act as a bonding agent (see Figure 8). The waste rock came from the Vulcan open-pit coal mine. The China United Cement Group Co., Ltd. Company in Zhejiang District, Xuzhou City, Jiangsu Province, was the supplier of the cement.

(1)

Waste rock

A crusher was used to reduce the size of the waste rock particle to less than 10 mm in order to improve experiment accuracy and decrease the influence of accidental errors. A vibro-stand and square-aperture sieves with 5 mm, 7.5 mm, 10 mm, and 2.5 mm apertures were used to gradually screen the material. Samples with particle sizes of 0–2.5 mm, 2.5–5 mm, 5–7.5 mm, and 7.5–10 mm were prepared. As can be seen in Figure 9, the sample of 0–10 mm for this experiment was created using a consistent mixing process at a ratio of 1:1:1:1.

(2)

Fly ash and cement

The particle size distribution of fly ash and cement was measured using the WINNER3009 Laser Particle Size Analyzer (Jinan Winner Particle Instrument Stock Co., Ltd., Jinan, China); the results are displayed in Figure 10 and Figure 11. Fly ash particle sizes range from the least to the greatest, 0.112 µm and 63.744 µm, and the diameters of the particles (D10, D50, and D90) are 22.177 µm, 61.359 µm, and 169.746 µm, respectively; that means only 10% of the particle sizes of fly ash are larger than 169.746 µm. The minimum and maximum particle sizes of cement are 0.112 µm and 63.744 µm, respectively; the values of D10, D50, and D90 are 21.545 µm, 56.603 µm, and 148.678 µm, respectively, which means that only 90% of the particle sizes of cement are smaller than 148.678 µm.

4.1.2. Sample Preparation

To make the backfilling paste, waste rock, fly ash, and cement were combined with water in the appropriate proportions. Several cubic molds measuring 70.7 mm × 70.7 mm × 70.7 mm were used to cast the paste.

The concrete sample mold was placed in a standard curing box with a temperature of 35 °C and a relative humidity of 90%. After curing for 1 day, 3 days, 7 days, and 28 days, each sample underwent a strength test to determine the stress–strain behavior of the paste at various mixing ratios. The samples were prepared according to the cement paste backfill procedure.

Figure 12 shows every testing facility used during the investigation.

Table 2. Specific parameters of each facility.

Number	Name	Type Specification
1	Strength testing facility	WAW-1000D (Jinan Hensgrand Instrument Co., Ltd., Jinan, China)
2	Digital curing chamber	SHBY-40B (Trading Company, Nanjing, China)
3	Cement mixer	NJ160 (Shaoxing Kare Instrument Equipment CO., Ltd., Shaoxing, China)
4	Mold	70.7 mm × 70.7 mm × 70.7 mm
5	Laser Particle Size Analyzer	WINNER3009
6	Laboratory Small Jaw Crusher	JXSC Machine (JXSC Mine Machinery, Ganzhou, China)
7	Vibro-stand and soil sieve

displays the particular parameters of every facility.

4.1.3. Testing Program

The orthogonal experimental design method was used to create the testing program. The fly ash content, cement content, and paste density were the three significant contributors.

Test specimens were created in the laboratory using a combination of cement percentages of 6%, 8%, and 10% for the cement content and 25%, 30%, 35%, and 40% for the fly ash content. See

Table 3. Factors and levels of the orthogonal experiment.

Level	Factor
	$\mathbf{Paste}\mathbf{Density}({\mathit{\rho }}_{\mathit{P}}$%)	$\mathbf{Fly}\mathbf{Ash}\mathbf{Content}({\mathit{X}}_1$%)	$\mathbf{Cement}\mathbf{Content}({\mathit{X}}_2$%)	Curing Time (d)
1	72	25	6	1
2	74	30	8	3
3	76	35	10	7
4	78	40	12	28

for factors and levels of the orthogonal experiment.

Thus, in accordance with

Table 4. Testing program.

Number	Curing Time (d)	$\mathbf{Paste}\mathbf{Density}({\mathit{\rho }}_{\mathit{P}}\%)$	$\mathbf{Fly}\mathbf{Ash}\mathbf{Content}({\mathit{X}}_1\%)$	$\mathbf{Cement}\mathbf{Content}({\mathit{X}}_2\%)$	$\mathbf{Waste}\mathbf{Rock}\mathbf{Content}({\mathit{X}}_3\%)$
S1	1	72	25	6	69
S2	1	74	25	8	67
S3	1	76	25	10	65
S4	1	78	25	12	63
S5	3	72	30	8	62
S6	3	74	30	10	60
S7	3	76	30	12	58
S8	3	78	30	6	64
S9	7	72	35	10	55
S10	7	74	35	12	53
S11	7	76	35	6	57
S12	7	78	35	8	57
S13	28	72	40	12	48
S14	28	74	40	6	54
S15	28	76	40	8	52
S16	28	78	40	10	50

, the testing program was created, and 16 samples, numbered from S1 to S16 (S1–S16), were tested. The masses of fly ash, cement, and waste rock added together equal the total solid mass. Also considered are the ratios of fly ash, cement, and waste rock to the total mass. The mass ratio of solids to the combined mass of solids and water is known as paste density. Equations (1)–(4) display the formulas for the waste rock content ($X_3$), fly ash content ($X_1$), cement content ($X_2$), and paste density (${\rho }_P$).

$${\rho }_P=\frac{F+C+R}{F+C+R+W}\times 100,$$

(1)

$$X_1\%=\frac{F}{F+C+R}\times 100,$$

(2)

$$X_2\%=\frac{C}{F+C+R}\times 100,$$

(3)

$$X_3\%=\frac{R}{F+C+R}\times 100=1-X_1-X_2.$$

(4)

where the masses of fly ash (F), cement (C), waste rock (R), and water (W) are represented.

4.2. Calculations and Analysis of Experimental Results

In this study, the data were analyzed using the variance analysis and intuitive analysis approaches. The best value of many components and their arrangement can be ascertained using the qualitative data analysis method known as intuitive analysis. Variance analysis is a quantitative method that may be used to ascertain each factor’s confidence and amount of influence on performance outcomes. In order to determine the ideal mix, these two analytical techniques can be utilized to more thoroughly determine the influence law of different influential components and levels on the performance of cemented backfilling materials. To process data, some specific formulas were used to input the necessary variables and perform the calculations accordingly.

The relationship between the unconfined compressive strength (UCS) and the factor of safety is not a direct correlation. However, we can establish a relationship between them through the concept of shear strength.

The factor of safety is a measure of the ability of a system to withstand loads without failing. In geotechnical engineering, the factor of safety is often calculated as the ratio of the shear strength of the soil to the shear stress applied.

The unconfined compressive strength (UCS) is a measure of the strength of a soil in unconfined compression. It is related to the shear strength of the soil, which is a critical parameter in determining the factor of safety. According to Equations (5)–(12), the parameter values were calculated [27,28,29]. The experimental results can be seen in

Table 5. Test results of paste fill samples in the laboratory.

Type of Paste Fill Specimen	Density (kg·m−3)	Peak Load (kN)	UCS (MPa)	Strain	Shear Stress (MPa)
6% Cement D1 = S1	34,571.4	3.0223	0.62	0.023	0.31
6% Cement D3 = S8	34,333.3	4.7335	0.97	0.018	0.485
6% Cement D7 = S11	34,523.8	12.3163	2.51	0.014	1.255
6% Cement D28 = S14	33,428.6	25.3666	5.18	0.028	2.59
8% Cement D1 = S2	34,095.2	5.6881	1.16	0.032	0.58
8% Cement D3 = S5	33,142.9	9.4608	1.93	0.036	0.965
8% Cement D7 = S12	33,571.4	27.4538	5.60	0.030	2.8
8% Cement D28 = 15	33,714.3	1.5099	12.22	0.022	6.11
10% Cement D1 = S3	34,095.2	13.7713	2.81	0.015	1.405
10% Cement D3 = S6	31,619.0	19.3474	3.95	0.028	1.975
10% Cement D7 = S9	33,571.4	36.4504	7.39	0.034	3.695
10% Cement D28 = S16	30,552.4	46.8446	9.56	0.025	4.78
12% Cement D1 = S4	33,619.0	23.9662	4.89	0.019	2.445
12% Cement D3 = S7	32,095.2	36.08	7.36	0.016	3.68
12% Cement D7 = S10	30,904.8	36.4504	7.44	0.019	3.72
12% Cement D28 = S13	31,333.3	66.055	13.48	0.017	6.74

.

The shear strength of a soil or cement past backfill can be estimated from the UCS using the following equation:

$${\tau }_{max}=cos\phi \ast UCS/2$$

(5)

where τ is the shear strength, φ is the internal friction angle, and $UCS$ is the unconfined compressive strength.

Once the shear strength is known, the factor of safety can be calculated as:

$$FOS={\tau }_{max}/\tau$$

(6)

where $FOS$ is the factor of safety, ${\tau }_{max}$ is the shear strength, and $\tau$ is the applied shear.

The axial strain was calculated as

$$\epsilon =∆L/L_0$$

(7)

where $\epsilon$ is the axial strain, $∆L$ is the change in measured axial length, and $L_0$ is the initial length of the sample.

The compressive stress was calculated as

$$\mathsf{\sigma }=\mathrm{P}/{\mathrm{A}}_0$$

(8)

where $\mathsf{\sigma }$ is the compressive stress, $\mathrm{P}$ is the load and ${\mathrm{A}}_0$, is the initial cross-section area of the specimen.

Therefore, the unconfined compressive strength is calculated for the maximum load applied:

$${\mathsf{\sigma }}_{\mathrm{U}\mathrm{C}\mathrm{S}}={\mathrm{P}}_{max}/{\mathrm{A}}_0$$

(9)

The shear stress was calculated as

$$\tau =\mathrm{F}/A$$

(10)

where $\tau$ is the shear stress, $\mathrm{F}$ is the force applied, and $A$ is the cross-sectional area of the material.

The sample density was calculated as

$$\gamma =m/v$$

(11)

where $\gamma$ is the sample density, $m$ is the sample mass, and $v$ is the sample volume, which was calculated by

$$\gamma =l\times w\times h$$

(12)

where $l$ = length, $w=$ width, and $h=$ height.

The Optimum Cemented Paste Fill

In order to meet engineering requirements, the goal of cemented paste backfill (CPB) mix optimization is to determine the ideal mix for artificial ground support in underground mines, taking into account both economic and performance factors. Stated differently, the goal of this research is to determine the ideal mixture for which the strength and elastic modulus satisfy engineering specifications while maintaining a fair cost. Backfill with an elastic modulus and sufficient strength can guarantee the stability and safety of the stope; however, excessive strength will result in excessive costs and needless waste. Consequently, “Strength and elastic modulus to meet the needs and cost to minimize” should be the guiding premise for filling mix optimization. The ideal paste density is 72%, the fly ash content is 40%, and the cement content is 12%, as demonstrated by the aforementioned criteria. It was determined to lower the cement concentration to 8% in light of the cement’s cost-effectiveness; the testing outcome is shown in Figure 13. It was observed that the equivalent strain was 0.022, and the strength of the cemented paste at the new mixing ratio was 12.22 MPa. Other important characteristics, such as flowability, were not assessed. This could be an important consideration for future research or practical applications of CPB.

5. Basic Theory and Definition

5.1. Limit Equilibrium Methods

Duncan provides a thorough overview of equilibrium methods. Limit equilibrium methods, which have a long history and a wealth of knowledge, are extensively used to examine slope stability with simple computation [30], including Price’s Method, Spencer’s Method, Bishop’s Modified Method, and the Method of Slices [30,31]. The reason that equilibrium approaches pose the most issues is that they are all based on the assumption that the failing soil mass may be separated into slices, which has implications for equilibrium. Due to its ability to meet strain compatibility and the static equilibrium equation without assuming the shape or location of the failure surface and slice side forces, the finite element method (FEM) has become increasingly popular for evaluating slope stability in situations where the linear Mohr–Coulomb failure criterion was frequently used [32]. Nonetheless, the experimental findings demonstrate that practically all geomaterials have distinctively nonlinear strength envelopes [28] and that a specific instance of a nonlinear failure criterion is the linear failure criterion. The majority of these nonlinear failure techniques are rather complex processes that depart greatly from straightforward calculation [33,34]. In this article, we use a simple combined failure criterion that combines the linear Mohr–Coulomb failure criterion with the maximum primary tensile stress criterion to determine the slope failure upon the shear failure zone and tensile failure zone [35,36,37].

5.2. Planar Failure

The block sitting on an inclined plane at limiting equilibrium is the most basic model for planar failure [38,39]. See Figure 14 for a block on an inclined plane at limiting equilibrium.

The following equations describe the forces acting on the block:

$$\tau =c+\sigma tan\varnothing ,$$

(13)

$$\sigma =\frac{N}{A}=\frac{W\cos \beta }{A},$$

(14)

$$\tau =c+\frac{W\cos \beta }{A}tan\varnothing$$

(15)

$$\begin{gathered} shear force=\tau A=resisting force \\ =cA+W\cos \beta ·tan\varnothing driving force=W\sin \beta \end{gathered}$$

where the following definitions hold:

$\tau$ = shear stress along the failure plane;

$c$ = cohesion along the failure plane;

$\sigma$ = normal stress on the failure plane;

$\varnothing$ = angle of internal friction for the failure plane;

$N$ = magnitude of the normal force across the failure plane;

$A$ = area of the base of the plane;

$w$ = weight of the failure mass;

$\beta$ = dip angle of the failure plane.

The factor of safety (FOS) can be calculated by equating the driving and opposing forces at limiting equilibrium.

$$F\mathrm{O}S=\frac{resisting forces}{driving forces}=\frac{cA+W\cos \beta tan\varnothing }{W\sin \beta }$$

(16)

5.3. Strength Reduction Finite Element Method

The factor of safety (FOS) of the slope is defined here as the factor by which the original shear strength parameters must be divided in order to bring the slope to failure [40]. And the factored shear strength parameters $C^{\prime }$ and ${\phi }^{\prime }$ are defined as follows, respectively:

$$C^{\prime }=\frac{C}{SRF},$$

(17)

$${\phi }^{\prime }=\arctan (\mathrm{tan\phi }/SRF)$$

(18)

where SRF is the “Strength Reduction Factor”, is the original friction angle (in degrees), and is the original cohesion. To find the exact factor of safety (FOS), it is necessary to initiate a systematic search for the SRF value that will just cause the slope failure, and FOS is determined as the corresponding SRF value, FOS = SRF. Based on this theory, any system has just one component: safety. If $\mathrm{F}\mathrm{O}\mathrm{S}\le 1.0$, a slope is regarded as unstable. However, it is frequently the case that many naturally stable slopes have factors of safety that are less than 1.0 in accordance with the generally accepted design practice [41,42]. The material may fail or distort as a result of dynamic loads, lowering the FOS values. Therefore, in order to design and build backfill systems that are stable and safe, the impacts of dynamic loads on the FOS values must be investigated.

5.4. Slope Failure Definition

There are a number of widely accepted definitions of failures, including tests where the slope profile bulges, shear stress limitation on the possible failure surface, and non-convergence of the solution. No stress distribution that satisfies both the failure criterion and global equilibrium may be discovered when the solution is unable to converge within a user-specified maximum number of iterations [42], and the majority of solutions choose a 1000-iteration ceiling, which imposes rather strict restrictions on geologists and civil engineers and mostly relies on the user’s experience. Before the solution’s non-convergence develops, there will be a running-through zone of plastic strain in the sliding surface, extending from the slope toe to the top [43], which is readily accessible and goes beyond the basic functionality of most commercial software. In this article, the slope failure time is assumed to be this running-through moment, and the related SRF is the FOS.

5.5. Mohr–Coulomb Plastic Criterion

According to the Mohr–Coulomb criterion, yield happens when a material’s shear stress at any given position reaches a value that is directly proportional to the normal stress in the same plane. See Figure 15 for the linear Mohr–Coulomb failure criterion. The yield line is the best straight line that touches these Mohr’s circles [44].

Therefore, the Mohr–Coulomb model is defined by

$$\tau =c+\sigma \mathrm{t}\mathrm{a}\mathrm{n}\phi$$

(19)

where $\sigma$ is positive in compression. From Mohr’s circle,

$$\tau =s·\mathrm{c}\mathrm{o}\mathrm{s}\phi ,$$

(20)

$$\sigma ={\sigma }_{\mathrm{m}}+s·\mathrm{s}\mathrm{i}\mathrm{n}\phi$$

(21)

Substituting for $\tau$ and $\sigma$, multiplying both sides by $cos\phi$, and reducing, the Mohr–Coulomb model can be written as

$$s+{\sigma }_{\mathrm{m}}sin\phi -\mathrm{c\; cos\phi }=0$$

(22)

$$s=\frac{1}{2}\left({\sigma }_1{-\sigma }_3\right)$$

(23)

$${\sigma }_{\mathrm{m}}=\frac{1}{2}\left({\sigma }_1{+\sigma }_3\right)$$

(24)

where $s$ is half of the difference between the maximum principal stress, ${\sigma }_1$, and the minimum principal stress, ${\sigma }_3;{\sigma }_{\mathrm{m}}$ is the average of the maximum and minimum principal stresses; and $\phi$ is the friction angle.

6. Limit Equilibrium Model with Cemented Paste Backfill

6.1. Model

The model was established in FLAC-Slope 8.1 [45]; the slope height is taken as 80 m, and the slope toe is 45°. Since the model size has some effect on the results, the distance from the slope foot to the left border is 40 m, and the left is 20 m. The distance from the slope top to the right border is 80 m. The model is shown in Figure 16 and Figure 17.

The main physical and mechanical parameters of each rock formation listed in Table 1 are simplified and classified; the input parameters for the model are presented in

Table 6. Input mechanical parameters for the model.

Number	Lithology	Thickness (m)	Density (kg·m−3)	Cohesion (MPa)	Internal Friction Angle (°)
1	Siltstone Sandstone	50.71	2460	2.45	40
2	Coal Siltstone	1.24	2050	2.45	40
3	Thin Variable Siltstone	0.97	2470	2.45	40
4	Coal	0.90	2050	3.5	24
5	Backfilling Body	Variable	Variable	Variable	Variable
6	Siltstone/Tillite	0.97	2590	2.45	40

. Each parameter of the cement paste backfill was applied in the model to analyze the effect of the strength of the cement paste backfill on slope stability; see

Table 7. Input parameters of cement paste backfill.

Type of Paste Fill Specimen	Density (kg·m−3)	UCS (MPa)	Strain	Shear Strength (MPa)	Cohesion (MPa)	Internal Friction Angle (°)
6% Cement D1 = S1	34,571.4	0.62	0.023	0.194	0.073	11.040
6% Cement D3 = S8	34,333.3	0.97	0.018	0.311	0.071	13.910
6% Cement D7 = S11	34,523.8	2.51	0.014	1.125	0.012	23.920
6% Cement D28 = S14	33,428.6	5.18	0.028	2.909	0.070	28.730
8% Cement D1 = S2	34,095.2	1.16	0.032	0.358	0.071	13.910
8% Cement D3 = S5	33,142.9	1.93	0.036	0.868	0.012	23.920
8% Cement D7 = S12	33,571.4	5.60	0.030	3.140	0.070	28.730
8% Cement D28 = 15	33,714.3	12.22	0.022	7.362	0.253	30.190
10% Cement D1 = S3	34,095.2	2.81	0.015	1.258	0.012	23.920
10% Cement D3 = S6	31,619.0	3.95	0.028	2.492	0.115	31.040
10% Cement D7 = S9	33,571.4	7.39	0.034	4.623	0.087	31.540
10% Cement D28 = S16	30,552.4	9.56	0.025	6.487	0.102	33.740
12% Cement D1 = S4	33,619.0	4.89	0.019	3.058	0.115	31.040
12% Cement D3 = S7	32,095.2	7.36	0.016	4.982	0.324	32.330
12% Cement D7 = S10	30,904.8	7.44	0.019	5.071	0.102	33.740
12% Cement D28 = S13	31,333.3	13.48	0.017	9.860	0.337	35.240

. The entire process of backfilling mining in accordance with the processes of mining and filling is simulated by using the Mohr–Coulomb model for the rock layers and the strain softening model for the coal.

6.2. Simulation Slope with a Different Cement Paste Backfilling Body

Simulated slope stability with a different cement paste backfilling body was a crucial aspect of understanding the behavior of cemented paste backfill (CPB) structures in underground mines. The strength development and distribution of CPB structures are influenced by various factors, including the backfilling strategy, the inclination angle of the stope, and the filling rate.

By using this model, the changes in CPB strength were investigated under various factors influencing the cement ratio. This study did not explicitly model the contact behavior between individual layers of the cemented paste backfill, which can significantly influence the overall mechanical response and stability of the backfill system.

Limit equilibrium on the slope was used with different cement paste backfilling to calculate the factor of safety for each cement percentage after 1 day, 3 days, 7 days, and 28 days of curing time (CT) to obtain the optimum compressive strength and shear straight of cemented paste backfill with high paste fill shear strength on the slope.

For the cement paste backfill with 6% cement for 3 days and 28 days, the paste fill density ($\gamma$) = 34,333.3 and 33,428.6 kg·m⁻³, UCS ($\sigma$) = 0.97 and 5.18 MPa, shear strength ($\sigma$) = 0.311 and 2.909 MPa, cohesion ($c$) = 0.071 and 0.070 MPa, and internal friction angle of paste fill ($\varnothing$) = 13.910$°$ and 28.730$°$, respectively. With these parameter values, the safety factor was calculated as 1.10 and 1.99. See Figure 18a,b.

For the cement paste backfill with 8% cement for 3 days and 28 days, the paste fill density ($\gamma$) = 31,619.0 and 30,552.4 kg·m⁻³, UCS ($\sigma$) = 3.95 and 9.56 MPa, shear strength ($\sigma$) = 2.492 and 6.487 MPa, cohesion ($c$) = 0.115 and 0.102 MPa, and internal friction angle of paste fill ($\varnothing$) = 31.040$°$ and 33.740$°$, respectively. With these parameter values, the safety factor was calculated as 1.23 and 3.57, and the results can be seen in Figure 19a,b.

For the cement paste backfill with 10% cement for 3 days and 28 days, the paste fill density ($\gamma$) = 31,619.0 and 30,552.4 ${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$, UCS ($\sigma$) = 3.95 and 9.56 MPa, shear strength ($\sigma$) = 2.492 and 6.487 MPa, cohesion ($c$) = 0.115 and 0.102 MPa, and internal friction angle of paste fill ($\varnothing$) = 31.040$°$ and 33.740$°$, respectively. With these parameter values, the safety factor was calculated as 1.23 and 3.57, and the results can be seen in Figure 20a,b.

For the cement paste backfill with 12% cement for 3 days and 28 days, the paste fill density ($\gamma$) = 32,095.2 and 31,333.3 ${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$, UCS ($\sigma$) = 7.36 and 13.48 MPa, shear strength ($\sigma$) = 4.982 and 9.860 MPa, cohesion ($c$) = 0.324 and 0.337 MPa, and internal friction angle of paste fill ($\varnothing$) = 32.330$°$ and 35.240$°$, respectively. With these parameter values, the safety factor was calculated at 4.36 and 4.74, and the results are contained in Figure 21a,b.

Table 8. Simulation results (FOS) with cement paste backfill.

Type of Paste Fill Specimen	Density (kg·m−3)	UCS (MPa)	Strain	Shear Strength (MPa)	Cohesion (MPa)	Internal Friction Angle (°)	FOS
6% Cement D1 = S1	34,571.4	0.62	0.023	0.194	0.073	11.040	1.1
6% Cement D3 = S8	34,333.3	0.97	0.018	0.311	0.071	13.910	1.23
6% Cement D7 = S11	34,523.8	2.51	0.014	1.125	0.012	23.920	0.97
6% Cement D28 = S14	33,428.6	5.18	0.028	2.909	0.070	28.730	1.99
8% Cement D1 = S2	34,095.2	1.16	0.032	0.358	0.071	13.910	1.23
8% Cement D3 = S5	33,142.9	1.93	0.036	0.868	0.012	23.920	0.98
8% Cement D7 = S12	33,571.4	5.60	0.030	3.140	0.070	28.730	1.99
8% Cement D28 = 15	33,714.3	12.22	0.022	7.362	0.253	30.190	3.57
10% Cement D1 = S3	34,095.2	2.81	0.015	1.258	0.012	23.920	0.97
10% Cement D3 = S6	31,619.0	3.95	0.028	2.492	0.115	31.040	2.59
10% Cement D7 = S9	33,571.4	7.39	0.034	4.623	0.087	31.540	2.31
10% Cement D28 = S16	30,552.4	9.56	0.025	6.487	0.102	33.740	2.67
12% Cement D1 = S4	33,619.0	4.89	0.019	3.058	0.115	31.040	2.53
12% Cement D3 = S7	32,095.2	7.36	0.016	4.982	0.324	32.330	4.36
12% Cement D7 = S10	30,904.8	7.44	0.019	5.071	0.102	33.740	2.66
12% Cement D28 = S13	31,333.3	13.48	0.017	9.860	0.337	35.240	4.74

presents a determination of the factor of safety (FOS) with cement paste backfill in a simulation and an analysis of the structural properties and behavior of the material under different conditions. Factors such as material strength, cohesion, internal friction angle, shear strength, and loading conditions play crucial roles in determining the FOS.

7. Discussion

When dealing with paste fill, geotechnical studies advise using FOS > 1.4. However, prior studies have stabilized the usage of paste fill; as a result, it is advised to use the FOS on a high scale, specifically between 2.5 and 5. The primary function of internal mechanical properties in backfill is to support the wall or roof of an underground stope aperture. It is necessary to initially check the shear strength if the mining technique involves filling with the aid of the current bearing wall paste. The compressive strength (σ) is designed as the primary parameter and can be related to other mechanical characteristics in the paste fill refilling system design phase. The UCS value should be at least 5 MPa to serve as a supplementary defense mechanism; for pillar extraction, it should be closer to 1–2 MPa.

In this research, the stability and strength of the cement paste fill for 3 days and 28 days, respectively, are known: for the mix cement, 6% reaches strength values of 0.97 and 5.18 MPa; for the mix cement, 8% reaches strength 1.93 and 12.22 MPa; for the mix cement, 10% reaches strength values of 3.95 and 9.56 MPa; and for the mix cement, 12% reaches strength values of 7.36 and 13.48 MPa. As can be seen in graphic 9a, the relationship between unconfined compressive strength (UCS) and curing time is a critical aspect of concrete properties; as the curing time increases, the UCS of concrete also increases. This is because a longer curing time allows for more complete hydration of the cement, resulting in stronger and more durable concrete. So, as shown in Figure 22, the value of UCS increased with a curing time of 28 days to reach the standard.

With 6% cement, FOS = 1.23 and 1.99; with 8% cement, FOS = 0.98 and 3.57; with 10% cement, FOS = 2.59 and 2.67; and with cement paste filled with 12% cement, FOS = 4.36 and 4.74 (see Figure 23). This study did not investigate whether filling excavations with cemented paste backfill affects the width, height, and length of the excavations. However, it is likely that the use of cemented paste backfill would influence the dimensions of the excavations, as it provides a more stable and supportive environment compared to other filling methods. The compacted backfill material would offer crucial lateral support to the excavated walls, preventing shifting or cracking, which could lead to changes in the width and height of the excavations.

The graph in Figure 23 can be used to analyze the simulation results for the safety criteria provided in Table 6. The safety factor for the failure model resulting from constrained cement paste filled with UCS increased at 28 days of curing time, with lesser values achieved at 1 day of curing time. As the cement paste fill line grows older, its mechanical strength increases, which accounts for the FOS value’s rise from one day to twenty-eight days. Cement paste fill’s physical and mechanical properties are also greatly influenced by the proportion of cement used to make it; the mechanical properties improve as the percentage of cement used as a binder does.

When mining ore with the mining wall method, which acts as a support cement paste backfill, when the factor of safety is greater than 1.4 (FOS > 1.4), the wall and slope are in stable condition. For each 12% percentage of cement for 28 days, the FOS was > 1.4. Curing time is the period during which concrete is allowed to hydrate and gain strength. Therefore, as cement paste fill cures and gains strength over time, its factor of safety can be expected to increase.

However, it is important to note that the relationship between cement paste fill strength and curing time is not always straightforward. Factors such as temperature, humidity, and the specific mix of cement paste fill can all affect the rate at which cement paste fill gains strength.

8. Conclusions

In this study, for the case of the slope in the Vulcan open-pit coal mine, this study applied the paste cut-and-backfill method and controlled its slope instability during the wall mining. The slope height is taken as 80 m, the slope toe is 45°, the distance from the slope foot to the left border is 40 m, and the left is 20 m. The distance from the slope top to the right border is 80 m.

The orthogonal experimental design method was used to create the testing program. The fly ash content, cement content, and paste density were three significant contributors.

Design samples for laboratory testing were produced with a mixture of cement percentages of 6%, 8%, and 10% for cement content, as well as 25%, 30%, 35%, and 40% for fly ash content (see Table 3).

Combined with the actual temperature of the actual mine, the cement paste sample mold was placed in the standard curing box, and the temperature was set to 35 °C, while the relative humidity was 90%. After 1 d, 3 d, 7 d, and 28 d of curing time, a strength test was conducted on each sample to capture the stress–strain behavior of the paste at different mixing ratios.

The experimental results were obtained, and intuitive analysis and variance analysis methodologies were employed in this study to analyze the data.

The objective of the mix optimization of cemented paste backfill was to obtain the optimum mix for determining the optimum compressive strength of cemented paste backfill for artificial ground support in wall mine economics and performance to meet engineering requirements. The cement paste fill was designed for strength (UCS) in the range of 0.62–13.48 MPa, where UCS ($\sigma$) = 12.2 MPa. This is the mix optimization of cemented paste backfills, whose cost is reasonable for artificial ground support in wall mine economics and performance to meet engineering requirements.

The stability and strength of the cement paste fill for 3 days and 28 days are known:

With 6% cement, FOS = 1.23 and 1.99, respectively.

With 8% cement, FOS = 0.98 and 3.57, respectively.

With 10% cement, FOS = 2.59 and 2.67, respectively.

With 12% cement, FOS = 4.36 and 4.74, respectively.

These results show that cement paste backfilling in a stable condition (FOS > 1.4) is recommended for cement paste backfill mines to meet the UCS standard, and cement paste backfilling in a condition of FOS $\le$ 1.4 is considered instable.

The relationship between unconfined compressive strength (UCS) and curing time is a critical aspect of concrete properties; as the curing time increases, the UCS of concrete also increases. This is because a longer curing time allows for more complete hydration of the cement, resulting in stronger and more durable concrete. So, as can be seen in graph 9b, the value of UCS increased with a curing time of 28 days to reach the standard.

The “Max shear strain-rate” can be seen in each model; it is a measure of the deformation rate of a material under shear stress, and it is an important parameter in the analysis of dynamic events that also can be used to evaluate the stability and strength of the model under different loading conditions.