1. Introduction
The ancestral hall buildings in Guangzhou are important representatives of regional culture, boasting a long history and unique architectural style. These buildings are not only numerous but also large in scale, making them a significant part of Guangzhou’s brick-and-wood historical structures. In recent years, some of these ancestral halls have undergone renovations and functional upgrades to meet the service demands of modern urban areas. However, inappropriate functional upgrades and spatial alterations may pose risks to their sustainable preservation. Located along the southeastern coast of China, Guangzhou frequently faces typhoon disasters during the summer and autumn seasons, which pose a primary natural hazard to historical buildings. Therefore, it is crucial to consider the impact of strong winds on these structures, especially given recent trends where some ancestral hall buildings have been enclosed with glass and their internal courtyards sealed off, potentially weakening the roofs’ wind resistance. Analyzing changes in roof wind pressure should be a focal point in the renovation of historical buildings in Guangzhou. This approach can mitigate the impact of retrofit strategies on wind resistance, help in selecting improvement measures by quantifying the risk of damage, and thereby enhance wind resilience.
The protection, renovation, and reuse of historical buildings require experience, interdisciplinary knowledge, and skills to minimize the negative impact of erroneous decisions. This comprehensive approach aims to enhance the resilience of historical buildings against natural disasters, human-induced hazards, and climate change [
1]. From the perspective of building materials and structures, the original design and construction of historical buildings took into account the local environment and climatic conditions [
2]. However, the rapidly changing global climate has introduced more extreme and frequent natural disaster events, such as heavy rainfall and strong winds, posing potential challenges to the preservation and adaptive reuse of aging historical buildings [
3,
4,
5].
Wood and brick–wood structures often exhibit poor load-bearing performance and are prone to brittle failure under seismic and strong wind loads. Consequently, in countries and regions where such structures are prevalent—such as China, Japan, South Korea, the Philippines, and Madagascar—local researchers have long focused their research on the impact of wind disasters, including typhoons and strong mountain winds, on historical buildings. Additionally, scholars in Europe, the Middle East, and North America have also observed the damage caused by hurricanes and strong winds to local brick–wood, stone, and steel historical buildings (
Table 1).
The aforementioned studies highlight an increasing international scholarly focus on assessing the risk of damage to historical buildings from wind disasters. Scholars employ semi-quantitative and quantitative analysis methods, such as computational fluid dynamics and finite element analysis, to conduct these risk assessments and formulate scientifically sound improvement and intervention strategies. However, the majority of these studies primarily address the damage inflicted by wind disasters on the historical buildings themselves, with limited exploration into the potential human-induced impairment of wind resistance performance resulting from the renovation and transformation of historical buildings. This aspect deserves greater attention and consideration. CFD simulation methods offer superior economic efficiency compared to traditional wind tunnel testing methods, with shorter experimental preparation times and lower costs. With advancements in computer technology and the optimization of turbulence models, CFD numerical simulations can now analyze complex fluid motion phenomena around building structures, yielding simulation results that closely match wind tunnel tests and on-site measurements [
17]. Various CFD software packages such as Phoenics, CFX, Fluent, and Star-CCM+ have been developed and widely applied in extensive research and practical engineering projects, validating the reliability of CFD simulation methods [
18]. Among these, Fluent software 2022R1 stands out for its integrated capabilities in modeling, computational setup, and solutions, which is why it was the CFD software tool used in this study.
The main objective of this study was to utilize CFD simulation techniques to analyze the impact of different renovation strategies on the wind resistance performance of typical ancestral hall buildings in Guangzhou. Specifically, this study compared the effects of two renovation approaches—installing glass curtain walls around the courtyard periphery and enclosing the courtyard with a glass roof—against the original state without renovation on wind load distribution. Quantitative assessment revealed that installing glass curtain walls around the courtyard effectively enhanced the wind resistance capability of the ancestral hall roofs. However, enclosing the courtyard with a glass roof may increase the risk of roof damage, particularly in strong wind environments. This study provides a scientific evaluation of renovation strategies for ancestral hall buildings, highlighting their specific impacts on the wind resistance performance of building roofs. It offers technical support and guidance for the protection and utilization of ancestral hall architectural heritage. The findings are significant not only for the renovation of ancestral hall architectural heritage but also for providing practical scientific methods and technical strategies for the conservation and renovation of similar historical buildings.
2. Materials and Methods
A combined approach of on-site case investigation and CFD numerical simulation was employed. The research comprised three main parts: an on-site investigation of representative ancestral hall buildings in Guangzhou, CFD simulations of typhoon wind environments for different renovation strategies, and a comparative evaluation of roof wind pressure distribution in ancestral halls (
Figure 1).
Firstly, an on-site investigation of representative ancestral hall buildings was conducted to gather detailed information, including structural features, materials, and architectural layout. Based on these data, SketchUp software 2023 was used to create three-dimensional geometric models and computational domain models of the ancestral halls, which were then imported into the CFD software Fluent for simulation analysis. In Fluent, mesh generation was performed, and boundary conditions and calculation parameters were set. During the CFD simulation phase, the software simulated and calculated the roof wind pressure distribution under different renovation strategies, including the unmodified state, installation of glass curtain walls around the courtyard periphery, and enclosing the courtyard with a glass roof.
Finally, through data analysis, the roof wind pressure distribution across different renovation scenarios was compared to quantitatively assess their impact on the wind resistance performance of the ancestral hall roofs. This systematic research method provides a scientific basis for evaluating the wind resistance performance of ancestral hall roofs under different renovation strategies, offering valuable insights for the protection and renovation of ancestral hall architectural heritage.
2.1. Case Study
Our case study focused on Lujiang Academy in Guangzhou, a representative ancestral hall building constructed in the 13th year of the Jiaqing period (1808) during the Qing Dynasty. Located within the ancient academy architectural complex of Liushui Well on Xihu Road in Yuexiu District, Guangzhou, Lujiang Academy is one of the best-preserved ancestral hall academies in the area. It covers a total area of approximately 1900 square meters, with a built-up area of about 2300 square meters. As part of its renovation and modernization efforts, Lujiang Academy has established the first financial museum in South China. The museum features seven exhibition halls dedicated to topics such as currency, banking, and traditional finance, offering functions related to financial collections, exhibitions, and cultural education (
Figure 2).
The Lujiang Academy primarily consists of ancestral hall buildings, oriented along a north–south axis with a width of approximately 13 m and a length of about 37 m. Built with traditional brick and wood structures, it features 35 cm thick brick mountain walls on both sides, joined by mortise and tenon joints in a wooden beam frame. The beams rest directly on bamboo and the mountain walls without rigid connections. Along the central axis from south to north, the academy comprises a head gate, nave, and apse. These halls have flush gable roof double slopes with overhanging eaves extending over 50 cm, covered in tiles. To accommodate museum exhibitions and visits, Lujiang Academy has renovated its indoor spaces while preserving the original style and layout. The primary renovation involved installing enclosed glass curtain walls around the two internal courtyards. These curtain walls, supported by independent steel structures, are positioned 400–500 mm lower than the indoor eaves, leaving ventilation gaps. This approach ensures natural ventilation for traditional building materials while creating a closed environment suitable for modern air conditioning systems, maintaining optimal conditions of temperature, humidity, and darkness for exhibit preservation.
During the on-site investigation, Lujiang Academy was meticulously surveyed and mapped, documenting its layout and spatial dimensions. Using SketchUp 3D modeling software, a comprehensive 3D model was created showcasing the academy’s scale, main entrance, and the arrangement of its main and ancillary halls along the axis (
Figure 3). The model accurately depicts the planned location of glass curtain walls around the two courtyards within the ancestral hall building.
Using glass to enclose courtyards is a common approach in the adaptive reuse of ancestral hall buildings. This is typically achieved by installing glass curtain walls and canopies over the courtyards. Given the inward-facing nature of ancestral halls, enclosing the courtyards with glass curtain walls often significantly enhances the usability of the interior space as a compromise. However, this practice also introduces several risks. It can alter the building’s silhouette, interfere with airflow, and affect wind load distribution on the building’s surfaces during typhoon conditions, thereby increasing the risk of wind damage. Consequently, conducting appropriate evaluations and analyses to assess these potential impacts is essential.
2.2. Application of CFD Simulation Method
The application process of CFD numerical simulation in this study primarily involves three stages: pre-processing, solving, and post-processing (
Figure 4). During the pre-processing stage, the main tasks include defining the scope of the historical building numerical simulation, establishing simulation conditions, and creating geometric models. Additionally, it is crucial to determine the spatial dimensions of the computational domain, create the computational domain model, and conduct grid generation and grid independence verification according to the flow field simulation requirements. In the solving stage, geometric model files are imported into the solver, and solving parameters are set. These parameters include turbulent models, air state parameters, surface material parameters of the architectural geometric model, inlet and outlet conditions of the computational domain, and boundary conditions. This stage also involves defining the numerical format of the solver and controlling convergence iterations, ultimately leading to the generation of calculation solution files. The post-processing stage involves visualizing the numerical simulation results, presenting data such as contour plots, isosurfaces, streamlines, and particle trajectories, and assessing the distribution of the wind pressure and wind pressure coefficients on the surfaces of the historical building under various conditions.
Numerical simulation methods for three-dimensional turbulence are typically classified into direct numerical simulation (DNS) and indirect numerical simulation [
19]. DNS involves solving the entire range of turbulence scales directly using the Navier–Stokes equation. This approach is the most accurate but is computationally intensive and impractical for high Reynolds number flows around buildings. Indirect numerical simulation includes Reynolds-averaged turbulence models and Large Eddy Simulation (LES) turbulence models. Among these, Reynolds-averaged turbulence models, including the standard k-ε model originally applied in wind engineering research, are widely used. Variants like the RNG k-ε model and the Realizable k-ε model have been developed to improve predictions of separation zones and surface pressure distributions on bluff bodies [
20]. In addition to the k-ε models, researchers have developed the standard k-ω turbulence model, suitable for low Reynolds numbers and compressible shear flow. This model accurately predicts the confined flow around building walls and the free shear flow and performs well in near-wall regions, wake flows, and flow around obstacles [
21]. The SST k-ω model (Shear Stress Transport model) is an enhancement of the standard k-ω model, incorporating turbulent shear stress propagation. This modification enhances the model’s accuracy and applicability in near-wall free flows. For analyzing the distribution of wind loads on the roofs and facades of historical buildings [
22], this study focused on employing the SST k-ω model due to its effectiveness in resolving complex flows around bluff bodies.
2.3. Simulation Conditions Settings
The spatial layout characteristics of ancestral hall building include two open courtyard spaces within the interior. However, in recent years, some ancestral hall buildings have undergone renovations involving the enclosure of courtyards with glass, potentially altering the building’s appearance and compromising its resistance to wind loads. Consequently, in designing the simulation experiments, consideration was given to the wind loads on Guangzhou ancestral hall buildings under typhoon conditions, as well as the interference of various courtyard enclosure configurations on these wind loads. To simplify the analysis, the potentially most unfavorable wind directions were considered at 0°, 45°, and 90° angles.
The experimental setup involved three sets of contrasting conditions under different wind directions (
Table 2):
A condition where the courtyard remains open, with the middle hall connected to both the front and rear courtyards;
A condition where the courtyard is enclosed with glass curtain walls on all four sides, with each courtyard enclosed independently;
A condition where the courtyard is covered with a glass canopy, with both courtyards enclosed.
The simulated condition corresponds to typhoon weather with a wind speed of 28.3 m/s. The selected wind directions are 0°, 45°, and 90°.
2.4. Setting of Computational Model and Boundary Conditions
The architectural and computational domain models for the CFD simulation experiments were both created using SketchUp software (
Figure 5). Based on various experimental wind directions and the maximum height (Hb) of the ancestral hall building, domain dimensions were calculated to meet specific requirements [
23,
24]: the distance from the inflow boundary to the building is 5xHb, and the distance from the outflow boundary to the building is 10xHb. The width of the domain must be greater than 4 times the windward width of the building [
25]. The distance from the top boundary to the building must be 4xHb, and the blockage ratio along the wind direction of the building should not exceed 5% (
Figure 6).
Grid partitioning in the Fluent software utilized an unstructured grid type with automatically generated tetrahedral (triangular) grids. The grid density for the ancestral hall building area was set to 0.25 m, while the grid density for the surrounding computational domain was set to 1 m. To ensure accurate boundary layer resolution, building surfaces were discretized using a combination of default tetrahedral grids and locally refined polyhedral grids, with a minimum of 10 layers ideally expanding to 20 layers for optimal results. The simulation employed a pressure-based solver with the SST k-ω turbulence model, known for its accuracy near walls without requiring wall functions.
While Large Eddy Simulation (LES) offers more precise results compared to the Reynolds-averaged Navier–Stokes (RANS) method [
19], it involves significantly higher computational complexity and costs, typically increasing by 80 to 100 times [
20]. Despite RANS simulations’ limitations in fully capturing turbulent kinetic energy, they serve as valuable engineering references [
26]. This explains their continued widespread use in both research and engineering applications [
27].
The entrance boundary condition used a gradient wind inlet with a wind speed profile defined by a user-defined function (UDF) file incorporating an exponential function [
17]. The power-law wind speed profile is described by Equation (1), with a turbulence intensity distribution calculated using Equation (2) [
28]. The roughness coefficient α was set to 0.22, typical for densely built urban areas, with a standard wind speed height of 10 m calibrated to match historical maximum wind speeds recorded during typhoons in Guangzhou, reaching 28.3 m/s. The turbulence intensity at 10 m height was set to 0.23.
where
is the height (m), and
represents the wind speed (m/s) at the height
.
where
represents the turbulence intensity at the height
.
The exit boundary condition was set to a pressure outlet, while the side and top boundaries were set to symmetric boundaries. The bottom boundary was configured as a no-slip wall. Due to the large volume of the ancestral hall building, the surface roughness of the roof and exterior walls has minimal impact on the results. Therefore, in the study, the surface of the building model was set to be a no-slip wall.
Coupling pressure and velocity was accomplished using the SIMPLE method, a common and effective coupling algorithm. To enhance the numerical accuracy, the least squares method was employed for discretization. Pressure gradients were managed using a second-order scheme to ensure numerical stability and accuracy. For convective terms, the second-order upwind differencing method was utilized, known for its validation and reliability in accurately capturing turbulent structures and flow characteristics in the flow field.
2.5. Calibration and Validation of Simulations
Our study involves comparing two potential renovation approaches and examining the impact of different typhoon conditions on roof wind pressures. While simulation results can typically be validated through wind tunnel experiments or field measurements, when both methods are impractical, validation work was completed prior to formal simulation. To verify the accuracy of the simulation for ancestral hall architecture, wind tunnel test results of a gabled-roof low-rise building with eaves from the Tokyo Polytechnic University (TPU) Aerodynamics Database were utilized. TPU conducted a series of wind tunnel tests on various geometric models and provided open-source software for data comparison and validation [
29].
Type O was selected from the TPU database as the validation case, representing low-sloped roof buildings with proportions similar to the hall volume in ancestral architecture and lacking significant eaves. The tested building model, depicted in
Figure 7, has dimensions of 24 m in length (D), 16 m in width (B), and 12 m in height, with a roof slope of 26.7°. The height-to-length ratio is 1:2, consistent with the proportions of the hall in ancestral architecture. The wind speed at a height of 10 m is 23.4 m per second, with an average wind speed profile exponent of 0.20. Steady-state simulations were conducted using the SST k-ω turbulence model to obtain the distribution of mean wind pressure coefficients on the building surfaces, which were subsequently compared with the TPU wind tunnel experimental results. As shown in
Figure 7, there is a high degree of consistency between the CFD simulation results and the TPU wind tunnel experimental results. Therefore, the CFD method employed demonstrates reliability and suitability for the preliminary analysis of the wind pressure distribution on building surfaces.
Before validating the simulation of the ancestral hall building, a grid resolution sensitivity analysis was conducted on the TPU building model to determine the optimal grid resolution for subsequent simulations. The effects of three grid sizes (0.1 m, 0.25 m, and 0.4 m) on the calculated roof wind pressure coefficients were compared. The results indicated that the deviation between the 0.25 m grid and the TPU results was small, with high computational efficiency. Thus, a grid size of 0.25 m was utilized for subsequent analysis. The turbulence model and computational settings for the validation analysis remained consistent with the previous settings, and the wind direction angles were set in accordance with the TPU database. The experiments showed that the wind pressure distribution calculated using the SST k-ω turbulence model was acceptable, with reasonable agreement between the numerical simulation and wind tunnel test results. This consistency indicates that the method is suitable for simulating the surface wind pressures of ancestral hall buildings.
3. Results
3.1. Wind Load Conditions for the Open Courtyard of the Ancestral Hall
3.1.1. Extreme Wind Pressure and Wind Pressure Coefficient on the Building Surface
Based on the wind pressure distribution and wind pressure coefficient distribution on the surface of the ancestral hall shown in
Figure 8 and
Figure 9, the following conclusions can be drawn:
At a wind angle of 0°, where the flow is perpendicular to the building ridge, the wind pressure distribution exhibits symmetrical characteristics, with positive pressure evenly distributed on the windward side. The open-style door of the front hall, serving as the typical windward face, demonstrates a typical positive pressure distribution. Additionally, extreme positive pressure values appear at the corners of the windward walls in the middle hall and rear hall. Extreme negative pressure values are observed at the junction of the side walls of the front hall and the eaves, as well as at the ridge of the first courtyard corridor on both sides and the ridge of the rear hall roof. These areas correspond to regions with negative wind pressure coefficients. The minimum wind pressure coefficient is observed at the ridge of the front hall and the rear hall roof, with a value of approximately −1. The middle hall roof of the ancestral hall does not exhibit extreme negative pressure values, likely due to the blocking effect of the front hall on the incoming flow, resulting in the separated airflow reattaching on the rear hall roof rather than the middle hall roof.
At a wind angle of 45°, significant variations in wind pressure distribution occur due to the differing heights of the roofs of each hall in the ancestral building. The most negative wind pressure tends to concentrate at the junction of the windward walls and the roof ridge of the entire structure. Specifically, the front hall exhibits the most negative pressure at its leeward roof ridge, extending across the entire leeward roof area. The middle hall’s negative pressure peak is situated at the midpoint of its leeward roof. Similarly, the rear hall’s negative pressure peak occurs at the eaves of the windward side and the roof ridge of the leeward side, albeit with a smaller negative pressure area than that of the front hall. Due to airflow deviations, noticeable negative and positive pressure extremes are observed at the roof ridge of the corridors linking the front and rear courtyards. The minimum negative wind pressure coefficient value is recorded at the rear hall’s roof ridge, measuring −3.2, while the wind pressure coefficient on the front hall’s roof ridge ranges from −1.8 to −2.8.
At a wind direction angle of 90°, where the airflow is parallel to the roof, the building roof predominantly experiences negative pressure. Wind pressure values decrease linearly along the airflow direction, with the most negative pressure occurring at the corners of the roof. Pronounced positive pressure changes are observed on the windward roofs of the courtyard corridors. Wind pressure coefficients on the roof are predominantly negative, with minimum values concentrated at the windward eaves, corners, and roof ridge, ranging from −1.5 to −2.3.
Between wind angles of 0° and 45°, the front hall of the ancestral hall experiences significant effects from incoming airflow, resulting in noticeable positive pressure on its windward facade (
Figure 9). At a wind angle of 0°, the distribution of positive pressure exhibits axial symmetry, with peak positive pressure occurring at the junctions of the front facade with the two side walls and on the inner surface of the side walls, reaching a maximum of 550 Pa. Meanwhile, the outer surface of the side walls experiences negative pressure peaks of around −700 Pa. At a wind angle of 45°, the positive pressure distribution on the front facade increases linearly along the wind direction, reaching a maximum of 520 Pa on the inner surface of the side walls. The outer surface of the side walls predominantly experiences negative pressure, approximately −350 Pa.
Therefore, under the combined effect of internal and external wind pressure, the walls of the front hall in the ancestral hall experience outward pulling forces at the junction with the eaves, potentially causing damage to structural elements such as the parapet and eaves. The parapet is a finely decorated component of the ancestral hall’s facade, embellished with brick carvings depicting various traditional auspicious patterns or stories, holding significant conservation value.
3.1.2. Vulnerable Parts under Comprehensive Wind Pressure Inside and Outside the Middle Hall
At a wind direction angle of 0°, the central hall is obstructed by the main entrance, resulting in negative pressure on the surface of the internal protective structure, ranging from −50 to −100 Pa, with wind suction on the inner surface of the roof. The majority of the windward surface of the roof’s exterior experiences positive pressure ranging from 0 to 150 Pa, representing wind pressure. Exceptional negative pressure occurs at the windward corner, with a maximum negative pressure of −80 Pa, resulting in downward wind pressure on the windward roof under the combined internal and external pressures. The leeward surface of the roof’s exterior experiences negative pressure throughout, forming symmetrical areas of negative pressure in the middle of the roof, ranging from −100 to −300 Pa. These areas on the leeward roof experience upward wind suction under the combined internal and external pressures (
Figure 10).
At a wind direction angle of 45°, the surface wind pressure on the internal protective structure of the central hall ranges from −250 to −300 Pa. On the exterior surface, the roof experiences uniformly negative wind pressure, with the highest negative pressures concentrated at the windward eaves, windward ridges, leeward eaves, and the center of the leeward roof, reaching −730 Pa. As a result, the roof of the central hall undergoes overall upward wind suction due to the combined internal and external wind pressures.
At a wind direction angle of 90°, the surface wind pressure on the internal protective structure of the central hall ranges from −350 to −400 Pa. Externally, the surface wind pressure shows a significant negative distribution, ranging from −250 to −700 Pa, gradually increasing in the direction of the incoming flow, with the maximum negative pressure concentrated at the eaves, ridges, and corners of the roof. Considering the combined wind pressures inside and outside the roof, it is evident that the windward near-end eaves, ridges, and corners experience wind suction, while the windward far-end eaves, ridges, and corners face downward wind pressure.
From the above observations, it can be concluded that the interior of the central hall building, which includes front and rear open courtyards, experiences negative pressure under various wind direction angles. The internal pressure of the building varies significantly depending on the wind direction angle. Considering the magnitude of wind pressure on the exterior surface of the roof, the central hall building is prone to upward wind suction at the eaves, ridges, and other locations, potentially resulting in roof damage.
3.2. Variation in Wind Loads after Installing Glass Curtain Walls in the Courtyard
After enclosing the glass curtain walls around the courtyard of the ancestral hall and comparing the wind pressure distribution maps before and after (
Figure 11), the following results were obtained:
At a wind direction angle of 0°, the extremes of wind pressure on the roof of the ancestral hall decreased overall. The wind pressure distribution on the windward side of the main entrance roof remains unchanged, but the negative pressure values and range on the leeward side have decreased, especially at the ridge and eaves. The positive pressure area on the windward side of the rear hall roof has increased, although the maximum positive pressure has decreased. Similarly, the maximum negative pressure on the leeward side has decreased, with changes in negative pressure concentrated at the ridge. The most significant change in roof wind load occurs in the central hall section, where the wind pressure on the windward side has shifted from positive to negative, ranging from −40 to −200 Pa, and there is a decrease in negative pressure on the leeward side.
At a wind direction angle of 45°, there is little change in the wind load on the roofs of the main entrance and rear hall of the ancestral hall. However, the negative pressure on the windward roof of the central hall has decreased. Conversely, negative pressure values at the windward corners, leeward corners, and leeward roof have significantly increased, accompanied by an expansion in the area affected by negative pressure.
At a wind direction angle of 90°, the wind load on the roof of the main entrance of the ancestral hall remains relatively unchanged. However, the range of maximum negative pressure on the roof of the rear hall has significantly decreased, particularly concentrated at the windward corners. Similarly, the range of maximum negative pressure on the roof of the central hall has also significantly decreased, with a greater concentration at the corners.
After enclosing the glass curtain walls around the courtyard of the ancestral hall, the most significant change in roof wind load occurs in the central hall, effectively reducing the negative pressure on the exterior surface of the roof. Following the enclosure of the courtyard and corridor, the indoor wind pressure in the central hall stabilizes at zero or maintains a weak negative pressure. Due to the combined effects of internal and external pressures, the upward wind suction on the roof decreases.
3.3. Changes in Wind Loads after Installing a Glass Canopy over the Courtyard
After enclosing the glass canopy over the courtyard of the ancestral hall and comparing the wind pressure distribution maps before and after (
Figure 12), the following results can be observed:
At a wind direction angle of 0°, the maximum positive and negative pressure values on the roof of the ancestral hall have decreased, particularly noticeable on the roofs of the front and rear courtyard corridors and the rear hall. At a wind direction angle of 45°, the most significant change in wind load occurs on the roof of the central hall of the ancestral hall, where both the magnitude and extent of negative pressure increase, posing challenges to roof wind protection. At a wind direction angle of 90°, changes in wind pressure on the roofs of various sections of the ancestral hall are minimal. However, there is an increase in negative pressure on the roofs of the corridors flanking the courtyard, with the glass canopy experiencing negative pressure.
After enclosing the glass canopy over the courtyard of the ancestral hall, an increase in negative pressure can be observed on the roof of the central hall under specific wind directions. This results in unfavorable negative pressure areas on the eaves, corridor roofs, and other sections, contributing to potential roof damage in the ancestral hall.
3.4. Summarizing and Comparing the Wind Pressure Distribution at Roof Control Points for Different Sets of Facade Enclosures
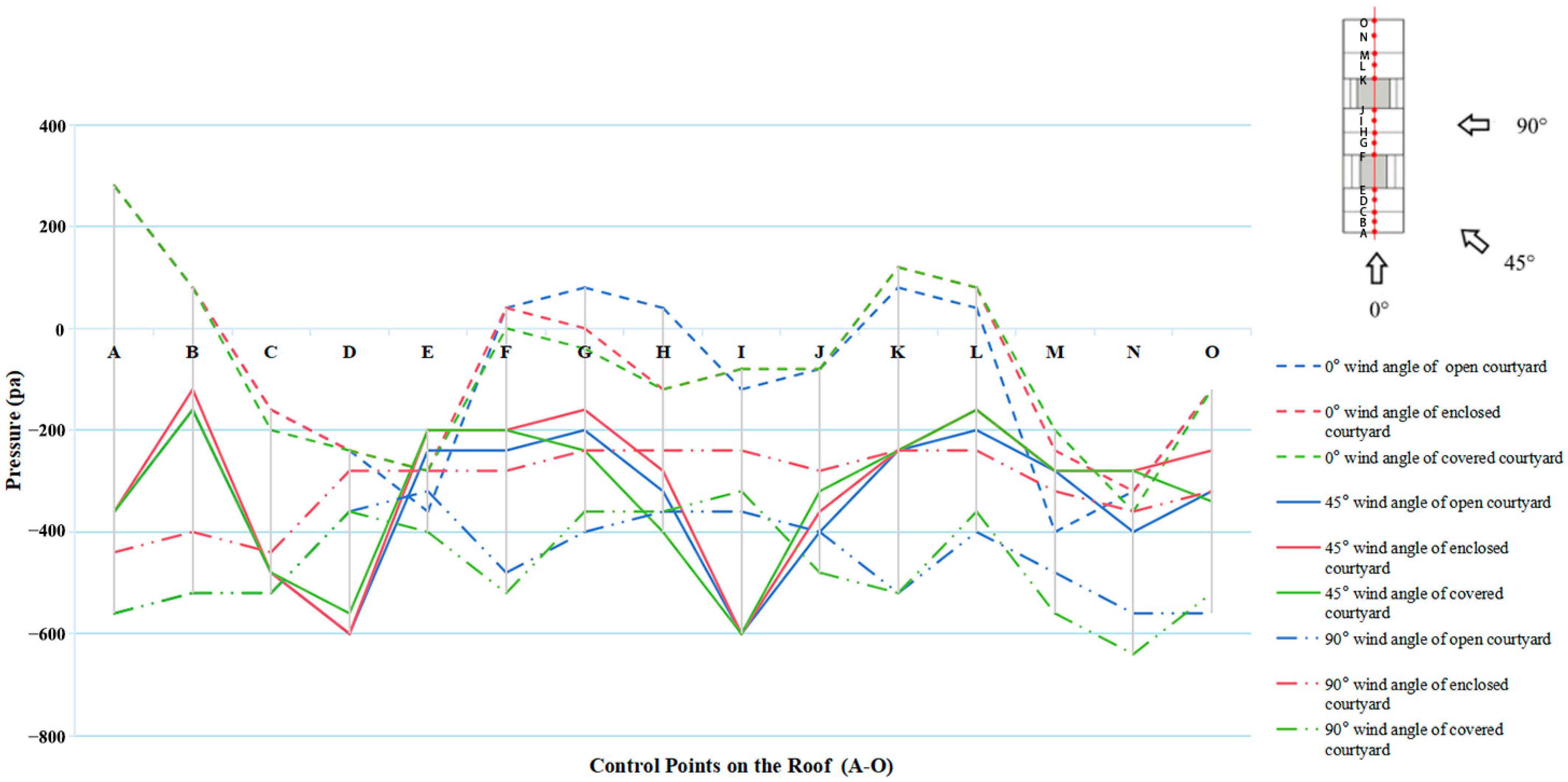
Along the central axis of the ancestral hall building, a series of control points labeled A to O were established on the roof to extract simulated wind pressure values, as depicted in
Figure 13. This figure summarizes and compares the wind pressure distribution characteristics on the roof of the temple building under different wind directions and facade enclosure configurations.
At a wind angle of 0°, methods such as enclosing courtyards with glass curtain walls and installing a glass canopy significantly increased the wind pressure on the windward side of the roof, while effectively reducing extreme positive and negative pressures on the leeward side. At a wind angle of 45°, both renovation methods had minimal impact on the distribution of wind pressure on the roof, with no amplification of negative pressure extremes observed. At a wind angle of 90°, enclosing courtyards with glass curtain walls significantly reduced extreme negative pressures on the roof, thereby enhancing its wind resistance performance. However, installing a glass canopy amplified negative pressure extremes at the building’s eaves.
Numerical simulation analysis data reveal significant changes in the internal pressure of the open halls of the ancestral hall under different wind directions, primarily negative pressure. These pressures, when combined with external forces, can easily lead to damage to roof eaves, ridges, etc. Enclosing the courtyard of the ancestral hall with glass curtain walls caused the most notable change in the wind load on the originally open roof of the central hall, effectively reducing upward suction forces and benefiting wind protection. Conversely, enclosing the courtyard with a glass canopy may increase unfavorable negative pressure areas on eaves, corridor roofs, etc., potentially leading to roof damage.
4. Discussion
Historical buildings in many countries and regions are often threatened by seasonal typhoons or strong winds [
2], which can cause irreparable damage [
30]. Researchers recognize the importance of protecting these structures from wind disasters [
31], employing qualitative and quantitative methods to assess and predict risks in windy environments [
32,
33]. However, less attention has been paid to how retrofitting and adaptive reuse affect the original wind resistance of historical buildings. In fact, such interventions may increase vulnerabilities to wind, a critical concern that warrants attention.
To advance this field, our study focused on the Lujiang Academy, a representative brick-and-wood ancestral hall in Guangzhou. CFD simulations under typhoon conditions were employed to compare the impacts of various retrofit strategies on wind resistance. CFD simulations are widely acknowledged for their effectiveness in such studies. Specifically, this study analyzed the impact of two retrofit approaches on wind pressure distribution within the ancestral hall’s internal courtyard: installing glass curtain walls and enclosing the courtyard with a glass canopy. Additionally, this study examined the wind pressure distribution on the original, unaltered roof. These retrofit methods are common in Guangzhou’s ancestral hall renovations, aiming to enclose courtyards and install indoor air conditioning systems for comfort, aligning with historical preservation goals [
34,
35].
Our findings revealed significant insights: installing glass curtain walls enhances the roof’s wind resistance, reducing internal pressure in the main hall and mitigating risks of eaves damage from negative pressure. Conversely, enclosing the canopy alters the building’s aerodynamic profile, potentially increasing roof damage risks and amplifying negative pressure effects on eaves and corridor roofs. This underscores the need for caution in retrofit strategies for historical buildings vulnerable to wind disasters, particularly in typhoon-prone areas or valleys.
Our study primarily focused on mean wind speeds to determine the average wind load distribution on the roof and facades of the ancestral hall. However, limitations in Reynolds-averaged methods precluded capturing information on surface fluctuating wind speeds and loads. Future studies will explore Large Eddy Simulation (LES) to better simulate fluctuating flow fields and assess peak wind loads on structural surfaces [
36]. Furthermore, for a comprehensive analysis of roof structural deformation under wind loads, mechanical monitoring and finite element simulation analysis will provide detailed mechanical behavior data, aiding in the preservation of historical building integrity [
37]. The insights gained will be valuable for similar contexts [
38]. Various modeling methods can be employed in the investigation of historical buildings instead of relying solely on SketchUp. For example, BIM (Building Information Modeling)-based models of historical buildings can help analyze changes in the overall structural forces under external wind forces after alterations to the building’s shape and contour [
39].
5. Conclusions
This paper combined on-site case studies and CFD numerical simulation methods to analyze the relationship between renovation strategies for ancestral hall buildings in Guangzhou and roof wind pressure distribution. The goal was to elucidate the impact of different renovation strategies on the buildings’ wind resistance performance and propose recommendations for their renovation and adaptive reuse. Based on the surveying, mapping, and investigation of the representative Guangzhou ancestral hall, Lujiang Academy, a 3D model of the ancestral hall was constructed using SketchUp. This model was then input into the CFD simulation software Fluent for domain setup, mesh generation, calculation parameter setting, and solution computation. Through CFD simulations, two renovation approaches within the ancestral hall’s courtyard were analyzed: installing enclosing glass curtain walls or installing enclosing glass canopies at the top. Additionally, the roof wind pressure distribution in its original, unaltered state was examined.
The CFD numerical simulation analysis data indicate significant variations in internal pressure within the open hall of the ancestral hall at different wind angles, primarily exhibiting negative pressure overall. Under the combined effects of internal and external pressures, this setup is prone to causing damage to roof eaves and ridges. However, when the ancestral hall courtyard is enclosed with glass curtain walls, the roof wind load variation on the originally open main hall roof is most pronounced. This retrofit method effectively reduces the upward suction effect on the roof, thus enhancing wind resistance. Conversely, enclosing the ancestral hall courtyard with a glass canopy results in increased adverse negative pressure areas on the eaves and corridor roofs, potentially leading to roof damage under certain wind conditions.
This study’s recommendations emphasize the importance of carefully assessing and analyzing the impact of various renovation measures on the wind resistance performance of historical buildings susceptible to seasonal typhoon disasters. Enhancing wind resistance should be a key criterion in the scientific evaluation of renovation projects for historical buildings. The CFD numerical simulation method used in this research is globally applicable for assessing historical buildings before renovation and adaptive reuse, aiding in achieving wind protection and preventative conservation goals. This analysis provides guidance for the conservation and utilization of Guangzhou’s ancestral hall buildings and similar historical structures with courtyard layouts. For highly protected ancestral hall heritage buildings, it is advisable to use glass curtain walls to enclose courtyards. This approach not only enhances the building’s wind resistance but also requires careful consideration of ventilation openings in the glass curtain walls and evacuation routes indoors to mitigate fire spread risks. For ancestral hall heritage buildings with lower protection levels, enclosing courtyards with glass canopies is recommended. However, special attention should be given to repairing and reinforcing eaves and corridor roofs in these cases. Implementing wind resistance enhancement measures is crucial to ensure the overall wind resistance capability of the building.
This study systematically evaluated renovation strategies for historical buildings, revealing in detail the specific impacts of different retrofit measures on the wind resistance performance of building roofs. Using Guangzhou’s ancestral hall buildings as an example, it provides clear technical support and guidance for their preservation and utilization. These methods and findings not only have significant implications for the renovation of ancestral hall heritage buildings but also offer practical scientific methods and technical strategies for the conservation and renovation of similar historical structures. These outcomes contribute to enhancing the buildings’ wind resistance capabilities in practical applications and effectively safeguard their historical and cultural value, advancing the scientific and systematic aspects of cultural heritage conservation efforts.
Author Contributions
Conceptualization, S.L. and X.Y.; methodology, S.L.; software, X.Y.; validation, Y.Z.; investigation, X.Y. and Y.G.; writing—original draft preparation, X.Y. and Y.Z.; review and editing, Y.G. and L.L.; visualization, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China (Grant No. 19ZD27) and supported by the China Postdoctoral Science Foundation (2024M750577).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to legal.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive and supportive feedback.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kurowska, A.; Nowogońska, B. Influence of the Decision to Select Renovated Elements in a Heritage Building on Further Stages of the Aging Process of the Building—A Case Study. Sustainability 2023, 15, 16926. [Google Scholar] [CrossRef]
- Mosoarca, M.; Keller, A.I.; Petrus, C.; Racolta, A. Failure analysis of historical buildings due to climate change. Eng. Fail. Anal. 2017, 82, 666–680. [Google Scholar] [CrossRef]
- Yavartanoo, F.; Kang, T.H.K. Retrofitting of unreinforced masonry structures and considerations for heritage-sensitive constructions. J. Build. Eng. 2022, 49, 103993. [Google Scholar] [CrossRef]
- Miran, F.D.; Husein, H.A. Introducing a Conceptual Model for Assessing the Present State of Preservation in Heritage Buildings: Utilizing Building Adaptation as an Approach. Buildings 2023, 13, 859. [Google Scholar] [CrossRef]
- You, X.; Zhang, Y.; Tu, Z.; Xu, L.; Li, L.; Lin, R.; Chen, K.; Chen, S.; Ren, W. Research on the Sustainable Renewal of Architectural Heritage Sites from the Perspective of Extenics—Using the Example of Tulou Renovations in LantianVillage, Longyan City. Int. J. Environ. Res. Public Health 2023, 20, 4378. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Chun, Q.; Xu, X.; Teng, Q.; Dong, Y.; Lin, Y. Wind effects on Chinese traditional timber buildings in complex terrain: The case of Baoguo Temple. J. Build. Eng. 2022, 59, 105088. [Google Scholar] [CrossRef]
- Li, Y.; Deng, Y.; Li, A. A nondestructive method for controlling wind loads and wind-induced responses of wooden pagoda. Wind Struct. 2022, 34, 525–538. [Google Scholar] [CrossRef]
- Fujita, K.; Hanazato, T.; Sakamoto, I. Earthquake response monitoring and seismic performance of five-storied timber pagoda. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 54. [Google Scholar]
- Son, M.; Kim, D.-Y. Analysis of Wind Flow around Architectural Heritage in Urban Area. Korea Spat. Plan. Rev. 2021, 109, 73–87. [Google Scholar]
- Sevieri, G.; Galasso, C. Typhoon risk and climate-change impact assessment for cultural heritage asset roofs. Struct. Saf. 2021, 91, 102065. [Google Scholar] [CrossRef]
- Song, B.; Galasso, C.; Garciano, L. Wind-uplift fragility analysis of roof sheathing for cultural heritage assets in the Philippines. Int. J. Disaster Risk Reduct. 2020, 51, 101753. [Google Scholar] [CrossRef]
- Taleb, R.; Ramanantoa, H.; Reynolds, T.; Beckett, C.T.; Huang, Y.; Rakotoarivony, M.; Gagnon, A.S.; Andriamaro, L. Fragility assessment of traditional wooden houses in Madagascar subjected to extreme wind loads. Eng. Struct. 2023, 289, 116220. [Google Scholar] [CrossRef]
- Sparks, P.S. Improving Hurricane Survivability of Heritage Structures. Adv. Mater. Res. 2010, 133–134, 867–872. [Google Scholar] [CrossRef]
- Khosrowjerdi, S.; Sarkardeh, H.; Kioumarsi, M. Effect of wind load on different heritage dome buildings. Eur. Phys. J. Plus 2021, 136, 1180. [Google Scholar] [CrossRef]
- Carter, A.J.; Taylor, P.H.; Santo, H.; Blakeborough, A. Wind loads on open truss structures: Applications of blockage to historic transporter bridges. Philos. Trans. R. Soc. A 2019, 377, 20190017. [Google Scholar] [CrossRef] [PubMed]
- Hussein, A.S.; El-Shishiny, H. Influences of wind flow over heritage sites: A case study of the wind environment over the Giza Plateau in Egypt. Environ. Model. Softw. 2009, 24, 389–410. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Sanyal, P.; Dalui, S.K. Computational fluid dynamics and artificial neural network-based analysis and forecasting of wind effects on obliquely parallel multiple building models using categorical variable encoding. Struct. Des. Tall Spec. Build. 2024, 33, e2105. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Van Hooff, T.; Blocken, B.; Tominaga, Y. On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- Yang, X.L.; Liu, Y. An improved k-ω-φ-α turbulence model applied to near-wall, separated and impinging jet flows and heat transfer. Comput. Math. Appl. 2018, 76, 315–339. [Google Scholar] [CrossRef]
- Zhao, M.; Wei, T.; Hao, S.; Ding, Q.; Liu, W.; Li, X.; Liu, Z. Turbulence simulations with an improved interior penalty discontinuous Galerkin method and SST k-ω model. Comput. Fluids 2023, 263, 105967. [Google Scholar] [CrossRef]
- Wegrzynski, W.; Lipecki, T. Wind and Fire Coupled Modelling—Part I: Literature Review. Fire Technol. 2018, 54, 1405–1442. [Google Scholar] [CrossRef]
- Wegrzynski, W.; Lipecki, T.; Krajewski, G. Wind and Fire Coupled Modelling—Part II: Good Practice Guidelines. Fire Technol. 2018, 54, 1443–1485. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Fan, Z.; Li, B.; Si, X.; Meng, L.; Zhu, J. Numerical Investigations of Wind Impacts on Chinese Ancient Architectural Roof Surfaces with Ridges and Semi-Cylindrical Tiles. Int. J. Archit. Herit. 2023, 1–18. [Google Scholar] [CrossRef]
- Blocken, B. 50 years of computational wind engineering: Past, present and future. J. Wind Eng. Ind. Aerodyn. 2014, 129, 69–102. [Google Scholar] [CrossRef]
- Gao, X.; Chun, Q.; Han, Y. Research on wind pressure characteristics of traditional timber buildings: A case study of the main hall of Shisi Temple. J. Wood Sci. 2024, 70, 12. [Google Scholar] [CrossRef]
- Quan, Y.; Tamura, Y.; Matsui, M.; Cao, S.; Yoshida, A. TPU aerodynamic database for low-rise buildings. In Proceedings of the 12th International Conference on Wind Engineering, Cairns, Australia, 2–6 July 2007; pp. 1615–1622. [Google Scholar]
- Sesana, E.; Gagnon, A.S.; Ciantelli, C.; Cassar, J.; Hughes, J.J. Climate change impacts on cultural heritage: A literature review. Wiley Interdiscip. Rev. Clim. Chang. 2021, 12, e710. [Google Scholar] [CrossRef]
- Blavier, C.L.S.; Huerto-Cardenas, H.E.; Aste, N.; Del Pero, C.; Leonforte, F.; Della Torre, S. Adaptive measures for preserving heritage buildings in the face of climate change: A review. Build. Environ. 2023, 245, 110832. [Google Scholar] [CrossRef]
- Pinelli, J.-P.; Simiu, E.; Gurley, K.; Subramanian, C.; Zhang, L.; Cope, A.; Filliben, J.J.; Hamid, S. Hurricane damage prediction model for residential structures. J. Struct. Eng. 2004, 130, 1685–1691. [Google Scholar] [CrossRef]
- Chettri, N.; Dhaurali, G.; Neopaney, T.; Cheki, T.; Gautam, D. Wind vulnerability and strengthening of Bhutanese vernacular roofs. Geomat. Nat. Hazards Risk 2022, 13, 1511–1534. [Google Scholar] [CrossRef]
- Cabeza, L.F.; de Gracia, A.; Pisello, A.L. Integration of renewable technologies in historical and heritage buildings: A review. Energy Build. 2018, 177, 96–111. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; De’rossi, F.; Vanoli, G.P. Energy retrofit of an educational building in the ancient center of Benevento. Feasibility study of energy savings and respect of the historical value. Energy Build. 2015, 95, 172–183. [Google Scholar] [CrossRef]
- Takemi, T.; Yoshida, T.; Horiguchi, M.; Vanderbauwhede, W. Large-eddy-simulation analysis of airflows and strong wind hazards in urban areas. Urban Clim. 2020, 32, 100625. [Google Scholar] [CrossRef]
- Hejazi, M.; Moayeian, S.M.; Daei, M. Structural analysis of Persian historical brick masonry minarets. J. Perform. Constr. Facil. 2016, 30, 04015009. [Google Scholar] [CrossRef]
- Hegyi, D.; Armuth, M.; Halmos, B.; Marotzy, K. The effect of wind on historical timber towers analyzed by plastic limit analysis in the focus of a collapse. Eng. Fail. Anal. 2022, 134, 105852. [Google Scholar] [CrossRef]
- Borkowski, A.S. Low-Cost Internet of Things Solution for Building Information Modeling Level 3B—Monitoring, Analysis and Management. J. Sens. Actuator Netw. 2024, 13, 19. [Google Scholar] [CrossRef]
Figure 1.
Methodology workflow utilized in this research.
Figure 1.
Methodology workflow utilized in this research.
Figure 2.
The interior space of Lujiang Academy after renovation and renovation. (a) Front hall; (b) Indoor exhibition display; (c) Glass curtain wall enclosed courtyard; (d) Indoor exhibition of courtyard corridor; (e) Corridor canopy.
Figure 2.
The interior space of Lujiang Academy after renovation and renovation. (a) Front hall; (b) Indoor exhibition display; (c) Glass curtain wall enclosed courtyard; (d) Indoor exhibition of courtyard corridor; (e) Corridor canopy.
Figure 3.
Design of Renewal and Renovation of Lujiang Academy. (a) Install glass curtain walls and canopies in the courtyard and corridor; (b) Newly added independent steel structure glass curtain wall in the courtyard; (c) Vertical section of ancestral hall.
Figure 3.
Design of Renewal and Renovation of Lujiang Academy. (a) Install glass curtain walls and canopies in the courtyard and corridor; (b) Newly added independent steel structure glass curtain wall in the courtyard; (c) Vertical section of ancestral hall.
Figure 4.
The application process of CFD numerical simulation method.
Figure 4.
The application process of CFD numerical simulation method.
Figure 5.
Definition of simulation test model and wind direction angles. (a) Courtyard remains open without enclosure; (b) courtyard enclosed with glass curtain walls on all sides; (c) courtyard equipped with a fully enclosed glass canopy; (d) setting of wind angles.
Figure 5.
Definition of simulation test model and wind direction angles. (a) Courtyard remains open without enclosure; (b) courtyard enclosed with glass curtain walls on all sides; (c) courtyard equipped with a fully enclosed glass canopy; (d) setting of wind angles.
Figure 6.
Geometries of the computational model: (a) computational domain; (b) front view; (c) computational grids; (d) top view and (e) side view.
Figure 6.
Geometries of the computational model: (a) computational domain; (b) front view; (c) computational grids; (d) top view and (e) side view.
Figure 7.
Comparison of CFD calculation results with TPU database: (a) geometric model; (b) TPU database; (c) CFD calculation results.
Figure 7.
Comparison of CFD calculation results with TPU database: (a) geometric model; (b) TPU database; (c) CFD calculation results.
Figure 8.
Wind pressure distribution on the roof: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 8.
Wind pressure distribution on the roof: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 9.
Wind pressure coefficient distribution on the roof: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 9.
Wind pressure coefficient distribution on the roof: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 10.
The distribution of wind pressure on the building surface: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 10.
The distribution of wind pressure on the building surface: (a) 0° wind angle; (b) 45° wind angle; (c) 90° wind angle.
Figure 11.
Distribution of surface wind pressure on the building after installing glass curtain walls in the courtyard. (a) Wind angle of 0°; (b) Wind angle of 45°; (c) Wind angle of 90°.
Figure 11.
Distribution of surface wind pressure on the building after installing glass curtain walls in the courtyard. (a) Wind angle of 0°; (b) Wind angle of 45°; (c) Wind angle of 90°.
Figure 12.
Distribution of surface wind pressure on the building after installing a glass canopy over the courtyard. (a) Wind angle of 0°; (b) Wind angle of 45°; (c) Wind angle of 90°.
Figure 12.
Distribution of surface wind pressure on the building after installing a glass canopy over the courtyard. (a) Wind angle of 0°; (b) Wind angle of 45°; (c) Wind angle of 90°.
Figure 13.
The wind pressure distribution at roof control points for different sets of facade enclosures.
Figure 13.
The wind pressure distribution at roof control points for different sets of facade enclosures.
Table 1.
Research on Wind Protection for Historical Buildings with different Structures.
Table 1.
Research on Wind Protection for Historical Buildings with different Structures.
| Countries and Regions | Researchers | Structure Type | Research Content and Method |
|---|
| China | Han Y. et al. [6] | Wood | Used Computational Fluid Dynamics (CFD) to evaluate the impact of wind on ancient wooden buildings and predict structural responses. |
| Li Y. et al. [7] | Wood | Used wind tunnel experiments to demonstrate that artificial plants are a non-destructive method that can reduce wind loads and damage to wooden towers. |
| Japan | Fujita K. et al. [8] | Wood | Focused on the wind resistance of traditional wooden pagodas and analyzed their dynamic response behavior during typhoons using long-term wind monitoring records. |
| South Korea | Minu S. et al. [9] | Brick–wood | Used CFD and geographic information systems (GIS) to analyze the interference effects of airflow separation and vortices in high-rise buildings on urban historical buildings. |
| Philippines | Sevieri G. et al. [10]
Song B. et al. [11] | Wooden structure and iron sheet roof | Evaluated the damage of typhoons to the roofs of historical buildings and proposed a simulation-based roof vulnerability analysis and risk assessment method. |
| Madagascar | Taleb R. et al. [12] | Wood | Tested the connection strength of traditional wooden roof components and developed a vulnerability curve to assess the risk of damage. |
| United States | Sparks P.S. [13] | Brick–wood | Assessed the vulnerability of historical buildings and proposed renovation methods to mitigate hurricane damage. |
| Iranian | Khosrowjerdi S. et al. [14] | Brick | Used CFD to compare roof wind pressure coefficients and determine the most suitable traditional dome form for windy areas. |
| British | Carter A.J. et al. [15] | Steel | Used finite element method to study the failure mode of bridges under wind load and evaluate the load-bearing performance of structural components. |
| Egyptian | Hussein A.S. et al. [16] | Stone | Studied the impact of environmental wind on the degradation of historical sites and simulated wind loads on the surface of pyramids. |
Table 2.
Simulation conditions.
Table 2.
Simulation conditions.
| No. | Simulation Conditions | Wind Direction Angle | Test Model |
|---|
| 1 | Courtyard remains open without enclosure | 0°, 45°, 90° | Case 1, Case 2, Case 3 |
| 2 | Courtyard enclosed with glass curtain walls on all sides | 0°, 45°, 90° | Case 4, Case 5, Case 6 |
| 3 | Courtyard equipped with a fully enclosed glass canopy | 0°, 45°, 90° | Case 7, Case 8, Case 9 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).