Wobble Board Performance: A Practical and Useful Quantification in Balance Assessment

Featured application

This work provides evidence for the use of computerized wobble boards in balance assessment and contributes to the clinical application of wobble board performance as a practical measure for monitoring purposes.

Abstract

Balance is integral in ankle injury prevention and therapy, especially in high-risk sports like volleyball. For balance assessment, the recommended wobble board (WB) performance (i.e., time at equilibrium) has never been compared with the gold standard. The objective was to investigate the relationships of force-plate-derived center of pressure (CoP) with WB performance and the accuracy of WB-derived CoP estimates. Twelve high-level volleyball players completed six unipedal standing trials on a computerized WB. WB tilt angles and CoP were obtained simultaneously via tri-axis accelerometers on the WB (200 Hz) and a force plate (1000 Hz), respectively. WB performance, polynomial-transformed CoP estimates, and CoP fractal sway, sway area, and mean sway velocity were assessed via Pearson and concordance correlation, root mean square errors, and dependent t-tests. WB performance was related with CoP sway and sway area (|r_linear| = 0.714–0.842, |r_nonlinear| = 0.833–0.910, p < 0.01). The strongest concordance (0.878–0.893, p < 0.001) and smallest errors (6.5–10.7%) were reported for anterior–posterior sway and sway area. Moderate to excellent relationships between the WB performance and force plate CoP variables supported the usefulness of WB performance and estimates (especially sway area) in balance assessment. Furthermore, this study presents recommendations for future analyses and modeling approaches to reflect the complexity of postural control.

1. Introduction

Balance control is a multifaceted skill crucial for physical activities, sports training, and rehabilitation therapies, serving as a preventive measure against injuries across various ages and performance levels [1,2,3]. It involves the ability to maintain the projection of the center of gravity within the base of support [1], e.g., in an upright position during standing [4]. Hereby, visual, vestibular, tactile, and proprioceptive systems supply sensory information for motor responses [3,5,6]. A variety of motor strategies such as ankle and hip strategies may be employed to successfully maintain balance [7], involving these joints to control postural sway. The inadequate execution of these strategies can deteriorate balance, posing serious health risks relevant for society (e.g., falls in the elderly) [8]. Due to the contribution of ankle functionality to maintain balance, individuals with ankle injuries often exhibit balance deficits, leading to increased risk of reinjury [9]. Sports like volleyball, notorious for ankle injuries especially among high-level competitors [10], necessitate specific injury prevention programs such as balance training [10].

For the effective monitoring and assessment of training outcomes, reliable and valid methods of balance testing are indispensable [3]. Balance tests can also detect pathologies that are associated with balance [5,11,12]. Timed unipedal stance tests yielded high reliability and were recommended as a suitable task for balance assessment [5]. Among various methodologies and devices (e.g., force plates, accelerometers, and functional tests), force plates and specifically the measurement of the center of pressure (CoP) sway are considered as the gold standard for balance assessment [13,14]. However, the costs, weight, and complexity in data processing limit the application of force plates in large-scale and in-field testing [5,15]. Therefore, alternative devices and practical protocols have been recommended [5,16], e.g., computerized wobble boards (WBs) [17,18]. Cheap and mobile in comparison with force plates, WBs are unstable platforms frequently used to train balance control [1,2,19]. When instrumented with accelerometers or gyroscope sensors, WBs can also be used for balance assessment [17,20,21]. Such instrumented WBs can obtain the tilt angle of the board during balance tasks. The change in the tilt angle over time mirrors CoP sway, with smaller tilt angles indicating better postural control.

One study compared the WB tilt angle derived from an inertia measurement unit with the angle derived from a Vicon motion capture system [22]. The authors reported great concurrent validity for the WB to measure tilt angles (R² > 0.99) [22]. When comparing WB tilt angles with force-plate-derived CoP, however, findings have been controversial [23,24]. One study reported correlation coefficients of −0.14–0.30 between WB tilt angle excursion and force plate CoP velocity in the sagittal and frontal plane separately [23]. Nevertheless, WB-derived CoP path length was able to reflect impaired balance in men with Achilles tendinopathy [25]. Another study investigated the resultant horizontal mean velocity of force-plate-derived CoP and documented a stronger correlation with WB tilt angle velocity (r = 0.77) [24]. In the latter study, a wide range of intra- and inter-session reliability was documented for various CoP variables, i.e., sway, horizontal mean velocity, and index of complexity (ICC = 0.17–0.76) [24]. This difference in reliability among CoP variables suggested that various CoP variables may not be equally appropriate for the practical purposes of balance assessment (e.g., longitudinal monitoring of development of balance performance). Moreover, different CoP variables may reflect different aspects of balance control, which makes it difficult to select a single best indicator for balance performance [13].

Alternatively, it was suggested to reflect balance performance as the time spent on the WB at a ~0° tilt angle during a 30 s standing test [17,21]. This time was then used as a measure of ‘WB performance’. The idea is to summarize the variety of balance strategies [7] and motor control systems in the human body [3] involved in postural control into a single representative expression of balance performance. This greatly simplifies data processing and interpretation, which facilitates practical use in the field. Reliability analyses of WB performance achieved ICC results of 0.71 [21] and 0.65–0.89 [17] in standing tests. Validity was only assessed in comparison with a functional balance test (i.e., Y-balance test) with poor results (r = −0.23–0.34) [17]. It was argued that the two tests may differ in their demands for postural control [17], which is in line with reported differences in strategies to maintain balance on WBs compared with firm surfaces [23]. The Y-balance test evaluates the ability to maintain equilibrium (steady state) on a stable surface, whereas the WB task requires dynamic adjustments to a moving platform, testing the ability to continuously regain balance [23]. As the WB is an unstable platform, the instrumented WB is effective in measuring dynamic, proactive balance performances, providing understandings into an individual’s ability to anticipate balance challenges. WB performance was able to accurately detect balance deficits in patients with chronic ankle instability [18,26]. However, WB performance as time spent at a ~0° tilt angle has never been validated against the gold standard in balance assessment (i.e., CoP variables derived from force plates) [13].

For concurrent validity, investigating the relationship of a tested system with the gold standard is common practice [27]. It is more likely to statistically confirm the relationship between two items in the overall population with a wide range of values (deviations from the mean) than in a specific sub-sample with a narrow range of values [28]. Therefore, an established relationship in the overall population does not imply that the relationship can also be confirmed within a specific sub-sample. Since training interventions are often administered to a specific group of individuals (e.g., athletes of a sports team, patients, elderly), the validation progress should reflect the system’s ability to relate with the gold standard within a sub-sample that is relevant in training reality. Otherwise, for example, the tested system may be valid for differentiating between sub-samples within the overall population but not for performance monitoring within a sub-sample (e.g., high-level athletes). High-level athletes are an appropriate sub-sample because inter-individual performance differences are usually smaller (i.e., narrow range of values) at high compared with low competition levels. Regarding a suitable sport for such investigation, volleyball represents a highly relevant choice because of the large number of ankle injuries and the importance of balance training as a prevention measure in volleyball [10].

Therefore, the objective of this study was to assess validity of WB performance by investigating the strength and nature of the relationship with CoP variables from force plates during a WB balance test in high-level volleyball players during unipedal stance. The relationship was hypothesized to be strong enough to reflect CoP variables accurately based on WB performance.

2. Materials and Methods

2.1. Study Design

Following a longitudinal study design, athletes participated repeatedly in three identical sessions of balance assessment to allow for familiarization and to control for potential developments over time. During each session, WB performance and CoP variables from force plates were obtained. The final analysis was cross-sectional, investigating the relationship between WB performance and CoP variables within the last session after familiarization.

All participants signed written consent before the first session, and this study received approval from the institutional ethics committee, following the Declaration of Helsinki.

2.2. Participants

Twelve female volleyball players (age: 22.8 ± 3.7 years, body mass: 69.9 ± 9.4 kg, body height: 1.78 ± 0.09 m, training experience: 11.8 ± 3.8 years) competing in the highest national league in Austria voluntarily participated in this study. They met the inclusion criteria if they actively trained and competed in the highest national league during the ongoing season and were healthy at the time of data collection. Players were excluded if they reported lower limb injuries within six weeks before testing or acute injuries that may affect balance performance (e.g., ankle sprains, concussion). The number of participants was limited to the size of the team and availability of players at this level. All healthy players of the team participated in this study. Statistical power analysis via gPower 3.1 showed that the sample size yielded a probability of approximately 80% to detect strong effects of a relationship (coefficients > 0.7) [29] at a significance level of α = 0.05.

2.3. Data Collection

Each participant completed three identical sessions of WB balance testing on a force plate to collect data simultaneously from both devices. The three sessions took place in 6-week intervals to represent a duration that is often required between measurements for various training interventions. The repeated sessions allowed for the investigation of long-term familiarization effects and testing whether the relationship between devices changed over time. Data from the final session were used for in-depth, within-session analysis.

Each session followed a validated protocol [17], including a mandatory familiarization with the WB by performing test trials in accordance with the protocol specifications. Then, the barefooted participants performed three unipedal stance tests per leg on the WB with their hands at their hips. A block of three trials with one leg was finished before a second block of another three trials on the other leg was conducted, and the sequence of blocks was randomized. This resulted in a total of six trials per participant. Each trial lasted 30 s, with a 1 min break between trials to prevent fatigue. During the entire duration of each the trial, the participants attempted to spend as much time as possible in a stable horizontal WB position (i.e., ~0° WB tilt angle).

The WB (Balance Board WSP, GSJ Service, Rome, Italy; maximal tilt angle = 20°) had a circular even surface of 40 cm diameter to stand on and a plastic hemisphere of 6 cm height and 20 cm width under the board to allow for 360° freedom of movement. It was equipped with tri-axis accelerometers (Phidget Spatial 0/0/3 Basic 1041, Phidgets Inc. 2016, Calgary, AB, Canada) placed in the hemisphere to measure mediolateral and anterior–posterior tilt angles at a sampling frequency of 200 Hz [17]. A USB connection with a computer via proprietary software (Software WSP version 1.0.0.1, GSJ Service, Rome, Italy) allowed for data collection and real-time display of the tilt angle. Visualized performance was displayed in real time on a screen in front of the participants via a validated software (GSJ Service, Rome, Italy), showing a moving dot that represented the CoP and a target zone that represented the ~0° WB tilt area [17]. A screen presented the dot and the target zone to the participants in real time during the trials, approximately one meter in front of the participants and one meter above the ground [17]. The WB was placed on an AMTI force plate (Watertown, MA, USA), obtaining ground reaction forces simultaneously at 1000 Hz. Visual3D v6 software (C-Motion Inc., Rockville, MD, USA) was used to calculate the CoP from ground reaction forces measured by the force plate. Force plate data were filtered in accordance with recommendations for CoP filtering [13] and the results of residual analysis performed for the specific data [30]. A fourth-order zero-lag Butterworth low-pass filter with a cut-off frequency of 10 Hz was applied.

2.4. Data Handling

WB performance was quantified as the time [%] spent at a ~0° tilt angle over the full span of the trial. Outliers in WB performance were defined as mean ± 2 times the standard deviation within a block of three trials (i.e., for each leg). Outliers (i.e., 2.4% of all data) were removed, and the remaining trials of the same leg were averaged. Then, each participant’s WB performances in both legs were averaged and used for further analyses, as this procedure has shown the highest reliability previously [17]. In line with a review specifically focused on the reliability of CoP variables for balance assessment [13], the following CoP variables were computed from ground reaction forces obtained from the force plate: (1) anterior–posterior sway as fractal standard deviation, (2) mediolateral sway as fractal standard deviation, (3) two-dimensional sway area defined by a 95% confidence ellipse, and (4) mean velocity of sway as the total distance of the CoP path, divided by trial duration.

2.5. Statistical Analysis

Statistical analyses and visualization were conducted in Office Excel 2019 (Microsoft Corporation, Redmond, WA, USA) and PASW Statistics 18 (SPSS Inc, Chicago, IL, USA). Data are presented as mean ± standard deviation. The Shapiro–Wilk test, skewness, and kurtosis confirmed normal distributions. As a standard for validation purposes [5,17], Pearson product-moment correlation (r) tested the linear relationship between WB performance and CoP variables in all three sessions.

Since all scatterplots regarding WB performance and CoP variables suggested nonlinear polynomial patterns, the nonlinear relationship was also tested during in-depth within-session analysis using the data from the final session. Results from polynomial least square fitting with two to six orders were compared via the models’ adjusted R², accounting for the number of predictors (i.e., polynomial order). The following formula calculated the adjusted R² = 1 − ((1 − R²) × (n − 1))/(n − k − 1), where n represents the number of observations, and k represents the number of predictors. The polynomial least square fit with the highest adjusted R² was selected for the assessment of the nonlinear relationship between WB performance and each CoP variable. Co-linearity among CoP variables was also calculated to check whether variables may reflect different aspects of balance control.

The final polynomial least square equations converted the practical WB performance into estimates of the respective force plate CoP variables (i.e., polynomial regression equations to predict CoP variables based on WB performance). In contrast to the original WB performance values, these predicted estimates were comparable with CoP values and, therefore, allowed for the testing of the concordance with force-plate-derived CoP variables. For each pair of polynomial-transformed WB performance and force plate CoP variables, the concordance correlation coefficient (CCC) was calculated as a recommended inferential measure of concordance between two items [31]. Dependent t-tests including Cohen’s d analyzed the difference between transformed WB performance and force plate CoP. Moreover, absolute [cm², mm, or mm·s⁻¹] and relative [%] root mean square errors (RMSEs) were presented. The relative RMSE was calculated as the absolute RMSE divided by the mean of the transformed WB performance and CoP variable.

Correlation results were interpreted as negligible, low, moderate, high, and very high at the thresholds of 0.3, 0.5, 0.7, and 0.9, respectively [29], and Cohen’s d as negligible, small, medium, and large at 0.2, 0.5, and 0.8 [32]. All statistical tests were conducted at a significance level of α = 0.05.

3. Results

Analysis of the correlation between WB and CoP variables during different measurement sessions derived coefficients r of −0.810 ± 0.027 for sway area, −0.776 ± 0.057 for anterior–posterior sway, −0.782 ± 0.059 for mediolateral sway, and −0.621 ± 0.050 for sway velocity across sessions (Figure 1).

Descriptive statistics of WB performance and CoP variables derived from both the force plate and the WB-based polynomial regression predictions are presented in

Table 1. Descriptive statistics as mean ± standard deviation (SD) and 95% confidence intervals (95% CI) for wobble board performance (WB), anterior–posterior sway (AP), mediolateral sway (ML), sway area (Area), and mean sway velocity (V) as well as the linear correlation matrix.

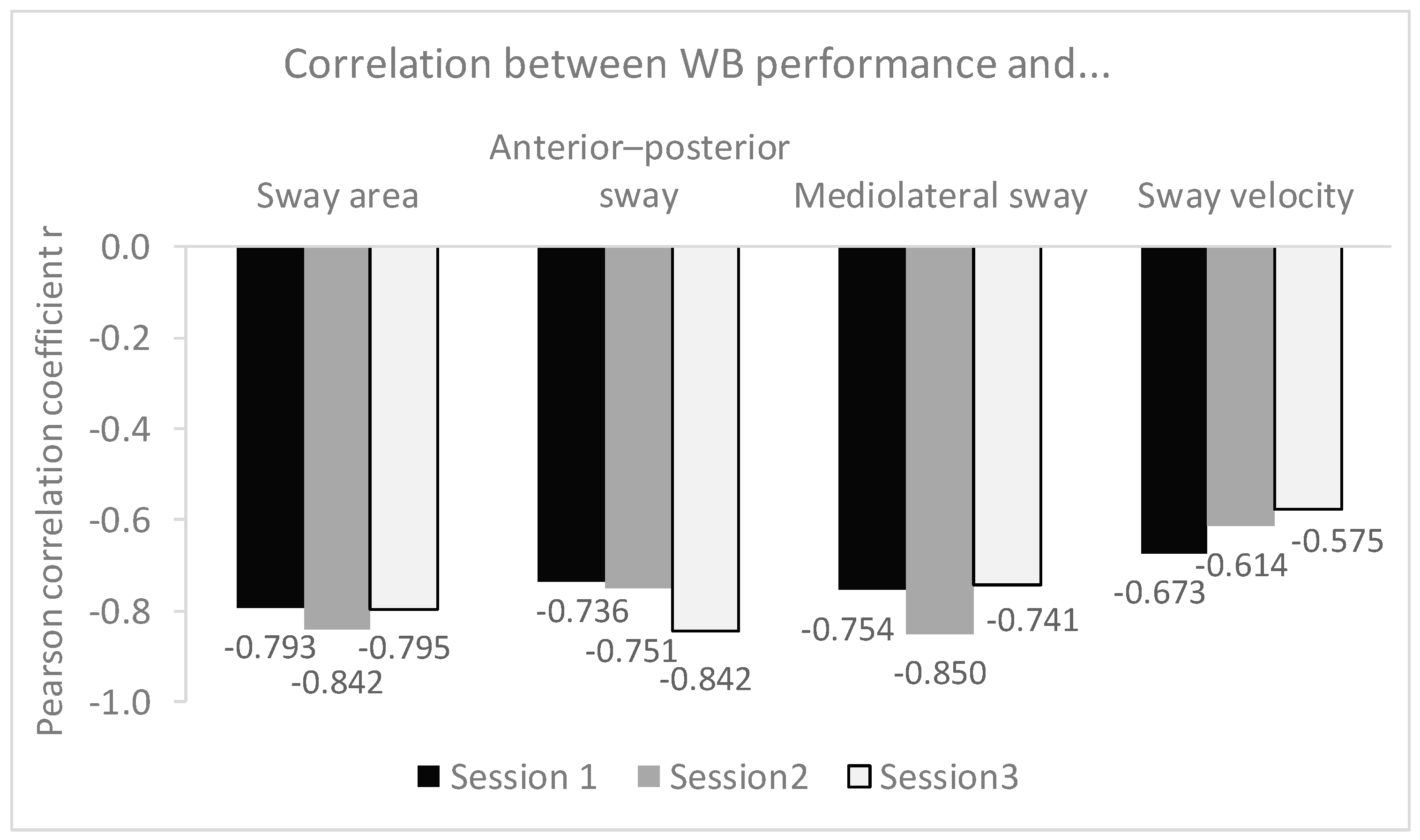
		WB [%]	AP [mm]	ML [mm]	Area [cm2]	V [mm·s−1]
mean ± SD		36.58 ± 22.09	7.30 ± 1.91 $ 7.47 ± 1.32 #	5.96 ± 1.11 $ 6.56 ± 0.80 #	8.43 ± 3.41 $ 8.43 ± 2.74 #	64.20 ± 9.26 $ 64.08 ± 6.06 #
95% CI		23.08–48.08	6.22–8.38 $ 6.73–8.21 #	5.33–6.59 $ 6.11–7.01 #	6.50–10.36 $ 6.88–9.98 #	58.96–69.44 $ 60.65–67.51 #
WB	r	1	−0.842	−0.714	−0.795	−0.575
	p		<0.001	0.009	0.002	0.051
AP	r		1	0.836	0.941	0.515
	p			<0.001	<0.001	0.087
ML	r			1	0.969	0.500
	p				<0.001	0.098
Area	r				1	0.510
	p					0.090
V	r					1
	p

Note: ^$ CoP values derived from force plate data; ^# predicted CoP values based on polynomial-transformed WB performance. Bold coefficients were statistically significant.

. The table also contains the correlation between WB performance and force plate CoP variables. Figure 2 displays the linear (|r_lin| = 0.575–0.842) and nonlinear (|r_non| = 0.728–0.910) relationship between WB performance and force plate CoP variables.

Table 2. R² and adjusted R² results of polynomial-transformed regression predictions of force-plate-derived center of pressure variables based on wobble board performance.

	Polynomial Order	Sway Area	Anterior–Posterior Sway	Mediolateral Sway	Sway Velocity
R2	2	0.738	0.778	0.683	0.496
	3	0.753	0.778	0.699	0.572
	4	0.781	0.817	0.706	0.634
	5	0.790	0.842	0.774	0.648
	6	0.802	0.843	0.799	0.648
Adjusted R2	2	0.713	0.757	0.653	0.448
	3	0.716	0.745	0.654	0.508
	4	0.735	0.778	0.644	0.557
	5	0.731	0.798	0.711	0.550
	6	0.732	0.788	0.728	0.524

Note: Bold coefficients indicate the highest adjusted R² for each variable. The respective polynomial order was applied for nonlinear transformation and nonlinear analysis.

displays the R² and adjusted R² results for all polynomial-transformed regression predictions, with the highest adjusted R² for polynomial transformation found in the fifth (anterior–posterior sway), sixth (mediolateral sway), and fourth order (sway area and velocity) at 0.798, 0.728, 0.735, and 0.557, respectively. The respective polynomial equations are included in Figure 2. The CCC (0.893, 0.685, 0.878, 0.778), absolute RMSE (0.09 mm, 0.13 mm, 0.16 cm², 0.07 mm·s⁻¹), and relative RMSE (6.5%, 12.1%, 10.7%, 5.2%) were documented between the transformed WB performance and anterior–posterior sway, mediolateral sway, sway area, and mean sway velocity, respectively. The transformed WB performance did not differ from the force plate anterior–posterior sway (d = 0.23, p = 0.439), sway area (d = 0.01, p = 0.984), and mean sway velocity (d = 0.02, p = 0.946) but differed from mediolateral sway (d = 1.01, p = 0.005).

4. Discussion

The objective of this study was to assess the validity of WB performance for balance evaluation based on the relationship with force plate CoP variables. For concurrent validity assessment, the linear relationship between a new and an established criterion has frequently been tested via Pearson’s or Spearman’s correlation analyses previously [17,24]. The current correlation coefficients remained consistent across three measurement sessions. The inter-session variability in the correlation coefficients showed small standard deviations, ranging from 0.027 to 0.059 for different CoP variables. No systematic deviations were noted over time, indicating the absence of long-term familiarization effects over multiple sessions. The stable correlation between WB and force-plate-derived CoP variables implied that the validity of WB performance was not session-dependent. Clinicians and coaches may use WB performance reliably across at least three repeated sessions in 6-week intervals without the necessity of a prior familiarization session.

During a single measurement session, the current coefficients showed a high correlation of WB performance with anterior–posterior (r = −0.842) and mediolateral (r = −0.741) sway and sway area (r = −0.795) of CoP derived from force plates. The correlation with mean sway velocity just missed significance (p = 0.051) and was only moderate (r = −0.575). These correlations were higher than the best correlation results (r = 0.52) between WB performance and another typical balance test (i.e., Y-balance test) [17,26]. Previous authors assumed that WB performance reflected different aspects of balance control than the Y-balance test [17]. Moreover, an intervention study showed that WB training improved WB performance and strategies, but balance performance on firm surfaces was not affected [33]. WB performance was, in the current study, more strongly associated with CoP variables (i.e., valid and reliable for balance assessment) [13,14] than with Y-balance test results in a previous study [17]. This comparison corroborated that WB performance may serve as a valid measure for dynamic instead of static balance assessment.

The adjusted R², accounting for the order in polynomial transformation, was higher for all transformed WB data than for raw WB performance. WB performance may be better described by a nonlinear than a linear relationship with force plate CoP variables. The coefficients for nonlinear relationships were high to very high. In line with the linear correlation results, the strongest nonlinear relationship was found in anterior–posterior sway (r = −0.915) and the weakest in velocity (r = −0.796).

Co-linearity was also the weakest between sway velocity and other CoP variables (r = 0.500–0.515, all nonsignificant) and high to very high among fractal sway and area (r ≥ 0.836). This suggested that velocity may reflect a different aspect of balance control than fractal sway and sway area. In recognition of the previously mentioned variety of factors contributing to balance control [3,5,6], the different strategies to maintain equilibrium [7,23], and specific effects of training interventions [33], it seemed reasonable that different biomechanical characteristics reflect different aspects of balance control. Therefore, velocity may be a valuable addition to fractal sway or sway area for holistic balance evaluation in research and practice.

To compare the results of different CoP variables, polynomial-transformed WB data allowed for more detailed analyses beyond traditional correlation analyses because the transformation provided estimates of the respective CoP variables. Thus, the comparison of exact values was feasible. For all CoP variables except for sway velocity, the 95% confidence intervals of WB-based polynomial regression estimates were narrower and within the intervals of force plate CoP variables. This corroborated the suitability of the derived equations and supported that WB performance aligned with force plate CoP variables. The strongest correlation and concordance with a small RMSE% between transformed WB performance and force plate CoP was found in anterior–posterior sway. Therefore, anterior–posterior sway represented the best single factor associated with WB performance. In contrast, mediolateral sway showed considerably lower correlation results, the weakest concordance, the largest RMSE%, and the only significant difference between the WB and force plate of all tests. For sway area, the correlation and concordance were slightly weaker but comparable with anterior–posterior sway with higher but perhaps acceptable RMSE%. Sway area may be considered if a two-dimensional representation of balance is preferred over the single best factor (i.e., anterior–posterior sway; one-dimensional). Despite the lowest errors, sway velocity showed the lowest correlation and a lower concordance than anterior–posterior sway and sway area. Therefore, velocity was not recommended as a single factor alternative to anterior–posterior sway and sway area. However, as explained before, the co-linearity results may suggest velocity as a potentially valuable addition in future multi-factorial strategies to assess general balance performance.

4.1. Limitations

First, the range of current WB balance performances (33–85%) exceeded the range of previously reported performances in uninjured and injured limbs of adults [17,26]. This wide range may suggest that the current data are representative of a more general population with respect to inter-individual variability in balance control. Although the current data represent a practically relevant sample (i.e., a team with its natural variability), it is unclear if comparable correlation results would also be achieved in samples with smaller inter-individual variability.

Second, the validity of the specific polynomial equations was limited to the current data because the current sample did not represent a wider population, and cross-validation against different sub-samples was not feasible. The purpose of the polynomial transformation was not to provide general predictive models for other samples. Instead, polynomial transformation served as the best fitting way to reflect the nonlinear relationship between WB performance and force plate CoP variables in this sample. Thus, the transformation produced values matching CoP variables based on WB. Consequently, this analysis allowed for the exploration of the nonlinear nature of the relationship and the analysis of concordance beyond the limitations of traditional correlation analyses.

Third, the sample size (n = 12) was relatively small due to limited accessibility to and availability of players at the highest level. Nevertheless, the sample was representative for the overall small size of the specific population of high-level female volleyball players. Furthermore, statistical power analysis revealed that the sample size was sufficient to detect at least strong effects with a widely accepted 80% chance at p < 0.05. Therefore, the results of moderate effects that closely missed significance should be interpreted carefully.

4.2. Practical Implications

An instrumented WB is a mobile and practical tool, and the variable of WB performance as time at equilibrium is easy to collect, process, and interpret. The observation that WB performance correlated with force-plate-derived CoP variables supported the validity of WB performance for balance assessment. Therefore, this study provided evidence to assess balance via WB performance, e.g., in clinical and sports practical settings.

The practicability of WB tests allows for frequent in-field applications, such as monitoring. Monitoring balance control for preventive purposes seems reasonable because balance control was identified as a predictor for the risk of ankle sprains [9]. It was suggested to perform pre-season screening of balance to assess the risk of ankle injuries and reoccurrence of injuries [34]. This may be especially important in high-risk sports like volleyball [10] because ankle injuries and chronic ankle instability are known to affect balance control [35] and movement strategies in jump landing and cutting movements [36].

5. Conclusions

Based on correlation and concordance results, a high concurrent validity of WB performance was concluded for anterior–posterior sway and sway area of CoP derived from force plates. In consideration of the mobility, affordability, and feasibility of WBs in addition to the previously reported high reliability, WB testing and specifically WB performance as a very practical criterion can be recommended for in-field balance assessment. The findings suggest that WBs are a suitable tool to assess balance performance in specific target groups with high injury risk. Considering practical feasibility in the field and the validity of WB performance relating to CoP variables, WB testing may be recommended for monitoring and risk assessment on site.