Mathematical Tools for Simulation of 3D Bioprinting Processes on High-Performance Computing Resources: The State of the Art
Abstract
1. Introduction
- Pre-printingIn the print cartridge, a cell-laden bioink can be considered a composite material. Therefore, even in the absence of different compounds such as rheological enhancers or additional biomaterials, high-cell-density suspensions behave as colloidal systems that exhibit printability. The impact of the cells embedding on the viscoelastic properties of the bioink is further complicated by the possibility that the cells are surrounded by a pericellular matrix, which could alter their mechanical characteristics, the hydrodynamic radius, and boundary conditions at the fluid interface [15].It is worth noting that cells can interact with each other, during the pre-printing phase and during the whole process, adding a further level of complexity to the overall system. Furthermore, different cell sources can be also considered when dealing with interface tissues such osteochondral one, which involves bone and cartilage tissues. Nonetheless, a bioink must prevent cell sedimentation to preserve a uniform cell suspension [16]. The cells in the ink are no longer evenly distributed when they settle. This may result in clogged nozzles as well as an uneven cell distribution in the finished printed structure (i.e., more cells in the early printed layers than in the latter ones). Creating bigger and more complex scaffolds may exacerbate the concerns related to cell sedimentation because these structures usually demand longer printing times (i.e., printing full-scale tissues or organs can take hours or even days). In conclusion, since cells can flow when a force is applied, a bioink would avoid cell sedimentation while yet remaining printable [14].Additionally, the volume occupied by the cells within a bioink varies according to their size and density. The hydrogel is excluded from the volume occupied by cells, which could affect the physicochemical and viscoelastic properties [15]. For example, cells may actually hinder the cross-linking process by limiting contact between reacting groups or acting as a physical barrier between various ink layers.
- During PrintingThis indicates that as a force is applied, their viscosity alters. Non-Newtonian fluids are primarily categorized into shear thickening (viscosity increases when shear rate increases) and shear thinning (viscosity reduces when shear rate increases) in response to this viscous tendency. Generally speaking, printability increases with material viscosity—at least to the point at which the internal pressures created can harm cells. Furthermore, some studies examine the impact of temperature on the viscosity of bioink. Nonetheless, they must be bioprinted at physiological conditions at 37 °C to preserve the cells [11]. Additionally, as a result of cell migration and proliferation, the distribution of cells during printing may change, which may have an impact on the bioink’s rheological characteristics. In fact, as cells interact with the matrix around them and with one other, traction forces are created that operate on the hydrogel macromolecules in a printed structure.
- Post-PrintingBioink needs to produce a 3D “milieu” that promotes cellular survival and function after printing. Because they offer an aqueous, cell-compatible environment that can mimic many of the mechanical and biochemical characteristics of the original tissue, hydrogels are frequently utilized in 3D cell culture. The simple passage of nutrients and waste products to and from encapsulated cells is made possible by their high water content and permeability. They can also provide a variety of signals to control cell phenotypic, differentiation, growth, and migration.
“What are the relevant mathematical tools for the simulation of the different phases of 3D bioprinting with a particular focus on the first principles-based (FP) models in macro and mesa-scales and how such tools should be modified/integrated to be compliant with the emerging computational resource in the Exascale Era?”.
| Sub-Search-1: | (bioprinting OR (cell-laden hydrogels) OR bioinks) |
| Sub-Search-2: | (simulation OR modeling OR (computational science)) |
| Sub-Search-3: | (macro or mesa scale FP models) |
| Sub-Search-4: | (numerical tools for computational solution of FP-model problems) |
| Sub-Search-5: | (Exascale models and algorithms). |
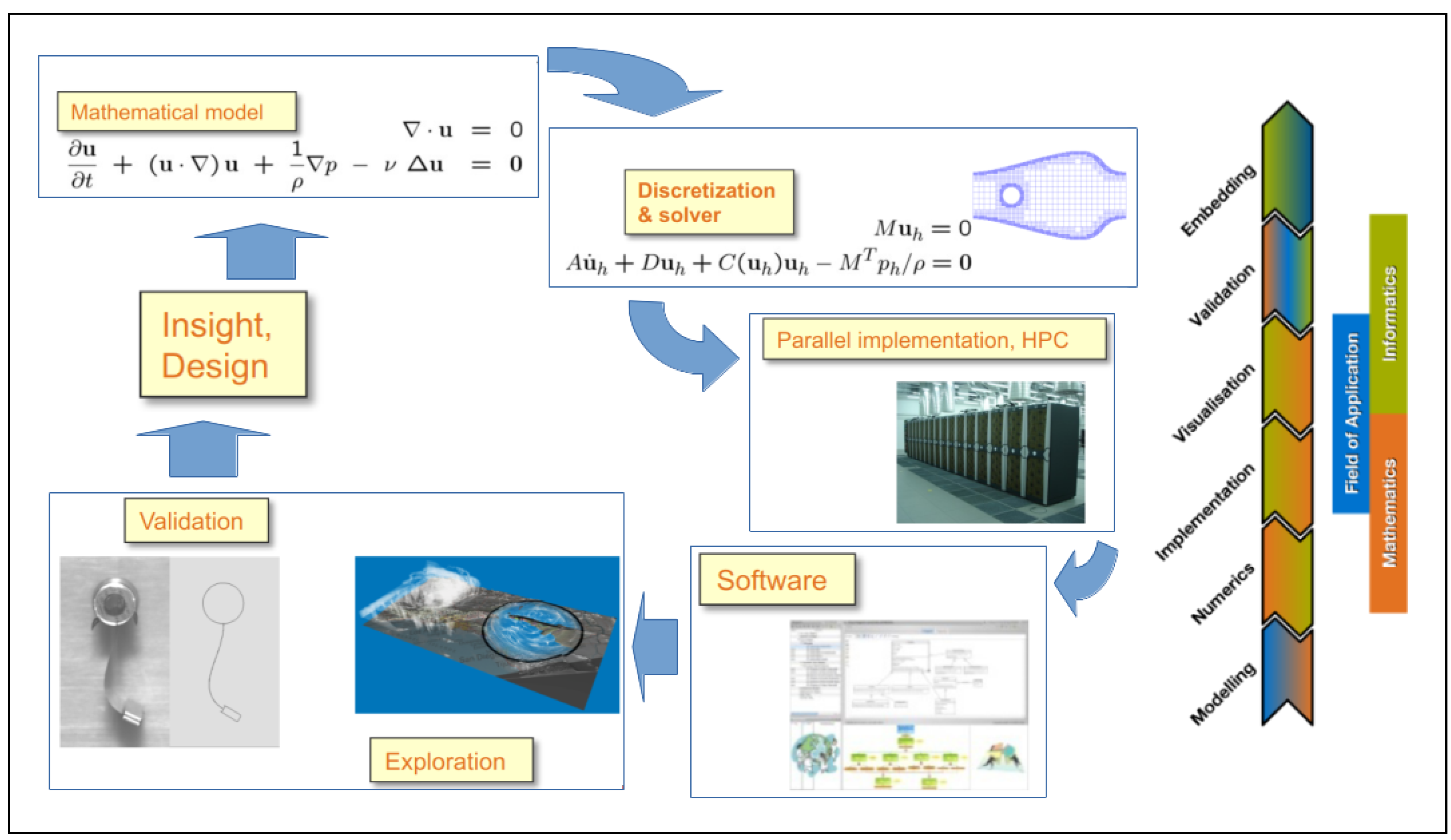
2. The Role of Computational Science (CS)
- Field experts and mathematicians jointly define the descriptive mathematical model of the problem.
- Mathematicians and computer scientists jointly define and implement the descriptive numerical model of the problem. The numerical model is described by an algorithm that can have a high computational cost due to the great number of operations. Therefore, it may be desirable to exploit the parallelism made available by resources for HPC [19,20,21,22,23,24,25].
- Field experts, mathematicians, and computer scientists jointly validate the correctness and accuracy of the numerical model and algorithm by executing its implementing software. Parallel algorithms and software are evaluated on the basis of their performance in terms of the number of performed operations per time unit, strong and weak scalability, and other useful metrics [26].
- If necessary, on the basis of the observations collected in the previous steps, a new formulation of the mathematical model is constructed.
3. An Inventory of the “In Silico” Experiments in 3D-Bioprinting of Cell-Laden Hydrogels
3.1. Pre-Printing
3.2. During Printing
3.3. Post-Printing
4. A “State of the Art” of HPC Systems in the Exascale Era
- Application programming support, which, in response to the complexity and scale of advanced computing hardware, makes available programming languages, numerical libraries, and programming models, eventually combined in hybrid and hierarchical approaches, exploit the multi-node, multi-core, and accelerators-based architecture of up-to-date HPC resources.
- New mathematical models and algorithms that can give solutions to the need for increasing amounts of data locality and the need to obtain much higher levels of concurrency and that can guarantee a high level of “scalability” [81] and “granularity” [82]. Then, it is now the time to develop new algorithms that are more energy-aware, more resilient, and characterized by reduced synchronization and communication needs.
5. Mathematical Models
5.1. Models at the Macro-Scale
5.1.1. The Navier–Stokes Equations for Viscoelastic Fluids
- Newtonian viscosity model
- Power-Law model
- Cross model
- Modified Cross model
- Carreau model
- Carreau–Yasuda model
5.1.2. The Two-Phase Flow Problem
- The representation and evolution in time of the interface.
- The way the imposed surface boundary conditions are treated.
- Representation and time evolution of the interface.To represent the two-phase flows with shifting inter-phase boundaries, various methodologies have been developed in response to the problem’s complexity, both numerically and physically. In principle, the methods can be divided into two classes: the so-called front-tracking (FT) methods and front-capturing (FC) methods.In these methods, two-phase flow is treated as a single flow with the density and viscosity smoothly varying across the moving interface which is captured in a Eulerian framework (FC) or in a Lagrangian, framework (FT), with the terms Eulerian and Lagrangian frameworks, meaning, meaning the following [100]:
- Lagrangian framework: In classical field theories, the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time.
- Eulerian framework: The Eulerian specification of the flow field is a way of looking at fluid motion that focuses on specific locations in the space through which the fluid flows as time passes.
The front-tracking method is based on a formulation in which a separate unstructured grid (surface grid) with nodes converging at a local velocity is used to represent the interface. One benefit of the technique is that interfacial conditions can be easily included because the interface is precisely established by the surface grid’s position. Moreover, a good approximation of the curvature allows for the consideration of surface tension force. The method’s drawback is that it requires the use of extra algorithms to compute flows with substantial interface deformations such bubble break-up and coalescence since the surface grid will be severely distorted.In contrast, the front-capturing approach uses a scalar function on a stationary grid to capture the interface as part of its implementation of the interface evolution. The ability to compute phenomena like bubble break-up and coalescence is made possible by the implicit interface capture provided by front-capturing techniques. The two main difficulties in using this approach are keeping a clear boundary between the different fluids and accurately calculating the surface tension forces [98].The Level Set approach was developed as a result of the front-capturing approach [59,60]. A different method, known as the Immersed Boundary (IB) method [58,101,102,103,104], was developed for flows across challenging geometries. It can be thought of as a combination of front-capturing and front-tracking procedures.- Level Set Method The idea on which the level set method is based is quite simple. Given an interface in of codimension one, bounding an open region , the LS method intends to analyze and compute its subsequent motion under a velocity field .This velocity depends on the position, time, the geometry of the interface (e.g., its normal or its mean curvature) and the external physics.The idea is to define a smooth function representing the interface as the set where .The level set function has the following properties:Thus, the interface is to be captured for all times t, by defining the set of points for which the values (levels) obey the following equationCoupling the level set method with problems related to two-phase Navier–Stokes incompressible flow needs the reformulation of Problem 1 as followsProblem 2.Equations of two-phase Navier–Stokes incompressible flow defined in using the level set methodwhere is the velocity field, p is the pressure field, is the gravitational acceleration, and are the piecewise constant fluid densities and stress tensors described by the Heaviside function, σ is the surface tension coefficient, κ is the curvature of the interface, is the unit normal vector outward to , and is a delta function.The function can have different format [105,106,107], which helps to avoid some disadvantages of the LS method related to the discrete solution of transport equations, which may be affected by numerical error leading to loss or gain of mass.In standard level set methods, the level set function is defined to be a signed distance functionwhere .To improve numerical robustness, “smoothed out” Heaviside functions (needed to represent density and viscosity discontinuities over the interface) are often used. For example [106],
- Immersed Boundary MethodThe Immersed Boundary Method (IBM) can be useful to describe fluid–structure interaction when the structure is intended to be an Immersed Body. In the IBM, the fluid is represented in a Eulerian coordinate system, and the configuration of the Immersed Body is described by a Lagrangian approach [101].Consider the simulation of incompressible flow around the body in Figure 4a, which is described by Problem 1 where . denotes the surrounding fluid domain occupied by the solid body domain with the boundary denoted by .In an IB method, the boundary condition would be imposed indirectly through a specification of Problem 1. In general, the specification takes the form of a source term (or forcing function) in the governing equations, which reproduces the effect of boundary [102].The original IBM, created by Peskin [58], is typically appropriate for flows with immersed elastic limits. It was designed for the combined modeling of blood flow and muscle contraction in a beating heart. A collection of massless points moves with the local fluid velocity , and these points serve as a Lagrangian tracker of the location of the Immersed Body, represented by a set of elastic fibers.Thus, the coordinate X of the Lagrangian point is governed by the equationThe effect of the Immersed Body on the surrounding fluid is essentially captured by transmitting the fiber’s stress to the fluid through a localized forcing term in the momentum equations, which is given bywhere is the Dirac delta function. The Dirac delta function in is formally defined by the following:and is also constrained to satisfy the identityThe function can be written aswhere is a given functional called “the elastic potential energy of the material” in configuration X and where the notation is shorthand for the “Fréchet derivative” of E with respect to X. Thanks to the use of the Dirac delta function, Equation (34) can be rewritten asThe forcing term is thought to be distributed over a band of cells surrounding each Lagrangian point (see Figure 4b), as the fiber locations typically do not coincide with the nodal points of the Eulerian grid. This distributed force is then imposed on the momentum equations of the surrounding nodes. As a result, a smoother distribution function, represented by d in this case, effectively replaces the delta function and may be applied to a discrete mesh. The d function allows for the rewriting of Equations (35) and (37) as follows:The choice of the distribution function d is a key ingredient in this method. Several different distribution functions were employed in the past (i.e., see [102] for a list of employed d).
Coupling the IB equations with problems related to the Navier–Stokes incompressible flow requires the reformulation of the Problem 1 as follows:Problem 3.Equations of the Navier–Stokes incompressible flow defined in surrounding an Immersed Body :where ρ is the density of the fluid, is the velocity field, p is the pressure field, is the gravitational acceleration, is the stress response to the deformation of the fluid, X is the Lagrangian coordinate of the generic point of the body, and E is the elastic potential energy of the body material. - Surface boundary conditions treatmentSince the second derivative of a discontinuous function determines the curvature , using front-capturing methods to compute the surface tension force requires particular considerations. Various methods were devised to precisely calculate the surface tension force. The most well-known method is presumably the continuum surface force (CSF) model [61]. The model considers surface tension force as a continuous, 3D effect across an interface, rather than as a boundary value condition on the interface. The continuum method eliminates the need for interface reconstruction. A model of a diffuse interface is examined, in which the surface tension force is converted into a volume force that distributes across several cell layers.We note (see Equation (20)) that surface tension per interfacial area at a point on the interface is given bywhere is the surface tension coefficient, is the curvature of the interface, and is the unit normal vector outward to .Suppose that the interface where the fluid changes from fluid 1 to fluid 2 discontinuously is replaced by a continuous transition. Applying a pressure jump at an interface brought on by surface tension is no longer appropriate. Instead, as can be shown in Figure 5, surface tension should be considered active everywhere in the transition area.As in [61], we choose a volume force at any point x of transition region aswhere is a smooth “color function” that approaches the “characteristic function”, , as the width h of the region approaches to zero,and where the “characteristic function” can be defined aswhere and represent the domains occupied by fluids 1 and 2, respectively. We note that for the curvature of the interface and for the unit normal vector outward to , the following equations are valid:The function can be defined as a convolution of the function with an interpolation function according to Brackbill et al. [61]:where has to satisfy the following conditions
- (a)
- ,
- (b)
- ,
- (c)
- is differentiable and decreases monotonically with increasing .
Volume force will result in the same total force as , but spread over the finite interface width, i.e.,Coupling the continuum surface force (CSF) model with problems related to two-phase Navier–Stokes incompressible flow requires the reformulation of the Problem 1 as follows:Problem 4.Equations of two-phase Navier–Stokes incompressible flow defined in using the CSF model:where is the velocity field, p is the pressure field, is the gravitational acceleration, and and are the piecewise constant fluid densities and stress tensors described by the Heaviside function.
5.1.3. Transport and Response of Biological and Chemical Species
5.2. Models at the Meso Scale
5.2.1. Monte Carlo-Based Methods
...a general method, suitable for fast electronic computing machines, of calculating the properties of any substance which may be considered as composed of interacting individual molecules. [111]
- .
- The -entry of the K-th power of gives the probability of transitioning from state i to state j in K steps.
- Irreducible if, for all states i and j, there exists K such that .
- A-periodic if, for all states i and j, the Greatest Common Divisor of the set is equal to 1.
- If is the stable distribution for an irreducible, a-periodic Markov Chain, then the Markov Chain can be used to sample from .
- Samples from can be used to approximate the properties of . For example, suppose f is any real-valued function on the state space S, and suppose that is a sample from ; then, the ergodic theorem [114] ensures thatwhere is the expected value .
5.2.2. Cellular Particle Dynamics
5.2.3. Cellular Automata Model
CA are simple mathematical idealizations of natural systems. They consist of a lattice of discrete identical sites, each site taking on a finite set of ... values. The values of the sites evolve in discrete time steps according to ... rules that specify the value of each site in terms of the values of neighboring sites. CA may thus be considered as discrete idealizations of the partial differential equations often used to describe natural systems [123].
- A grid of individual cells.
- A group of ingredients.
- A collection of local rules dictating how the constituents behave.
- Identified starting conditions.
- The grid, the cells, and the ingredients: A cellular automaton consists of a regular grid of cells. The grid can be in any finite number of dimensions N. Every grid cell can typically exist in a limited number of “states”, which specify the cell’s occupancy. The cell may be empty or hold a specified ingredient, which, if it is present, may be a type of particle, a specific molecule, or some other relevant thing for the topic under consideration. An illustration of a bi-dimensional CA grid with cells each, whereby some cells are occupied by ingredient A (red cells) and other cells by ingredient B (blue cells), can be found in Figure 7a.Movements and other actions on the grid are controlled by rules that are only dependent on the characteristics of the cells that are closest to the ingredient. The neighborhood of a cell is its immediate surroundings. The “Von Neumann neighborhood” is the most often employed neighborhood in two-dimensional CA investigations (see Figure 7d, where the blue cell neighborhood is pictured by the four red cells).Another common neighborhood is the “Moore neighborhood”, pictured by the red cells surrounding the blue cell in Figure 7c. Another useful neighborhood is the “extended Von Neumann neighborhood”, shown in Figure 7d by the red and green cells surrounding the blue cell.Every grid cell’s value will be impacted by how its neighborhoods are managed, including cells that are on the edge of the CA grid. Keeping the values in those cells constant is one approach that might be taken. Using distinct neighborhood definitions for these cells is an additional strategy. They might have fewer neighbors, but it is also possible to define more elaborate strategies for the cells that are closest to the edges.These cells are typically handled in a toroidal manner; for instance, in a bi-dimensional grid, one cell “goes off the top” and “enters” at the corresponding position on the bottom, and one cell “enters on” the right when it “goes off” the left (this is sometimes referred to as periodic boundary conditions in the field of partial differential equations). To illustrate this, consider taping the rectangle’s left and right sides to create a tube, and then the top and bottom edges to create a torus (see Figure 7b).
- The rules: The behaviors of the ingredients on the grid, and consequently the evolutions of the CA systems, are governed by a variety of rules. According to what is described in [69], a list of potential rule types is provided below.
- Movement rules: Movement rules define the condition that, during an iteration, the ingredients move to neighborhood cells. These rules take several forms [120]:
- The “breaking” probability, , defines the condition that two adjacent ingredients A and B may remain linked to each other.
- The “joining” parameter, , defines the condition that, if two ingredients A and B are separated by an empty cell, ingredient A moves toward or away from ingredient B.
- The “free-moving” probability of an ingredient A defines the ingredient’s propensity to move on the grid more rapidly or slowly.
- Transition rules: Transition rules define the condition that, during an iteration, an ingredient will transform to some other species. These rules take several forms [120]:
- The “simple first-order transition” probability defines the condition that an ingredient of species A will change to species B.
- The “reaction” probability defines the condition that ingredients A and B will transform into ingredients C and D, respectively, in case they “encounter” each other during their movements in the grid.
The critical characteristics of all these rules are their local nature, focusing solely on the ingredient in question and potentially any nearby ingredients.All the probabilities listed above are enforced using a random-number generator in the CA algorithm. For example, suppose we use a random-number generator which generates numbers in the interval . Suppose that one of the above rule probabilities is set to and that the random-number generator generates a number r; the ingredient A can make the “move” prescribed by the rule if and “cannot move” otherwise. - The initial conditions: The remaining conditions of the simulation must be determined after the grid type, size, and governing rules have been established, the latter by giving particular values to the previously mentioned parameters. These consist of (1) the types and quantities of the beginning ingredients; (2) the setup of the system’s initial state; (3) the number of simulation runs that are to be performed; and (4) the duration of the runs or the number of iterations they should contain.About points (3) and (4) above, it needs to be emphasized that when the CA rules are stochastic, i.e., probabilistic, each simulation run is, in effect, an independent “experiment”. This implies that the outcomes of different runs could theoretically be different. A single ingredient’s activity is typically totally unpredictable. But for the majority of cases, we will look at which collective outcome—from a run with a lot of ingredients or from a lot of runs with few ingredients—tends to show a similar pattern. As a result, two further simulation-related details must be determined: the number of independent runs that must be completed and their duration (in iterations). These numbers will be heavily influenced by the type of simulation that will be run. In certain situations, it will be preferable to let the runs continue for a sufficient amount of time in order to reach an equilibrium or steady-state condition [120].
6. Numerical Methods and Algorithms
6.1. Models at the Macro-Scale
6.1.1. Discretization in the Space-Time Domain
- Finite Elements A strong computational method for solving differential and integral equations that come up in many applied scientific and engineering domains is the Finite Element Method (FEM) [125].The fundamental idea behind the FEM is to consider a given domain as a collection of basic geometric shapes called finite elements, for which the approximation functions required to solve a differential equation can be generated systematically. Indeed, the solution u of a differential equation can be approximated, on each element e, by a linear combination of unknown parameters and appropriately selected functions :For a given differential equation, it is possible to develop different finite element models, depending on the choice of a particular type of approximation method (e.g., Galerkin, weak-form Galerkin, least-squares, subdomain, collocation, and so on). The finite element model is a set of algebraic relations among the unknown parameters of the approximation: so, solving the problem to find an approximation of u requires the solution of a system of algebraic equations with the unknown parameters .The major steps in the finite element formulation and analysis of a typical problem are as follows.
- Discretization of the domain into a set of selected finite elements. This is accomplished by subdividing the given domain into a set of subdomains where and , called finite elements (see Figure 8a). The phrase “finite element” often refers to both the geometry of the element and degree (or order) of approximation: The form of the element can be either triangle or quadrilateral, and the degree of interpolation over it can take on various forms, including linear and quadratic. The finite element mesh of the domain is the non-overlapping total (or assembly) of all elements used to represent the actual domain, and it is represented by . In general, may not equal the actual domain because of its potentially complex geometry. Nodal points, also known as nodes, are typically taken at appropriate positions in the structure, usually to simplify the element. They are used to characterize the individual elements and subsequently the complete mesh structure (see Figure 8b).
- Construction of a statement, often a weighted-integral in a weak-form statement according to Weighted Residual Methods (WRMs) [130], which is equivalent (in some sense) to the differential equation to be analyzed over a typical element. A general class of techniques, called the Weighted Residual Method, was created to obtain an approximate solution to the problem of the formwhere is a general linear differential operator. If is just an approximation of the true solution function u of (86), then an error or residual will exist such thatThe idea at the basis of WRM is to force the residual to zero in some average sense over the domain , namely,where values are the so-called weight functions. Depending upon the nature of the weight function, different types of Weighted Residual Methods can be used. The Point Collocation Method, Subdomain Collocation Method, Least Square Method, and Galerkin Method are a few of the common ones. The trial functions themselves are selected as the weight functions in the Galerkin variant of the Weighted Residual Method. So, in the Galerkin method, we set and the weak-form Galerkin model, for each element e is the following set of algebraic relations obtained from (88) and (85):or, in matrix form,whereare, respectively, an matrix and two vectors of length l. We assume that the vectors also include both the “essential” and the “natural” boundary conditions (see [125] for details). The drawback of this model for second- and higher-order differential equations is that the approximation functions should be differentiable as many times as the actual solution .The weak form in Equation (86) requires that the approximation chosen for should be at least linear in x. In addition, it requires that be made continuous across the elements. The approximation functions , in each element e, are chosen to have the so-called interpolation property, that is,where are the nodal points of the element e. The scalar is defined as follows:Then, the values of in Equation (85) coincide with the values that takes on at the same nodal points:Therefore, solving the Equation (90) allows one to identify the values that the approximation takes on in the nodal points of each element e. Functions that satisfy the interpolation property (91) are known as the Lagrange interpolation functions. The shape and number of nodes of the element are determined by the number l of linearly independent terms in the representation of . Not all geometric shapes qualify as finite element domains. It turns out that triangle- and quadrilateral-like shapes, with an appropriate number of nodes, qualify as elements.
- Finite element assembly to produce the global system of algebraic equations of the formwhere , , and are, respectively, am matrix and two vectors of length and where denotes the number of the nodes (the global grid node) of all the elements composing the finite element mesh. Therefore, the assembly procedure represents the realization of the global displacement boundary conditions as well as the inter-element compatibility of the approximation functions and the displacement field. Indeed, each global grid node is shared by different finite elements which all contribute to the solution of the unknown values on the involved nodes. Let us denote withthe set of such global grid nodes; then, a transformation exists that “maps” the “local” index i of the i-th node of the element e into the “global” index I of the same node (see Figure 8c). Thanks to the validity of the “superposition” property in FEM context due to the linear nature of the problem, for the global matrix and the global vector , the following equalities are valid:
If u is a function defined both in space and time and the linear differential operator has the following form:where does not contain terms with differentiation with respect to the time variable t, then Equation (92) can be rewritten as:where is a vector of the values assumed by the approximation in all the nodal points of the finite elements mesh and where the symbol denotes the partial derivative of the function u respect to time t: . The nonlinear Equation (96) represents an approximation to the original system of partial differential equations, which is discrete in space and continuous in time. - Finite Differences [127] The basic idea of FDM is to compute an approximation of the solution u of (86) by mean an approximation of all the differential operators defining . As for FEM, the major steps in the finite element formulation and analysis of a typical problem are:
- Discretization of the space domain into a set of nodes . This is accomplished by subdividing the given domain by mean of a grid of nodes which represent the finite difference mesh (see Figure 9a).
- Construction of approximation statements, based on a finite difference, for all the differential operators present in . Thanks to the use of Taylor expansion, the validity of the following relations can be demonstrated [137]:where , and are, respectively, named the n-th order forward, backward, and central differences with respect to and are given by, respectively.
- Forward difference
- Backward difference
- Central differencewhere .
- By substituting one of the above approximations to each space derivative operator in , we obtain the so-called space approximated operator , which can be written generally as a nonlinear algebraic operator as follows:where and m depend on the type of approximation chosen.
- The set of the following algebraic equationswhich are obtained by evaluating the equation in each node of finite difference mesh can be written, after the inclusion of boundary conditions, in matrix form aswhere , , and are, respectively, a matrix and two vectors whose generic elements arewhere . Therefore, solving Equation (103) allows us to identify the values at which the approximation takes on the nodal points of the finite element mesh. It is obvious that the accuracy of depends on the type of approximation chosen for the derivative operators that are present in .
- Finite Volumes [127,138] A space discretization technique called the finite volume approach works well for numerical modeling of several kinds of conservation laws that are represented by PDEs of the form (86) where the linear differential operator can be expressed asAs for FEM and FDM, the major steps in the finite element formulation and analysis of a typical problem are
- Discretization of the domain into a set of selected subdomains. This is accomplished by subdividing the given domain into a set of subdomains where and , called control volumes or cells (see Figure 9b), forming the finite volume mesh. Planar surfaces in 3D or straight edges in 2D define the boundaries of the control volumes. Consequently, flat faces or straight edges are used to approximate the bounding surface, if it is curved. Cell faces, or just faces, are the names given to these bounding discrete surfaces.
- Construction of approximation statements needed to identify the approximation function for the actual solution u of (104). Following the approach described for the FEM framework and based on Weighted Residual Methods, from (88), where the weight functions are chosen to be constant and equal to identity, it follows thatfor each cell of the finite volume mesh. By using the Divergence Theorem, Equation (105) can be rewritten asThanks to the use of mean value theorem, in each subdomain , Equation (106) can be re-written aswhere are the mean values respectively of functions f in subdomain (which can be considered as values of f in cell center ) and where the symbol is used to represent the volume/area/length of respectively a 3D/2D/1D space domain.One can substitute the integral on the left side of Equation (107) with a summation over the faces enclosing the c-th cell, resulting inwhere is the number of faces of the c-th cell and represents the f-th face of the c-th cell. Details about the forms for the restriction of on each are available in the literature (i.e., see [139,140]), but, for the sake of semplicity, assume, as in [139], that, on each cell, is a constant function whose value is ; then, Equation (108) can be rewritten aswhere is an approximation of F that can be defined using a variety of approaches. For this purpose, Taylor series expansions have historically been employed [141]. The end result of approximating F by in terms of cell center values (that is, the constant values ), followed by substitution into Equation (109) and by the boundary conditions incorporation, is a set of discrete linear algebraic equations of the formwhere , , and are, respectively, an matrix and two vectors. The solution u of (110) allows us to calculate the values of for all the representing the finite volume mesh.
6.1.2. Solution of the “Discrete in Space” Model
- The Time Integration algorithm The proposed space discretization methods allow the construction of similar discrete problems since they all lead to a generally non-linear system of algebraic equations in the following form:which represents an ordinary differential equation (ODE) with respect to the time variable.Depending on the type of the approximation of the time derivative present in the left term of Equation (111) and the discretization of the temporal domain , different methods are available to solve the problem described by Equation (111), which is discrete in space and continuous in time.Assuming that is the time interval and that it is discretized by a set of equally spaced points , where and , then there exist different methods—called “Time Integration Schemes (TIS)”—to compute the approximation of u at the time as a function of just the approximation of u and at the time (explicit methods) or as a function of u and at the times and (implicit methods).See [142] for a classification of such schemes.Among the rich set of available TIS, a one-parameter family of methods, called the -family, is commonly used [143]. In this family of methods, a weighted average of time derivative of a dependent variable u is approximated at two consecutive time steps by a linear interpolation of the values of the same variable u at the same two steps:By substituting Equation (112) into Equation (111), the following relation is obtainedwhereand whereSince at time (i.e., ), the right-hand side is computed using the initial values defined in the time boundary conditions, and since the vector is always known, for both times and , then the approximation of u at time (when ) can be computed by Algorithm 1.For different values of the parameter , several well-known time approximation schemes are obtained:
- , the forward difference Euler explicit scheme. The problem (113) is linear, the schema is conditionally stable, and its order of accuracy (see Definition 2 for a definition of the “order of accuracy” terms) is ;
- , the Crank–Nicolson implicit scheme. The problem (113) is nonlinear, the schema is unconditionally stable, and its order of accuracy is ;
- , the Galerkin implicit scheme. The problem (113) is nonlinear, the schema is unconditionally stable, and its order of accuracy is ;
- , the backward difference Euler implicit scheme. The problem (113) is nonlinear, the schema is unconditionally stable, and its order of accuracy is .
Algorithm 1 The algorithm implementing the -family methods for the approximated solution of the discrete in space and continuous in time problem described by Equation (111). - 1:
- procedure TimeIntegrator(, , , , , , , , T, , )
- 2:
- Input: , , , , , , , T,
- 3:
- Output:
- 4:
- Compute , and
- 5:
- for to do
- 6:
- Compute
- 7:
- Compute
- 8:
- Compute
- 9:
- Solve
- 10:
- Compute
- 11:
- Compute
- 12:
- end for
- 13:
- end procedure
For , the scheme is stable, and for , the scheme is stable only if the time step meets the following restrictions (i.e., conditionally stable schemes) (see Reddy [136]):where the greatest eigenvalue of the eigenvalue problem related to the matrix Equation (113) is denoted by :See [144] for further definitions and descriptions of the “stability” and “accuracy” terms. Generally, Algorithm 1 requires the solution of a nonlinear problem (see line 9) that can be solved by methods described in the next point 2. If the problem degenerates into a linear one (i.e., when ) its solution can be obtained by methods described at next point 3. - The Non-linear problem solver Let us consider the following nonlinear algebraic system:where and are vectors in . Assuming the existence of a solution for the system (122), an approximation of that solution can be obtained by different methods. The “Newton–Raphson methods”, and their derivatives, should be cited as the most commonly used [145]. Such methods iteratively compute an approximation of , and they are based on a Taylor series development of the left term of (122) at an already known statewhere is the Jacobi matrix of at , i.e.,Let ; thenTherefore, an approximation of can be computed using the iterative algorithm represented in Algorithm 2. The rate of convergence of the Newton-Raphson scheme is characterized by the following inequality:
Algorithm 2 The algorithm implementing the “Newton–Raphson methods” for the approximated solution of Equation (122). - 1:
- procedure NewtonSolver(, , N, )
- 2:
- Input: , , N
- 3:
- Output:
- 4:
- for to do
- 5:
- Compute
- 6:
- Compute
- 7:
- Solve
- 8:
- Compute
- 9:
- end for
- 10:
- end procedure
Depending on the approach used to approximate/compute the Jacobi-matrix (or tangent matrix) of , different derivations of the scheme can be obtained: Table 8 lists some of them. Also, when the application of the BFGS-update is considered, Algorithm 2 can be used. Only the equation system at the line 7 of Algorithm 2 has to be reformulated by introducing the BFGS-update of the inverse of the secant matrix. See Algorithm 3 for details on the BFGS reformulation of Algorithm 2.Algorithms 2 and 3 require the solution of a linear problem (see, respectively, lines 6 and 7) that can be solved by methods described in the next point 3.Details about convergence and other numerical issues are available in the literature (see [145]).Algorithm 3 The algorithm implementing the “BFGS” reformulation of the Newton–Raphson method. - 1:
- procedure BFGSNewtonSolver(, , N, )
- 2:
- Input: , , N
- 3:
- Output:
- 4:
- Compute
- 5:
- Compute
- 6:
- Solve
- 7:
- Compute
- 8:
- for to do
- 9:
- Compute
- 10:
- Compute
- 11:
- Compute
- 12:
- Compute
- 13:
- Compute
- 14:
- Compute
- 15:
- end for
- 16:
- Compute
- 17:
- end procedure
- The linear problem solver: Let us consider the linear problem of the formwhere , and are, respectively, a matrix and two vectors in and . Since the matrices coming from the discretization of problems of interest for this review are sparse if not even structured—for example, see matrices generated for the solution of Navier–Stokes equations for viscoelastic fluids in Section 6.1.3, which have a lot of zero elements (or have zero blocks)—particular attention will be spent in this work to describe methods to be used for the solution of (125) when is sparse (or structured) (see [146] for a more precise definition of the sparsity concept).There are three fundamental classes of methods that are used to solve Equation (125):
- Direct methods The direct solution of (125) is generally based on a technique called “ decomposition” [147]. This technique consists of factoring the matrix as in Equation (126) (by algorithms whose computational complexity is generally on the order of ), and it is based on the concept that triangular systems of equations are “easy” to solve:where and are, respectively, lower triangular and upper triangular matrices and where and are permutation matrices. A permutation matrix is used to represent row or column interchanges in matrix , and it is obtained from the identity matrix by applying on it the same sequence of row or column interchanges. The row or column permutations on are often required for both numerical and sparsity issues [146].The decomposition facilitates the solution of (125) effectively, particularly when solving several systems that share the same matrix . In fact, if a matrix already has a decomposition available, the linear system in (125) can be solved by (1) the solution of (forward substitution), followed by (2) the solution of (backward substitution) where . Then, the values of all the unknowns can be obtained by permuting the rows of based on the permutation matrix . The execution of both a forward and a backward substitution has a general computational complexity of ).If the matrix is symmetric and positive definite (that is, if i for all nonzero vectors x), then the decomposition of becomes and is called “Cholesky” factorization.Numerical issues related to the stability and accuracy of the presented direct solver can be found in [146].With the aim to present and discuss methods useful in computing the decomposition of sparse matrices, we propose the “Frontal methods”. Such methods have their origin in the solution of finite-element problems, but they are not restricted to this application. They are of great interest in their own right since the extension of these ideas to multiple fronts, regardless of the origin of the problem, will offer a great opportunity for parallelism [146,148,149].In the context of “Frontal methods” the matrix can be considered as the sum of submatrices of varying sizes, as happens for the matrices that are the result of the assembly process underlying the discretization using finite elements. That is, each entry is computed as the sum of one or more values:Entry in (127) is said to be fully summed (or fully assembled) if all the operations (127) have been performed, and the index of the unknown k is said to be fully summed if all the entries in its row (i.e., ) and its column (i.e., ) are fully summed.The fundamental notion of frontal techniques is to limit decomposition operations to a frontal matrix , on which Level 3 BLAS [150] is used to execute dense matrix operations. (The BLAS (Basic Linear Algebra Subprograms) are routines that provide optimized standard building blocks for performing primary vector and matrix operations. BLAS routines can be classified depending on the type of operands: Level 1: operations involving just vector operands; Level 2: operations between vectors and matrices; and Level 3: operations involving just matrix operands.) In the frontal scheme, the factorization proceeds as a sequence of partial factorization on frontal matrices , which can be represented, up to some row or column permutations, by a blocks structure:where is related to the unknown indices that are fully summed.The decomposition by Frontal methods can be described by Algorithm 4.A variation of frontal solvers is the Multifrontal method. It could be considered an improvement of the frontal solver, which, based on an appropriate order or coupling of the addends in the summation in (127), can lead to the use of several independent fronts paving the way, naturally, to the development of parallel algorithms. Efficient parallel and sequential decomposition algorithms based on Frontal and Multifrotal methods should be able to perform an analysis of the structure of matrix to define all the needed reorganizations of its row and columns (i.e., by the definition of appropriate permutations) to better exploit sparsity, preserve “good” numerical properties, and define the order of front assembly. See [146] for details about techniques to be used in such analyses.
Algorithm 4 The algorithm implementing the “Frontal method”. - 1:
- procedure FrontalDecomposition(, L)
- 2:
- Input: , L
- 3:
- Output: ,
- 4:
- 5:
- for to L do
- 6:
- Compute
- 7:
- Factorize
- 8:
- Solve
- 9:
- Solve
- 10:
- Compute
- 11:
- end for
- 12:
- 13:
- 14:
- end procedure
- Iterative methods: Direct methods could exploit the sparse linear system structure as much as possible to avoid computations with zero elements and zero-element storage. However, these methods are often too expensive for large systems, except where the matrix has a special structure. For many problems, the direct solution methods will not lead to solutions in a reasonable amount of time. So, researchers have long tried to iteratively approximate the solution starting from a “good ” initial guess for the solution [151].The Krylov subspace iteration methods (KSMs) are among the most important iterative techniques for solving linear systems because they have significantly altered how users approach huge, sparse, non-symmetric matrix problems. The techniques in question were recognized as one of the top ten algorithms that had the biggest impact on the advancement and application of science and engineering during the 1900s [110], and they seem to have also confirmed their importance in the current century due to the effort spent to improve their effectiveness and efficiency in up-to-date computing architecture.Like the majority of feasible iterative methods now in use for resolving large linear equation systems, KSM makes use of a projection process. A projection process is the standard method for taking an approximation from a subspace to the solution of a linear system [152].Let and be two N-dimensional subspaces of . Finding an approximate solution to (125) requires a projection technique onto the subspace and orthogonal to . This is carried out by imposing the conditions that belongs to and that the new residual vector is orthogonal to , where is the initial guess to the solution; that is,Note that if is written in the form , and the initial residual vector is defined as , then the above condition becames,In other words, the approximate solution can be defined aswhere the symbol denotes the Euclidean inner product. In the most general form, this is a basic projection step. A series of these projections is used in the majority of common techniques. A new pair of subspaces, and , are used in a new projection step to compute . An initial guess, , is equal to the most recent solution estimate obtained from the previous projection step. Many well-known techniques in scientific computing, such as the more complex KSM procedure or the simpler Gauss–Seidel step, have a unifying framework that is provided by projection methods.A Krylov subspace method is a method for which the subspace is the Krylov subspace [152]Variations in the choices of subspace give rise to different Krylov subspace methods. The most popular methods arise from two general options for .The first is simply and the minimum residual variation . The most representative among the KSMs is related to the choice , and it will be described in this work: the “Generalized Minimum Residual Method (GMRES)”. The second class of methods is based on defining to be a Krylov subspace method associated with , namely, (see [152] for details).The GMRES method can be used to solve sparse linear systems whose matrix is general (i.e., not necessarily symmetric or positive definite). Let matrices whose columns are an orthonormal basis for space , then can be expressed as as where . Furthermore, let and definewhere is the spectral norm, that is, the matrix norm induced by the Euclidean vector’s inner product.Then, condition (129) (or equivalently the condition (131)) is satisfied by if, and only if, is the solution to the following minimum problem (see Proposition in Saad [152]):A schema for the GMRES iterative algorithm, useful to compute the approximation of the solution for problem (125), is represented in Algorithm 5.
Algorithm 5 The GMRES iterative algorithm. - 1:
- procedure GMRES(, , , N, )
- 2:
- Input: , , N
- 3:
- Output:
- 4:
- Compute
- 5:
- Assign
- 6:
- for to N do
- 7:
- Compute an orthonormal basis for
- 8:
- Compute
- 9:
- Compute
- 10:
- end for
- 11:
- end procedure
Different methods can be used to perform steps at line 7 of Algorithm 5. The most common ones are related with the Gram–Schmidt or Householder procedures, which both compute, at the step n, both the matrix and the upper Hessenberg matrix (see [153] for the definition of upper Hessenberg matrix) , for which the following relation is valid [152]:Thanks to Equation (135) (see Proposition in Saad [152]), the function can be rewritten aswhere is the constant vector defined as . The solution to the minimum problem at line 8 of Algorithm 5 is easy and inexpensive to compute since it requires the solution of an least-squares problem where n is typically small and where the coefficient matrix is an upper triangular matrix.Although KS methods are well founded theoretically, they are all likely to experience slow convergence when dealing with problems arising from applications where the numerical features of the coefficient matrix are not “good”. The matrix’s “condition number” is the primary parameter that describes its numerical “goodness”. The condition number of a square matrix is defined asIn numerical analysis, the condition number of a matrix is a way of describing how well or badly a linear system with as a coefficient matrix could be numerically solved in an effective way: if is small, the problem is well-conditioned; otherwise, the problem is rather ill-conditioned and it can hardly be solved numerically in an effective way [147].In these situations, preconditioning is essential to the effectiveness of Krylov subspace algorithms. Preconditioners, in general, are modifications to initial linear systems that make them “easier” to solve.Identifying a preconditioning matrix is the first stage in the preconditioning process. The matrix can be defined in a variety of ways, but it must meet a few minimal requirements. The most crucial one is that linear system must be cheap to solve because the preconditioned algorithms will need to solve linear systems with coefficient matrix at each stage. Furthermore, should be nonsingular and “close” to matrix in some sense (i.e., ) [152].For example, if the preconditioner is applied from the left, the modification leads to the preconditioned linear systemwhose coefficients matrix should have better numerical features than because it is “near” the identity matrix . An incomplete factorization of the original matrix is one of the easiest ways to define a preconditioner. This involves taking into account the formula , in which represents the residual or factorization error and and represent the lower and upper portions of , respectively, with the same nonzero structure. Calculating this incomplete factorization, often known as , is not too difficult or expensive.More sophisticated preconditioners are available, such as the preconditioners based on Domain Decomposition Methods and those based on Multigrid Methods (i.e., see [152] for the basic panoramic of such tools).It is worth mentioning that if the matrix is symmetric and positive definite, then specialized algorithms exist in the context of KSM: the Conjugate Gradient (CG) method is the most famous among those [152]. - Hierarchical/Multilevel methods: When solving linear systems resulting from discretized partial differential equations (PDEs), preconditioned Krylov subspace algorithms tend to converge more slowly as the systems get bigger. There is a significant loss of efficiency because of this decline in the convergence rate. The convergence rates that the Multigrid method class can achieve, on the other hand, are theoretically independent of the mesh size. Discretized elliptic PDEs are the primary focus of Multigrid methods, which distinguish them significantly from the preconditioned Krylov subspace approach. Later, the technique was expanded in many ways to address nonlinear PDE problems as well as problems not described by PDEs [152]. The most important contribution in this sense is related to the Algebraic Multigrid (AMG) [154]. The main ingredients of multilevel methods to solve (125) are as follows.
- (a)
- A hierarchyof H problems along with restriction and prolongation operators to move between levels, whereand wherewithfor each ;
- (b)
- A relaxation operator, , for “smoothing”. is in general a tool to compute iteratively an approximation for the solution of the linear system from the initial guess .
Algorithm 6 describes the recursive implementation schema of AMG methods based on the ingredients listed above, where is the initial guess for solution .Algorithm 6 Implementation schema of AMG methods. - 1:
- function AMG (H, , , , , , )
- 2:
- Input:H, , , , , ,
- 3:
- Output:
- 4:
- Pre-smooth times
- 5:
- Get residual
- 6:
- Restrict residual
- 7:
- Restrict matrix
- 8:
- if then
- 9:
- Solve Coarse System
- 10:
- else
- 11:
- 12:
- for to do
- 13:
- Recursive Solve
- 14:
- end for
- 15:
- end if
- 16:
- Correct by prolongation
- 17:
- Post-smooth times
- 18:
- return
- 19:
- end function
The Multigrid schema is defined by the parameter , which controls the number of times AMG is iterated in line 13 of Algorithm 6. The V-cycle Multigrid is obtained for the situation . The W-cycle Multigrid is the case where . The illustrations in Figure 10 show how complicated the ensuing inter-grid up and down moves can be. Seldom is the case used [152].
Details about restriction, prolongation, and relaxation operators can be found in Stuben [154]. - The Saddle Point Problem solvers Let us consider the block linear systems of the formwhere , and . If one or more of the following requirements are met by the constituent blocks A, , , and C, then the linear system (143) defines a (generalized) “Saddle Point problem” [155]:
- C1 A is symmetric ();
- C2 the symmetric part of A, , is positive semidefinite;
- C3 ;
- C4 C is symmetric and positive semidefinite;
- C5 .
In addition to the standard differentiation between direct and iterative techniques, generalized Saddle Point problem-solving algorithms can be broadly classified into two groups: segregated and coupled methods [155].- Segregated methods and , the two unknown vectors, are computed independently via segregated procedures. This method entails solving two linear systems (referred to as reduced systems), one for each of , that are less in size than . Each reduced system in segregated techniques can be addressed using an iterative or direct approach. The Schur complement reduction method, which is based on a block LU factorization of the block matrix in Equation (143) (also known as the global matrix ), is one of the primary examples of the segregated approach. Indeed, if A is nonsingular, the Saddle Point matrix admits the following block triangular factorization:where is the Schur complement of A in . It follows that if is nonsingular, S is also nonsingular. Using Equation (144), the linear system (143) can be transformed intoor equivalently,
Algorithm 7 The algorithm of the segregated approach to the solution of a generalized Saddle Point system. - 1:
- procedure SaddlePointSegregatedMethod(A, , , C, , , , )
- 2:
- Input:A, , , C, ,
- 3:
- Output: ,
- 4:
- Solve
- 5:
- Compute
- 6:
- Solve
- 7:
- Compute
- 8:
- Solve
- 9:
- end procedure
Then, the solution of the linear system (143) by the segregated method can be performed using Algorithm 7. Solution of linear systems at the lines 4, 6 and 8 of Algorithm 7 can be solved either directly or iteratively. This approach is attractive if the order m of the reduced system at line 6 of Algorithm 7 is small and if linear systems with coefficient matrix A can be solved efficiently. Since the solution of two linear systems with coefficient matrix A is required, it should be convenient to perform just one LU factorization of A to be used twice. The two main drawbacks are that A must be nonsingular and that the Schur complement S can be full, making it prohibitively expensive to factor or compute. When creating S, numerical instability could potentially be an issue, particularly if A is not well conditioned [155]. If S is too costly to form or factor, a Schur complement reduction can still be used by solving related linear systems using iterative techniques like KSM, which only require S in the form of matrix-vector products that involve the matrices , , and C, as well as by solving a linear system with matrix A. These techniques do not require access to individual entries of S. It is possible that the Schur complement system is not well conditioned, in which case preconditioning will be necessary. - Coupled methods Coupled methods deal with the system (143) as a whole, computing and (or approximations to them) simultaneously. Among these approaches are direct solvers based on triangular factorizations of the global matrix , as well as iterative algorithms such as KSM applied to the system as a whole (143), usually preconditioned in some way.For direct methods based on triangular factorizations of , we give a brief overview limited to the symmetric case (that is, where , and ), since no specialized direct solver exists for a nonsymmetric Saddle Point problem. Furthermore, we assume that A is positive definite and B has full rank, then the Saddle Point matrix admits the following factorization,where is a diagonal matrix and is a unit lower triangular matrix. To be more precise, A is positive definite, so its decomposition is , where is the unit lower triangular and is the diagonal (also positive definite); additionally, the Schur complement is negative definite, so its decomposition is . Thus, we are able to writewhere . Note that . However, in practice, with the original ordering, the factors will be fairly dense, and sparsity preservation requires the employment of symmetric permutations . Not every sparsity-preserving permutation is suitable, though. It is demonstrated that there are permutation matrices such that the factorization of , where is a diagonal matrix, is not available for . Moreover, some permutations might result in issues with numerical instability [155].Iterative methods are preferred for solving the linear system (143) using coupled methods, as sparse factorization methods are not completely foolproof, especially for Saddle Point systems arising from PDE problems.About the usage of iterative algorithms, we wrote some words about the use of preconditioned KSM for iterative solution of the entire linear system (143). Various preconditioning strategies designed for (generalized) Saddle Point systems are explained. To develop high-quality preconditioners for Saddle Point problems, one must take advantage of the problem’s block structure and possess a comprehensive understanding of the origin and structure of each block [155].We consider block diagonal and block triangular preconditioners for KSM applied to the coupled system as in (143). The basic block diagonal preconditioner is given bywhere both and are approximations of A and S, respectively. Several different approximations have been considered in the literature. A fairly general framework considers a splitting of A intowhere D is invertible and easy to invert. Then and are chosen.The basic block (upper) triangular preconditioner has the formand, on the other hand, the form of a (lower) triangular preconditioner iswhere, as before, both and are approximations of A and S, respectively.For the coupled solution of a linear system (143) using KSM, the availability of reasonable approximations for the block A and the Schur complement S is necessary for the development of excellent block diagonal and block triangular preconditioners. Such approximations are difficult to build and heavily rely on the specific problem at hand.
For other details about the treatment of Saddle Point problems, we suggest reading the monograph by Benzi et al. [155].
6.1.3. The Discrete Model of the Navier–Stokes Equations for Viscoelastic Fluids
- , , and are vectors of basis functions (the symbol denotes the transposition operation);
- M, N, and K indicate the number of nodal points , and at which the various unknowns are defined in each element e;
- , and are vectors of unknowns into the nodal points in each element e, i.e.,
- Continuity equation
- Momentum equation
- Constitutive equation
6.2. Models at the Meso Scale
6.2.1. The Markov Chain Monte Carlo Algorithms
| Algorithm 8 The MCMC Metropolis–Hastings algorithm. |
|
6.2.2. The Cellular Particle Dynamics Algorithms
6.2.3. The Cellular Automata Model Algorithms
- A N-dimensional grid of cells where, for each of them, the set of neighborhood is defined;
- A set of ingredients, i.e., ;
- A set of rules, i.e., .
| Algorithm 9 The asynchronous cellular automata algorithm. |
|
7. Algorithms for HPC Systems in the Exascale Era
7.1. Models for Exascale Computing
Description of multiphysics modeling, associated implementation issues such as coupling or decoupling approaches, and example applications are available in Keyes et al. [162].“Because we strongly advocate examining coupling strength before pursuing a decoupled or split strategy for solving a multiphysics problem, we propose “coupled until proven decoupled” as a perspective worthy of 21st-century simulation purposes and resources.” [162]
7.2. Parallel Solvers for Exascale Computing
- Extreme-scale computers might consist of millions of nodes with thousands of light cores or hundreds of thousands of nodes with more aggressive cores, according to technological advancements. In any case, solvers will need to enable billion-way concurrence with small thread states [157].
- Extreme-scale systems will probably encounter a high number of hardware malfunctions since they will be constructed on a vast number of components, highlighting a resilient and non-deterministic behavior. Applications should therefore anticipate a high frequency of soft mistakes (such as data value changes due to logic latch faults) and hard interruptions (device failure). Current fault-tolerance methods (those based on traditional, full checkpoint/restart) may cause significant overhead and be impractical for these systems. Solvers must therefore be equipped with methods for locating and resolving software errors and interruptions to reduce any detrimental consequences on an application [157].
- Compared to memory technologies, the cost of devices designed for floating-point operations is decreasing more quickly. Recent system trends indicate that the memory per node is already modestly increasing while memory per core is dropping. Therefore, to take advantage of parallelism, solvers will need to reduce synchronization, increase computation on local data, and shift their focus from the typical scenario of weak scaling, which involves using more resources to solve problems of larger sizes, to one that favors strong scaling, which involves using more resources to solve a problem of fixed size in order to reduce the time to solution (see [163] for a definition of weak vs. strong scaling) [157].
- Power consumption will be a major issue for future HPC systems. Although low-energy accelerators and other hardware design elements can lower the needed power, more steps must be taken to further minimize energy consumption. An approach that could be used is algorithmic study [157].
- Communication- and synchronization-avoiding algorithms The expected costs of computation at the Exascale (also in terms of energy consumption) will be more conditioned by movements from/to the memory or between different memories (i.e., “a communication”) than by the execution of floating point operations. So, when solving huge problems on parallel architectures with extreme levels of concurrency, the most significant concern becomes the cost related to communication and synchronization overheads. This is especially the case for preconditioned Krylov methods (see Section 6.1.2). New versions of such algorithms “minimizing communication” should be investigated to address the critical issue of such communication costs (see Section 7.2.3). Likewise, such popular algorithms execute tasks requiring synchronization points, for example, the computation of BLAS operators and the preconditioner applications. Then, additive algorithmic variants (with no synchronization among components) may be more attractive compared to their multiplicative counterparts [164]. Such considerations are taken into account also by “Time integrators” in the Exascale context (see Section 7.2.1). Furthermore, the linear solution process, which is at the base of the solution of almost all described problems in the previous sections, requires constantly moving the sparse matrix entries from the main memory into the CPU, without register or cache reuse. Therefore, methods that demand less memory bandwidth need to be researched. There are promising linear techniques, such as coefficient-matrix-free representations [165], that totally avoid sparse matrices, or Fast Multipole Methods (see Section 7.2.4) [157].
- Mixed-Precision Arithmetic Algorithms Using a combination of single- and double-precision arithmetic in a calculation is known as mixed-precision arithmetic. Single-precision arithmetic is typically faster than double-precision arithmetic, but some computations may be so susceptible to roundoff errors that the entire computation is typically not possible to complete with just a single precision, so mixed-precision arithmetic can be used. In order to quantify the situations in which using mixed-precision arithmetic is advantageous for a given class of algorithms, further research is required, with a particular focus on the numerical behavior of this technique. In addition to speeding up problem-solving, mixed-precision arithmetic might also need less memory. When working with mixed-precision arithmetic, it is crucial to understand how round-off errors spread and affect computed value accuracy [157]. Section 7.2.3 provides examples of mixed-precision techniques for solving linear problems.
- Fault-tolerant and resilient algorithms Allowing for nondeterminism in both data and operations is a beneficial—and perhaps essential—feature that makes fault-tolerant and robust algorithms possible. Algorithms based on pseudorandom number generators offer a multitude of possibilities at the extreme scale. Monte Carlo-like methods, or more in general, stochastic-based algorithms such as Cellular Automata, can identify resilient implementations by using stochastic replications, which can improve concurrency by several orders of magnitude by employing stochastic replications to find robust implementations [157] (see Section 7.2.5). Regarding fault-tolerant algorithms, a possible solution to the problem of global synchronous checkpoint/restart on extreme-scale systems is the use of localized checkpoints and asynchronous recovery. Recent work is focused on algorithm-based fault tolerance (ABFT): for example, much of the ABFT work on linear solvers is based on the use of checksum [157,166].
7.2.1. “Implicit-Explicit” and “Parallel in Time” Solvers
- The initial approximation vectors (see lines 5–7 of Algorithm 10) can be computed concurrently and independently of each other in an “embarrassingly parallel” approach (no communications are needed among tasks);
- The initial vectors (see lines 8–10 of Algorithm 10) can be computed by all the P tasks concurrently and independently of each other;
- In each iteration of the iterative method that is needed to refine the approximation of the vectors (see lines 11–17 of Algorithm 10), the computation of vectors can be performed concurrently and locally to the assigned task p. To complete the computation of , task p should eventually send the vector to its right neighbor task and should receive the vector from its left neighbor task .
| Algorithm 10 The algorithm of the Parallel-In-Time iterative solution of ODE. |
|
7.2.2. Composite Nonlinear Solver
| Algorithm 11 The algorithm implementing the “Newton–Krylov methods” for the approximate solution of Equation (194). |
|
7.2.3. Parallel Iterative and Direct Linear Solver
- Mixed-precision dense and sparse LU factorization based on Iterative Refinement (IR);
- Mixed-Precision GMRES based on IR;
- Compressed-Basis (CB) GMRES.
- Orthonormalize against the orthonormal basis and compute ,
- Orthonormalize columns of by a QR factorization [147].
| Algorithm 12 The m-th step of block-based GMRES Method. |
|
7.2.4. Fast Multipole Methods and “Hierarchical” Matrices
- Each node of is a subset of the index set I;
- I is the root of (i.e., the node at the 0-th level of );
- If is a leaf (i.e, a node at the L-th level of ), then ;
- If is not a leaf whose set of sons is represented by , then and
| Algorithm 13 Procedure for building the block quad-tree corresponding to a cluster tree and an admissibility condition . The index set and the value l to be used in the first call to the recursive BlockClusterQuadTree procedure are such that . |
|
| Algorithm 14 Matrix-vector multiplication of the -matrix (defined on block cluster quad-tree ) with vector . The index sets to be used in the first call to the recursive HMatrix-MVM procedure are such that . |
|
7.2.5. Parallel Monte Carlo Based Methods
- Communication- and synchronization-avoiding: To implement parallelism in an MC-like algorithm, the named dynamic bag-of-work model can be used [191]. Using such a strategy, a large task, related to the computation of M states, is split into smaller independent P subtasks, where each task computes states and where all the P subtasks are executed independently of each other in an “embarrassingly parallel” approach.
- Fault-Tolerant and Resilient: To make an MC-like algorithm resilient to hard failures, an P-out-of-Q strategy can be used [191]. Since MC-based applications “accuracy” depend only on the number M of computed states and not on which random sample set is estimated (provided that all the random samples are independent in a statistical sense), the actual size of the computation is obtained by increasing the number of subtasks from P to Q, where . The whole task is considered to be completed when P partial results, from each subtask of size states, are ready. In the P-out-of-Q approach, more subtasks are needed than are actually scheduled. Therefore, none of these subtasks will become a “key” subtask and at most faulted subtasks can be tolerated. The critical aspect is properly choosing the value Q since a “good” value for Q may prevent a few subtasks from delaying or halting the whole computation. On the other hand, an excessive value for Q could result in a much higher calculation workload with little gain to the computation outcomes. The proper choice of Q in the P-out-of-Q strategy can be determined by considering the average job-completion rate in the computing system. Suppose c is the completion probability of subtasks up to time t in the computing system. Clearly, should be approximately P, i.e., the fraction of the Q subtasks finished should equal to P. Thus, a good choice is [191].To make an MC-like algorithm resilient to a soft fault causing an error in the computation, for example, due to a change in data value in memory, strategies such as the “duplicate checking” or the “majority vote” [191] could be considered. Subtasks are repeated and executed on separate nodes in these algorithms. Comparing the outcomes of the same subtask carried out on other nodes might help identify inaccurate computational results (e.g., by ensuring that the results fall within a suitable confidence interval). When performing duplicate checking, an incorrect result must be found by doubling computations. It takes at least three times as much calculation to find an incorrect computation result in a majority vote.
8. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- D’Amora, U.; Ronca, A.; Scialla, S.; Soriente, A.; Manini, P.; Phua, J.W.; Ottenheim, C.; Pezzella, A.; Calabrese, G.; Raucci, M.G.; et al. Bioactive Composite Methacrylated Gellan Gum for 3D-Printed Bone Tissue-Engineered Scaffolds. Nanomaterials 2023, 13, 772. [Google Scholar] [CrossRef] [PubMed]
- D’Amora, U.; Soriente, A.; Ronca, A.; Scialla, S.; Perrella, M.; Manini, P.; Phua, J.W.; Ottenheim, C.; Di Girolamo, R.; Pezzella, A.; et al. Eumelanin from the Black Soldier Fly as Sustainable Biomaterial: Characterisation and Functional Benefits in Tissue-Engineered Composite Scaffolds. Biomedicines 2022, 10, 2945. [Google Scholar] [CrossRef] [PubMed]
- Ferroni, L.; Gardin, C.; D’Amora, U.; Calzà, L.; Ronca, A.; Tremoli, E.; Ambrosio, L.; Zavan, B. Exosomes of mesenchymal stem cells delivered from methacrylated hyaluronic acid patch improve the regenerative properties of endothelial and dermal cells. Biomater. Adv. 2022, 139, 213000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; D’Amora, U.; Ronca, A.; Li, Y.; Mo, X.; Zhou, F.; Yuan, M.; Ambrosio, L.; Wu, J.; Raucci, M.G. In vitro and in vivo biocompatibility and inflammation response of methacrylated and maleated hyaluronic acid for wound healing. RSC Adv. 2020, 10, 32183–32192. [Google Scholar] [CrossRef] [PubMed]
- Arjoca, S.; Robu, A.; Neagu, M.; Neagu, A. Mathematical and computational models in spheroid-based biofabrication. Acta Biomater. 2023, 165, 125–139. [Google Scholar] [CrossRef] [PubMed]
- Szychlinska, M.A.; Bucchieri, F.; Fucarino, A.; Ronca, A.; D’Amora, U. Three-dimensional bioprinting for cartilage tissue engineering: Insights into naturally-derived bioinks from land and marine sources. J. Funct. Biomater. 2022, 13, 118. [Google Scholar] [CrossRef]
- Lepowsky, E.; Muradoglu, M.; Tasoglu, S. Towards preserving post-printing cell viability and improving the resolution: Past, present, and future of 3D bioprinting theory. Bioprinting 2018, 11, e00034. [Google Scholar] [CrossRef]
- Bradley, W.; Kim, J.; Kilwein, Z.; Blakely, L.; Eydenberg, M.; Jalvin, J.; Laird, C.; Boukouvala, F. Perspectives on the integration between first-principles and data-driven modeling. Comput. Chem. Eng. 2022, 166, 107898. [Google Scholar] [CrossRef]
- Kovalchuk, S.V.; de Mulatier, C.; Krzhizhanovskaya, V.V.; Mikyška, J.; Paszyński, M.; Dongarra, J.; Sloot, P.M. Computation at the Cutting Edge of Science. J. Comput. Sci. 2024, 102379. [Google Scholar] [CrossRef]
- Naghieh, S.; Chen, X. Printability—A key issue in extrusion-based bioprinting. J. Pharm. Anal. 2021, 11, 564–579. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Blanco, J.C.; Mancha-Sànchez, E.; Marcos, A.C.; Matamoros, M.; Dìaz-Parralejo, A.; Pagador, J.B. Bioink Temperature Influence on Shear Stress, Pressure and Velocity Using Computational Simulation. Processes 2020, 8, 865. [Google Scholar] [CrossRef]
- Karvinen, J.; Kellomaki, M. Design aspects and characterization of hydrogel-based bioinks for extrusion-based bioprinting. Bioprinting 2023, 32, e00274. [Google Scholar] [CrossRef]
- Carlier, A.; Skvortsov, G.A.; Hafezi, F.; Ferraris, E.; Patterson, J.; Koç, B.; Oosterwyck, H.V. Computational model-informed design and bioprinting of cell-patterned constructs for bone tissue engineering. Biofabrication 2016, 8, 025009. [Google Scholar] [CrossRef]
- Hull, S.M.; Brunel, L.G.; Heilshorn, S.C. 3D Bioprinting of Cell-Laden Hydrogels for Improved Biological Functionality. Adv. Mater. 2021, 34, 2103691. [Google Scholar] [CrossRef] [PubMed]
- Schwab, A.; Levato, R.; D’Este, M.; Piluso, S.; Eglin, D.; Malda, J. Printability and Shape Fidelity of Bioinks in 3D Bioprinting. Chem. Rev. 2020, 120, 11028–11055. [Google Scholar] [CrossRef] [PubMed]
- D’Amora, U.; D’Este, M.; Eglin, D.; Safari, F.; Sprecher, C.M.; Gloria, A.; De Santis, R.; Alini, M.; Ambrosio, L. Collagen density gradient on three-dimensional printed poly(ϵ-caprolactone) scaffolds for interface tissue engineering. J. Tissue Eng. Regen. Med. 2018, 12, 321–329. [Google Scholar] [CrossRef] [PubMed]
- Hölzl, K.; Lin, S.; Tytgat, L.; Vlierberghe, S.V.; Gu, L.; Ovsianikov, A. Bioink properties before, during and after 3D bioprinting. Biofabrication 2016, 8, 032002. [Google Scholar] [CrossRef] [PubMed]
- USA National Institute of Standards and Technology (NIST). Computational Science. Available online: https://www.nist.gov/computational-science (accessed on 31 March 2024).
- Carracciuolo, L.; Lapegna, M. Implementation of a non-linear solver on heterogeneous architectures. Concurr. Comput. Pract. Exp. 2018, 30, e4903. [Google Scholar] [CrossRef]
- Mele, V.; Constantinescu, E.M.; Carracciuolo, L.; D’Amore, L. A PETSc parallel-in-time solver based on MGRIT algorithm. Concurr. Comput. Pract. Exp. 2018, 30, e4928. [Google Scholar] [CrossRef]
- Carracciuolo, L.; Mele, V.; Szustak, L. About the granularity portability of block-based Krylov methods in heterogeneous computing environments. Concurr. Comput. Pract. Exp. 2021, 33, e6008. [Google Scholar] [CrossRef]
- Carracciuolo, L.; Casaburi, D.; D’Amore, L.; D’Avino, G.; Maffettone, P.; Murli, A. Computational simulations of 3D large-scale time-dependent viscoelastic flows in high performance computing environment. J. -Non-Newton. Fluid Mech. 2011, 166, 1382–1395. [Google Scholar] [CrossRef]
- Carracciuolo, L.; D’Amore, L.; Murli, A. Towards a parallel component for imaging in PETSc programming environment: A case study in 3D echocardiography. Parallel Comput. 2006, 32, 67–83. [Google Scholar] [CrossRef]
- Murli, A.; D’Amore, L.; Carracciuolo, L.; Ceccarelli, M.; Antonelli, L. High performance edge-preserving regularization in 3D SPECT imaging. Parallel Comput. 2008, 34, 115–132. [Google Scholar] [CrossRef]
- D’Amore, L.; Constantinescu, E.; Carracciuolo, L. A Scalable Space-Time Domain Decomposition Approach for Solving Large Scale Nonlinear Regularized Inverse Ill Posed Problems in 4D Variational Data Assimilation. J. Sci. Comput. 2022, 91, 59. [Google Scholar] [CrossRef]
- Foster, I. Designing and Building Parallel Programs: Concepts and Tools for Parallel Software Engineering; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1995. [Google Scholar]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Benson, S.; Brown, J.; Brune, P.; Buschelman, K.; Constantinescu, E.M.; Dalcin, L.; Dener, A.; et al. PETSc Web Page. Available online: https://petsc.org/ (accessed on 31 March 2024).
- The Trilinos Project Web Page. Available online: https://trilinos.org (accessed on 31 March 2024).
- The German Priority Programme “Software for Exascale Computing” (SPPEXA) Web Page. Available online: http://www.sppexa.de/ (accessed on 31 March 2024).
- Nasrollahzadeh, N.; Applegate, L.A.; Pioletti, D.P. Development of an Effective Cell Seeding Technique: Simulation, Implementation, and Analysis of Contributing Factors. Tissue Eng. Part Methods 2017, 23, 485–496. [Google Scholar] [CrossRef] [PubMed]
- Olivares, A.L.; Lacroix, D. Simulation of Cell Seeding within a Three-Dimensional Porous Scaffold: A Fluid-Particle Analysis. Tissue Eng. Part Methods 2012, 18, 624–631. [Google Scholar] [CrossRef] [PubMed]
- Dechriste, G.; Fehrenbach, J.; Griseti, E.; Lobjois, V.; Poignard, C. Viscoelastic modeling of the fusion of multicellular tumor spheroids in growth phase. J. Theor. Biol. 2018, 454, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Reid, J.A.; Mollica, P.A.; Johnson, G.D.; Ogle, R.C.; Bruno, R.D.; Sachs, P.C. Accessible bioprinting: Adaptation of a low-cost 3D-printer for precise cell placement and stem cell differentiation. Biofabrication 2016, 8, 025017. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Tian, X.; Schreyer, D.J.; Chen, X. Effect of needle geometry on flow rate and cell damage in the dispensing-based biofabrication process. Biotechnol. Prog. 2011, 27, 1777–1784. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.; Cortres-Rodriguez, C.J.; Hazur, J.; Reakasame, S.; Boccaccini, A.R. Rational Design of a Triple-Layered Coaxial Extruder System: In silico and in vitro Evaluations Directed Toward Optimizing Cell Viability. Int. J. Bioprinting 2020, 6, 282. [Google Scholar] [CrossRef] [PubMed]
- Sego, T.J.; Kasacheuski, U.; Hauersperger, D.; Tovar, A.; Moldovan, N.I. A heuristic computational model of basic cellular processes and oxygenation during spheroid-dependent biofabrication. Biofabrication 2017, 9, 024104. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Tian, X.; Kozinski, J.A.; Chen, X.; Hwang, D.K. Modeling Mechanical Cell Damage in the Bioprinting Process Employing a Conical Needle. J. Mech. Med. Biol. 2015, 15, 1550073. [Google Scholar] [CrossRef]
- Liravi, F.; Darleux, R.; Toyserkani, E. Additive manufacturing of 3D structures with non-Newtonian highly viscous fluids: Finite element modeling and experimental validation. Addit. Manuf. 2017, 13, 113–123. [Google Scholar] [CrossRef]
- Samanipour, R.; Wang, Z.; Ahmadi, A.; Kim, K. Experimental and computational study of microfluidic flow-focusing generation of gelatin methacrylate hydrogel droplets. J. Appl. Polym. Sci. 2016, 133, 43701. [Google Scholar] [CrossRef]
- Prendergast, M.E.; Burdick, J.A. Computational Modeling and Experimental Characterization of Extrusion Printing into Suspension Baths. Adv. Healthc. Mater. 2021, 11, 2101679. [Google Scholar] [CrossRef] [PubMed]
- Carlier, A.; Geris, L.; Bentley, K.; Carmeliet, G.; Carmeliet, P.; Van Oosterwyck, H. Correction: MOSAIC: A Multiscale Model of Osteogenesis and Sprouting Angiogenesis with Lateral Inhibition of Endothelial Cells. PLoS Comput. Biol. 2013, 9, e1002724. [Google Scholar] [CrossRef]
- Gironi, P.; Petraro, L.; Santoni, S.; Dede’, L.; Colosimo, B.M. A computational model of cell viability and proliferation of extrusion-based 3D-bioprinted constructs during tissue maturation process. Int. J. Bioprinting 2023, 9, 741. [Google Scholar] [CrossRef]
- Göhl, J.; Markstedt, K.; Mark, A.; Håkansson, K.; Gatenholm, P.; Edelvik, F. Simulations of 3D bioprinting: Predicting bioprintability of nanofibrillar inks. Biofabrication 2018, 10, 034105. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wang, Q. Modeling and simulations of multicellular aggregate self-assembly in biofabrication using kinetic Monte Carlo methods. Soft Matter 2013, 9, 2172–2186. [Google Scholar] [CrossRef]
- Jakab, K.; Norotte, C.; Damon, B.; Marga, F.; Neagu, A.; Besch-Williford, C.L.; Kachurin, A.; Church, H.K.; Park, H.; Mironov, V.; et al. Tissue Engineering by Self-Assembly of Cells Printed into Topologically Defined Structures. Tissue Eng. Part A 2008, 14, 413–421. [Google Scholar] [CrossRef] [PubMed]
- Cristea, A.; Neagu, A. Shape changes of bioprinted tissue constructs simulated by the Lattice Boltzmann method. Comput. Biol. Med. 2016, 70, 80–87. [Google Scholar] [CrossRef]
- Shafiee, A.; McCune, M.; Forgacs, G.; Kosztin, I. Post-deposition bioink self-assembly: A quantitative study. Biofabrication 2015, 7, 045005. [Google Scholar] [CrossRef] [PubMed]
- McCune, M.; Shafiee, A.; Forgacs, G.; Kosztin, I. Predictive modeling of post bioprinting structure formation. Soft Matter 2014, 10, 1790–1800. [Google Scholar] [CrossRef]
- Flenner, E.; Marga, F.; Neagu, A.; Kosztin, I.; Forgacs, G. Relating Biophysical Properties Across Scales. In Multiscale Modeling of Developmental Systems; Current Topics in Developmental Biology Series; Schnell, S., Maini, P.K., Newman, S.A., Newman, T.J., Eds.; Academic Press: Cambridge, MA, USA, 2008; Volume 81, pp. 461–483. [Google Scholar] [CrossRef]
- Mohammadrezaei, D.; Moghimi, N.; Vandvajdi, S.; Powathil, G.; Hamis, S.; Kohandel, M. Predicting and elucidating the post-printing behavior of 3D printed cancer cells in hydrogel structures by integrating in-vitro and in-silico experiments. Sci. Rep. 2023, 13, 1211. [Google Scholar] [CrossRef] [PubMed]
- Kuan, H.S.; Pönisch, W.; Jülicher, F.; Zaburdaev, V. Continuum Theory of Active Phase Separation in Cellular Aggregates. Phys. Rev. Lett. 2021, 126, 018102. [Google Scholar] [CrossRef] [PubMed]
- Beaune, G.; Sinkkonen, L.; Gonzalez-Rodriguez, D.; Timonen, J.V.; Brochard-Wyart, F. Fusion Dynamics of Hybrid Cell-Microparticle Aggregates: A Jelly Pearl Model. Langmuir 2022, 38, 5296–5306. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, I.N.; Smith, L.J.; Olivos, D.J., III; Chu, T.M.G.; Kacena, M.A..; Wagner, D.R. Scaffold-free bioprinting of mesenchymal stem cells with the regenova printer: Optimization of printing parameters. Bioprinting 2019, 15, e00048. [Google Scholar] [CrossRef]
- Semple, J.L.; Woolridge, N.; Lumsden, C.J. Review: In Vitro, In Vivo, In Silico: Computational Systems in Tissue Engineering and Regenerative Medicine. Tissue Eng. 2005, 11, 341–356. [Google Scholar] [CrossRef]
- Bardini, R.; Di Carlo, S. Computational methods for biofabrication in tissue engineering and regenerative medicine—A literature review. Comput. Struct. Biotechnol. J. 2024, 23, 601–616. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Liu, Q.; Casillas, J.; Mcanally, M.; Mubtasim, N.; Gollahon, L.S.; Wu, D.; Xu, C. Prediction of cell viability in dynamic optical projection stereolithography-based bioprinting using machine learning. J. Intell. Manuf. 2022, 33, 995–1005. [Google Scholar] [CrossRef]
- Lee, J.; Oh, S.J.; An, S.H.; Kim, W.D.; Kim, S.H. Machine learning-based design strategy for 3D printable bioink: Elastic modulus and yield stress determine printability. Biofabrication 2020, 12, 035018. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level Set Methods: An Overview and Some Recent Results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef]
- Gibou, F.; Fedkiw, R.; Osher, S. A review of level-set methods and some recent applications. J. Comput. Phys. 2018, 353, 82–109. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Cherizol, R.; Sain, M.; Tjong, J. Review of Non-Newtonian Mathematical Models for Rheological Characteristics of Viscoelastic Composites. Green Sustain. Chem. 2015, 5, 6–14. [Google Scholar] [CrossRef]
- Nair, K.; Gandhi, M.; Khalil, S.; Yan, K.C.; Marcolongo, M.; Barbee, K.; Sun, W. Characterization of cell viability during bioprinting processes. Biotechnol. J. 2009, 4, 1168–1177. [Google Scholar] [CrossRef] [PubMed]
- Burova, I.; Wall, I.; Shipley, R.J. Mathematical and computational models for bone tissue engineering in bioreactor systems. J. Tissue Eng. 2019, 10, 2041731419827922. [Google Scholar] [CrossRef] [PubMed]
- Flenner, E.; Janosi, L.; Barz, B.; Neagu, A.; Forgacs, G.; Kosztin, I. Kinetic Monte Carlo and cellular particle dynamics simulations of multicellular systems. Phys. Rev. E 2012, 85, 031907. [Google Scholar] [CrossRef]
- Kosztin, I.; Vunjak-Novakovic, G.; Forgacs, G. Colloquium: Modeling the dynamics of multicellular systems: Application to tissue engineering. Rev. Mod. Phys. 2012, 84, 1791–1805. [Google Scholar] [CrossRef]
- Yang, X.; Mironov, V.; Wang, Q. Modeling fusion of cellular aggregates in biofabrication using phase field theories. J. Theor. Biol. 2012, 303, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Plan, E.L.C.M., VI; Yeomans, J.M.; Doostmohammadi, A. Active matter in a viscoelastic environment. Phys. Rev. Fluids 2020, 5, 023102. [Google Scholar] [CrossRef]
- Bonchev, D.; Thomas, S.; Apte, A.; Kier, L.B. Cellular automata modelling of biomolecular networks dynamics. SAR QSAR Environ. Res. 2010, 21, 77–102. [Google Scholar] [CrossRef]
- A Supercomputing Journey Inspired by Curiosity—History of Cray Supercomputers. Available online: https://www.hpe.com/uk/en/compute/hpc/cray.html (accessed on 31 March 2024).
- Reed, D.A.; Dongarra, J. Exascale Computing and Big Data. Commun. ACM 2015, 58, 56–68. [Google Scholar] [CrossRef]
- Edelman, A.; Chapter 6 of the Selected Lecture Notes from Applied Parallel Computing (SMA 5505) Course. Massachusetts Institute of Technology. Parallel Machines. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/77902/18-337j-spring-2005/contents/lecture-notes/chapter_6.pdf (accessed on 31 March 2024).
- Becker, D.J.; Sterling, T.; Savarese, D.; Dorband, J.E.; Ranawak, U.A.; Packer, C.V. BEOWULF: A Parallel Workstation For Scientific Computation. In Proceedings of the 24th International Conference on Parallel Processing, Urbana-Champain, IL, USA, 14–18 August 1995; CRC Press: Boca Raton, FL, USA, 1995; pp. 11–14. [Google Scholar]
- Gara, A.; Blumrich, M.A.; Chen, D.; Chiu, G.L.; Coteus, P.; Giampapa, M.; Haring, R.A.; Heidelberger, P.; Hoenicke, D.; Kopcsay, G.V.; et al. Overview of the Blue Gene/L system architecture. IBM J. Res. Dev. 2005, 49, 195–212. [Google Scholar] [CrossRef]
- Tuomi, I. The Lives and Death of Moore’s Law. First Monday 2002, 7, 11. [Google Scholar] [CrossRef]
- Petitet, A.; Whaley, R.C.; Dongarra, J.J.; Cleary, A. A Portable Implementation of the High-Performance Linpack Benchmark for Distributed-Memory Computers; Innovative Computing Laboratory: Knoxville, TN, USA, 2000; Available online: https://icl.utk.edu/hpl/index.html (accessed on 31 March 2024).
- Top 500—The List. Available online: https://www.top500.org/ (accessed on 31 March 2024).
- Top 500 List—June 2022. Available online: https://www.top500.org/lists/top500/2022/06/ (accessed on 31 March 2024).
- Geist, A.; Lucas, R. Major Computer Science Challenges At Exascale. Int. J. High Perform. Comput. Appl. 2009, 23, 427–436. [Google Scholar] [CrossRef]
- Chen, W. The demands and challenges of Exascale computing: An interview with Zuoning Chen. Natl. Sci. Rev. 2016, 3, 64–67. [Google Scholar] [CrossRef][Green Version]
- Kumar, V.; Gupta, A. Analyzing Scalability of Parallel Algorithms and Architectures. J. Parallel Distrib. Comput. 1994, 22, 379–391. [Google Scholar] [CrossRef]
- Kwiatkowski, J. Evaluation of Parallel Programs by Measurement of Its Granularity. In Proceedings of the Parallel Processing and Applied Mathematics, Naleczow, Poland, 9–12 September 2001; Wyrzykowski, R., Dongarra, J., Paprzycki, M., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 145–153. [Google Scholar] [CrossRef]
- European Union. The EU Enters the Exascale Era with the Announcement of New Supercomputing Hosting Sites. Available online: https://digital-strategy.ec.europa.eu/en/news/eu-enters-Exascale-era-announcement-new-supercomputing-hosting-sites (accessed on 31 March 2024).
- Matsuoka, S.; To Exascale and Beyond. Japan RIKEN Center for Computational Science. Available online: https://www.riken.jp/en/news_pubs/research_news/rr/2019spring/ (accessed on 31 March 2024).
- US Exascale Computing Project. The Office of Science (SC) and the National Nuclear Security Administration (NNSA) organizations of U.S. Department of Energy (DOE). Available online: https://www.Exascaleproject.org/ (accessed on 31 March 2024).
- Barone, G.B.; Boccia, V.; Bottalico, D.; Carracciuolo, L. SCoPE@Scuola: (In)-formative Paths on Topics Related with High Performance, Parallel and Distributed Computing. In Proceedings of the Euro-Par 2017: Parallel Processing Workshops, Santiago de Compostela, Spain, 28–29 August 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 191–202. [Google Scholar] [CrossRef]
- Yelick, K. Beyond Exascale Computing. Available online: https://www.isc-hpc.com/conference-keynote-2024.html (accessed on 13 May 2024).
- Yelick, K. Beyond Exascale Computing. Available online: https://people.eecs.berkeley.edu/~yelick/talks/exascale/PostExascale-ICPP2023.pdf (accessed on 20 May 2024).
- National Academies of Sciences, Engineering, and Medicine. Charting a Path in a Shifting Technical and Geopolitical Landscape: Post-Exascale Computing for the National Nuclear Security Administration; The National Academies Press: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Dongarra, J.; Deelman, E.; Hey, T.; Matsuoka, S.; Sarakar, V.; Bell, G.; Foster, I.; Keyes, D.; Kranzlmueller, D.; Lucas, B.; et al. Can the United States Maintain Its Leadership in High-Performance Computing? A Report from the ASCAC Subcommittee on American Competitiveness and Innovation to the ASCR Office; Report, The Advanced Scientific Computing Advisory Committee (ASCAC) Subcommittee on American Competitiveness and Innovation: Washington, DC, USA, 2023. Available online: https://science.osti.gov/-/media/ascr/ascac/pdf/meetings/202306/ASCAC_Subcommittee_on_American_Competitiveness_202306.pdf (accessed on 20 May 2024).
- Burini, D.; Chouhad, N. A multiscale view of nonlinear diffusion in biology: From cells to tissues. Math. Model. Methods Appl. Sci. 2019, 29, 791–823. [Google Scholar] [CrossRef]
- Fish, J.; Wagner, G.J.; Keten, S. Mesoscopic and multiscale modelling in materials. Nat. Mater. 2021, 20, 774–786. [Google Scholar] [CrossRef] [PubMed]
- Amani, A.; Balcàzar, N.; Naseri, A.; Rigola, J. A numerical approach for non-Newtonian two-phase flows using a conservative level-set method. Chem. Eng. J. 2020, 385, 123896. [Google Scholar] [CrossRef]
- Ahmadi, M.; Farsani, A. CFD simulation of non-Newtonian two-phase fluid flow through a channel with a cavity. Therm. Sci. 2018, 2018, 151. [Google Scholar] [CrossRef]
- Irgens, F. Rheology and Non-Newtonian Fluids; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Bush, J. Surface tension. In New Trends in the Physics and Mechanics of Biological Systems: Lecture Notes of the Les Houches Summer School: July 2009; Oxford University Press: Oxford, UK, 2011; Volume 92, pp. 27–64. [Google Scholar] [CrossRef]
- López-Herrera, J.; Popinet, S.; Castrejón-Pita, A. An Adaptive Solver for Viscoelastic Incompressible Two-phase Problems Applied to the Study of the Splashing of Weakly viscoelastic droplets. J. -Non-Newton. Fluid Mech. 2019, 264, 144–158. [Google Scholar] [CrossRef]
- Wielage, K. Analysis of Non-Newtonian Two-Phase Flows. Ph.D. Thesis, University of Paderborn, Paderborn, Germany, 2005. Available online: https://d-nb.info/978191463/34 (accessed on 31 March 2024).
- Keslerova, R.; Reznicek, H.; Padelek, T. Numerical modelling of generalized Newtonian fluids in bypass tube. Adv. Comput. Math. 2019, 45, 2047–2063. [Google Scholar] [CrossRef]
- Lagrangian and Eulerian Specification of the Flow Field—Wikipedia Page. Available online: https://en.wikipedia.org/wiki/Lagrangian_and_Eulerian_specification_of_the_flow_field#cite_note-Batchelor-1 (accessed on 31 March 2024).
- Bhalla, A.P.S.; Bale, R.; Griffith, B.E.; Patankar, N.A. A unified mathematical framework and an adaptive numerical method for fluid–structure interaction with rigid, deforming, and elastic bodies. J. Comput. Phys. 2013, 250, 446–476. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, G. Immersed Boundary Methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Zhang, L.; Gerstenberger, A.; Wang, X.; Liu, W.K. Immersed Finite Element Method. Comput. Methods Appl. Mech. Eng. 2004, 193, 2051–2067. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.K. Extended immersed boundary method using FEM and RKPM. Comput. Methods Appl. Mech. Eng. 2004, 193, 1305–1321. [Google Scholar] [CrossRef]
- Balcazar, N.; Jofre, L.; Lehmkuhl, O.; Castro, J.; Rigola, J. A finite-volume/level-set method for simulating two-phase flows on unstructured grids. Int. J. Multiph. Flow 2014, 64, 55–72. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G.; Zahedi, S. A conservative level set method for two phase flow II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- O’Dea, R.; Byrne, H.; Waters, S. Continuum Modelling of In Vitro Tissue Engineering: A Review. In Computational Modeling in Tissue Engineering; Springer: Berlin/Heidelberg, Germany, 2013; pp. 229–266. [Google Scholar] [CrossRef]
- Extracellular Matrix—Wikipedia Page. Available online: https://en.wikipedia.org/wiki/Extracellular_matrix (accessed on 31 March 2024).
- Dongarra, J.; Sullivan, F. Guest Editors’ Introduction: The Top 10 Algorithms. Comput. Sci. Eng. 2000, 2, 22–23. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 2004, 21, 1087–1092. [Google Scholar] [CrossRef]
- Richey, M. The Evolution of Markov Chain Monte Carlo Methods. Am. Math. Mon. 2010, 117, 383–413. [Google Scholar] [CrossRef]
- Larget, B. Introduction to Markov Chain Monte Carlo Methods in Molecular Evolution. In Statistical Methods in Molecular Evolution; Springer: New York, NY, USA, 2005; pp. 45–62. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains; Cambridge Series in Statistical and Probabilistic Mathematics Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Barker, A.A. Monte Carlo Calculations of the Radial Distribution Functions for a Proton-electron Plasma. Aust. J. Phys. 1965, 18, 119–134. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics, 4th ed.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Newman, T.J. Modeling Multicellular Structures Using the Subcellular Element Model. In Single-Cell-Based Models in Biology and Medicine; Birkhäuser: Basel, Switzerland, 2007; pp. 221–239. [Google Scholar] [CrossRef]
- van Kampen, N. Chapter IX—The Langevin Approach. In Stochastic Processes in Physics and Chemistry, 3rd ed.; North-Holland Personal Library; Elsevier: Amsterdam, The Netherlands, 2007; pp. 219–243. [Google Scholar] [CrossRef]
- Kier, L.B.; Seybold, P.G.; Cheng, C.-K. Modeling Chemical Systems Using Cellular Automata; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- von Neumann, J. Theory of Self-Reproducing Automata; University of Illionois Press: Champain, IL, USA, 1966. [Google Scholar]
- Ulam, S. Random processes and transformations. In Proceedings of the International Congress of Mathematicians, Cambridge, MA, USA, 30 August–6 September 1950; American Mathematical Society: Providence, RI, USA, 1952; Volume 2, pp. 264–275. [Google Scholar]
- Wolfram, S. Cellular Automata. Los Alamos Sci. 1983, 9, 2–27. [Google Scholar]
- Menshutina, N.V.; Kolnoochenko, A.V.; Lebedev, E.A. Cellular Automata in Chemistry and Chemical Engineering. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar] [CrossRef]
- Alves, M.A.; Oliveira, P.J.; Pinho, F.T. Numerical Methods for Viscoelastic Fluid Flows. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Chung, T. Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Fontes, E.; FEM vs. FVM. Available online: https://www.comsol.com/blogs/fem-vs-fvm (accessed on 31 March 2024).
- Sjodin, B. What’s the Difference between FEM, FDM and FVM? Available online: https://www.machinedesign.com/3d-printing-cad/fea-and-simulation/article/21832072/whats-the-difference-between-fem-fdm-and-fvm (accessed on 31 March 2024).
- Hatami, M. Chapter 2—Weighted Residual Methods Principles and Modifications. In Weighted Residual Methods; Hatami, M., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 83–152. [Google Scholar] [CrossRef]
- Baaijens, P.T.F. Mixed Finite Element Methods for viscoelastic flow analysis: A review. J. -Non-Newton. Fluid Mech. 1998, 79, 361–385. [Google Scholar] [CrossRef]
- Marchandise, E.; Geuzaine, P.; Chevaugeon, N.; Remacle, J.F. A stabilized Finite Element Method using a discontinuous level set approach for the computation of bubble dynamics. J. Comput. Phys. 2007, 225, 949–974. [Google Scholar] [CrossRef]
- Chen, T.; Minev, P.D.; Nandakumar, K. A projection scheme for incompressible multiphase flow using adaptive Eulerian grid. Int. J. Numer. Methods Fluids 2004, 45, 1–19. [Google Scholar] [CrossRef]
- Pillapakkam, S.; Singh, P. A Level-Set Method for Computing Solutions to Viscoelastic Two-Phase Flow. J. Comput. Phys. 2001, 174, 552–578. [Google Scholar] [CrossRef]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method, 2nd ed.; McGraw-Hill Higher Education: Boca Raton, FL, USA, 1993; ISBN 9780070513556. [Google Scholar]
- Gerald, C.; Wheatley, P. Applied Numerical Analysis; Featured Titles for Numerical Analysis; Pearson/Addison-Wesley: London, UK, 2004. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite Volume Methods. In Handbook of Numerical Analysis; Lions, J.L., Ciarlet, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 7, pp. 713–1020. [Google Scholar] [CrossRef]
- Chen, L. Finite Volume Methods. In Lecture Notes for the Course Math 226: Computational PDEs; University of California: Irvine, CA, USA; Available online: https://www.math.uci.edu/~chenlong/lectures.html (accessed on 31 March 2024).
- Cai, Z. On the finite Volume element methods. Numer. Math. 1990, 58, 713–735. [Google Scholar] [CrossRef]
- Mazumder, S. Chapter 6—The Finite Volume Method (FVM). In Numerical Methods for Partial Differential Equations; Mazumder, S., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 277–338. [Google Scholar] [CrossRef]
- Kumar, S. A Time Integration Scheme for Dynamic Problems. Ph.D. Thesis, Department of Mechanical Engineering, Indian Institute of Technology Guwahati, Guwahati, India, 2015. [Google Scholar] [CrossRef]
- Geradin, M.; Rixen, D. Mechanical Vibrations: Theory and Application to Structural Dynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Duff, I.S.; Erisman, A.M.; Reid, J.K. Direct Methods for Sparse Matrices, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Duff, I.S.; Reid, J.K. The Multifrontal Solution of Indefinite Sparse Symmetric Linear. ACM Trans. Math. Softw. 1983, 9, 302–325. [Google Scholar] [CrossRef]
- Amestoy, P.; Buttari, A.; Duff, I.; Guermouche, A.; L’Excellent, J.Y.; Uçar, B. Multifrontal Method. In Encyclopedia of Parallel Computing; Springer: Boston, MA, USA, 2011; pp. 1209–1216. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J.; Kincaid, D.R.; Krogh, F.T. Basic Linear Algebra Subprograms for Fortran Usage. ACM Trans. Math. Softw. 1979, 5, 308–323. [Google Scholar] [CrossRef]
- van der Vorst, H.A. Krylov subspace iteration. Comput. Sci. Eng. 2000, 2, 32–37. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Other Titles in Applied Mathematics, Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar] [CrossRef]
- Dubrulle, A.A.; Weisstein, E.W.; Hessenberg Matrix. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/HessenbergMatrix.html (accessed on 31 March 2024).
- Stüben, K. A review of algebraic Multigrid. J. Comput. Appl. Math. 2001, 128, 281–309. [Google Scholar] [CrossRef]
- Benzi, M.; Golub, G.H.; Liesen, J. Numerical Solution of Saddle Point Problems. Acta Numer. 2005, 14, 1–137. [Google Scholar] [CrossRef]
- Dongarra, J.; Hittinger, J.; Bell, J.; Chacon, L.; Falgout, R.; Heroux, M.; Hovland, P.; Ng, E.; Webster, C.; Wild, S. Applied Mathematics Research for Exascale Computing; Technical Report LLNL-TR-651000; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2014. [Google Scholar] [CrossRef]
- Ang, J.; Evans, K.; Geist, A.; Heroux, M.; Hovland, P.D.; Marques, O.; Curfman McInnes, L.; Ng, E.G.; Wild, S.M. Report on the Workshop on Extreme-Scale Solvers: Transition to Future Architectures; Department of Energy, ASCR: Washington, DC, USA, 2012. Available online: https://science.osti.gov/-/media/ascr/pdf/program-documents/docs/reportExtremeScaleSolvers2012.pdf (accessed on 31 March 2024).
- Khaleel, M.A. Scientific Grand Challenges: Crosscutting Technologies for Computing at the Exascale—February 2–4, 2010, Washington, D.C.; Technical Report; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2011. [Google Scholar] [CrossRef][Green Version]
- Liu, W.K.; Park, H.S.; Karpov, E.G.; Farrell, D. Bridging Scale Method and Its Applications. In Meshfree Methods for Partial Differential Equations III; Springer: Berlin/Heidelberg, Germany, 2007; pp. 185–205. [Google Scholar] [CrossRef]
- Park, H.S.; Liu, W.K. An introduction and tutorial on multiple-scale analysis in solids. Comput. Methods Appl. Mech. Eng. 2004, 193, 1733–1772. [Google Scholar] [CrossRef]
- Chacon, L.; Chen, G.; Knoll, D.A.; Newman, C.; Park, H.; Taitano, W.; Willert, J.A.; Womeldorff, G. Multiscale high-order/low-order (HOLO) algorithms and applications. J. Comput. Phys. 2017, 330, 21–45. [Google Scholar] [CrossRef]
- Keyes, D.E.; McInnes, L.C.; Woodward, C.; Gropp, W.; Myra, E.; Pernice, M.; Bell, J.; Brown, J.; Clo, A.; Connors, J.; et al. Multiphysics simulations: Challenges and opportunities. Int. J. High Perform. Comput. Appl. 2013, 27, 4–83. [Google Scholar] [CrossRef]
- HPC Wiki—Scaling. Available online: https://hpc-wiki.info/hpc/Scaling#Strong_or_Weak_Scaling (accessed on 1 March 2024).
- Keyes, D.E. Exaflop/s: The why and the how. Comptes Rendus MéCanique 2011, 339, 70–77. [Google Scholar] [CrossRef]
- Brown, P.N.; Hindmarsh, A.C. Matrix-Free Methods for Stiff Systems of ODE’s. SIAM J. Numer. Anal. 1986, 23, 610–638. [Google Scholar] [CrossRef]
- Davies, T.; Karlsson, C.; Liu, H.; Ding, C.; Chen, Z. High performance linpack benchmark: A fault tolerant implementation without checkpointing. In Proceedings of the International Conference on Supercomputing, Tucson, AZ, USA, 31 May–4 June 2011; pp. 162–171. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo Zaglia, M. Studies in Computational Mathematics 2. In Extrapolation Methods Theory and Practice; Studies in Computational Mathematics Series; Elsevier: Amsterdam, The Netherlands, 1991; Volume 2. [Google Scholar] [CrossRef]
- Hairer, E.; Norsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar] [CrossRef]
- Althaus, K. Theory and Implementation of the Adaptive Explicit Midpoint Rule Including Order and Stepsize Control. Bachelor’s Thesis, Department of Mathematics, Technische Universitat Munchen, Munchen, Germany, 2018. Available online: https://github.com/AlthausKonstantin/Extrapolation/blob/master/Bachelor%20Theseis.pdf (accessed on 1 March 2024).
- Constantinescu, E.M.; Sandu, A. Extrapolated Implicit-Explicit Time Stepping. SIAM J. Sci. Comput. 2010, 31, 4452–4477. [Google Scholar] [CrossRef]
- Constantinescu, E.M.; Sandu, A. Achieving Very High Order for Implicit Explicit Time Stepping: Extrapolation Methods; Report Preprint ANL/ANL/MCS-TM-306; Argonne National Laboratory: Lemont, IL, USA, 2009. Available online: https://www.mcs.anl.gov/uploads/cels/papers/TM-306.pdf (accessed on 1 March 2024).
- Gander, M.J. 50 Years of Time Parallel Time Integration. In Proceedings of the Multiple Shooting and Time Domain Decomposition Methods, Heidelberg, Germany, 6–8 May 2013; Carraro, T., Geiger, M., Körkel, S., Rannacher, R., Eds.; Springer: Cham, Switzerland, 2015; pp. 69–113. [Google Scholar]
- Gander, M.J.; Lunet, T.; Ruprecht, D.; Speck, R. A Unified Analysis Framework for Iterative Parallel-in-Time Algorithms. SIAM J. Sci. Comput. 2023, 45, A2275–A2303. [Google Scholar] [CrossRef]
- Brune, P.R.; Knepley, M.G.; Smith, B.F.; Tu, X. Composing Scalable Nonlinear Algebraic Solvers. SIAM Rev. 2015, 57, 535–565. [Google Scholar] [CrossRef]
- Balay, S.; Gropp, W.D.; McInnes, L.C.; Smith, B.F. Efficient Management of Parallelism in Object Oriented Numerical Software Libraries. In Modern Software Tools in Scientific Computing; Arge, E., Bruaset, A.M., Langtangen, H.P., Eds.; Birkhäuser Press: Basel, Switzerland, 1997; pp. 163–202. [Google Scholar]
- Smith, B.; McInnes, L.C.; Constantinescu, E.; Adams, M.; Balay, S.; Brown, J.; Knepley, M.G.; Zhang, H. PETSc’s Software Strategy for the Design Space of Composable Extreme-Scale Solvers. In Proceedings of the DOE Exascale Research Conference; Portland, OR, USA, 16–18 April 2012, Report Preprint ANL/MCS-P2059-0312; Argonne National Laboratory: Lemont, IL, USA, 2012. Available online: http://www.mcs.anl.gov/uploads/cels/papers/P2059-0312.pdf (accessed on 31 March 2024).
- Pawlowski, R.P.; Shadid, J.N.; Simonis, J.P.; Walker, H.F. Globalization Techniques for Newton–Krylov Methods and Applications to the Fully Coupled Solution of the Navier–Stokes Equations. SIAM Rev. 2006, 48, 700–721. [Google Scholar] [CrossRef][Green Version]
- Dolean, V.; Gander, M.J.; Kheriji, W.; Kwok, F.; Masson, R. Nonlinear Preconditioning: How to Use a Nonlinear Schwarz Method to Precondition Newton’s Method. SIAM J. Sci. Comput. 2016, 38, A3357–A3380. [Google Scholar] [CrossRef]
- Carson, E. Communication-Avoiding Krylov Subspace Methods in Theory and Practice. Technical Report No. UCB/EECS-2015-179. Ph.D. Thesis, Electrical Engineering and Computer Sciences, University of California at Berkeley, Berkeley, CA, USA, 2015. Available online: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2015/EECS-2015-179.pdf (accessed on 31 March 2024).
- Anzt, H.; Boman, E.; Falgout, R.; Ghysels, P.; Heroux, M.; Li, X.; Curfman McInnes, L.; Tran Mills, R.; Rajamanickam, S.; Rupp, K.; et al. Preparing sparse solvers for Exascale computing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190053. [Google Scholar] [CrossRef] [PubMed]
- Abdelfattah, A.; Anzt, H.; Ayala, A.; Boman, E.; Carson, E.; Cayrols, S.; Cojean, T.; Dongarra, J.; Falgout, R.; Gates, M.; et al. Advances in Mixed Precision Algorithms: 2021 edition; Technical Report LLNL-TR-825909; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2021. [Google Scholar] [CrossRef]
- Hoemmen, M. Communication-avoiding Krylov Subspace Methods. Technical Report No. UCB/EECS-2010-37. Ph.D. Thesis, Electrical Engineering and Computer Sciences, University of California at Berkeley, Berkeley, CA, USA, 2010. Available online: https://www2.eecs.berkeley.edu/Pubs/TechRpts/2010/EECS-2010-37.pdf (accessed on 31 March 2024).
- Bai, Z.; Hu, D.; Reichel, L. A Newton basis GMRES implementation. IMA J. Numer. Anal. 1994, 14, 563–581. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Cipra, B.A. The Best of the 20th Century: Editors Name Top 10 Algorithms. SIAM News 2000, 33, 1–2. [Google Scholar]
- Beatson, R.; Greengard, L. A Short Course on Fast Multipole Methods. Available online: http://math.nyu.edu/faculty/greengar/shortcourse_fmm.pdf (accessed on 31 March 2024).
- Martinsson, P.G. Fast Multipole Methods. In Encyclopedia of Applied and Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 498–508. [Google Scholar] [CrossRef]
- Fenn, M.; Steidl, G. FMM and H-Matrices: A Short Introduction to the Basic Idea. 2002. Available online: https://madoc.bib.uni-mannheim.de/744/ (accessed on 31 March 2024).
- Hackbusch, W.; Grasedyck, L.; Börm, S. An introduction to hierarchical matrices. Math. Bohem. 2002, 127, 229–241. [Google Scholar] [CrossRef]
- Weisstein, E.W.; Binary Tree. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/BinaryTree.html (accessed on 31 March 2024).
- Li, Y.; Mascagni, M. Grid-Based Monte Carlo Application. In Proceedings of the Grid Computing—GRID 2002, Baltimore, MD, USA, 18 November 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 13–24. [Google Scholar] [CrossRef]
- Rosenthal, Jeffrey S. Parallel computing and Monte Carlo algorithms. Far East J. Theor. Stat. 2000, 4, 207–236. [Google Scholar]
- Advanced Materials 2030 Initiative. Materials 2030 Manifesto—A Systemic Approach of Advanced Materials for Prosperity—A 2030 Perspective; EU Publications Office: Brussels, Belgium, 2022; Available online: https://research-and-innovation.ec.europa.eu/system/files/2022-02/advanced-materials-2030-manifesto.pdf (accessed on 31 March 2024).
- Abbadessa, A.; Landín, M.; Oude Blenke, E.; Hennink, W.E.; Vermonden, T. Two-component thermosensitive hydrogels: Phase separation affecting rheological behavior. Eur. Polym. J. 2017, 92, 13–26. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Mimona, M.A.; Islam, M.A.; Hossain, N.; Zohura, F.T.; Imtiaz, I.; Rimon, M.I.H. Scope of machine learning in materials research—A review. Appl. Surf. Sci. Adv. 2023, 18, 100523. [Google Scholar] [CrossRef]
- Yamanaka, A.; Maeda, Y.; Sasaki, K. Ensemble Kalman filter-based data assimilation for three-dimensional multi-phase-field model: Estimation of anisotropic grain boundary properties. Mater. Des. 2019, 165, 107577. [Google Scholar] [CrossRef]
- Evensen, G.; Vossepoel, F.C.; Van Leeuwen, P.J. Data Assimilation Fundamentals: A Unified Formulation of the State and Parameter Estimation Problem; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Carlberg, K.; Brencher, L.; Haasdonk, B.; Barth, A. Data-Driven Time Parallelism via Forecasting. SIAM J. Sci. Comput. 2019, 41, B466–B496. [Google Scholar] [CrossRef]
- An, J.; Chua, C.K.; Mironov, V. A perspective on 4D bioprinting. Int. J. Bioprinting 2016, 2, 3–5. [Google Scholar] [CrossRef]

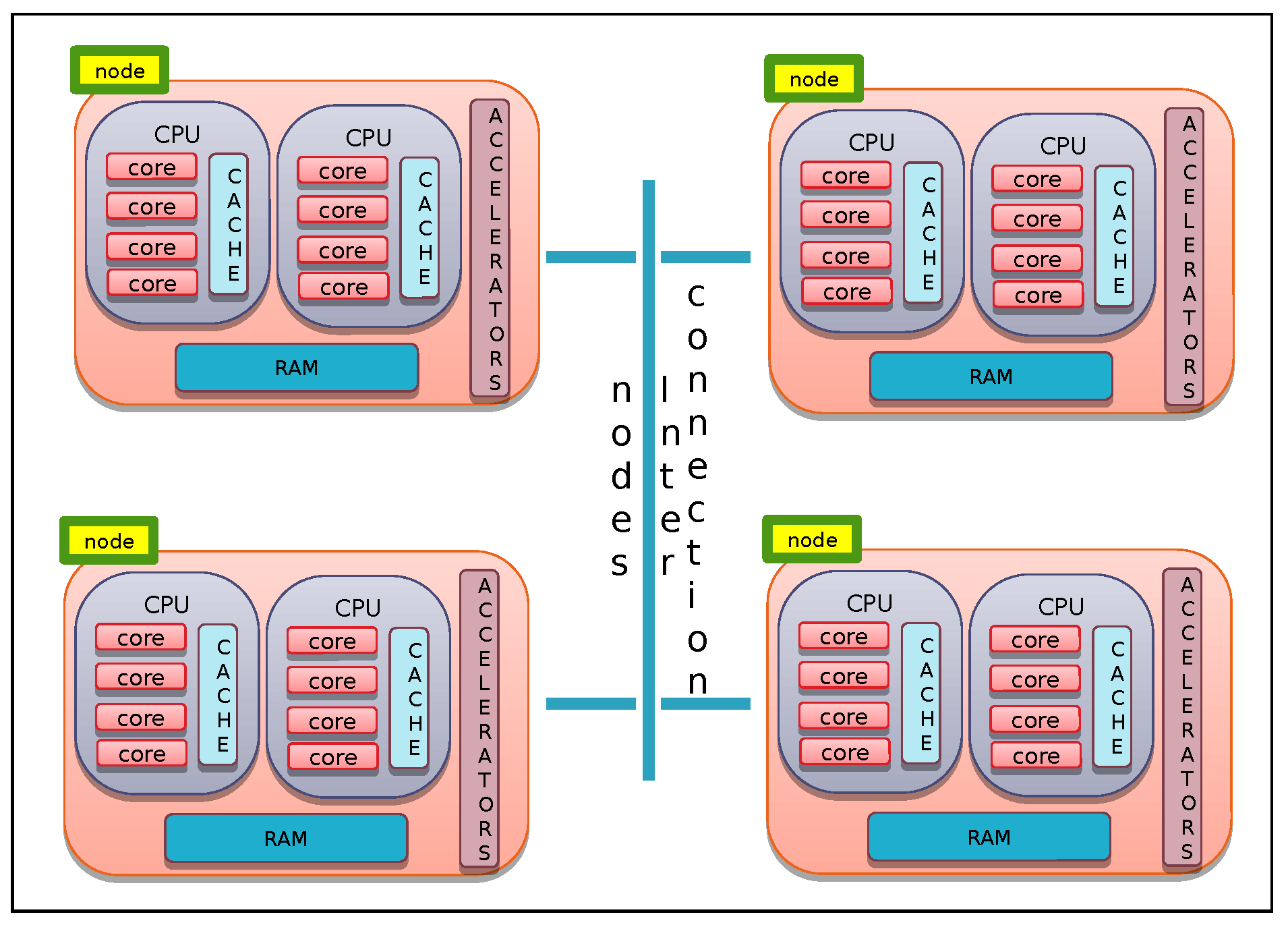







| Transversal Contents | |||
|---|---|---|---|
| Introduction on Computational Science (Section 2) | |||
| “State of the Art” of HPC Systems (Section 4) | |||
| Inventory of Mathematiacl Tools for Computational Simulation of Bioprinting Processes (Section 3) | |||
| Models | Numerical Tool | Exascale Numerical Tool | |
| Discretization | Algorithms | ||
| Fluid Flows Equations or coupled continuos equations (Two-Phase flow problem, transport and response of species, Section 5.1) Cellular Particle Dynamics (Section 5.2.2) | FEM, FDM, FVM (Section 6.1.1) Cellular Particle Dynamics Algorithm (Section 6.2.2) |
|
|
| Monte Carlo approach (Section 5.2.1) | The Markov Chain Monte Carlo Algorithms (Section 6.2.1) | Parallel Monte Carlo based methods (Section 7.2.5) | |
| The Cellular Automata Model (Section 5.2.3) | The Cellular Automata Model Algorithms (Section 6.2.3) | General considerations on stochastic-based algorithms (Section 7.2) | |
| Model | Aim | Refs. | |
|---|---|---|---|
| Pre-Printing | Fluid Flows Equations | Evaluate the influence of a seeding loading regime on suction pressure and infiltration velocity of the cell suspension. | [30] |
| Introduce a new methodology to simulate the cell-seeding process under perfusion conditions. The cells are treated as spherical particles dragged by the fluid media. | [31] | ||
| Design a model describing the fusion of growing cell clusters, such as embryo cell aggregates or tumor cell spheroids. | [32] | ||
| During Printing | Fluid Flows Equations | Used to study the influence of needle geometries on cell clogging during printing. | [33] |
| Determine how printing process parameters affect the flow velocity of cell-laden printing material and the survivability of cells within printed structures. | [34] | ||
| Aid the design of an extruder system for the biofabrication of vascular networks with the goal of maintaining cell viability throughout the printing process. | [35] | ||
| Monte Carlo approach | Used to study cellular adhesiveness and motility, interactions with concentration fields, and concentration-dependent, stochastic cell dynamics, driven by metabolite-dependent cell death. | [36] | |
| Immersed Boundary Method | Used to study cell deformation during the extrusion/ injection-based bioprinting processes. | [37] | |
| Two-Phase Level Set Methods | Used to study droplet formation. | [38,39] | |
| Computational simulations of bioink printing process in suspension baths. | [40] | ||
| Used to assess the influence of bioink temperature on shear stress, pressure, and velocity. | [11] | ||
| Models for transport and response of biological and chemical species | Optimize printing process parameters in order to achieve the required cell dispersion and maintain cell viability. | [41] | |
| Investigate the distribution of oxygen and glucose in bioprinted structures, as well as examine the reality of the diffusion and consumption phenomena and their impact on the growth and demise of cells. | [42] | ||
| Surface Tension Model | Study the filament deposition and the final bioprinted shape during the extrusion/ injection-based bioprinting processes. | [43] | |
| Post-Printing | Monte Carlo approach | Study cell self-assembly and cellular aggregate fusion of multicellular aggregate systems. | [44] |
| Study early morphogenesis of 3D tissue structures formed through the post-printing fusion of the bioink particles, | [45] | ||
| Fluid Flows Equations | Study post-printing cell rearrangement to forecast the geometry and stability of printed structures | [46] | |
| Cellular Particle Dynamics | Study the discrete bioink units’ ability to self-assemble into the intended form after deposition and their deposition rate. | [47,48,49] | |
| Cellular Automata | Simulate post-printing cell behavior within the 3D bioprinted complex under a variety of bioprinting conditions. | [50] |
| Model | “Pros’’ | “Cons” |
|---|---|---|
| The Navier–Stokes equations for Viscoelastic Fluids (Section 5.1.1) | The most comprehensive way to describe complex fluid dynamics. | The definition of model parameters could be very hard. |
| The Level Set Method (LSM) for the two-phase flow problem (Section 5.1.2) | LSM is based on a front-capturing approach that uses a scalar function on a stationary grid to capture the interface evolution. The ability to compute phenomena like bubble break-up and coalescence is made possible by the implicit interface capture. | The main difficulty in using this approach is keeping a clear boundary between the different fluids. |
| The Immersed Boundary Method (IBM) for the two-phase flow problem (Section 5.1.2) | IBM is based on a combination of front-capturing and front-tracking approaches. It can be useful to describe fluid–structure interaction when the structure is intended to be an immersed body. | IBM could inherit drawbacks of front-tracking approaches in describing interfaces with complex geometries. Moreover, the correct definition of the distribution function d could be crucial. |
| The continuum surface force (CSF) model for the two-phase flow problem (Section 5.1.2) | The probably most famous approach used to compute the surface tension force needed by the application of front capturing methods. The model considers surface tension force as a continuous, 3D effect across an interface, rather than as a boundary value condition on the interface. | The definition of the transition region and of the “color” function . |
| Transport and response of biological and chemical species (Section 5.1.3) | Models used to study how the tissue reacts to the chemical and mechanical environment in the culture medium. They can be considered a strict framework of conservation laws for mixes of interacting continua that describe the transfer of mass and momentum between different component phases. | The definition of model parameters could be very hard. |
| Oldroyd B | FENE-P | FENE-CR | Linear PTT | |
|---|---|---|---|---|
| No-slip | The boundary is considered as a rigid wall where no fluid comes out of the wall. On the boundary, the following equation is valid [98]: |
| Free-slip |
No fluid comes out of the wall, but in contrast to the no-slip condition, no friction acts along the wall.
Therefore, on the boundary, the following equation is valid [98]
|
| Inflow |
In this case, all velocity components are stated [98], i.e.,
|
| Outflow |
In order to prescribe boundary conditions at the outlet, many technics exist.
Practicable importance can be attributed to the so-called “do-nothing” method, which is described by the following equation
|
| Periodic |
In the case of a one-directional periodical problem with periodic length , the velocities and the pressure have to be equal on both sides of the periodical
direction. If we assume that the problem is periodic in the direction, it follows that [98]
|
| Model | “Pros” | “Cons” |
|---|---|---|
| Monte Carlo-based methods (MCMs) (Section 5.2.1) | MCMs are a broad category of computing methods for assessing sums and integrals or estimates of energy or other macro-parameters in a physical or biological system. They are universally appreciated for their power and easy implementation beyond their versatility and flexibility. | They can only be used to assess equilibrium states. |
| The cellular automata method (Section 5.2.3) | An approach where the behaviors of the species under study are determined by rules which can be probabilistic or deterministic. CA could be particularly significant in managing the behaviors of systems where the traditional, differential-equation-based methodologies are either useless or difficult to adopt due to the numerous complex interconnections between the system constituents. | They can only be used to assess equilibrium states. Either synchronous or asynchronous rule applications lead to CA development but serious practical implementations limit the use of CA to an asynchronous rule application. |
|
The cellular particle dynamics (CPD) (Section 5.2.2) | CPD is based on the idea of constructing a cell from a cloud of sub-cellular entities called elements. All the elements, through their relative positions, and in response to cell internal and external forces, determine the dynamics of all the cells. | The definition of model parameters could be very difficult. |
| Discretization Methods | “Pros” | “Cons” | Refs. |
|---|---|---|---|
| Finite Element Method (FEM) |
| The mathematics needs are advanced. | [11,30,33,35] |
| Finite Difference Method (FDM) |
| Managing curved boundaries or material discontinuities might be challenging. | [46] |
| Finite Volume Method (FVM) |
| The functions that approximate the solution cannot be easily made of higher order. | [31] |
| Discrete Newton |
The matrix is approximated by where
|
| Modified Newton |
The matrix substitutes . It is considered to be equal to for all steps n, i.e.,
|
| Quasi-Newton |
The tangent matrix is approximated by the “secant matrix” for which the following relation is valid:
|
| Methods | |||
|---|---|---|---|
| DBJ | − | ||
| ABJ | − | ||
| ABGS | − | ||
| Parareal | − | ||
| TMG | |||
| TMGc | − | ||
| TMGf | |||
| PFASST |
| Composite | ||
|---|---|---|
| Type | Statement | Abbreviation |
| Additive | ||
| Multiplicative | ||
| Preconditioning | ||
| Type | Statement | Abbreviation |
| Left | ||
| Right | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carracciuolo, L.; D’Amora, U. Mathematical Tools for Simulation of 3D Bioprinting Processes on High-Performance Computing Resources: The State of the Art. Appl. Sci. 2024, 14, 6110. https://doi.org/10.3390/app14146110
Carracciuolo L, D’Amora U. Mathematical Tools for Simulation of 3D Bioprinting Processes on High-Performance Computing Resources: The State of the Art. Applied Sciences. 2024; 14(14):6110. https://doi.org/10.3390/app14146110
Chicago/Turabian StyleCarracciuolo, Luisa, and Ugo D’Amora. 2024. "Mathematical Tools for Simulation of 3D Bioprinting Processes on High-Performance Computing Resources: The State of the Art" Applied Sciences 14, no. 14: 6110. https://doi.org/10.3390/app14146110
APA StyleCarracciuolo, L., & D’Amora, U. (2024). Mathematical Tools for Simulation of 3D Bioprinting Processes on High-Performance Computing Resources: The State of the Art. Applied Sciences, 14(14), 6110. https://doi.org/10.3390/app14146110







