NOx Formation Mechanism and Emission Prediction in Turbulent Combustion: A Review

Abstract

The field of nitric oxide (NOx) production combined with turbulent flow is a complex issue of combustion, especially for the different time scales of reactions and flow in numerical simulations. Around this, a series of approach methods, including the empirical formula approach, the computational fluid dynamics (CFD) approach coupling with an infinite rate chemical reaction, the chemical reaction networks (CRNs), and the CFD approach coupling with CRNs, were classified, and we discussed its advantages and applicability. The empirical-formula approach can provide an average range of NOx concentration, and this method can be involved only in special scenarios. However, its simplicity and feasibility still promote practical use, and it is still widely applied in engineering. Moreover, with the help of artificial intelligence, this method was improved in regard to its accuracy. The CFD approach could describe the flow field comprehensively. In compliance with considering NOx formation as finite-rate chemical reactions, the NOx concentration distribution via simulation cannot match well with experimental results due to the restriction caused by the simplification of the combustion reaction. Considering NOx formation as a finite-rate chemical reaction, the CRNs approach was involved in CFD simulation, and the CRNs approach could forecast the NOx concentration distribution in the flow field. This article mainly focuses on the simulation method of nitric oxide (NOx) production in different combustion conditions. This review could help readers understand the details of the NOx formation mechanism and NOx formation prediction approach.

1. Introduction

As a kind of air pollutant, nitric oxide (NOx) is the main factor that causes serious air pollution, such as photochemical smog and acid rain. To protect the environment and human health, the International Civil Aviation Organization (ICAO) published more stringent regulations on nitric oxide (NOx) emissions [1]. Hence, in the process of designing a combustion chamber, the calculation of nitric oxide (NOx) emissions has become a necessary step, and how to reduce the amount of nitric oxide (NOx) has become the research focus.

Nitric oxide (NOx) emissions derived from the combustion of an engine experience a high-temperature environment, coupled with a complex turbulent flow, inside the combustion chamber. In addition, the complex geometry of the combustion chamber also plays an important role in influencing the airflow movement. Subsequently, predicting nitric oxide (NOx) concentrations is a complex task in a turbulent flow situation. First, the nitric oxide (NOx) generation process is a multi-scale process [2], including the flow and the chemical reaction process. The flow is coupled with the chemical reactions, especially in the chemical reaction process under turbulent conditions. Second, the process of nitric oxide (NOx) generation is relatively slow compared to the rapid process of the oxidative decomposition of hydrocarbon fuels [3]. Because the airflow stays in the combustion chamber for a short time, the amount of nitrogen oxide (NOx) generation would not reach an equilibrium state after leaving the combustion chamber, NOx could still continue to be generated, and the concentration of each component associated with NOx could continue to change. The key point of approach to predict nitric oxide (NOx) emissions should be coupled with the temperature and flow field. This also makes it difficult to predict the rate of nitric oxide (NOx) production. In addition, nitric oxide (NOx) emissions were affected by the turbulent state and fuel type [4]. With the development of Sustainable Aviation Fuel (SAF), the change in fuel composition affects its physical and chemical properties, in turn affecting its atomization performance [5]. Reforming the atomization of droplets for liquid fuels has a significant impact on emission performance, including nitrogen oxides and particulate matter emissions.

In earlier studies, the level of nitric oxide (NOx) emissions could be estimated roughly through empirical formulas [6]. The main idea is to treat the rate of reactant formation as an average constant dependent on the operating conditions. Even though this method could be applied to special scenarios, such as the gas turbine cycle analysis and preliminary design frameworks, its simplicity and feasibility still make it become a common way in practical use. In recent years, artificial intelligence and neural networks have been applied to predict nitric oxide (NOx) emissions to improve accuracy [7,8,9], but they still have drawbacks, such as the simplicity of the application scenarios and the huge amount of data that should be given to train the model.

With the development of computers and the computing method, the capability and reliability of computational fluid dynamics (CFD) in combustion performance are well-known to use in NOx prediction [10]. In general, the computational fluid dynamics (CFD) method could describe the flow in detail and also solve the fuel oxidation process, which is considered as an infinite rate of chemical reaction. However, compared with the fuel oxidation process, the production of nitric oxide (NOx) is a finite-rate process, which means that the integration of the source item is complex. It is essential in a turbulent combustion regime to introduce a combustion model, which determines the reaction rate in the reacting flow [11]. In some research, the computational fluid dynamics (CFD) method was applied to predict nitric oxide (NOx) production [12,13]. Due to a mismatch between the flow and chemical reaction in the field of time and length scale, the computational fluid dynamics (CFD) method may entail a substantial computational burden or pose challenges in terms of precision.

The chemical reaction networks (CRNs) method has successfully improved the prediction of nitric oxide (NOx) emissions by sacrificing part of the accuracy in the field of flow [14,15,16,17]. The accuracy of nitric oxide (NOx) prediction relies on ensuring a precise temperature and reactant concentration, which could be achieved through the utilization of the chemical reaction networks (CRNs) method, as supported by comprehensive reaction mechanisms. Moreover, by combining information from the computational fluid dynamics (CFD) method, the chemical reaction networks (CRNs) method could improve the accuracy of nitric oxide (NOx) emissions with only an increase in simulation time. This method was applied in several research studies and showed applicability with the experiment results [18,19,20]. Therefore, the CRNs method combined with the computational fluid dynamics (CFD) method would predict the nitric oxide (NOx) concentration in a flow field.

This article mainly focuses on the prediction method of nitric oxide (NOx) production in different combustion chambers. Through the review of the methods that are mainly applied in current situations, the advantages and disadvantages were compared, and we discussed those appropriate application scenarios. The empirical formula provided a large scope of application due to easy access. With the help of artificial intelligence, this method’s application could be extended further in practical use with accuracy improvement. The computational fluid dynamics (CFD) method can capture the combined behavior of flow, temperature, and reactant concentration. In the prediction of nitric oxide (NOx) generation field, the simulation by the direct numerical simulation method (DNS) is limited due to its enormous calculation cost. The other computational fluid dynamics (CFD) methods were restricted by the accuracy of their simplified combustion model, with 10–20% deviation. Moreover, the computational fluid dynamics (CFD) method would be applied only to the types of fuels that contain a finite number of reactants and reaction mechanisms, which would not be suitable for the complex components of fuel. The chemical reaction networks (CRNs) method focuses on the chemical reactions by sacrificing the flow of information, and the chemical reaction networks (CRNs) method is more suitable than computational fluid dynamics (CFD) for the simple flow. The chemical reaction networks (CRNs) method should be combined with computational fluid dynamics (CFD), as the prediction of NOx would be improved by coupling both advantages.

2. NOx Formation Mechanism

The classification of the NOx route could be identified as thermal NO route, prompt NO route, N₂O route, NNH route, and fuel-N route. The thermal NO route plays a significant role because of the high temperature in the combustion chamber. The prompt NO route, N₂O route, and NNH route would contribute to NOx generation under special conditions. The fuel-N route may be disregarded in the absence of nitrogen-containing in aviation fuel.

2.1. Thermal NOx Route

The thermal NOx route could also be called the Zeldovich way, which was first proposed in 1964 [21]. The details of its elementary reactions include the following:

$$\mathrm{O}· + {\mathrm{N}}_2\to \mathrm{NO} + \mathrm{N}·$$

(1)

$$\mathrm{N}· + {\mathrm{O}}_2\to \mathrm{NO} + \mathrm{O}·$$

(2)

With the situation of the production existing water, the thermal pathway could expand as follows:

$$\mathrm{N}· + \mathrm{OH}\to \mathrm{NO} + \mathrm{H}·$$

(3)

The strength of the thermal NO route is mainly affected by temperature. The higher the reaction temperature, the more thermal NO route is generate. In the research of Löffler et al. [22], a simplified NOx generation mechanism was built through the steady-state approximation and showed a good agreement in a wide range of conditions with the detailed mechanism. Based on this simplified mechanism, the different percentages of each route during CH₄ combustion are shown in Figure 1. The results showed that the thermal NO route would be crucial when the temperature is above 1600 °C, which is the same as the practical test. The reason is that, at the beginning of the chain reaction, R1 needs to break the chemical bound of N-N, which needs activity energy of about 318 kJ/mol.

Owing to the temperature of the chamber being higher than 1800 K, the thermal NOx route plays a leading role in all pathways. The thermal NO route contributes to the main emission of NOx in the high-temperature area [23,24,25].

The second influence factor on the thermal NOx pathway is residence time. NOx is continuously generated during the flue gas flowing in the combustion chamber. Restricted by the reaction rates of NOx generation, the partial chemical equilibrium would not be achieved in a short time. This is quite different from the fuel decomposition process, which is considered fast chemistry. Hence, the more residence time, the more NOx production exists [26].

2.2. Prompt NO Route

The prompt NO route is also called the Fenimore pathway. It occurred at the fuel-rich flame, which mainly occurred in the fuel consumption area. The prompt NOx pathway is first observed in the experiment; the whole pathway is very complex. The current research supposed that the prompt NOx has a relationship with the radical [CH∙], and the beginning of the chain reaction is as follows:

$$\mathrm{CH}·+{\mathrm{N}}_2\to \mathrm{HCN}·+\mathrm{N}·$$

(4)

$$\mathrm{C}·+{\mathrm{N}}_2\to \mathrm{CN}·+\mathrm{N}·$$

(5)

Equations (4) and (5) are the initial chain reactions; then, [HCN∙] and [CN∙] oxidized, generating [NCO∙]; [NCO∙] was hydrogenated to product [NH∙]; and [NH∙] was finally transferred to NO.

The prompt NOx route mainly occurred under fuel-rich conditions because the radical [C₂H₂∙] is the predecessor of radical [CH∙] [27]. Through the measurement, the presence of high concentrations of [CH∙] occurred at the regions of peak NOx, which proved that the prompt NO route generated the NOx [28]. Similarly, the prompt route was strongly coupled to the concentration of peak [CH∙] and flow residence time within the CH∙ layer [29].

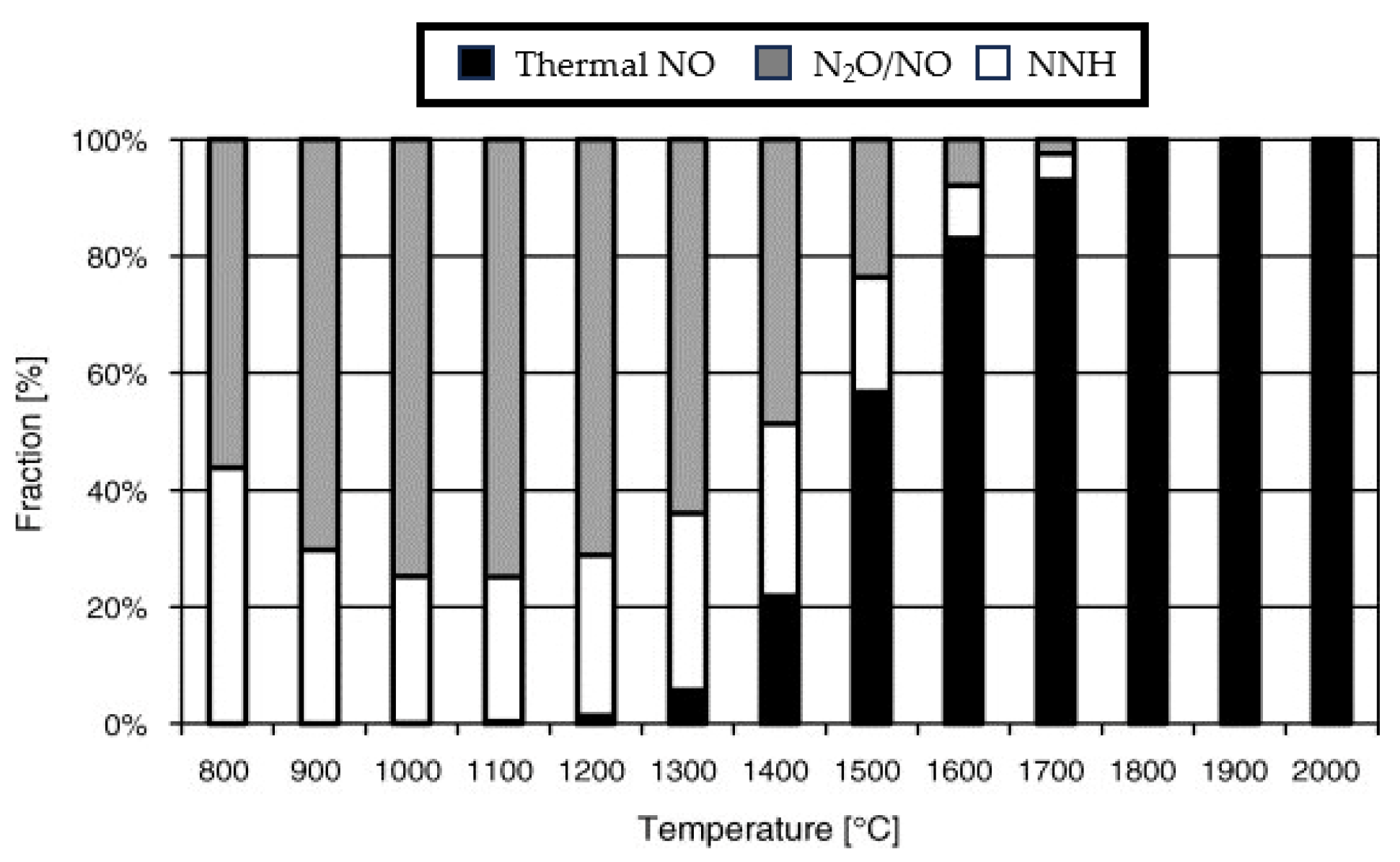
2.3. N₂O Route

The mechanism of the N₂O pathway is similar to the thermal NOx pathway, namely the radical [O∙] impacts the nitrogen. However, the N₂O pathway is a three-molecular mechanism that needs a M to exist. The main elementary reactions are as follows:

$${\mathrm{N}}_2+\mathrm{O}·+\mathrm{M}\to {\mathrm{N}}_2\mathrm{O}+\mathrm{M}$$

(6)

$${\mathrm{N}}_2\mathrm{O}+\mathrm{O}·\to 2\mathrm{NO}$$

(7)

The N₂O route would be dominant in the lean-fuel situation [30]. This pathway is often ignored because it is attributed to a small amount of NOx generation. However, when the situation is in lean-fuel conditions, the radical [CH∙] would be a small amount, the prompt pathway would be restrained, the low temperature would occur in lean-fuel conditions, and the thermal pathway would also be suppressed. At that time, the N₂O pathway would be mainly the route to product NO, especially when pressure is high, and the three-body reaction is still active, because of the existence of the third molecule, M.

The low reactor temperature and oxygen environment would prompt the N₂O route. In the moderate or intense low-oxygen dilution (MILD) combustion of the CH₄/H₂ fuel-blend system, with the reactor temperature increasing, the N₂O route decreased, and with the initial mass fraction of oxygen increased, the N₂O route increased [31]. Analogically, in methane oxy-fuel combustion, the N₂O route dominates the NO production at the area of mass fraction of oxygen from around 3% to 10% [32].

2.4. NNH Route

The NNH route, as a new pathway, was discovered in 1995 [33]. Through radical [O∙] and [NNH∙] combining and decomposing rapidly, it would finally generate the radical [NH∙] and NO.

$${\mathrm{N}}_2+\mathrm{H}·\to \mathrm{NNH}·$$

(8)

$$\mathrm{NNH}·+\mathrm{O}\to \mathrm{NO}+\mathrm{H}·$$

(9)

With the environment around oxygen atoms, the NNH is a dominant way to generate NO. In addition, the NNH pathway at lower mixture temperatures and short residence times contributes more to NO production [34]. Especially for the short residence times, the NNH route plays a dominant role in NO generation [35].

2.5. Fuel-N Route

The nitrogen in fuel could decompose with the combustion process, producing NH₃ and HCN∙. These would continue to be oxidated, finally producing NO. The fuel-N pathway usually occurs in coal combustion. However, for aviation fuel, because of the purification technology, the contents of jet fuel contained little nitrogen.

In summary, the formation process of NOx is a complex process coupled with different routes based on different equivalence ratios, temperatures, pressures, and residence times. The concentration of radicals changed with the residence time and directly affected the strength of elementary reactions about the NOx generation. Hence, to predict the NOx correctly, it is necessary to calculate the temperature and concentration fields accurately.

3. NOx Formation-Kinetics Approach

The mechanism utilization for NOx formation could be divided into two categories: the simplified mechanisms and the detailed mechanisms.

3.1. Simplified Kinetics

The first method is to estimate NOx formation using a steady-state hypothesis. By classifying the formation mechanism of nitrogen oxides, the formation rate of nitrogen oxides is expressed in the form of compound concentrations product. By using the quasi-steady-state hypothesis and the steady-state hypothesis, the concentration of radicals in the elementary reaction is expressed by the concentration of compounds, thus reducing the difficulty of calculation. The concentration field distribution of NOx was obtained by solving the transport equation of species. Generally, this method mainly was involved in the post-treatment of CFD, and it is believed that the generation of nitrogen oxides is small and has a weak influence on the generation process of fuel combustion.

Taking the thermal mechanism as an example, the nitrogen oxide generation rate, synthesized by the reaction of the three elementary elements, can be expressed as

$$\frac{\mathrm{d}[\mathrm{N}\mathrm{O}]}{\mathrm{d}\mathrm{t}} ={\mathrm{k}}_1[{\mathrm{N}}_2][\mathrm{O}·]+{\mathrm{k}}_2[\mathrm{N}·][{\mathrm{O}}_2]+{\mathrm{k}}_3[\mathrm{N}·][\mathrm{OH}·],$$

(10)

Combined on the assumption of the quasi-equilibrium of [N∙]

$$\frac{\mathrm{d}[\mathrm{N}·]}{\mathrm{d}\mathrm{t}} ={\mathrm{k}}_1[{\mathrm{N}}_2][\mathrm{O}·]-{\mathrm{k}}_2[\mathrm{N}·][{\mathrm{O}}_2]-{\mathrm{k}}_3[\mathrm{N}·][\mathrm{OH}·]=0,$$

(11)

Combining these formulas, the thermal NO production rate is [36]

$$\frac{\mathrm{d}[\mathrm{N}\mathrm{O}]}{\mathrm{d}\mathrm{t}}=2{\mathrm{k}}_1[{\mathrm{N}}_2][\mathrm{O}·],$$

(12)

Because the [O∙] is hard to calculate or measure, in practice, the concentration of radicals usually transfers to the concentrations of compounds, and this transfer can be performed via a calculation or measurement. Hence, the [O∙] usually can be expressed differently based on various compounds. For an equilibrium system of combustion, the [O∙] could be expressed as follows:

$$[\mathrm{O}·]={\mathrm{K}}_1\frac{\left[H_2\right]\left[O_2\right]}{\left[H_2\mathrm{O}\right]},$$

(13)

For an oxygen-rich environment, the [O∙] could be expressed as follows:

[O·] = K₂[O₂]^0.5.

(14)

Similarly, the prompt NO formation rate could be expressed as follows [37]:

$$\frac{\mathrm{d}\left[\mathrm{N}\mathrm{O}\right]}{\mathrm{d}\mathrm{t}} ={\mathrm{f}}_{\mathrm{C}}\times {\mathrm{k}}_{\mathrm{prompt}}\times {\left[{\mathrm{O}}_2\right]}^{\mathrm{a}}[{\mathrm{N}}_2][\mathrm{F}]\exp (-\mathrm{Ea}/\mathrm{R}/\mathrm{T}).$$

(15)

where a is the order of reaction, and f_C is a correction factor dependent on the air-to-fuel ratio and fuel type. Also, k_prompt equals 6.4 × 10⁶, and Ea equals 72,500 cal/g mol.

This simplified mechanism is commonly used in the CFD simulation, despite the fact that this method is relatively simple compared with the detailed mechanism. The possible error can be summarized at two points. Firstly, the simplified mechanism could not include all pathways of NOx generation but only express the average NOx formation, and the pathways of NOx generation are complex and affect each other based on different reaction environments. Secondly, in the combustion process, there is a super-equilibrium state which occurs after the fuel decomposes. Although the time period is relatively short, the concentrations of radicals would exceed the equilibrium ones by hundreds of times.

3.2. Detailed Mechanisms

The other approach is the detailed mechanisms, which combine all reactions that are related to the NOx generation. Usually, the chemical document would combine the fuel oxidization process and the detailed process of NOx generation. The NOx generation process would consist of thermal pathways and prompt pathways with specific elementary reactions. If the time steps are short enough, the calculation would be accurate compared with the real situation. Even though the calculation of this method is quite huge, it is still worth performing for significant compounds, such as evaluating the NOx production. The direct numerical calculation and the chemical reaction networks are all applied this way.

The common reactions assembled from detailed reactions are GRI-Mech 2.11 or 3.0 version, which is relative to the natural gas oxidization process. Waluyo and Aziz [38] investigated the hydrogen/air turbulent non-premixed flame on the model burner and applied the GRI-Mech 3.0 mechanism and partial Mevel mechanism to predict the NO emission. The results showed a better NO prediction of the GRI-Mech 3.0 because of the more elaborative nitrogen reactions. Tasdemir and Karyeyen [39] applied GRI-Mech 3.0 chemical kinetics integrated into the eddy dissipation-concept combustion model to predict the temperature and NOx profile emission of coke oven gas under a colorless distributed combustion technique. The consistency was achieved almost the same for NOx profiles between the measured and predicted ones.

4. The Empirical Formula Approach

At the early stage, the computer was not able to support the computational fluid dynamics of the NOx generation. Hence, making use of a large amount of experiment results could predict the tendency of NOx production.

Aiming at evaluating several gas turbine combustors, Lefebvre [40] proposed a method of evaluation that incorporates the product of reaction rate, mean residence time, and mixing coefficient into the following calculation:

$$NOx=A\left(\frac{P{V}_C}{{\dot{m}}_{A}T}\right){\left(\frac{\Delta P}{P}\right)}^x\exp \left(zT\right)$$

(16)

where $A$, $x$, and $z$ are constants representing the empirical coefficients of NOx generation; $\Delta P$ represents the pressure differential; and $T$ and $P$ represent the temperature and pressure in the combustion chamber, respectively.

The reaction rate could be represented as a function comprising the exponential of temperature and pressure. The mean residence time can be determined by considering the mass flow rate, density, and volume of the reactor. The fitting results showed that the NOx generation depended on the operating conditions and residence time and had little relationship with the fuel properties. The subsequent research followed this idea to calculate the NOx amount by correcting parameters in the empirical formula.

Odgers and Kretschmer [41] pointed out that fuel type, steam and water, and fuel vaporization affected the accuracy of the empirical formula for the gas turbine. And the empirical formula could be expressed as follows:

$$E{I}_{NOx}=29\exp \left(-\mathrm{21,670}/T\right)P_3^{0.66}\left(1-\exp \left(-250\tau \right)\right)$$

(17)

where $\tau$ represents the residence times; $P_3$ represents the combustor inlet pressure; and $T$ represents the effective flame temperature, which is relative to the combustor inlet pressure and temperature.

The revised empirical formula could be within the margin of error of 20%. At the same time, to overcome the shortcomings of the empirical formula, they designed a method based on the simplest chemical reaction rate model to predict NOx emission as follows, which has a stronger theoretical basis and is preliminarily considered more satisfactory than the empirical formula.

$$E{I}_{NOx}=\exp \left(A-B/T\right)\tanh (C\times P_3^D\times T_3^E\times {\varphi }^F\times \tau )$$

(18)

where $A$, $B$, $C$, $D$,$E$, and $F$ are the empirical coefficients; T represents the effective flame temperature, which is relative to the combustor inlet pressure and temperature; $P_3$ represents the combustor inlet pressure; $T_3$ represents the combustor inlet temperature; $\varphi$ represents the equivalence ratios; and $\tau$ represents residence times.

Based on the traditional empirical formula for predicting NOx emissions, Rizk and Mongia [42] took into account the influence of droplet evaporation and droplet size and combustor type, including the RQL combustor, diffusion flame combustor, and premixed combustor. By improving the prediction accuracy to modify the empirical formula, the simulation results were verified in the 3D model, and good matching results were obtained. The error between calculation and measurement is around 10%, which provides support for the subsequent utilization in advanced combustion systems.

Laviolette and Perez [43] used mathematical methods that introduced a large range of experimental data to optimize the coefficients of Lefebvre’s empirical formula and Odger and Kretschmer’s modified formula:

$$E{I}_{NOx}=1.902\times {10}^5\frac{P_3^{0.4048}\left(1-\exp \left(-480\tau \right)\right)}{\exp \left(\mathrm{37,902}/T\right)}$$

(19)

where $\tau$ represents residence times; $P_3$ represents the combustor inlet pressure; and $T$ represents the effective flame temperature, which is relative to the combustor inlet pressure and temperature. By increasing the coefficient of determination and smaller standard deviation, the experiment results can match the prediction results well.

Saravanan et al. [44] developed correlations to predict the NOx emissions of a stationary CI engine fueled with biodiesel at the standard and retarded injection timing.

$$\begin{array}{ll}NOx in ppm=& \mathrm{20,956.69}\rho \\ & \times \left[1+C\left[-5.740\times {10}^{-3}{L}^2+0.0995L-0.603\right]\right]\\ & \times \exp \left(0.948\times ID-18.83\right)\times \exp \left(4626.44/T_f\right)\end{array}$$

(20)

where $L$ represents the load, $ID$ represents the ignition delay, and $T_f$ represents the flame temperature.

The error between the prediction and the experiment is quite marginal at standard and retarded injection timing.

The advantages of this empirical-formula method are that it can simplify computational complexity and obtain data quickly. For the engineers who designed the combustion chamber, these advantages satisfied their requirement, which is that, by changing design parameters, they could obtain the response data quickly. However, this empirical-formula approach only includes temperature and pressure information; it does not contain the concentration of species and temperature distribution. For researchers who aim to reduce the production of NOx, this oversimplified method has many drawbacks, so it cannot give an accurate description of the temperature field, along with reactants and radical species’ concentrations [45].

With the development of artificial intelligence, neural networks were introduced to improve models. Shen et al. [46] applied a hybrid neural network architecture combining the convolutional neural network (CNN) and long short-item memory (LSTM) neural network to predict NOx emissions. The results demonstrated that the fitting coefficient of the CNN-LSTM network model is 0.977. Similarly, Park et al. [47] developed a machine-learning model for predicting NOx, using the Random Forest method to reduce the negligible input features. The final model showed an accuracy of R² = 0.965. Han et al. [48] proposed a hybrid deep neural network model for NOx emission prediction. In this model, an adversarial denoising autoencoder (ADAE) and the least support vector regression (LSSVR) were in the model to extract flame–deep features and to analyze the extracted features, respectively. The satisfactory prediction accuracy of this model is 0.97, meaning that it outperforms other state-of-art models.

The application of artificial intelligence and neural networks could effectively improve the prediction accuracy of the model, but the large number of training data required and the small adaptation range of the models are still the disadvantages of this method. According to empirical formula, the formation of NOx is mainly related with combustion temperature, oxidant concentration or its partial pressure, and retention time in the high-temperature region.

5. The Chemical Reaction Network Method

Although the CFD method coupled with the finite rate chemical reaction has achieved good results in the prediction of temperature and the results of infinite reaction rate, for the NOx generation process, which is a finite chemical rate process, the CFD method was limited by its turbulence reaction model, which showed the characteristics of huge calculation and accuracy problems. These drawbacks are deeply ingrained in the CFD method and limit the CFD method applied to the practical issue.

Unlike the CFD method, which needed to introduce reaction models to approach the concentrations, the chemical reaction networks (CRNs) method completely predicts the NOx generation via detailed mechanisms. In the CFD method, the concentrations of each point were calculated. But in the CRNs method, only the values at the exit are of concern. By sacrificing the accurate flow characteristics, the CRNs method could ensure the accuracy of concentrations. Also, with the decoupling of the flow, the calculation would be decreased [49]. Hence, the CRNs approach method is an economical and convenient method to evaluate NOx production compared with the other methods.

Except for the simulation of the results of combustion, the CRNs method could also be applied to research the effect of the coefficients.

Sharma et al. [50] built a skeletal chemical reactor network, which consists of two PSR units, to research the NO prediction for pure dimethyl ether by the effect of the equivalence ratio. Through applying two different mechanisms, the PSR model could approach the experiment date with 7.1 NOx dry ppm to 7.0 dry ppm at 3% O₂ at the equivalence ratio of 1.0.

Liu et al. [51] applied a Mixer and a PSR model to build a model for researching the relationship between adiabatic combustion temperature and heat loss. The results showed that, considering the heat loss, the PSR model showed NOx emissions increased slightly with increasing hydrogen content, which has a similar tendency to the experimental results.

Liu et al. [52] applied the CRNs model to simulate the NOx emission of a syngas-fueled gas turbine combustor using rich-burn, quick-mix, lean-burn (RQL) architecture, and the impacts of combustor design/operating parameters on NOx were investigated. The most significant parameter for NOx control is temperature. Following the mixing in the rich-burn zone, the airflow split emerges as a highly influential parameter. However, with the combustor outlet temperature increase, the residence time split and the mixing in the quick-mix zone become important.

In most cases, the chemical reaction networks (CRNs) model is widely applied to overcome the drawbacks of the CFD method, which showed a good agreement with the experiment results. For example, Xiao et al. [53] applied the CRNs model to simulate modern aircraft engine combustion chambers. The final result showed that the EI NOx predicted by the CRNs model approached the experiment results, especially at take-off and climb conditions. With the approach and idle condition, even the biggest deviation between them is under 12%. Xu et al. [54] applied the CRNs model to a rectangular section of a gas turbine combustor. The tolerance between experiment and simulation at two full-power and idle conditions is smaller than 10.13%. The results showed a good agreement with the practical. Rizk et al. [55] simulated the emission of the diffusion flame combustion chamber. The emission index of NOx through simulation was 42, and the experimental result was 44 at take-off conditions. The simulation result could match well with experiment one. Andreini and Facchini [56] used PSR and PFR models to simulate different types of combustion chambers, and the simulation results showed good accuracy compared with the experiment results. For the single-chemical reaction networks (CRNs) method, Villette et al. [57] divided the combustor into three sections to predict the accurate pollutant emission and combustion efficiency estimations. The CRNs approach to NOx emissions displayed a notable absolute accuracy for all power settings in all simulations.

The main constituent of the CRNs method are two kinds of ideal models, which are the perfect stirred reactor (PSR model) and the plug flow reactor (PFR model). There are two other models, namely the MIX model and the partially stirred reactor (PaSR model), that could also be applied to assist the simulation. The PSR model is mainly used to simulate the area of combustion, and the PFR one is used to stimulate the diffusion area. An essential element of the perfect stirred reactor model is the assumption that the reactor is sufficiently mixed to be described well by spatially averaged or bulk properties, in which the Damkohler number approaches zero [58]. The partially stirred reactor model is similar to the PSR model, but the difference between them is the mixing time scale. When the mixing time scale is small enough that the properties inside the reactor are homogeneously mixed, the PaSR model becomes the PSR model. The PFR models describe the steady-state tube-flow reactor that could be used for process design, optimization, and control. Each model represents a small region that has a small variation in physical and chemical parameters [59].

Through the combination of these four types of models with different amounts, the inner space of the combustion chamber could be rebuilt. The quantities of ideal models depend on the geometry of combustion. In the simplest case, a main reactor and a diffusion area could be applied to express a combustor [42]. The more ideal models are applied in the simulation system, the more accurate the flow pattern rebuilt by these models is. The few quantities of the ideal model could describe simple geometry, which usually applies dozens of PSR models and several PFR models in the examples mentioned above. In general, the CRNs model could independently operate without CFD results, but with the help of CFD information, the simulation could be more accurate. The complex geometries should be divided by the CFD_CRNs method, which would describe the latter.

Compared with the CFD method, the CRNs method has two advantages. First, the CRNs model decoupled with the chemical and flow process, meaning that the calculation would be decreased. Second, the calculation method of NOx emissions in the CRNs method is more accurate than that in the CFD approach. In the CFD approach to evaluate NOx emissions, the main method of calculation of the NOx reaction rate is through the concentration of compounds, but in the CRNs method, the detail radicals could be considered by thermal pathway, prompt pathway, N₂O pathway, NNH pathway, and so on. The quantities of species and elementary steps in the CRNs-approach method could be ten times than the CFD-approach method. With the detailed mechanisms applied in the CRNs model, more information would be enhanced compared with the approach of the only CFD simulation. The quantities of species and elementary steps in the CRNs-approach method could be dozens of times compared with the CFD-approach method.

6. Turbulent Combustion Simulation Approach

The computational fluid dynamics (CFD) method is a mathematical calculation method that makes the approximate-solution approach the real value by solving discrete functions in the domain. Because it can solve the Navier–Stokes equation effectively, it is widely applied in the calculation of hydrodynamics and thermal dynamics to predict flow patterns and temperature, which has obtained excellent achievements.

In conventional CFD calculations, the chemical reaction of fuel combustion is usually considered as a source item, and the subsequent flow process is used to diffuse the reaction product. This approximation has been successful in predicting hydrocarbon combustion. This is based on the fact that the decomposition of hydrocarbon fuels could be completed in an extremely short time. However, in response to the rapid decomposition of hydrocarbon fuels, the formation of NOx is as long as the order of seconds, and the formation is accompanied by the flow of the entire flue gas in the combustion chamber. The chemical reaction rate of NOx should be calculated with the whole flow process. Therefore, it is difficult to calculate the NOx formation using traditional calculation methods. Several different calculation methods were proposed to solve this problem, such as the direct numerical simulation method (DNS), probability density function method (PDF), and flame-let model (FLM). These methods of CFD are applied in the field of NOx generation in turbine combustors due to their convenience [60].

6.1. Direct Numerical Simulation Method

The direct numerical simulation method is a method that is based on the continuity equation, Navier–Stokes equations, energy equation, and transport equations of species, without considering any turbulence model. Compared with the other methods that contain turbulence models, the direct numerical simulation method introduces errors via the truncation error and round-off error.

Although the DNS method is straightforward in principle, it is computationally intensive. The number of grid scales depends on the flow pattern, chemical reaction, and thermodynamics. From the view of the flow pattern, the length scale of the mesh would range from the largest length scale to the smallest one, namely from the maximum turbulence integration length scale to the minimum length scale of turbulence, which is the Kolmogorov scale Lk, relating to viscosity. These length scales span a wide number of magnitudes, which is a function of the Reynolds number. Not only the flow effect should be considered, but also the chemical reaction led to refining the mesh, increasing the quantities of mesh. From the view of the laminar flame-let concept, which was widely applied in turbulent combustion, chemical time and length scales are sufficiently smaller than the smallest length and time scales of the turbulence [61]. Hence, to ensure the accuracy of this simulation calculation, not only the length scale of the mesh should consider the Kolmogorov scale, but also the ones corresponding to the chemistry scales. This would enlarge the amount of mesh inevitably. In addition, the interaction between flow and thermodynamics that introduced the Karlovitz number should also be considered. The number of grid-point scales, N, could be evaluated by this formula:

$$\mathrm{N}={\left(\frac{L}{{2l}_T}\right)}^3\mathrm{Da}\times \mathrm{Ka}\times {\mathrm{Re}}^{7/4},$$

(21)

where $L$ represents the one-dimensional turbulence length, $l_T$ represents the integration length scale of the fluctuating field, Da represents the Damkohler number, and Ka represents the Karlovitz number. With the computational capacity of current computers, it is imperative to regulate the mesh size within an acceptable range; the number of Damkohler, Karlovitz, and Reynolds should not be huge [62]. The DNS approach is exclusively applicable under conditions where the Reynolds number and Damkohler number are moderate, while the Karlovitz number is high. For the high Reynolds number condition, the DNS method could not be satisfied with the current computing ability [63].

The DNS method could be directly used to simulate the production of NOx and achieve the detailed structure of flames. Bédat et al. [64] applied the DNS method to simulate premixed combustion with methane. The authors attempted to apply three-step reactions to simulate the NO generation to reduce the calculation. When comparing the simulation results with the detailed mechanism, it was found that the abstract mechanism could not replace the detailed ones. Ohta et al. [65] used the DNS method to simulate three-dimensional compressible mixing layers with non-premixed hydrogen/air combustion with a detailed chemical reaction mechanism with NOx production. The results show that in the mixing layers, the formation and expansion of the combustion region by the roller vortices, and the baroclinic torque had a significant impact on NO production. The chemical reaction consists of 31 chemical species and 241 elementary reactions. Dinesh et al. [66] applied a 3D direct numerical simulation of the syngas non-premixed jet flame to discover the NO pollutant formation at a Reynolds number of 6000, and the GRI-Mech 3.0 mechanism was applied.

Not only the DNS method could evaluate NOx production, but also its generated data could be applied to build a lookup table for query and proofreading. In the research of Ren et al. [67], a lookup table was established through the NO source and various NO pathways averaged with the process variable and mixture fraction, which comes from a direct numerical simulation (DNS) database of turbulent stratified premixed flames. A similar application occurred in the works of Luo et al. [68]. They used the DNS database of combustion to verify the correction of a new model.

6.2. CFD with Different Combustion Models

In the prediction of nitrogen oxides, in addition to direct numerical methods, other CFD approaches must introduce turbulence models, combustion models, and NOx generation models. The introduction of turbulence models is typically aimed at resolving the closure problem in the Navier–Stokes equations arising from the Reynolds stress term.

The combustion model correlates the fuel reaction rate with the flow dynamics. Owing to the presence of turbulent fluctuation terms, the calculation of chemical reaction rates demonstrates non-linearity. Specifically, the average chemical reaction rate calculated using mean values (including temperature, reactant concentration, and density) does not equate to the average chemical reaction rate. Turbulent combustion models are required to provide closure for the mean reaction rates in the RANS species transport equations [45]. Hence, the inclusion of a combustion model is imperative for accurately determining the reaction rate of chemical reactions.

Typical combustion models encompass a range of approaches, including the eddy breakup (EBU) model, eddy dissipation model (EDM), eddy dissipation concept (EDC) model, conditional moment closure (CMC) model, probability density function (PDF) model, flame-let model (FLM) model, etc.

Various combustion models are based on specific assumptions and applicable ranges and could be categorized according to whether or not they can incorporate finite reaction rates. The EBU, EDM, steady laminar flame-let model, etc., were built as the fundamental assumption of the fast chemistry model. Because of the slow chemistry process of NOx generation, the NOx could not be calculated directly by these combustion models. Hence, the NOx approach of these combustion models would mainly have relied on the steady-state hypothesis calculation method. And the EDC, the composition PDF model, could calculate the finite-rate chemistry model. Therefore, they could approach the NOx with combustion models themselves. Based on the above content, whether these combustion models are compatible with finite reaction rates determines the approach of NOx models. The approach of NOx models was already discussed in Section 3.

6.2.1. Combustion Models with Fast Chemistry Hypothesis

The EBU combustion model was effectively utilized to predict the temperature and concentration of key species [69,70,71]. The standard EBU combustion model neglects chemical kinetics under the assumption of the reaction rate dictated by the turbulent mixing time scale [72]. Mobasheri and Shahrokhi-Dehkordi [73] applied the standard $k-\epsilon$ model, EBU combustion model, and NOx equilibrium assumption to predict the combustion process and NOx emission on a modified four-cylinder MPFI SI engine. The result showed that the EBU model with global assumption has the least deviations on the NOx emission. However, according to the results figure, it only compared with the result of the 420-degree crank angle, which has few results to prove this model could approach the NOx emission.

The EDM combustion model is also based on the infinite fast-chemistry assumption. The rate of reactions in EDM depends only on the behavior of the turbulent flow. Moreover, the EDM combustion model only handles the global kinetic mechanisms with a maximum of a few reactions. Hence, the model cannot discriminate between slow and fast chemistry [74]. Hosseini et al. [75] applied the standard $k-\epsilon$ model, the EDM combustion model, and the NOx equilibrium assumption to research the NOx emission of a methane/air diffusion flame. The simulation results showed that increasing the swirl number could reduce exhaust NOx values.

The PDF method treats the turbulent flow field from a completely random point of view. There are two approaches to determining the PDF in the modeling of a turbulent reacting flow. The presumed PDF method with a fast chemistry assumption could be employed to investigate the reaction–turbulence interactions. The transported PDF method is discussed in the next section.

Ribert et al. [76] and Robin et al. [77] provided a variety of presumed PDF shapes, and the most commonly used method is the form of the beta function. Bazdidi-Tehrani and Zeinivand [78] used the beta function to represent the probability density function containing 10 compounds related to the oxidative decomposition of hydrocarbon fuels. At the same time, the NOx generation rate was calculated with the quasi-steady-state hypothesis. Under the effect of the thermal radiation model, the concentration of NOx prediction reached a value of approximately 9 ppm, in good agreement with the experiment measurements. Hashemi et al. [79] researched the effect of air turbulence intensity on NO formation in the combustion of mixed hydrogen–hydrocarbon fuel. The turbulence–combustion interaction was chosen as a presumed beta PDF model due to its better results for the turbulent non-premixed reacting flow. The NO concentration increased with the axial distance increasing, and the deviation between the present results and numerical results reached the maximum value at the end of the axial distance, about 160 ppm, approximately 19% of the present results. Hashemi et al. [80] investigated the effect of air inlet conditions on NOx emission in a co-flowing methane/air diffusion flame. The beta PDF combustion model was applied to simulate the NOx emission. The average NOx emission at the exit of the combustors was 601 ppm, according to the present results, compared with 553 ppm from the other simulation results with similar conditions; thus, this simulation showed a good model validation. A similar method also appeared in Hashemi et al. [81] and Mohapatra et al. [82].

These combustion models were built under the assumption of fast chemistry. Because of the combustion models, the NOx approach method was applied to the equilibrium hypothesis. The reason is that the fast chemistry assumption is not compatible with the process of NOx generation.

6.2.2. Combustion Models with Detailed Mechanisms

Following the last section, another approach is through the joint probability density method. The joint probability density function not only contains composition but also could be combined with velocity or velocity–frequency. The main advantage of the PDF conservation equation is that the chemical reaction item is only related to the chemical variable, and no turbulence combustion model needs to be introduced. Therefore, PDF conservation equations can handle arbitrarily complex chemical reaction models. For instance, through the pure-composition PDF method to evaluate NOx production, Sahin [83] applied the PDF/Mixture fraction combustion model to provide more accurate results for the fuels that are a mixture of gases and more practical. Pashchenko [12] simulated a swirling flame of synthetic fuel combustion. By applying a composition PDF transport model to simulate finite-rate kinetic effects in reacting flow, this model not only could calculate the production of CO and NOx but also could be applied to simulate flame extinction and ignition. The main advantage of a PDF model is the possibility of obtaining an accurate value of NOx emission. The root-mean-square error of NOx emission is about 6% between the experiment and CFD calculation. Also, Tang et al. [84] applied a joint velocity–composition–turbulence–frequency probability density function method to calculate the production of a series of piloted-jet non-premixed methane flames. There are 19 species and 15 reactions, including NO formation. Compared with the experimental data of flames D and E, the NO mass fractions conditioned on mixture fraction at different axial locations showed agreement with the experimental data in the whole range, but in some locations, a slightly underpredicted phenomenon occurred. Paul et al. [85] also used a detailed zero-dimensional velocity–composition–frequency transported probability density function model (0D-VCF-tPDF) for numerical simulation, and the NOx mechanism was used in the chemical model. Compared with the 3D-CFD method, the 0D-VCF-tPDF method showed similar accuracy in the field of the predicted normalized engine-out NOx; the coefficient of determination is 0.867 to 0.866, respectively.

The composition PDF method has greater advantages in the fields of finite chemical rate and NOx production issues, but it has a large amount of computation, especially for its Monte Carlo method to solve the PDF equations. Usually, this method would be very expensive in the calculation field, needing a computation time of about two orders of magnitude greater than that for a PDF with a fast chemistry model [86].

Another method that allowed for finite chemistry is the EDC combustion model. The EDC model could be applied to overcome the drawbacks of the EBU model, which could consider the complex chemistry reaction. Zhang et al. [87] applied the standard $k-\epsilon$ model and the EDC combustion model with GRI-Mech 2.2 to predict the NOx emission of a moderate and intense low-oxygen dilution (MILD) combustion of natural gas. The simulation results showed a common tendency and small deviations with the experimental data at the different traverses. However, because of the integration to calculate the chemical composition equations within each cell, the calculation of this method is enormous [88], and it increased with the species numbers [89].

The CMC model is promising for predicting NOx emissions [90]. Tao et al. [91] combined the $k-\epsilon$ model and SIMPLE method with an elliptic-type CMC model to predict flow characteristics, conditional averaged temperature, and NO concentration with detailed mechanisms of the fuels. Reasonable agreement between experiments and predictions was obtained, which further confirmed the CMC model’s applicability in predicting the species concentration and temperature in turbulent non-premixed combustion. Even though the CMC model has several advantages in the field of NOx prediction, the CMC model’s calculation is enormous when there are complex chemical reactions, and the series expansion would introduce errors in calculating the time-average reaction rate. This method for turbulent premixed flames depends on the precision of the conditional scalar dissipation-rate model [92].

Finally, the FLM model was applied to the combustion models. The thermodynamic and chemical parameters are mapped to several control variables under the flame-let hypothesis, and a flame-let lookup table for turbulent combustion simulation is constructed based on the PDF function. The thermodynamic and chemical parameters of the flow field are obtained by solving the control variable in the flow field and looking up the table. This method realizes the decoupling of turbulence and chemical reaction, greatly reduces the degree of freedom in flow field solution, simplifies the complexity of combustion simulation, and can consider complex chemical-reaction mechanisms.

Yue et al. [93] applied two different flame-let libraries with GRI-Mech 2.2 that were generated by one-dimensional unstretched premixed flame and the one-dimensional counterflow diffusion flame, respectively, to predict NOx emissions in Sandia Flame D. To improve the accuracy of NOx emission prediction, two additional variables of mixture fraction variance and enthalpy loss were added. The mixture fraction used for the presumed probability density function integration, and the enthalpy loss took into account the non-adiabatic effect. Compared with the experimental data, the results applying the counter-flow diffusion flame library model to simulate over-estimate 4.2 times at the location of the maximum error occurred; as a comparison, the unstretched premixed flame library only over-estimated by 0.5 times. Yao et al. [94] used the steady-diffusion flame-let (SDF) model with detailed mechanisms to predict the generation of NOx; however, this method is not very suitable for the prediction of NOx emissions. This is because, in most examples, the mass percentage of NOx is overestimated by this method. This is because the elementary reactions involved in the production of NOx are relatively slow. Therefore, using the FLM model will cause the results to be too large. However, the prediction of the overall trend of NOx production is accurate.

Above all, the combustion models with detailed mechanisms would increase the predict accuracy and also increase the calculation cost.

Several references are listed to exhibit the CFD method in the field of NOx generation in the

Table 1. Several references are listed to exhibit the CFD method in the field of NOx generation.

Fuel	Premixed/ Non-Premixed	Turbulence Model	Reaction Model	Mechanisms	Deviation	Reference
Ammonia/dimethyl-ether	Premixed	DNS	-	A reduced model with 48 species and 294 reactions	Close to experimental data	[96]
Hydrogen	Non-premixed	DNS	-	Konnov mechanism with 31 species and 241 reactions	-	[65]
CnHm	premixed	Standard $k-\epsilon$	EDU	NOx equilibrium assumption	Only one point compared with the experimental data	[73]
Methane/air	Non-premixed	Standard  $k-\epsilon$	EDM	NOx equilibrium assumption	-	[75]
CH4/H2	Non-premixed	Realizable $k-\epsilon$	Presumed PDF	Thermal and prompt pathway	19% approximately	[79]
Synthetic (hydrogen-rich) fuel	Premixed	RNG $k-\epsilon$	Transported PDF	-	Root-mean-square error for NOx emission about 6%	[12]
Methane/air	Non-premixed	-	Transported PDF	19 species, 15 reactions	Agreement with the experimental data	[84]
Natural gas	Non-premixed	standard $k-\epsilon$ model	EDC	GRI-Mech 2.2	Small deviations with the experimental data	[87]
Fuel	Non-premixed	$k-\epsilon$ model	CMC	-	Reasonable agreement between experiments and predictions	[91]
CH4-air	Premixed	Standard  $k-\epsilon$	FLM	GRI-Mech 2.11	0.5 times overestimation referring to the experimental data	[93]

. The table shows that the CFD method could evaluate NOx emissions in different combustion chambers. The CFD method could predict the tendency of NOx emissions successfully [95], but the deviation in prediction NOx would approach around 10–20%, even though, in some specific cases, the deviation would be approximately 6%. Moreover, the species of the fuel commonly are methane, natural gas, or hydrogen, which has limited quantities of reactants and reaction mechanisms.

Through the above review, it could be found that CFD as a prediction of NOx-generation calculation methods contained many pathways. Although each of these methods has its advantages, they still have the same shortcomings in some respects:

First, the number of reactants involved in the production of NOx is relatively small in most examples. In most of the examples, it is considered that the formation of NOx has no strong influence on the combustion process. Therefore, with a few exceptions, only a limited number of compound concentrations are used in most of the examples to represent the thermal mechanism, prompt mechanism, and N₂O mechanism on the formation of NOx. This method is often based on the assumption of a quasi-steady state or partial steady state, but in the initial stage of combustion, overbalance occurs very easily, so the prediction results based on the steady-state assumption are often small.

Secondly, the calculation process is prone to errors due to the mismatch between the mesh length scale of turbulent motion and the length scale corresponding to the chemical reaction time. If the number of grids needs to be encrypted to meet the needs of predicting chemical reactions, this result will inevitably lead to a substantial increase in computing capacity, far beyond the current computing capacity. If the chemical reaction accuracy is sacrificed, the predicted concentration of each reactant will be inaccurate. Although most CFD approach methods, except the DNS method, try to decouple the flow from the chemical reaction process, it is still impossible to avoid the occurrence of mismatches.

Finally, the chemical framework’s ordinary differential equation (ODE) exhibits stiffness phenomena. In the practical of chemical dynamics, the subprocess would be encountered with multiple interactions but very different rates of change, which leads to the solution of the corresponding ordinary differential equation containing some variables that decay very quickly and other variables that change relatively slowly. When trying to solve this kind of problem numerically on the slow variable interval of the solution, although the value of the fast variable component has declined to negligible at this time, the rapid change in the interference still seriously affects the stability and accuracy of the numerical solution and brings great substantial difficulties to the whole calculation. This phenomenon is called the stiffness of ODE, and the initial value problem of the ordinary differential equation describing this kind of process becomes a rigid problem. Especially in the process of predicting the formation of NOx at a finite rate of chemical reaction, the stiffness of the differential equation of substance concentration prediction will lead to the inaccuracy of the calculation results.

6.2.3. Combustion Models with CRNs Method

Not only could the CRNs model be used alone to simulate the prediction of NOx generation, but it also can further improve the prediction accuracy of NOx generation based on the flow-fitting results of CFD. NOx formation is a chemical reaction process with a strong correlation between temperature and reactant concentration. However, the temperature gradient and concentration gradient in the combustion chamber vary greatly during the combustion process, after combustion, and after air mixing, so more detailed flow information and temperature-concentration information are needed to provide more accurate guidance for CRNs modeling. The CRNs method combined with the CFD information has become a common method in current research.

In a complex flow field, the complexity of the flow field is related to the number of CRNs units required. In theory, more CRNs simulation units could describe the changes in temperature and concentration in the flow field with more detail; especially in areas with large temperature gradients and large concentration changes, it is more necessary to increase the number of CRNs simulation units. By comparing the fitting results of a different number of units, it can be found that the prediction results of 12 PSR models, 1 PFR model, and 3 MIX models using complex models are closer to the experimental results than that of 5 PSR models, 1 PFR model, and 1 MIX model using simple models [97]. A similar conclusion was also obtained by Monaghan et al. [98]. They compared the precision of the CRNs model in predicting NOx and CO concentration with different numbers of PSR models. The results showed that as the number of PSR models increased, the accuracy of NOx generation progressively increased and approached the experimental results. It is important to note that an increase in the number of CRNs analog units will lead to a substantial rise in computational workload [99].

The combined method of CRNs and CFD could effectively predict the NOx generation. Xue et al. [100] applied the combined CFD–CRNs method to research the impact of steam addition on combustion and NOx emissions in a model annular-type gas turbine combustor. Through the information provided by the CFD simulation, a 14-element CRNs model using the Jet-A fuel was built. The CRNs model prediction was compared with the ICAO databank at different operation conditions. The whole EI NOx showed almost the same results in different power settings, except for one that is on the idle power point, in which the relative error is about 10%. Ahmad et al. [101] analyzed the pollutant discharged NOx from a gas turbine ignition chamber using methane gas. Two kinds of CRNs models were built through the CFD simulation, providing flow information. The simple CRNs model contained 5 PSR reactors, and the complex CRNs model contained 12 PSR reactors. Compared with the experimental value, the NOx emission from the complex CRNs model showed the same tendency at the equivalence ratio from 0.5 to 0.8. the biggest error occurred at ER = 0.8, which is about 11.1%. Nguyen et al. [102] established a model of NOx emission level in lean oil-premixed combustors by combining CFD and CRNs models. Among them, the CRNs model used 41 reaction units, and its reaction mechanism was GRI-Mech 3.0. The simulation results showed that when the equivalent ratio is 0.5, 0.6, and 0.7, the predicted results of the NOx model jointly established by CRNs and CFD are closer to the test results than those obtained by CFD post-processing. Truc Huu, Kim, Park, Jung, and Kim [97] simulated a lean combustion gas turbine using natural gas. By combining CFD and CRNs methods, it could be used to predict the change in temperature and reactant concentration. Among them, CFD is used to simulate the temperature field and velocity field of the flow field, providing effective data support for the material flow exchange in the CRNs model, where the chemical reaction uses the two-step global reaction of methane. The results show that the combined modeling of the CFD and CRNs models could effectively and quickly predict the changes in velocity, temperature, and concentration in the flow field more accurately. Chang et al. [103] used a two-step global reaction of methane to simulate combustion with CFD, followed by a GRI-Mech 3.0 mechanism to simulate NOx generation in the combustion chamber. The CRNs model includes five PSR models and one PFR model. Through the combination of the CRNs model and CFD, the prediction of NOx generation is effectively solved. Nguyen [104] used 24 CRNs units to predict NOx emissions in a lean combustion chamber, and the error between the reaction group prediction and the test results was less than 1.2%. Zhang et al. [105] established two kinds of CRNs models based on CFD flow simulation results, among which the simple model included 7 PSR models and the detailed model included 15 PSR models. The reaction mechanism file in the CRNs model is the detailed JP10 reaction mechanism, which includes 82 substances reacting with 374 step elements. Compared with the experimental results, the results of the detailed CRNs model are closer to the results of the empirical formula than that of the simple CRNs model. For the CRNs combined with the CFD method, Chaturvedi et al. [106] applied this method to simulate the NOx emission of ammonia–hydrogen-blend fuel on the premixed combustion. The results showed that, in a large range of equivalence ratio of 0.65–1.2, the approach tendency is correct compared with the experimental data.

Through these examples, the CFD simulation could apply a global reaction or two-step mechanisms of the fuel to provide the flow field information, mainly about the temperature field. Even though this operation would reduce the accuracy of the flow field, considering that the fuel oxidation process is independent of the NOx generation, this sacrifice was acceptable for most cases. Without the complex mechanism, the CFD simulation could reduce the cost of time and CPU resources. Then, the CRNs model could add detailed mechanisms, which include the NOx-generation process to ensure the accuracy of NOx generation.

The methods that were used for CFD to be combined with the CRNs built model could be summarized by several methods. In some cases, the combustor is divided by flow patterns from the CFD simulation results, such as streamlines and temperature [103,107,108,109,110], or based on the local temperature gradient [99]. By partitioning the combustion volume based on temperature or flow-pattern characteristics, a preliminary model was developed. And then, through several iterations, the research goals would fit with the experiments. In some instances, the CFD data were utilized through a blend of unsupervised clustering and graph-scanning algorithms to automatically construct a CRN model for enhanced accuracy [52,111].

Several references are listed in the

Table 2. Several references were listed to exhibit the CRN and CFD_CRNs methods in the field of NOx generation.

CRNs/CFD_CRNs	Fuel	Object	Mechanism	Units	Deviation	Reference
CRNs	Dimethyl ether and its mixtures with methane/hydrogen	Flameless furnace	NUIG-Mech 1.1 and CRECK kinetic schemes	2 PSRs	7.1 dry ppm @3% O2 to 7.0 of experimental data	[50]
CRNs	Hydrogen/methane blends	Moderate or intense low-oxygen dilution (MILD) combustion	GRI-Mech 3.0	1 Mixer and 1 PSR	Similar tendency to the experimental results	[51]
CRNs	Syngas-fueled	Gas turbine combustor with RQL	a dedicated syngas mechanism with 44 species and 251 reactions	9 PSRs, 1 Mixer, and 1 PFR	-	[52]
CRNs	RP-3 kerosene	LESS combustor	a surrogate of Jet-A fuel mechanism	10 PSRs, 2 PFRs	Maximum 10.13%	[54]
CFD_CRNs	Jet-A fuel	A model annular-type gas turbine combustor	Jet-A fuel	10 PSRs, 1 PFR, and 3 Mixer	Maximum 10%	[100]
CFD_CRNs	Methane gas	Gas turbine ignition chamber	GRI-Mech 3.0	12 PSRs, 1 PFR, and 1 Mixer	Maximum 11.1%	[101]
CFD_CRNs	CH4	Lean–premixed gas turbine combustors	2-step model of CFD GRI-Mech 3.0 of CRNs	39 PSRs, 1 PFR, and 1 Mixer	Similar tendency to the experimental results	[102]
CFD_CRNs	CH4/air	Gas turbine combustor	GRI-Mech 3.0 of CRNs	17 PSRs, 2 PFRs, and 5 Mixers	The error estimate is smaller than 1.2%	[104]
CFD_CRNs	JP10	Aero-engine combustor	detailed JP10 mechanism of CRNs	15 PSRs, 1 PFR, and 3 Mixer	EI_NOx was 24 g/kg to 26.4 g/kg of the experiment at 100% load	[105]

. From the content of the table, it could be found that the CRNs and the CFD_CRNs method could predict the NOx emission with a small deviation, which is approximately 10%. And it could be widely applied under different conditions. The CRNs method and the CFD_CRNs method focused on the chemical reaction; and the types of fuel could be abundant, which could simulate the NOx emission of the aviation fuel. This is another advantage of this method.

The CRNs method is more focused on the concentrations of each reactant compared with the flow field of the CFD method. Through the more detailed reaction documents applied, the CRNs method could be based on the concentration to calculate the reaction rate in each time node. This avoids the introduction of the combustion model, which would easily lead to errors in the chemical condition. This is the key point of the CRNs method to improve accuracy. With the sacrifice of the flow characters, the steps of the time scale could decrease enough to avoid the problem of stiffness in ODE equations. This would enhance the accuracy of the calculation in comparison to the CFD approach, without introducing additional computational overhead. Finally, the CRNs method could be applied based on the condition of the early stage. Because of the independence of the geometry, the CRNs method could be applied without detailed flow information, only through the residence time, temperature, and pressure.

Even though there are several advantages to the CRNs method, it still has limitations in application. First and foremost, the accuracy of the CRNs method remains contingent upon the geometric characteristics of the combustor chamber. The more units applied, the more accurate simulation would become; however, there is still a limitation of quantities of units. And with the quantities increased, the time of calculation would also increase rapidly. There is a balance between the time cost and the accuracy of NOx production. Moreover, the methods to divide models in some specific ways are still not universally relevant for each case, which needs to state the guidelines to satisfy each case.

7. Conclusions

The empirical formula provided a large scope of application due to easy access. With the help of artificial intelligence, this method could be extended further application in practical use with accuracy improvement. According to the empirical formula, the formation of NOx is mainly related with combustion temperature, oxidant concentration or its partial pressure, and retention time in the high-temperature region.

The computational fluid dynamics (CFD) methods can capture the combined behavior of flow, temperature, and reactant concentration. In the prediction of the nitric oxide (NOx) generation field, the simulation by the direct numerical simulation method (DNS) is limited due to its enormous calculation. The other computational fluid dynamics (CFD) methods were restricted by the accuracy of their combustion model, with 10–20% deviation. Moreover, the computational fluid dynamics (CFD) method would be applied only to the types of fuels that contain a finite number of reactants and reaction mechanisms, which would not be suitable for the complex components of fuel.

The chemical reaction networks (CRNs) method focuses on the chemical reactions by sacrificing the flow of information. The chemical reaction networks (CRNs) method is more suitable than computational fluid dynamics (CFD) for the simple flow.

The chemical reaction networks (CRNs) method should be combined with computational fluid dynamics (CFD), as the prediction of NOx would be improved by coupling both advantages.