Metrics for Evaluating Synthetic Time-Series Data of Battery

Abstract

The advancements in artificial intelligence have encouraged the application of deep learning in various fields. However, the accuracy of deep learning algorithms is influenced by the quality of the dataset used. Therefore, a high-quality dataset is critical for deep learning. Data augmentation algorithms can generate large, high-quality datasets. The dataset quality is mainly assessed through qualitative and quantitative evaluations. However, conventional qualitative evaluation methods lack the objective and quantitative parameters necessary for battery synthetic datasets. Therefore, this study proposes the application of the rate of change in linear regression correlation coefficients, Dunn index, and silhouette coefficient as clustering indices for quantitatively evaluating the quality of synthetic time-series datasets of batteries. To verify the reliability of the proposed method, we first applied the TimeGAN algorithm to an open-source battery dataset, generated a synthetic battery dataset, and then compared its similarity to the original dataset using the proposed evaluation method. The silhouette coefficient was confirmed as the most reliable index. Furthermore, the similarity of datasets increased as the silhouette index decreased from 0.1053 to 0.0073 based on the number of learning iterations. The results demonstrate that the insufficient quality of datasets used for deep learning can be overcome and supplemented. Furthermore, data similarity can be efficiently evaluated regardless of the learning environment. In conclusion, we present a new synthetic time-series dataset evaluation method that is more reliable than the conventional representative evaluation method (the training loss rate).

1. Introduction

Deep learning has recently been employed in various industries, and its applications include failure diagnosis in manufacturing [1], autonomous driving in the automotive industry [2], and battery state estimation in the energy industry [3]. Deep learning creates models through data-based learning; therefore, datasets are an essential element of deep learning. Notably, using a small training dataset can cause overfitting or underfitting problems. Moreover, the learning model accuracy decreases when many outliers are present in the training dataset. Therefore, building high-quality datasets is crucial to improve the performance of deep learning algorithms.

The Kaggle and KITTI datasets [4] are representative open-source datasets used for training in deep learning algorithms. However, the availability of difficult-to-measure or specialized open-source datasets is limited. Datasets can be built through experiments or generated using generative adversarial networks (GANs). Representative data augmentation algorithms include deep convolutional GAN (DCGAN) [5], Wasserstein GAN (WGAN) [6], least squares GAN (LSGAN) [7], continuous recurrent neural network with GAN (C-RNN-GAN) [8], recurrent conditional GAN (RCGAN) [9], and time-series GAN (TimeGAN) [10]. In particular, NASA’s battery dataset has a small amount of cell data measured under the same conditions (temperature, battery usage pattern, etc.) [11], so it is necessary to generate a synthetic battery dataset through an augmentation algorithm.

Although a GAN algorithm can generate large amounts of battery data, it also generates abnormal data. In particular, when using the GAN-generated battery data for state of things (SoX) estimation algorithms, the accuracy of the algorithm is affected if the dataset contains an excessive amount of data with abnormal characteristics. Therefore, it is essential to evaluate the quality of synthetic datasets—i.e., their similarity to the original datasets—before using them in estimation algorithms.

In general, qualitative and quantitative evaluation methods are used to evaluate synthetic datasets generated through GAN. A typical qualitative evaluation method involves visually evaluating data similarities. The similarity between the original and synthetic data is determined by experts from multiple perspectives [6,7]. The image data are evaluated based on composite data. The time-series data are visually evaluated through a graph according to the time axis [12]. In addition, in the case of time-series data, data features are extracted and qualitatively evaluated using heat maps [13], which express the connection between the features, and dimension reduction algorithms such as t-distributed stochastic neighbor embedding (t-SNE) and principal component analysis (PCA) [10,14] that represent samples as one point. This evaluation method has a limitation—the evaluation results are fluid, as there is no objective criterion, and reflect the subjectivity of the evaluator.

The quality and diversity of the images generated through the Inception model are learned and evaluated by the Inception Score (IS) and Frechet Inception Distance (FID) [15]. Images are also evaluated using the CID Index, which reflects their creativity, inheritance, and diversity [16]. This evaluation method is generally suitable for evaluating image data (a field of computer vision) but not for synthetic battery data.

Time-series data evaluation methods include quantitative evaluation through the learning of the loss rate of the GAN algorithm and the accuracy of the classification algorithm, which varies depending on the learning environment. Among the evaluation methods based on statistical techniques used for the time-series analysis, dynamic time warping (DTW) has been used to compare data similarity at various time axes [12]. Furthermore, data have been evaluated using the Euclidean and Wasserstein distances [13] between data points. The DTW evaluation technique can evaluate data that repeat a specific cycle and are classified under the same label, and it is difficult to evaluate the non-clusterable data (i.e., battery) used in estimation and prediction algorithms.

Generally, the use of qualitative techniques (which express results visually) reflects the subjective evaluation of the evaluator; however, their accuracy and reliability are poor. In quantitative techniques, learning loss is generally used as an evaluation criterion; however, an objective comparison is difficult because the loss varies based on the learning environment.

Data augmentation addresses the insufficiency problem of battery data. To ensure the reliability of such augmented battery data, this study proposes three quantitative indicators (namely, the rate of change of linear correlation coefficients, the Dunn index, and silhouette coefficients) that directly evaluate the quality of synthetic battery data, specifically, its similarity to the original data. Similarity can be visualized through existing qualitative evaluation methods, such as t-SNE, but they are not suitable for evaluating the battery data of estimation algorithms. Moreover, visual evaluation is affected by the subjectivity of the evaluator. Therefore, to overcome this limitation, the quality of synthetic battery data is quantitatively evaluated using the adopted correlation coefficient and clustering technique (Dunn index [17] and silhouette coefficient [18]) using visual evaluation (t-SNE [19]).

The contributions of this study are as follows:

• The proposed method can satisfy and compensate for the quality of insufficient datasets in deep learning-based battery estimation and fault diagnosis.
• By evaluating the quality of the data, high-quality data can be obtained for battery estimation and fault diagnosis.
• The proposed method can efficiently evaluate battery data both visually and quantitatively, regardless of the learning environment.
• The proposed method can also evaluate the synthetic battery data generated using data generation techniques other than TimeGAN for similarity.
• The proposed method can be used for data other than battery data to evaluate the similarity of data.

2. TimeGAN

TimeGAN [10] is a time-series data augmentation algorithm that incorporates temporal characteristics into the GAN algorithm. The GAN algorithm comprises a generator and a discriminator. Its basic structure is shown in Figure 1. Synthetic data similar to the original data are generated by using random noise as the input to the generator, whereas the discriminator distinguishes between the original and synthetic data. This algorithm can be expressed as show in Equation (1).

$${\mathit{min}}_G{\mathit{max}}_{D}V(D,G)=E_{x{P}_{data}\left(x\right)}\left[logD\left(x\right)\right]+E_{Z{P}_Z\left(z\right)}\left[log(1-D\left(G\left(z\right)\right))\right]$$

(1)

where D represents the discriminator that classifies the original data and synthesized data of the battery, G represents the generator that generates virtual battery data, E denotes the expected value, and $V(D,G)$ denotes the value function of the GAN algorithm. The GAN algorithm learns along the direction in which the value function is maximized, that is, along the direction in which it is difficult to distinguish between the synthesized and original battery data. When discriminator D determines that the original battery data x is True and the synthesized battery data $G\left(z\right)$ is False, the value function is maximized.

Based on this working principle, TimeGAN, which adds functions to generate battery data by learning the temporal characteristics of data based on the GAN algorithm, has a framework consisting of an autoencoder and a GAN, as shown in Figure 2. The autoencoder rapidly learns the features of the input data by reducing the data to a lower dimension, whereas the GAN generates and evaluates the synthetic battery data. Therefore, data reflecting both the static and temporal (dynamic) characteristics of the battery data are generated by reconstructing the reduced dimensions and generating data.

3. Proposed Evaluation Method

A sufficient battery dataset is required for battery SoX estimation through deep learning. However, battery datasets require data generation because the amount of cell data obtained under similar conditions is small. If there are many abnormal features in the generated battery dataset, the accuracy of the algorithm is degraded; therefore, it is necessary to evaluate the composite data. Existing evaluation techniques have limitations in that these are not suitable for battery datasets and/or are affected by the subjectivity of evaluators. Therefore, to ensure the quality of the synthetic battery dataset, we propose three quantitative evaluation methods in the t-SNE plot through dimension reduction. The quality of the dataset is quantitatively evaluated using a correlation coefficient of linear regression, which allows data to be compared for linearity, and a clustering evaluation index (Dunn index, silhouette coefficient), which compares the classification accuracy of two clusters). To compare the changes in the linear characteristics of the data, the rate of change in the correlation coefficient was used, and the clustering evaluation index was used to utilize the distance information of the data.

3.1. t-SNE

t-SNE [19], a dimensionality reduction technique that represents high-dimensional data in a low-dimensional form and visualization, compensates for the disadvantages of the Gaussian distribution in SNE.

SNE reduces high-dimensional data to low dimensions while preserving the distance information between close data points as probabilities; these probabilities, representing the distances, follow the Gaussian distribution, as shown in Equation (2). However, the Gaussian distribution has a limitation, in that learning is not reflected beyond a certain distance owing to large changes in probability values.

$$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}$$

(2)

To overcome this limitation, the t-SNE dimensionality reduction technique uses t-distribution, which has a wider predictive range than that of the normal distribution. The t-distribution, defined in Equation (3), has thick tails on either side due to its larger variance than that of the standard normal distribution (see Figure 3), indicating a wide predictive range.

$$t=\frac{\overline{x}-\mu }{s/\sqrt{n}}$$

(3)

The t-SNE uses the t-distribution to compute similarity between two points in the low-dimensional space to regenerate the axis for the new feature.

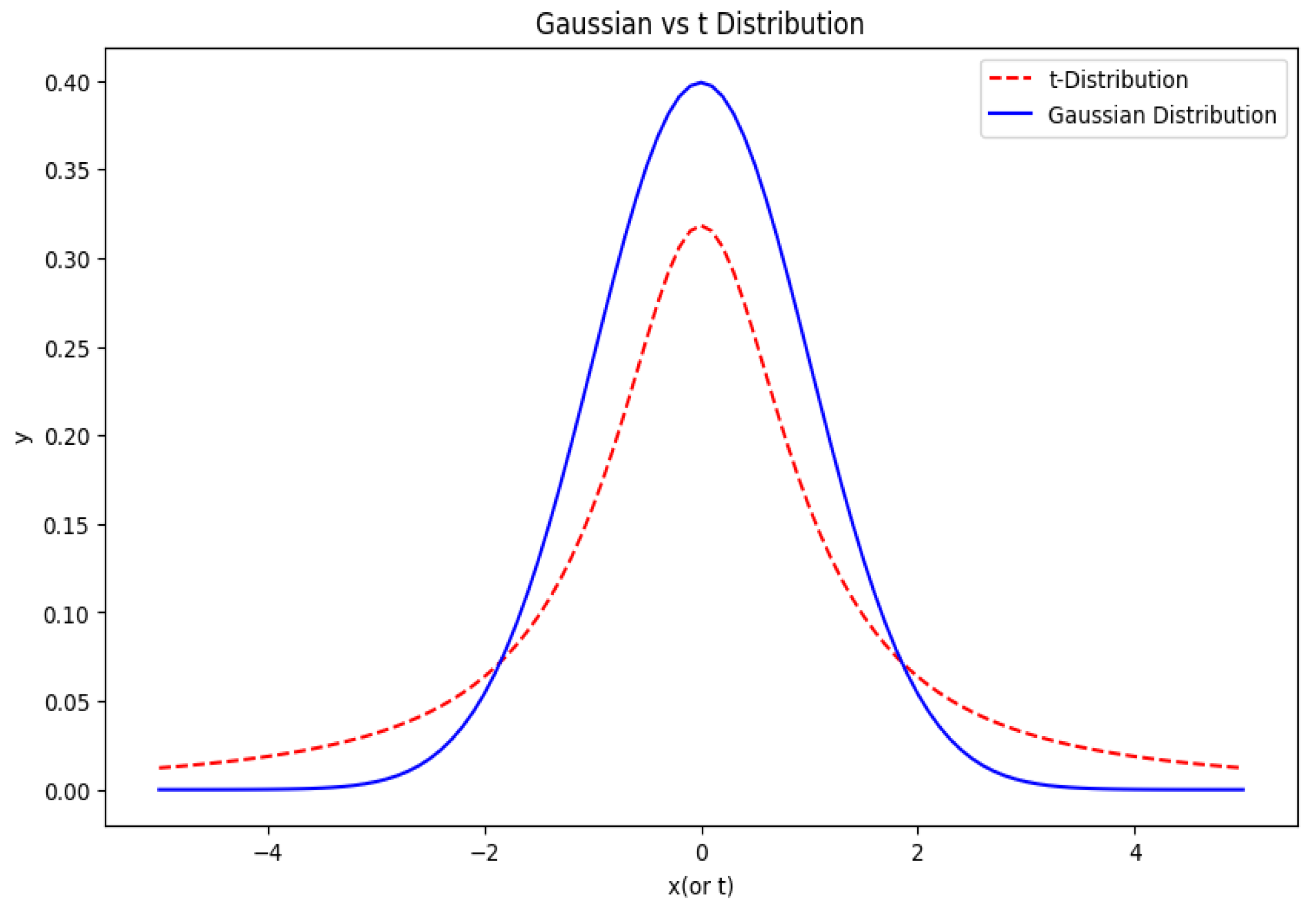
3.2. Rate of Change in Correlation Coefficient of Linear Regression

Linear regression, an analysis technique that models the linear correlation between two variables from the given data, describes the relationship between variables by finding the correlation coefficient that expresses the tendency of the given data.

In this study, the quality of the data is evaluated by comparing the correlation coefficients of the linear regressions of the original dataset and the dataset to which the composite data is added. The more similar the linear characteristics of the data, the more similar the correlation coefficient between these datasets.

The reliability of the correlation coefficient is ensured through the determination coefficient [20], and the correlation coefficients of the original dataset and synthetic dataset including original data are calculated. The calculated correlation coefficient is applied to Equation (4) to calculate the rate of change (ROC) in the correlation coefficient. The quality of the data is evaluated using the rate of change in the correlation coefficient.

$$RateOfChange(\%)=\frac{|r_{\mathit{ori}}-r_{syn}|}{r_{\mathit{ori}}}$$

(4)

where $r_{ori}$ and $r_{syn}$ represent the correlation coefficients of the original dataset and synthetic dataset including original data, respectively. When the linear characteristics of the original and composite datasets are similar, the rate of change of the correlation coefficient has a value close to 0. When the linear characteristics of the original and composite datasets differ, the rate of change of the correlation coefficient has a large value.

3.3. Dunn Index

Among the clustering evaluation indicators, the Dunn index is a representative indicator for evaluating clustering in the field of clustering research, such as keyword classification [21] and validity evaluation [22] of documents. The Dunn index determines whether the data classification according to the characteristics (char.) of the data is efficiently performed based on the ratio of the distance outside the cluster, and calculates it as show in Equation (5).

$${\mathit{DI}}_{\mathit{K}}=\frac{\mathit{min}\delta \left(C_{\mathit{i}},C_{\mathit{j}}\right)}{\mathit{max}{\Delta }_{\mathit{k}}}$$

(5)

where ${\Delta }_k$ represents the Euclidean distance between objects within the same cluster, and $\delta \left(C_{i,}{C}_j\right)$ represents the Euclidean distance between objects belonging to different clusters.

In this study, the concept of Dunn index is applied in reverse to evaluate the data quality. The Dunn index is calculated from the maximum and minimum distance between the original and composite datasets. The more similar the characteristics of the data, the smaller the minimum distance between the datasets; therefore, it has a smaller value.

To apply the Dunn index, data are expressed through dimension reduction. First, the distance between the two farthest data within the original dataset and the distance between the closest data between the original and composite datasets are obtained. The Dunn index is then calculated by applying the two values in Equation (5), and the similarity of the data is thus determined.

When the Dunn index has a small value, the composite and original datasets have similar characteristics and may be interpreted as the same cluster. When the index has a large value, it may be interpreted that the characteristics of the datasets differ because the two datasets are divided into different clusters. A high-quality synthetic dataset should have characteristics similar to those of the original dataset; thus, the Dunn index should have a small value.

3.4. Silhouette Coefficient

Along with the Dunn index, the silhouette coefficient is another evaluation index for clustering [18]. This coefficient evaluates the classification of data by comparing the average distance between data in the cluster and the average distance between the clusters. This index is calculated as show in Equation (6)

$$\mathit{S}\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\mathit{max}\{a\left(i\right),b\left(i\right)\}}$$

(6)

where $a\left(i\right)$ represents the average distance to other data within the cluster, and $b\left(i\right)$ represents the average distance to data in other clusters.

In this study, the absolute value of the silhouette coefficient is used as the average distance between the original and composite datasets to evaluate data similarity. The data quality is determined using the value of the silhouette coefficient applied in the clustering technique. As the characteristics of the data are similar, the average distance between the datasets and the average distance within the dataset are also similar. Therefore, its value is close to 0.

To apply the silhouette coefficient, data are expressed through dimensional reduction, and the average distance within the original dataset and the average distance between the original and composite datasets are obtained. After substituting for the average distance in Equation (6), the absolute value is obtained, and the data similarity is evaluated through the size.

When the absolute value of the silhouette coefficient is close to 1, the composite dataset does not reflect the characteristics of the original dataset or only partially reflects the characteristics of the original dataset. When the value of the silhouette coefficient is close to 0, it is inferred that the original and composite datasets have similar characteristics (and thus cannot be distinguished) and a high-quality composite dataset has been generated. Therefore, the silhouette coefficient should be close to 0 for a composite dataset with quality similar to that of the original dataset.

4. Results and Analysis

To validate the proposed evaluation method, we generated a synthetic battery dataset based on TimeGAN using the NASA battery dataset. To facilitate the comparison between the original and synthetic time-series datasets, we applied the proposed evaluation method of reduced dimensions. Subsequently, we compared the proposed evaluation method with the existing indirect evaluation method of training loss. The software and hardware environments were as follows: Ubuntu 22.04 LTS, Python 3.7.12, TensorFlow 1.15.0, CUDA 12.2, Nvidia Driver 535.54, Intel Xeon CPU, and NVIDIA A30.

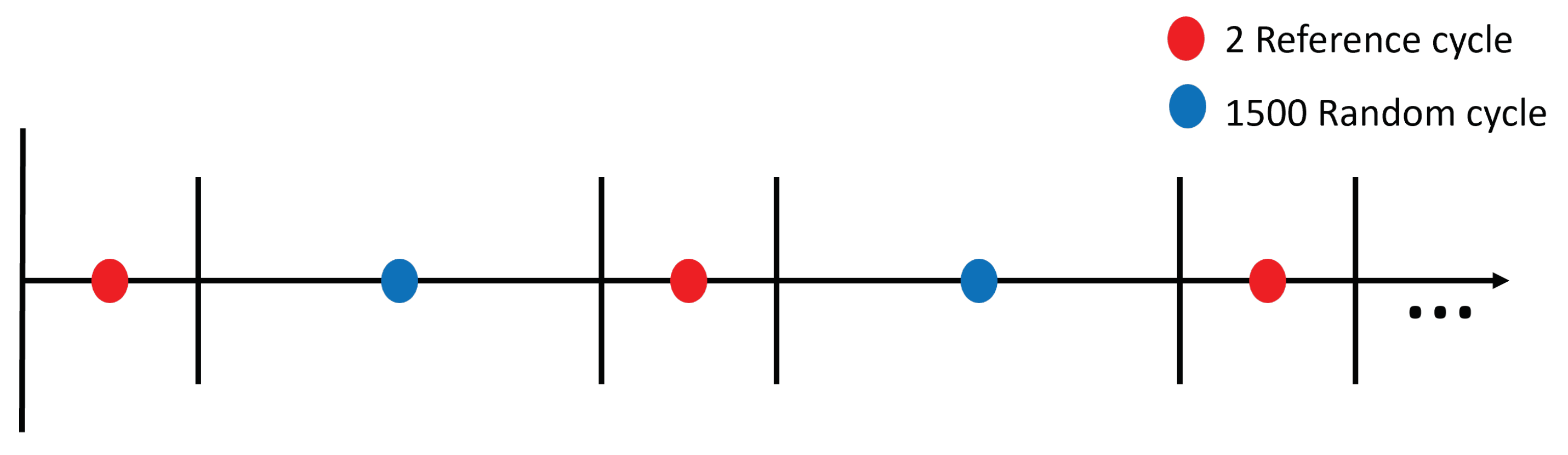
4.1. Test Dataset

In this study, we used the NASA Randomized Battery Dataset [11]. To validate the proposed data evaluation method, we utilized discharge datasets from RW9, RW10, RW11, and RW12 cells—tested by random charging and discharging at room temperature. The dataset was tested by repeating the reference charge/discharge cycle and random charge/discharge cycle as shown in Figure 4. The randomly charged and discharged current ranged from −4.5 A to 4.5 A and lasted 1500 random cycles. The condition for discharge termination was that the reference cycle should be performed when the voltage range exceeded or the random cycle lasted for 5 min or longer. The specifications of the used battery are listed in

Table 1. Data specifications for battery.

Characteristic/Parameter	Value
Battery properties	18,650 LIBs
Chemistry	18,650 lithium cobalt oxide vs. graphite
Nominal capacity	2.10 Ah
Capacity range	0.80–2.10 Ah
Voltage range	3.2–4.2 V

.

4.2. Application of the Proposed Evaluation Method

After representing the original and synthetic datasets generated through TimeGAN in low dimensions using t-SNE, we calculated the Dunn index, silhouette coefficient, and rate of change in the correlation coefficient of the linear regression between the two dataset clusters.

The t-SNE plot of the dimensionally reduced time-series data is shown in Figure 5. In this figure, the black and red points represent the original and synthetic data, respectively.

Through t-SNE, the similarity of data based on the number of learning iterations can be partially evaluated. When the original and synthetic battery datasets are distributed close together, the similarity is evaluated as high. However, it is difficult to objectively confirm the similarity when comparing t-SNE plots in which the difference is not visually evident. Different evaluators may consider different parts to be similar, and the evaluation is likely based on individual subjectivities.

Furthermore, the similarity of battery data can be evaluated using learning loss as shown in Figure 6; this is the most widely used quantitative evaluation method. However, the loss varies depending on the learning environment, and it is difficult to compare loss values when the learning environments differ.

Therefore, the proposed evaluation method objectified the similarity of the synthetic dataset through quantitative and qualitative evaluation, as shown in Figure 7 and

Table 2. Result of the proposed evaluation method (bold indicates best performance).

Data	Evaluation Method		Iteration
			100	1000	10,000
RW9	Existing	Training loss	0.3900	0.1800	0.1200
	Proposed	Rate of change in correlation coefficient	Not used	0.0813	0.0027
		Dunn index	0.3127	0.3030	0.2540
		Silhouette coefficient	0.1053	0.0308	0.0073
RW 10	Existing	Training loss	0.2850	0.2550	0.1450
	Proposed	Rate of change in correlation coefficient	Not used	0.0325	0.0291
		Dunn index	0.2718	0.3533	0.2719
		Silhouette coefficient	0.0381	0.0889	0.0089
RW 11	Existing	Training loss	0.4700	0.2200	0.1050
	Proposed	Rate of change in correlation coefficient	Not used	0.0382	0.0320
		Dunn index	0.3223	0.2722	0.2639
		Silhouette coefficient	0.2172	0.0199	0.0084
RW 12	Existing	Training loss	0.2850	0.3200	0.1540
	Proposed	Rate of change in correlation coefficient	Not used	0.1444	0.0414
		Dunn index	0.6826	0.2900	0.2938
		Silhouette coefficient	0.0267	0.0295	0.0156

. To ensure the reliability of the quantitative indicator, it was compared with the learning loss calculated in the same learning environment. In general, as shown in the Figure, as the number of learning iterations of the data augmentation algorithm increases, the learning loss decreases, and the synthetic dataset further reflects the characteristics of the original dataset.

First, the similarity between the original and composite datasets was determined using the rate of change in the correlation coefficient by comparing the linear relationship of the data using linear regression in t-SNE. Before judging the similarity, it was confirmed that the linear regression equation could sufficiently explain the data using the determination coefficient. If the determination coefficient was sufficient (0.7 or more), the similarity of the data was confirmed using the rate of change of the correlation coefficient. In Figure 7, the linear regression is indicated using a solid line for 1000 and 10,000 iterations, for the determination coefficient of 0.7 or more. The solid black line is the linear regression for the original dataset, and the solid blue line is the linear regression for the dataset comprising the composite and original datasets. When the number of iterations is 100, evaluation is difficult because linear characteristics do not appear. When the number of iterations is 1000 or more (as listed in Table 2), the rate of change in the correlation coefficient decreases as the number of iterations increases; consequently, a composite dataset close to the original dataset is generated. The rate of change of linear regression correlation coefficient is characterized by linearity in data characteristics; therefore, evaluation is possible only when the determination coefficient is greater than or equal to 0.7, and the evaluation is limited when the characteristics of the data are nonlinear. In this case, clustering indicators such as the Dunn index and silhouette coefficient should be used.

Second, the Dunn index indicates that the smaller the value, the more similar the original and composite datasets are, and the higher the quality of the composite dataset. As the number of iterations increases to 100, 1000, and 10,000, it is evident from the data in Table 2 that the Dunn index value generally decreases and has a value close to 0, which quantitatively indicates that the original and composite datasets are similar. In Figure 7, when some data are distributed far from the dataset to which they belong, such as 100 learning results of RW10 cells or 1000 learning results of RW12 cells, the Dunn index has a small value even though the data has relatively low similarity owing to the nature of the Dunn index, which utilizes the maximum minimum distance of the data. The Dunn index can evaluate the similarity of data relatively simply by utilizing the maximum minimum distance of the dataset; however, it is difficult to accurately evaluate when the dataset is distributed in several clusters. Therefore, this index is suitable when there is no outlier in the distribution of the dataset. Furthermore, when the distribution of the dataset is far away, evaluation through a linear regression or silhouette coefficient (which is not sensitive to specific data) should be performed together.

Finally, the closer the silhouette coefficient is to 0, the more difficult it is to classify the original and the composite data. Therefore, the composite data is inferred to similarly simulate the quality of the original data. In contrast, the closer the value of this coefficient is to 1, the more distinct the characteristics between the datasets, indicating that the composite dataset is not similar to the original dataset. As opposed to the Dunn index, the value of the silhouette coefficient decreases consistently and approaches 0 as the number of iterations increases to 100, 1000, and 10,000 for four datasets. Accurate evaluation is possible even when some data are distributed far within the group, and the value of the silhouette coefficient ranges from 0 to 1; thus, this index is most suitable for quantifying similarity.

The learning loss evaluation to validate the proposed evaluation method confirmed that the value decreased as the number of iterations increased. As the learning loss decreased, the accuracy of learning increased, thus improving the quality of the composite dataset. In general, the three proposed evaluation metrics tended to decrease as the number of iterations increased, and the reliability of the evaluation method was improved compared to that of the existing evaluation method based on learning loss.

Contrary to the learning loss method, the proposed evaluation method can quantitatively evaluate data similarities by directly comparing the datasets. The silhouette coefficient demonstrated the best accuracy for similarity based on the number of iterations. This is because this coefficient does not depend on data characteristics (such as linearity) and uses the average distance of all data rather than the distance between specific data.

5. Conclusions

In this study, we investigated methods for quantitatively evaluating the quality of synthetic time-series battery data generated using data augmentation algorithms. The existing qualitative evaluation methods (such as t-SNE based on visualization) are not suitable for battery data generated using estimation algorithms because visual evaluation methods are subjective.

We proposed a method to quantitatively evaluate the similarity between the original dataset and the dataset generated by TimeGAN by representing the generated dataset as a two-dimensional graph using t-SNE and utilizing three evaluation metrics—the rate of change in the linear regression correlation coefficient, Dunn index for clustering, and silhouette coefficient. We also confirmed the similarity between the original and synthetic datasets through the proposed evaluation metrics.

The rate of change in the correlation coefficient of linear regression, Dunn index, and silhouette coefficient tended to decrease as the number of iterations of the GAN algorithm increased. The rate of change in the linear regression correlation coefficient is characterized by the linearity of the data; thus, evaluation is possible even when the determination coefficient has a value of 0.7 or more. Because the Dunn index utilizes the maximum–minimum distance of the dataset, its evaluation result is accurate only when no outlier exists in the dataset distribution. The silhouette coefficient provided accurate evaluations even when some data points are distributed far apart within a cluster. Therefore, the results of the three proposed direct evaluation metrics are similar to those obtained using the existing indirect evaluation methods (training loss). Thus, the usefulness of the proposed method was confirmed. We also conclude that the silhouette coefficient is the most reliable indicator among the three proposed quantitative metrics.

As the proposed evaluation method is based on t-SNE plot and suitable for the synthetic time-series dataset of batteries, we expect it to be utilized as a universal evaluation method for other synthetic time-series datasets.

In the future, we will develop a comprehensive scoring system based on the correlation between the three indicators and conduct an integrated algorithm study for real-time data quality evaluation.