Efficient Solution Resilient to Noise and Anchor Position Error for Joint Localization and Synchronization Using One-Way Sequential TOAs
Abstract
1. Introduction
- A new closed-form solution using nullspace projection to generate the initial guess.
- A robust iteration solution based on factor graphs and message passing, resilient to noise and AN position error, ensuring global convergence.
- Theoretical analysis corroborating the optimality in the RMSE of the proposed RIS.
- Extensive simulations validating the analytical results, demonstrating the best bias performance, and confirming the manageable computational complexity.
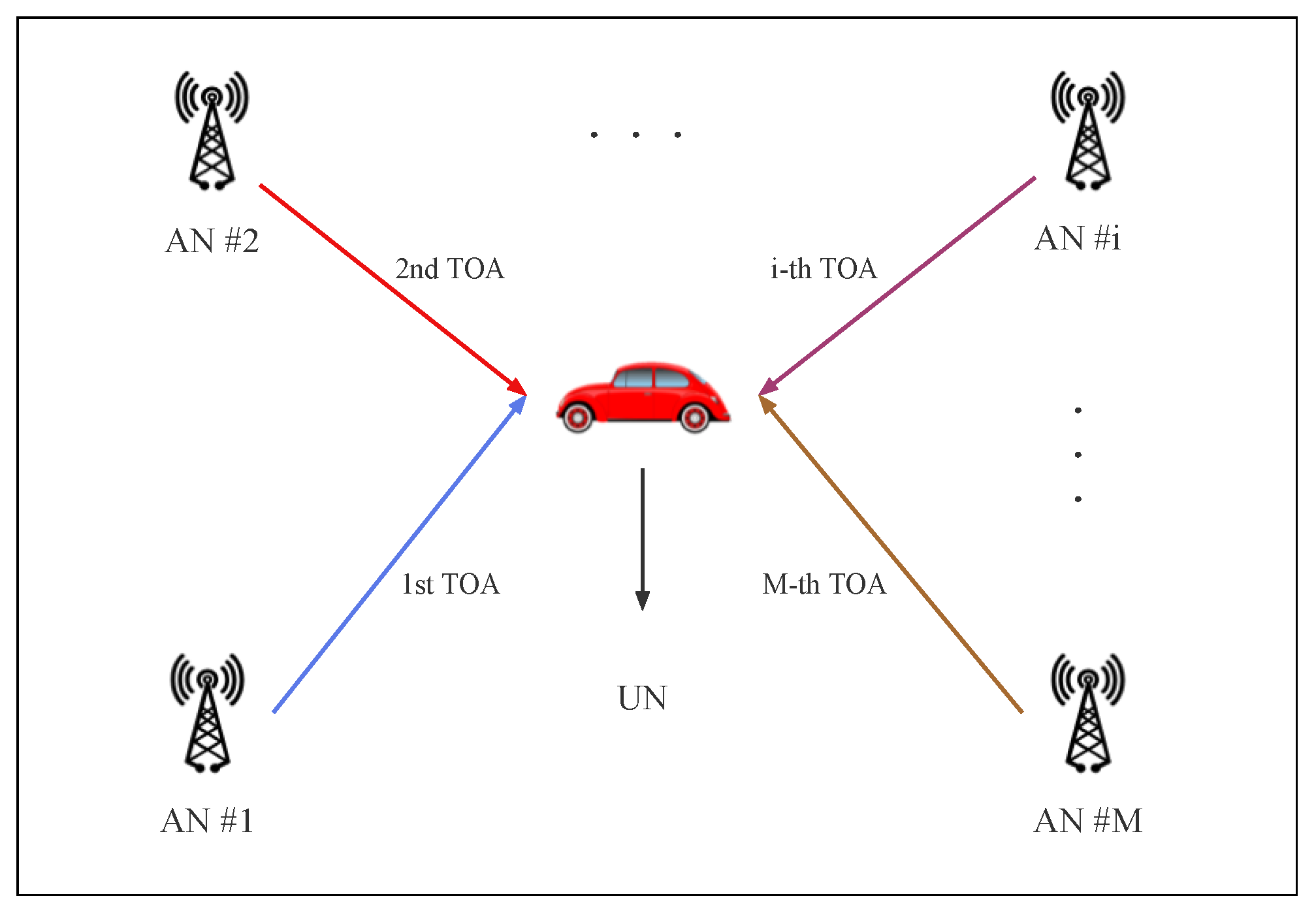
2. One-Way TOA Measurement Model
3. Proposed Solutions
3.1. Problem Formulation
3.2. Closed-Form Solution by Nullspace Projection
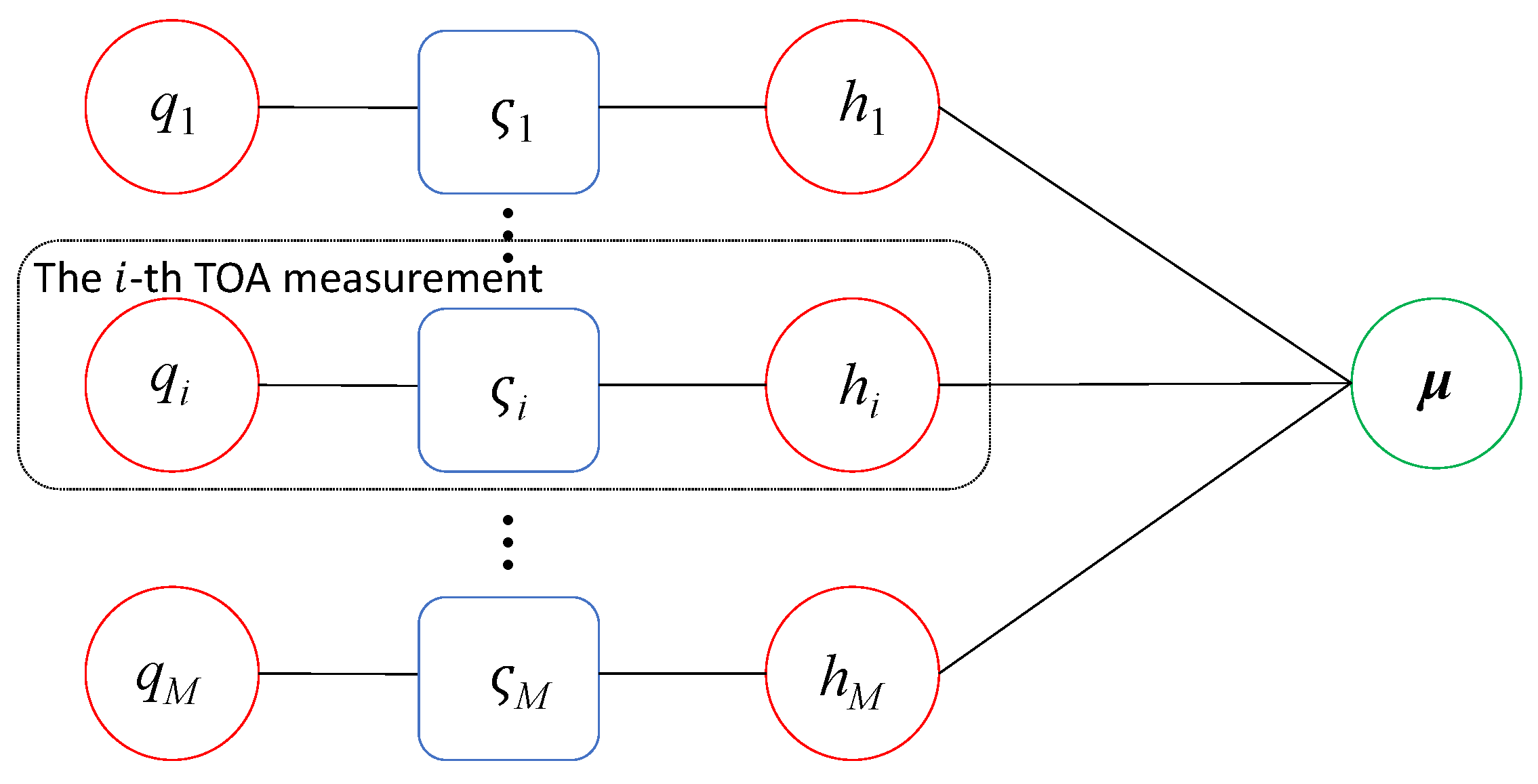
3.3. Robust Iterative Solution
4. Analysis
4.1. CRLB Derivation
4.2. Theoretical Error Analysis
4.3. Complexity Analysis
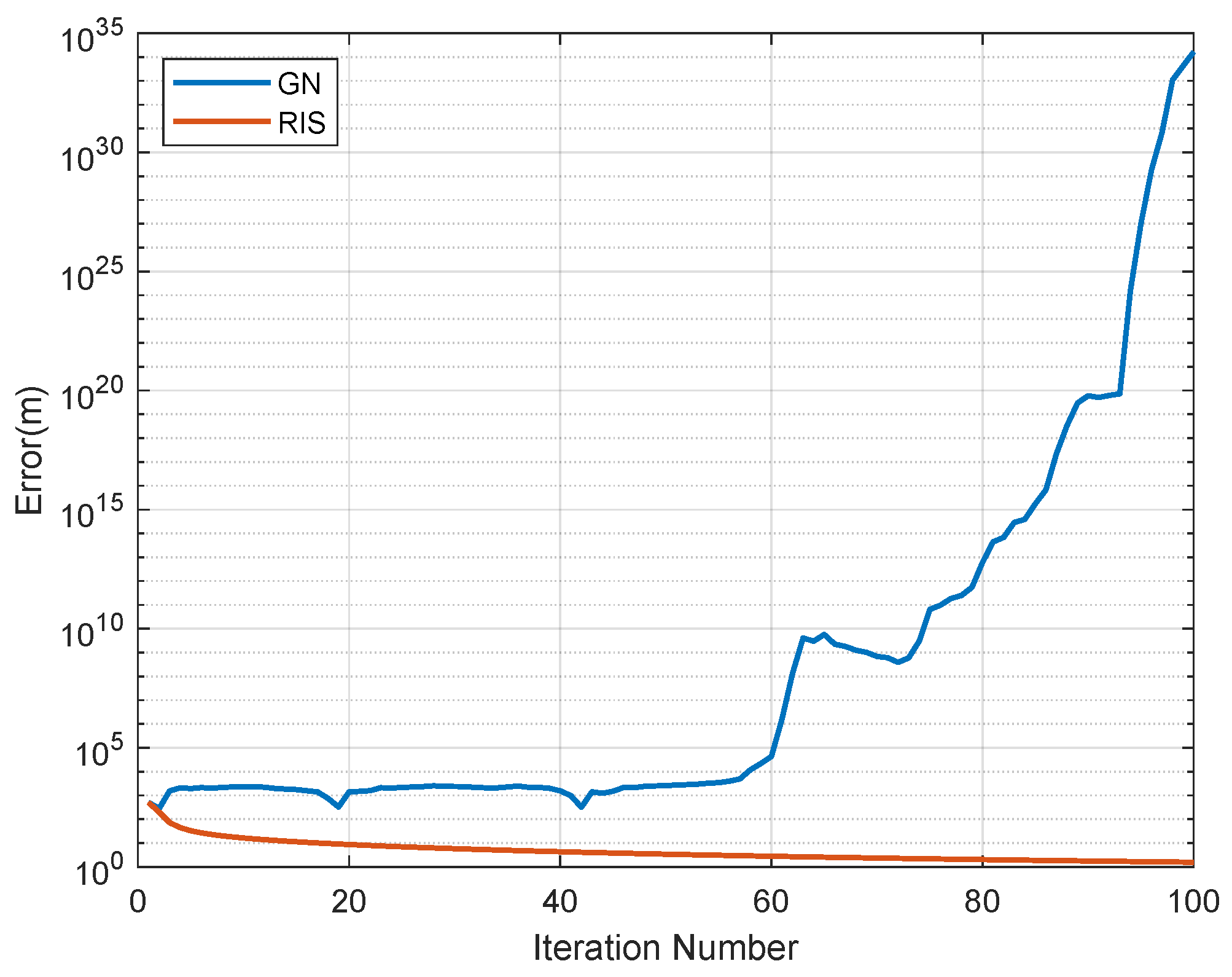
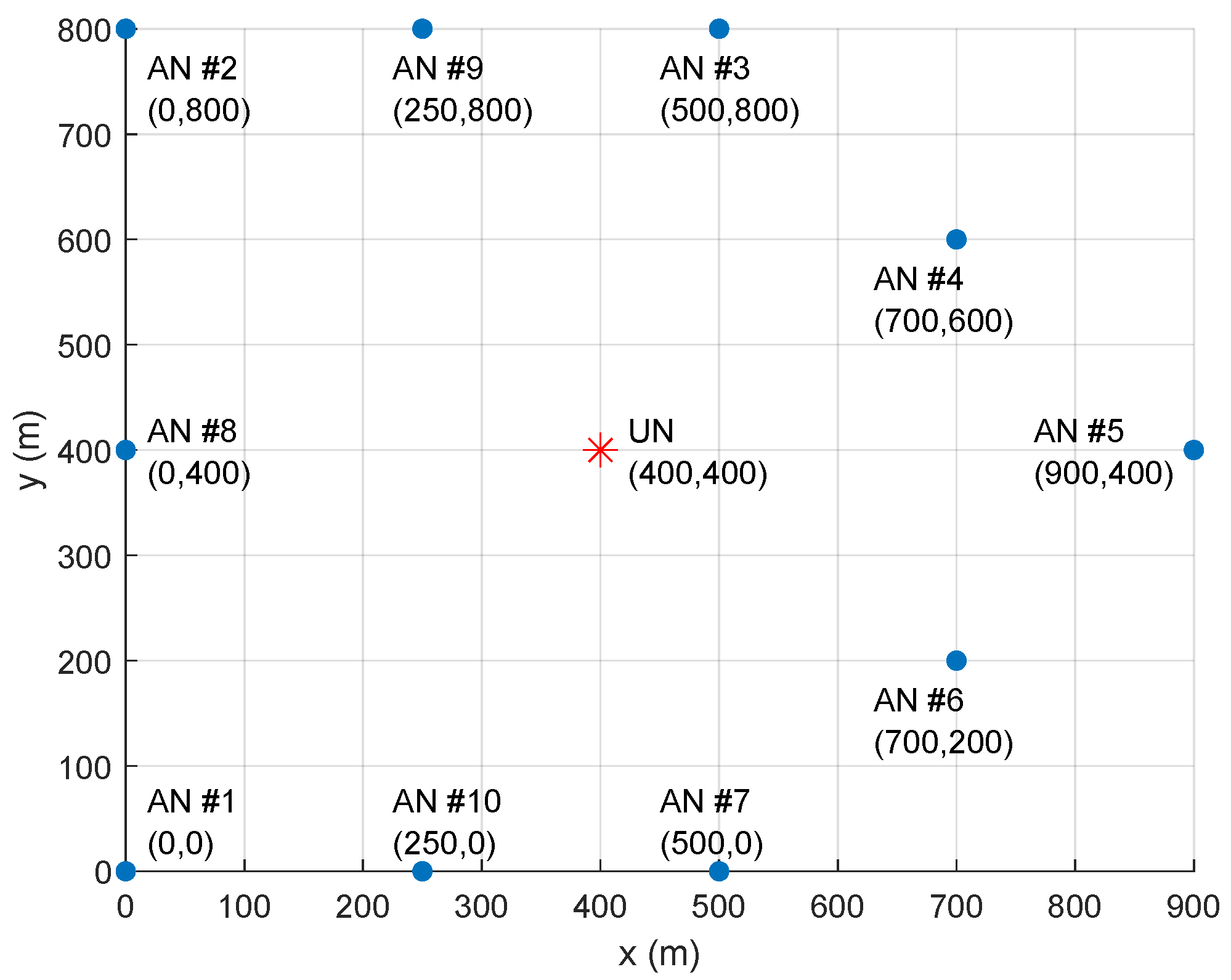
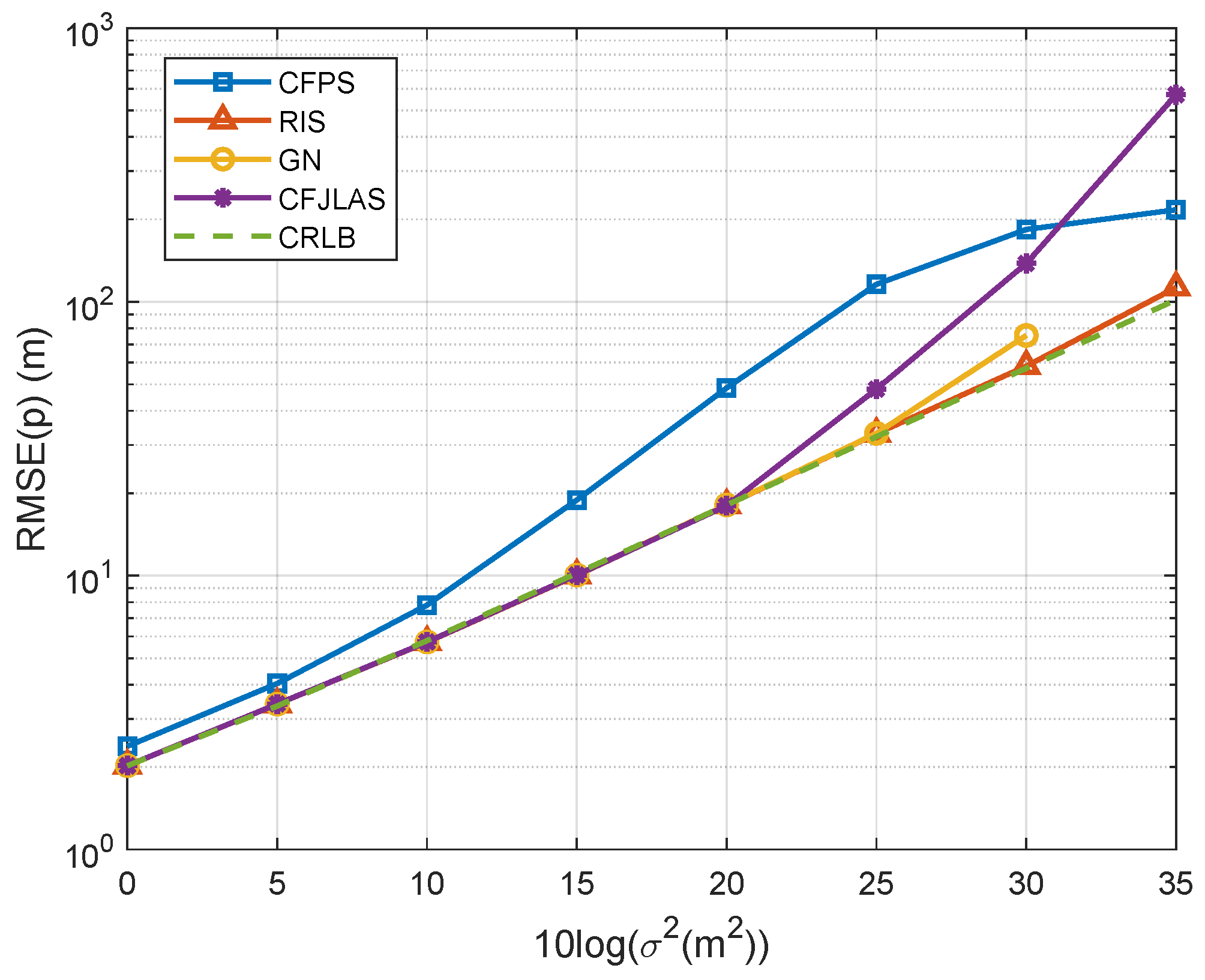
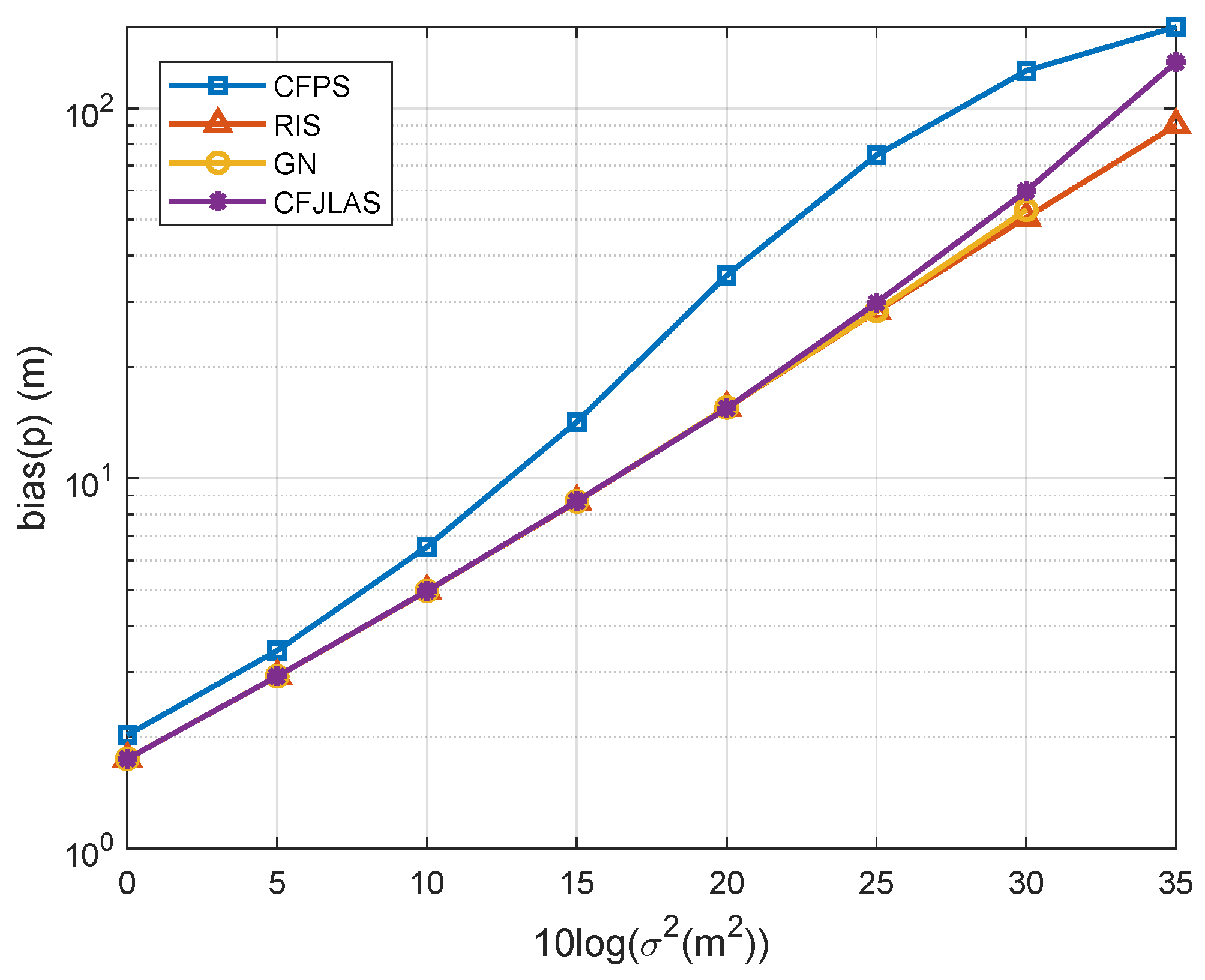
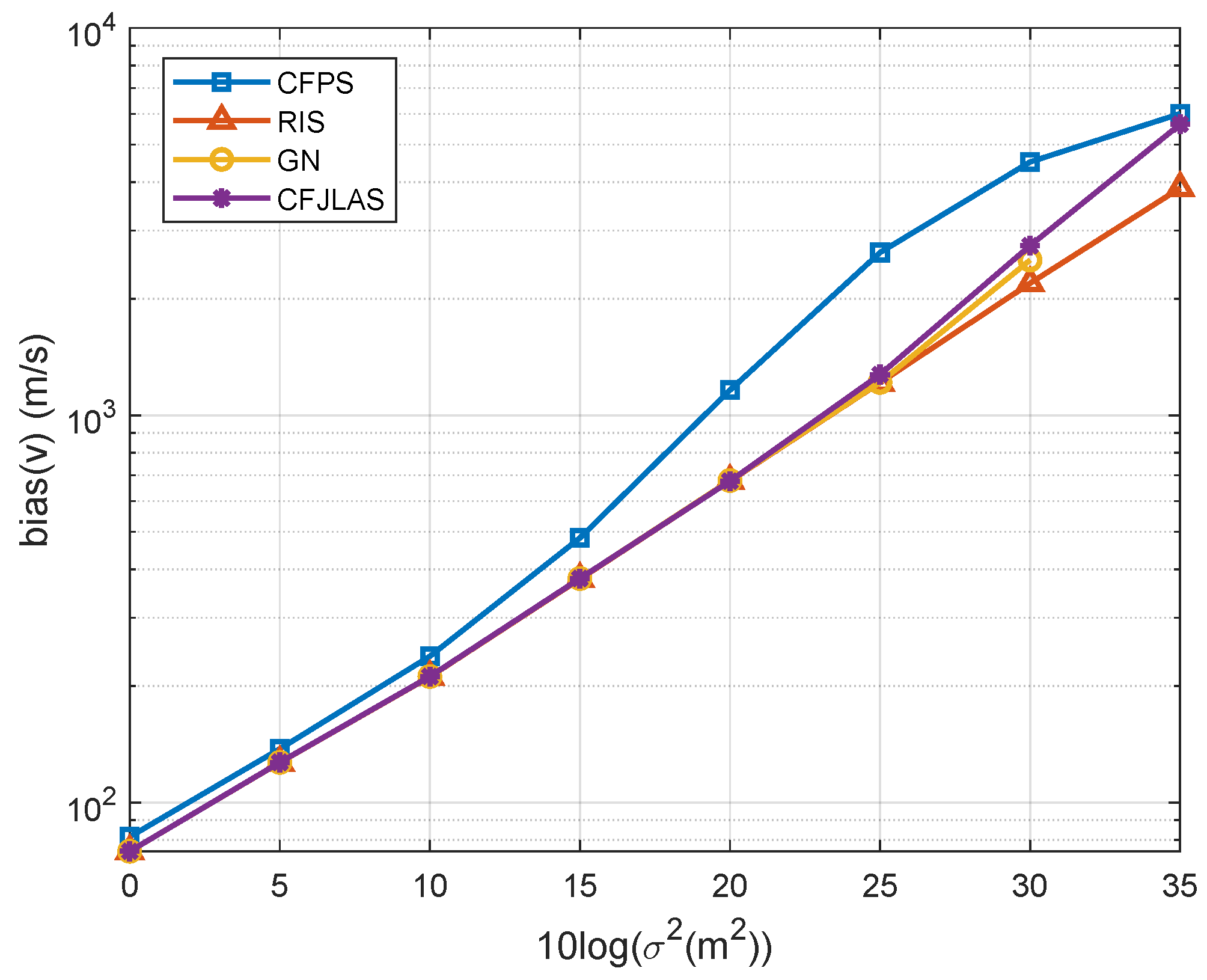
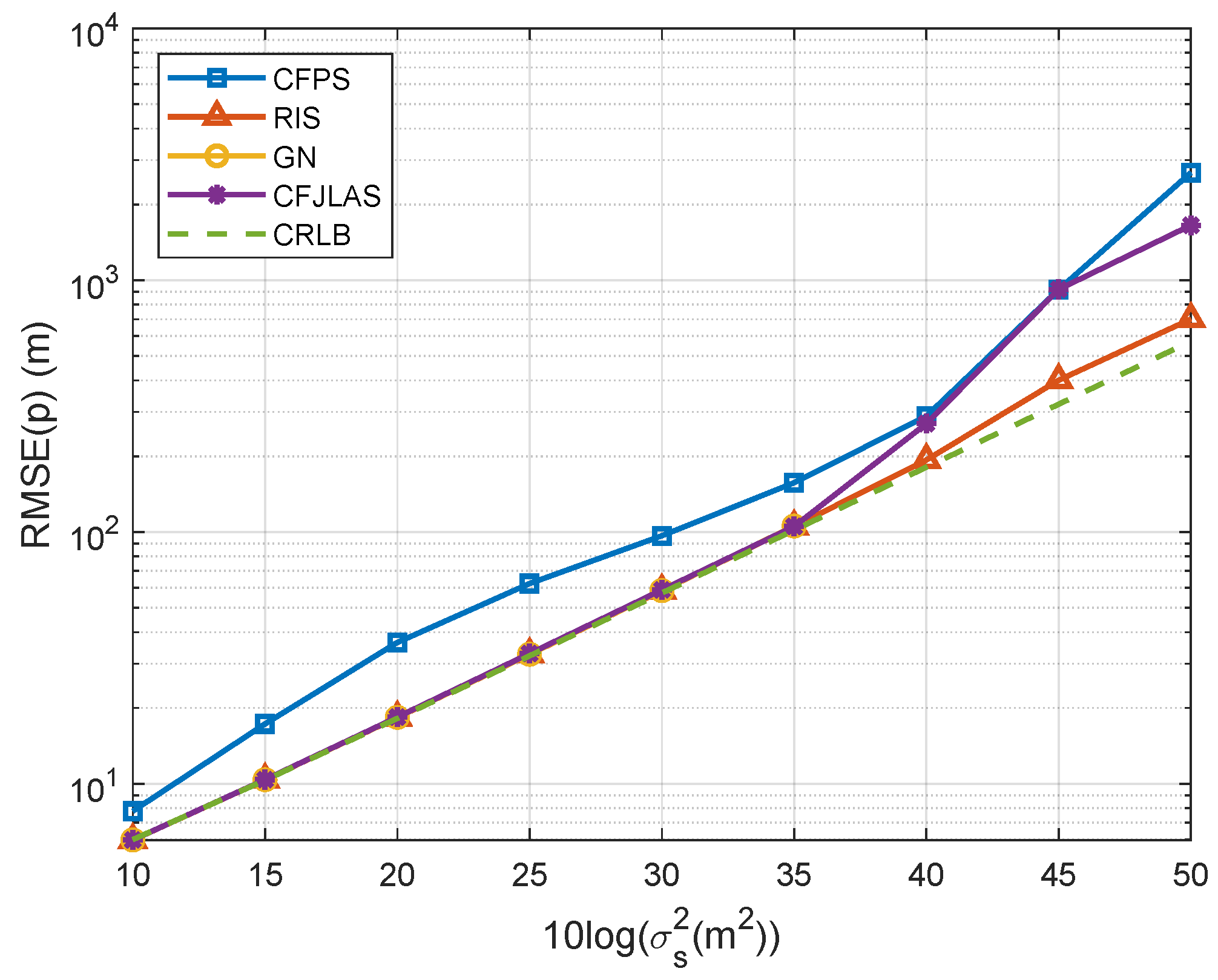
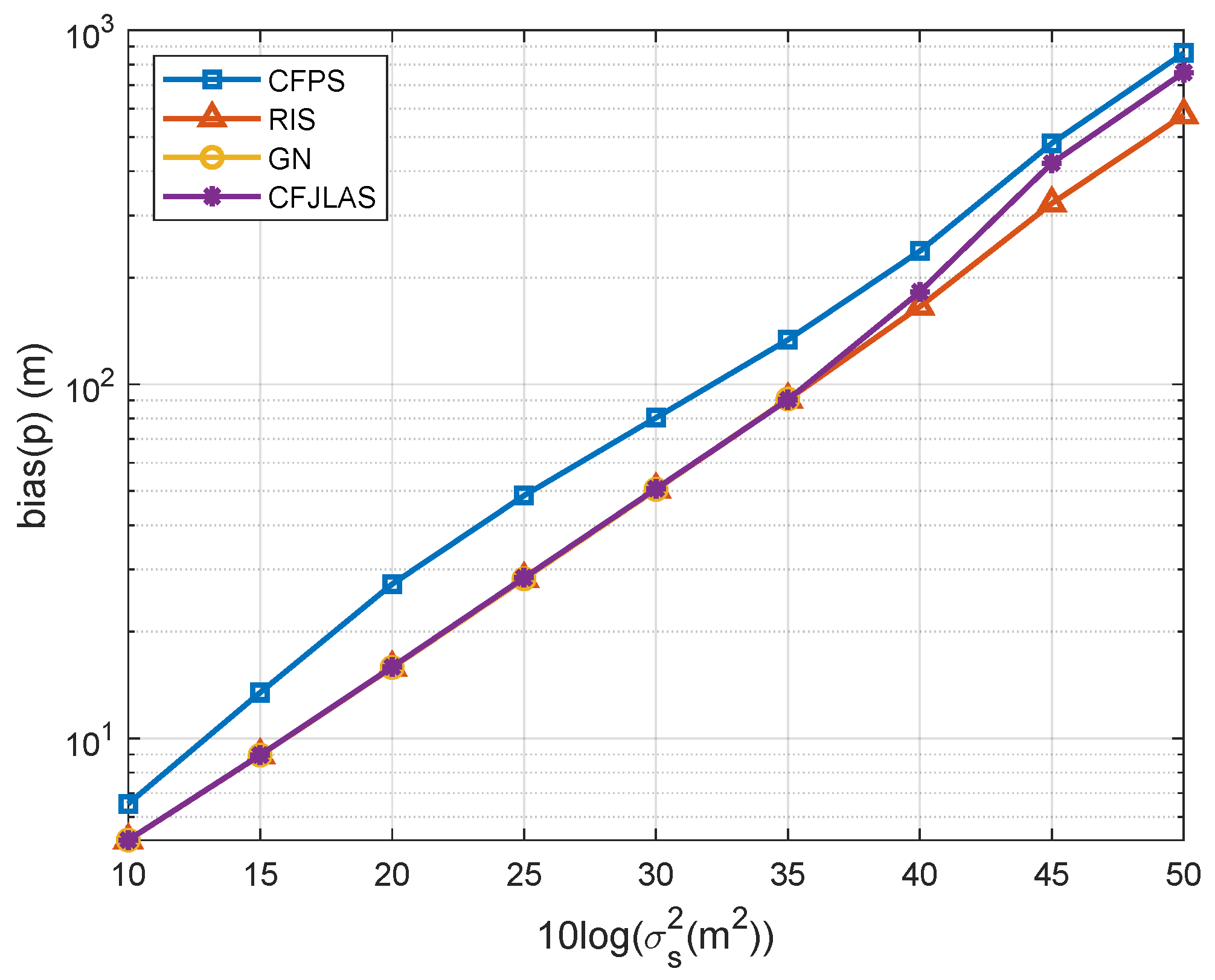
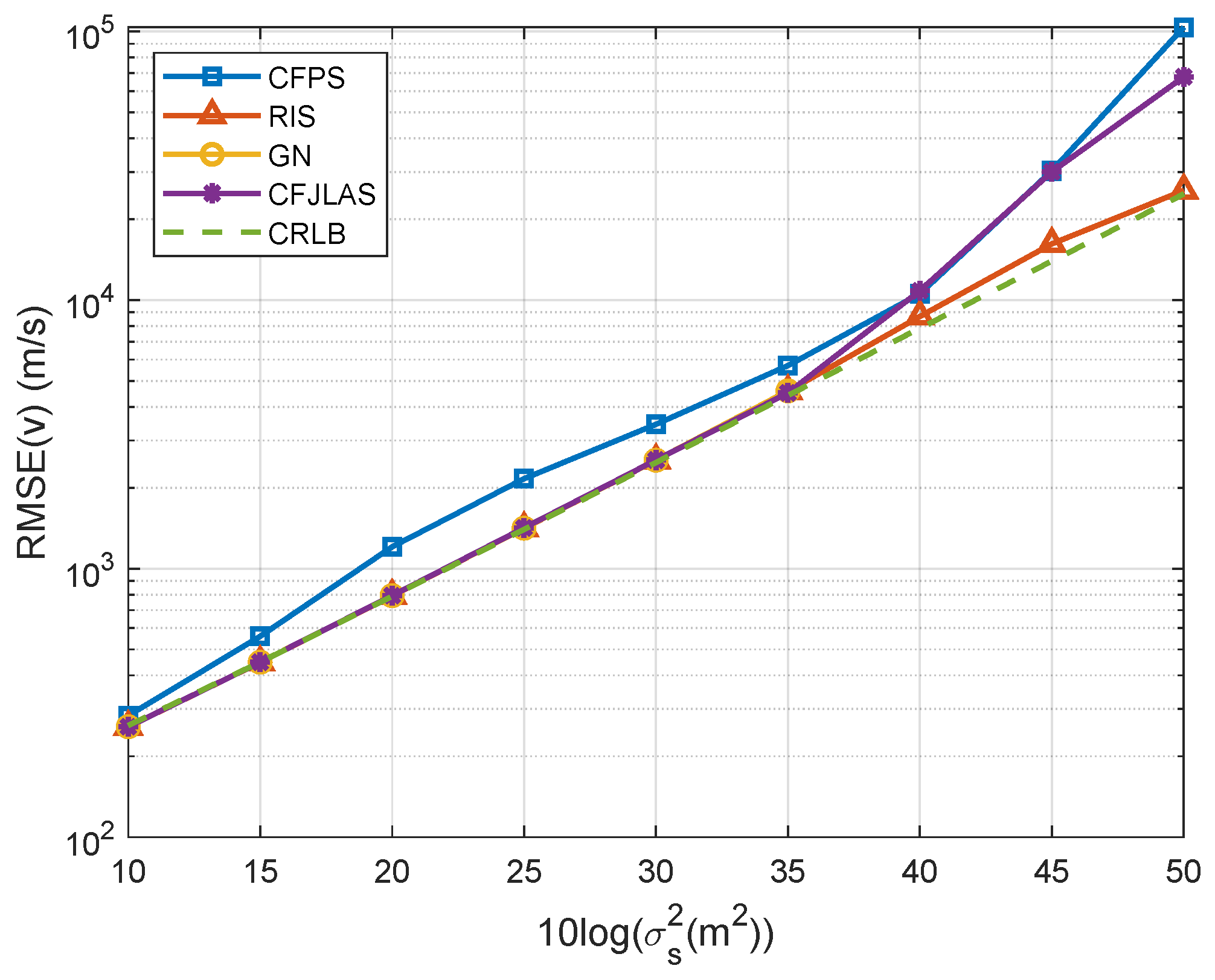
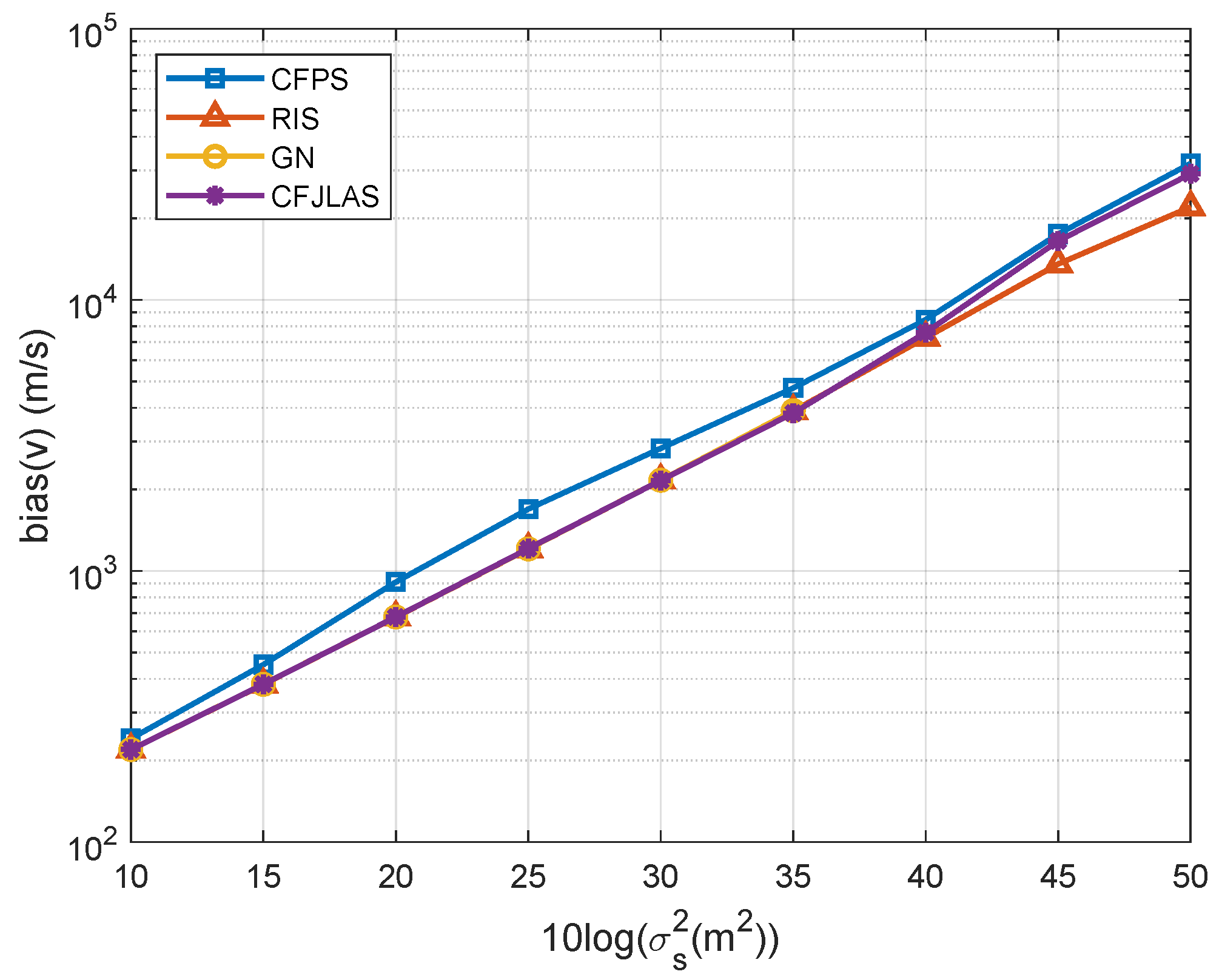
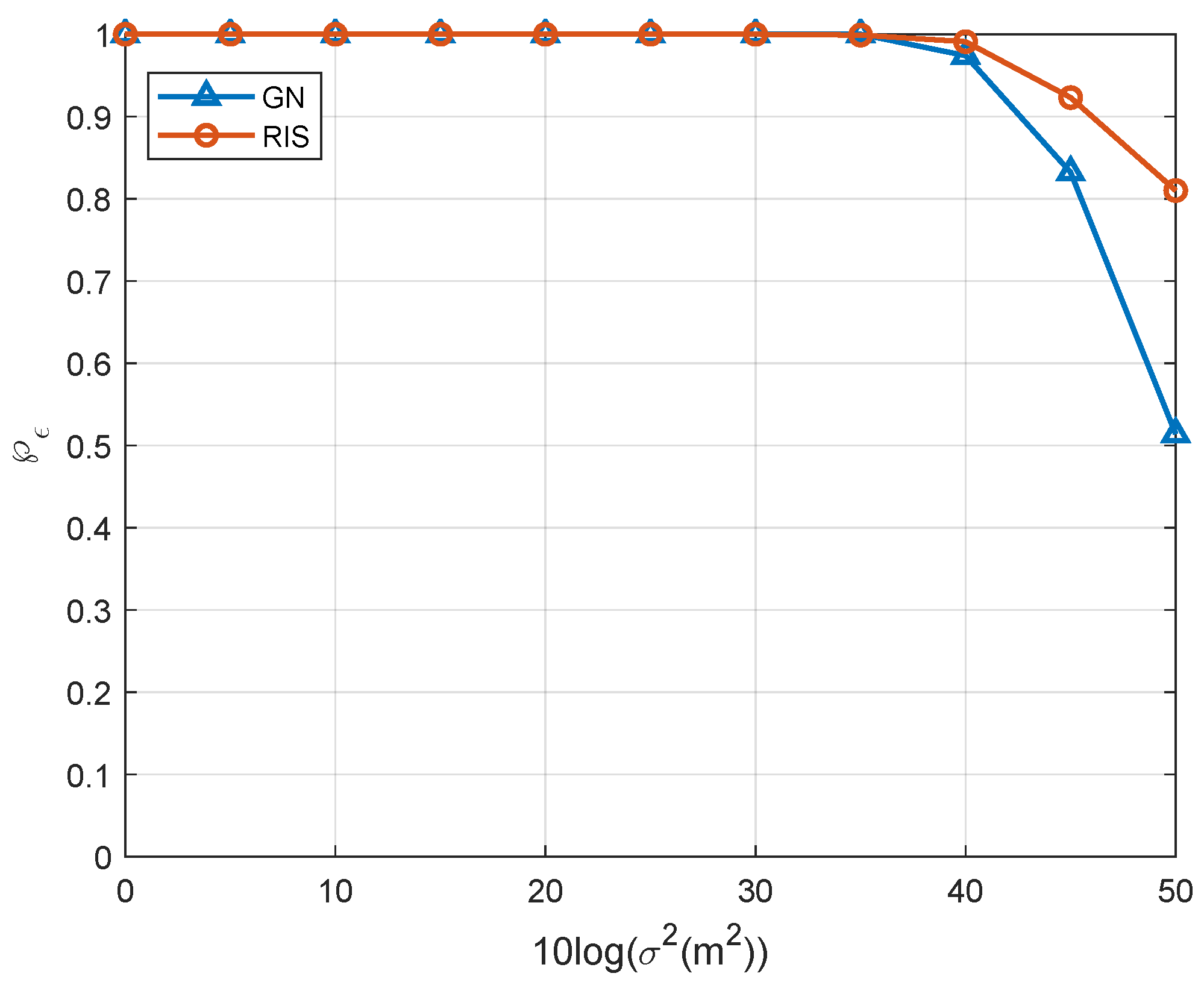
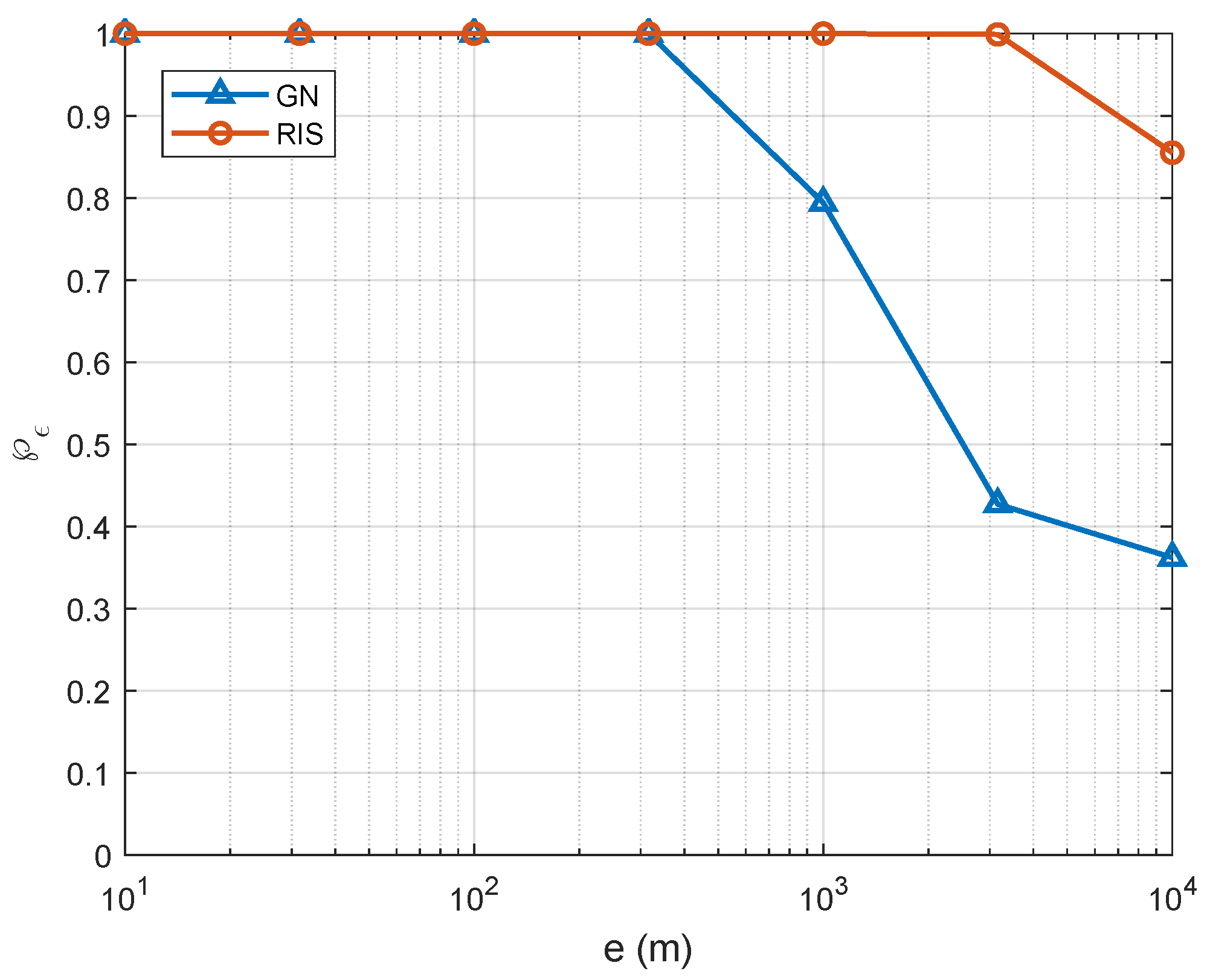
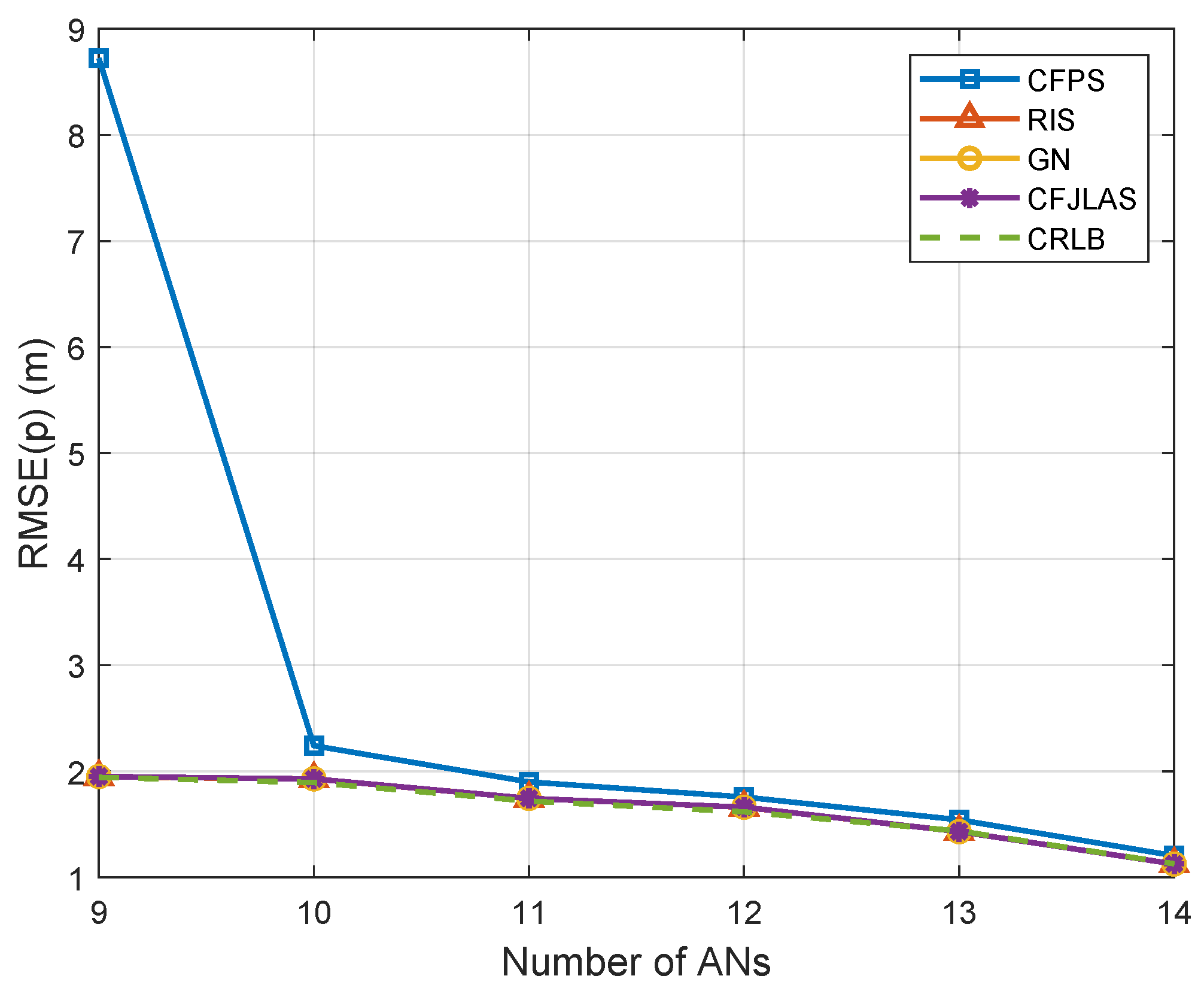
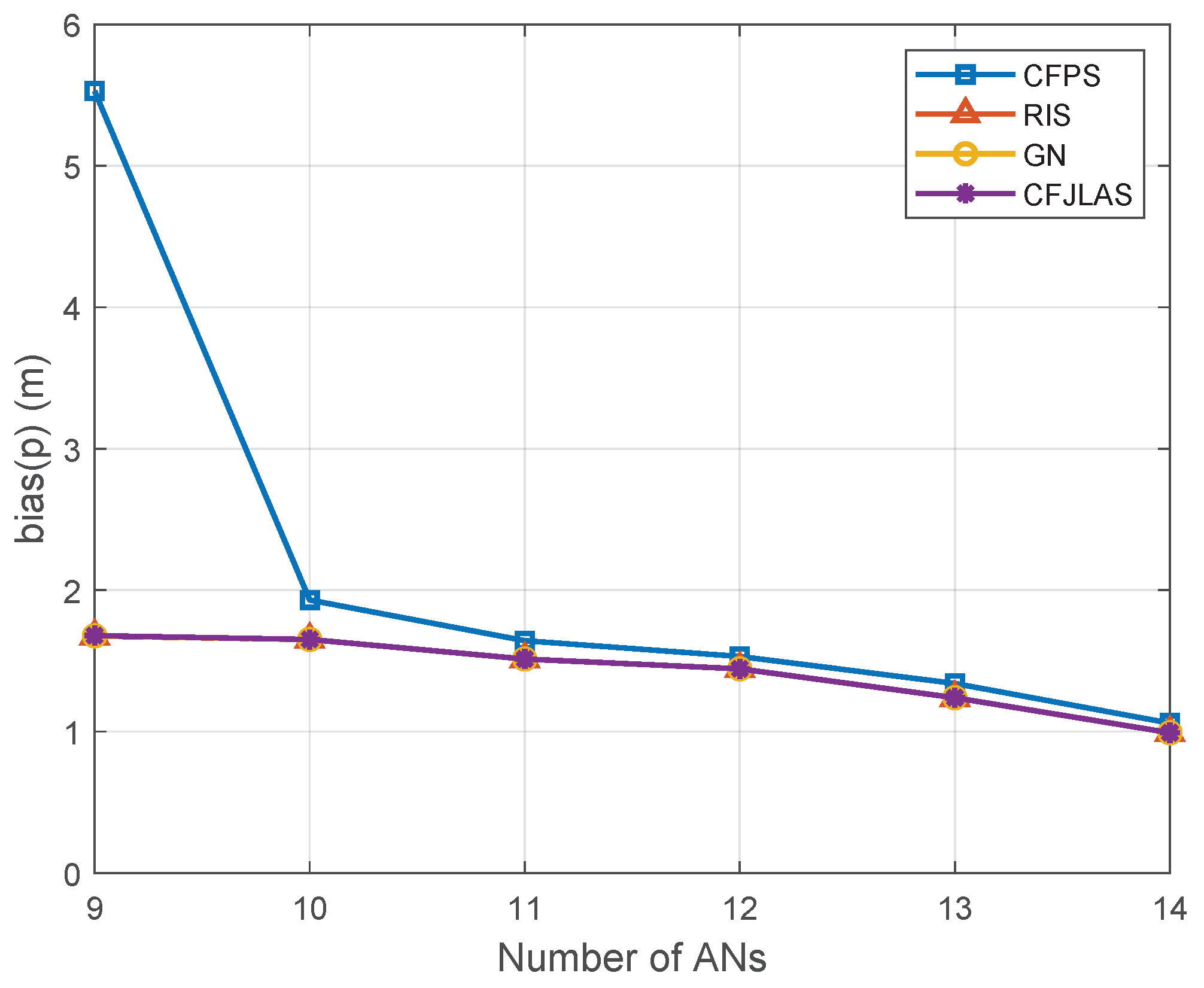
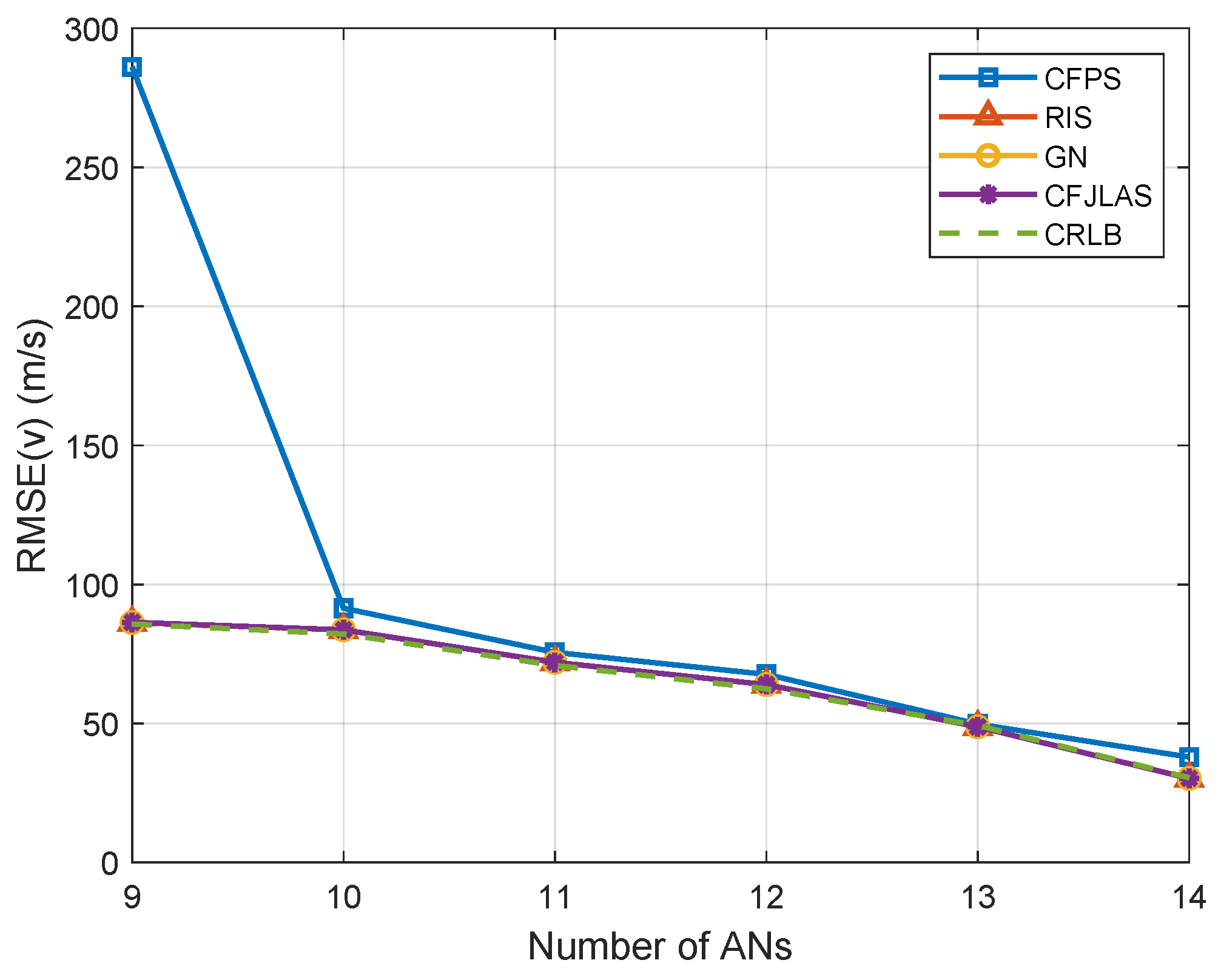
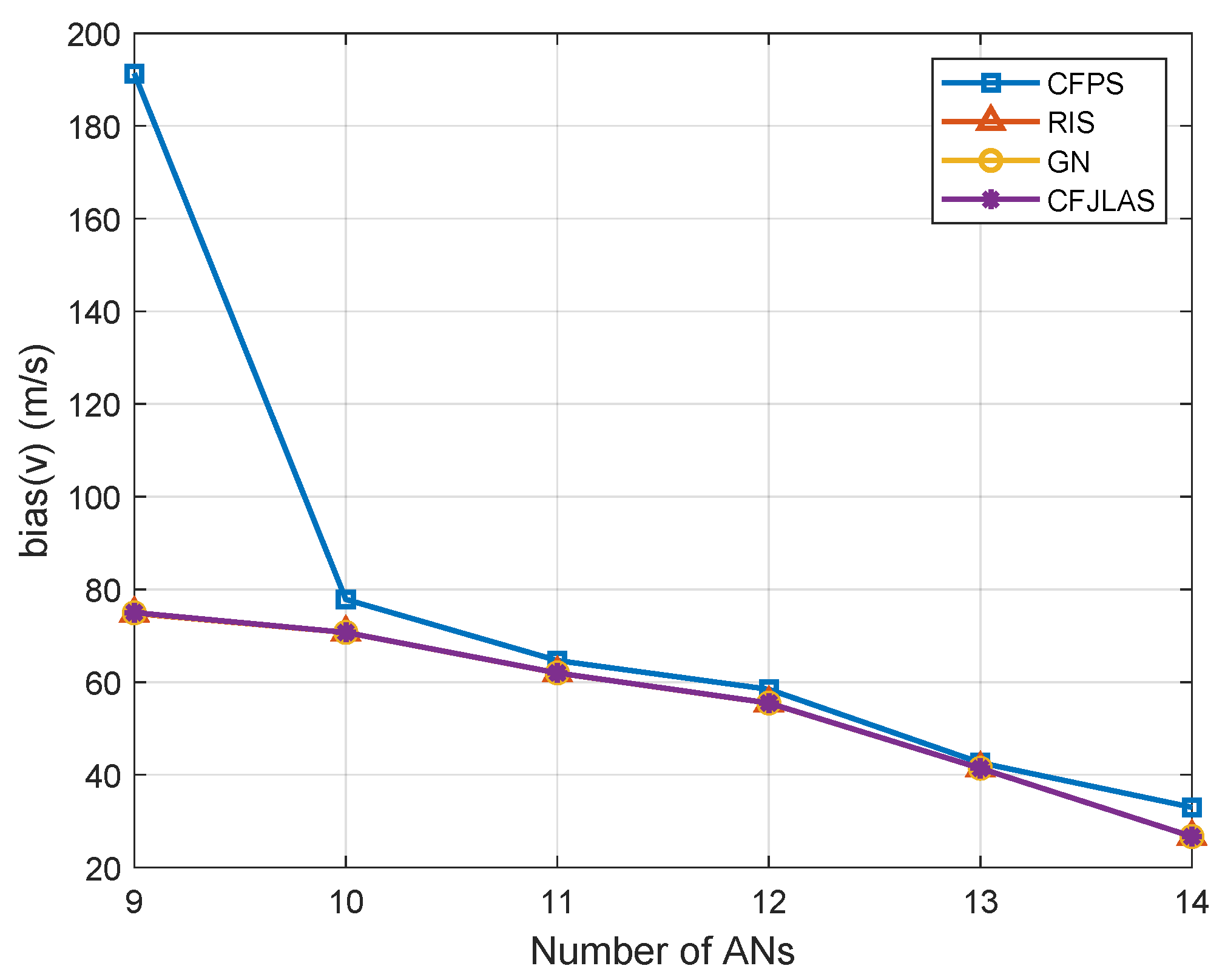
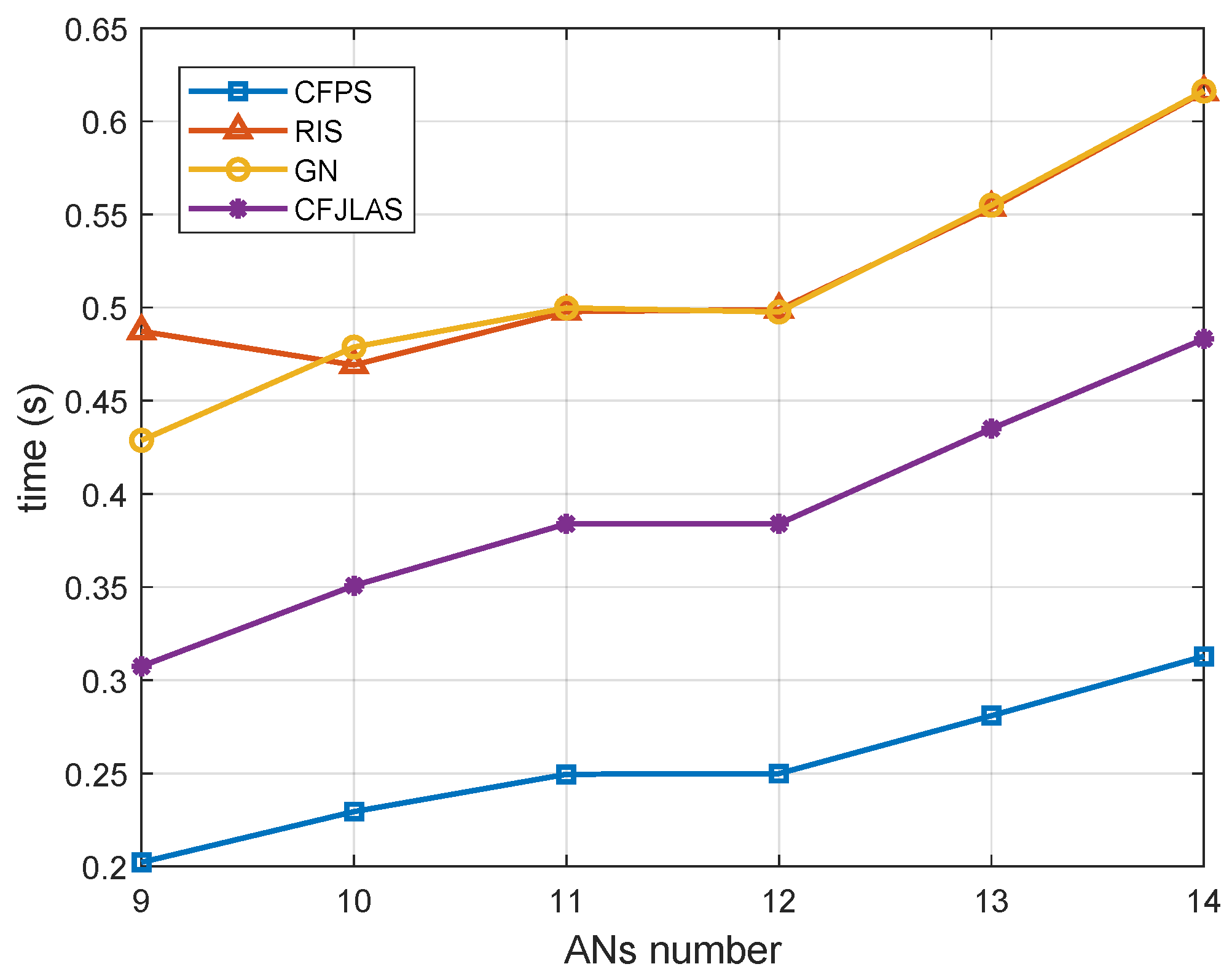
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Symbol | Explanation |
| lowercase a | scalar |
| bold lowercase | vector |
| bold uppercase | matrix |
| Euclidean norm of a vector | |
| subvector constructed by the i-th to j-th elements of | |
| the i-th element of | |
| the i-th column of the matrix | |
| Dirac delta function | |
| M | number of ANs |
| N | dimension of the ANs and UNs |
| , , | position, clock offset, and clock drift of AN |
| , | UN’s position and velocity vector |
| , | UN’s clock offset and skew |
| measured TOA from AN | |
| collective form of | |
| the error of vector | |
| time interval from the beginning of the TD broadcast round to | |
| AN ’s transmission time | |
| , | measurement noise and position error from AN |
| , | variance of measurement noise and position error for AN |
| , | collective of noise and error |
| parameter vector, = | |
| , | covariance matrices of and , respectively |
| unit vector from the UN to AN | |
| the zero matrix | |
| the identity matrix |
Acronyms
| Acronyms | Full words |
| TOA | Time-of-arrival |
| JLAS | Joint localization and synchronization |
| UNs | User nodes |
| ANs | Anchor nodes |
| CRLB | Cramér-Rao lower bound |
| RIS | Robust iterative solution |
| RMSE | Root mean square error |
| RF | Radio frequency |
| WSNs | Wireless sensor networks |
| TOF | Time-of-flight |
| IoT | Internet of Things |
| FD | Frequency division |
| CD | Code division |
| TD | Time division |
| WLS | Weighted least squares |
| SDP | Semidefinite programming |
| TSWLS | Two-step weighted least squares |
| MLE | Maximum likelihood estimator |
| GN | Gauss-Newton |
| CFPS | Closed-form projection solution |
| CWLS | Constrained WLS |
| MSE | Mean-square error |
| FG | Factor graph |
| SPA | Sum-product algorithm |
| ML | Maximum likelihood |
| ZZB | Ziv-Zakai bound |
| AGVs | Automatic guided vehicles |
References
- Gonçalves Ferreira, A.F.G.; Fernandes, D.M.A.; Catarino, A.P.; Monteiro, J.L. Localization and Positioning Systems for Emergency Responders: A Survey. IEEE Commun. Surv. Tut. 2017, 19, 2836–2870. [Google Scholar] [CrossRef]
- Farahsari, P.S.; Farahzadi, A.; Rezazadeh, J.; Bagheri, A. A Survey on Indoor Positioning Systems for IoT-Based Applications. IEEE Internet Things J. 2022, 9, 7680–7699. [Google Scholar] [CrossRef]
- Yang, H.; Zhong, W.D.; Chen, C.; Alphones, A. Integration of Visible Light Communication and Positioning within 5G Networks for Internet of Things. IEEE Netw. 2020, 34, 134–140. [Google Scholar] [CrossRef]
- Wen, F.X.; Wymeersch, H.; Peng, B.L.; Tay, W.P.; So, H.C.; Yang, D.G. A survey on 5G massive MIMO localization. Digit. Signal Process. 2019, 94, 21–28. [Google Scholar] [CrossRef]
- Saeed, N.; Alouini, M.S.; Al-Naffouri, T.Y. 3D Localization for Internet of Underground Things in Oil and Gas Reservoirs. IEEE Access 2019, 7, 121769–121780. [Google Scholar] [CrossRef]
- Tabella, G.; Ciuonzo, D.; Paltrinieri, N.; Rossi, P.S. Bayesian Fault Detection and Localization Through Wireless Sensor Networks in Industrial Plants. IEEE Internet Things J. 2024, 11, 13231–13246. [Google Scholar] [CrossRef]
- Shi, Q.; Cui, X.; Zhao, S.; Lu, M. Sequential TOA-Based Moving Target Localization in Multi-Agent Networks. IEEE Commun. Lett. 2020, 24, 1719–1723. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, X.P.; Cui, X.; Lu, M. Optimal Localization with Sequential Pseudorange Measurements for Moving Users in a Time-Division Broadcast Positioning System. IEEE Internet Things J. 2021, 8, 8883–8896. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, X.P.; Cui, X.; Lu, M. Optimal Two-Way TOA Localization and Synchronization for Moving User Devices with Clock Drift. IEEE Trans. Veh. Technol. 2021, 70, 7778–7789. [Google Scholar] [CrossRef]
- Zhao, S.; Guo, N.; Zhang, X.P.; Cui, X.; Lu, M. Closed-Form Two-Way TOA Localization and Synchronization for User Devices with Motion and Clock Drift. IEEE Signal Process. Lett. 2022, 29, 100–104. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, S.; Zhang, X.P.; Yao, Z.; Cui, X.; Lu, M. New Closed-Form Joint Localization and Synchronization Using Sequential One-Way TOAs. IEEE Trans. Signal Process. 2022, 70, 2078–2092. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Algebraic Solution for Joint Localization and Synchronization of Multiple Sensor Nodes in the Presence of Beacon Uncertainties. IEEE Trans. Wirel. Commun. 2014, 13, 5196–5210. [Google Scholar] [CrossRef]
- Goodarzi, M.; Sark, V.; Maletic, N.; Terán, J.G.; Caire, G.; Grass, E. DNN-Assisted Particle-Based Bayesian Joint Synchronization and Localization. IEEE Trans. Commun. 2022, 70, 4837–4851. [Google Scholar] [CrossRef]
- Ge, T.; Tharmarasa, R.; Lebel, B.; Florea, M.; Kirubarajan, T.T. A Multidimensional TDOA Association Algorithm for Joint Multitarget Localization and Multisensor Synchronization. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2083–2100. [Google Scholar] [CrossRef]
- Kazemi, S.A.R.; Amiri, R.; Behnia, F. Efficient Joint Localization and Synchronization in Distributed MIMO Radars. IEEE Signal Process. Lett. 2020, 27, 1200–1204. [Google Scholar] [CrossRef]
- Shams, R.; Otero, P.; Aamir, M.; Hanif, F. E2JSL: Energy Efficient Joint Time Synchronization and Localization Algorithm Using Ray Tracing Model. Sensors 2020, 20, 7222. [Google Scholar] [CrossRef] [PubMed]
- Myung, H.G.; Lim, J.; Goodman, D.J. Single carrier FDMA for uplink wireless transmission. IEEE Veh. Technol. Mag. 2006, 1, 30–38. [Google Scholar] [CrossRef]
- Picois, A.V.; Samama, N. Near-far interference mitigation for pseudolites using double transmission. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2929–2941. [Google Scholar] [CrossRef]
- Shi, Q.; Cui, X.; Zhao, S.; Xu, S.; Lu, M. BLAS: Broadcast Relative Localization and Clock Synchronization for Dynamic Dense Multiagent Systems. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3822–3839. [Google Scholar] [CrossRef]
- Dwivedi, S.; Zachariah, D.; De Angelis, A.; Handel, P. Cooperative Decentralized Localization Using Scheduled Wireless Transmissions. IEEE Commun. Lett. 2013, 17, 1240–1243. [Google Scholar] [CrossRef]
- Hamer, M.; D’Andrea, R. Self-Calibrating Ultra-Wideband Network Supporting Multi-Robot Localization. IEEE Access 2018, 6, 22292–22304. [Google Scholar] [CrossRef]
- Zachariah, D.; De Angelis, A.; Dwivedi, S.; Händel, P. Self-Localization of Asynchronous Wireless Nodes with Parameter Uncertainties. IEEE Signal Process. Lett. 2013, 20, 551–554. [Google Scholar] [CrossRef]
- Carroll, P.; Mahmood, K.; Zhou, S.; Zhou, H.; Xu, X.; Cui, J.H. On-Demand Asynchronous Localization for Underwater Sensor Networks. IEEE Trans. Signal Process. 2014, 62, 3337–3348. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, X.; Luo, X.; Wang, Y.; Chen, C.; Guan, X. Asynchronous Localization with Mobility Prediction for Underwater Acoustic Sensor Networks. IEEE Trans. Veh. Technol. 2018, 67, 2543–2556. [Google Scholar] [CrossRef]
- Sun, M.; Yang, L. On the joint time synchronization and source localization using TOA measurements. Int. J. Distrib. Sens. Netw. 2013, 9, 794805. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, X.P.; Cui, X.; Lu, M. Semidefinite Programming Two-Way TOA Localization for User Devices with Motion and Clock Drift. IEEE Signal Process. Lett. 2021, 28, 578–582. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, Y.; Shen, Y. Joint Localization and Synchronization for Moving Agents Using One-Way TOAs in Asynchronous Networks. IEEE Internet Things J. 2023, 10, 11844–11857. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.C.; Wan, Q. Solution and Analysis of TDOA Localization of a Near or Distant Source in Closed-Form. IEEE Trans. Signal Process. 2019, 67, 320–335. [Google Scholar] [CrossRef]
- Jia, T.Y.; Liu, H.W.; Ho, K.C.; Wang, H.Y. Mitigating Sensor Motion Effect for AOA and AOA-TOA Localizations in Underwater Environments. IEEE Trans. Wirel. Commun. 2023, 22, 6124–6139. [Google Scholar] [CrossRef]
- Zou, Y.; Fan, J.; Wu, L.; Liu, H. Fixed Point Iteration Based Algorithm for Asynchronous TOA-Based Source Localization. Sensors 2022, 22, 6871. [Google Scholar] [CrossRef]
- Yu, Z.; Li, J.; Guo, Q.; Sun, T. Message Passing Based Robust Target Localization in Distributed MIMO Radars in the Presence of Outliers. IEEE Signal Process. Lett. 2020, 27, 2168–2172. [Google Scholar] [CrossRef]
- Yu, Z.; Li, J.; Guo, Q.; Ding, J. Efficient Direct Target Localization for Distributed MIMO Radar with Expectation Propagation and Belief Propagation. IEEE Trans. Signal Process. 2021, 69, 4055–4068. [Google Scholar] [CrossRef]
- Yu, Z.; Li, J.; Guo, Q. Message Passing Based Target Localization Under Range Deception Jamming in Distributed MIMO Radar. IEEE Signal Process. Lett. 2021, 28, 1858–1862. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.C.; Yang, Y.; Zhang, L.; Chen, L. Robust Iterative Solution for Linear Array-Based 3-D Localization by Message Passing. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Zhang, Z.; Shi, Z.; Gu, Y.; Greco, M.S.; Gini, F. Ziv-Zakai Bound for Compressive Time Delay Estimation From Zero-Mean Gaussian Signal. IEEE Signal Process. Lett. 2023, 30, 1112–1116. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, Z.; Zhou, C.; Yan, C.; Gu, Y. Ziv-Zakai Bound for Compressive Time Delay Estimation. IEEE Trans. Signal Process. 2022, 70, 4006–4019. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, Z.; Shao, C.; Chen, J.; Greco, M.S.; Gini, F. Ziv-Zakai Bound for 2D-DOAs Estimation. IEEE Trans. Signal Process. 2024, 72, 2483–2497. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Bernstein, D.S. Matrix mathematics: Theory, Facts, and Formulas with Application to Linear Systems Theory; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Wu, L.; Sahu, N.; Xu, S.; Babu, P.; Ciuonzo, D. Optimization Based Sensor Placement for Multi-Target Localization with Coupling Sensor Clusters. IEEE Trans. Signal Inf. Process. Netw. 2023, 9, 596–611. [Google Scholar] [CrossRef]

| Commun. Tech. | Bandwidth Occupation | Commun. Mode | Short Comings | Advantages | TOA Measurements |
|---|---|---|---|---|---|
| Frequency division | Large | Simultaneous | Energy-consuming, complex RF design | Obtain TOAs after one communication round | Non-sequential |
| Code division | Small | Simultaneous | Near-far effect | Obtain TOAs after one communication round | Non-sequential |
| Time division | Small | One pair by one pair | Longer temporal duration | Energy-saving, frequency spectrum resource-saving, simple design | Sequential |
| Paper | Measurements | Methods | Complexity |
|---|---|---|---|
| [7] | One-way TOA | TSWLS | Low |
| [8,27] | One-way TOA | GN | Medium |
| [11] | One-way TOA | WLS | Low |
| [19] | One-way TOA | Distributed state estimation | High |
| [20] | Two-way TOA | WLS | Low |
| [23] | Two-way TOA | Exhaustive search and a multi-grid search | High |
| [25] | Two-way TOA | WLS | Low |
| [26] | Two-way TOA | SDP | Medium |
| Anchor | Position | Anchor | Position |
|---|---|---|---|
| AN #1 | m | AN #8 | m |
| AN #2 | m | AN #9 | m |
| AN #3 | m | AN #10 | m |
| AN #4 | m | AN #11 | m |
| AN #5 | m | AN #12 | m |
| AN #6 | m | AN #13 | m |
| AN #7 | m | AN #14 | m |
| Method | RIS | GN | CFPS | CFJLAS |
|---|---|---|---|---|
| Times (s) | 60.2648 | 26.6622 | 1.8245 | 2.7523 |
| Rel. Times | 21.89 | 9.69 | 0.66 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xu, Y.; Tang, B.; Yang, Y.; Sun, Y. Efficient Solution Resilient to Noise and Anchor Position Error for Joint Localization and Synchronization Using One-Way Sequential TOAs. Appl. Sci. 2024, 14, 6069. https://doi.org/10.3390/app14146069
Zhang S, Xu Y, Tang B, Yang Y, Sun Y. Efficient Solution Resilient to Noise and Anchor Position Error for Joint Localization and Synchronization Using One-Way Sequential TOAs. Applied Sciences. 2024; 14(14):6069. https://doi.org/10.3390/app14146069
Chicago/Turabian StyleZhang, Shuyi, Yihuai Xu, Beichuan Tang, Yanbing Yang, and Yimao Sun. 2024. "Efficient Solution Resilient to Noise and Anchor Position Error for Joint Localization and Synchronization Using One-Way Sequential TOAs" Applied Sciences 14, no. 14: 6069. https://doi.org/10.3390/app14146069
APA StyleZhang, S., Xu, Y., Tang, B., Yang, Y., & Sun, Y. (2024). Efficient Solution Resilient to Noise and Anchor Position Error for Joint Localization and Synchronization Using One-Way Sequential TOAs. Applied Sciences, 14(14), 6069. https://doi.org/10.3390/app14146069







