Analysis of Bullet Impact Locations in the 10 m Air Pistol Men’s Competition Based on Covariance
Abstract
1. Introduction
2. Related Works
3. Methods
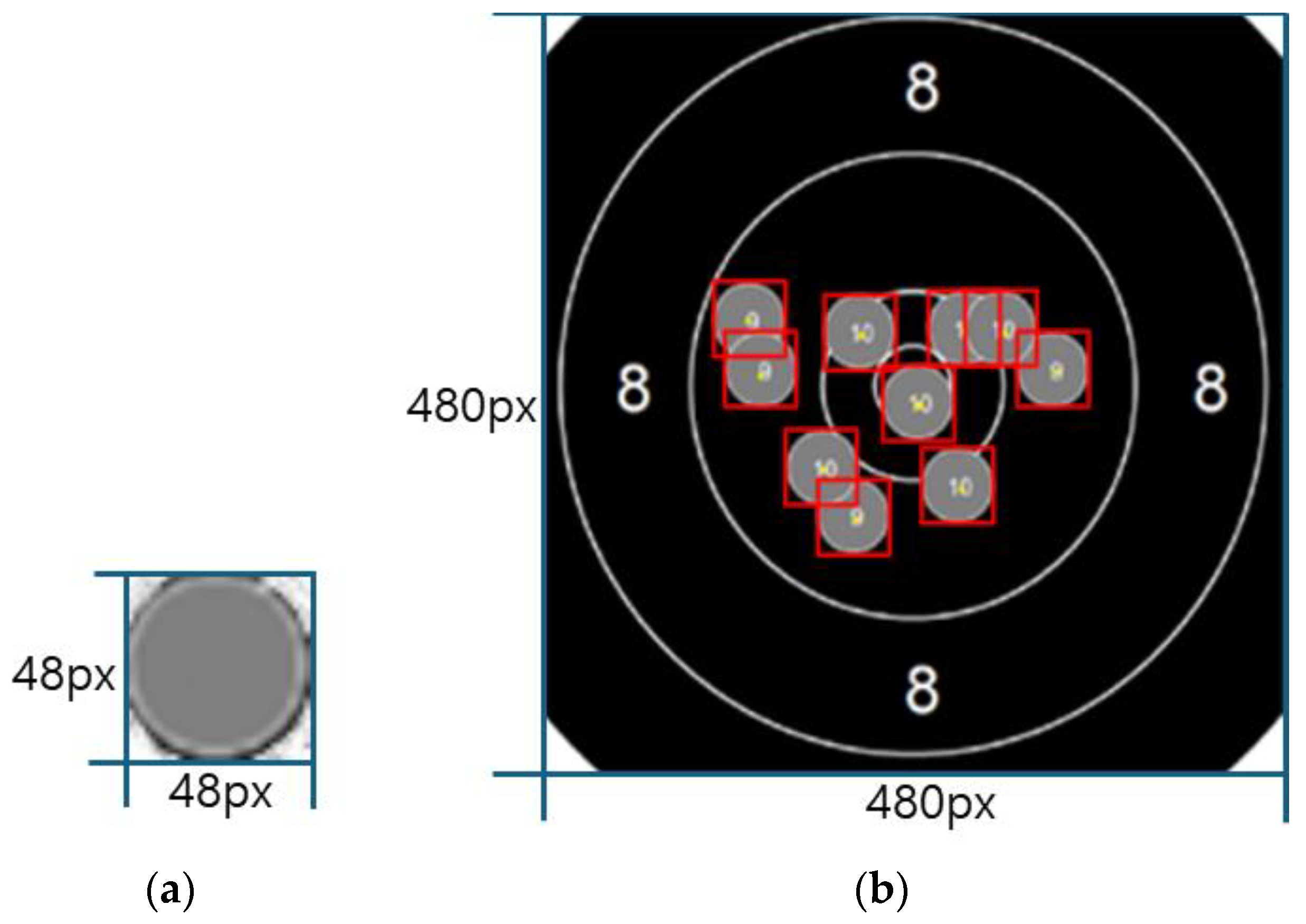
3.1. Extraction of Bullet Impact Point Location Information
3.1.1. Extraction of Image x and y Coordinates
3.1.2. Calculation of Bullet Impact Position Coordinates
3.1.3. Calculation of Scores by x, y Coordinates
3.2. Data Collection and Statistical Analysis
3.3. Feature Indicators
- X-variance
- Y-variance
- Covariance
- X-mean
- Y-mean
- Root mean square error (RMSE)
- X-mean score
- Y-mean score
4. Results
4.1. Competition Analysis Results
4.2. Correlation Analysis between Rankings and Key Indicators
4.3. Player-Specific Case Analysis
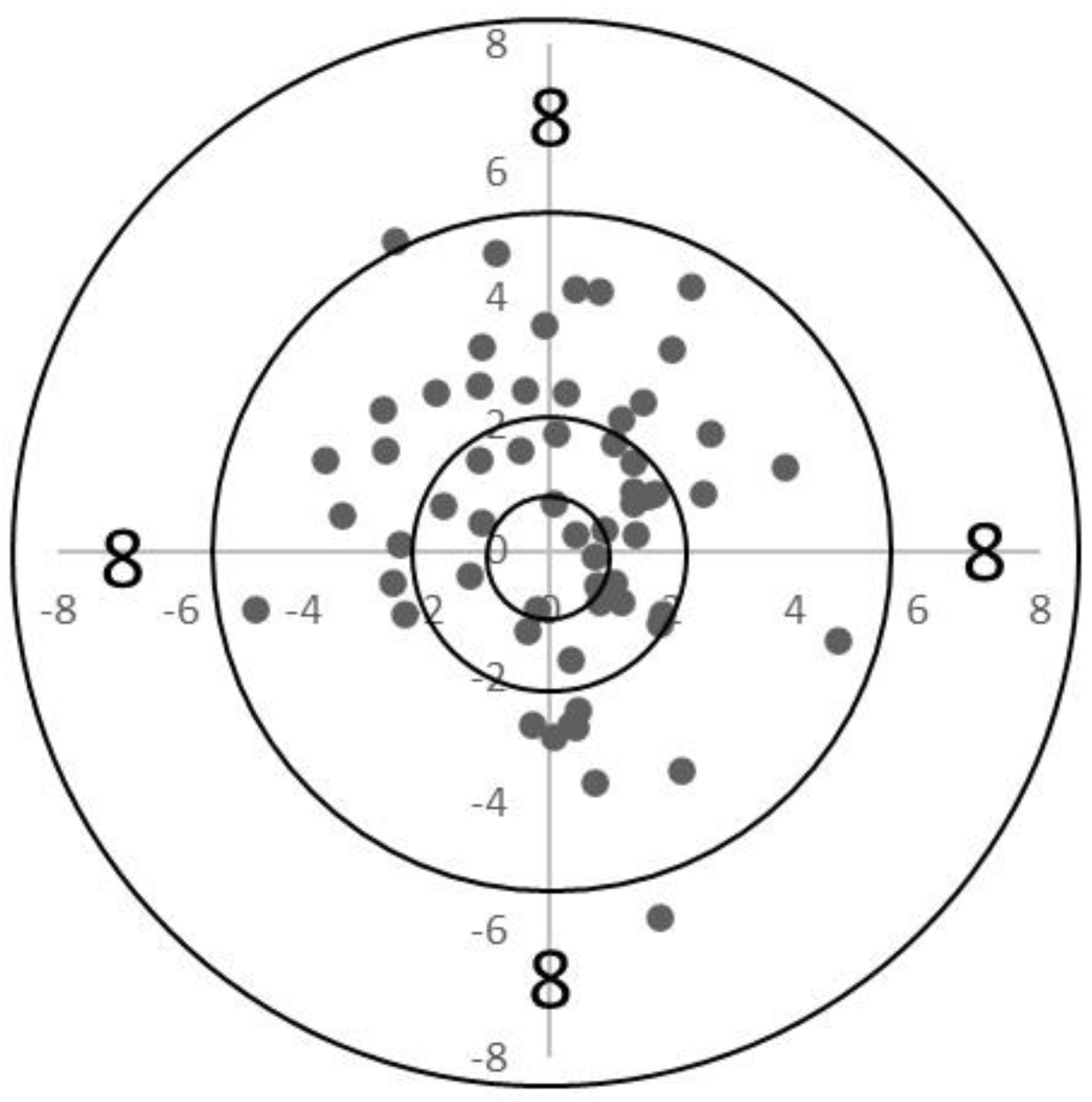
4.3.1. Shooting Pattern Analysis #1
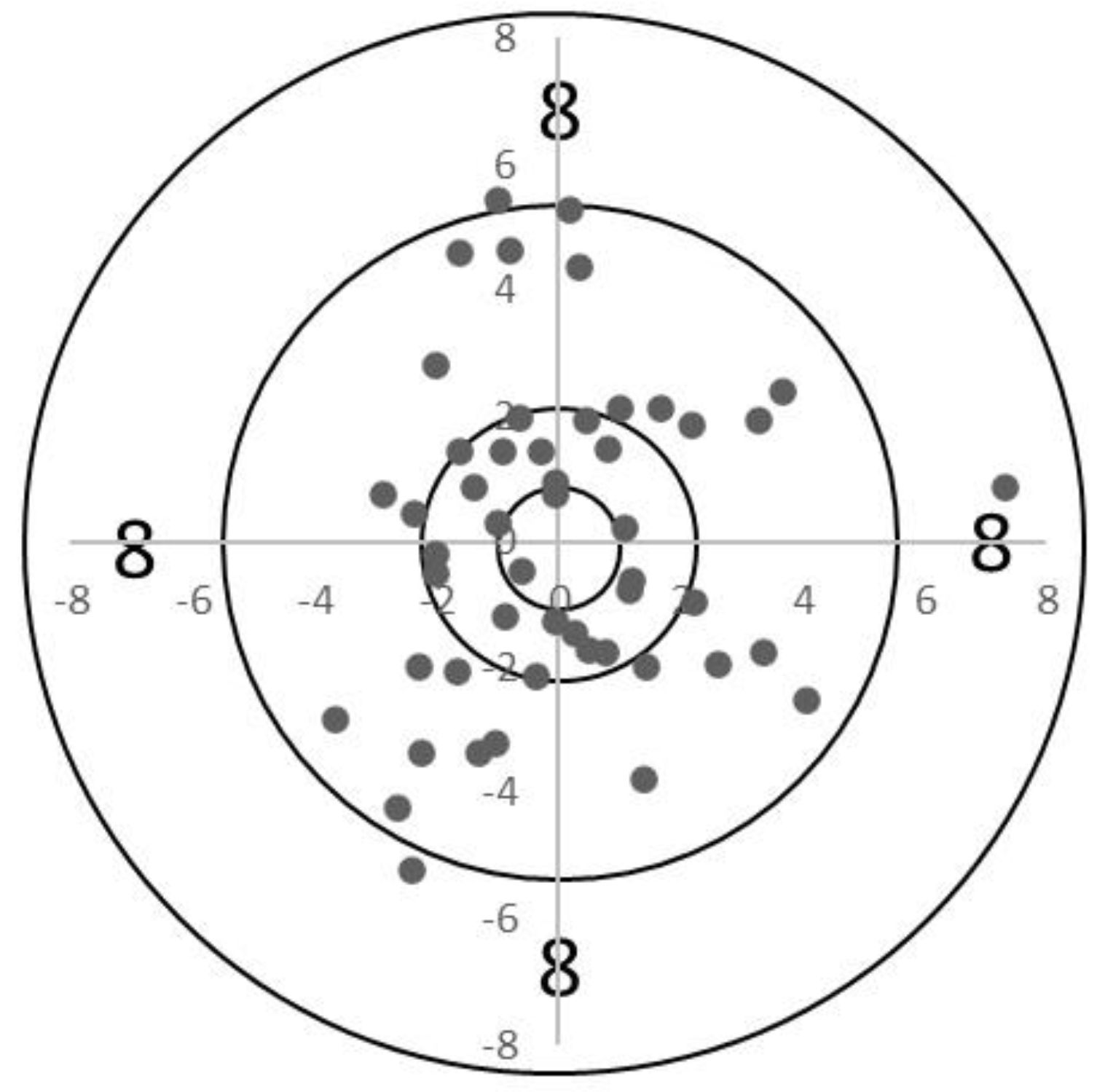
4.3.2. Shooting Pattern Analysis #2
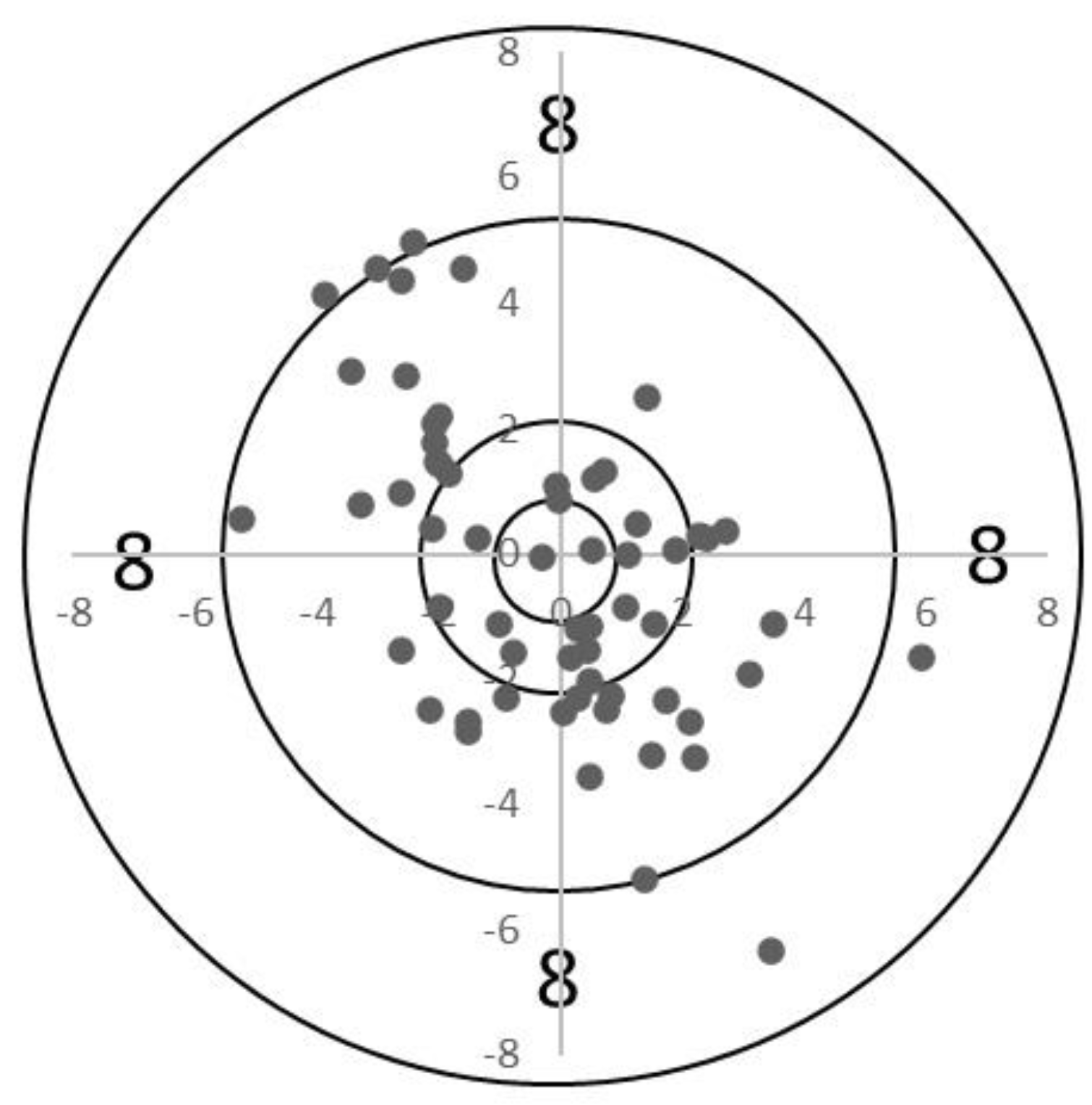
4.3.3. Shooting Pattern Analysis #3
4.3.4. Shooting Pattern Analysis #4
4.3.5. Shooting Pattern Analysis #5
5. Discussion
5.1. Competition Analysis
5.2. Rankings and Feature Indicator Correlation
5.3. Player-Specific Case Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hwang, S.Y.; Park, J. A descriptive review of shooting skills and physical factors of shooters. Sports Sci. 2023, 41, 217–228. [Google Scholar] [CrossRef]
- Jeong, I.S. A study on the effect of coaching machine training on improving the performance of shooting players. J. Korean Soc. Sports Sci. 2020, 29, 1159–1167. [Google Scholar]
- Hawkins, R. Identifying mechanic measures that best predict air-pistol shooting performance. Int. J. Perform. Anal. Sport 2011, 11, 499–509. [Google Scholar] [CrossRef]
- Joo, D.Y.; Kim, M.G. The effect of body stability on a shooter’s aiming shot. Korean Sports Res. 2004, 15, 551–566. [Google Scholar]
- Woo, C.H.; Lee, G.S. Kinematic analysis of pistol shooting. Korean J. Kinesiol. 2000, 9, 81–101. [Google Scholar]
- Lee, Y.; Kim, S. The effect of core muscle strengthening exercises using an unstable support surface on the balance ability and shooting scores of shooters. J. Orthop. Sports Phys. Ther. 2020, 16, 77–84. [Google Scholar] [CrossRef]
- Kim, S.; Lee, K.C. The effect of air pistol aiming on scoring. Coach. Competency Dev. J. 2004, 6, 165–173. [Google Scholar]
- Eom, H.J.; Kim, J.A.; Choi, H. Analysis of the efficiency of volleyball game analysis program input information settings and technical performance: Focusing on women’s games in the 2018–2019 professional volleyball regular season. Korean J. Phys. Educ. Meas. Eval. 2020, 22, 137–161. [Google Scholar]
- Choi, J.; Kim, A. A literature review on the improvement of physical strength and performance of shooting athletes. J. Korean Soc. Sports Converg. 2021, 19, 27–33. [Google Scholar]
- Kim, S.E.; Cho, C.R. The impact of each technical factor on air rifle shooting on scoring. Korean J. Sports Sci. 2004, 13, 753–761. [Google Scholar]
- Kim, Y.; Kim, G.S. Kinematic analysis of air pistol shooting posture between excellent and non-excellent athletes. Korean J. Kinesiol. 2009, 19, 509–517. [Google Scholar]
- Kim, K.W.; Jeon, G.G. The effect of stabilization of muzzle and posture on performance when shooting an air rifle. J. Korean Soc. Sports Sci. 2013, 22, 1169–1178. [Google Scholar]
- Dall, I.; Park, J.L. Shot distribution in target archery, with application to arrow selection. Proc. Inst. Mech. Engineers. J. Sports Eng. Technol. 2022, 17543371221130537. [Google Scholar] [CrossRef]
- Mononen, K.; Konttinen, N.; Viitasalo, J.; Era, P. Relationships between postural balance, rifle stability and shooting accuracy among novice rifle shooters. Scand. J. Med. Sci. Sports 2007, 17, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.W.; Kong, B. A shooting training and instructing system based on image analysis. In Proceedings of the 2006 IEEE International Conference on Information Acquisition, Veihai, China, 20–23 August 2006; IEEE: New York, NY, USA; pp. 961–966. [Google Scholar]
- Mon-López, D.; Tejero-González, C.M. Validity and reliability of the Target Scan ISSF Pistol & Rifle application for measuring shooting performance. Scand. J. Med. Sci. Sports 2019, 29, 1707–1712. [Google Scholar] [PubMed]
- Lang, D.; Zhou, A. Determinants of shooting performance in elite air rifle shooters. Sports Biomech. 2022, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Baca, A.; Kornfeind, P. Stability analysis of motion patterns in biathlon shooting. Hum. Mov. Sci. 2012, 31, 295–302. [Google Scholar] [CrossRef] [PubMed]
- Quan, C.H. Relationship between aiming patterns and scores in archery shooting. Korean J. Appl. Biomech. 2016, 26, 353–360. [Google Scholar] [CrossRef]
- Olsson, E.; Laaksonen, M.S. Key technical components for air pistol shooting performance. Int. J. Perform. Anal. Sport 2021, 21, 348–360. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, S. The design and implementation of shooting training and intelligent evaluation system. In Emerging Computation and Information Technologies for Education: Proceedings of 2012 International Conference on Emerging Computation and Information Technologies for Education (ECICE 2012); Springer: Berlin/Heidelberg, Germany, 2012; pp. 107–115. [Google Scholar]
- Ding, P.; Zhang, X.; Fan, X.; Cheng, Q. Design of automatic target-scoring system of shooting game based on computer vision. In Proceedings of the 2009 IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009; pp. 825–830. [Google Scholar]
- Kim, S. Real-time scoring of air rifle shooting using image processing techniques. J. Korean Soc. Inf. Technol. 2015, 13, 33–41. [Google Scholar]
- Lee, T.G.; Lim, C.G.; Kim, K.C.; Kim, Y.M. Extracting the Point of Impact from Simulated Shooting Target based on Image Processing. J. Internet Comput. Serv. 2010, 11, 117–128. [Google Scholar]
- Rudzinski, J.; Luckner, M. Low–cost computer vision based automatic scoring of shooting targets. In Knowledge Engineering, Machine Learning and Lattice Computing with Applications: 16th International Conference, KES 2012, San Sebastian, Spain, 10–12 September 2012; Revised Selected Papers 16; Springer: Berlin/Heidelberg, Germany, 2013; pp. 185–195. [Google Scholar]
- Aryan, P.R. Vision based automatic target scoring system for mobile shooting range. In Proceedings of the 2012 International Conference on Advanced Computer Science and Information Systems (ICACSIS), Depok, Indonesia, 1–2 December 2012; pp. 325–329. [Google Scholar]
- Ali, F.; Mansoor, A.B. Computer vision based automatic scoring of shooting targets. In Proceedings of the 2008 IEEE International Multitopic Conference, Karachi, Pakistan, 23–24 December 2008; pp. 515–519. [Google Scholar]




| Research Area | Author(s) & Year | Title | Main Content |
|---|---|---|---|
| Shooting performance | Liang and Kong, 2006 [15] | A shooting training and instructing system based on image analysis | Designing and implementing a computer-assisted shooting training and coaching system. After the camera captures the target image, the aiming point marked by the laser spot is extracted from the image, and the corresponding score is calculated and printed on the screen in real-time. |
| Mon-Lopez and Tejero-Gonzalez, 2019 [16] | Validity and reliability of the Target Scan ISSF Pistol & Rifle application for measuring shooting performance | Confirming the validity and reliability of the Target Scan ISSF Pistol and Rifle application, an automatic mobile application that measures shooter performance through image analysis | |
| Lang and Zhou, 2022 [17] | Determinants of shooting performance in elite air rifle shooters | Confirming the determinants of shooting ability in elite 10 m air rifle shooters using the SCATT optical shooting test system and force platform | |
| Shooting patterns | Baca and Kornfeind, 2012 [18] | Stability analysis of motion patterns in biathlon shooting | Analyzing the aiming stability of nine biathlon athletes. Reconstructing the horizontal and vertical movements of the rifle barrel using a video-based system. |
| Quan, 2016 [19] | Relationship between aiming patterns and scores in archery shooting | Investigating the relationship between archery aiming patterns and scores using nine accelerometers on four middle school students at the elementary school level | |
| Target analysis | Olsson and Laaksonen, 2021 [20] | Key technical components for air pistol shooting performance | Using an optical training device to measure shooting scores and 17 trajectory variables of aiming points |
| Lin and Wu, 2012 [21] | The design and implementation of shooting training and intelligent evaluation system | Automatic target scoring and skill assessment through tracking records of shooting aiming points obtained via video acquisition |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 584 | 3.021 | 2.916 | −0.711 | −0.143 | −0.681 | 0.696 | 9.950 | 9.933 |
| 2 | 582 | 4.330 | 3.358 | −0.576 | −0.206 | −0.782 | 0.809 | 9.900 | 9.950 |
| 3 | 581 | 3.712 | 3.977 | −0.799 | 0.39 | −0.477 | 0.616 | 9.800 | 9.900 |
| 4 | 581 | 3.913 | 3.596 | −0.526 | 0.254 | 0.274 | 0.374 | 9.850 | 9.850 |
| 5 | 578 | 3.366 | 4.988 | −0.558 | 0.156 | 0.519 | 0.542 | 9.917 | 9.767 |
| 6 | 577 | 3.536 | 5.918 | 0.046 | −0.184 | −0.268 | 0.325 | 9.900 | 9.817 |
| 7 | 577 | 4.159 | 5.878 | 0.631 | −0.019 | 0.038 | 0.042 | 9.820 | 9.820 |
| 8 | 575 | 3.164 | 4.567 | 0.123 | −0.521 | −0.500 | 0.722 | 9.900 | 9.950 |
| 9 | 575 | 4.888 | 4.258 | −0.492 | 0.788 | −0.430 | 0.898 | 9.717 | 9.867 |
| 10 | 574 | 4.734 | 5.107 | −1.62 | 0.403 | −0.862 | 0.952 | 9.740 | 9.900 |
| 11 | 574 | 4.604 | 5.721 | −2.681 | −0.201 | −0.260 | 0.329 | 9.850 | 9.850 |
| 12 | 574 | 5.291 | 5.453 | −0.327 | −0.888 | −0.696 | 1.128 | 9.850 | 9.900 |
| 13 | 573 | 7.228 | 3.560 | −0.356 | 0.408 | −0.309 | 0.512 | 9.700 | 9.883 |
| 14 | 573 | 3.574 | 5.882 | −0.892 | −0.355 | −0.083 | 0.365 | 9.900 | 9.750 |
| 15 | 573 | 4.723 | 4.389 | −0.293 | −0.224 | −0.895 | 0.923 | 9.883 | 9.950 |
| 16 | 573 | 3.146 | 2.910 | −0.665 | −0.147 | −0.699 | 0.714 | 9.950 | 9.933 |
| 17 | 572 | 5.807 | 4.481 | −0.971 | 0.195 | −0.368 | 0.416 | 9.783 | 9.917 |
| 18 | 571 | 4.573 | 7.299 | 0.312 | 0.085 | −0.757 | 0.762 | 9.867 | 9.867 |
| 19 | 570 | 4.991 | 5.862 | 1.231 | 0.216 | −0.352 | 0.413 | 9.800 | 9.820 |
| 20 | 570 | 3.896 | 5.422 | −0.771 | −0.486 | −1.570 | 1.644 | 9.883 | 9.967 |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 584 | 3.021 | 2.916 | −0.711 | −0.143 | −0.681 | 0.696 | 9.950 | 9.933 |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 578 | 3.366 | 4.988 | −0.558 | 0.156 | 0.519 | 0.542 | 9.917 | 9.767 |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 7 | 577 | 4.159 | 5.878 | 0.631 | −0.019 | 0.038 | 0.042 | 9.820 | 9.820 |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 574 | 4.604 | 5.721 | −2.681 | −0.201 | −0.260 | 0.329 | 9.850 | 9.850 |
| Ranking | Total Score | X-Variance | Y-Variance | Covariance | X-Mean | Y-Mean | RMSE | X-Mean Score | Y-Mean Score |
|---|---|---|---|---|---|---|---|---|---|
| 13 | 573 | 7.228 | 3.560 | −0.356 | 0.408 | −0.309 | 0.512 | 9.700 | 9.883 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.-Y.; Lee, E. Analysis of Bullet Impact Locations in the 10 m Air Pistol Men’s Competition Based on Covariance. Appl. Sci. 2024, 14, 6006. https://doi.org/10.3390/app14146006
Moon J-Y, Lee E. Analysis of Bullet Impact Locations in the 10 m Air Pistol Men’s Competition Based on Covariance. Applied Sciences. 2024; 14(14):6006. https://doi.org/10.3390/app14146006
Chicago/Turabian StyleMoon, Ji-Yeon, and Euichul Lee. 2024. "Analysis of Bullet Impact Locations in the 10 m Air Pistol Men’s Competition Based on Covariance" Applied Sciences 14, no. 14: 6006. https://doi.org/10.3390/app14146006
APA StyleMoon, J.-Y., & Lee, E. (2024). Analysis of Bullet Impact Locations in the 10 m Air Pistol Men’s Competition Based on Covariance. Applied Sciences, 14(14), 6006. https://doi.org/10.3390/app14146006







