Thermodynamic Study on the Vortex Teeth of Electric Scroll Compressors Based on Gradient Tooth Height
Abstract
:1. Introduction
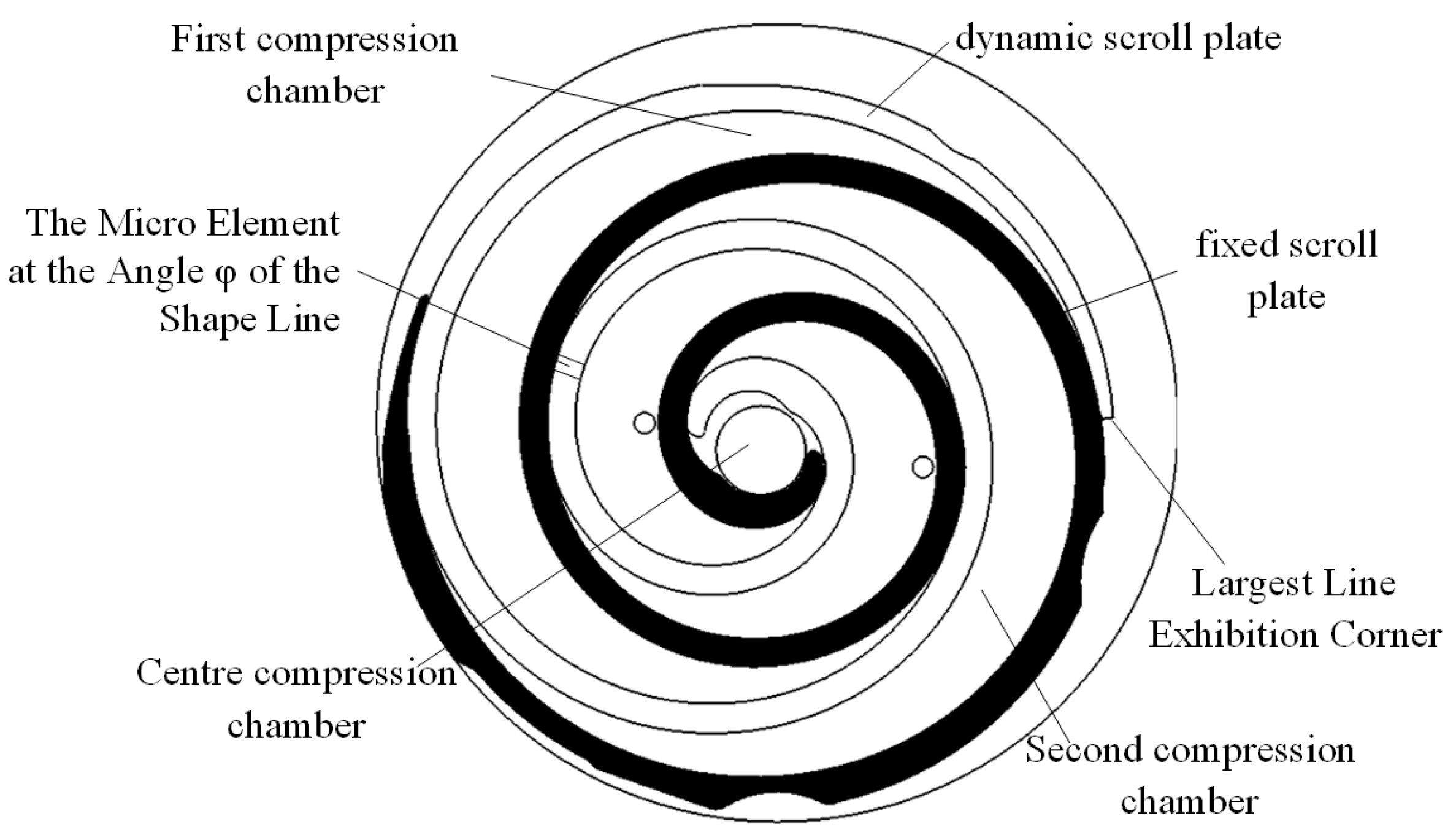
2. Vortex Tooth Temperature Distribution Model
2.1. Model Analysis and Assumptions
- (1)
- The average gas temperature and the convective heat transfer coefficient associated with the scroll teeth are maintained throughout the operation cycle.
- (2)
- The focus is exclusively on the change in temperature distribution along the profile axis.
- (3)
- The influence of spindle rotation speed fluctuations on temperature distribution has been ignored, assuming that it remains constant.
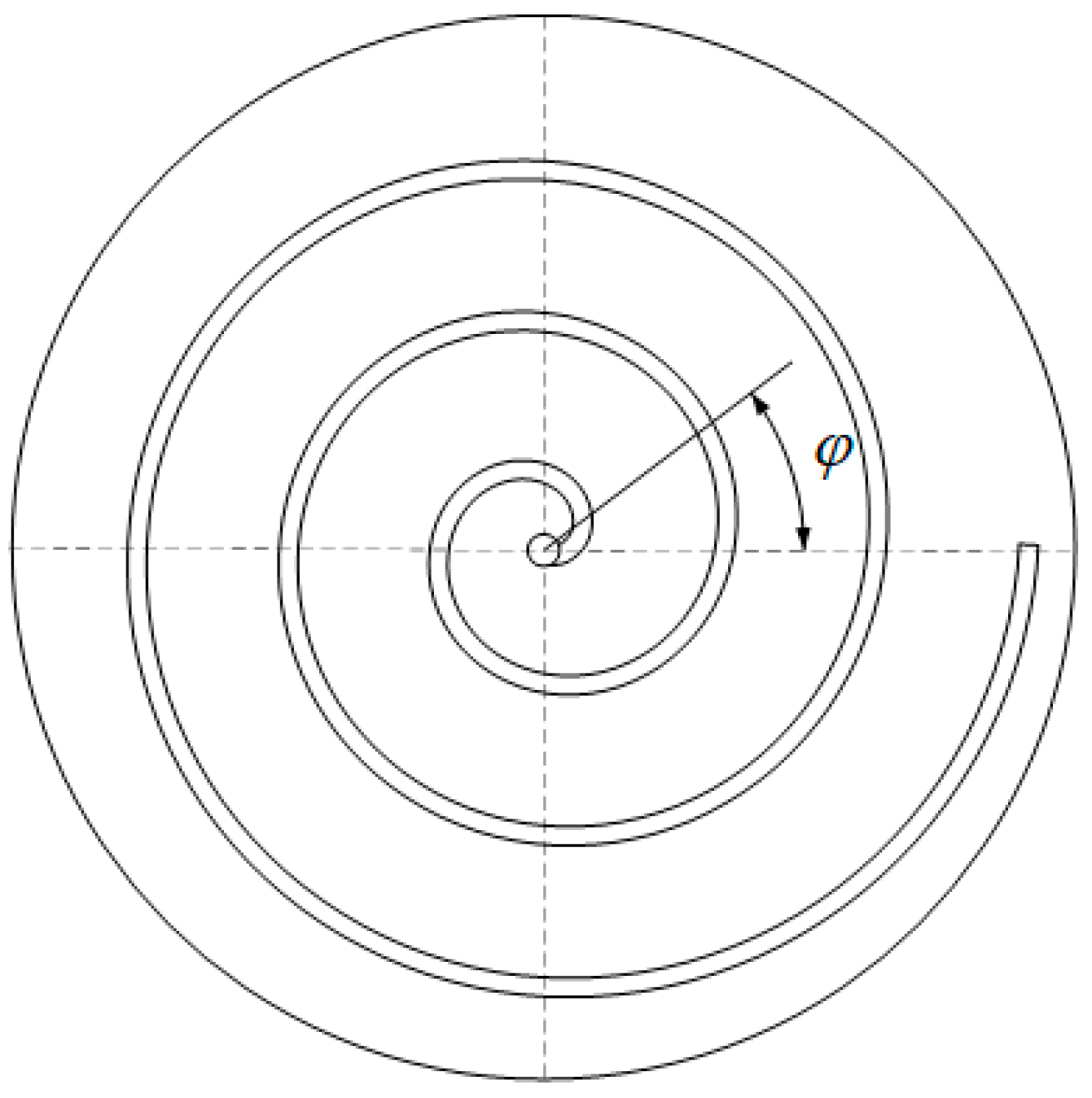
2.2. Steady-State Temperature Function of the Wall Surface of the Vortex Tooth
2.3. Scroll Tooth Temperature Distribution Solution
3. Finite Element Modeling
3.1. Geometric Modeling and Meshing
3.2. Restrictive Condition
- (1)
- The rotational freedom of the movable scroll disc along the Z-axis is constrained to zero.
- (2)
- The dynamic bearing bore of the scroll disc is completely fixed in both the X and Y directions.
3.3. Acting Load
4. Simulation Analysis
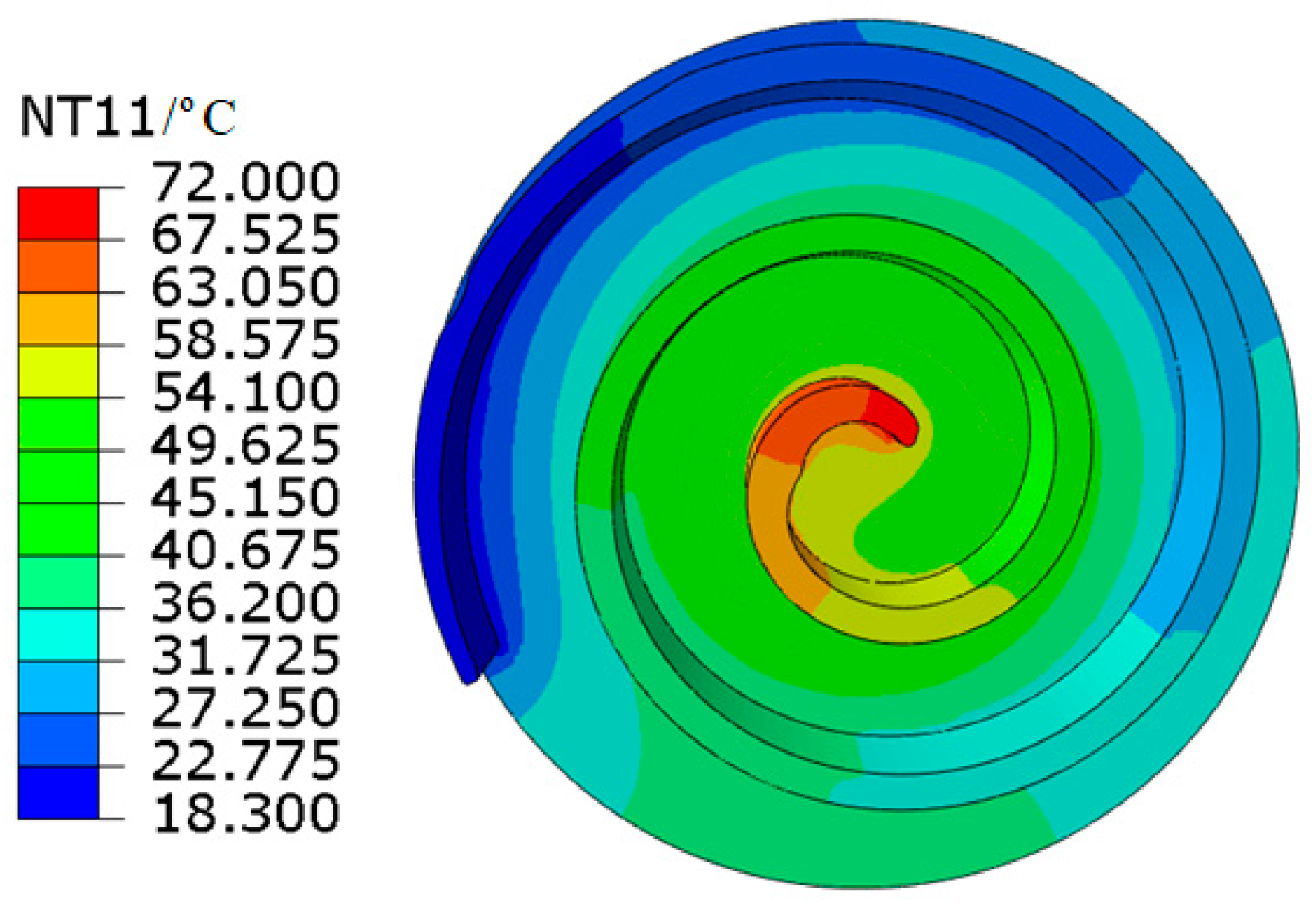
4.1. Temperature Load
4.2. Gas Pressure Load
4.3. Multi-Load
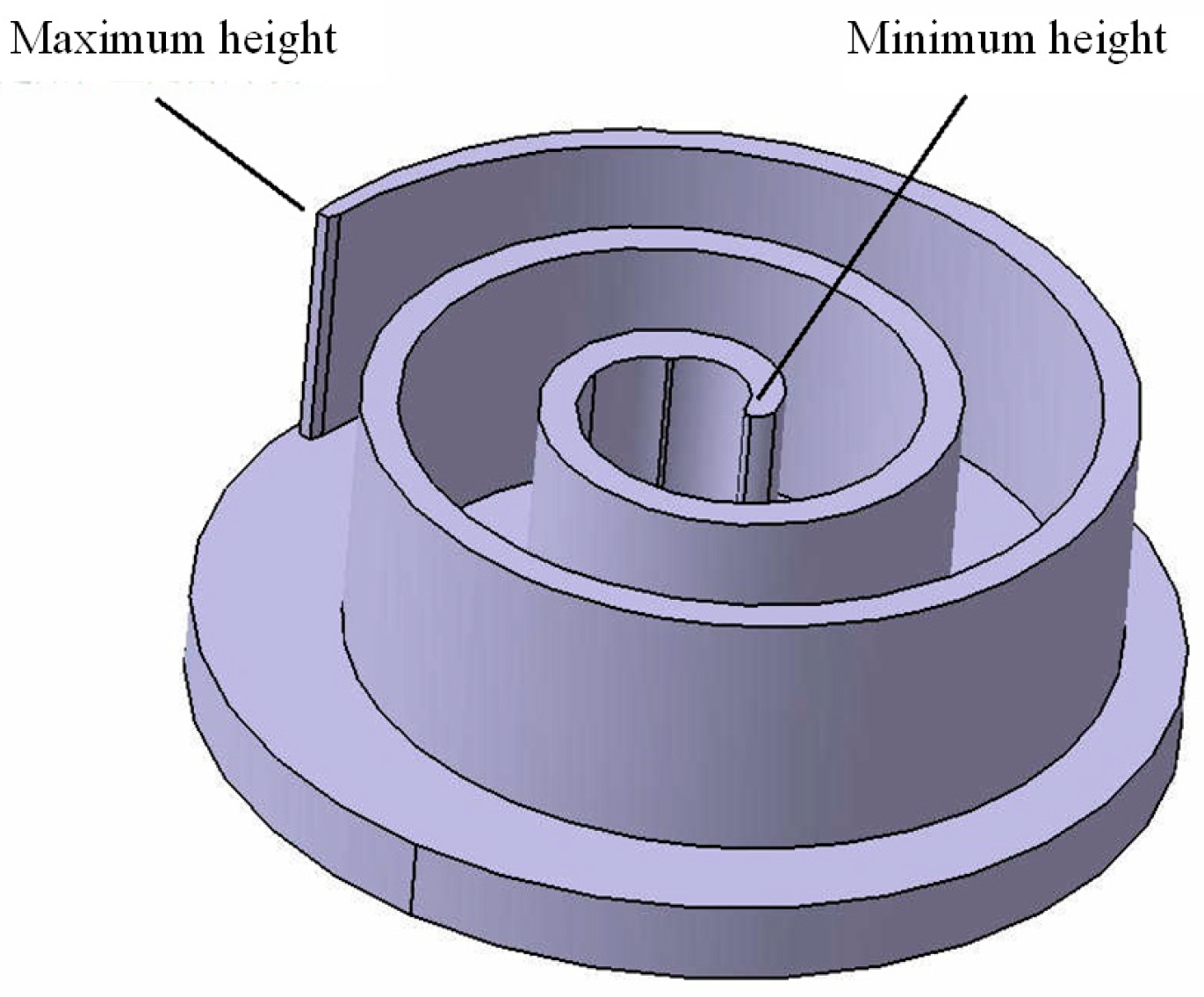
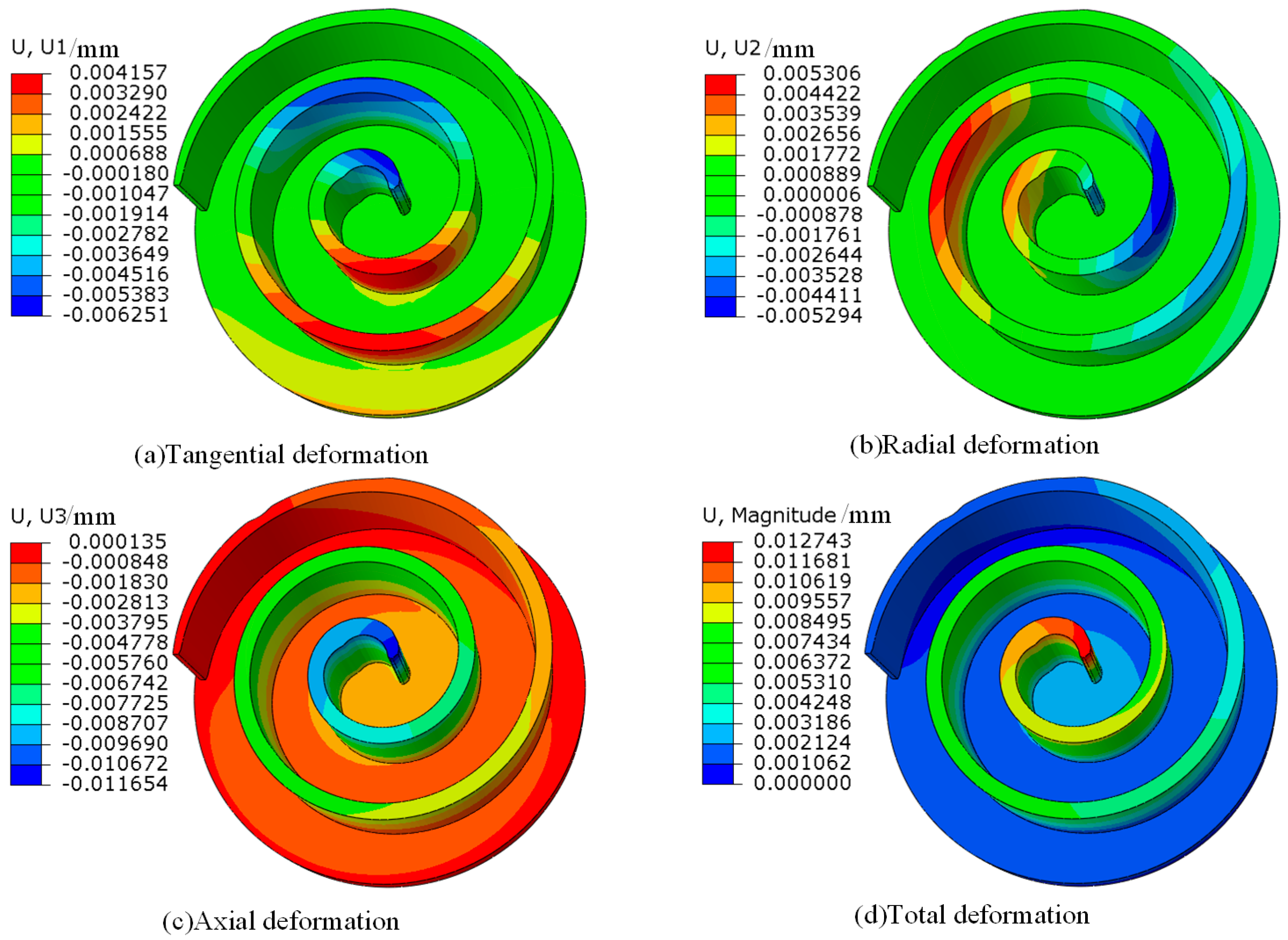
4.4. Deformation Law of Asymptotic Tooth Height under Multiple Loads
4.5. Result Reliability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Liu, J.; Zhao, H.J.; Jiang, Y.; Huang, X.Y. Aerodynamic noise analysis of suction and discharge valves of linear compressor based on multi physical field coupling. Chin. Hydraul. Pneum. 2023, 47, 68–76. [Google Scholar]
- Zhang, Y.B.; Peng, B.; Zhang, P.C.; Sun, J.; Liao, Z.X. Key technologies and application of electric scroll compressors: A review. Energies 2024, 17, 1790. [Google Scholar] [CrossRef]
- Peng, Q.H.; Du, Q.G. Progress in heat pump air conditioning systems for electric vehicles—A review. Energies 2016, 9, 240. [Google Scholar] [CrossRef]
- Cheng, J.M.; Yang, Z.J. Summarization of flow field analysis of scroll compressor compression chamber. Petro-Chem. Equip. 2016, 19, 49–50. [Google Scholar]
- Tian, S.G.; Wang, C.; Zhao, Y.Y. Research progress and development trend of scroll compressor. Refrig. Air-Cond. 2021, 21, 72–77+86. [Google Scholar]
- Liu, G.P.; Li, J.F.; Gong, Q. Finite element analysis based on moving thermal boundary for orbiting scroll wrap’s temperature distribution. Chin. Hydraul. Pneum. 2019, 1, 65–70. [Google Scholar]
- Wang, J.T.; Liu, G.P.; Hu, R.H.; Yu, T.F. Temperature-fields simulation of scroll gears of wind-cooling oil-free scroll air Compressor. Chin. J. Vac. Sci. Technol. 2015, 35, 1225–1230. [Google Scholar]
- Wang, J.T.; Liu, G.P.; Yu, T.F.; Xiao, G.F.; Song, H.G. Research of scroll air compressor with asynchronous discharge of symmetric chambers. China Mech. Eng. 2014, 25, 2715–2718. [Google Scholar]
- Li, Y.Z. Flow Field Characteristics of the Scroll Compressor and Stress-Strain Analysis of Orbiting Scroll Wrap. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2023. [Google Scholar]
- Hirano, T.; Hagimoto, K.; Maeda, M. Study on scroll profile for scroll fluid machines. Trans. Jpn. Soc. Refrig. Air Cond. Eng. 2011, 8, 53–64. [Google Scholar]
- Meng, H.; Li, A.; Li, H.S.; Feng, W.G.; Chen, J.H.; Cui, Z. Research on deformation behavior of grooved scroll teeth for oil-free scroll compressor. Fluid Mach. 2022, 50, 66–72+104. [Google Scholar]
- Li, X.R.; Wu, W.F.; Zhang, J.; Guo, C.Q.; Ke, F.; Jiang, F.Q. Analysis of 3D transient flow in a high-speed scroll refrigeration compressor. Energies 2023, 16, 3089. [Google Scholar] [CrossRef]
- Ballani, A.; Pasunurthi, S.S.; Srinivasan, C.; Maiti, D. Performance Prediction of an e-Compressor Using 3D CFD Simulation; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2023. [Google Scholar]
- Cavazzini, G.; Giacomel, F.; Benato, A.; Nascimben, F.; Ardizzon, G. Analysis of the inner fluid-dynamics of scroll compressors and comparison between CFD numerical and modelling approaches. Energies 2021, 14, 1158. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Q.; Jiang, Y.; Wang, Z.L.; Cha, H.B. Temperature distribution and deformation of scroll wraps for scroll compressors. J. Eng. Thermophys. 2016, 37, 2344–2348. [Google Scholar]
- Wu, Z.; Feng, Z.G.; Su, Y.F. Simulation and analysis of internal flow field in scroll compressor with circular involute profile. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 1840–1846. [Google Scholar]
- Li, X.Q.; Wang, Z.L.; Wang, J. A simplified method of calculating working chamber volumes for scroll machinery. Compress. Technol. 2009, 5, 25–28. [Google Scholar]
- Li, J.F. Structure Optimization Design of Scroll Compressor for Scroll Based on Thermodynamics. Master’s Thesis, Nanchang University, Nanchang, China, 2019. [Google Scholar]
- Yang, M.H. Research on the Methods to Decrease Discharge Temperature of R32 Scroll Compressor. Master’s Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Li, C.; Xie, W.J.; Zhao, M. Deformation and stress analysis of orbiting scroll under the multi-field coupling. Fluid Mach. 2013, 41, 16–20. [Google Scholar]
- Xie, W.J. The Finite Element Analysis on Orbiting and Fixed Scrolls of Oil-Free Scroll Compressor. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2013. [Google Scholar]
- Wei, N. Scroll Compressor Based on Combined Profile Change Study on Performance of working CHAMBER. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2023. [Google Scholar]



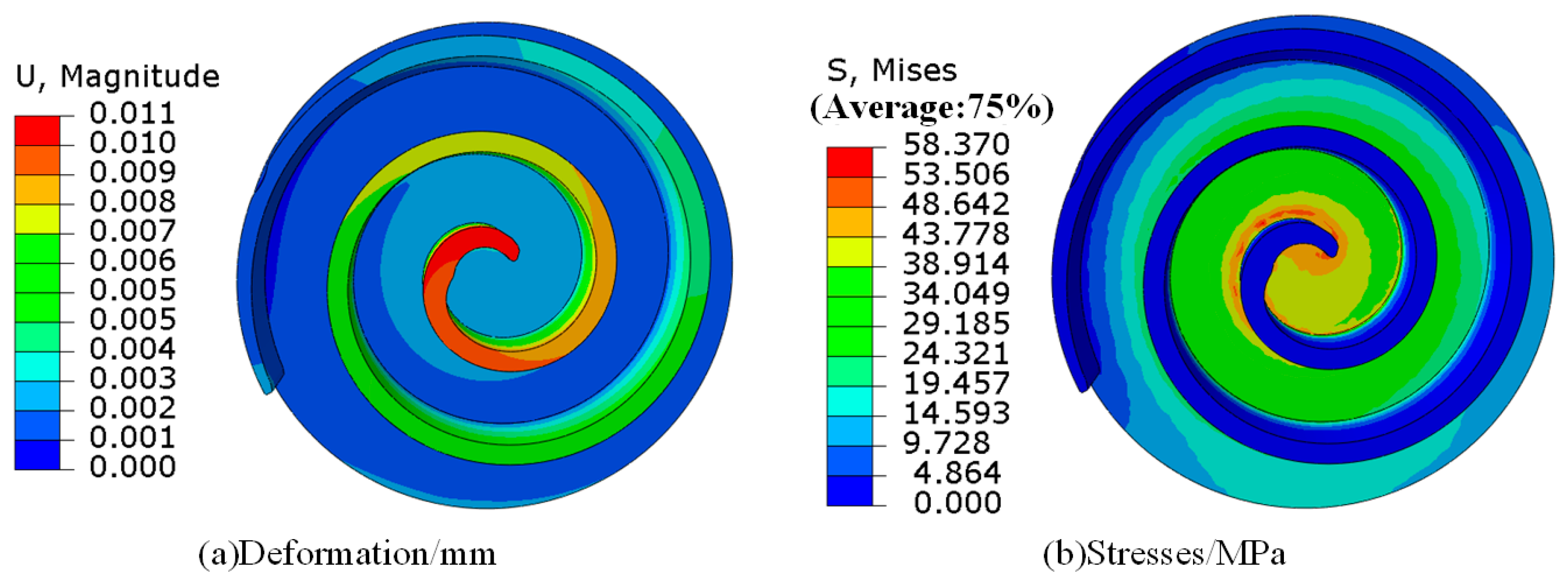
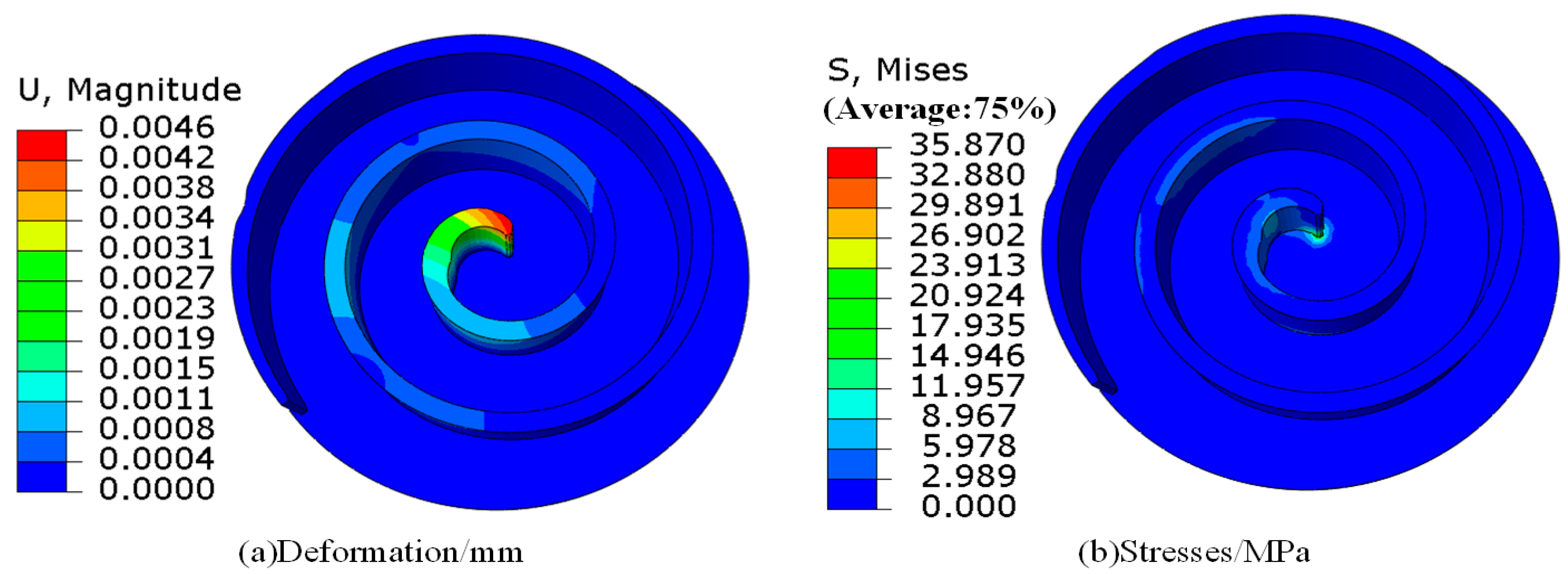
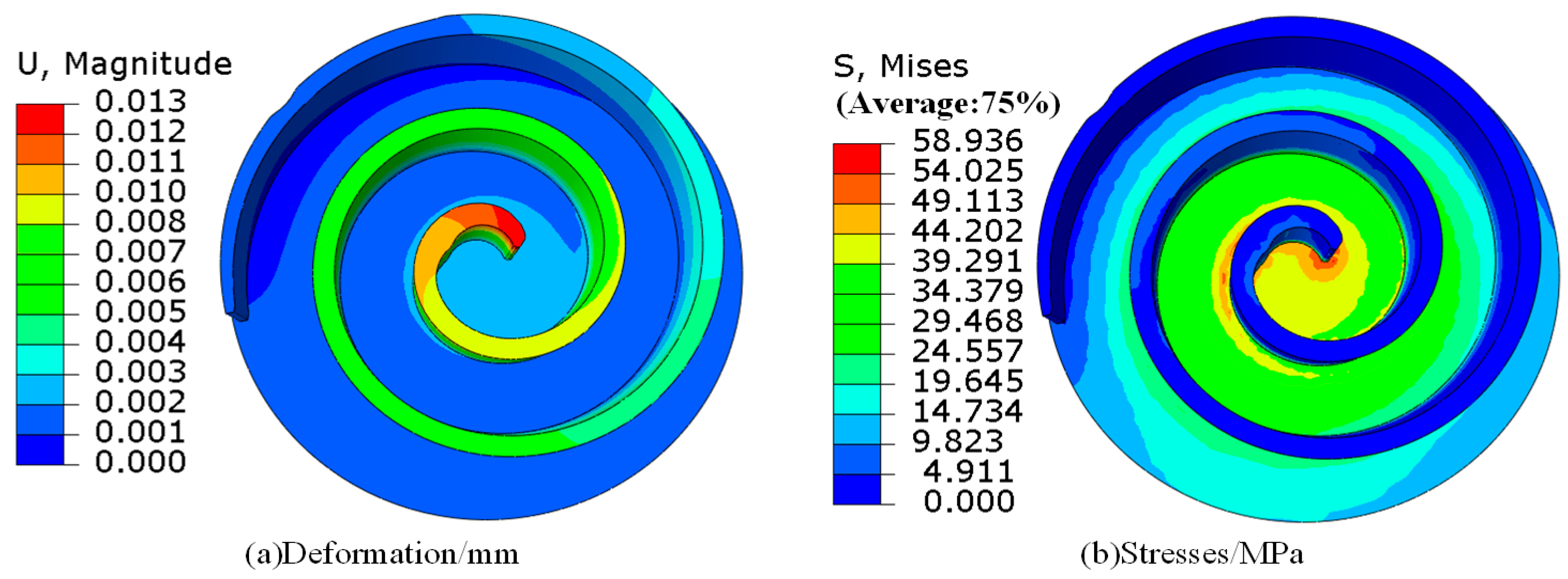
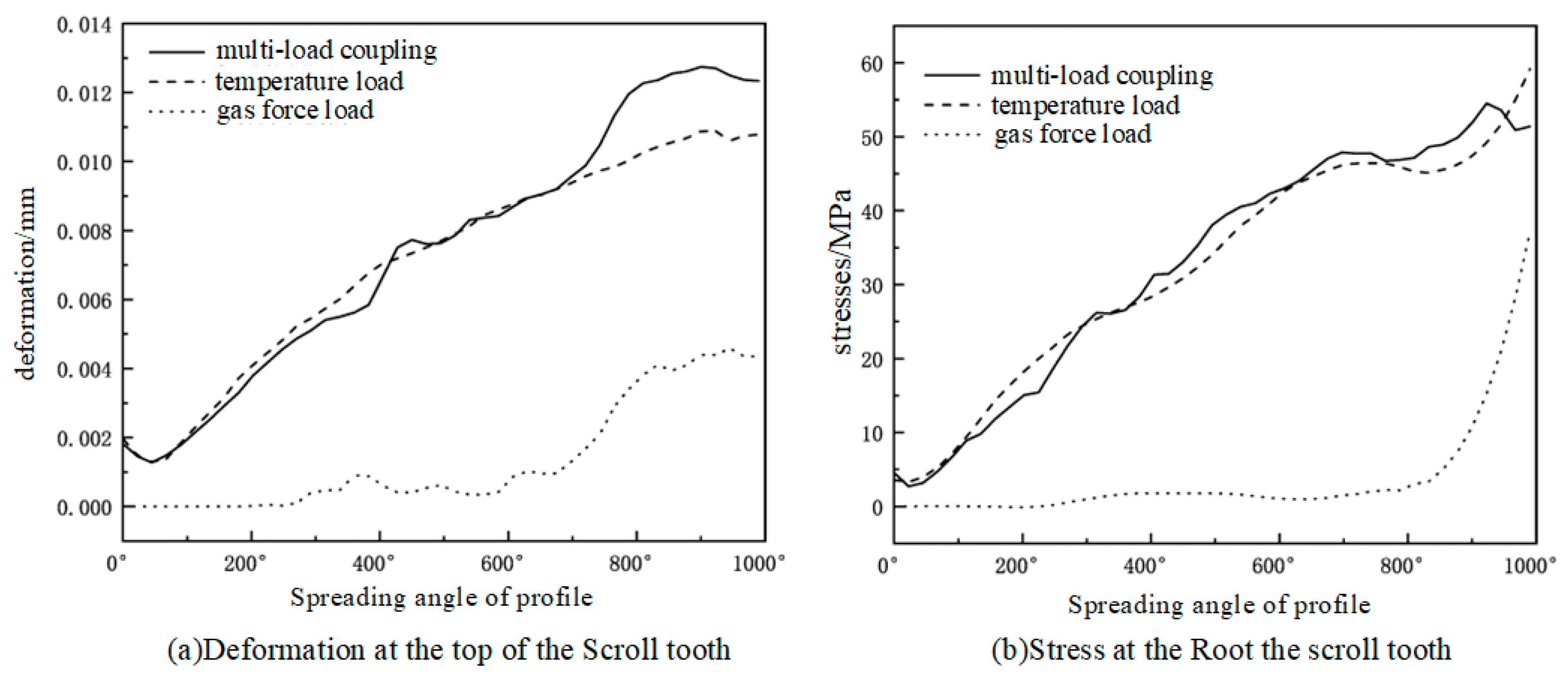

| Name of Material | Numerical Value |
|---|---|
| Modulus of elasticity (MPa) | 1.38 × 105 |
| Poisson’s ratio | 0.156 |
| Density (t/mm3) | 7.28 × 10−9 |
| Coefficient of thermal expansion (m/(m·K)) | 8.2 × 10−6 |
| Heat transfer coefficient (W/(mm·K)) | 0.045 |
| Specific heat capacity (mJ/(t·K)) | 510 |
| Deformation Rate | ||
|---|---|---|
| 10 | 13.1 | 1.58 |
| 11 | 12.8 | 0.93 |
| 12 | 12.9 | 0.48 |
| 13 | 12.5 | 0.26 |
| 14 | 12.5 | 0.79 |
| 15 | 12.9 | 1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Li, A.; Yuan, M.; Wu, J.; Gao, F.; Ge, M. Thermodynamic Study on the Vortex Teeth of Electric Scroll Compressors Based on Gradient Tooth Height. Appl. Sci. 2024, 14, 5977. https://doi.org/10.3390/app14145977
Yang B, Li A, Yuan M, Wu J, Gao F, Ge M. Thermodynamic Study on the Vortex Teeth of Electric Scroll Compressors Based on Gradient Tooth Height. Applied Sciences. 2024; 14(14):5977. https://doi.org/10.3390/app14145977
Chicago/Turabian StyleYang, Bin, Annan Li, Mengli Yuan, Jinguo Wu, Feng Gao, and Mengqi Ge. 2024. "Thermodynamic Study on the Vortex Teeth of Electric Scroll Compressors Based on Gradient Tooth Height" Applied Sciences 14, no. 14: 5977. https://doi.org/10.3390/app14145977
APA StyleYang, B., Li, A., Yuan, M., Wu, J., Gao, F., & Ge, M. (2024). Thermodynamic Study on the Vortex Teeth of Electric Scroll Compressors Based on Gradient Tooth Height. Applied Sciences, 14(14), 5977. https://doi.org/10.3390/app14145977






