Challenges of Using Synthetic Data Generation Methods for Tabular Microdata

Featured Application

This study’s findings hold significant implications for enhancing data privacy and utility in healthcare analytics. By evaluating synthetic data generation methods like CTGAN, TVAE, CopulaGAN and Copula across diverse medical datasets containing sensitive patient information, such as genetic profiles and medical histories, the research aims to improve the development of predictive models without compromising patient privacy.

Abstract

The generation of synthetic data holds significant promise for augmenting limited datasets while avoiding privacy issues, facilitating research, and enhancing machine learning models’ robustness. Generative Adversarial Networks (GANs) stand out as promising tools, employing two neural networks—generator and discriminator—to produce synthetic data that mirrors real data distributions. This study evaluates GAN variants (CTGAN, CopulaGAN), a variational autoencoder, and copulas on diverse real datasets of different complexity encompassing numerical and categorical attributes. The results highlight CTGAN’s sensitivity to training parameters and TVAE’s robustness across datasets. Scalability challenges persist, with GANs demanding substantial computational resources. TVAE stands out for its high utility across all datasets, even for high-dimensional data, though it incurs higher privacy risks, which is indicative of the curse of dimensionality. While no single model universally excels, understanding the trade-offs and leveraging model strengths can significantly enhance synthetic data generation (SDG). Future research should focus on adaptive learning mechanisms, scalability enhancements, and standardized evaluation metrics to advance SDG methods effectively. Addressing these challenges will foster broader adoption and application of synthetic data.

1. Introduction

Despite initiatives for open-linked data and the enforcement of FAIR (Findable, Accessible, Interoperable, Reusable) principles, there is still a lack of publicly available microdata for training machine learning models [1,2]. One issue is the uncertainty regarding the associated privacy breach risk, which is primarily addressed through technical and organizational measures such as the establishment of a scientific review board, federated learning, and signing of terms-of-use clauses [3,4]. While this reduces the risk, it results in researchers having to reapply repeatedly for datasets and being unable to create a larger collection of data across different institutions. Synthetic data generation (SDG) promises a viable solution for this purpose and is driven by two distinct communities [5,6]: on the one hand, the statistical community, which already leans towards synthetic data with multiple imputation and requires explicit modeling of relationships in the data [7,8]; and on the other hand, the computer science community, which attempts to generate synthetic data without the modeling effort by using neural networks (NNs) as approximators of real-world data distributions [9,10]. A significant challenge lies in ensuring that synthetic data accurately represent the statistical properties of the original data. Synthetic data may fail to capture all the nuances of the original dataset, leading to potential inaccuracies in representation. This can result in discrepancies in distributions and correlations, which are crucial for maintaining the integrity of data-driven research. Therefore, it is imperative to employ advanced methods and rigorous validation techniques to ensure that synthetic data preserves the essential statistical properties of the original data.

Statisticians often rely on explicit modeling of relationships within the data. Two prominent R packages in this context are synthpop [11] and simpop [12]. By explicitly modeling the data, statisticians can ensure that the distributions, correlations, and other statistical properties are preserved. They validate the synthetic data through rigorous statistical tests and comparisons with the original data, adjusting their models as necessary to achieve high fidelity. This approach allows for a clear understanding and control over the generated data, ensuring that it reflects the original data’s nuances accurately. On the other hand, computer scientists leveraging NNs employ a more automated, black-box approach to SDG. NNs, particularly Generative Adversarial Networks (GANs) and their variants, are trained to learn the underlying patterns and distributions of the original data without the need for explicit modeling. The sophisticated black-box nature of NNs allows them to capture complex, non-linear relationships that might be difficult to model explicitly. However, this approach also requires careful tuning and validation to ensure the generated data are accurate. Both approaches have their strengths: the statistical methods provide transparency and control, while NNs offer the ability to capture complex patterns with less manual intervention.

GANs are currently one of the most promising NNs for generating synthetic data that are difficult to model explicitly and operate according to the Turing test principle [13,14]. GANs consist of two NNs: a generator and a discriminator. The generator creates candidates, in our case a synthetic dataset, by way of learning to mimic the real data distribution. The discriminator, on the other hand, attempts to distinguish the generator’s results from the real data. Over multiple iterations, the generator and discriminator are trained in competition with each other: the generator aims to produce increasingly better synthetic datasets that closely resemble the real data, while the discriminator is trained to better distinguish the generator’s results from the real data. The goal of this process is for the generator to produce synthetic data that the discriminator cannot distinguish from real data. At the end, the generator becomes a random generator for a complex distribution, which is learned by gradient-based training on real data. Once this distribution is learned, the corresponding dataset is generated from a uniformly or normally distributed random variable (another prior could be used as well).

Here, the aim is to outline challenges for the application of GANs and similar synthetic data techniques, namely CTGAN [15], TVAE [15], CopulaGAN [16], and Copula [17,18], based on an empirical study. The datasets under consideration include a range of numerical and categorical attributes, as well as different task types such as regression and classification. We want to gain insights into how the effectiveness of these methods depends on various characteristics of the data, such as the proportion of numerical versus categorical attributes and the nature of the task. The assumption that SDG automatically serves to protect privacy and leads out-of-the-box to high-quality data is often too naive. Balancing the trade-off between maintaining data utility and ensuring privacy is a complex and challenging task. In the next section, details of the datasets and the SDG methods will be introduced. After describing our study design, we present our results together with the observed challenges. These will then be generalized, and the next steps for deepening our understanding of SDG methods will be presented.

2. Materials and Methods

The datasets chosen for this study are listed in

Table 1. Details on several UCI Machine Learning datasets used in the study.

Abbreviation	Name	# Train- Set (80%)	# Test- Set (20%)	# Numerical (cont.)	# Categorical	Task Type
AP	Apartment	2345	587	6	12	Regression
AQ	Air Quality	661	166	13	0	Regression
BC	Breast Cancer	455	114	30	2	Regression
MB	Metabric	873	219	493	200	Regression
MU	Musk	380	166	168	1	Classification

. They have been specifically selected due to their diverse characteristics, making them ideal for benchmarking SDG techniques. The varying proportions of numerical and categorical attributes, as well as the inclusion of both regression and classification tasks, provide a comprehensive framework for evaluating the dependency of SDG methods on different data features. In particular, the number of attributes is assumed to pose a significant challenge for the various methods. By using these datasets, we aim to elucidate the unique challenges and performance metrics associated with applying GANs and related techniques across a spectrum of real-world scenarios.

We employ several advanced SDG methods, namely CTGAN, TVAE, CopulaGAN, and Copula. Conditional Tabular GAN (CTGAN) is designed to handle tabular data with mixed data types, effectively learning from complex relationships and distributions. Tabular Variational Autoencoder (TVAE) uses a variational autoencoder framework to generate synthetic data, capturing the underlying data distribution while providing flexibility in handling missing values and mixed data types. CopulaGAN combines the strengths of GANs with copula functions to model the dependency structure between variables, enhancing the generation of realistic synthetic data for tabular datasets. Lastly, the Copula method leverages statistical copulas to capture the dependence structure among variables, allowing for the generation of synthetic data that preserves the original data’s correlations. Categorical variables are converted to continuous before using the Copula method. These methods are thus well-suited for generating synthetic data that include both numerical and categorical attributes, making them ideal for the datasets selected in this study. For the implementation of the SDG methods, we utilize the Synthetic Data Vault (SDV [19]) library. SDV offers a comprehensive suite of algorithms for generating synthetic data. Various algorithms are integrated into the SDV framework, providing a unified platform for experimentation and evaluation. By leveraging SDV, we ensure consistency and reproducibility in our experimental setup.

The performance of the SDG methods is evaluated using utility measures derived from Random Forest (RF) models trained on the generated synthetic data. The utility of the synthetic data is compared against the original datasets’ performance, serving as the baseline. The utility measures are calculated across 100 runs to ensure statistical significance and the robustness of the results. The experimental setup is as follows:

• Train-test split: Each dataset is split into train (80%) and test (20%) sets. The SDG methods are trained on the train set and then evaluated on the test set.
• Model hyperparameters: The SDG methods are trained for 300, 1000, and 10,000 epochs to observe the effect of training duration on the quality of the generated data. In order to gauge the effects of sample size, the SDG methods are trained with batch sizes of 60 and 500 each.
• Utility comparison: The performance of models trained on synthetic data is compared to those trained on the original data using utility scores. For regression tasks, the mean $R^2$ score and for classification tasks the mean $F_1$ score is reported. These scores indicate how well the synthetic data preserves the predictive power of the original datasets. Hyperparameter tuning for all RF models is performed through a cross-validated grid search on the training split of the original dataset (see

  Table A1. Hyperparameters for RF models across datasets. The table shows the grid search parameters and the selected best hyperparameters for each dataset.

  	n_Estimators	Max_Depth	Min_Samples_Split	Min_Samples_Leaf	Max_Features	Bootstrap
  Search Grid	[50, 100, 200]	[None, 10, 20]	[2, 5, 10]	[1, 2, 4]	[auto, sqrt]	[True, False]
  AP	200	20	5	1	sqrt	False
  AQ	100	20	2	1	sqrt	False
  BC	100	None	2	1	sqrt	False
  MB	200	None	2	1	sqrt	False
  MU	50	20	10	1	sqrt	False

  in the appendix for details).
• Assessment of re-identification risk: To approximate the inherent re-identification risk in synthetic data, we utilize the concept of ε-Identifiability [6,20]. This metric quantifies the likelihood that the i-th record in the original data has a smaller weighted distance to its nearest synthetic observation (${\widehat{r}}_i)$ than to its nearest real observation ($r_i$), with ε representing the threshold of closeness. For all occurrences where the measurement ${\widehat{r}}_i$ is smaller than $r_i$, we calculate the proportion of these occurrences.

Generating high-quality synthetic data can be computationally intensive, necessitating substantial computational resources. The experiments in this study, conducted on a robust server setup, underscore the resource demands associated with SDG. Utilizing NVIDIA H100 PCIe 80 GB graphics cards and Intel Xeon Silver 4416+ processors, along with a significant amount of RAM (1008 GB), highlights the need for powerful hardware to handle the complex computations involved in SDG. Such resources enable the processing of large datasets and the implementation of advanced models, which are critical for ensuring the quality and accuracy of synthetic data. This computational intensity is a crucial consideration for researchers and organizations aiming to employ SDG methods, as it necessitates access to high-performance computing infrastructure to achieve optimal results.

In addition to the SDG methods evaluated in our benchmark, we also considered two additional methods: ADS-GAN [6] and PATE-GAN [21]. ADS-GAN (Anonymization through Data Synthesis Generative Adversarial Network) is a framework developed to address privacy concerns by generating synthetic data that closely resemble real data while protecting sensitive information. Like traditional GANs, the generator creates synthetic data ($\widehat{x})$ by taking a real dataset ($x)$ and random noise $\left(z\right)$ as input. Additionally, an identifiability loss is calculated to assess how similar the synthetic data are to the real data, measured by the weighted Euclidean distance ${\mathbb{E}}_{x,\widehat{x}|x}\left[-‖w\left(x-\widehat{x}\right)‖\right]$. This similarity is controlled by a parameter called Lambda (see Algorithm 1 in [6]), which dictates the allowable similarity between the datasets. A higher value for Lambda allows the generator to deviate more from a specific distribution, resulting in more private generated data. PATE-GAN (Private Aggregation of Teacher Ensembles Generative Adversarial Network) is another framework designed to address privacy concerns in GANs. First, multiple teacher models $T_1,T_2,\dots , T_k$ are trained on disjoint partitions of the real data. Each teacher learns to classify the data into different categories, contributing to an ensemble of diverse classifiers. When presented with a new data sample, each teacher independently provides its classification. To preserve privacy, these individual outputs are aggregated using a noise mechanism. This noisy aggregation ensures that no single teacher’s decision dominates and leaks sensitive information. A student model (the generator in the GAN framework) is trained using the aggregated teacher outputs as labels. The student’s objective is to generate synthetic data that resemble the real data as closely as possible while minimizing the privacy risk. Only a student is trained to avoid directly involving the teachers in the optimization algorithm, as they are trained on the real data, and their parameter values could reveal substantial information about the real data.

We have opted not to include both approaches in our evaluation due to problems encountered in their respective implementations during internal evaluations. Nonetheless, we include them in our discussion to highlight the challenges associated with GANs (see also [22] for a more non-technical view on this).

3. Results

Table 2. RF-utility results across various SDG models and epochs/batch sizes on the UCI Machine Learning datasets.

Model	Epochs	Batch Size	AP	AQ	BC	MB	MU
Original	-	-	0.782 ± 0.003	0.896 ± 0.005	0.880 ± 0.006	0.586 ± 0.031	0.831 ± 0.010
CTGAN	300	60	0.362 ± 0.060	0.148 ± 0.057	0.840 ± 0.019	−0.028 ± 0.017	0.483 ± 0.018
		500	−1.721 ± 0.412	−0.037 ± 0.147	−0.341 ± 0.148	−0.016 ± 0.020	0.430 ± 0.047
	1000	60	0.501 ± 0.043	0.381 ± 0.049	0.839 ± 0.021	−0.017 ± 0.024	0.492 ± 0.011
		500	0.562 ± 0.059	−0.603 ± 0.194	0.824 ± 0.018	−0.031 ± 0.019	0.526 ± 0.046
	10,000	60	0.629 ± 0.023	0.656 ± 0.029	0.877 ± 0.030	DNF	0.732 ± 0.030
		500	0.662 ± 0.021	0.547 ± 0.036	0.896 ± 0.015	−0.019 ± 0.032	0.672 ± 0.031
TVAE	300	60	0.702 ± 0.011	0.363 ± 0.039	0.899 ± 0.019	0.298 ± 0.036	0.721 ± 0.032
		500	0.697 ± 0.011	0.359 ± 0.039	0.892 ± 0.017	0.118 ± 0.034	0.730 ± 0.027
	1000	60	0.707 ± 0.014	0.535 ± 0.033	0.890 ± 0.021	0.412 ± 0.034	0.722 ± 0.031
		500	0.669 ± 0.012	0.547 ± 0.034	0.897 ± 0.019	0.348 ± 0.036	0.730 ± 0.027
	10,000	60	0.706 ± 0.018	0.671 ± 0.029	0.880 ± 0.023	DNF	0.712 ± 0.033
		500	0.699 ± 0.013	0.656 ± 0.026	0.887 ± 0.022	0.478 ± 0.033	0.712 ± 0.036
Copula GAN	300	60	0.524 ± 0.031	−0.069 ± 0.111	0.797 ± 0.038	−0.031 ± 0.018	0.492 ± 0.021
		500	0.082 ± 0.126	−0.212 ± 0.167	−0.385 ± 0.012	−0.029 ± 0.019	0.531 ± 0.043
	1000	60	0.463 ± 0.041	0.388 ± 0.054	0.812 ± 0.036	−0.029 ± 0.020	0.541 ± 0.033
		500	0.612 ± 0.027	0.087 ± 0.121	0.649 ± 0.082	−0.036 ± 0.023	0.542 ± 0.034
	10,000	60	0.671 ± 0.022	0.682 ± 0.029	0.863 ± 0.040	DNF	0.703 ± 0.032
		500	0.672 ± 0.017	0.571 ± 0.031	0.814 ± 0.037	−0.030 ± 0.024	0.572 ± 0.022
Copula	-	-	0.400 ± 0.056	0.808 ± 0.021	0.604 ± 0.072	0.285 ± 0.042	0.116 ± 0.055

outlines the RF performance of various models, including the original, CTGAN, TVAE, CopulaGAN, and Copula, across different datasets. Results for the low-dimensional three datasets AP, AQ, and BC will be analyzed first. The original model serves as a baseline, demonstrating high accuracy across all datasets: 0.782 ± 0.003 for AP, 0.896 ± 0.005 for AQ and 0.880 ± 0.006 for BC.

The CTGAN model exhibits varied performance across the three datasets and different training configurations. Notably, CTGAN’s performance improves with an increase in epochs and a decrease in batch size. For the AQ dataset, the accuracy starts low (worse than random guess) at −0.037 ± 0.147 (300 epochs & 500 batch size) but significantly improves to 0.656 ± 0.029 (10,000 epochs & 60 batch size), though this is still below the baseline results. The AP dataset shows a similar trend, with improved performance at higher epochs and lower batch sizes, although the improvement is less pronounced compared to AQ. Interestingly, the BC dataset, despite being the smallest, achieves the best results with CTGAN, even surpassing the baseline accuracy. The accuracy reaches 0.896 ± 0.015 (10,000 epochs & 500 batch size), indicating that CTGAN effectively learns the general data distribution. This superior performance on the BC dataset can be attributed to the smaller number of instances (455), allowing the model to learn more efficiently and accurately with extensive training. As this pattern can be observed with other models as well (TVAE and CopulaGAN), we assume that the dataset is not challenging.

The TVAE model shows a more consistent performance improvement compared to CTGAN. For the AQ dataset, the accuracy starts at 0.363 ± 0.039 (300 epochs & 60 batch size) and improves to 0.671 ± 0.029 (10,000 epochs & 60 batch size). For the AP and BC datasets, the TVAE model consistently performs well, with accuracies reaching up to 0.707 ± 0.014 (1000 epochs & 60 batch size) for AP and 0.899 ± 0.019 (300 epochs & 60 batch size) for BC. This consistency highlights the robustness of the TVAE model in handling different datasets and suggests that it can effectively learn from the data with less sensitivity to parameter changes compared to CTGAN.

The CopulaGAN model exhibits similar mixed results as CTGAN. For the AQ dataset, the accuracy improves from −0.069 ± 0.111 (300 epochs & 60 batch size) to 0.682 ± 0.029 (10,000 epochs & 60 batch size). On the AP and BC datasets, the performance fluctuates slightly less than CTGAN, with accuracies ranging from 0.524 ± 0.031 (300 epochs & 60 batch size) to 0.672 ± 0.017 (10,000 epochs & 500 batch size) for AP and from 0.385 ± 0.002 (300 epochs & 500 batch size) to 0.863 ± 0.040 (1000 epochs & 60 batch size) for BC. While CTGAN shows potential for high performance, its sensitivity to training parameters makes it less predictable. In contrast, CopulaGAN’s more stable performance across different datasets and training configurations can be advantageous in real-world applications where model reliability is critical. Blending the Copula and GAN approach tends to outperform the plain Copula model, demonstrating the added value of adversarial training in capturing complex data patterns.

The Copula model results indicate moderate performance, with accuracies of 0.808 ± 0.021 for the AQ dataset, 0.400 ± 0.056 for the AP dataset, and 0.604 ± 0.072 for the BC dataset. These results are generally lower compared to the original data and some GAN-based models, highlighting the challenges in capturing intricate data patterns with simpler statistical models. Specifically, for the AQ dataset, the accuracy is reasonably high compared to other models. On the AP dataset, the performance is notably lower, which is probably due to the higher number of categorical features, which must be transformed to continuous ones. The Copula model struggles to capture the underlying relationships as effectively as GAN-based models. On the BC dataset, the Copula model achieves an accuracy that is also significantly lower than the original model’s 0.880 ± 0.006. The higher feature count likely exacerbates the model’s limitations in capturing complex dependencies.

The characteristics of each dataset—such as the number of instances, features, and the mix of numerical and categorical features—play a crucial role in determining model performance. The AQ dataset, with 661 instances and 12 features, represents a regression task that generally showed better performance with models like TVAE and CopulaGAN when sufficient training epochs were used. The AP dataset, with 2345 instances and 17 features, presented more challenges, likely due to its higher feature count and mixed numerical and categorical data, leading to more varied model performance. The BC dataset, with 455 instances and 31 features, performed consistently well across models, indicating that it is indeed the number of categorical data that poses the highest difficulty.

Next, we highlight the differences between the high-dimensional datasets MU and MB and the other datasets (AP, AQ, BC). The baseline performance on the MB dataset is notably low, reflecting its complexity. This complexity results in poor performance across most SDG models, with TVAE being a notable exception. TVAE demonstrated relatively robust performance, particularly with a high number of categorical variables. The best results for TVAE were obtained with the highest number of epochs, although it should be noted that training for 10,000 epochs with a batch size of 60 did not finish in under 60 h. For the MU dataset, the original performance is relatively high, and the results are comparable to those obtained from the low-dimensional datasets. This suggests that while the total number of columns is a factor, the number of categorical columns is the primary challenge in SDG. Interestingly, this observation is not reflected in the results from the Copula model. While Copula performed poorly on the MU dataset, it was the second-best-performing model on the MB dataset after TVAE. This indicates that the Copula model’s ability to recognize interdependencies in continuous data can partially compensate for the difficulties posed by categorical variables. The contrasting performance of the Copula model on MU and MB datasets underscores the need for models that can effectively manage both continuous and categorical data interdependencies. In our comparative evaluations, TVAE demonstrates a higher capability of achieving this outcome than traditional GAN models.

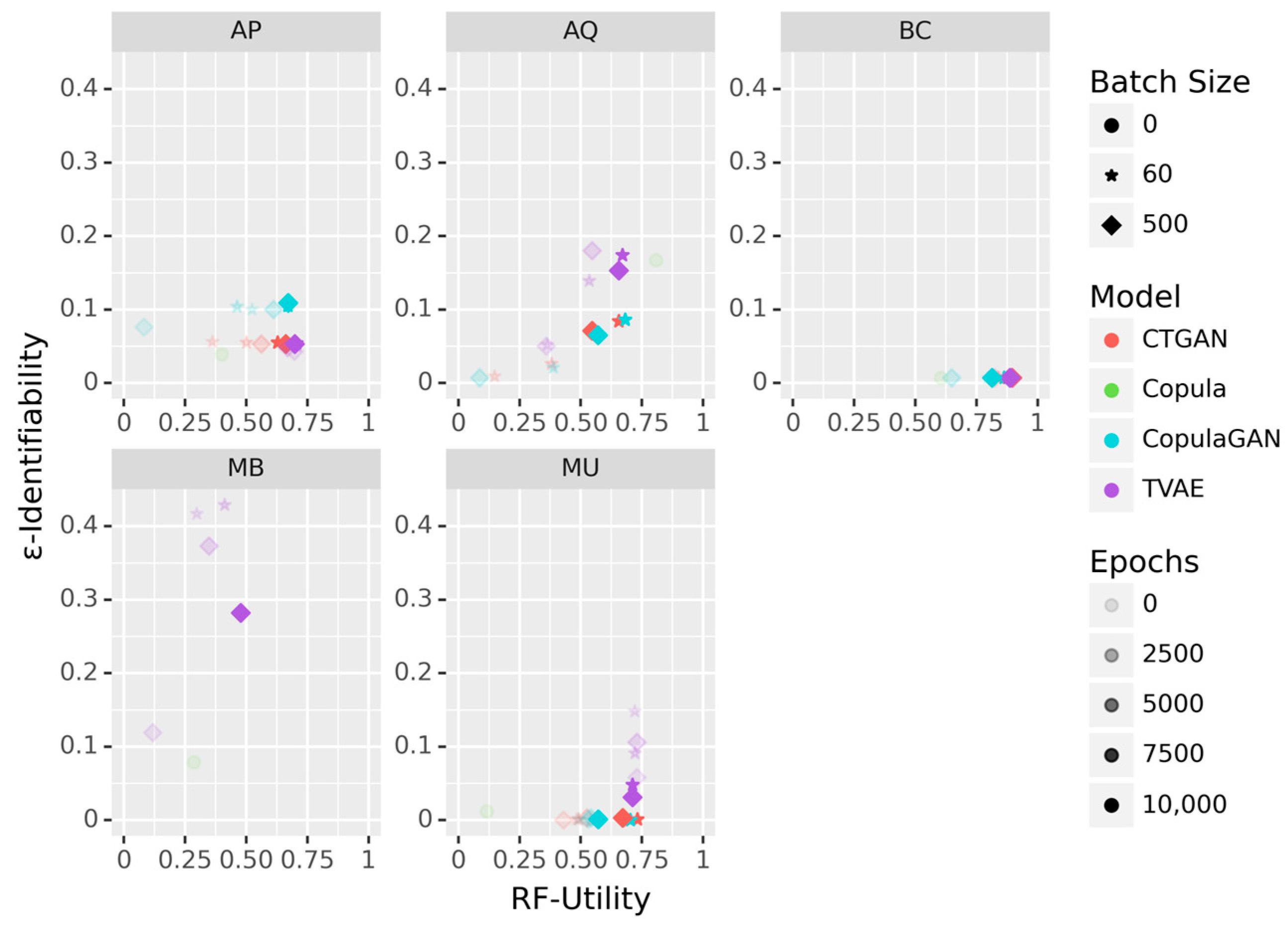
Figure 1 presents scatter plots illustrating the relationship between ε-Identifiability and RF-utility across five different datasets (see also

Table A2. ε-Identifiability, i.e., the proportion of records that are at risk of being identified by syn-thetic observations using k-nearest neighbor.

Model	Epochs	Batch Size	AP	AQ	BC	MB	MU
CTGAN	>300	60	0.056 ± 0.002	0.009 ± 0.003	0.007 ± 0.005	0.247 ± 0.022	0.001 ± 0.001
		500	0.047 ± 0.003	0.002 ± 0.001	0.007 ± 0.005	0.409 ± 0.021	0.000 ± 0.000
	>1000	60	0.055 ± 0.002	0.026 ± 0.006	0.007 ± 0.005	0.206 ± 0.020	0.001 ± 0.002
		500	0.053 ± 0.002	0.006 ± 0.002	0.007 ± 0.005	0.200 ± 0.023	0.003 ± 0.002
	10,000	60	0.055 ± 0.002	0.084 ± 0.009	0.007 ± 0.005	DNF	0.001 ± 0.001
		500	0.053 ± 0.002	0.071 ± 0.010	0.007 ± 0.005	0.421 ± 0.020	0.003 ± 0.002
TVAE	>300	60	0.051 ± 0.003	0.052 ± 0.003	0.007 ± 0.005	0.417 ± 0.019	0.148 ± 0.016
		500	0.043 ± 0.002	0.050 ± 0.001	0.007 ± 0.005	0.119 ± 0.005	0.058 ± 0.009
	>1000	60	0.050 ± 0.003	0.139 ± 0.005	0.007 ± 0.005	0.429 ± 0.020	0.091 ± 0.015
		500	0.048 ± 0.003	0.180 ± 0.002	0.007 ± 0.005	0.373 ± 0.022	0.106 ± 0.015
	10,000	60	0.054 ± 0.003	0.174 ± 0.010	0.007 ± 0.005	DNF	0.048 ± 0.011
		500	0.053 ± 0.003	0.153 ± 0.009	0.007 ± 0.005	0.282± 0.016	0.031 ± 0.009
Copula GAN	>300	60	0.100 ± 0.004	0.008 ± 0.003	0.007 ± 0.005	0.210 ± 0.020	0.001 ± 0.001
		500	0.076 ± 0.004	0.002 ± 0.001	0.007 ± 0.005	0.334 ± 0.020	0.001 ± 0.002
	>1000	60	0.104 ± 0.005	0.021 ± 0.005	0.007 ± 0.004	0.143 ± 0.017	0.000 ± 0.001
		500	0.100 ± 0.004	0.007 ± 0.002	0.007 ± 0.005	0.183 ± 0.024	0.003 ± 0.002
	10,000	60	0.105 ± 0.005	0.086 ± 0.010	0.007 ± 0.005	DNF	0.000 ± 0.001
		500	0.109 ± 0.004	0.065 ± 0.009	0.007 ± 0.005	0.397 ± 0.023	0.001 ± 0.001
Copula	-	-	0.039 ± 0.002	0.167 ± 0.013	0.007 ± 0.005	0.079 ± 0.010	0.012 ± 0.005

for the individual ε-Identifiability values). The plots use different symbols to represent various batch sizes: circles for 0, stars for 60, and diamonds for 500. Colors indicate different models: red for CTGAN, green for Copula, blue for CopulaGAN and purple for TVAE. The color intensity corresponds to the number of epochs, with lighter colors for fewer epochs and darker colors for more epochs. The Copula model (green) consistently demonstrates very low ε-Identifiability across all datasets, making it a strong candidate for privacy preservation. However, it tends to have lower utility compared to other models, except in the Breast Cancer (BC) dataset, where it maintains relatively high utility. CopulaGAN (blue) exhibits moderate to high ε-Identifiability, which is especially noticeable in the AP dataset, with generally high utility except in the MB dataset. Lower batch sizes (60) and more epochs increase both ε-Identifiability and utility, indicating a strong privacy-utility trade-off. CTGAN (blue) shows a pattern similar to CopulaGAN but with slightly lower ε-Identifiability values and comparable utility, suggesting a better privacy-utility trade-off. TVAE (purple) generates high ε-Identifiability and utility values, with these metrics being less dependent on epoch and batch sizes. This model is best suited for scenarios where high utility is crucial, and some level of privacy risk is acceptable. It is notably the only method that provides acceptable utility for high-dimensional data despite the increased risk known as the curse of dimensionality in anonymization [23,24]. These insights underscore the complexities involved in balancing privacy and utility in SDG.

4. Challenges

SDG holds promise as a solution to data scarcity and privacy concerns in machine learning applications. However, its implementation faces several challenges that must be addressed to ensure efficacy and reliability across diverse datasets. This section discusses key challenges in SDG, focusing on insights from empirical studies and, afterwards, considering advanced techniques.

One significant challenge lies in the sensitivity of SDG models to training parameters such as epochs and batch sizes. Our empirical study reveals varying performance based on these parameters across different datasets. Models like TVAE demonstrate more consistent performance with fewer parameter adjustments compared to CTGAN, which shows greater variability. This sensitivity underscores the need for robust methodologies that can adapt to different data characteristics without compromising data quality or privacy. Addressing the sensitivity of SDG models requires advances in algorithmic design and training strategies that minimize reliance on specific parameter configurations. Techniques that incorporate adaptive learning mechanisms or automated parameter tuning may offer pathways to mitigate these challenges, enhancing the robustness and applicability of synthetic data methods.

Scalability remains a persistent challenge in SDG, particularly when scaling up to larger datasets or diverse data types. While models like Copula and CopulaGAN offer simpler statistical approaches, their performance may not effectively scale with increasing dataset complexity or size. GAN-based methods show potential for scaling by leveraging neural network architectures, provided the dataset is not overly complex. However, GANs require substantial computational resources. For high-dimensional datasets with many categorical variables, even that can be insufficient, highlighting the need to precisely define the limitations of GANs and explore alternative solutions for such scenarios. TVAE emerges as a promising alternative not only due to its superior performance on high-dimensional, complex data but also because it is four times faster than other GAN models, providing a significant advantage in terms of efficiency. In addition to that, techniques such as distributed training, parallel processing, and advanced optimization algorithms should be considered to scale training processes efficiently across multiple computing resources. By implementing these strategies, it may be possible to overcome the scalability limitations currently hindering the broader application of SDG in complex and diverse datasets.

In our analysis, significant differences were observed between the high-dimensional datasets (MU and MB) and the other datasets (AP, AQ, BC). The MB dataset, in particular, posed considerable challenges, as evidenced by its low baseline performance. This complexity was reflected in the generally poor performance of most SDG models, with TVAE being a notable exception. TVAE showed relatively robust results, especially when dealing with a high number of categorical variables. Conversely, the original performance on the MU dataset was relatively high, and the results from synthetic models were comparable to those from the low-dimensional datasets, suggesting that the primary challenge in SDG is not just the total number of columns but the number of categorical columns. The performance of the Copula model highlights the importance of developing SDG models that can effectively handle both continuous and categorical data interdependencies. Overall, TVAE consistently demonstrated superior capabilities in managing these complexities compared to traditional GAN models, underscoring its potential as a robust tool for SDG in high-dimensional datasets.

We have provided significant insights into the trade-offs between ε-Identifiability and RF-utility. Each model exhibits distinct characteristics, emphasizing the complexities involved in balancing privacy and utility. No single model universally excels across all metrics. Instead, the choice of model should be guided by specific application needs, balancing the critical aspects of privacy and utility. We were especially surprised by the performance of TVAE on the high-dimensional dataset MB. This model is also less sensitive to variations in batch size and epochs, indicating its stability and reliability for producing high-quality synthetic data.

Effective benchmarking and evaluation of SDG methods pose additional challenges. Assessing the utility of generated data against original datasets requires robust evaluation metrics and consistent experimental protocols. Traditional evaluation metrics may not adequately capture the utility and privacy preservation aspects of the synthetic data, requiring the development of specialized evaluation frameworks [25]. For instance, the Wasserstein Distance is a general-purpose metric that is not optimal for categorical variables [26]. Additionally, we observed variations in the implementation of distance metrics in practice. For instance, ADS-GAN does not utilize the Wasserstein metric as claimed. While this deviation may not be inherently problematic [27], it can cause confusion for users aiming to establish a reproducible pipeline, especially when encountering unexpected negative values. Presently, there is a lack of a standardized metric for mixed continuous and categorical data. Consequently, practitioners often resort to special-purpose metrics. The use of utility measures derived from machine learning models, such as RFs, provides insights into the performance of synthetic data across different tasks like regression and classification. However, ensuring the reproducibility and reliability of these metrics across diverse datasets remains a critical area for improvement in synthetic data research. This is not the place to introduce new metrics but rather to highlight the challenges. In an accepted paper, which will be published soon, we propose a robust metric for measuring risk.

Ethical and regulatory considerations surrounding the use of synthetic data pose challenges that extend beyond technical limitations. Ensuring compliance with data privacy regulations, ethical guidelines, and institutional policies requires careful governance frameworks. Initiatives like federated learning and scientific review boards attempt to mitigate privacy risks associated with SDG but introduce administrative overhead and procedural complexities that can hinder widespread adoption. To address these concerns, one potential approach is the development of standardized protocols and guidelines for synthetic data creation and usage. These standards could be developed by a consortium of industry, academic, and governmental bodies to ensure they are comprehensive and widely accepted. Educational initiatives aimed at increasing the awareness and understanding of synthetic data’s benefits and limitations among regulators, practitioners, and the public can also play a crucial role. By fostering a collaborative environment where stakeholders are well informed and engaged, it is possible to create a more favorable landscape for the adoption of SDG methods.

While ADS-GAN and PATE-GAN offer promising approaches to address privacy concerns in the context of SDG that go beyond the methods we evaluated here, they face several additional challenges and limitations in practice [28]. The main concerns we have encountered are related to the uncertainty regarding utility and the privacy-utility trade-off. For instance, we have internally used the liver transplant data from the UNOS dataset [29], which comprises various other subsets. The target variable is related to the question of whether a transplanted liver has been rejected. We selected only continuous predictors, such as BMI of the donor and the recipient, due to the fact that the handling of categorical variables was messy and came down to a simple binarization. We were surprised about the instability of the algorithms and the unreliability of the results in terms of risks. Especially, outliers pose problems, as too much noise would have to be added, resulting in near-zero utility. In classical anonymization, an algorithm would simply enforce suppression [30]. Two central challenges are still data utility and risks.

Data utility: One of the primary concerns with both ADS-GAN and PATE-GAN is ensuring that the generated synthetic data retain sufficient utility for downstream tasks. If the synthetic data do not accurately represent the underlying patterns and characteristics of the real data, it may not be useful for analysis or model training. The basic trust that a neural network will learn these structures is only justified when using a well-established architecture in practice for the given scenario. However, such an architecture does not yet exist. Datasets can possess so many idiosyncrasies that it becomes difficult to arrive at a general architecture [31]. This, in turn, leads to the realization that, contrary to the promise that there is hardly any manual work involved when using GANs, here one still needs to invest more in the design and substantive understanding of the data. This is not inherently bad but should be factored into consideration when working with GANs. For useful data, one often has to get one’s hands dirty, even with GANs.

Re-identification risk: In terms of limiting the risk, there are similar issues as with Differential Privacy (DP [32]). Even though DP is a semantically sound concept, it is often misapplied because DP is not about protecting microdata but rather ensuring that for a query for an aggregated measure, it does not matter whether a specific entity was included in the query or not [33]. Similarly, the mechanisms of ADS-GAN and PATE-GAN are not designed to directly limit the risk of microdata but rather to either not allow too little Euclidean distance (so if, for example, the ID is the same, but the address is new, it would be less dangerous) or to not allow insight into the parameters of the teacher. This can lead to unexpected results in both directions: unnecessary noise may be injected or too little. Various privacy risks remain, including linkability and inference attacks, which exploit vulnerabilities in the synthesized data to infer sensitive information about individuals [34]. Such risks and the associated instability make it cumbersome for practical use, and it also shows that more work would need to be invested than is actually expected.

5. Discussion

As evidenced by empirical studies and advancements in methodologies like ADS-GAN and PATE-GAN, several critical issues must be carefully navigated to ensure the efficacy and reliability of synthetic data across diverse datasets.

Firstly, one of the foremost issues lies in the sensitivity of SDG models to training parameters such as epochs and batch sizes. Our study underscores the variability in model performance across different datasets based on these parameters. While models like TVAE exhibit more consistent performance with fewer parameter adjustments, GAN-based methods like CTGAN show greater sensitivity, necessitating robust algorithmic designs. Future research directions should focus on developing adaptive learning mechanisms and automated hyperparameter tuning strategies. These innovations can enhance the resilience of SDG methods to parameter variations, ensuring more reliable outcomes across various data scenarios.

Scalability poses a hurdle in SDG, which is particularly evident when tackling larger and more diverse datasets. While statistical models like Copula and CopulaGAN offer simplicity, their effectiveness diminishes as the dataset complexity grows. Conversely, GAN-based methods leverage NNs, showing promise in scaling tasks, albeit demanding significant computational resources. This becomes particularly challenging with high-dimensional datasets rich in categorical variables, where GANs may falter. TVAE emerges as a compelling alternative, excelling in handling complex data while maintaining efficiency, which is crucial for practical applications. Moreover, integrating distributed training, parallel processing, and advanced optimization techniques holds the potential to bolster scalability, offering a pathway to address current limitations and foster wider adoption of synthetic data across diverse and intricate datasets.

There are also issues with model robustness and generalization: GANs rely on the assumptions that the underlying data distribution remains consistent and that the trained models generalize well to unseen data. However, real-world data may exhibit complex and dynamic patterns, making it challenging for the models to generalize effectively. This is, of course, a general problem, but it is exacerbated here by the fact that we do not know what has been generalized from the data and what has not. This black-box nature makes it difficult to adjust GANs accordingly, as would be the case with parameterized statistical models, for example. This is one reason why so many different GANs are now available and why new GANs need to be trained for each case [35]. This is unsatisfactory in the long run. It would be beneficial to develop transfer models here, analogous to image classification, that generalize sufficiently for certain scenarios.

Our empirical study also elucidates the intricate balance between privacy and utility in SDG. The findings reveal that the Copula model excels in privacy preservation with consistently low ε-Identifiability, albeit at the cost of lower utility in most datasets, except the BC dataset. CopulaGAN and CTGAN offer a more balanced privacy-utility trade-off, with CopulaGAN showing higher ε-Identifiability but also higher utility, particularly when tuned with larger batch sizes and more epochs. CTGAN, while similar, provides slightly better privacy with comparable utility. TVAE stands out for its high utility across all datasets, even for high-dimensional data, though it incurs higher privacy risks, which is indicative of the curse of dimensionality. While no single model universally excels, understanding the trade-offs and leveraging model strengths can significantly enhance SDG.

Ethical and regulatory considerations present significant challenges in the practical application of SDG techniques. Compliance with stringent data privacy regulations and ethical guidelines necessitates robust governance frameworks. While initiatives like federated learning and scientific review boards help mitigate privacy risks associated with synthetic data, they introduce administrative complexities that may impede widespread adoption. Future research efforts should prioritize enhancing these governance frameworks by incorporating comprehensive technical and organizational measures for data protection. Focusing solely on specific anonymization techniques may no longer suffice, emphasizing the need for a holistic approach to ensure efficient and effective data privacy safeguards across all possible avenues.

In summary, while SDG holds significant promise, overcoming its challenges requires interdisciplinary efforts spanning algorithmic innovation, computational infrastructure, regulatory compliance, and ethical governance. By comprehensively addressing these challenges, future research can advance SDG methods towards broader adoption and impactful applications in machine learning and beyond. Understanding the limitations of these methods and assessing the potential benefits of increased computational power are essential steps forward. Therefore, one of the critical next steps is to expand frameworks like SDV to provide insights into suitable and unsuitable deployment scenarios based on the characteristics of the data being modeled.