Three-Dimensional Guidance Laws for Spacecraft Propelled by a SWIFT Propulsion System
Abstract
1. Introduction
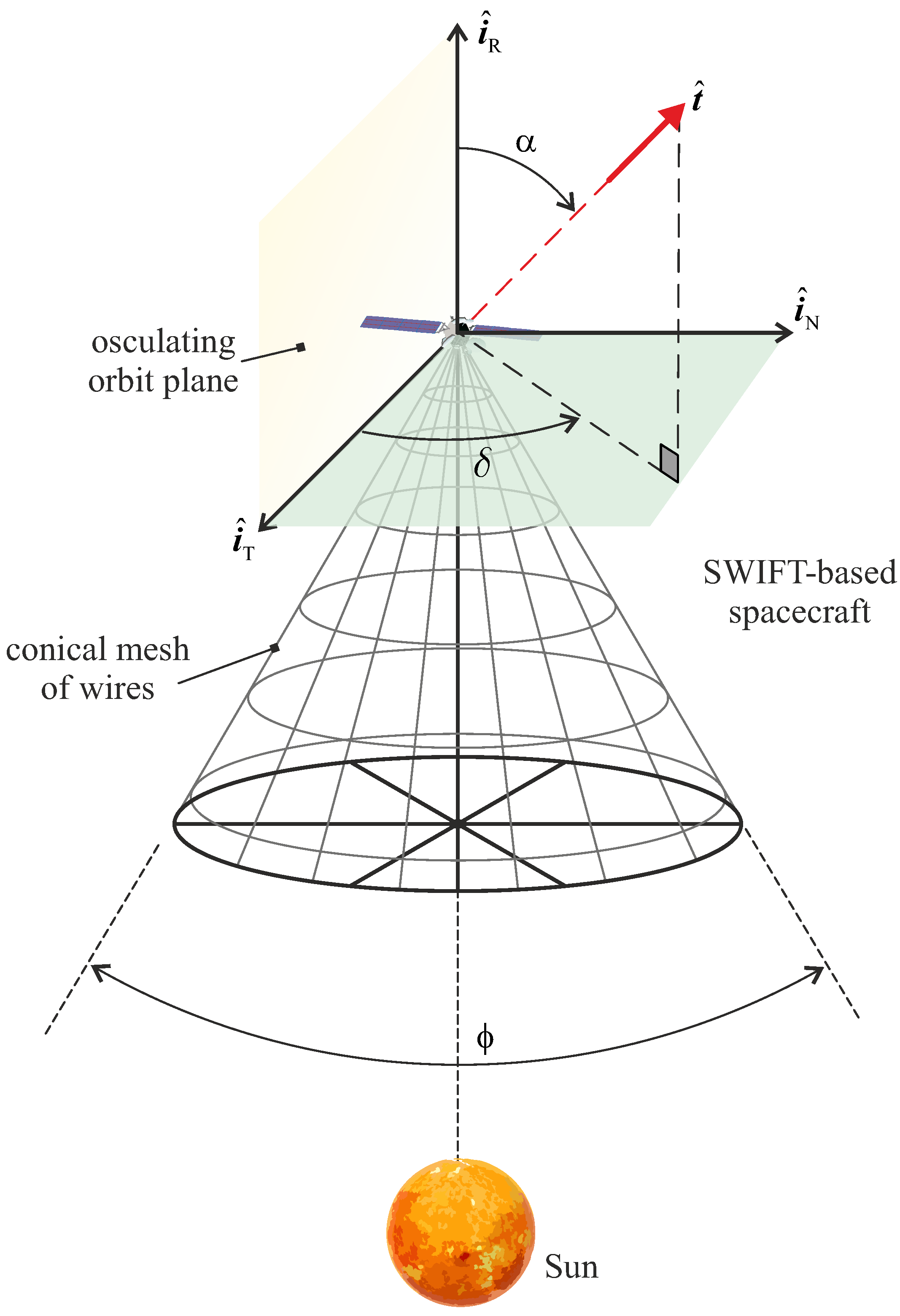
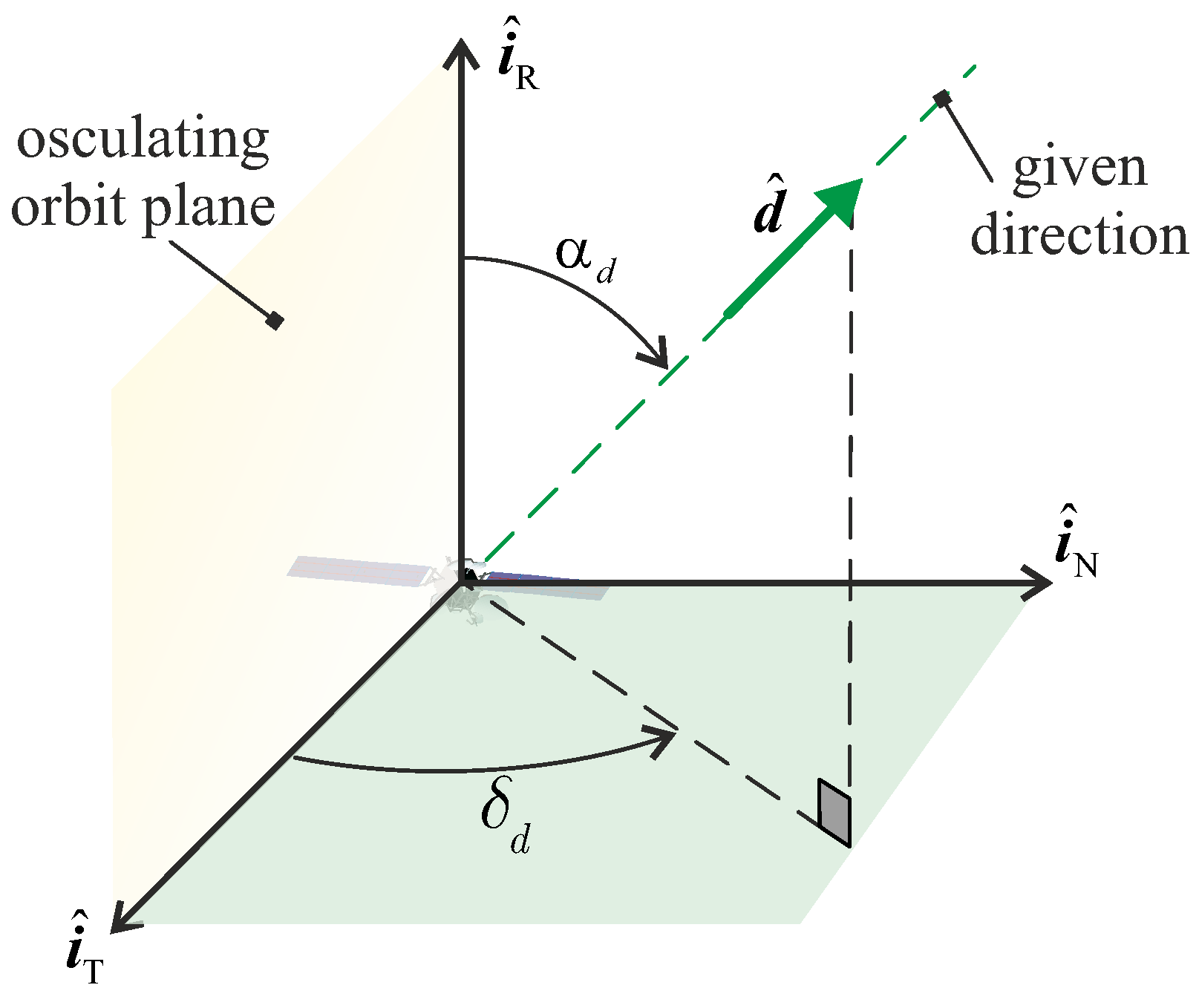
2. Thrust Vector Model for Trajectory Design in a 3D Mission Scenario
Maximization of the Projection of Vector along a Given Direction
3. Optimal Guidance Laws
3.1. Spacecraft State in Terms of Cartesian Components of Position and Velocity Vector
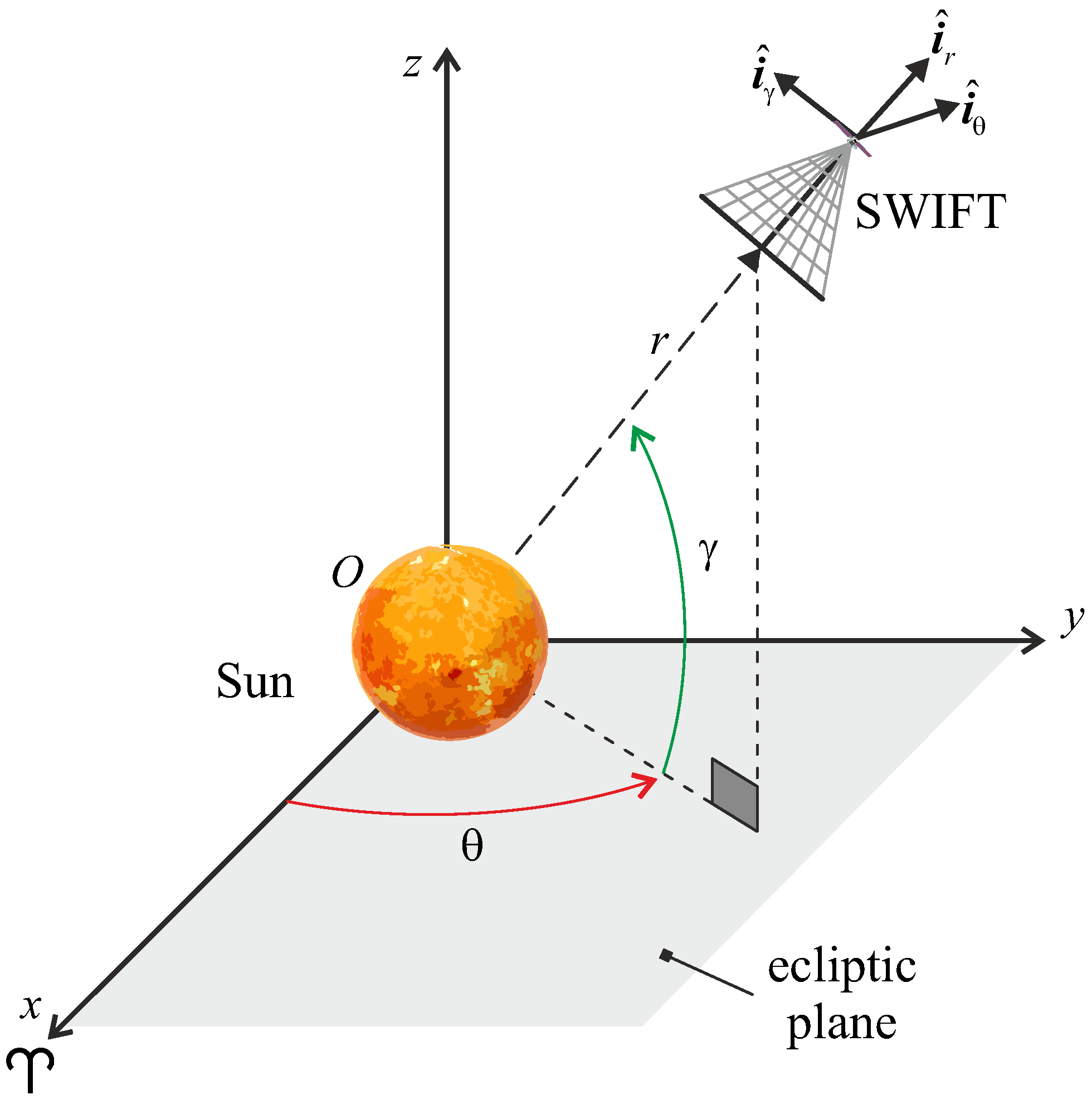
3.2. Spacecraft Dynamics in a Heliocentric Spherical Reference Frame
3.3. Spacecraft Dynamics in Terms of Variation of the Walker’s Modified Equinoctial Orbital Elements
3.4. Spacecraft Dynamics in Terms of Classical Orbital Elements
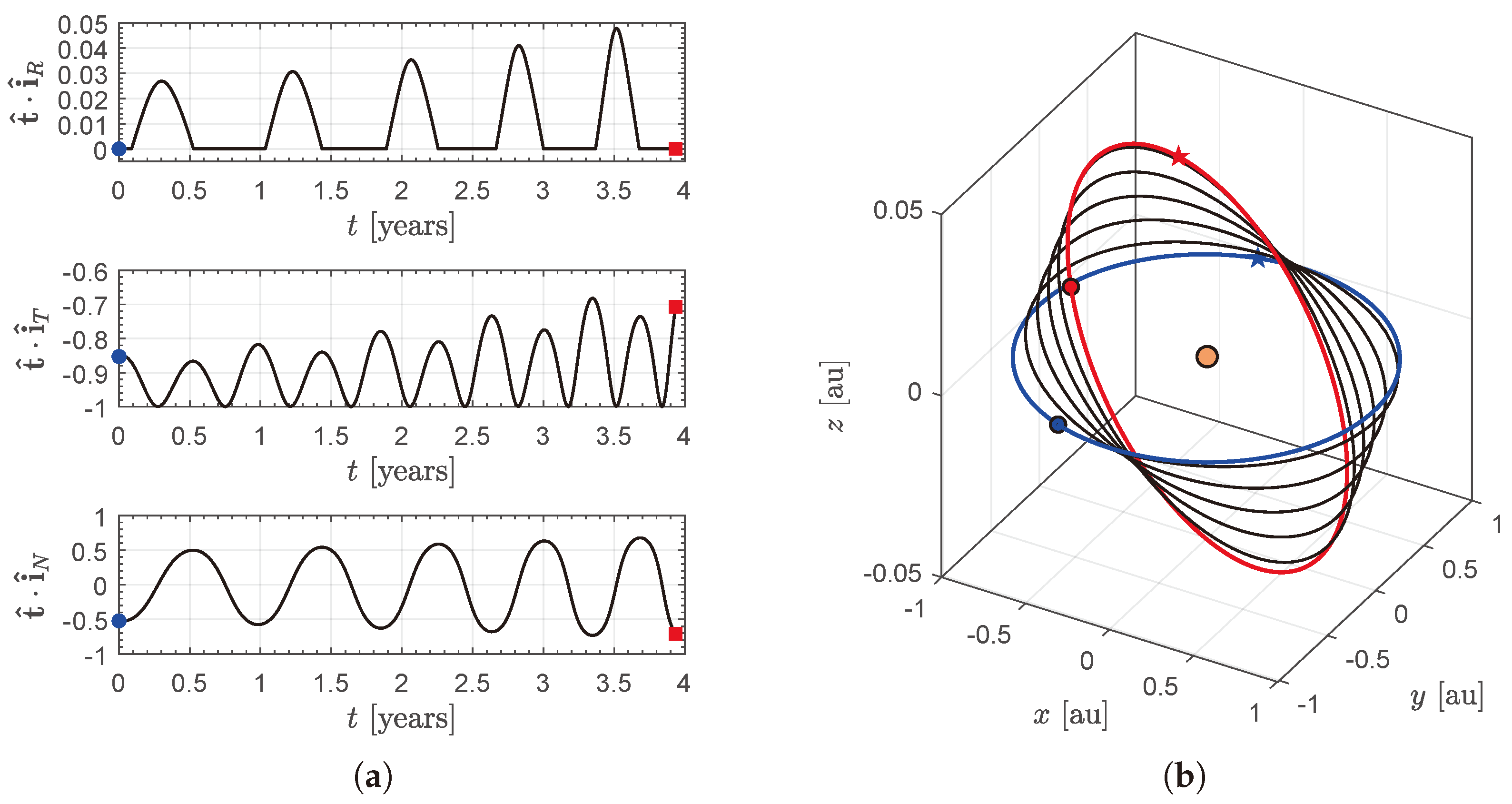
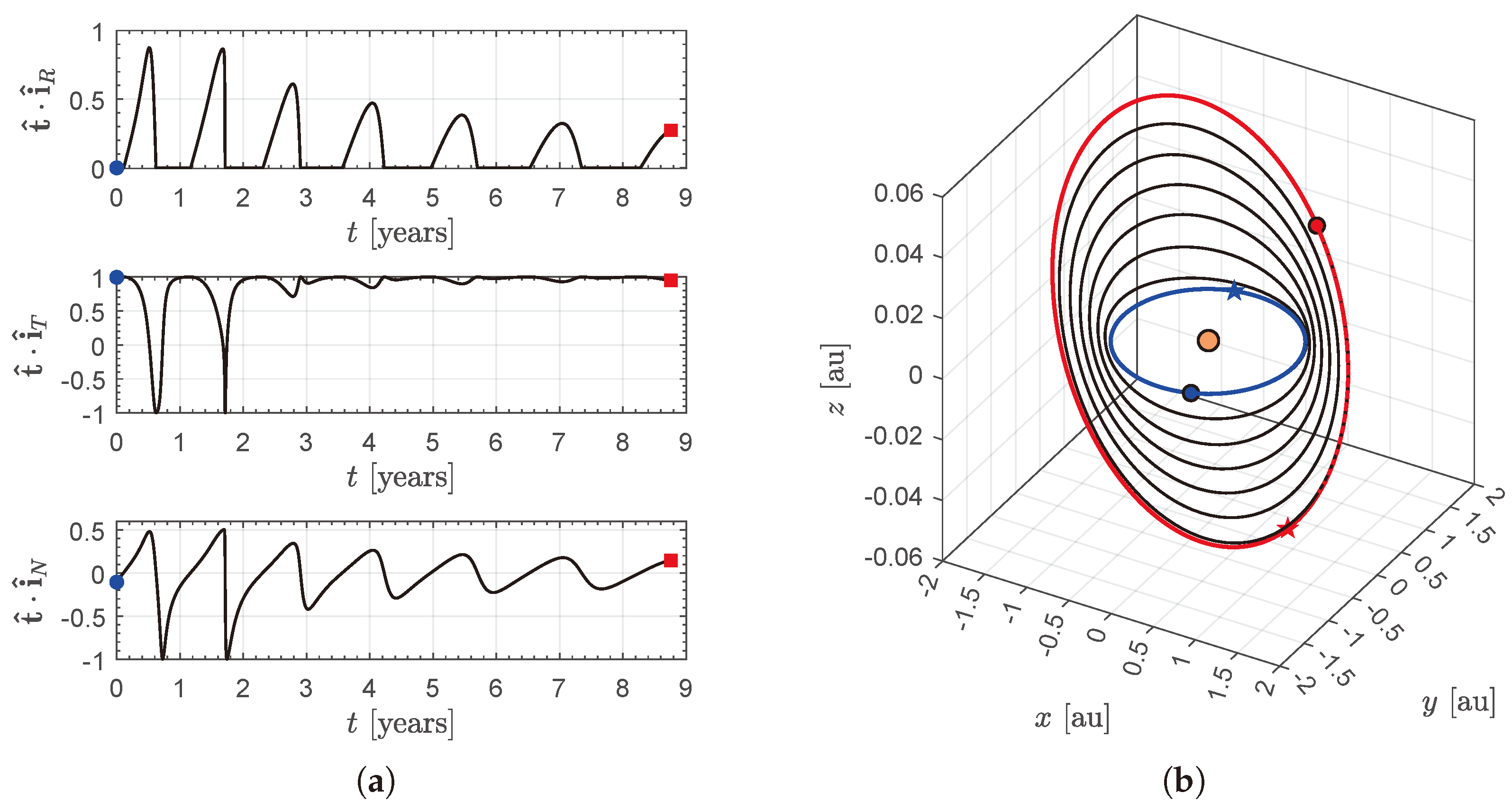
4. Potential Transfer Trajectories and Case Study
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
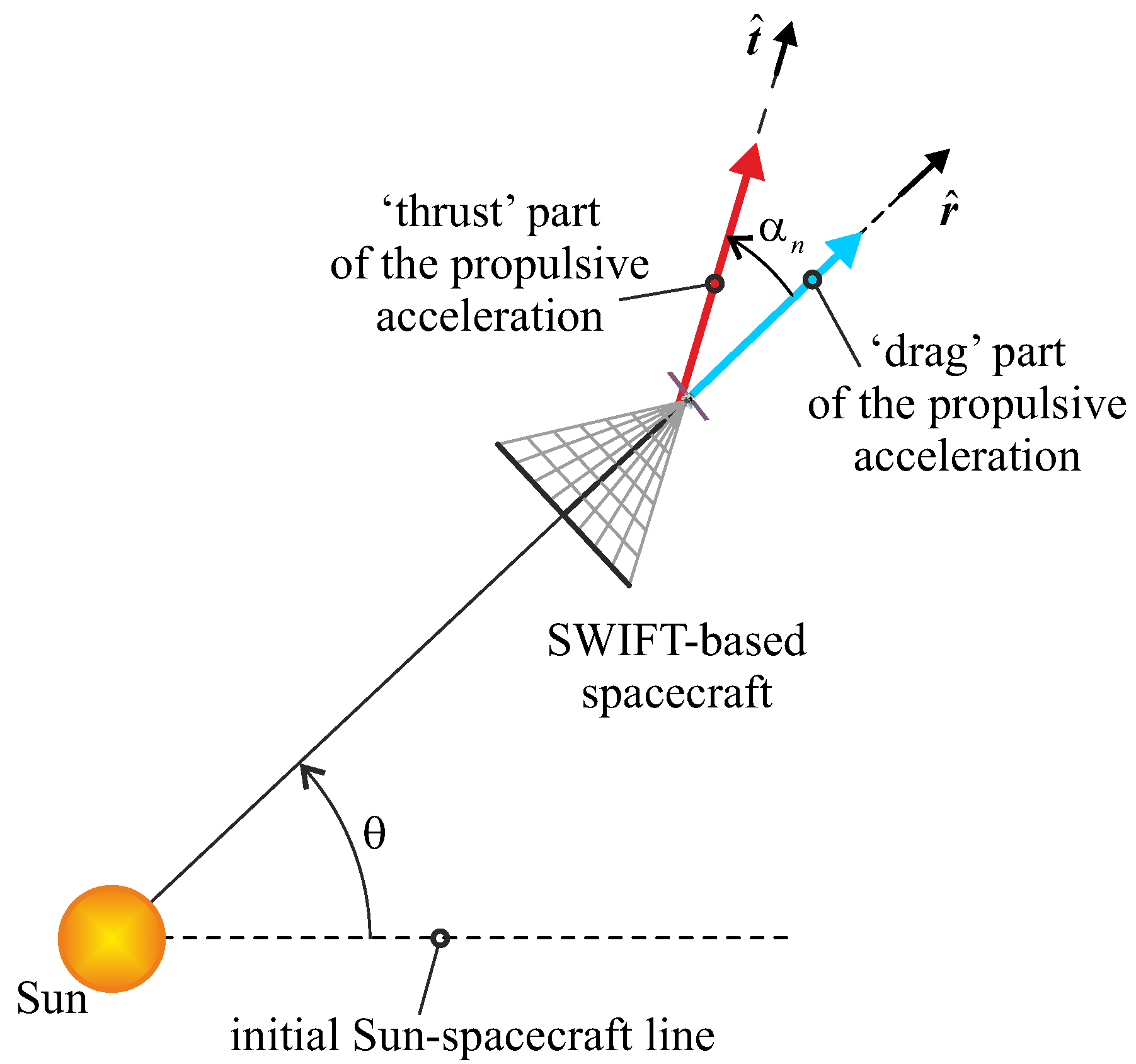
Appendix A. SWIFT Thrust Vector Model and Spacecraft Dynamics for 2D Mission Scenarios
References
- Gemmer, T.R.; Yoder, C.D.; Mazzoleni, A.P. Performance Analysis and Parametric Studies of the Solar Wind Ion Focusing Thruster (SWIFT) for Interplanetary Travel. J. Br. Interplanet. Soc. 2021, 74, 30–40. [Google Scholar]
- Gemmer, T.R.; Mazzoleni, A.P. Introduction and Performance Analysis of the Solar Wind Ion Focusing Thruster (SWIFT). In Proceedings of the 65th International Astronautical Congress, Toronto, ON, Canada, 29 September–3 October 2014. [Google Scholar]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instruments 2010, 81, 111301. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 100768. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Janhunen, P.; Sandroos, A. Simulation study of solar wind push on a charged wire: Basis of solar wind electric sail propulsion. Ann. Geophys. 2007, 25, 755–767. [Google Scholar] [CrossRef]
- Quarta, A.A.; Niccolai, L.; Mengali, G.; Bassetto, M. Optimal Interplanetary Transfer of Solar Wind Ion Focusing Thruster-based Spacecraft. Appl. Sci. 2023, 13, 3820. [Google Scholar] [CrossRef]
- Spencer, D.A.; Johnson, L.; Long, A.C. Solar sailing technology challenges. Aerosp. Sci. Technol. 2019, 93, 105276. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, C.; Li, Y. Design and application of solar sailing: A review on key technologies. Chin. J. Aeronaut. 2023, 36, 125–144. [Google Scholar] [CrossRef]
- Zubrin, R.M.; Andrews, D.G. Magnetic sails and interplanetary travel. J. Spacecr. Rocket. 1991, 28, 197–203. [Google Scholar] [CrossRef]
- Andrews, D.G.; Zubrin, R.M. Magnetic sails and interstellar travel. J. Br. Interplanet. Soc. 1990, 43, 265–272. [Google Scholar]
- Perakis, N.; Hein, A.M. Combining magnetic and electric sails for interstellar deceleration. Acta Astronaut. 2016, 128, 13–20. [Google Scholar] [CrossRef]
- Garwin, R. Solar Sailing—A Practical Method of Propulsion Within the Solar System. Jet Propuls. 1958, 28, 188–190. [Google Scholar]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1992; pp. 223–233. ISBN 978-2881248429. [Google Scholar]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer-Praxis Series in Space Science and Technology; Springer: Berlin, Germany, 1999; pp. 46–54, 119–120. [Google Scholar] [CrossRef]
- Hintz, G.R. Orbital Mechanics and Astrodynamics; Springer: New York, NY, USA, 2015; Chapter 5; pp. 214–216. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal Trajectories of Diffractive Sail to Highly Inclined Heliocentric Orbits. Appl. Sci. 2024, 14, 2922. [Google Scholar] [CrossRef]
- von Stryk, O.; Bulirsch, R. Direct and indirect methods for trajectory optimization. Ann. Oper. Res. 1992, 37, 357–373. [Google Scholar] [CrossRef]
- Liu, H.; Tongue, B.H. Indirect Spacecraft Trajectory Optimization Using Modified Equinoctial Elements. J. Guid. Control Dyn. 2010, 33, 619–623. [Google Scholar] [CrossRef]
- Taheri, E.; Arya, V.; Junkins, J.L. Costate mapping for indirect trajectory optimization. Astrodynamics 2021, 5, 359–371. [Google Scholar] [CrossRef]
- Kopp, R.E. Optimization Techniques with Applications to Aerospace Systems; Mathematics in Science and Engineering; Elsevier: New York, NY, USA, 1962; pp. 255–279. [Google Scholar] [CrossRef]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. [Google Scholar]
- Walker, M.J.H. A set of modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419, Erratum in Celest. Mech. 1986, 38, 391–392. [Google Scholar] [CrossRef]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: New York, NY, USA, 1971; Chapter 2; pp. 54–55, 58–61. [Google Scholar]
- Curtis, H.D. Orbital Mechanics for Engineering Students; Elsevier: Oxford, UK, 2014; Chapter 4; pp. 187–237. [Google Scholar] [CrossRef]
- Lawden, D.F. Optimal Trajectories for Space Navigation; Butterworths & Co.: London, UK, 1963; pp. 54–60. [Google Scholar]
- Prussing, J.E. Optimal Spacecraft Trajectories; Oxford University Press: Oxford, UK, 2018; Chapter 4; pp. 32–40. [Google Scholar]
- Zheng, M.; Luo, J.; Dang, Z. Optimal impulsive rendezvous for highly elliptical orbits using linear primer vector theory. Chin. J. Aeronaut. 2024, 37, 194–207. [Google Scholar] [CrossRef]
- Oguri, K.; Lantoine, G. Indirect trajectory optimization via solar sailing primer vector theory: Minimum solar-angle transfers. Acta Astronaut. 2023, 211, 405–415. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal three-dimensional interplanetary rendezvous using nonideal solar sail. J. Guid. Control Dyn. 2005, 28, 173–177. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M. Optimal Solar Sail Transfers to Circular Earth-Synchronous Displaced Orbits. Astrodynamics 2020, 4, 193–204. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Broucke, R.A.; Cefola, P.J. On the equinoctial orbit elements. Celest. Mech. 1972, 5, 303–310. [Google Scholar] [CrossRef]
- Kechichian, J.A. Optimal low-thrust rendezvous using equinoctial orbit elements. Acta Astronaut. 1996, 38, 1–14. [Google Scholar] [CrossRef]
- Lagona, E.; Hilton, S.; Afful, A.; Gardi, A.; Sabatini, R. Autonomous Trajectory Optimisation for Intelligent Satellite Systems and Space Traffic Management. Acta Astronaut. 2022, 194, 185–201. [Google Scholar] [CrossRef]
- Coverstone, V.L.; Prussing, J.E. Technique for Escape from Geosynchronous Transfer Orbit Using a Solar Sail. J. Guid. Control Dyn. 2003, 26, 628–634. [Google Scholar] [CrossRef]
- Quarta, A.A.; Abu Salem, K.; Palaia, G. Solar sail transfer trajectory design for comet 29P/Schwassmann-Wachmann 1 rendezvous. Appl. Sci. 2023, 13, 9590. [Google Scholar] [CrossRef]
- Betts, J.T. Very low-thrust trajectory optimization using a direct SQP method. J. Comput. Appl. Math. 2000, 120, 27–40. [Google Scholar] [CrossRef]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics, Revised ed.; AIAA: Reston, VA, USA, 1999; Chapter 10; pp. 488–490. [Google Scholar] [CrossRef]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; Chapters 3 and 6; pp. 166–172, 312. [Google Scholar]
- Quarta, A.A. Fast initialization of the indirect optimization problem in the solar sail circle-to-circle orbit transfer. Aerosp. Sci. Technol. 2024, 147, 109058. [Google Scholar] [CrossRef]
- Quarta, A.A. Initial costate approximation for rapid orbit raising with very low propulsive acceleration. Appl. Sci. 2024, 14, 1124. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Stengel, R.F. Optimal Control and Estimation; Dover Books on Mathematics; Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Prussing, J.E. Spacecraft Trajectory Optimization; Cambridge University Press: Cambridge, UK, 2010; Chapter 2; pp. 16–36. [Google Scholar] [CrossRef]
- Gemmer, T.R.; Mazzoleni, A.P. Solar wind ion focusing thruster (SWIFT) Orbital Performance Analysis. In Proceedings of the 66th International Astronautical Congress, Jerusalem, Israel, 12–16 October 2015. [Google Scholar]
- Gemmer, T.R.; Mazzoleni, A.P. Comparative orbital performance study of a solar wind ion focusing thruster (SWIFT). In Proceedings of the 67th International Astronautical Congress, Guadalajara, Mexico, 26–30 September 2016. [Google Scholar]
- Gemmer, T.R.; Yoder, C.; Mazzoleni, A.P. Increasing the accuracy of electric sail mission performance estimates. In Proceedings of the 68th International Astronautical Congress, Adelaide, Australia, 25–29 September 2017; Volume 14, pp. 8992–8997. [Google Scholar]
- Rishikof, B.H.; McCormick, B.R.; Pritchard, R.E.; Sponaugle, S.J. SeGRAm: A practical and versatile tool for spacecraft trajectory optimization. Acta Astronaut. 1992, 26, 599–609. [Google Scholar] [CrossRef]
- Rubinsztejn, A.; Sandel, C.G.; Sood, R.; Laipert, F.E. Designing trajectories resilient to missed thrust events using expected thrust fraction. Aerosp. Sci. Technol. 2021, 115, 106780. [Google Scholar] [CrossRef]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]


| Orbital Parameter | Earth | Venus | Mars |
|---|---|---|---|
| semimajor axis a [au] | |||
| eccentricity e | |||
| inclination i [deg] | |||
| long. of the asc. node [deg] | |||
| arg. of perihelion [deg] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A. Three-Dimensional Guidance Laws for Spacecraft Propelled by a SWIFT Propulsion System. Appl. Sci. 2024, 14, 5944. https://doi.org/10.3390/app14135944
Quarta AA. Three-Dimensional Guidance Laws for Spacecraft Propelled by a SWIFT Propulsion System. Applied Sciences. 2024; 14(13):5944. https://doi.org/10.3390/app14135944
Chicago/Turabian StyleQuarta, Alessandro A. 2024. "Three-Dimensional Guidance Laws for Spacecraft Propelled by a SWIFT Propulsion System" Applied Sciences 14, no. 13: 5944. https://doi.org/10.3390/app14135944
APA StyleQuarta, A. A. (2024). Three-Dimensional Guidance Laws for Spacecraft Propelled by a SWIFT Propulsion System. Applied Sciences, 14(13), 5944. https://doi.org/10.3390/app14135944








