Anisotropic Mechanical Properties and Fracture Mechanism of Transversely Isotropic Rocks under Uniaxial Cyclic Loading
Abstract
1. Introduction
2. Materials and Methods
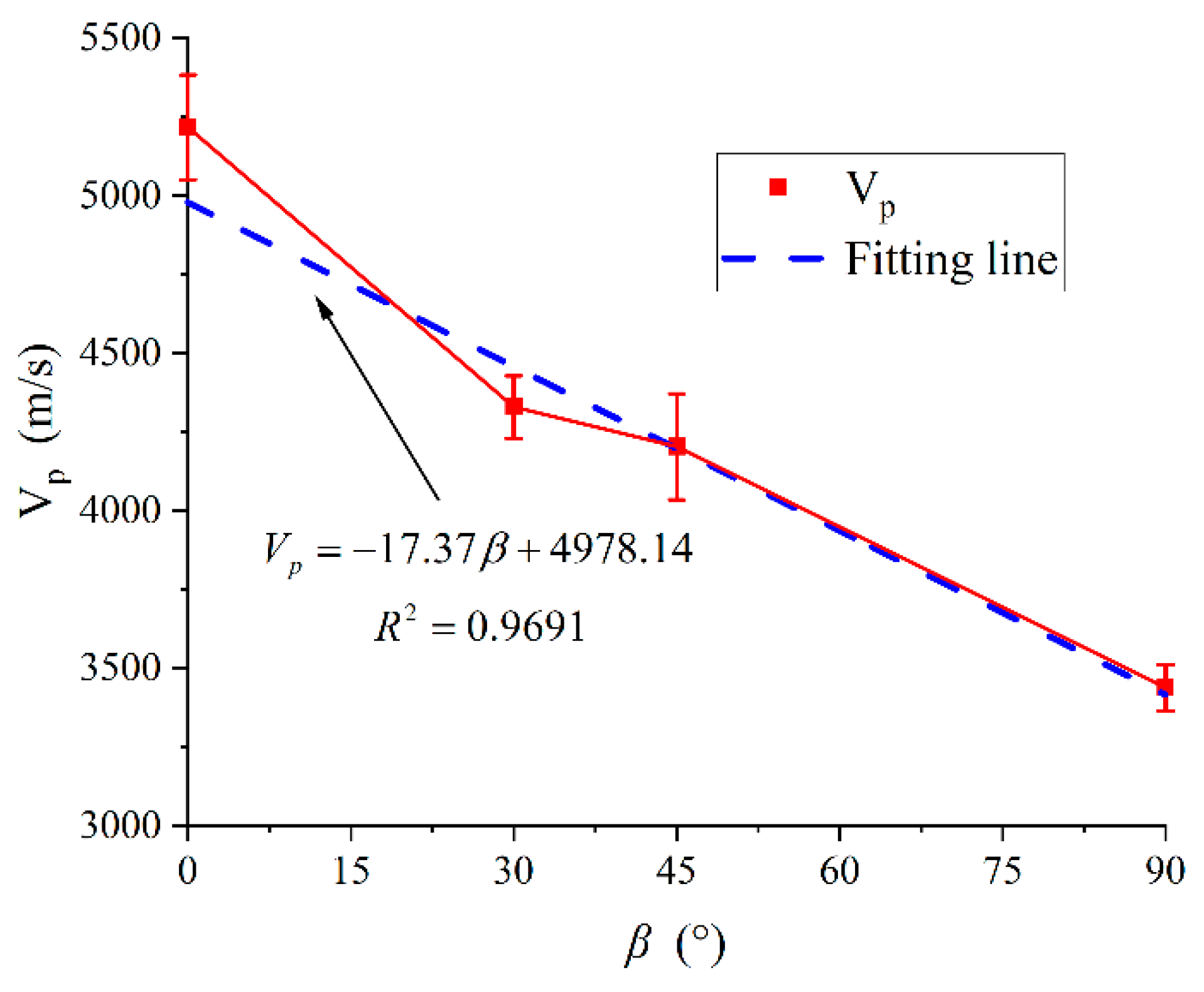
2.1. Specimen Preparation
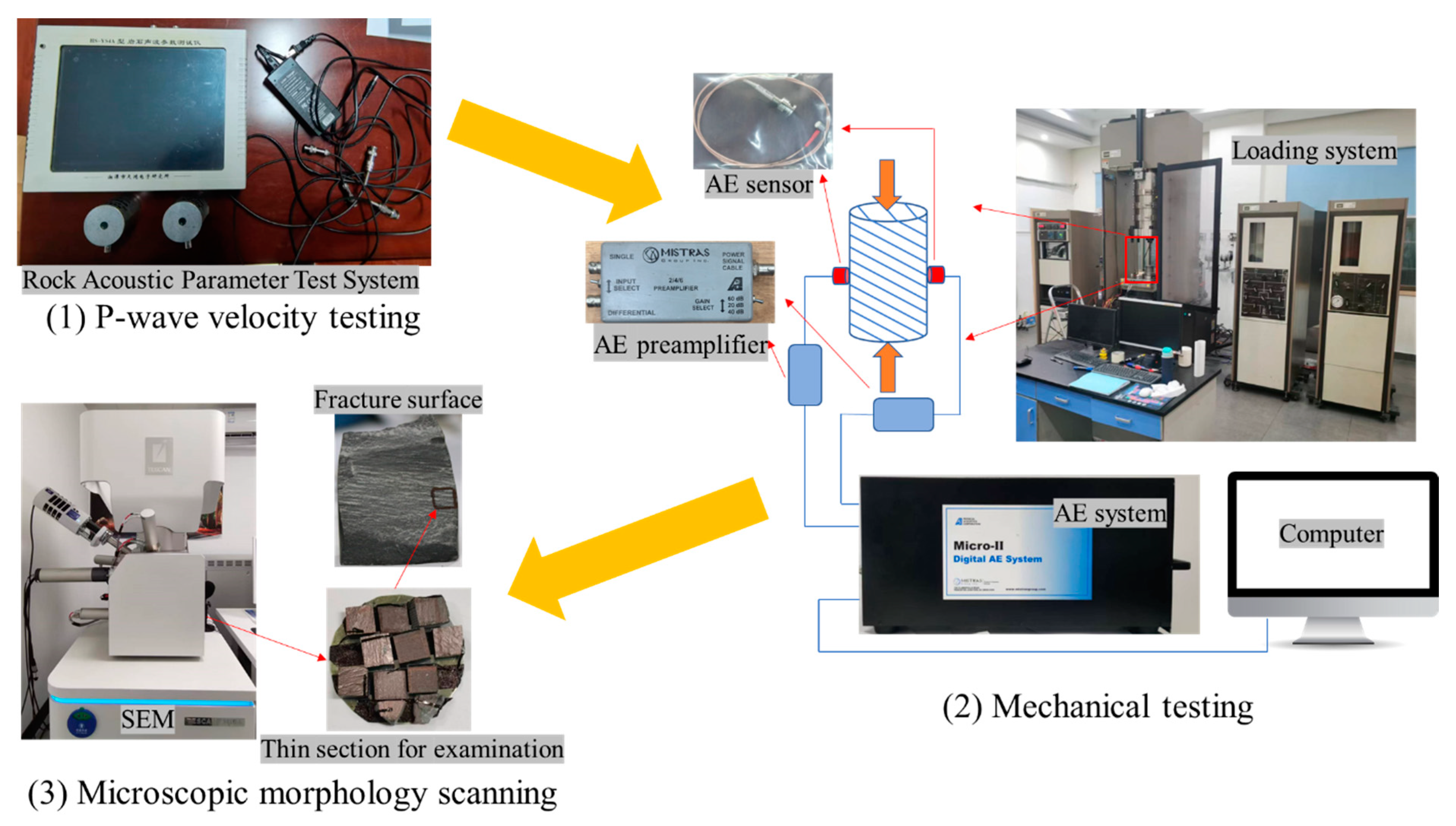
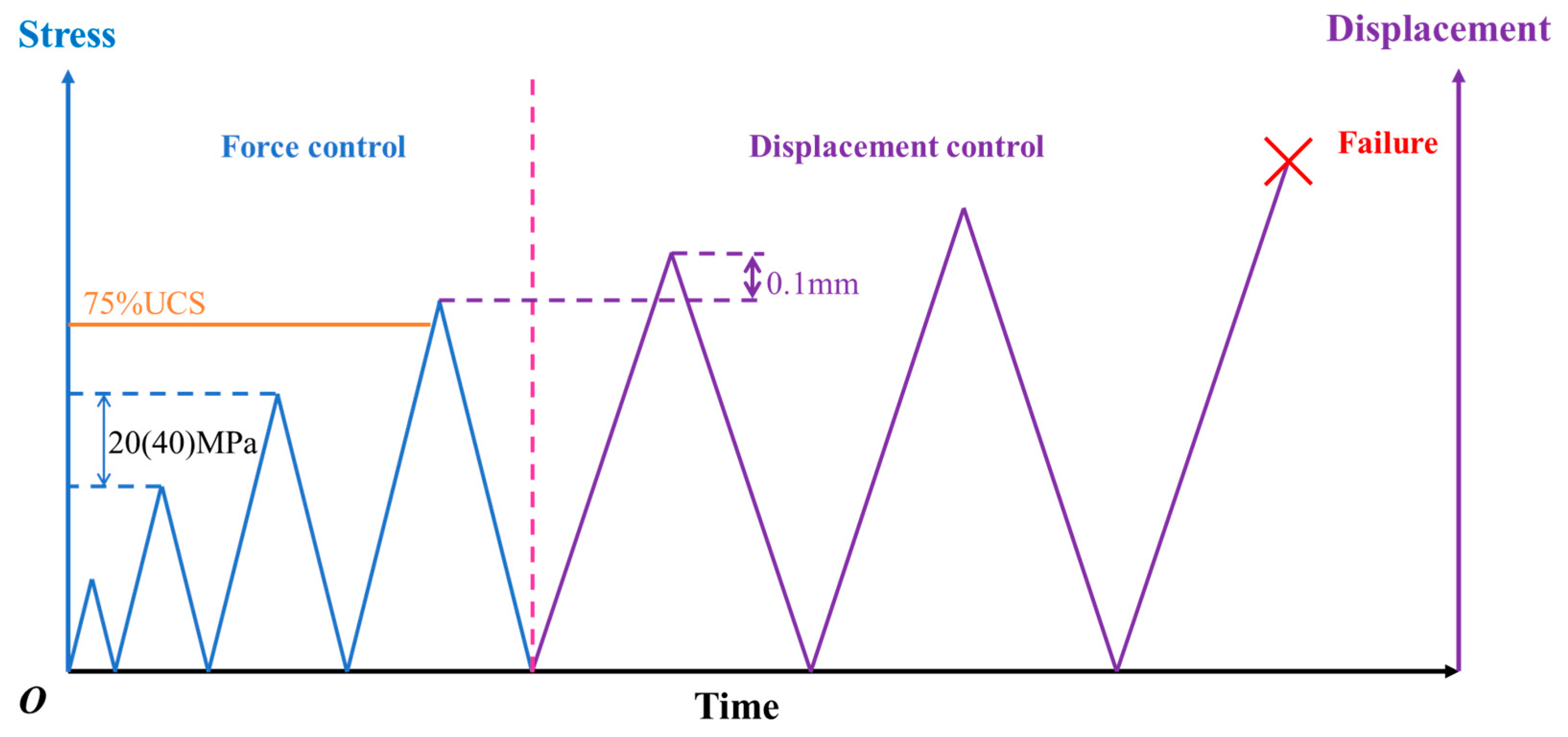
2.2. Test Equipment and Methods
3. Results and Discussion
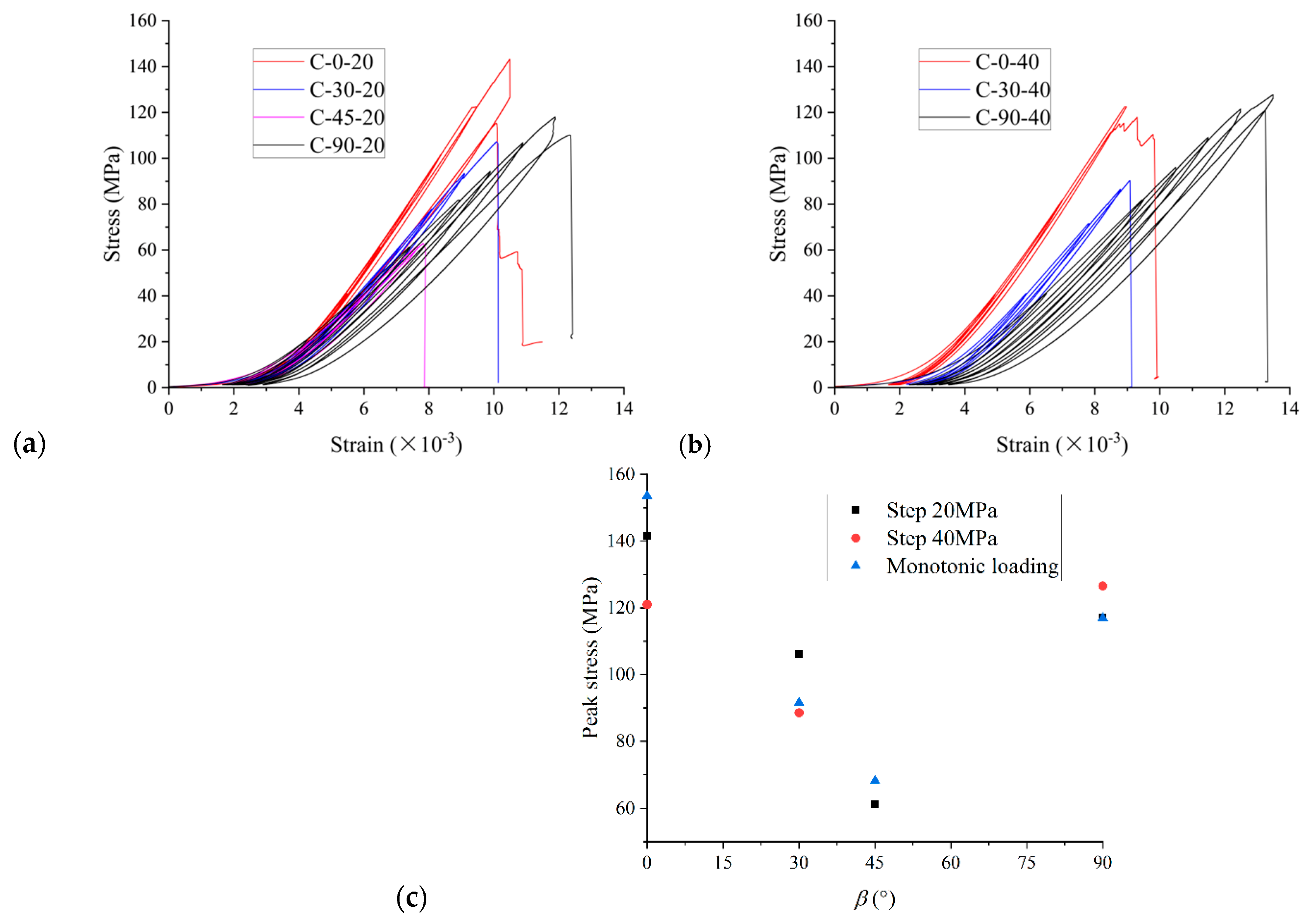
3.1. Mechanical Properties
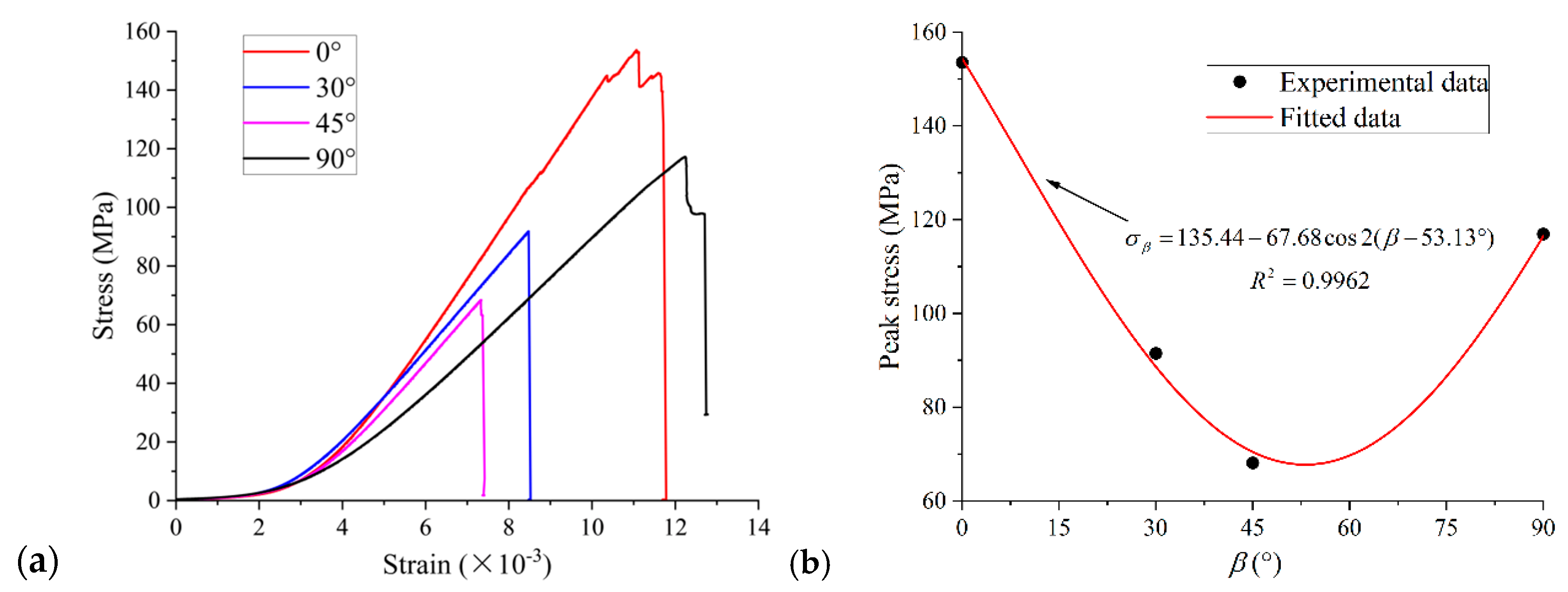
3.1.1. Peak Strength
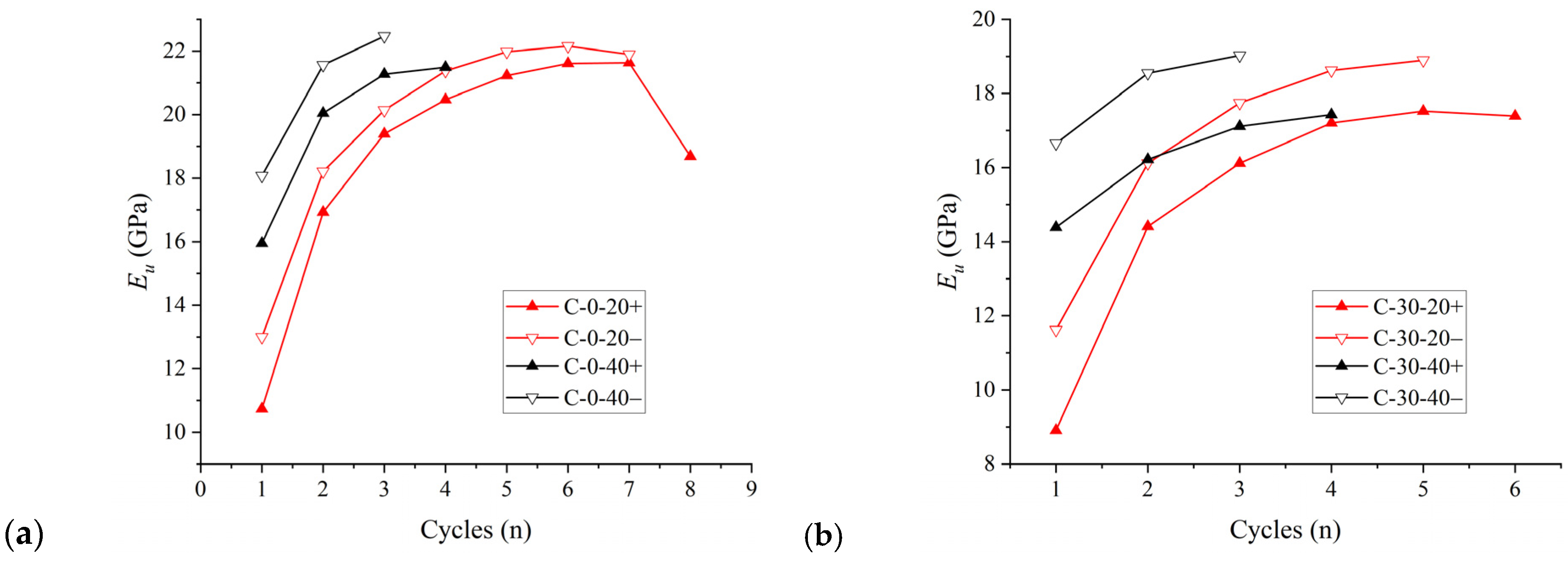
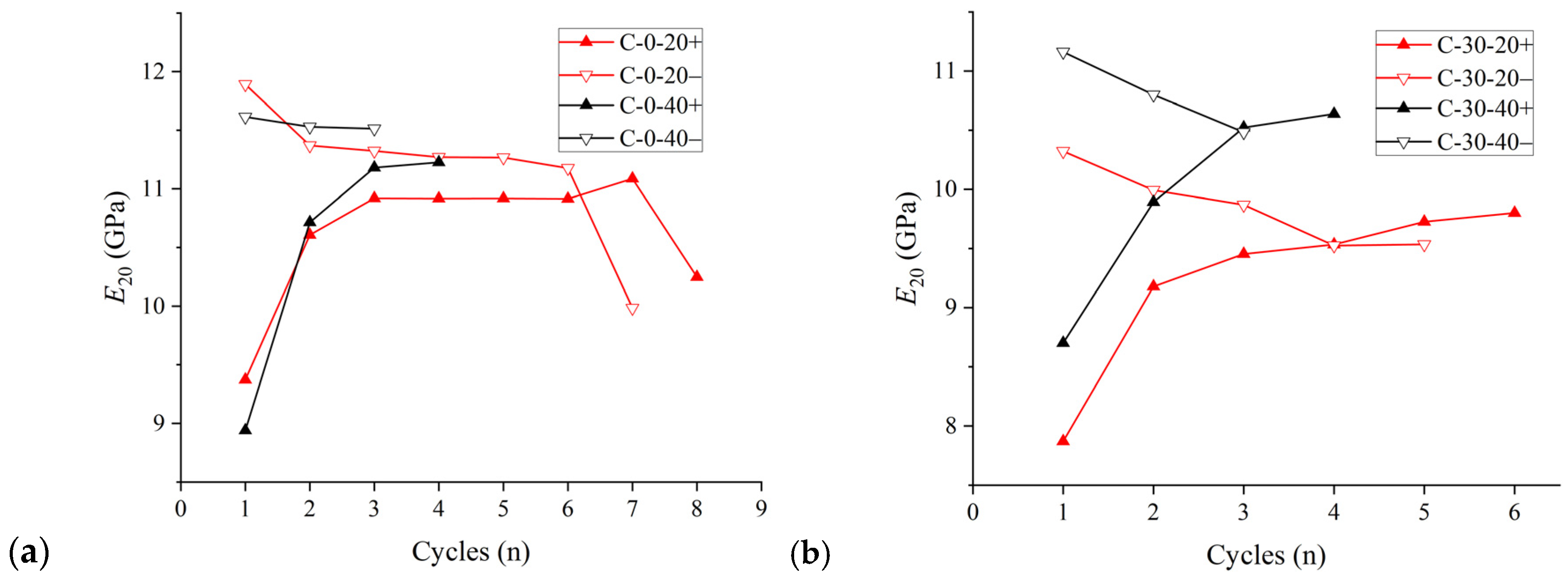
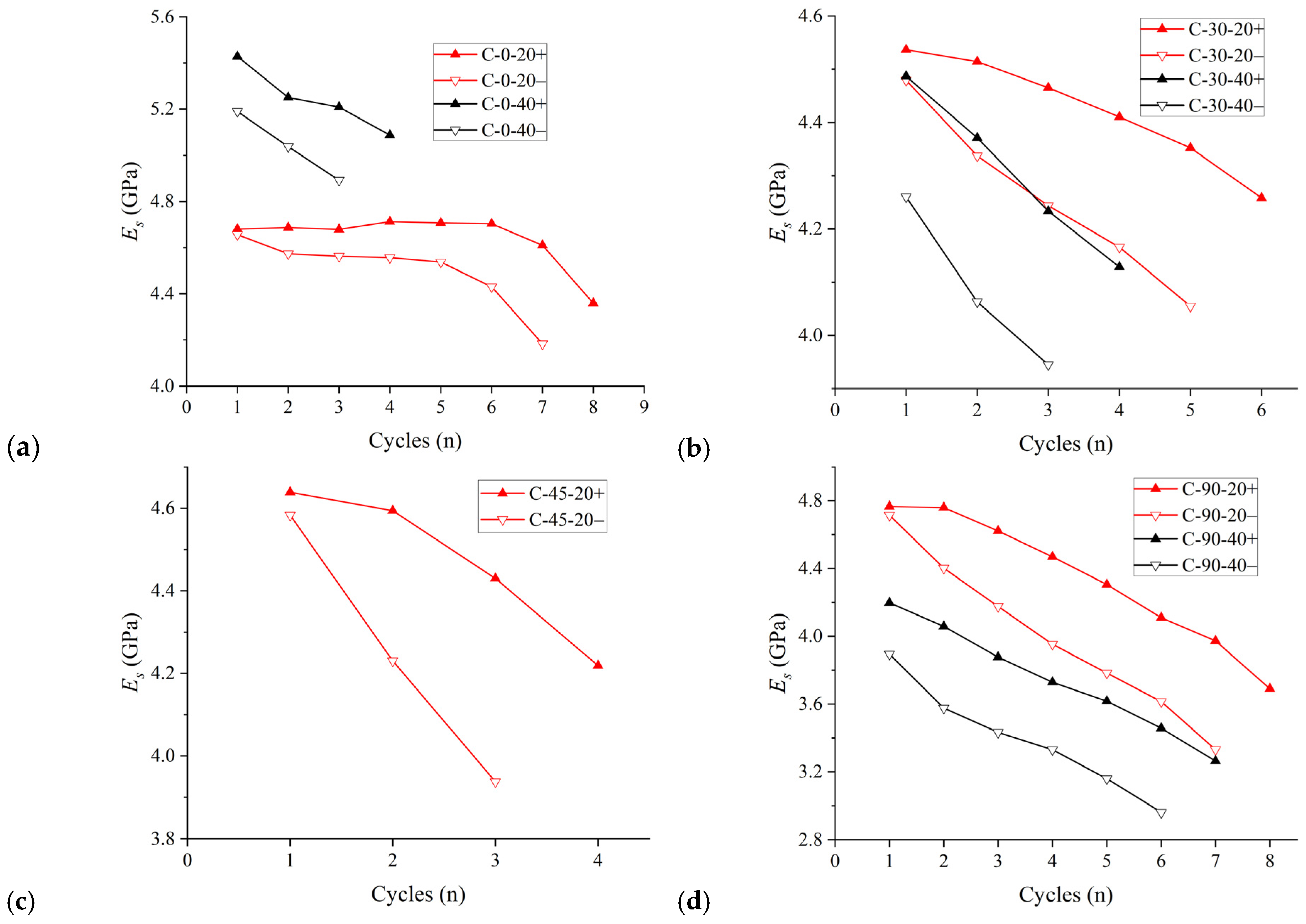
3.1.2. Elastic Modulus
3.2. Damage Evolution
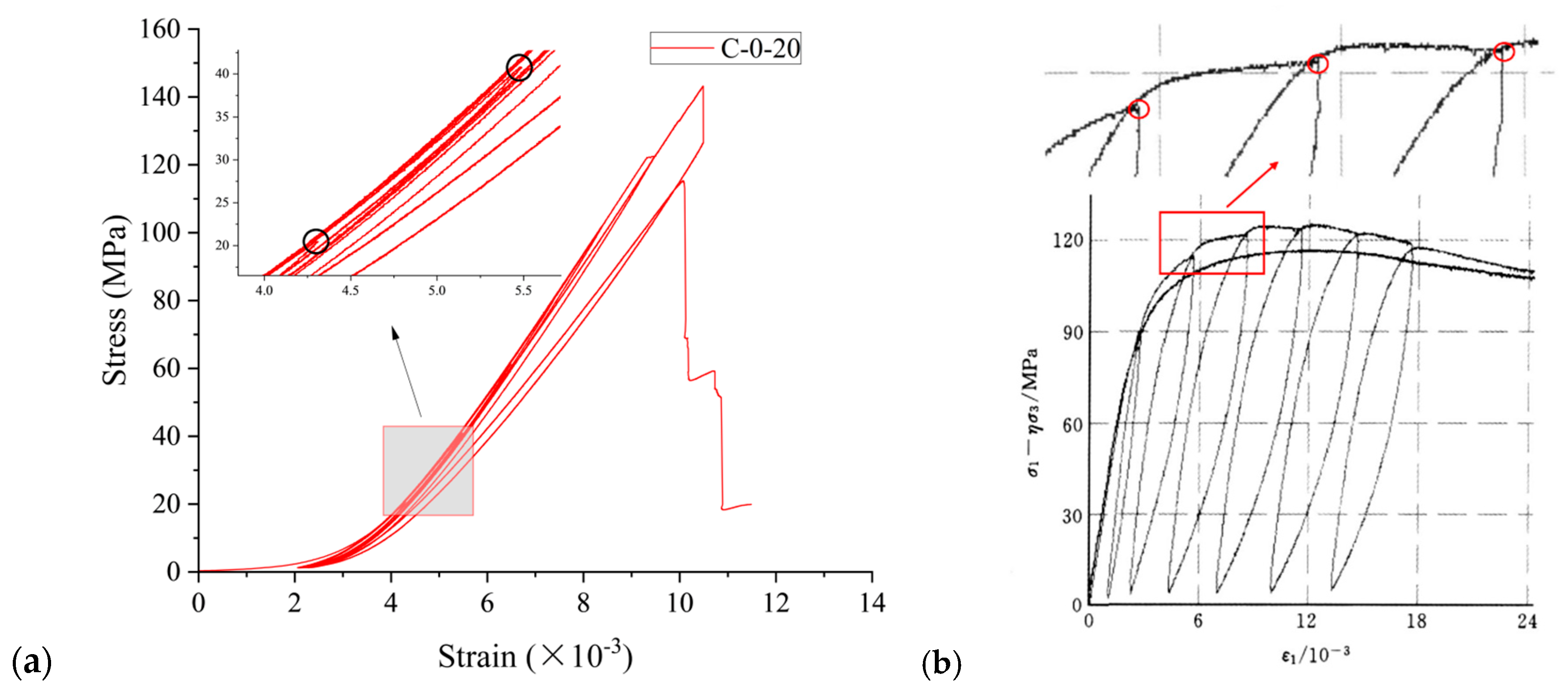
3.2.1. Deformation Evolution Process
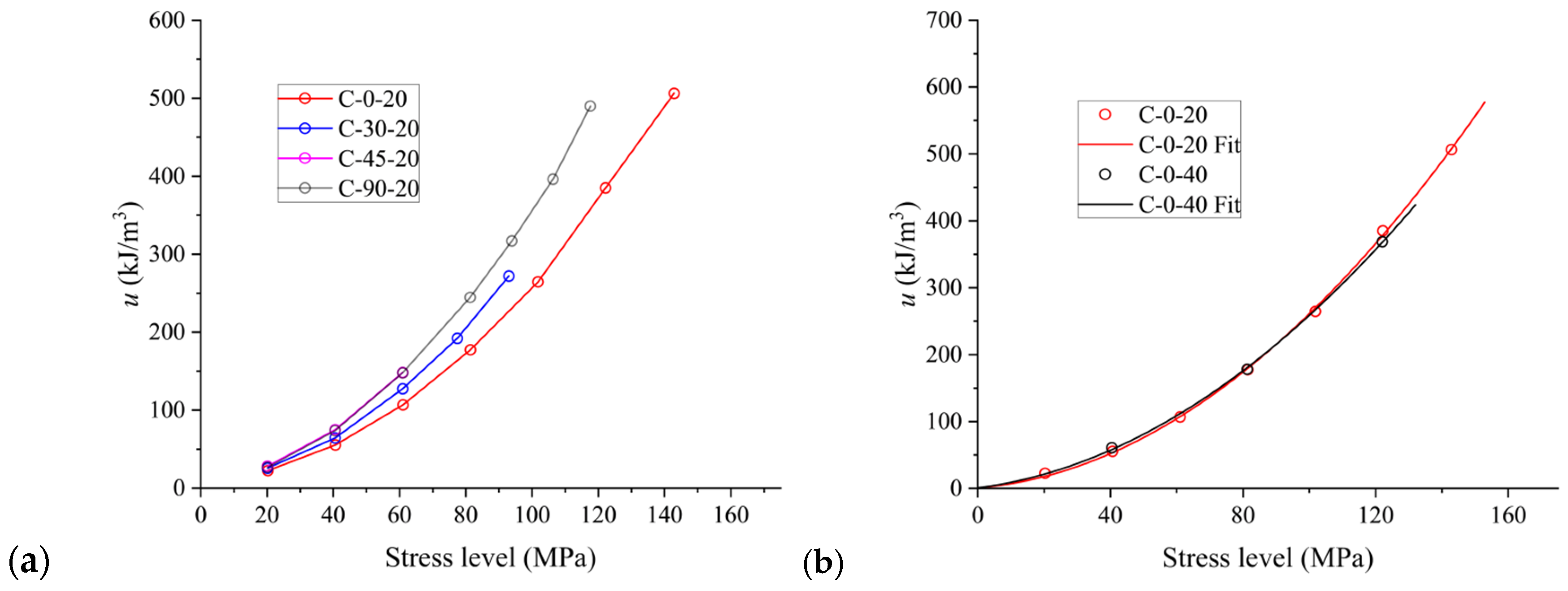
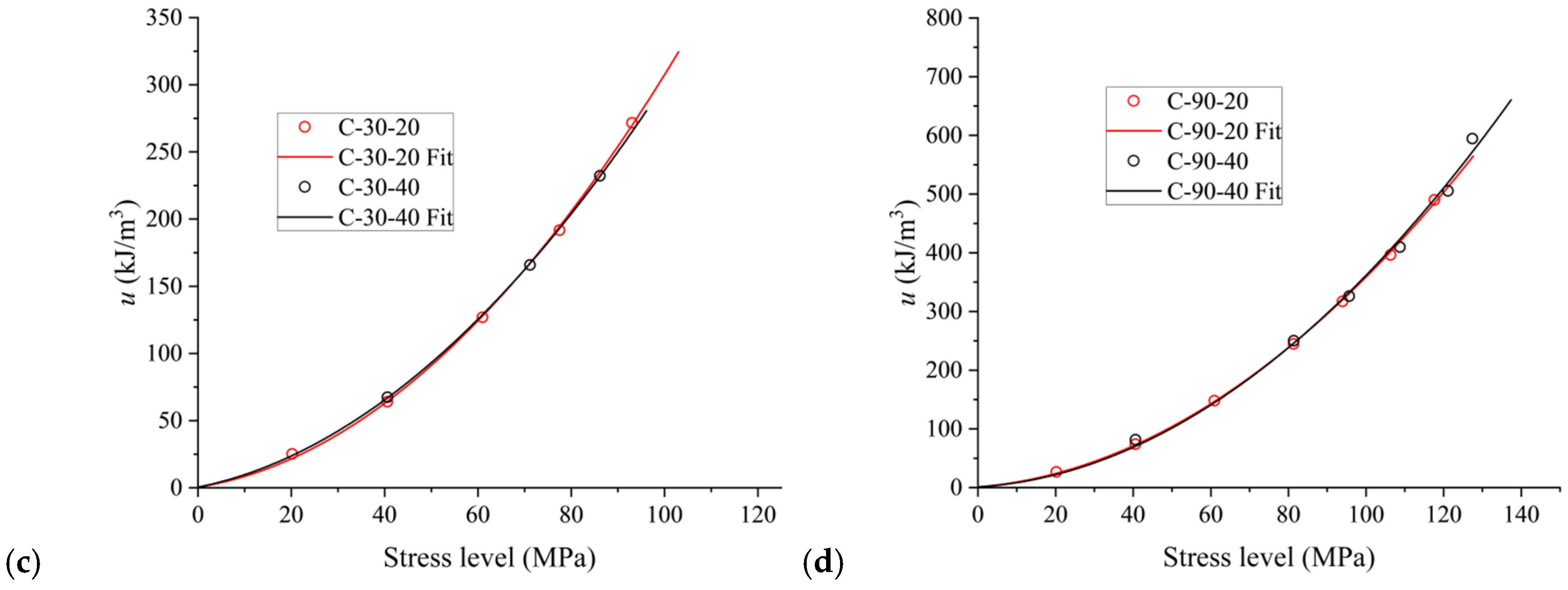
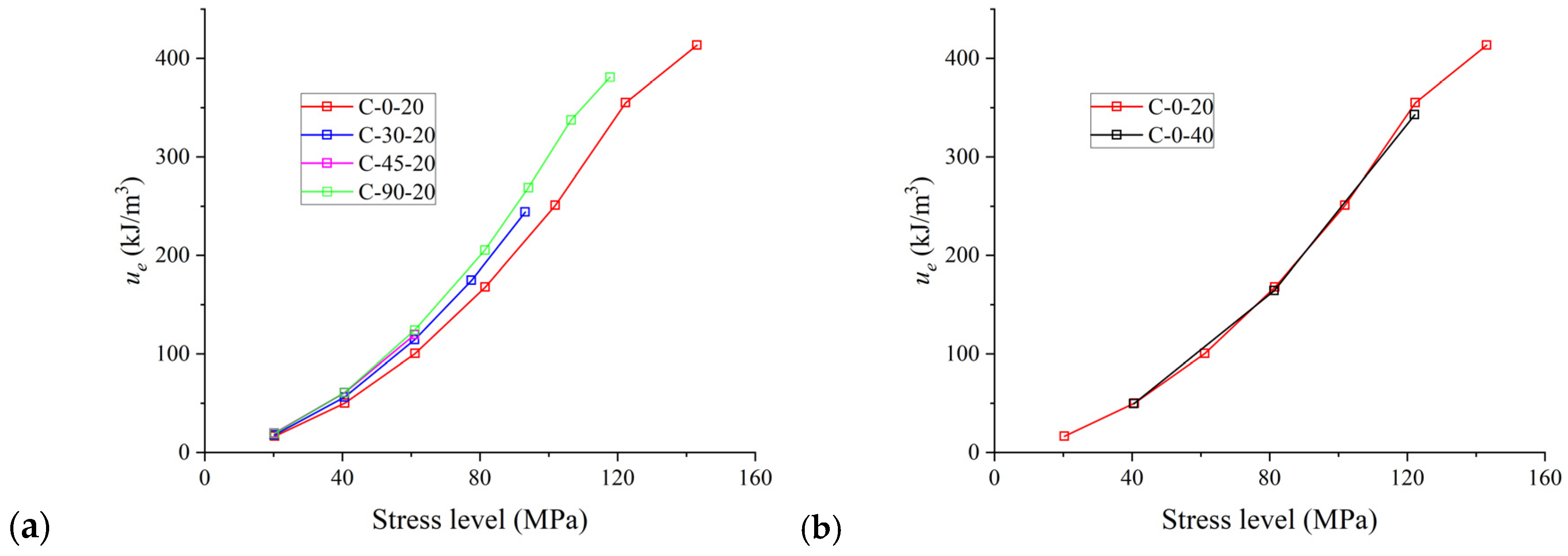
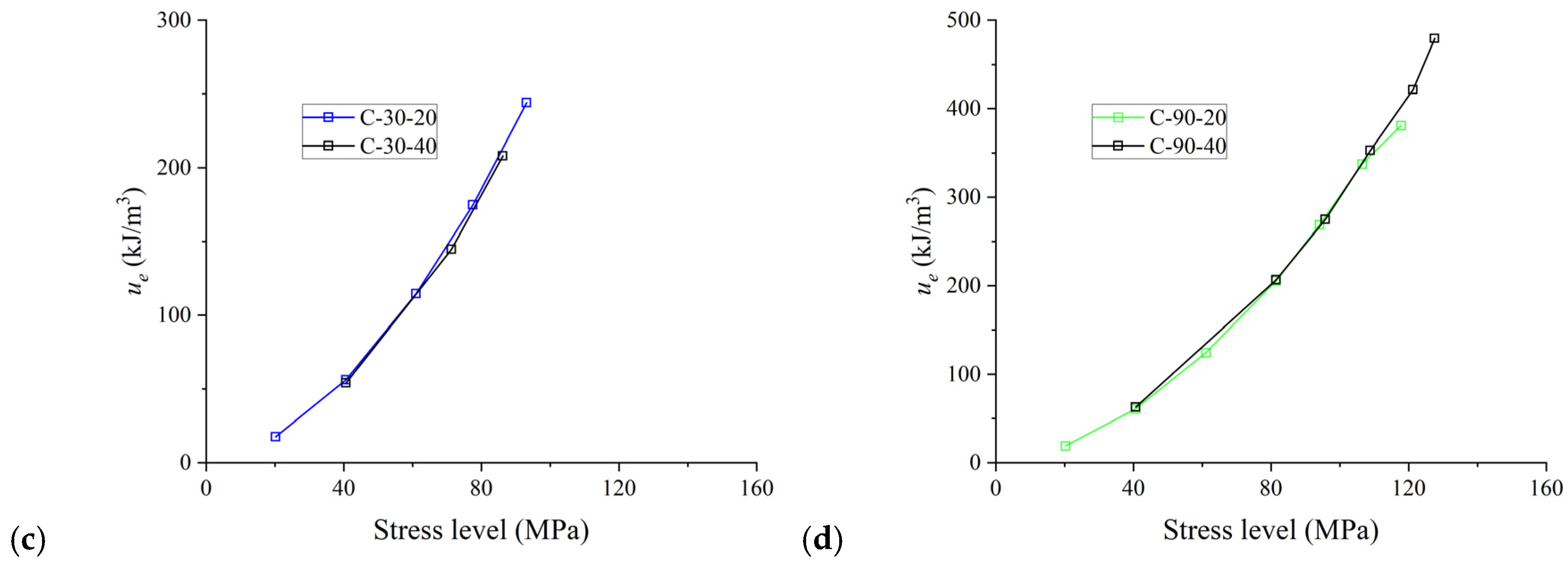
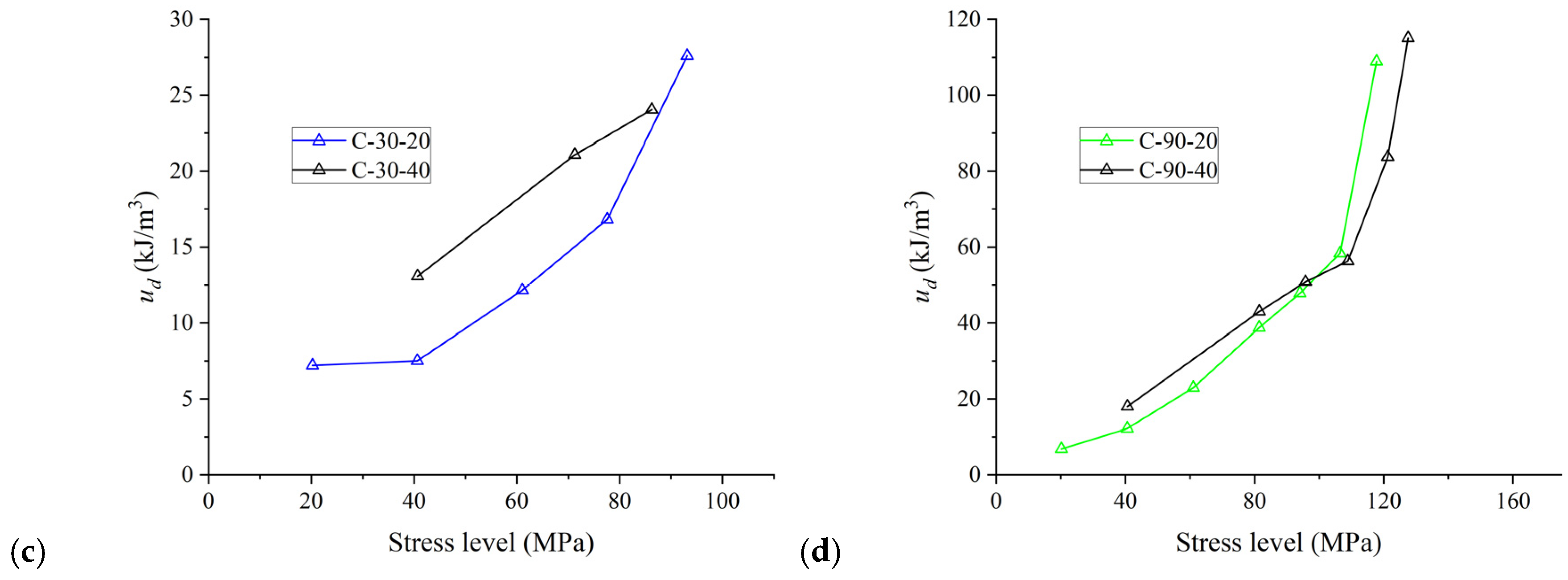
3.2.2. Energy Evolution Process
3.2.3. Damage Variable
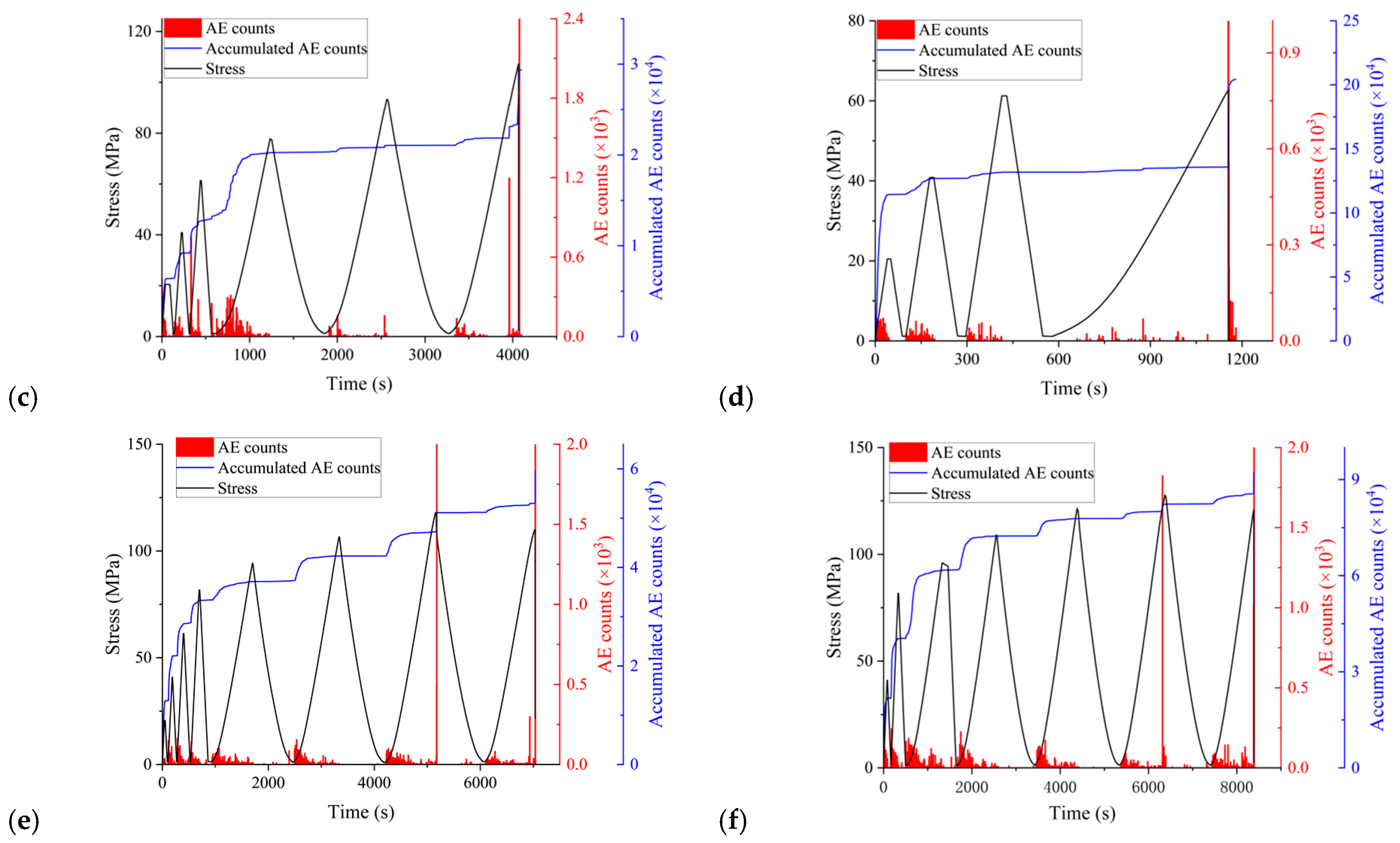
3.3. Acoustic Emission Characterization
3.3.1. AE Characteristics under Monotonic Loading
3.3.2. AE Characteristics under Cyclic Loading
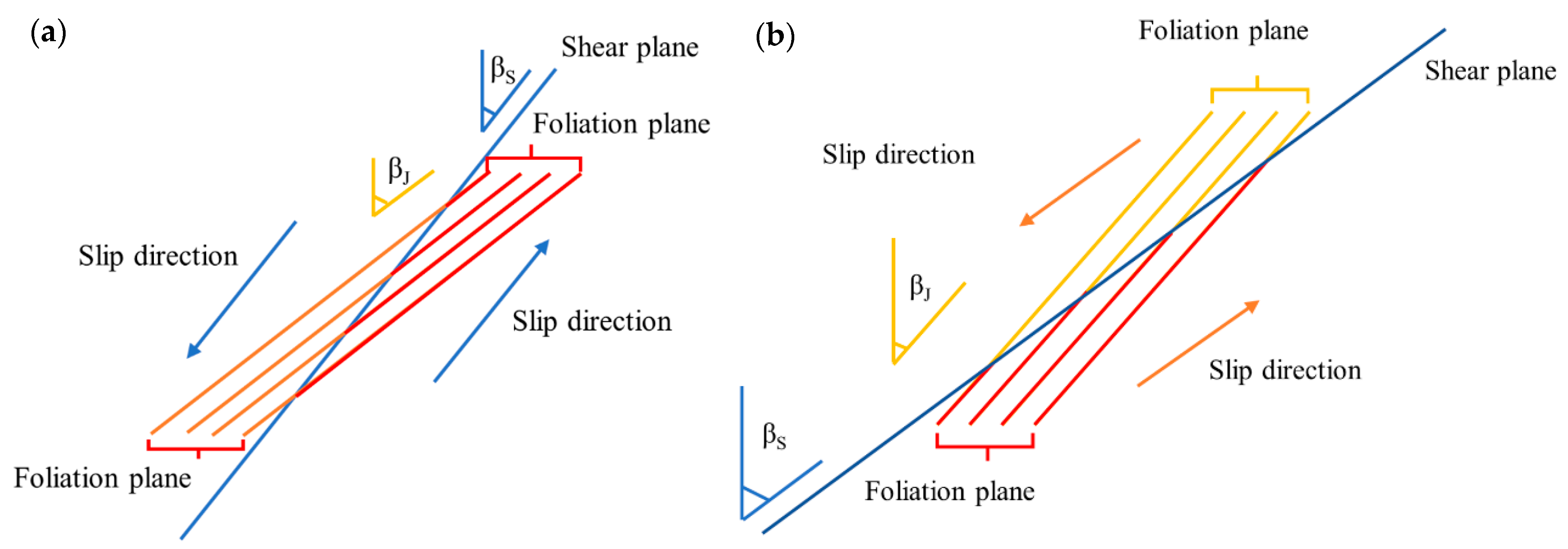
3.4. Fracture Mechanism
3.4.1. Macroscopic-Fracture Characteristics
3.4.2. Microscopic-Fracture Characteristics
4. Conclusions
- (1)
- The peak strength of specimens varies with the loading–foliation angle under cyclic loading, exhibiting a U-shaped trend similar to that observed under monotonic loading. The strength of the specimens at the same loading–foliation angle is close under both loading paths. The variation in elastic modulus of the specimens under uniaxial cyclic loading confirms the transversely isotropic model.
- (2)
- The secant moduli at different positions of the stress–strain curve exhibit unique variation characteristics under cyclic loading. These moduli can reflect the damage evolution process of the specimen with respect to various aspects. Eu and E20 reflect the influence of compaction and the damage effects on the specimen during cyclic loading and unloading. Es mainly reflects the damage of the specimen caused by the loading–unloading cycles, with Es− being more effective in characterizing this feature than Es+.
- (3)
- The input of the total energy density of the specimen is mainly dependent on the loading–foliation angle at the same stress level. The elastic-energy density and the dissipated-energy density are affected by the loading–foliation angle, cyclic stress step and number of cycles. When the degree of damage in the rock is low, increasing the stress level of the cyclic load or increasing the number of cycles can reduce the proportion of dissipated energy. The damage variable is influenced by both the loading–foliation angle and the cyclic stress step.
- (4)
- The AE characteristics of the specimen are closely related to the loading condition and the loading–foliation angle, presenting an obvious anisotropy. Under cyclic loading, regardless of cyclic stress step, the AE counts of specimens at β = 0° are concentrated near the peak region, consistent with the Kaiser effect, whereas those of specimens at the other loading–foliation angles are mainly distributed in the early stage of each cyclic-loading process, exhibiting an obvious Felicity effect.
- (5)
- The failure mechanism of slate specimens is jointly determined by the loading–foliation angle, loading condition, and cyclic stress step. The fracture modes are classified into four categories: the tensile fracture along the foliation plane (β = 0°, 90°), the tensile fracture through the foliation plane (β = 30°, 90°), the shear fracture along the foliation plane (β = 30°, 45°) and the shear fracture through the foliation plane (β = 45°, 90°). The SEM images of corresponding fracture surfaces show different characteristics, with more rock debris formed in the fracture surface of the specimen subjected to cyclic loading than to monotonic loading.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amadei, B. Importance of anisotropy when estimating and measuring in situ stresses in rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 293–325. [Google Scholar] [CrossRef]
- Jianyong, P. Strength of Transversely Isotropic Rocks. Ph.D. Thesis, Massachusetts Institute of Technology, Massachusetts Ave, Cambridge, UK, 2008. [Google Scholar]
- Li, K.; Yin, Z.-Y.; Han, D.; Fan, X.; Cao, R.; Lin, H. Size Effect and Anisotropy in a Transversely Isotropic Rock Under Compressive Conditions. Rock Mech. Rock Eng. 2021, 54, 4639–4662. [Google Scholar] [CrossRef]
- Wittke, W. Rock Mechanics Based on an Anisotropic Jointed Rock Model (AJRM), 1st ed.; Ernst & Sohn: Berlin, Germany, 2014; pp. 5–7. [Google Scholar]
- Li, K.; Yin, Z.Y.; Cheng, Y.; Cao, P.; Meng, J. Three-dimensional discrete element simulation of indirect tensile behaviour of a transversely isotropic rock. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1812–1832. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, B.; Yang, K.; Guo, P.; Tao, Z. Large Deformation Mechanism of Foliated Rock and NPR Anchor Cable Support Technology in the Changning Tunnel: A Case Study. Rock Mech. Rock Eng. 2022, 55, 7243–7268. [Google Scholar] [CrossRef]
- Plúa, C.; Vu, M.N.; de La Vaissière, R.; Armand, G. In Situ Thermal Hydrofracturing Behavior of the Callovo-Oxfordian Claystone within the Context of the Deep Geological Disposal of Radioactive Waste in France. Rock Mech. Rock Eng. 2023. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F. A review of experimental and theoretical research on the deformation and failure behavior of rocks subjected to cyclic loading. J. Rock Mech. Geotech. 2021, 13, 1203–1230. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, M.; Tan, H.; Lin, H.; Li, K. Effect of temperature on pure mode III fracture behavior and fracture morphology of granite after thermal shock. Theor. Appl. Fract. Mech. 2023, 127, 104024. [Google Scholar] [CrossRef]
- Wang, M.; Li, J.; Tan, H.; Wang, J.; Shi, Z.; Li, K. Study on fatigue characteristics and thermal damage mechanism of red sandstone under high temperature-cyclic load coupling. Int. J. Fatigue 2023, 168, 107405. [Google Scholar] [CrossRef]
- He, M.C.; Ren, F.Q.; Cheng, C. Experimental and numerical analyses on the effect of stiffness on bedded sandstone strain burst with varying dip angle. Bull. Eng. Geol. Environ. 2019, 78, 3593–3610. [Google Scholar] [CrossRef]
- Ge, X.R.; Jiang, Y.; Lu, Y.; Ren, J. Testing study on fatigue deformation law of rock under cyclic loading. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2003, 22, 1581–1585. [Google Scholar] [CrossRef]
- Yang, S.Q.; Ranjith, P.G.; Huang, Y.H.; Yin, P.F.; Jing, H.W.; Gui, Y.L.; Yu, Q.L. Experimental investigation on mechanical damage characteristics of sandstone under triaxial cyclic loading. Geophys. J. Int. 2015, 201, 662–682. [Google Scholar] [CrossRef]
- Jiang, C.; Duan, M.; Yin, G.; Wang, J.G.; Lu, T.; Xu, J.; Zhang, D.; Huang, G. Experimental study on seepage properties, AE characteristics and energy dissipation of coal under tiered cyclic loading. Eng. Geol. 2017, 221, 114–123. [Google Scholar] [CrossRef]
- Peng, K.; Zhou, J.; Zou, Q.; Song, X. Effect of loading frequency on the deformation behaviours of sandstones subjected to cyclic loads and its underlying mechanism. Int. J. Fatigue 2020, 131, 105349. [Google Scholar] [CrossRef]
- Meng, Q.-b.; Liu, J.-f.; Huang, B.-x.; Pu, H.; Wu, J.-y.; Zhang, Z.-z. Effects of Confining Pressure and Temperature on the Energy Evolution of Rocks Under Triaxial Cyclic Loading and Unloading Conditions. Rock Mech. Rock Eng. 2022, 55, 773–798. [Google Scholar] [CrossRef]
- Yang, S.Q.; Huang, Y.H.; Tang, J.Z. Mechanical, acoustic, and fracture behaviors of yellow sandstone specimens under triaxial monotonic and cyclic loading. Int. J. Rock Mech. Min. Sci. 2020, 130, 104268. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhao, Y.L.; Liu, Q.; Li, Y.; Lin, H.; Ma, J.J. Energy Evolution Law of Sandstone Material during Post-Peak Cyclic Loading and Unloading under Hydraulic Coupling. Sustainability 2024, 16, 24. [Google Scholar] [CrossRef]
- Sinaie, S.; Heidarpour, A.; Zhao, X.L.; Sanjayan, J.G. Effect of size on the response of cylindrical concrete samples under cyclic loading. Constr. Build. Mater. 2015, 84, 399–408. [Google Scholar] [CrossRef]
- Peng, K.; Zhou, J.; Zou, Q.; Zhang, J.; Wu, F. Effects of stress lower limit during cyclic loading and unloading on deformation characteristics of sandstones. Constr. Build. Mater. 2019, 217, 202–215. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F.; Feng, P.; Xu, N.-w. Mechanical behavior of intermittent jointed rocks under random cyclic compression with different loading parameters. Soil Dyn. Earthq. Eng. 2018, 113, 12–24. [Google Scholar] [CrossRef]
- Duan, H.; Yang, Y. Deformation and Dissipated Energy of Sandstone Under Uniaxial Cyclic Loading. Geotech. Geol. Eng. 2018, 36, 611–619. [Google Scholar] [CrossRef]
- Tang, J.H.; Chen, X.D.; Dai, F. Experimental study on the crack propagation and acoustic emission characteristics of notched rock beams under post-peak cyclic loading. Eng. Fract. Mech. 2020, 226, 106890. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Liu, J.H.; Zhang, C.S.; Liao, J.; Zhu, S.T.; Zhang, L.Y. Mechanical behavior of sandstone during post-peak cyclic loading and unloading under hydromechanical coupling (vol 33, pg 927, 2023). Int. J. Min. Sci. Technol. 2023, 33, 1317. [Google Scholar] [CrossRef]
- Xiao, J.-Q.; Ding, D.-X.; Jiang, F.-L.; Xu, G. Fatigue damage variable and evolution of rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2010, 47, 461–468. [Google Scholar] [CrossRef]
- Li, T.T.; Pei, X.J.; Wang, D.P.; Huang, R.Q.; Tang, H. Nonlinear behavior and damage model for fractured rock under cyclic loading based on energy dissipation principle. Eng. Fract. Mech. 2019, 206, 330–341. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, N.; Feng, X.; Kan, J.; Pan, D.; Qian, D. Experimental Investigation of Sandstone under Cyclic Loading: Damage Assessment Using Ultrasonic Wave Velocities and Changes in Elastic Modulus. Shock. Vib. 2018, 2018, 7845143. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.K.; Li, C.H. On anisotropic fracture and energy evolution of marble subjected to triaxial fatigue cyclic-confining pressure unloading conditions. Int. J. Fatigue 2020, 134, 105524. [Google Scholar] [CrossRef]
- Bao, H.; Pei, R.; Lan, H.; Yan, C.; Xu, J.; Zhai, Y.; Xu, X. Damage evolution of Biotite quartz schist caused by mineral directional arrangement under cyclic loading and unloading. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2021, 40, 2015–2026. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, W.Y.; Wang, H.L.; Wang, R.B.; Yan, L.; Hu, M.T. Anisotropic mechanical behaviour of columnar jointed rock masses subjected to cyclic loading: An experimental investigation. Int. J. Rock Mech. Min. Sci. 2021, 148, 14. [Google Scholar] [CrossRef]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1999, 36, 281–289. [Google Scholar]
- Li, K.; Cheng, Y.; Yin, Z.-Y.; Han, D.; Meng, J. Size Effects in a Transversely Isotropic Rock Under Brazilian Tests: Laboratory Testing. Rock Mech. Rock Eng. 2020, 53, 2623–2642. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, Q.; Hao, S.; Geng, J.; Lv, C. Experimental study on the variation of physical and mechanical properties of rock after high temperature treatment. Appl. Therm. Eng. 2016, 98, 1297–1304. [Google Scholar] [CrossRef]
- Jaeger, J.C. Shear Failure of Anistropic Rocks. Geol. Mag. 1960, 97, 65–72. [Google Scholar] [CrossRef]
- Donath, F.A. Experimental study of shear failure in anisotropic rocks. GSA Bull. 1961, 72, 985–989. [Google Scholar] [CrossRef]
- Saeidi, O.; Vaneghi, R.G.; Rasouli, V.; Gholami, R. A modified empirical criterion for strength of transversely anisotropic rocks with metamorphic origin. Bull. Eng. Geol. Environ. 2013, 72, 257–269. [Google Scholar] [CrossRef]
- Zhang, J.; Du, R.; Chen, Y.; Huang, Z. Experimental Investigation of the Mechanical Properties and Energy Evolution of Layered Phyllite Under Uniaxial Multilevel Cyclic Loading. Rock Mech. Rock Eng. 2023, 56, 4153–4168. [Google Scholar] [CrossRef]
- Cho, J.W.; Kim, H.; Jeon, S.; Min, K.B. Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist. Int. J. Rock Mech. Min. Sci. 2012, 50, 158–169. [Google Scholar] [CrossRef]
- Li, C.; Gao, C.; Xie, H.; Li, N. Experimental investigation of anisotropic fatigue characteristics of shale under uniaxial cyclic loading. Int. J. Rock Mech. Min. Sci. 2020, 130, 104314. [Google Scholar] [CrossRef]
- You, M.; Su, C. Experimental study on strengthening of marble specimen in cyclic loading of uniaxial or pseudo-triaxial compression. Guti Lixue Xuebao/Acta Mech. Solida Sin. 2008, 29, 66–72. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock Mech. Geotech. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Wang, J.A.; Park, H.D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn. Undergr. Space Technol. 2001, 16, 49–57. [Google Scholar] [CrossRef]
- Scruby, C.B. An introduction to acoustic emission. J. Phys. E Sci. Instrum. 1987, 20, 946. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Jing, H.-W.; Wang, S.-Y. Experimental Investigation on the Strength, Deformability, Failure Behavior and Acoustic Emission Locations of Red Sandstone Under Triaxial Compression. Rock Mech. Rock Eng. 2012, 45, 583–606. [Google Scholar] [CrossRef]
- Yin, T.; Yin, J.; Wu, Y.; Yang, Z.; Liu, X.; Zhuang, D. Water saturation effects on the mechanical characteristics and fracture evolution of sandstone containing pre-existing flaws. Theor. Appl. Fract. Mech. 2022, 122, 103605. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Cui, Z.; Cheng, C.; Jian, Z. Investigation of the fracture modes of red sandstone using XFEM and acoustic emissions. Theor. Appl. Fract. Mech. 2016, 85, 283–293. [Google Scholar] [CrossRef]
- Xu, G.; He, C.; Su, A.; Chen, Z. Experimental investigation of the anisotropic mechanical behavior of phyllite under triaxial compression. Int. J. Rock Mech. Min. Sci. 2018, 104, 100–112. [Google Scholar] [CrossRef]
- Erarslan, N.; Williams, D.J. Mechanism of rock fatigue damage in terms of fracturing modes. Int. J. Fatigue 2012, 43, 76–89. [Google Scholar] [CrossRef]
- Fan, J.; Chen, J.; Jiang, D.; Ren, S.; Wu, J. Fatigue properties of rock salt subjected to interval cyclic pressure. Int. J. Fatigue 2016, 90, 109–115. [Google Scholar] [CrossRef]















| Loading Path | Specimen Name | β (°) | Cyclic Stress Step (MPa) | Number of Cycles (Force Control + Displacement Control) |
|---|---|---|---|---|
| Monotonic loading | U-0 | 0 | \ | \ |
| U-30 | 30 | \ | \ | |
| U-45 | 45 | \ | \ | |
| U-90 | 90 | \ | \ | |
| Cyclic loading and unloading | C-0-20 | 0 | 20 | 6 + 2 |
| C-0-40 | 0 | 40 | 3 + 1 | |
| C-30-20 | 30 | 20 | 3 + 3 | |
| C-30-40 | 30 | 40 | 2 + 2 | |
| C-45-20 | 45 | 20 | 3 + 1 | |
| C-90-20 | 90 | 20 | 4 + 4 | |
| C-90-40 | 90 | 40 | 3 + 4 |
| β (°) | 0 | 30 | 45 | 90 |
| E (GPa) | 20.39 | 16.15 | 15.49 | 13.57 |
| Specimen Name | Quadratic Coefficient | Primary Term Coefficient | Number of Fit Points | Correlation Coefficient |
|---|---|---|---|---|
| C-0-20 | 0.022 | 0.399 | 8 | 0.9998 |
| C-0-40 | 0.020 | 0.624 | 4 | 0.9999 |
| C-30-20 | 0.025 | 0.553 | 6 | 0.9998 |
| C-30-40 | 0.023 | 0.701 | 4 | 1.0000 |
| C-45-20 | 0.027 | 0.741 | 4 | 0.9999 |
| C-90-20 | 0.030 | 0.536 | 8 | 0.9998 |
| C-90-40 | 0.032 | 0.409 | 7 | 0.9981 |
| Specimen Name | uN (kJ/m3) | ue,N (kJ/m3) | ud,N (kJ/m3) |
|---|---|---|---|
| C-0-20 | 382.58 | 306.05 | 76.53 |
| C-0-40 | 453.46 | 255.23 | 198.23 |
| C-30-20 | 359.82 | 292.96 | 66.85 |
| C-30-40 | 247.14 | 215.93 | 31.21 |
| C-45-20 | 147.91 | 115.80 | 32.11 |
| C-90-20 | 482.01 | 331.05 | 150.97 |
| C-90-40 | 512.15 | 396.38 | 115.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Du, G.; Li, J.; Han, D.; Wang, Y. Anisotropic Mechanical Properties and Fracture Mechanism of Transversely Isotropic Rocks under Uniaxial Cyclic Loading. Appl. Sci. 2024, 14, 4988. https://doi.org/10.3390/app14124988
Li K, Du G, Li J, Han D, Wang Y. Anisotropic Mechanical Properties and Fracture Mechanism of Transversely Isotropic Rocks under Uniaxial Cyclic Loading. Applied Sciences. 2024; 14(12):4988. https://doi.org/10.3390/app14124988
Chicago/Turabian StyleLi, Kaihui, Guangzhen Du, Jiangteng Li, Dongya Han, and Yan Wang. 2024. "Anisotropic Mechanical Properties and Fracture Mechanism of Transversely Isotropic Rocks under Uniaxial Cyclic Loading" Applied Sciences 14, no. 12: 4988. https://doi.org/10.3390/app14124988
APA StyleLi, K., Du, G., Li, J., Han, D., & Wang, Y. (2024). Anisotropic Mechanical Properties and Fracture Mechanism of Transversely Isotropic Rocks under Uniaxial Cyclic Loading. Applied Sciences, 14(12), 4988. https://doi.org/10.3390/app14124988








