Fuzzy-FMEA Theory Approach for Prioritizing Supply Chain Nervousness Factors
Abstract
1. Introduction
2. Literature Review
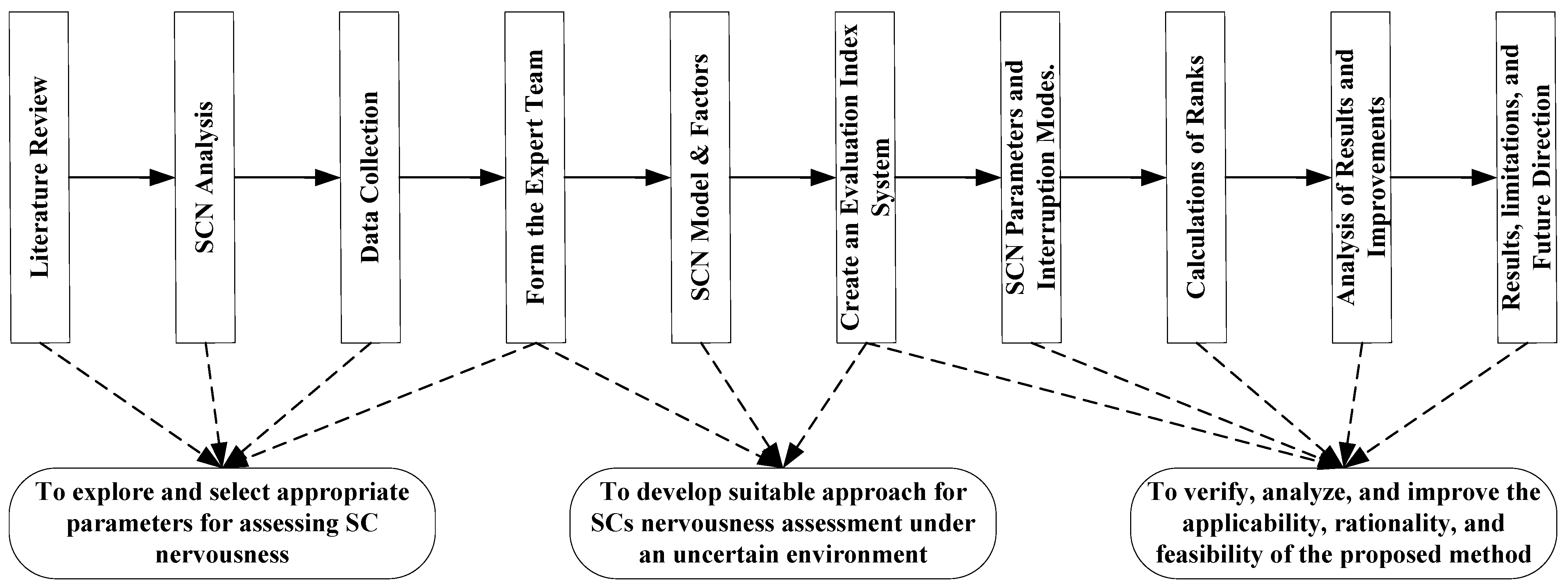
3. Research Methodology
3.1. Assessment of SCN
3.2. SCN Model
4. Illustrative Application of the SCN Model
Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Disney, S.M. Revisiting Rescheduling: MRP Nervousness and the Bullwhip Effect. Int. J. Prod. Res. 2016, 55, 1992–2012. [Google Scholar] [CrossRef]
- Mousavi, B.A.; Azzouz, R.; Heavey, C.; Ehm, H. MRP analysis of the nervousness within semiconductors supply chain planning: Insight from a case study. In Proceedings of the Winter Simulation Conference (WSC), National Harbor, MD, USA, 8–11 December 2019; pp. 2396–2407. [Google Scholar]
- Kaipia, R.; Korhonen, H.; Hartiala, H. Planning nervousness in a demand supply network: An empirical study. Int. J. Logist. Manag. 2006, 17, 95–113. [Google Scholar] [CrossRef]
- Law KM, Y.; Gunasekaran, A. A comparative study of schedule nervousness among high-tech manufacturers across the straits. Int. J. Prod. Res. 2010, 48, 6015–6036. [Google Scholar] [CrossRef]
- Maryanto, M.; Zendrato, R.; Wicaksana, B. Reduction of Supply Chain Nervousness with Vendor Managed Inventory Approach. Tekinfo|Sci. J. Ind. Inf. Eng. 2012, 1, 1–11. [Google Scholar]
- Wangsa, I.D.; Iskandar, B. Pengembangan Model Consignment Stock pada Sistem Rantai Pasok Dua Eselon dengan Permintaan Berfluktuasi dan Perubahan Order Awal. J. Tek. Ind. 2013, 15, 1–12. [Google Scholar] [CrossRef][Green Version]
- Tunc, H.; Kilic, O.A.; Tarim, S.A.; Eksioglu, B. A simple approach for assessing the cost of system nervousness. Int. J. Prod. Econ. 2013, 141, 619–625. [Google Scholar] [CrossRef]
- Magableh, G.M.; Mistarihi, M.Z. Causes and Effects of Supply Chain Nervousness: Mena case study. Acta Logist. 2022, 9, 223–235. [Google Scholar] [CrossRef]
- Magableh, G.M.; Mistarihi, M.Z. Global Supply Chain Nervousness (GSCN). Sustainability 2023, 15, 12115. [Google Scholar] [CrossRef]
- Kropp, D.H.; Carlson, R.C. Lot-Sizing Algorithm for Reducing Nervousness in MRP Systems. Manag. Sci. 1984, 30, 240–244. [Google Scholar] [CrossRef]
- Ho, C.J.; Ireland, T.C. Correlating MRP system nervousness with forecast errors. Int. J. Prod. Res. 1998, 36, 2285–2299. [Google Scholar] [CrossRef]
- Kropp, D.H.; College, D.; Carlson, R.C.; Jucker, J.V. Concepts, Theories, and Techniques Heuristic Lot-Sizing Approaches for Dealing with MRP System Nervousness. Decis. Sci. 1983, 14, 156–169. [Google Scholar] [CrossRef]
- Ho, C.J. Evaluating the impact of operating environments on MRP system nervousness. Int. J. Prod. Res. 1989, 27, 1115–1135. [Google Scholar] [CrossRef]
- Blackburn, J.D.; Kropp, D.H.; Millen, R.A. MRP System Nervousness: Causes and Cures. Eng. Costs Prod. Econ. 1985, 9, 141–146. [Google Scholar] [CrossRef]
- Blackburn, J.D.; Kropp, D.H.; Millen, R.A. Comparison of Strategies to Dampen Nervousness in MRP Systems. Manag. Sci. 1986, 32, 413–429. [Google Scholar] [CrossRef]
- Ho, C.J. Evaluating dampening effects of alternative lot-sizing rules to reduce MRP system nervousness. Int. J. Prod. Res. 2002, 40, 2633–2652. [Google Scholar] [CrossRef]
- Ho, C.J.; Carter, P.L. An investigation of alternative dampening procedures to cope with MRP system nervousness. Int. J. Prod. Res. 1996, 34, 137–156. [Google Scholar] [CrossRef]
- Ho, C.J.; Ho SJ, K. Evaluating the effectiveness of using lot-sizing rules to cope with MRP system nervousness. Prod. Plan. Control 1999, 10, 150–161. [Google Scholar] [CrossRef]
- Ho, C.J.; Ireland, T.C. A diagnostic analysis of the impact of forecast errors on production planning via MRP system nervousness. Prod. Plan. Control 1993, 4, 311–322. [Google Scholar] [CrossRef]
- Ho, C.-J.; Narasimhan, R.; Melnyk, S.A.; Carter, P.L. Research Framework for Investigating the Effectiveness of Dampening Procedures to Cope with MRP System Nervousness. Int. J. Oper. Prod. Manag. 1992, 12, 30–43. [Google Scholar] [CrossRef]
- Braun, M.W.; Schwartz, J.D. A control theoretic evaluation of schedule nervousness suppression techniques for master production scheduling. In Decision Policies for Production Networks; Springer: London, UK, 2012; pp. 143–171. [Google Scholar]
- Ave, G.D.; Alici, M.; Harjunkoski, I.; Engell, S. An Explicit Online Resource-Task Network Scheduling Formulation to Avoid Scheduling Nervousness. In Computer Aided Chemical Engineering; Elsevier B.V.: Amsterdam, The Netherlands, 2019; Volume 46, pp. 61–66. [Google Scholar] [CrossRef]
- Hasachoo, N.; Masuchun, R. Reducing Schedule Nervousness in Production and Operations Under Non-Stationary Stochastic Demand: The Case of an Airline Catering Company. In Proceedings of the IEEM2016: 2016 International Conference on Industrial Engineering and Engineering Management, Bali, Indonesia, 4–7 December 2016; pp. 941–946. [Google Scholar]
- Pujawan, I.N. Schedule nervousness in a manufacturing system: A case study. Prod. Plan. Control 2004, 15, 515–524. [Google Scholar] [CrossRef]
- Kadipasaoglu, S.N.; Sridharan, V. Alternative approaches for reducing schedule instability in multistage manufacturing under demand uncertainty. J. Oper. Manag. 1995, 13, 193–211. [Google Scholar] [CrossRef]
- Inderfurth, K. Nervousness in inventory control: Analytical results. OR Spektrum 1994, 16, 113–123. [Google Scholar] [CrossRef]
- Atadeniz, S.N.; Sridharan, S.V. Effectiveness of nervousness reduction policies when capacity is constrained. Int. J. Prod. Res. 2020, 58, 4121–4137. [Google Scholar] [CrossRef]
- Herrera, C.; Thomas, A. Simulation of less master production schedule nervousness model Simulation of less master production schedule nervousness model Simulation of Less Master Production Schedule Nervousness Model. IFAC Proc. 2009, 42, 1585–1590. [Google Scholar] [CrossRef]
- Roberta Minifie, J.; Davis, R.A. Interaction effects on MRP nervousness. Int. J. Prod. Res. 1990, 28, 173–183. [Google Scholar] [CrossRef]
- Carlson, R.C.; Jucker, J.V.; Kropp, D.H. Less Nervous MRP Systems: A Dynamic Economic Lot-Sizing Approach. Manag. Sci. 1979, 25, 754–761. [Google Scholar] [CrossRef]
- Koca, E.; Yaman, H.; Aktürk, M.S. Stochastic lot sizing problem with nervousness considerations. Comput. Oper. Res. 2018, 94, 23–37. [Google Scholar] [CrossRef]
- Mistarihi, M.; Magableh, G. Unveiling Supply Chain Nervousness: A Strategic Framework for Disruption Management under Fuzzy Environment. Sustainability 2023, 15, 11179. [Google Scholar] [CrossRef]
- Mistarihi, M.; Magableh, G. Supply Chain Nervousness Optimization using Fuzzy-ELECTRE Technique. In Proceedings of the International Conference On Mechanical, Industrial and Production Engineering—(ICMIPE-23), Davanagere, India, 30 April 2023. [Google Scholar]
- Shanker, S.; Sharma, H.; Barve, A. Assessment of risks associated with third-party logistics in restaurant supply chain. Benchmarking 2021, 28, 2432–2464. [Google Scholar] [CrossRef]
- Munir, M.; Jajja, M.S.S.; Chatha, K.A.; Farooq, S. Supply chain risk management and operational performance: The enabling role of supply chain integration. Int. J. Prod. Econ. 2020, 227, 107667. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A novel plithogenic TOPSIS-CRITIC model for sustainable supply chain risk management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Brusset, X.; Teller, C. Supply Chain Capabilities, Risks, and Resilience. Int. J. Prod. Econ. 2016, 184, 59–68. [Google Scholar] [CrossRef]
- Aqlan, F.; Lam, S.S. Supply chain optimization under risk and uncertainty: A case study for high-end server manufacturing. Comput. Ind. Eng. 2016, 93, 78–87. [Google Scholar] [CrossRef]
- Sreedevi, R.; Saranga, H. Uncertainty and supply chain risk: The moderating role of supply chain flexibility in risk mitigation. Int. J. Prod. Econ. 2017, 193, 332–342. [Google Scholar] [CrossRef]
- Yu, R.; Wu, Z.; Qu, S. Optimal Strategy of Supply Chain considering Interruption Insurance. Complexity 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Linqiao, Y.; Xuedong, L.; Fumin, D.; Zhaoxia, G. Risk Assessment of Supply Chain Based on Combination Weighting Method and Grey Theory. In Proceedings of the 2015 IEEE IEEM, Singapore, 6–9 December 2015; pp. 895–899. [Google Scholar]
- Shao, L.; Jin, S. Resilience assessment of the lithium supply chain in China under impact of new energy vehicles and supply interruption. J. Clean. Prod. 2020, 252, 119624. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, W.; Lu, J.; Wu, S.; Wang, X. Research on dynamic analysis and mitigation strategies of supply chains under different disruption risks. Sustainability 2021, 13, 2462. [Google Scholar] [CrossRef]
- Duan, W.; Ma, H.; Xu, D.S. Analysis of the impact of covid-19 on the coupling of the material flow and capital flow in a closed-loop supply chain. Adv. Prod. Eng. Manag. 2021, 16, 5–22. [Google Scholar] [CrossRef]
- Guo, H.; Wang, S.; Zhang, Y. Supply interruption supply chain network model with uncertain demand: An application of chance-constrained programming with fuzzy parameters. Discret. Dyn. Nat. Soc. 2021, 2021, 6686992. [Google Scholar] [CrossRef]
- Dudek-Burlikowska, M. Monitoring of the production processing in a metallurgical company using FMEA method. Arch. Metall. Mater. 2017, 62, 2089–2094. [Google Scholar] [CrossRef]
- Fattahi, R.; Khalilzadeh, M. Risk evaluation using a novel hybrid method based on FMEA, extended MULTIMOORA, and AHP methods under fuzzy environment. Saf. Sci. 2018, 102, 290–300. [Google Scholar] [CrossRef]
- Wan, C.; Yan, X.; Zhang, D.; Qu, Z.; Yang, Z. An advanced fuzzy Bayesian-based FMEA approach for assessing maritime supply chain risks. Transportation Research Part E: Logistics and Transportation Review LJMU Research Online An advanced fuzzy Bayesian-based FMEA approach for assessing maritime supply chain risks. Transp. Res. Part E-Logist. Transp. Rev. 2019, 125, 222–240. [Google Scholar] [CrossRef]
- Mangla, S.K.; Luthra, S.; Jakhar, S. Benchmarking the risk assessment in green supply chain using fuzzy approach to FMEA: Insights from an Indian case study. Benchmarking 2018, 25, 2660–2687. [Google Scholar] [CrossRef]
- Zhu, Q.; Golrizgashti, S.; Sarkis, J. Product deletion and supply chain repercussions: Risk management using FMEA. Benchmarking 2021, 28, 409–437. [Google Scholar] [CrossRef]
- Arabsheybani, A.; Paydar, M.M.; Safaei, A.S. An integrated fuzzy MOORA method and FMEA technique for sustainable supplier selection considering quantity discounts and supplier’s risk. J. Clean. Prod. 2018, 190, 577–591. [Google Scholar] [CrossRef]
- Rathore, R.; Thakkar, J.J.; Jha, J.K. Evaluation of risks in foodgrains supply chain using failure mode effect analysis and fuzzy VIKOR. Int. J. Qual. Reliab. Manag. 2021, 38, 551–580. [Google Scholar] [CrossRef]
- Liu, Y.; Kong, Z.; Zhang, Q. Failure modes and effects analysis (FMEA) for the security of the supply chain system of the gas station in China. Ecotoxicol. Environ. Saf. 2018, 164, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Altubaishe, B.; Clarke, J.; McWilliams, C.; Desai, S. Comparative Analysis of Risk Management Strategies for Additive Manufacturing Supply Chains. Am. J. Appl. Sci. 2019, 16, 273–282. [Google Scholar] [CrossRef]
- Curkovic, S.; Scannell, T.V.; Wagner, B.J.; Scannell, T.; Wagner, B. Using FMEA for Supply Chain Risk Management. Modern Manag. Sci. Eng. 2013, 1, 251–265. [Google Scholar]
- Kudláč, Š.; Štefancová, V.; Majerčák, J. Using the Saaty Method and the FMEA Method for Evaluation of Constraints in Logistics Chain. Procedia Eng. 2017, 187, 749–755. [Google Scholar] [CrossRef]
- Bogataj, D.; Bogataj, M. Measuring the supply chain risk and vulnerability in frequency space. Int. J. Prod. Econ. 2007, 108, 291–301. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Zhou, H.; Kong, Y. An Integrated Method of Supply Chains Vulnerability Assessment. Sci. Program. 2016, 2016, 2819238. [Google Scholar] [CrossRef]
- Ivanov, D.; Pavlov, A.; Dolgui, A.; Sokolov, B. Hybrid fuzzy-probabilistic approach to supply chain resilience assessment Hybrid fuzzy-probabilistic ap-proach to supply chain resilience assessment Hybrid fuzzy-probabilistic approach to supply chain resilience assessment. IEEE Trans. Eng. Manag. 2018, 65, 303–315. [Google Scholar] [CrossRef]
- Patidar, A.; Sharma, M.; Agrawal, R. Prioritizing drivers to creating traceability in the food supply chain. Procedia CIRP 2021, 98, 690–695. [Google Scholar] [CrossRef]
- Lin, K.P.; Tseng, M.L.; Pai, P.F. Sustainable supply chain management using approximate fuzzy DEMATEL method. Resour. Conserv. Recycl. 2018, 128, 134–142. [Google Scholar] [CrossRef]
- Sufiyan, M.; Haleem, A.; Khan, S.; Khan, M.I. Evaluating food supply chain performance using hybrid fuzzy MCDM technique. Sustain. Prod. Consum. 2019, 20, 40–57. [Google Scholar] [CrossRef]
- Magableh, G.M. Supply Chains and the COVID-19 Pandemic: A Comprehensive Framework. Eur. Manag. Rev. 2021, 18, 363–382. [Google Scholar] [CrossRef]
- Magableh, G.M.; Mistarihi, M.Z. Applications of MCDM approach (ANP-TOPSIS) to evaluate supply chain solutions in the context of COVID-19. Heliyon 2022, 8, e09062. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Bai, L.; Zhang, R. Prevention schemes for future fresh agricultural products (FAPs) supply chain: Mathematical model and experience of guaranteeing the supply of FAPs during the COVID-19 pandemic. J. Sci. Food Agric. 2021, 101, 6368–6383. [Google Scholar] [CrossRef]
- Lahmar, A.; Galasso, F.; Chabchoub, H.; Lamothe, J. Conceptual Framework of Supply Chain Vulnerability. In Proceedings of the 6th International Conference on Information Systems, Logistics and Supply Chain, Bordeaux, France, 1–4 June 2016. [Google Scholar]
- Wang, H.; Zhang, Y.M.; Yang, Z. A risk evaluation method to prioritize failure modes based on failure data and a combination of fuzzy sets theory and grey theory. Eng. Appl. Artif. Intell. 2019, 82, 216–225. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, H. Improvement on Judgement Matrix Based on Triangle Fuzzy Number. Fuzzy Syst. Math. 2003, 2, 011. [Google Scholar]
- Liu, L.; Liu, H.; Lin, Q. An improved FMEA using fuzzy evidential reasoning approach and grey theory. Fuzzy Syst. Math. 2011, 2, 72–80. [Google Scholar]
| Reference | Problem Addressed | Methodology |
|---|---|---|
| [1] | MRP nervousness | Order-up-to (OUT) policy and the proportional OUT policy (POUT). |
| [2] | Assessing internal nervousness in semiconductors SC planning system | Simulation-based analysis |
| [3] | Demand supply network nervousness | Experiential study |
| [4] | Evaluating the relationships between the different determinants of schedule nervousness | Statistical analysis |
| [5] | Studying the relationship between nervousness and the bullwhip effect | Vendor managed inventory (VMI) approach |
| [6] | Reducing demand nervousness | Mathematical modeling |
| [7] | System nervousness cost | Mathematical modeling |
| [8] | Exploring causes and effects of SCN in the MENA region | Delphi-based AHP |
| [9] | Identifying combinations of factors linked to GSCN | Delphi-FAHP |
| [10] | Examining setups added to production scheduling nervousness and costs | Wagner–Whitin algorithm |
| [11] | Scheduling stability and forecast errors | Simulation experiment |
| [12] | Reducing MRP system nervousness | Modified Wagner–Whitin algorithm |
| [13] | MRP nervousness | Simulation modeling |
| [14] | Investigating alternative strategies dealing with nervousness | Simulation experiments |
| [15] | Order nervousness | Simulation modeling |
| [16] | Lot-sizing rules and MRP nervousness | Simulation modeling |
| [17] | Nervousness in manufacturing firms | Simulation modeling |
| [18] | MRP nervousness | Simulation modeling |
| [19] | Cost-performance of the MRP system and forecast errors | Simulation modeling |
| [20] | Classifying nervousness-dampening procedures and their relative effectiveness | Static dampening procedure |
| [21] | Studying the schedule nervousness increased by uncertainty in the demand forecast | Empirical transfer function estimate (ETFE) |
| [22] | Reducing frequent revisions of the schedule, which leads to scheduling nervousness | Resource–task network (RTN) |
| [23] | Comparing the effectiveness of the planning policy for reducing demand uncertainty | Mixed-integer linear programming (MILP) |
| [24] | Quantifying nervousness in scheduling nervousness based on field observations | Mathematical modeling and analytical hierarchy process (AHP) |
| [25] | Nervousness in MRP systems under uncertainty | Simulation modeling |
| [26] | Quantify nervousness in stochastic inventory control demand | Rolling horizon planning procedure |
| [27] | Examining solutions for overcoming master production schedule nervousness | Simulation model |
| [28] | Exploring undesirable effects of nervousness master production scheduling | Simulation and mixed-integer programming model |
| [29] | Addressing the implications of the statistical findings compared to simulated MRP environments | Simulation model |
| [30] | Considering the economic effect of the production schedule caused by nervousness | Wagner–Whitin method |
| [31] | Stochastic lot sizing nervousness problem | Mixed-integer programming |
| [32] | Unveiling SCN and presenting a strategic framework for disruption management under a fuzzy environment | Fuzzy-DEMATEL |
| [33] | SCN analysis | Fuzzy-ELECTRE |
| [9] | Introduction of global supply chain nervousness (GSCN) | Delphi–fuzzy-AHP |
| Level I Elements | Level II Elements | Interruption Mode |
|---|---|---|
| Planning (P) | Demand (P1) | P1I1: Reduced satisfaction |
| P1I2: Excess inventory | ||
| Supply (P2) | P2I1: Increased disruptions | |
| P2I2: Governmental interventions | ||
| Risk (P3) | P3I1: Increased vulnerability | |
| P3I2: Raise of safety and security issues | ||
| Visibility (V) | Collaboration (V1) | V1I1: Less transparency |
| V1I2: Competitiveness among partners | ||
| Integration (V2) | V2I1: Lack of consistent decision-making | |
| V2I2: Lack of trust and willingness | ||
| Communication (V3) | V3I1: Shortages/lack of exchange information | |
| V3I2: Low employees confidence | ||
| Stability (S) | Policies (S1) | S1I1: Lack of prioritization |
| S1I2: Design change | ||
| Disaster recovery (S2) | S2I1: Mismatch between supply and demand | |
| S2I2: Long recovery time | ||
| Stable roles and regulations (S3) | S3I1: Difficulties of regulatory compliance | |
| S3I2: Changes in government policies | ||
| DSS (D) | Expertise (D1) | D1I1: Variations in skills |
| D1I2: Scarcity of special competencies | ||
| Powerful tools (D2) | D2I1: Selecting the right tool | |
| D2I2: Criteria, process mapping, and flow problems | ||
| Technology (D3) | D3I1: Technological constraints (implementation) | |
| D3I2: Digital transformation (SC transformation) | ||
| Flexibility (F) | Awareness (L1) | L1I1: Lack of trends and situational awareness |
| L1I2: Deficiencies in traceable and sustainable awareness | ||
| Resilience (L2) | L2I1: Lack of resistance, recovery, and redundancy systems (plans) | |
| L2I2: Unexpected changes (external changes) | ||
| Innovation (L3) | L3I1: Slow reaction to modern innovations | |
| L3I2: Adoption of significant changes |
| Semantic Element | Severity (Se) | Occurrence (Oc) | Detection (De) |
|---|---|---|---|
| EU | SC is not affected | Interruptions barely occur | Almost all interruptions are detected |
| VU | SC is slightly affected | Interruptions infrequently/rarely occur | The probability that an error is not recognized is low |
| UL | Some SC processes are slightly affected, but the flows work appropriately | Interruptions occur less | The probability that a fault will not be detected is quite low |
| NE | The flows fairly work, but some important processes are affected as long as there is no unsatisfied customer | Interruptions occur occasionally/intermittently | The error is not recognized infrequently |
| LK | The flows fairly work, but some important processes are seriously affected, and some customers are not satisfied | Interruptions occur often/in moderate amounts | Not being recognized is a common occurrence |
| VL | The process and flows have problems and have lost their basic functions | Interruptions occur recurrently | Most of the time, errors cannot be recognized |
| EL | SC operations completely lose their basic functions and endanger personal safety or violate laws | Interruptions are almost unpredictable | Errors are almost undetectable |
| Expert | EU | VU | UL | NE | LK | VL | EL | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.15 | (0, 1.1, 2.7) | (0.9, 2.5, 3.6) | (2.9, 4.6, 6.4) | (3.1, 5.6, 7.4) | (5.8, 7.5, 8.7) | (7.1, 8.9, 9.8) | (9.6, 10, 10) |
| 2 | 0.14 | (0, 1.3, 2.8) | (0.7, 2.4, 3.9) | (2.8, 4.5, 6.3) | (3.4, 5.8, 7.8) | (6.1, 7.1, 8.3) | (7.7, 8.8, 9.9) | (9.4, 10, 10) |
| 3 | 0.11 | (0, 1.2, 2.8) | (0.6, 2.3, 3.2) | (3.1, 4.5, 6.3) | (3.6, 5.9, 7.9) | (5.7, 7.8, 8.7) | (8.3, 8.9, 9.7) | (9.3, 10, 10) |
| 4 | 0.097 | (0, 1.4, 2.4) | (0.8, 2.6, 3.5) | (2.7, 4.7, 6.6) | (3.2, 6.2, 7.6) | (5.4, 7.9, 8.2) | (8.2, 8.7, 9.9) | (9.4, 10, 10) |
| 5 | 0.089 | (0, 1.5, 2.3) | (0.7, 2.7, 3.7) | (2.9, 4.2, 6.2) | (3.9, 6.3, 8.1) | (5.8, 8.1, 9.1) | (7.9, 9.1, 9.8) | (9.5, 10, 10) |
| 6 | 0.086 | (0, 1.7, 3.1) | (0.7, 2.8, 3.6) | (2.5, 5.2, 6.7) | (3.1, 5.7, 8.3) | (6.3, 6.9, 7.8) | (7.7, 9.3, 9.9) | (9.6, 10, 10) |
| 7 | 0.078 | (0, 2.1, 2.2) | (0.9, 2.5, 3.8) | (2.4, 4.1, 6.6) | (3.2, 5.4, 7.5) | (4.8, 7.6, 8.6) | (7.4, 8.6, 9.7) | (9.7, 10, 10) |
| 8 | 0.077 | (0, 1.3, 2.7) | (1.1, 3.1, 4.2) | (2.6, 4.5, 7.1) | (3.3, 5.3, 7.8) | (6.5, 7.8, 8.7) | (8.4, 9.1, 9.8) | (9.7, 10, 10) |
| 9 | 0.066 | (0, 1.2, 2.8) | (0.8, 2.4, 3.3) | (2.5, 4.7, 6.1) | (4.1, 5.6, 7.9) | (6.6, 7.7, 8.5) | (7.5, 8.7, 9.9) | (9.8, 10, 10) |
| 10 | 0.059 | (0, 1.1, 2.6) | (0.8, 2.3, 3.4) | (2.5, 4.1, 6.2) | (3.4, 5.8, 7.6) | (6.4, 7.9, 8.8) | (7.6, 8.8, 9.9) | (9.9, 10, 10) |
| 11 | 0.048 | (0, 1.4, 2.5) | (1.2, 2.1, 3.5) | (2.6, 4.6, 6.3) | (3.5, 5.7, 7.7) | (6.8, 7.6, 8.6) | (7.8, 8.9, 9.9) | (9.8, 10, 10) |
| Total/Average | 1.00 | (0, 1.4, 2.6) | (0.8, 2.5, 3.6) | (2.7, 4.5, 6.4) | (3.4, 5.8, 7.8) | (5.9, 7.6, 8.5) | (7.8, 8.9, 9.8) | (9.6, 10, 10) |
| Evaluation Rate | EU | VU | UL | NE | LK | VL | EL |
|---|---|---|---|---|---|---|---|
| Crisp value | 1.34 | 2.37 | 4.56 | 5.68 | 7.42 | 8.84 | 9.89 |
| Factor/Expert | Se | Avg. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| P1I1 | EL | NE | VL | LK | EL | VU | LK | VL | EL | NE | VL | 7.7 |
| 9.9 | 5.7 | 8.8 | 7.4 | 9.9 | 2.4 | 7.4 | 8.8 | 9.9 | 5.7 | 8.8 | ||
| P1I2 | VL | NE | LK | VL | VL | NE | UL | VL | UL | LK | NE | 6.9 |
| 8.8 | 5.7 | 7.4 | 8.8 | 8.8 | 5.7 | 4.6 | 8.8 | 4.6 | 7.4 | 5.7 | ||
| P2I1 | VL | EL | VL | LK | EL | LK | VL | VL | LK | EL | NE | 8.4 |
| 8.8 | 9.9 | 8.8 | 7.4 | 9.9 | 7.4 | 8.8 | 8.8 | 7.4 | 9.9 | 5.7 | ||
| P2I2 | EL | VL | LK | UL | VU | NE | VL | LK | VL | EL | VL | 7.4 |
| 9.9 | 8.8 | 7.4 | 4.6 | 2.4 | 5.7 | 8.8 | 7.4 | 8.8 | 9.9 | 7.4 | ||
| P3I1 | VL | EL | VL | UL | NE | NE | UL | LK | NE | UL | VL | 6.7 |
| 8.8 | 9.9 | 8.8 | 4.6 | 5.7 | 5.7 | 4.6 | 7.4 | 5.7 | 4.6 | 7.4 | ||
| P3I2 | NE | LK | LK | NE | EU | VU | UL | VU | VL | NE | UL | 5.1 |
| 5.7 | 7.4 | 7.4 | 5.7 | 1.3 | 2.4 | 4.6 | 2.4 | 8.8 | 5.7 | 4.6 | ||
| Level I Factors | Level II Factors | Failure Mode | Se Weight Ƚ1% | Oc Weight Ƚ2% | De Weight Ƚ3% | ||||
|---|---|---|---|---|---|---|---|---|---|
| P | 28% | P1 | 40% | P1I1 | 61% | 51% | 12% | 37% | 0.068 |
| P1I2 | 39% | 44% | 21% | 35% | 0.044 | ||||
| P2 | 38% | P2I1 | 68% | 53% | 11% | 36% | 0.072 | ||
| P2I2 | 32% | 54% | 8% | 38% | 0.034 | ||||
| P2 | 22% | P3I1 | 72% | 52% | 27% | 23% | 0.044 | ||
| P3I2 | 28% | 38% | 29% | 33% | 0.017 | ||||
| V | 24% | V1 | 54% | V1I1 | 66% | 65% | 7% | 28% | 0.086 |
| V1I2 | 34% | 43% | 31% | 26% | 0.044 | ||||
| V2 | 30% | V2I1 | 52% | 38% | 42% | 20% | 0.037 | ||
| V2I2 | 48% | 32% | 34% | 34% | 0.035 | ||||
| V3 | 16% | V3I1 | 49% | 56% | 9% | 35% | 0.019 | ||
| V3I2 | 51% | 39% | 8% | 53% | 0.020 | ||||
| S | 21% | S1 | 35% | S1I1 | 53% | 40% | 11% | 49% | 0.039 |
| S1I2 | 47% | 41% | 14% | 45% | 0.035 | ||||
| S2 | 33% | S2I1 | 78% | 56% | 26% | 18% | 0.054 | ||
| S2I2 | 22% | 34% | 21% | 45% | 0.015 | ||||
| S3 | 32% | S3I1 | 36% | 47% | 15% | 48% | 0.024 | ||
| S3I2 | 64% | 58% | 7% | 35% | 0.043 | ||||
| D | 17% | D1 | 40% | D1I1 | 57% | 39% | 35% | 26% | 0.039 |
| D1I2 | 43% | 29% | 18% | 53% | 0.029 | ||||
| D2 | 28% | D2I1 | 59% | 31% | 22% | 47% | 0.028 | ||
| D2I2 | 41% | 59% | 29% | 22% | 0.020 | ||||
| D3 | 32% | D3I1 | 33% | 42% | 23% | 35% | 0.018 | ||
| D3I2 | 67% | 57% | 27% | 16% | 0.036 | ||||
| F | 10% | L1 | 19% | L1I1 | 55% | 41% | 16% | 43% | 0.010 |
| L1I2 | 45% | 38% | 15% | 47% | 0.009 | ||||
| L2 | 46% | L2I1 | 51% | 58% | 22% | 20% | 0.023 | ||
| L2I2 | 49% | 62% | 10% | 28% | 0.023 | ||||
| L3 | 35% | L3I1 | 53% | 58% | 7% | 35% | 0.019 | ||
| L3I2 | 47% | 59% | 15% | 26% | 0.016 |
| Element | Ƚ1% | Ƚ2% | Ƚ3% | |||||
|---|---|---|---|---|---|---|---|---|
| P1I1 | 61% | 51% | 7.7 | 12% | 6.1 | 37% | 7.4 | 0.068 |
| P1I2 | 39% | 44% | 6.9 | 21% | 5.3 | 35% | 6.8 | 0.044 |
| P2I1 | 68% | 53% | 8.4 | 11% | 7.2 | 36% | 7.2 | 0.072 |
| P2I2 | 32% | 54% | 7.4 | 8% | 4.2 | 38% | 8.1 | 0.034 |
| P3I1 | 72% | 52% | 6.7 | 27% | 5.5 | 23% | 6.5 | 0.044 |
| P3I2 | 28% | 38% | 5.1 | 29% | 4.2 | 33% | 7.4 | 0.017 |
| V1I1 | 66% | 65% | 8.6 | 7% | 7.1 | 28% | 6.8 | 0.086 |
| V1I2 | 34% | 43% | 6.2 | 31% | 6.2 | 26% | 6.6 | 0.044 |
| V2I1 | 52% | 38% | 7.2 | 42% | 8.4 | 20% | 5.8 | 0.037 |
| V2I2 | 48% | 32% | 6.1 | 34% | 6.8 | 34% | 7.8 | 0.035 |
| V3I1 | 49% | 56% | 8.9 | 9% | 2.8 | 35% | 7.6 | 0.019 |
| V3I2 | 51% | 39% | 6.3 | 8% | 2.6 | 53% | 8.6 | 0.020 |
| S1I1 | 53% | 40% | 8.4 | 11% | 3.4 | 49% | 8.4 | 0.039 |
| S1I2 | 47% | 41% | 5.2 | 14% | 4.4 | 45% | 8.1 | 0.035 |
| S2I1 | 78% | 56% | 7.4 | 26% | 5.4 | 18% | 4.6 | 0.054 |
| S2I2 | 22% | 34% | 6.4 | 21% | 4.8 | 45% | 4.4 | 0.015 |
| S3I1 | 36% | 47% | 8.9 | 15% | 3.6 | 48% | 5.1 | 0.024 |
| S3I2 | 64% | 58% | 5.1 | 7% | 2.6 | 35% | 6.8 | 0.043 |
| D1I1 | 57% | 39% | 7.5 | 35% | 6.6 | 26% | 5.8 | 0.039 |
| D1I2 | 43% | 29% | 6.8 | 18% | 4.8 | 53% | 8.2 | 0.029 |
| D2I1 | 59% | 31% | 8.2 | 22% | 5.2 | 47% | 7.8 | 0.028 |
| D2I2 | 41% | 59% | 5.6 | 29% | 6.4 | 22% | 5.1 | 0.020 |
| D3I1 | 33% | 42% | 7.6 | 23% | 5.3 | 35% | 6.6 | 0.018 |
| D3I2 | 67% | 57% | 6.8 | 27% | 6.1 | 16% | 4.4 | 0.036 |
| L1I1 | 55% | 41% | 8.8 | 16% | 4.8 | 43% | 7.4 | 0.010 |
| L1I2 | 45% | 38% | 6.2 | 15% | 4.2 | 47% | 7.8 | 0.009 |
| L2I1 | 51% | 58% | 8.2 | 22% | 5.2 | 20% | 5.1 | 0.023 |
| L2I2 | 49% | 62% | 6.2 | 10% | 2.8 | 28% | 6.2 | 0.023 |
| L3I1 | 53% | 58% | 7.4 | 7% | 2.6 | 35% | 6.4 | 0.019 |
| L3I2 | 47% | 59% | 5.1 | 15% | 3.4 | 26% | 6.2 | 0.016 |
| Rank | Rank | Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| P1F1 | 0.068 | 0.0177 | 3 | P1 | 0.4 | 0.0286 | 2 | P | 0.28 | 0.0707 | 1 |
| P1F2 | 0.044 | 0.0109 | 6 | ||||||||
| P2F1 | 0.072 | 0.0198 | 2 | P2 | 0.38 | 0.0286 | 3 | ||||
| P2F2 | 0.034 | 0.0088 | 12 | ||||||||
| P3F1 | 0.044 | 0.01 | 9 | P3 | 0.22 | 0.0135 | 10 | ||||
| P3F2 | 0.017 | 0.0035 | 26 | ||||||||
| V1F1 | 0.086 | 0.023 | 1 | V1 | 0.54 | 0.0331 | 1 | V | 0.24 | 0.062 | 2 |
| V1F2 | 0.044 | 0.0101 | 8 | ||||||||
| V2F1 | 0.037 | 0.0105 | 7 | V2 | 0.3 | 0.0185 | 5 | ||||
| V2F2 | 0.035 | 0.008 | 15 | ||||||||
| V3F1 | 0.019 | 0.0052 | 21 | V3 | 0.16 | 0.0104 | 13 | ||||
| V3F2 | 0.02 | 0.0052 | 20 | ||||||||
| S1F1 | 0.039 | 0.0111 | 5 | S1 | 0.35 | 0.0192 | 4 | S | 0.21 | 0.049 | 3 |
| S1F2 | 0.035 | 0.0081 | 14 | ||||||||
| S2F1 | 0.054 | 0.0116 | 4 | S2 | 0.33 | 0.0144 | 8 | ||||
| S2F2 | 0.015 | 0.0028 | 29 | ||||||||
| S3F1 | 0.024 | 0.0063 | 18 | S3 | 0.32 | 0.0154 | 7 | ||||
| S3F2 | 0.043 | 0.0091 | 11 | ||||||||
| D1F1 | 0.039 | 0.0095 | 10 | D1 | 0.4 | 0.0171 | 6 | D | 0.17 | 0.0412 | 4 |
| D1F2 | 0.029 | 0.0076 | 16 | ||||||||
| D2F1 | 0.028 | 0.0072 | 17 | D2 | 0.28 | 0.0113 | 11 | ||||
| D2F2 | 0.02 | 0.0041 | 23 | ||||||||
| D3F1 | 0.018 | 0.0041 | 24 | D3 | 0.32 | 0.0128 | 9 | ||||
| D3F2 | 0.036 | 0.0087 | 13 | ||||||||
| L1F1 | 0.01 | 0.0029 | 28 | L1 | 0.19 | 0.005 | 15 | L | 0.1 | 0.0233 | 5 |
| L1F2 | 0.009 | 0.0021 | 30 | ||||||||
| L2F1 | 0.023 | 0.0057 | 19 | L2 | 0.46 | 0.0105 | 12 | ||||
| L2F2 | 0.023 | 0.0048 | 21 | ||||||||
| L3F1 | 0.019 | 0.0046 | 22 | L3 | 0.35 | 0.0078 | 14 | ||||
| L3F2 | 0.016 | 0.0032 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magableh, G.M.; Mumani, A.A.; Obaidat, S.F.; Mistarihi, M.Z. Fuzzy-FMEA Theory Approach for Prioritizing Supply Chain Nervousness Factors. Appl. Sci. 2024, 14, 4747. https://doi.org/10.3390/app14114747
Magableh GM, Mumani AA, Obaidat SF, Mistarihi MZ. Fuzzy-FMEA Theory Approach for Prioritizing Supply Chain Nervousness Factors. Applied Sciences. 2024; 14(11):4747. https://doi.org/10.3390/app14114747
Chicago/Turabian StyleMagableh, Ghazi M., Ahmad A. Mumani, Sinan F. Obaidat, and Mahmoud Z. Mistarihi. 2024. "Fuzzy-FMEA Theory Approach for Prioritizing Supply Chain Nervousness Factors" Applied Sciences 14, no. 11: 4747. https://doi.org/10.3390/app14114747
APA StyleMagableh, G. M., Mumani, A. A., Obaidat, S. F., & Mistarihi, M. Z. (2024). Fuzzy-FMEA Theory Approach for Prioritizing Supply Chain Nervousness Factors. Applied Sciences, 14(11), 4747. https://doi.org/10.3390/app14114747







