Featured Application
This study belongs to the field of intelligent non-destructive testing and proposes a CNN-based method for accurate quantification of defect characterized by ultrasonic diffraction method. The innovation in this study lies in several key aspects: (1) Development of a CNN architecture that automatically classifies A-scan signals in the scan path; (2) Connectivity region solving algorithm to accurately calculate the defect-region size according to the classification results; (3) An intelligent noise reduction framework that enables accurate identification of defective areas in complex noise situations.
Abstract
The purpose of this paper is to automate the interpretation of data during ultrasonic diffraction using a non-destructive testing (NDT) technique to accurately size defects for assisting in decision-making. A convolutional neural network (CNN) architecture was developed to automatically measure the length of the defect. Using the architecture, the population of A-scan signals in the scanning path was classified. The defect region was extracted and its size in the scanning direction was obtained by the connected region solution algorithm based on the classification results. The arrival time of diffraction waves was accurately identified by the intelligent denoising framework proposed, combined with Hilbert transform, and then the height of defects was calculated by corresponding geometric relations. The estimation results demonstrate that the measurement method can be considered as a useful technique for crack sizing in industrial structures, even in the case of complex noise.
1. Introduction
When ultrasonic waves propagating through a material encounter a discontinuity, reflected waves are generated at the surface of the discontinuity. The conventional ultrasonic non-destructive testing (NDT) techniques, pulse-echo testing techniques, exploit this reflex phenomenon to detect flaws inside materials, and have been widely used in the inspection of industrial structures and parts. Although pulse-echo techniques show excellent performance in defect characterization, such as location and quantification of defects, the particular directionality of echo, which can only be received by the transducer at a specific position, limits the defect detection rate. In the late 1970s, an innovative ultrasonic testing technique based on diffracted waves from acute ends of the crack was first invented by Silk at the Harwell Laboratory [1,2]. The advantage of diffracted waves is that they travel in any direction and can therefore be received by the transducers at many positions. Additionally, defect assessment for the ultrasonic diffraction method only depends on the arrival times of diffracted waves rather than their amplitudes [3]. Hence, the ultrasonic diffraction method is sensitive to defects, especially cracks [4,5]. The defect detection rate of the ultrasonic diffraction method is comparable to or exceeds that of radiographic detection [6].
In this technology, two angle probes, one for the transmitter and the other for the receiver, are separated by a certain distance, called the probe center separation (PCS), fixed with a scanning device and step-by-step moved along the direction to be detected. Figure 1a illustrates the ultrasonic diffraction inspection schematic at a cross-section of a weld, where the scanning direction is parallel to the center line of the weld, that is, perpendicular to the screen. At each position or cross-section, an A-scan signal is obtained. Each A-scan always has two typical waves, one that propagates along the surface of the weld (surface wave), and another that is reflected on the backwall (backwall wave), as shown in Figure 1b. When the ultrasonic beam encounters an internal defect, diffracted waves from top and bottom tip of the defect are generated between the surface wave and backwall wave. The presence of a defect can be established by the detection of diffracted waves. Measuring the arrival time of the waves, the depth and height of the defect can be calculated by corresponding geometric relation. All A-scans in the scanning path will constitute ultrasonic diffraction image where every pixel is the sample amplitude in the A-scan and a column of pixels corresponds to an A-scan, as shown in Figure 2. The length of the defect can be determined by identifying the region where the defect occurs in the ultrasonic diffraction image.
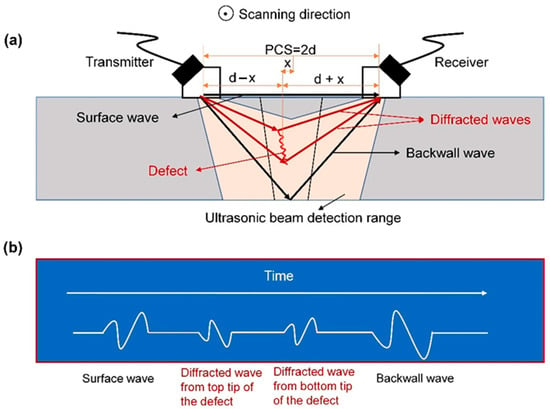
Figure 1.
Schematic diagram of the ultrasonic diffraction technique. (a) is the formation of diffracted waves generated by the defect and the two inherent waves generated by the interfaces of the tested specimen, respectively, called surface wave and backwall wave; (b) is the representation of the typical ultrasonic diffraction A-scan.
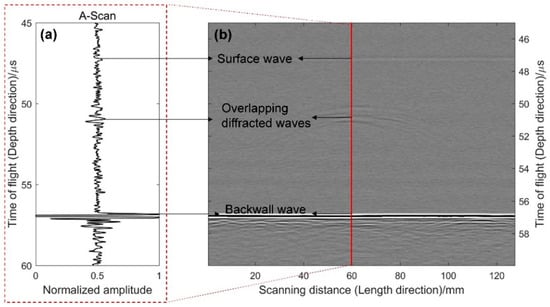
Figure 2.
An example of ultrasonic diffraction data actually acquired. (a) is the A-scan signal at position 60 of the scanning axis; (b) is the ultrasonic diffraction image (B-scan) generated by all A-scan signals in the scanning path.
The sizing accuracy for the ultrasonic diffraction method includes two aspects, length measurement and height measurement. The length measurement accuracy is related to accurate identification of the region where the defect occurs in the ultrasonic diffraction image. In the image, the defect usually appears as a flat parabola, as shown in Figure 3. This results from the large angle range of the ultrasonic beam in the ultrasonic diffraction method. At present, the standard measurement method is to manually fit two small parabolas with the two cambered ends of the defect, and the resulting distance between the vertex of the two parabolas is the length of the defect (Figure 3). However, the measurement results depend on and vary with the experience of the inspector. Different results are obtained even by the same inspector at different times. Additionally, the noise caused by the material grains and the measurement system may make cambered ends of the defect invisible. As shown in Figure 3, they can hardly be found. Therefore, the above method cannot be executed effectively. The height measurement accuracy is related to the arrival time measurements from the diffracted waves. However, the diffracted waves are likely to overlap and contain the noise, as exhibited in Figure 2a, which is very detrimental to the measurement. In addition, if large structures, such as pipelines and reactors, are inspected, the number of obtained data for interpretation will be considerable. Therefore, developing an effective and automatic data analysis method is imperative to enhancing measurement accuracy and efficiency.
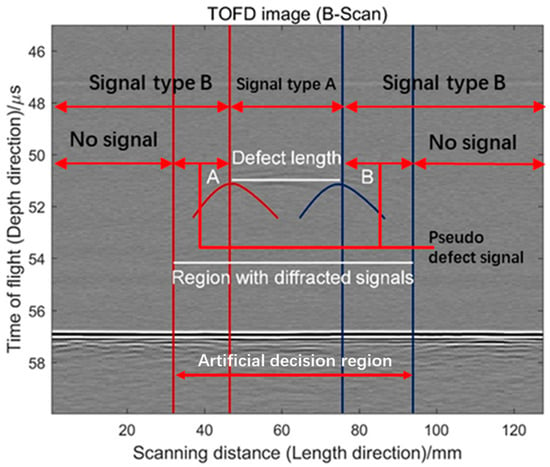
Figure 3.
Schematic diagram of the conventional method to determine the length of defect in the ultrasonic diffraction image.
In this context, Bolland et al. first proved that when a crack appears in a structure, a group of parabolas with a principal axis is present in the ultrasonic diffraction image [7]. Thus, the crack in the structure can be located by examining these parabolas and determining the position of their summit points. Thouraya used a mathematical morphology approach, the watershed technique, to extract relevant pixels corresponding to the presence of a defect, and subsequently adopted a skeletonization technique to characterize the defect [8]. Some works employed different means and then used the Hough transform (HT) to automatically detect parabolic shapes for locating crack tips in B-scan images [9,10]. To save calculation and processing time, matched filtering was used to detect parabolic forms when the shapes in ultrasonic diffraction images are intact [11].
In terms of A-scan signal processing, various signal processing techniques have been employed for estimating the parameters of diffracted echoes, such as the methods based on cross-correlation (CC) and its enhanced forms [12,13]. The CC method considers a white Gaussian noise presence in the acquired signal and needs a reference signal, which will affect the estimation accuracy. Demirli developed a model-based method [14,15] to overcome the limitations and evaluate the parameters of ultrasonic signals by the Levenberg–Marquart or Gauss–Newton algorithms that can solve the non-linear optimization problem. However, these methods cannot ensure the convergence of an estimation problem due to dependence on the initial guesses. So, they can have trouble processing complex signals. Ruiz-Reyes et al. conquered this difficulty by applying an MP approach [16]. In the approach, a signal is estimated through matching it to a minimum number of elementary functions selected from a large dictionary. Further, Nabil estimated the ultrasonic diffraction signals by the envelope extraction using Hilbert transform (HT) and subsequently the envelope estimation using a matching pursuit (MP) approach that is optimized by differential evolution to reach fast and accurate results [17]. Zelin Zhi et al. proposed a Faster R-CNN model for TOFD signal processing that can classify and localize various defect signals, providing a localization accuracy of 92.43 ± 1.25% [18]. Duje Medak et al. proposed an ultrasound B-scan (S-scan) imaging technique that utilizes machine vision, which achieved a detection accuracy of 91.3% [19].
Although considerable successes have been achieved in ultrasonic diffraction data analysis by various techniques, they can only estimate the perfect ultrasonic data without noise or with simple noise (white Gaussian noise). The real data, however, contain multifarious complicated noises caused by grain or surface roughness of the structure to be detected. These methods can run into difficulty in complicated situations. In addition, systematic studies on both the length and height estimation of defects in the ultrasonic diffraction method have not been reported.
In this paper, a deep learning-based ultrasonic diffraction data analysis method is proposed to overcome the above difficulties. It can automate the interpretation of ultrasonic data to accurately size defects for assisting in decision-making. Firstly, a convolutional neural network (CNN) architecture is developed to automatically measure the length of the defect. Using the architecture, the population of A-scan signals in the scanning path is classified. The defect region is extracted and its size in the scanning direction is obtained by the connected region solution algorithm based on the classification results. Secondly, in determining the height of defects (size in the direction of ultrasonic propagation), the arrival time of diffraction waves is accurately identified by the intelligent denoising framework previously proposed, combined with Hilbert transform, and then the height of defects is calculated by corresponding geometric relations. Two welded joints, with five embedded artificial cracks in the middle and at the root, respectively, were prepared to verify the effectiveness of the method. The estimation results demonstrate that the measurement method can be considered as a useful technique for crack sizing in industrial structures, even in the case of complex noise.
2. Ultrasonic Diffraction Theory Background
Ultrasonic diffraction method is a well-established ultrasonic NDT technique that exhibits high defect detection rate and sizing accuracy. This technique is based on using the diffracted waves from the defect edges to detect defects. Since diffracted waves travel in any direction, its detection probability barely relies on the positions of the transducers and is not affected by orientations of defects that can be unfavorable for ultrasonic pulse-echo methods. Hence, it has been widely used in the inspection of industrial structures and parts.
2.1. Flight Diffraction Model
The ultrasonic diffraction system contains two angle probes in a transmitter–receiver configuration, as shown in Figure 1a. They are separated PCS distance by a rigid bar on the scanning device. The PCS is determined by the following equation:
T is the thickness of the specimen to be detected and θ is the main beam angle of the probe. When an ultrasonic pulse is generated by the transmitter, two typical waves will generally be received by the receiver. One is the surface wave that propagates along the surface of the weld, and the other is backwall wave that is reflected on the backwall. When a crack is present in the specimen under test, two diffracted waves from the top and bottom tip of the defect appear between the surface wave and backwall wave, as shown in Figure 1b. The presence of defect can be established by the detection of diffracted waves. Measuring the arrival time of the waves, the depth and height of the defect can be calculated by corresponding geometric relation.
The arrival time of diffracted waves is calculated by Equation (2):
where is the depth at which the diffracted wave is generated, is half of PCS, c is the ultrasound velocity, and is the distance of the defect away from the middle of the probes (see Figure 1a). In actual detection, can be ignored. So, Equation (2) is reduced to this form.
Further, the depth of the diffracted wave is derived from Equation (3).
Therefore, the height of the defect is given by Equation (5).
and are, respectively, the arrival time of diffracted waves from the top and bottom tip of the defect, which can be measured using an A-scan signal. From Equations (4) and (5), it is apparent that whether the arrival time can be accurately measured directly determines the measurement accuracy of defect height and depth.
2.2. Image Generation
As mentioned in Section 1, when scanner device with the probes is moved along the direction to be detected, an ultrasonic diffraction image (B-scan) can be synthesized by all A-scans in the scanning path. In the image, every pixel is the sample amplitude in the A-scan and a column of pixels corresponds to an A-scan, as shown in Figure 3. Low amplitudes are shown as black pixels, high amplitudes as white pixels, and zero amplitude as gray pixels [20]. The A-scan at each probe position always contains a surface wave and a backwall wave. The thickness of the specimen and PCS are constant, which makes the arrival time of these two waves in each A-scan the same. Thus, two gray horizontal bands appear at the top and bottom in the image. They, respectively, represent the surface wave and backwall wave.
The presence of the defect must lie in the region between these two bands, according to ultrasonic time of flight. The defect generally appears as a flat parabola in this region (see Figure 3) due to the large beam range of the ultrasonic diffraction probe. In the scanning process, when the probes are close to but do not begin to overlap with the defect, part of the ultrasound wave with large diffusion angle has actually encountered the defect and the corresponding diffracted wave is received by the receiver, which will cause arc-shaped features at both ends of the defect in the ultrasonic diffraction image. Therefore, the length of the defect cannot be measured simply by the presence of a region with diffraction signals. Obviously, this amplifies the length of the defect to a great extent. Considering this, a standard measurement method is adopted. It manually fits two small parabolas with the two cambered ends of the defect, and the resulting distance ( in Figure 3) between the vertex of the two parabolas is the length of the defect.
However, the measurement results depend on and vary with the experience of the inspector due to the subjective nature of this operation. The different results are obtained even by the same inspector at different times, as in the manually discriminated area in Figure 3, where a defect with an actual length of 30 mm may have a diffracted wave area radiating up to 60 mm. In the region encompassed by diffracted waves, the reliability of manual determination is limited, and the application of machine learning can enhance the consistency of determination outcomes through the comprehensive extraction and recognition of defective signals. In addition, the noise caused by the material grains and the measurement system may make cambered ends of the defect invisible. As shown in Figure 3, they can hardly be found. Therefore, the above method cannot be executed effectively [21].
3. Deep Learning-Based Crack Sizing Method
3.1. Length Measurement Architecture
The efficiency of the conventional manual measurement method varies with the experience of the inspector. Additionally, the noise caused by the material grains and the measurement system can further aggravate this. Therefore, developing an effective and automatic data analysis method is imperative to enhancing the measurement accuracy and efficiency and mitigate the interpretation burden of operators.
According to the analysis in Section 2.2, the core problem of accurately measuring the defect length is how to effectively determine the left and right ends of the defect in ultrasonic diffraction images or the scanning path. Hence, an automatic measurement strategy was conceived. The population of A-scan signals in the scanning path is classified by the corresponding intelligent algorithm. The TOFD dataset is classified by performing complete feature extraction and defect signal recognition. This technique precisely detects defects area on the B-scan and the area size correlates directly with the defect length. The defect region is extracted and its size in the scanning direction is obtained by the connected region solution algorithm based on the classification results.
Some artificial intelligence techniques, especially neural networks, have widely been used to automatically classify flaws in ultrasonic testing during the last several decades [22]. A. Masnata employed a three-layered neural network to automatically classify cracks, porosity, and slag defects based on features extracted from ultrasonic pulse echoes using Fisher discriminant analysis [23]. Later, a large number of recognition networks and feature extraction techniques for ultrasonic signal were developed and utilized to achieve better recognition accuracy [24,25,26]. Although good performance has been achieved, the complexity of feature extraction by signal processing techniques and the sensitivity of the selected feature to operating conditions limit its application in practice. As computing power increases incredibly and has the ability to process large quantities of dimensional data, a fully connected deep neural network (DNN) was developed to classify various defects by original ultrasonic signals without any feature extraction [27]. Since the fully connected DNN shows relatively poor performance at low signal-to-noise ratio, a robust DNN framework with convolution layers, called a convolutional neural network (CNN), was successfully adopted to identify flaws under noisy conditions [28] and to classify the delamination and void defects in CFRP specimens [29]. The CNN was firstly proposed by LeCun [30], which later provided amazing performance in the fields of speech recognition and computer vision [31,32].
So, in this paper, a CNN framework is designed to automatically classify the ultrasonic diffraction A-scans for measuring the length of the defect, as illustrated in Figure 4. The deep learning architecture is composed of two convolutional layers followed by a pooling layer behind each, two fully connected (FC) layers, and one output layer. Convolutional layers combined with pooling layers are used for feature extraction while FC layers are used for classification.
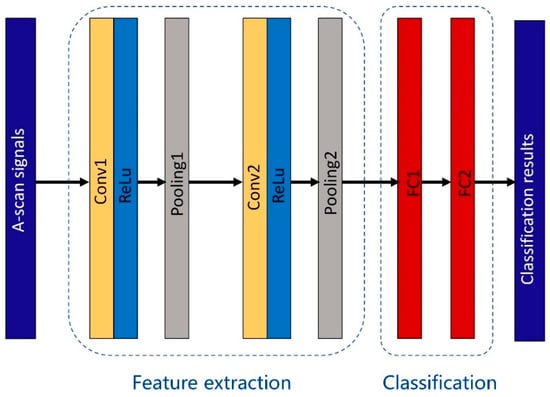
Figure 4.
The designed CNN framework for automatically classifying the ultrasonic diffraction A-scans.
Sixteen 8 × 1 kernel filters are applied to the input signal with 896 samples in the first convolutional layer, followed by non-linear operation with an activation function to generate sixteen 445 × 1 feature maps. Here, the activation function, , is adopted. Subsequently, the feature maps are down-sampled to obtain sixteen 223 × 1 feature maps by the 2 × 1 kernel filters in the first pooling layer. In the second convolutional layer and the second pooling layer, similar convolutional and pooling options are conducted on the new feature maps to generate thirty-two 56 × 1 feature maps. In this multiple-layer stacking manner, the features of signals can be extracted, non-linearly combined, hierarchically compressed, and assembled into high-level features by the proposed architecture. This is the advantage of the convolution layer, unlike the FC layer, not connected with each node in the adjacent layer, but with the local regions of interest through convolutional kernels. Therefore, the convolution layer is very competent for feature extraction.
The final feature maps are reshaped and then passed to the first FC layer with a dropout probability of 0.25 to save computing time and avoid overfitting. After that, through the second FC layer with 200 nodes and the output layer with 2 nodes, the classification results are obtained. The number of nodes in the FC layer was determined through many trials and the number with good performance was selected. The detailed configuration parameters and operation results of the architecture are shown in Table 1.

Table 1.
Parameters of the designed CNN framework.
The regularized cost function, MSEreg, is applied during the training process, defined as follows:
where denotes the weight and γ is a super-parameter that can be adjusted manually. MSE is mean square error, defined as follows:
where is the target value and is the predicted value based on input data by neural network.
3.2. Height Measurement Architecture
It is observed in Equation (5) that the height measurement accuracy is related to the arrival time measurements from the diffracted waves. However, the diffracted waves are likely to overlap and contain noise, as shown in Figure 2a, which is very detrimental to the measurement. Current signal processing technologies for measuring the parameters of ultrasonic diffraction waves have shortcomings in one way or another, as described in Section 1. Therefore, these sophisticated methods need to be further developed to accurately estimate ultrasonic diffraction signals. In this study, the arrival time of diffraction waves is precisely identified by the intelligent denoising framework previously proposed [29,30], combined with Hilbert transform.
The intelligent denoising framework can achieve signal reconstruction from noisy ultrasonic data by combining basic statistical analysis with a series of machine learning algorithms. The proposed framework analyzes abundant information from numerous raw signals to distinguish the desired signal from complicated noises, avoiding the limitation of information provided by only a single signal. Its complete workflow is shown in Figure 5. Firstly, the database of the ultrasonic signals taken from test specimens is set up. The database is later delivered to our self-developed machine learning algorithms. The algorithms start with similarity analysis in signals, especially for the database with various complicated noises, using a k-means algorithm. These highly similar signals or the same class of signals are subsequently passed on to the core part, the denoising autoencoder, for training it. With the trained autoencoder, we will move on to the denoising step where the noise can be automatically reduced according to the rule learned by the autoencoder. The detailed steps of removing noise were shown in the previous work [33,34]. It has been successfully applied to various complicated noises in practice, e.g., grain noises and surface roughness noise, which are almost the same as the desired signal.
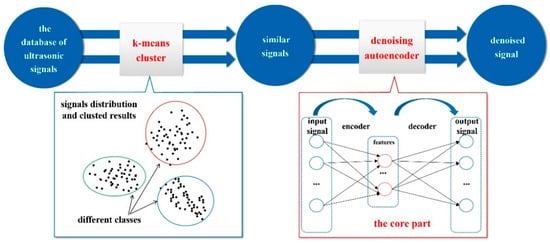
Figure 5.
The intelligent denoising framework.
So, the original ultrasonic diffraction signals acquired are denoised through the above framework. The envelopes of the clean signals are extracted by Hilbert transform. In this way, the arrival time of diffracted waves can successfully be determined in the envelope.
4. Data Acquisition
4.1. Experimental Setup
To validate the proposed method, some testing experiments were conducted. Two flat plate welded joints (600 mm× 400 mm× 90 mm) were prepared by joining flat plates made of 20# carbon steel using argon arc welding in combination with arc welding. Five artificial cracks were embedded in the middle of one (called Joint1) and at the root of the other (called Joint2), respectively, which were evenly spaced in the weld. Table 2 gives details of the defects. In the middle of Joint1, five defects of the same size were set. To increase the difficulty for the proposed method, five defects of varying size were set at the root of Joint2, as is shown in Figure 6. As these defects are far from the probe, the diffracted signal will become weak, which may make it more difficult for the measurement method to identify defects. Meanwhile, its measurement performance can be checked under varying conditions.

Table 2.
Detailed parameters for defects embedded in welded joints.
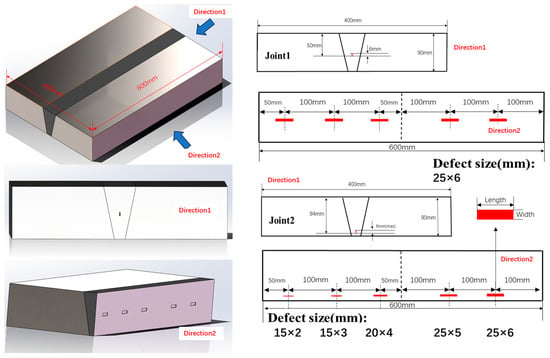
Figure 6.
Drawings of joints and simulation defects.
The ultrasonic diffraction equipment in the experiments contains an ultrasonic transmitter–receiver module, a computer system controlling the ultrasonic module through the matched software, two probes (transmitter and receiver) in pitch–catch configuration, and a scanner device for fixing the probes. The computer sends corresponding instructions to the ultrasonic module to generate ultrasonic pulses in the transmitter and receive the response pulses in the receiver. The received pulses are digitized and stored on the computer. The scanner device is used to carry the two probes to scan the weld and record the signal at each position. Here, the step of the scanner is set to 1 mm, meaning that one signal is recorded every 1 mm. The used ultrasonic probes have a beam angle of 60° and central frequency of 5 MHz, and the sampling frequency is 100 MHz. As the defects exist in the lower part of the weld, the distance between two probes is set to 208 mm according to Equation (1), i.e., PCS = 252 mm. Figure 7 shows the experimental setup.
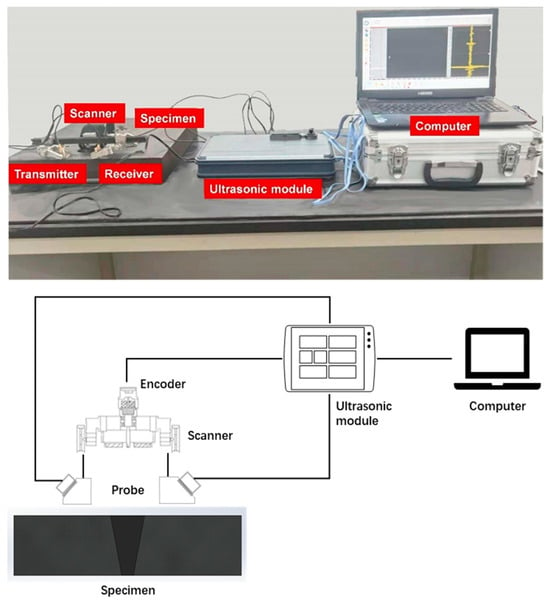
Figure 7.
The ultrasonic diffraction equipment in experiments.
Figure 8 shows an example of ultrasonic diffraction images obtained from the two welded joints. The image of Joint1 obviously demonstrates the five cracks in its middle while careful observation needs to be taken to see the cracks in the image of Joint2. The diffracted waves from the cracks at the root of Joint2 travel for so long that they suffer from large attenuation. Therefore, weak defect signals appear in its image, which increases the difficulty of defect evaluation, especially by manual means.
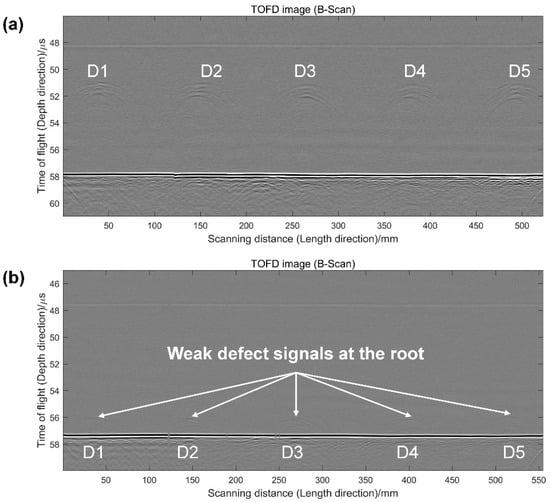
Figure 8.
Ultrasonic diffraction images obtained from the two welded joints: (a) image of Joint1; (b) image of Joint2.
4.2. Ultrasonic Dataset
Since the ultrasonic equipment for inspection and the specimens to be tested with realistic flaws are generally awfully expensive, acquiring the ultrasonic data is a costly process. Additionally, due to the small proportion of defect region in the tested specimen, a large number of defect signals are difficult to collect. This shortcoming can be remedied by generating or simulating signals to develop a deep learning model. Though these methods may be useful for training models, estimation should be conducted on an actual dataset to guarantee the credibility of the results obtained. So, in acquiring data, we scanned the weld back and forth in both directions and repeated twice to obtain more defect data. The original database acquired contains a total of 4400 signals, including 900 defect signals and 3500 non-defect signals.
However, notice that the allocation of classes within the database is unbalanced, i.e., the non-defect class has significantly more signals than the defect class. The number of non-defect class signals was reduced to that of the defect class to deal with this imbalance by taking random samples from the non-defect class. Meanwhile, the reduced database was divided into training and testing datasets where 90% of each class is reserved for training and the remaining 10% for testing. The reason for this is that the trained model can present good performance on the seen examples while possibly failing to estimate the unseen examples. Hence, common practice is that the data are divided into training and testing datasets to investigate the practical performance of the model. The model is trained on training datasets and its performance is evaluated on testing datasets.
All the signals were normalized before feeding to the neural network with Equation (8). This normalization was used to obtain all the signals on the same scale, which can avoid activation function saturation [35].
5. Results and Discussion
5.1. Length Measurement Results and Discussion
In this work, the designed CNN model was achieved in TENSORFLOW (Version 1.12.0, Google, Amphitheatre Pkwy, Mountain View, CA, USA) on a desktop with an intel core-i5 9400 CPU, 16 GB of RAM, and a 256 GB SSD. The deep learning model was trained for 10,000 iterations. The initial learning rate was set to 0.01, which decays by 0.001 every 100 iterations to avoid gradient disappearance caused by an excessive learning rate. The batch size was 100 and the training error was recorded every 100 iterations; the designed network achieved good convergence at 8000 iterations.
Performance of the CNN model trained was evaluated on the testing dataset. The accuracy achieved on the testing dataset for the network was 99.23%, while the performance on the training dataset was also estimated and the achieved result was 99.68%. It was observed that the accuracy on the training dataset was slightly higher than that on the testing dataset. This is methodologically normal, since, for a network it, is better at identifying the seen samples. Anyway, the accuracy of the model is considerable.
However, even an accurate A-scan identification is of little significance without the context from its surrounding area, since the sizing, estimation and decision-making of a defect is not only dependent on a single A-scan but the A-scans in a certain abnormal area. Figure 9, further, shows that the classification results of two tested specimens vary with the spatial position of the probe, where 0 denotes non-defect A-scan and 1 denotes defect A-scan. It can clearly be seen that the defect areas in both Joint1 and Joint2 have been well identified. It is worth noting that recognition results at the edge of some defects float back and forth between 0 and 1, e.g., part of the defects (D4 and D5) in Joint1, and almost all defects (D2, D3, D4, and D5) in Joint2. This may result from a low signal-to-noise ratio in the ultrasonic data, making the boundary between classes blurred. So, the features extracted from the signals at the edge of the defect by the proposed CNN can be between that of non-defect and defect, which leads to difficult decision-making for the CNN. This instability at the edge of the defect is exacerbated in Joint2, further confirming this suspicion. From the B-scan image in Figure 8b, the defect signal is so weak that it is barely distinguishable to the naked eye. Despite the slight instability, the CNN accurately identified the defect areas.
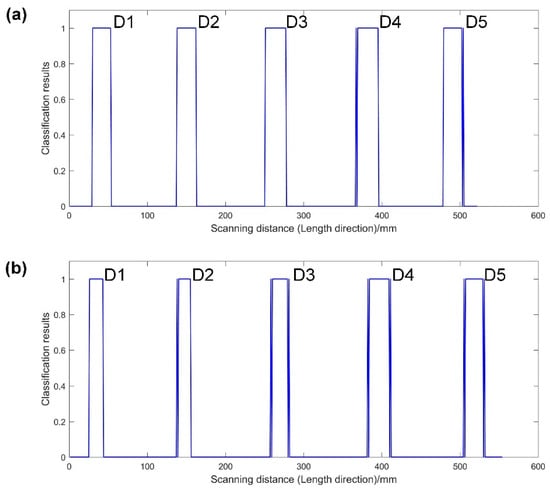
Figure 9.
The classification results of two tested specimens in the space of the probe positions: (a) the results of Joint1; (b) the results of Joint2.
Length of the defect can be automatically measured by the connected region solution algorithm based on the classification results corresponding to the probe positions. This algorithm can extract the non-zero regions of a binarized sequence. The classification results shown in Figure 9 constitute the sequence. Nonetheless, the instability mentioned above will affect the automatic process, which can make the algorithm mistake a small floating area at the edge of the defect for a small flaw. This drawback can be solved by setting a minimum size of the region. When the size of the connected region is greater than this size, it is extracted. Since the instability is random, the minimum size can be set to 1. Hence, the length of defect is obtained automatically, as listed in Table 3.

Table 3.
Comparisons of the lengths measured by proposed method and designed values.
To evaluate the measurement performance of this deep learning model, the length values measured by it were compared with the designed values. Figure 10 shows the comparison results, where (a) and (b) are, respectively, the comparisons of Joint1 and Joint2, and (c) and (d) are, respectively, the deviations from the designed values corresponding to Joint1 and Joint2. It can be seen from Figure 10a,b that the measured values of defects in the two tested joints are both close to the designed values. The deviation of Joint1 is between −0.040 and +0.080, and the mean deviation is ±0.074. The deviation of Joint2 is between −0.133 and +0.042, and the mean deviation is ±0.056. By comparing the deviations of Joint2 to Joint1, the model consistently performs well, despite weak signals and complex defects in Joint2.
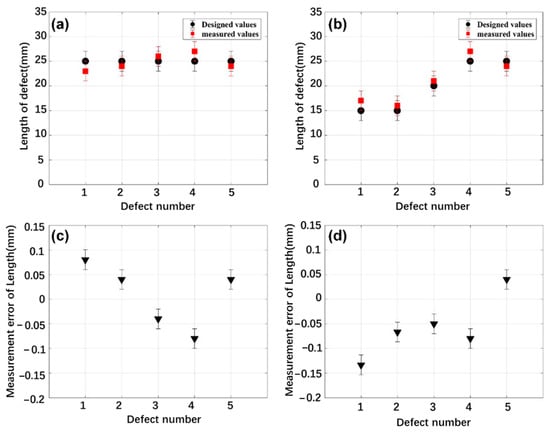
Figure 10.
Comparisons of the lengths measured by the proposed method and the designed values: (a) comparison of Joint1; (b) comparison of Joint2; (c) deviations from the designed values of Joint1; (d) deviations from the designed values of Joint2.
5.2. Height Measurement Results and Discussion
The height measurement accuracy is related to the arrival time measurements from the diffracted waves. However, the diffracted waves are likely to overlap and contain noise, which is very detrimental to the measurement. Current signal processing technologies for measuring the parameters of ultrasonic diffraction waves have shortcomings in one way or another, as described in Section 1. Therefore, these sophisticated methods need to be further developed to accurately estimate ultrasonic diffraction signals. The original A-scan signals acquired are firstly denoised through the denoised framework proposed in Section 3.2 to avoid the adverse effect of noise on the signal. The envelops of the clean signals are further extracted by Hilbert transform. In this way, the arrival time of diffracted waves can successfully be determined in the envelope.
Figure 11 displays two examples of processed results from Joint1 and Joint2, respectively, where (a) is the processed result of defect D3 in Joint1 and (b) is the processed result of defect D1 in Joint2. Here, surface and backwall waves are cut off to highlight the region of interest. As can be seen from Figure 11a, although the diffracted signals from the top and bottom tips of the defect are strong enough before denoising, they are seriously disturbed by noise, so that the top and bottom tips of the defects cannot be determined in the envelope obtained by Hilbert transform. Moreover, they are intertwined. After denoising by the proposed method, the two tips are extracted successfully in the new envelope. For the original signal of defect D1 in Joint2, in addition to the above problems, it encounters the risk of being drowned out by noise due to its weakness. However, the method is still competent for tip recognition in this case, as shown in Figure 11b.
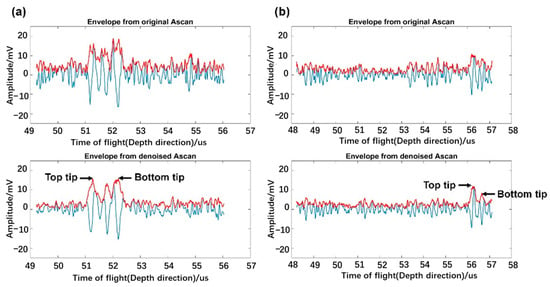
Figure 11.
Two examples of the envelopes extracted by the proposed method: (a) the processed results from defect D3 in Joint1; (b) the processed results from defect D1 in Joint2.
For defect D3 in Joint1, the arrival time of the top and bottom tips is, respectively, estimated to be 51.26 µs and 52.15 µs using the method. For defect D1 in Joint2, the arrival time is estimated to be 56.26 µs and 56.66 µs. According to Equation (5), the heights of the two defects are computed to be 6.4 mm and 1.8 mm, respectively. Similarly, heights of other defects can be obtained through the above estimation process. Table 4 displays the estimation results of the proposed method.

Table 4.
The comparisons of the heights measured by the proposed method and the designed values.
To highlight its measurement performance, the estimated values were compared with the designed values. Figure 12 shows the comparison results, where (a) and (b) are, respectively, the comparisons of Joint1 and Joint2, and (c) and (d) are, respectively, the deviations from the designed values corresponding to Joint1 and Joint2. It can be observed from Figure 12a,b that the measured values of defects in the two joints are also both close to the designed values. The deviation of Joint1 is between −0.083 and +0.033, and the mean deviation is ±0.050. The deviation of Joint2 is between −0.067 and +0.010, and the mean deviation is ±0.073. Therefore, it can be concluded that the method is suitable for the estimation of defect height using the ultrasonic diffraction method.
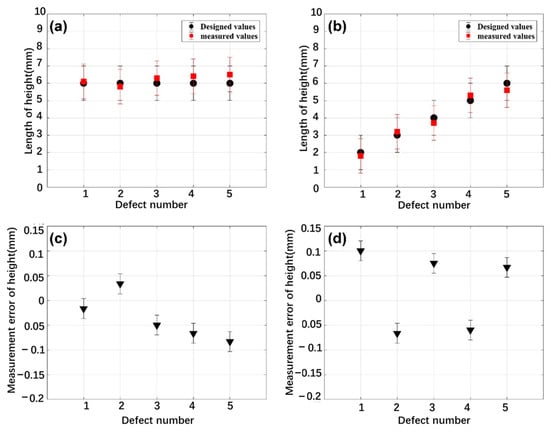
Figure 12.
Comparisons of the heights measured by the proposed method and the designed values: (a) comparison of Joint1; (b) comparison of Joint2; (c) deviations from the designed values of Joint1; (d) deviations from the designed values of Joint2.
6. Conclusions
This paper presents a deep learning-based ultrasonic diffraction data analysis method for the automatic interpretation of ultrasonic data, with the objective of accurately measuring defects. A series of defects in weld joints of varying depths, heights, and lengths were created to test the efficacy of the proposed method. In terms of length measurement, the lengths of defects can be automatically determined by the designed convolutional neural network (CNN) architecture in conjunction with a connected-region-based method. The mean measurement accuracy is ±0.065. In the case of height measurement, the arrival time of the diffracted waves can be accurately estimated by the proposed intelligent denoising architecture in conjunction with the Hilbert transform. Furthermore, the height of the defects can be calculated by means of the corresponding geometric relation. The mean measurement accuracy can be estimated to be ±0.061. Consequently, the proposed method can be employed for the automated analysis of ultrasonic data and the precise estimation of the ultrasonic diffraction technique in practice, even in the presence of noise and a weak signal.
The study presented in this paper demonstrates that the proposed convolutional neural network (CNN) model is capable of accurately identifying the boundary of the tip diffraction signal and noise reduction through signal classification. This enables the realization of high-precision quantification of defects under noise interference conditions. In other instances of common weld seam defects, such as porosity clusters and imperfections, the characteristics of defect signals undergo significant alterations. Consequently, the generalizability of the proposed method and the capacity to identify defect types based on comprehensive defect signal feature extraction and quantification require further in-depth investigation.
Author Contributions
Conceptualization, W.X.; methodology, W.X. and J.Z.; investigation, Q.F., J.C. and L.J.; writing—original draft preparation, Q.F. and J.C.; writing—review and editing, J.Z. and J.Y.; supervision, H.D.; project administration, J.Y. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Project of China, grant number 2018YFB1106100.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to thank Xiaohong Li for her assistance in the research of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Silk, M.G. Interpretation of TOFD data in the light of ASME XI and similar rules. Brit. J. Non Destr. Test. 1989, 31, 242–251. [Google Scholar]
- Silk, M.G.; Lidington, B.H. Defect sizing using an ultrasonic time delay approach. Brit. J. Non Destr. Test. 1975, 17, 33–36. [Google Scholar]
- Jin, S.; Wang, X.; Wang, Z.; Luo, Z. Defect detection of spherical heads by time-of-flight diffraction. Appl. Acoust. 2024, 216, 109787. [Google Scholar] [CrossRef]
- Silk, M.G.; Lidington, B.H. The potential of scattered or diffracted ultrasound in the determination of crack depth. Non Destr. Test. 1975, 8, 146–151. [Google Scholar] [CrossRef]
- Han, Q.; Wang, P.; Zheng, H. Modified ultrasonic time-of-flight diffraction testing with Barker code excitation for sizing inclined crack. Appl. Acoust. 2018, 140, 153–159. [Google Scholar] [CrossRef]
- Carvalho, A.; Rebello, J.; Souza, M.; Sagrilo, L.; Soares, S. Reliability of non-destructive test techniques in the inspection of pipelines used in the oil industry. Int. J. Press. Vessel. Pip. 2008, 85, 745–751. [Google Scholar] [CrossRef]
- Bolland, P.; Voon, L.L.; Gremillet, B.; Pillet, L.; Diou, A.; Gorria, P. The application of Hough transform on ultrasonic images for the detection and characterization of defects in non-destructive inspection. In Proceedings of the Third International Conference on Signal Processing (ICSP’96), Beijing, China, 18 October 1996; Volume 391, pp. 393–396. [Google Scholar]
- Merazi-Meksen, T.; Boudraa, M.; Boudraa, B. Mathematical morphology for TOFD image analysis and automatic crack detection. Ultrasonics 2014, 54, 1642–1648. [Google Scholar] [CrossRef] [PubMed]
- Bolland, P.; Voon, L.L.; Gorria, P.; Gremillet, B.; Pillet, L. Gradient-based Hough transform for the detection and characterization of defects during non-destructive inspection. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Tokyo, Japan, 20 June 1997; p. 33. [Google Scholar]
- Maalmi, K.; Benslimane, R.; Voon, L.L.Y.; Eric, F. Towards automatic analysis of ultrasonic time-of-flight diffraction data using genetic-based Inverse Hough Transform. Insight 2009, 51, 184–191. [Google Scholar] [CrossRef]
- Petcher, P.A.; Dixon, S. Parabola detection using matched filtering for ultrasound B-scans. Ultrasonics 2012, 52, 138–144. [Google Scholar] [CrossRef]
- Hirata, S.; Kurosawa, M.K. Ultrasonic distance and velocity measurement using a pair of LPM signals for cross-correlation method: Improvement of Doppler-shift compensation and examination of Doppler velocity estimation. Ultrasonics 2012, 52, 873–879. [Google Scholar] [CrossRef]
- Queiros, R.; Girao, P.S.; Serra, A.C. Cross-Correlation and Sine-Fitting Techniques for High Resolution Ultrasonic Ranging. IEEE Trans. Instrum. Meas. 2006, 59, 552–556. [Google Scholar]
- Demirli, R.; Saniie, J. Model-based estimation of ultrasonic echoes. Part I: Analysis and algorithms. IEEE Trans. Ultrason Ferroelectr. Freq. Control. 2001, 48, 787–802. [Google Scholar] [CrossRef]
- Demirli, R.; Saniie, J. Model-based estimation of ultrasonic echoes. Part II: Nondestructive evaluation applications. IEEE Trans. Ultrason Ferroelectr. Freq. Control. 2001, 48, 803–811. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Reyes, N.; Vera-Candeas, P.; Curpián-Alonso, J.; Mata-Campos, R.; Cuevas-Martínez, J.C. New matching pursuit-based algorithm for SNR improvement in ultrasonic NDT. Non Destr. Test. E Int. 2005, 38, 453–458. [Google Scholar] [CrossRef]
- Yacef, N.; Bouden, T.; Grimes, M. Accurate ultrasonic measurement technique for crack sizing using envelope detection and differential evolution. Non Destr. Test. E Int. 2019, 102, 161–168. [Google Scholar] [CrossRef]
- Zhi, Z.; Jiang, H.; Yang, D.; Gao, J.; Wang, Q.; Wang, X.; Wang, J.; Wu, Y. An end-to-end welding defect detection approach based on titanium alloy time-of-flight diffraction images. J. Intell. Manuf. 2023, 34, 1895–1909. [Google Scholar] [CrossRef]
- Medak, D.; Posilović, L.; Subašić, M.; Budimir, M.; Lončarić, S. DefectDet: A deep learning architecture for detection of defects with extreme aspect ratios in ultrasonic images. Neurocomputing 2022, 473, 107–115. [Google Scholar] [CrossRef]
- Felice, M.V.; Fan, Z. Sizing of flaws using ultrasonic bulk wave testing: A review. Ultrasonics 2018, 88, 26–42. [Google Scholar] [CrossRef]
- Browne, B. Time of flight diffraction its limitations–actual & perceived. E-J. Non. Destr. Test. 1997, 2. Available online: https://www.ndt.net/?id=179 (accessed on 6 April 2024).
- Hu, Q.; Wei, X.; Guo, H.; Xu, H.; Li, C.; He, W.; Pei, B. Study on intelligent and visualization method of ultrasonic testing of composite materials based on deep learning. Appl. Acoust. 2023, 207, 109363. [Google Scholar] [CrossRef]
- Masnata, A.; Sunseri, M. Neural network classification of flaws detected by ultrasonic means. Non Destr. Test. E Int. 1996, 29, 87–93. [Google Scholar] [CrossRef]
- Margrave, F.W.; Rigas, K.; Bradley, D.A.; Barrowcliffe, P. The use of neural networks in ultrasonic flaw detection. Measurement 1999, 25, 143–154. [Google Scholar] [CrossRef]
- Drai, R.; Khelil, M.; Benchaala, A. Time frequency and wavelet transform applied to selected problems in ultrasonics NDE. Non Destr. Test. E Int. 2002, 35, 567–572. [Google Scholar] [CrossRef]
- Filho, E.F.S.; Silva, M.M.; Farias, P.C.M.A.; Albuquerque, M.C.S.; Silva, I.C.; Farias, C.T.T. Flexible decision support system for ultrasound evaluation of fiber–metal aminates implemented in a DSP. Non Destr. Test. E Int. 2016, 79, 38–45. [Google Scholar]
- Munir, N.; Kim, H.-J.; Song, S.-J.; Kang, S.-S. Investigation of deep neural network with drop out for ultrasonic flaw classification in weldments. J. Mech. Sci. Technol. 2018, 32, 3073–3080. [Google Scholar] [CrossRef]
- Munir, N.; Kim, H.-J.; Park, J.; Song, S.-J.; Kang, S. Convolutional neural network for ultrasonic weldment flaw classification in noisy conditions. Ultrasonics 2019, 94, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Xu, W.; Li, X.; Zhang, J.; Xue, Z.; Cao, J. Ultrasonic signal enhancement for coarse grain materials by machine learning analysis. Ultrasonics 2021, 117, 106550. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhang, J.; Li, X.; Yuan, S.; Ma, G.; Xue, Z.; Jing, X.; Cao, J. Intelligent denoise laser ultrasonic imaging for inspection of selective laser melting components with rough surface. Non Destr. Test. E Int. 2022, 125, 102548. [Google Scholar] [CrossRef]
- Rashid, T. Make Your Own Neural Network; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).