Abstract
In the development of geothermal resources in hot dry rocks, deep underground rock masses are typically subjected to real-time high-temperature environments. High temperatures alter the physical and mechanical properties of the rocks, directly affecting the safe and efficient utilization of hot dry rock resources. Therefore, a grain-based model (GBM) of particle flow code (PFC) was constructed based on uniaxial compression tests, and the model was verified according to macroscopic mechanical parameters and damage modes, in order to carry out the simulation study of the uniaxial compression of granite and explore the meso-failure mechanism of granite under real-time high temperature. The relationships between stress–strain curves and crack derivation, the evolution of microcracks, and the characteristics of acoustic emission activity and energy changes at different temperatures were investigated in conjunction with the results of laboratory tests. The results show that crack development, acoustic emission activity, and energy evolution during uniaxial compression include four main stages: initial compression, elasticity, plastic strengthening, and post-peak damage. The failure of granite is primarily controlled by mica and feldspar. During loading, intergranular tensile cracks first emerge within the granite, followed by intragranular tensile cracks, with shear cracks appearing last. As the temperature increases, the total number of microcracks continuously rises, the frequency of acoustic emission events increases, and both dissipated energy and boundary energy gradually decrease, showing an upward trend in the energy dissipation ratio, indicating an increase in thermal damage due to high temperatures. At 400 °C, the rate of microcrack formation increases significantly, with intergranular and intragranular cracks starting to coalesce into macroscopic cracks that extend outward. In the post-peak stage, the phenomenon of multiple peaks in acoustic emission events begins to appear. At 600 °C, the rate of microcrack formation reaches its maximum, with cracks extending throughout the sample to form a network of fractures, resulting in the granite exhibiting ductile failure characteristics.
1. Introduction
As conventional energy sources gradually deplete, hot dry rock (HDR) has attracted widespread attention among various new energy sources due to its abundant reserves, renewability, and clean and efficient characteristics [1]. HDR is primarily stored in high-temperature rock formations located 3–10 km below the surface, which contain little to no fluid, mainly composed of granite, with temperatures ranging from 150 to 650 °C [2]. During the extraction process of HDR, the deep underground reservoir rocks are typically in a real-time high-temperature state, which can lead to changes in the mineral composition, microstructure, and mechanical properties of granite [3,4,5,6]. Therefore, studying the microscopic damage and failure mechanisms of granite under real-time high temperatures is of great significance for the development of geothermal energy resources from HDR.
A considerable number of researchers have conducted studies on the physical and mechanical properties of rocks under high-temperature conditions. Lei et al. [7], Zhang et al. [8], and Li et al. [9] analyzed the influence of high temperature on the physical and mechanical properties of granite, such as strength, peak strain, elastic modulus, porosity, and wave velocity. Chen et al. [10] indicated the existence of a threshold temperature for thermal damage in granite and identified 400 °C as a temperature turning point for changes in its mechanical properties. Liu et al. [11] found that the permeability of granite gradually increased with temperature after high-temperature cooling treatment, followed by a rapid increase, and the brittle–ductile transition temperature range of granite was found to be 500 °C to 600 °C. Zuo et al. [12], Li et al. [13], and Nasseri et al. [14] conducted Type I fracture toughness tests on sandstone at different temperatures using three-point bending, and the experimental results revealed a transition in the fracture mechanism of sandstone from transgranular fractures to a mixture of transgranular and intergranular fractures under high temperatures, ultimately transitioning to thermal cracking. Li et al. [15] utilized acoustic emission technology to observe the process of granite fracturing and found that thermal cracking was the primary cause of deterioration in the mechanical properties of granite. David et al. [16] and Zhang et al. [17] analyzed the microstructure and morphology of granite after exposure to high temperatures through CT and scanning electron microscope experiments, indicating that differences in the mineral composition and crack size of samples would affect the strength of granite. Guo et al. [18] and Yang et al. [19] conducted a series of triaxial compression tests on granite under different confining pressures and temperatures, indicating that the mechanical properties of granite weakened with increasing temperature.
However, relying solely on laboratory experiments makes it challenging to observe the micromechanical behavior of rock during the failure process, necessitating further analysis using numerical methods [20,21,22]. Common numerical methods include the finite element method (FEM), boundary element method (BEM), finite difference method (FDM), and discrete element method (DEM). Among these, the particle flow code (PFC) program, based on the discrete element model framework, is widely used for simulating the microcrack development, thermal cracking process, and damage evolution of rocks under high temperatures. In early studies on granite rock samples, the parallel-bonded model (PBM) was primarily used to simulate the mechanical behavior of intact and fractured rock masses by employing parallel-bonded contacts (PB). However, this model has limitations, such as a low internal friction angle and a low tensile-to-compressive strength ratio [23,24]. To address these limitations, researchers have proposed new improvement methods, primarily by altering particle shapes and constitutive relationships within the model. For instance, Deisman [25] developed the Flat-Joint (FJ) contact model, which simulates the mechanical behavior of bonding, failure, and local contacts within a polygonal crystal structure by assuming finite-length segments and finite-area surfaces. To simulate expansion and interlocking forces by changing grain shapes, Cho et al. [26] introduced the Cluster and Clump elements. The Cluster element involves the aggregation of multiple particles to simulate boundaries, while the Clump element allows particles within the unit to overlap freely without undergoing failure under force. These methods offer certain advantages but still fail to accurately reproduce the failure processes occurring within and at the boundaries of rock crystals. Therefore, Potyondy et al. [27] proposed the Grain-Based Model (GBM), which consists of crystals represented by different polygons. Within the mineral crystals, particles are connected by parallel-bond (PB) contacts, while the boundaries between crystals are defined by smooth-joint (SJ) contacts, allowing for deformation and failure of the crystals. This model not only simulates the mechanical behavior within crystals but also replicates the interactions between crystals, providing a more realistic representation of rock mechanical behavior. Consequently, GBM is currently considered one of the most suitable tools for studying the mechanical response mechanisms of rock materials, particularly crystalline rocks. Tian et al. [28,29] established a GBM granite model based on granular flow, studying the evolution of the cracks and stress–strain curves of granite with different crystal grain sizes and under different high temperatures. Zhang et al. [30] improved the traditional Voronoi GBM model using digital image processing techniques to consider the actual microscopic structure of rocks, integrating discrete crack networks into the model to account for the influence of microcracks. Yang et al. [31] developed a thermo-mechanical grain-based model (TM-GBM) that reflects the actual mineral distribution to study the multi-scale damage of granite during heating, cooling, and uniaxial loading processes. Their findings revealed that, under the same thermal shock temperature, the thermal stress magnitude and the number of thermal cracks during the heating process were significantly lower than those during the cooling process. From the above analysis, it can be observed that it is challenging to fully capture the entire damage and fracture process of granite in real-time high-temperature environments through indoor experiments alone. Therefore, numerical simulation methods are needed for analysis. However, current high-temperature simulation studies on granite are mainly focused on post-high-temperature conditions, while there is relatively less research on the micromechanical behavior of granite under real-time high-temperature conditions. However, the mechanical properties of rocks differ between real-time high-temperature and post-high-temperature exposure conditions. Luo et al. [32], Yin et al. [33], and Zhang et al. [34] found that compared to samples cooled naturally after high-temperature exposure, the degradation of various mechanical properties of real-time high-temperature specimens is more pronounced when the temperature is below 400 °C. However, after reaching 400 °C, samples cooled naturally exhibit a temperature turning point, with the degree of degradation higher than that of real-time high-temperature specimens.
Based on the above considerations, given the geological conditions of real-time high-temperature exploitation in deep dry hot rocks, it is essential to conduct research on the microscopic damage of rocks under real-time high-temperature conditions. Therefore, this paper utilizes the discrete element software PFC6.0 to construct a GBM based on laboratory experiments. The study simulates the mechanical behavior of granite under real-time high-temperature conditions. Through analysis of microcrack development, acoustic emission activity, and energy evolution characteristics, the paper investigates the impact of high temperature on the damage characteristics of granite, revealing its microscopic failure mechanisms under real-time high-temperature conditions. This research aims to provide a theoretical basis for the safe and efficient exploitation of geothermal resources in dry hot rocks.
2. Materials and Methods
2.1. Materials
The granite samples used in this study were obtained from Huangbai Town, Yueyang City, Hunan Province, China. According to international standards of rock mechanics, the granite was processed into cylindrical samples with a diameter of 38 mm and a height of 76 mm. The surface of the samples is smooth and even, with uniform particles. The natural density of the granite is 2.675 g/cm3, and the porosity is 0.926%, as shown in Figure 1a. Figure 1b displays a polarized microscope image (magnification: 5×) of the internal structure of the granite sample. From the image, it can be observed that at the microscopic level, the granite is a heterogeneous material composed of different minerals, with variations in the physical and chemical properties between different minerals reflected in the color differences in the polarized image.

Figure 1.
Granite sample and polarized light microscopy image: (a) granite sample; (b) polarized microscope image of granite.
2.2. Methods
This research conducted uniaxial compression tests at six real-time temperatures (25 °C, 200 °C, 300 °C, 400 °C, 500 °C, and 600 °C). In order to ensure the accuracy of the experiments and minimize the experimental errors caused by variations in the composition of the granite structures, three samples were tested simultaneously at each temperature. The experimental apparatus, as illustrated in Figure 2, primarily consisted of three systems: loading, temperature control, and data acquisition, operated by a microcomputer-controlled electronic universal testing machine. The loading system included a reaction force frame, high-temperature clamps, a high-temperature furnace, and displacement sensors (LVDTs). The heating rate was set to 5 °C/min. Upon reaching the target temperature, to mitigate the thermal gradient effect on the granite and ensure the uniform heating of the samples, the samples were held at a constant temperature for 2 h before testing commenced. The tests were conducted under displacement-controlled loading at a rate of 0.1 mm/min, with a fixed force attenuation amplitude of 60%. The samples were loaded continuously until failure, with the axial force and displacement changes recorded throughout the entire process. The final test results are presented in Table 1.

Figure 2.
Real-time high-temperature electronic universal testing machine.

Table 1.
Uniaxial compression test results at real-time temperatures.
3. Modeling
3.1. Generation Procedure of GBM
This research fully utilizes the characteristics of “rblock” units and “geometry” units in PFC. The main process can be divided into three steps, as shown in Figure 3:
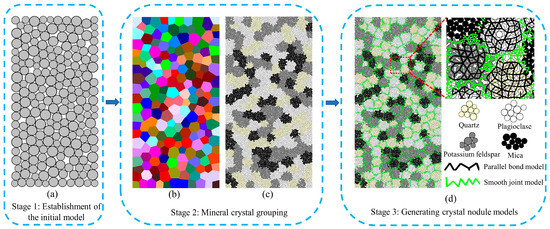
Figure 3.
Model setup: (1) Initial model building; (2) Mineral crystal grouping; (3) Contact model assignment.
- Establishment of initial model: Based on the actual dimensions of the granite samples, an initial model of granular flow with a diameter of 38 mm and a height of 76 mm is established. Particles are randomly generated within the boundary, with radii ranging from 1.5 mm to 2.4 mm. Each particle represents an individual mineral (Figure 3a).
- Grouping of mineral crystals: The “block” unit set is constructed using the particles from the initial model (Figure 3b). Based on the results of polarized light microscopy observation (Figure 3b) and XRD analysis, the main mineral components and their respective proportions in granite are determined. The “block” unit set is grouped accordingly. The grouped “block” unit set is then transformed into a “geometry” unit set, and particle filling is performed (Figure 3c).
- Assignment of contact models: The contact model between particles inside the crystals is replaced with a parallel-bond model (PBM), and the corresponding microscopic parameters are assigned. The contact between different crystals is replaced with a smooth-joint model (SJM), and smooth-joint parameters are assigned (Figure 3d).
3.2. Heating and Loading Process
In PFC2D thermal–solid coupling, thermal storage and conduction processes can be simulated. The thermal conduction between particles is achieved through thermal pipes, where the medium storing heat is the particles, and the contact between particles serves as the thermal conduction pipes. Thermal strain is generated through the interaction between the thermal expansion of particles and temperature changes. The thermal expansion radius of particles can be calculated using the following formula:
where denotes the change in particle radius; is the particle expansion coefficient; is the particle radius; is the temperature increment.
When particles are connected through parallel-bond connections, it is assumed that particle expansion only causes an incremental change in normal stress , while the contact radius of the particle uniformly expands. Therefore, the change in normal stress due to interactions between particles can be expressed as follows:
where denotes the normal stiffness of the bond; is the contact area of the bond; and is the average thermal expansion coefficient.
Figure 4 depicts a schematic illustration of the thermal–mechanical calculation in PFC2D, demonstrating a network-like thermal conduction structure composed of thermal reservoirs and thermal pipes. In this structure, both particle thermal expansion and the interaction of contact bonding contribute to the thermal strain generated in the numerical model. When the temperature changes, the thermal conduction between particles is realized through predetermined thermal parameters, including the specific heat capacity, thermal expansion coefficient, and thermal conductivity of different mineral grains. For specific parameter values, specific parameters are provided in Table 2.
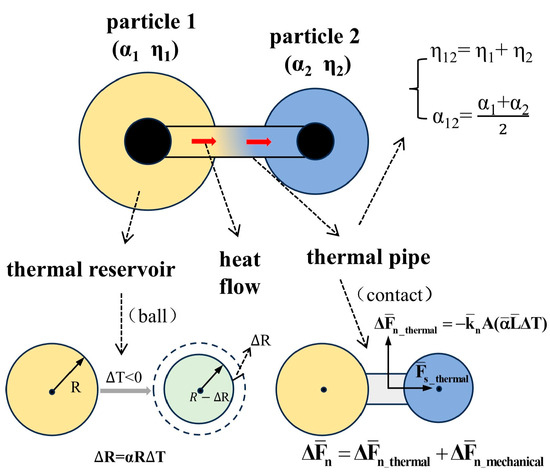
Figure 4.
PFC2D schematic of thermal calculation [35].

Table 2.
Thermal properties of granite [36].
The initial temperature of the GBM is set to 20 °C, and particles in contact with the walls are designated as boundary conditions. The samples are heated to 200 °C, 300 °C, 400 °C, 500 °C, and 600 °C, respectively. To minimize thermal shock, a gradual heating approach is adopted to simulate uniform heating. Mechanical equilibrium is achieved every 10 °C increment during heating. After reaching the target temperatures, the command “model thermal active off” is used to complete the calculation of the high-temperature effects on the physical and mechanical properties of the particles. Subsequently, uniaxial compression tests are simulated. The loading speed is set to 0.05 m/s. This choice is made to balance computational efficiency and accuracy [37]. Chen [38] found through research that this critical point is 0.1 m/s. When the loading rate is less than 0.1 m/s, the results obtained from numerical simulations are in good agreement with laboratory experiments, while when the rate exceeds this value, numerical simulations fail to reproduce the mechanical behavior of the rock well. The entire loading process records in real-time the development of cracks, acoustic emission activity, and energy changes. Throughout the loading process, the real-time monitoring of crack development, acoustic emission activity, and energy changes is conducted.
3.3. Model Calibration and Validation
3.3.1. Model Calibration
In PFC, due to the lack of a direct correspondence between microscale parameters and macroscopic mechanical behavior, a trial-and-error method is commonly employed for calibration. This involves continuously adjusting microscale parameters by comparing the macroscopic mechanical parameters obtained from numerical simulations with those from laboratory experiments, including uniaxial compressive strength, elastic modulus, peak strain, and failure modes, to match the results of PFC simulations with laboratory experiments [39]. Based on the mechanical performance relationship between different mineral crystals in granite (quartz > feldspar > mica > intergranular), and referring to the range of microscale parameter values used in previous studies, different parameters are assigned to intragranular and intergranular contacts [27,28]. At room temperature (20 °C), with a loading speed set to 0.05 m/s, the elastic modulus and bonding strength within and between mineral crystals were adjusted. Suitable parameters were chosen for the uniaxial compression test. The stress–strain curve obtained from simulation was compared with the results from laboratory experiments (Figure 5), revealing a good agreement. Additionally, both exhibited a distinct X-shaped failure pattern, indicating the effectiveness of the parameter calibration.
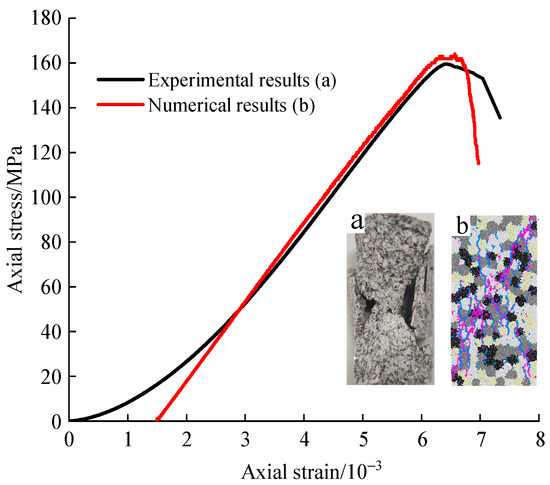
Figure 5.
Comparison of stress–strain curve and failure modes of granite at room temperature.
To better illustrate the trend of stress–strain behavior with temperature variations, it is necessary to readjust the elastic modulus and bond strength within and between mineral crystals to match the mechanical properties of granite at different temperatures. Typically, the aforementioned process needs to be repeated several times until reasonable microscopic parameters are obtained. The final calibrated results are presented in Table 3 and Table 4.

Table 3.
Microparameters of intra-grain in the granite sample.

Table 4.
Microparameters of inter-grain in the granite sample.
3.3.2. Model Validation
Figure 6 compares the compressive strength and elastic modulus of granite obtained from the experimental and numerical simulations at different temperatures. As shown in Figure 6a, the uniaxial compressive strength obtained through numerical simulation follows a trend consistent with the experimental results as temperature varies. At temperatures below 200 °C, the high-temperature effect leads to an increase in the uniaxial compressive strength of granite. Between 300 °C and 500 °C, the uniaxial compressive strength gradually decreases with increasing temperature. At 600 °C, the compressive strength significantly decreases. As shown in Figure 6b, currently, there is no effective method in PFC to simulate mineral transformation and chemical reactions during the heating process under real-time high-temperature conditions for granite. Consequently, the deformation of particles after 400 °C is underestimated, resulting in elastic modulus values higher than those obtained from experimental results [40].
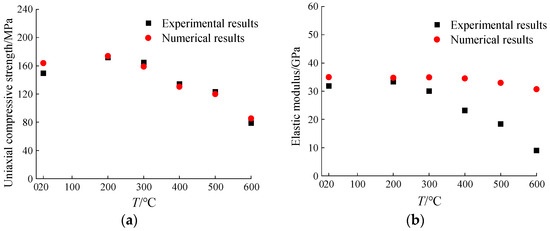
Figure 6.
Comparison of test results: (a) uniaxial compressive strength; (b) elastic modulus.
Figure 7 compares the final failure modes obtained from experiments and numerical simulations at different temperatures. It can be observed that under uniaxial compression, the samples primarily fail in shear, and the fragments of the failed samples are mainly in the form of strips and blocks. With increasing temperature, the number of fine particles produced by fracture gradually increases. Similarly, in the numerical simulation, there are two distinct oblique crack bands in the failed samples, forming an X-shaped conjugate shear failure along the axial loading direction. As the temperature rises, the distribution of thermal damage-induced microcracks becomes more dispersed, and a greater number of cracks begin to propagate and combine, forming a network of microcracks around the mineral crystals. Through the above comparison, it can be observed that the numerical simulation results are in good agreement with the experimental results, which to some extent accurately reflect the mechanical properties of granite under real-time high-temperature conditions.
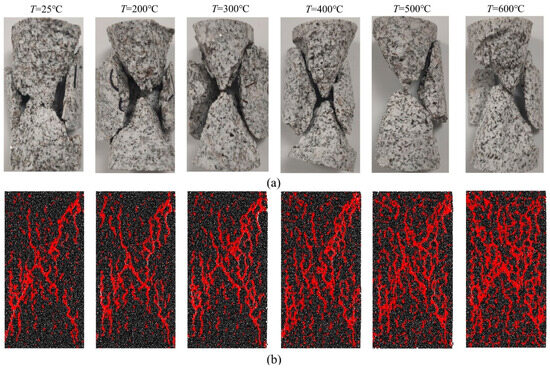
Figure 7.
Comparison results of failure modes: (a) experimental results; (b) numerical results.
4. Results
4.1. Stress–Strain and Crack Propagation
To visually illustrate the entire process of crack initiation and propagation within granite, the crack evolution during the compression process of granite at room temperature is divided into four stages, as shown in Figure 8. (1) Initial densification stage (curve ab): The stress–strain relationship is linear, indicating that cracks have not yet initiated due to the relatively small load. (2) Elastic stage (curve bc): The number of cracks gradually increases with the increase in load. Compared to intragranular contacts, the intergranular contacts are weaker. When the tensile stress on the sample exceeds the tensile strength between mineral crystals, dispersed intergranular tensile cracks rapidly form. (3) Plastic strengthening stage (curve cd): The rate of crack development further increases, with a significant increase in the number of intragranular tensile cracks compared to the elastic stage. Additionally, shear failure cracks begin to appear during this stage. At point d, where the peak stress is reached, crack development becomes concentrated, and the failure mode of the sample becomes foreseeable. (4) Post-peak failure stage (curve de): The slope of both intergranular and intragranular tensile crack curves significantly increases compared to the previous stage. Although a certain number of intergranular shear cracks have formed, tensile failure cracks still dominate. At this stage, crack propagation weakens the overall strength of the material, leading to a gradual decrease in stress and the eventual macroscopic fracture of the sample.
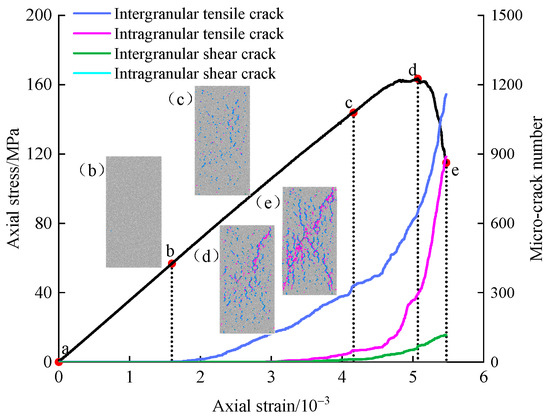
Figure 8.
Stress–strain versus crack derivation curves.
To investigate the influence of high temperature on the damage and failure of granite under uniaxial compression, Figure 9 presents a statistical analysis of the total number of microcracks and the proportions of different types of cracks observed in the samples at different temperatures. It is observed that at 200 °C, the effect of high temperature on the mechanical properties of the granite samples is minimal, with the number of microcracks remaining relatively unchanged compared to that at room temperature (20 °C). Due to the lowest intergranular tensile strength, intergranular tensile cracks constitute the majority of cracks, accounting for 92.8% of the total microcracks. This result is consistent with the viewpoint proposed by Kranz [41] that shear strength exceeds tensile strength in brittle materials. At 300 °C, the differential coefficients of thermal expansion of the mineral crystals result in the uneven expansion of the sample, accelerating the development of microcracks, albeit with a slight decrease in the proportion of intergranular tensile cracks. Between 400 °C and 500 °C, the continued weakening of intergranular bonding leads to a further increase in the rate of microcrack formation due to structural damage to the mineral crystals. During this period, the rate of intragranular crack expansion remains lower than that of intergranular cracks. Upon reaching 600 °C, there is a sharp increase in the number of microcracks, nearly doubling compared to that at 20 °C.
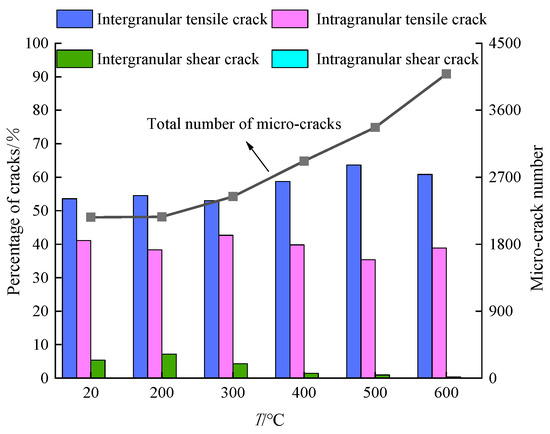
Figure 9.
Total number of microcracks and the proportion of each type of crack at different temperatures.
In summary, the crack development in granite during uniaxial compression mainly undergoes four stages: initial compression, elasticity, plastic strengthening, and post-peak failure. Intergranular tensile cracks dominate the initiation process, followed by intragranular tensile cracks, with only a few shear cracks starting to propagate in the later stages. This result is also consistent with the experimental and simulation findings of Liu et al. [42]. With the increase in temperature, the number of microcracks gradually increases. Compared to the growth rate of cracks between 300 °C and 500 °C, there is a significant increase in crack growth at 600 °C, with intergranular tensile cracks exhibiting the most pronounced changes.
4.2. Microcrack Evolution
Figure 10 illustrates the distribution of local microcracks in the granite samples after failure at different temperatures. It is observed that when the temperature does not exceed 200 °C, microcracks are randomly distributed within the sample, with little apparent connection between them. Intragranular cracks mainly occur within the feldspar and mica crystals, with few occurring within the quartz. After 300 °C, cracks at the boundaries of mineral crystals significantly increase, with a small number of cracks beginning to propagate and combine. At 400 °C, as shown in Figure 10d at points 1 and 2, numerous cracks appear within and at the boundaries of the mica crystals. This is because the thermal expansion coefficient of mica is smaller than that of other minerals, making it easier for tensile stress to concentrate near mica under high-temperature conditions. After 500 °C, as shown in Figure 10e at point 3, tensile cracks begin to aggregate at the boundaries of quartz crystals. When the temperature reaches 600 °C, Figure 10f at point 4 displays a large number of intragranular tensile cracks within the quartz crystals. Additionally, from Figure 10f at points 5 and 6, it can be observed that cracks at the grain boundaries increase, forming a network of interconnected cracks. Overall, the main areas where microcracks gather at different temperatures are within the mica and feldspar, indicating that the compression failure of granite under real-time high-temperature conditions is mainly controlled by these minerals. This observation aligns with the experimental and simulation results of Yang et al. and Gao et al. [43,44]. On the other hand, high temperature significantly affects crack evolution. As the temperature increases, the aggregation of tensile cracks within and between various types of crystals gradually intensifies, leading to a more severe failure of granite due to the formation of a crack network.

Figure 10.
Evolution of granite microcracking with temperature.
Figure 11 presents scanning electron microscope images of the fracture surfaces of the granite samples after real-time high-temperature uniaxial compression tests. The development of microcracks in the samples at different temperatures varies significantly, indicating a significant influence of high temperature on the microcrack evolution in granite. At 25 °C, the fracture surface of the granite sample contains only a few native microcracks, indicating that the internal structure of the granite is nearly intact, with mineral particles arranged relatively closely. At 200 °C, the effect of high temperature causes some initial microcracks to begin closing, and the expansion of mineral particles improves the microstructure of the granite. When the temperature rises to 300 °C, internal stress between particles increases, resulting in the deformation and delamination of mica, leading to a continuous increase in intergranular cracks [45]. With the temperature further increasing, thermal damage becomes more severe. Between 400 °C and 500 °C, the fracture surface becomes rougher, with a significant increase in the number of dense cracks. The widths and lengths of the cracks also increase, and the damaged zones along the crack edges are more prone to initiate new cracks under the interaction of frictional forces. This also leads to the connection and propagation of some intergranular and intragranular cracks, forming distinct crack aggregation zones [46]. After 600 °C, due to the α-β phase transition of quartz at 573 °C, transgranular cracks appear abundantly on the fracture surface, with a wider distribution and deeper aggregation. Many crystals are divided into small pieces, forming a honeycomb-like structure, accompanied by a large amount of debris generation [47].
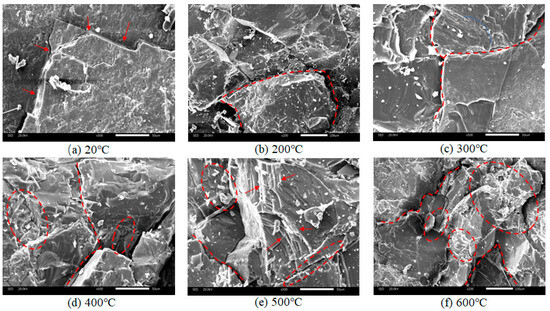
Figure 11.
Scanning electron micrographs of granite fracture surfaces at different temperatures.
By searching for the crack quantity within a certain range and utilizing the “scalar” units in PFC, the crack heatmap of the sample after failure is plotted, as shown in Figure 12. It can be observed that from 20 °C to 200 °C, cracks mainly develop along two diagonal shear bands, with a relatively concentrated distribution. In the image, this is manifested by narrow crack bands and a lower degree of crack aggregation. From 300 °C to 400 °C, the two main crack bands gradually expand outward, with some cracks starting to extend around them. At this point, the thermal damage to the granite becomes significantly aggravated, and the degree of crack aggregation increases. At 500 °C, the crack bands start to become “blurry”, and cracks at the edges quickly connect to the main cracks, indicating a further increase in the impact of high temperature on the sample. When reaching 600 °C, cracks have extended throughout the entire sample, with a more uniform distribution, indicating that the granite sample becomes tougher with increasing temperature.
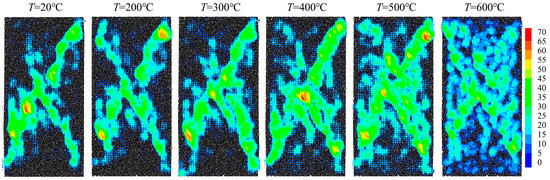
Figure 12.
Cracking hotspot map of granite at different temperatures.
4.3. Acoustic Emission and Energy
In PFC, particles are used to construct a computational model, and when the stress exceeds the bond strength between particles, the bond breaks and releases energy, corresponding to an acoustic emission event [48]. In addition, from the energy point of view, assuming that the heat exchange from the sample to the outside world is not taken into account, the total input energy is all converted into the strain energy and dissipation energy of the rock:
where denotes the boundary energy, which is the work performed by the upper and lower walls on the sample; is the strain energy, including the strain energy of the particles themselves and the model strain energy; is the frictional energy, including the frictional energy, damping energy, kinetic energy, etc., between particles. Through the built-in Fish language in PFC, real-time monitoring and recording of acoustic emission events and energy evolution during the loading process are conducted. Eventually, different temperature-dependent full-process acoustic emission and energy development curves of granite under uniaxial compression are obtained, as shown in Figure 13.
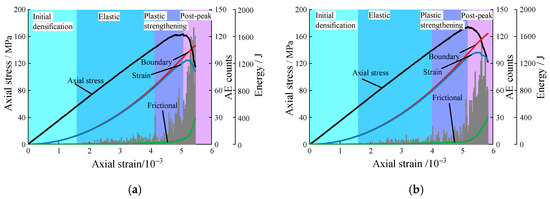
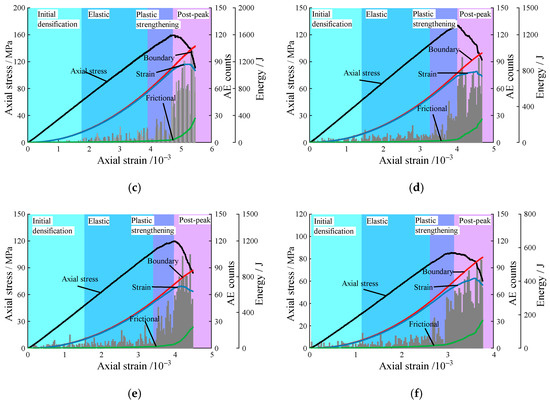
Figure 13.
Acoustic emission events and energy evolution of granites at different temperatures: (a) 20 °C; (b) 200 °C; (c) 300 °C; (d) 400 °C; (e) 500 °C; (f) 600 °C.
For the room temperature samples, as shown in Figure 13a, the results correspond to the four stages of stress–strain curve and crack development of the granite mentioned above, with different characteristics in acoustic emission activity and energy evolution. In the initial densification stage, there are very few acoustic emission signals. The bonds between particles are not yet broken, and the energy is still in an accumulation state. The boundary energy is entirely converted into strain energy stored between the bonds. The strain energy curve coincides with the boundary energy curve, exhibiting a nonlinear parabolic growth, with a very small growth rate. In the elastic stage, acoustic emission events gradually appear, but the amplitude and frequency are still small. With the increase in stress, the frictional energy slightly increases, and the boundary energy begins to separate from the strain energy curve. In the plastic strengthening stage, acoustic emission activity gradually becomes frequent, with an increase in amplitude and frequency. Although the strain energy still shows an increasing trend, the growth rate gradually decreases and drops to zero at the peak point. The strain energy stored between particles is released. Upon entering the post-peak failure stage, the number of acoustic emission events sharply increases, and the amplitude intensifies. When reaching the peak stress, the number of acoustic emission events does not reach its peak but lags behind the peak stress point. At this point, the strain energy is at a critical value, and the work performed by external forces mainly converts into frictional energy.
As shown in Figure 13b–f, for the granite subjected to high-temperature effects, its acoustic emission activity differs significantly from that at the room temperature state. In the initial densification stage, there are minor acoustic emission events starting at 200 °C. When the temperature reaches 400 °C, acoustic emissions become active in the early stages of loading. This indicates that with the increase in temperature, the thermal damage caused to the sample gradually increases, and internal cracks develop and begin to release energy earlier than at room temperature. Upon entering the elastic stage, the level of acoustic emission activity shows a slight increase due to the higher temperature. In the post-peak stage, the higher the temperature, the more pronounced the multi-peak phenomenon of acoustic emissions becomes. However, the amplitude intensity is less intense than that at room temperature. This is because the higher temperature enhances the ductility of the granite, resulting in more energy being released near the peak stress, while the energy released at the peak stress decreases [49]. In summary, high-temperature effects lead to increased initial damage to the sample, manifesting as a higher likelihood of acoustic emission events occurring in the early stages of loading. However, due to the enhanced ductility of granite at high temperatures, its progressive failure process is slower than that at room temperature. Therefore, acoustic emission activity during real-time high-temperature conditions may not be as intense as that at room temperature, particularly from the plastic strengthening stage onwards, but the activity near the peak stress region becomes broader.
Figure 14 illustrates the variation in boundary energy and dissipation energy of the granite sample during failure as a function of temperature. Compared to ambient temperature conditions, at 200 °C, the boundary energy increases while Ud/U decreases, indicating an increase in the released strain energy during failure and a slight enhancement in the strength of the granite sample. As the temperature rises from 200 °C to 500 °C, the curves of boundary energy and dissipation energy continue to decrease. Particularly at 400 °C, the boundary energy sharply decreases, indicating a significant weakening of the ability of the granite to store strain energy internally. Consequently, the damage caused by the release of strain energy after reaching peak strength diminishes. Meanwhile, during this temperature range, the Ud/U curve gradually increases, indicating that with the rise in temperature, the particles are more prone to movement and slipping. Upon reaching 600 °C, the Ud/U value further increases, indicating that high-temperature effects lead to a more gradual failure of the granite, with weakened resistance to deformation and enhanced ductility.
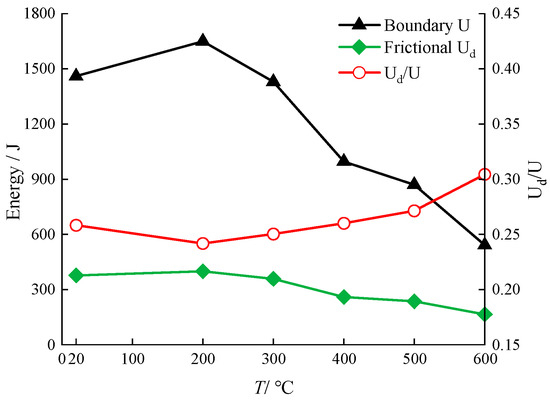
Figure 14.
Boundary and frictional energies and the relationship between the ratio of them for granite damage at different temperatures.
5. Conclusions
This research conducted real-time uniaxial compression simulations under high temperatures using a PFC-GBM constructed based on laboratory experiments. The stress–strain relationship, crack propagation, and evolution of acoustic emission activity and energy with temperature were analyzed. The main conclusions obtained are as follows:
- During uniaxial loading, intergranular tensile cracks in granite initiate first and dominate throughout the entire process, with shear cracks appearing after the peak strength point and being minimal in number. As the temperature increases, the total number of microcracks gradually increases, becoming significant after 400 °C, and reaching the maximum development rate at 600 °C.
- Combining SEM (scanning electron microscopy) results, the distribution of microcracks in granite at different temperatures reveals that the damage under uniaxial compression is mainly controlled by mica and feldspar. As the temperature rises, the internal crack distribution in granite becomes more uniform, with edge cracks rapidly developing to connect with the main crack to form a fracture network, indicating a transition to ductile failure characteristics.
- With increasing temperature, acoustic emission events begin to occur during the initial compression stage, and their distribution becomes wider near the peak strength region with a decrease in amplitude. Multiple peaks in acoustic emission events gradually appear in the post-peak stage. Concurrently, both dissipated energy and boundary energy gradually decrease, and the energy consumption ratio increases, indicating more severe thermal damage to the granite.
Author Contributions
Conceptualization, K.L. and F.Z.; formal analysis, K.L.; data curation, K.L.; writing—original draft preparation, K.L.; writing—review and editing, K.L. and F.Z.; supervision, F.Z. The results were discussed and conclusions were drafted jointly by all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work was jointly supported by the National Natural Science Foundation of China (Grant No. 51979100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martin, G.M.; Iribarren, D.; Dufour, J. On the environmental suitability of high- and low-enthalpy geothermal systems. Geothermics 2015, 53, 27–37. [Google Scholar] [CrossRef]
- Breede, K.; Dzebisashvili, K.; Liu, X.L.; Falcone, G. A systematic review of enhanced (or engineered) geothermal systems: Past, present and future. Geotherm. Energy 2013, 1, 4. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, D.; Wang, Z.L.; Guo, T.K.; Wang, C.G.; He, J.Y.; Zhang, L.; Zheng, P.; Qu, Z.Q. Study on permeability evolution and damage mechanism along the EGS fracture in heat mining stage under thermal stress/cracking. Geotherm. Energy 2023, 11, 31. [Google Scholar] [CrossRef]
- Scott, S.; Yapparova, A.; Weis, P.; Houde, M. Hydrological constraints on the potential of enhanced geothermal systems in the ductile crust. Geotherm. Energy 2024, 12, 10. [Google Scholar] [CrossRef]
- Bahrami, B.; Ayatollahi, M.R.; Mirzaei, A.M.; Yahya, M.Y. Support type influence on rock fracture toughness measurement using semi-circular bending specimen. Rock Mech. Rock Eng. 2020, 53, 2175–2183. [Google Scholar] [CrossRef]
- Kelkar, S.; Woldegabriel, G.; Rehfeldt, K. Lessons learned from the pioneering hot dry rock project at Fenton Hill, USA. Geothermics 2016, 63, 5–14. [Google Scholar] [CrossRef]
- Lei, D.; Zhang, P.; He, J.T.; Bai, P.X.; Zhu, F.P. Fatigue life prediction method of concrete based on energy dissipation. Constr. Build. Mater. 2017, 145, 419–425. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Sun, Q.; Hao, S.Q.; Geng, J.S.; Lv, C. Experimental study on the variation of physical and mechanical proper-ties of rock after high temperature treatment. Appl. Therm. Eng. 2016, 98, 1297–1304. [Google Scholar] [CrossRef]
- Li, B.; Ju, F.; Xiao, M.; Ning, P. Mechanical stability of granite as thermal energy storage material: An experimental investigation. Eng. Fract. Mech. 2019, 211, 61–69. [Google Scholar] [CrossRef]
- Chen, Y.; Ni, J.; Shao, W.; Azzam, R. Experimental study on the influence of temperature on the mechanical proper-ties of granite under uni-axial compression and fatigue loading. Int. J. Rock Mech. Min. 2012, 56, 62–66. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.Y. An experimental study on the physico-mechanical properties of two post-high-temperature rocks. Eng. Geol. 2015, 185, 63–70. [Google Scholar] [CrossRef]
- Zuo, J.P.; Xie, H.P.; Dai, F.; Ju, Y. Three-point bending test investigation of the fracture behavior of siltstone after ther-mal treatment. Int. J. Rock Mech. Min. 2014, 70, 133–143. [Google Scholar] [CrossRef]
- Li, C.; Hu, Y.Q.; Meng, T.; Zhang, C.W.; Gao, R.; Jin, P.H.; Hu, Y.F. Mode-I fracture toughness and mechanisms of Salt-Rock gypsum interlayers under real-time high-temperature conditions. Eng. Fract. Mech. 2020, 240, 107357. [Google Scholar] [CrossRef]
- Nasseri, M.H.B.; Schubnel, A.; Young, R.P. Coupled evolutions of fracture toughness and elastic wave velocities at high crack density in thermally treated Westerly granite. Int. J. Rock Mech. Min. 2007, 44, 601–616. [Google Scholar] [CrossRef]
- Li, B.Q.; Gonçalves, D.S.B.; Einstein, H. Laboratory hydraulic fracturing of granite: Acoustic emission observations and interpretation. Eng. Fract. Mech. 2019, 209, 200–220. [Google Scholar] [CrossRef]
- David, C.; Menéndez, B.; Darot, M. Influence of stress-induced and thermal cracking on physical properties and microstructure of La Peyratte granite. Int. J. Rock Mech. Min. 1999, 36, 433–448. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Zhang, F.; Yang, K.; Cai, Z.Y. Effects of real-time high temperature and loading rate on deformation and strength behavior of granite. Geofluids 2022, 2022, 9426378. [Google Scholar] [CrossRef]
- Guo, L.L.; Zhang, Y.B.; Zhang, Y.J.; Yu, Z.W.; Zhang, J.N. Experimental investigation of granite properties under different temperatures and pressures and numerical analysis of damage effect in enhanced geothermal system. Renew. Energy 2018, 126, 107–125. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Li, Y.B.; Huang, Y.H. Experimental investigation on triaxial mechanical and permeability behavior of sandstone after exposure to different high temperature treatments. Geothermics 2017, 69, 93–109. [Google Scholar] [CrossRef]
- Shahani, N.M.; Kamran, M.; Zheng, X.G.; Liu, C.C.; Guo, X.W. Application of gradient boosting machine learning algorithms to predict uniaxial compressive strength of soft sedimentary rocks at Thar Coalfield. Adv. Civ. Eng. 2021, 2021, 2565488. [Google Scholar] [CrossRef]
- Kamran, M.; Kidega, R.; Ondiaka, N.; Maina, D.; Jonah, K. Decision based uncertainty model to predict rockburst in underground engineering structures using gradient boosting algorithms. Geomech. Eng. 2022, 30, 259–272. [Google Scholar] [CrossRef]
- Kamran, M.; Jiskani, I.M.; Wang, Z.M.; Zhou, W. Decision intelligence-driven predictive modelling of air quality index in surface mining. Eng. Appl. Artif. Intel. 2024, 133, 108399. [Google Scholar] [CrossRef]
- Wu, S.C.; Xu, X.L. A study of three intrinsic problems of the classic discrete element method using Flat-Joint model. Rock Mech. Rock Eng. 2016, 49, 1813–1830. [Google Scholar] [CrossRef]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The impact of porosity and crack density on the elasticity, strength and friction of cohesive granular materials: Insights from DEM modelling. Int. J. Rock Mech. Min. 2009, 46, 250–261. [Google Scholar] [CrossRef]
- Deisman, N.; Mas, I.D.; Pierce, M. PFC2D Smooth joint contact model numerical experiments. In Proceedings of the GeoEdmonton 2008: The 61th Canadian Geotechnical Conference and the 9th Joint CGS/IAH-CNC Groundwater Conference, Edmonton, AB, Canada, 21–24 September 2008. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Potyondy, D.O. A grain-based model for rock: Approaching the true microstructure. In Proceedings of the Rock Mechanics in the Nordic Countries, Kongsberg, Norway, 9–12 June 2010; pp. 225–234. [Google Scholar]
- Tian, W.L.; Yang, S.Q.; Huang, Y.H. Macro and micro mechanics behavior of granite after heat treatment by cluster model in particle flow code. Acta Mech. Sin. 2018, 34, 175–186. [Google Scholar] [CrossRef]
- Tian, W.L.; Yang, S.Q.; Huang, Y.H.; Hu, B. Mechanical behavior of granite with different grain sizes after high-temperature treatment by particle flow simulation. Rock Mech. Rock Eng. 2020, 53, 1791–1807. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Wong, L.N.Y.; Chan, K.K. An extended grain-based model accounting for microstructures in rock deformation. J. Geophys. Res. Solid Earth 2019, 124, 125–148. [Google Scholar] [CrossRef]
- Yang, Z.; Tao, M.; Ranjith, P.G.; Zhuang, D.D.; Memon, M.B.; Luo, H. Multiscale damage and thermal-stress evolution characteristics of rocks with thermal storage potential under thermal shocks. J. Energy Storage 2024, 83, 110631. [Google Scholar] [CrossRef]
- Luo, S.Y.; Dou, B.; Tian, H.; Chen, J.; Xiao, P.; Zhang, S. Comparative experimental study on physical and mechanical properties of granite after natural cooling and under real-time high temperature. Earth Sci. Front. 2020, 27, 178–184. [Google Scholar] [CrossRef]
- Yin, T.B.; Shu, R.H.; Li, X.B.; Wang, P.; Liu, X.L. Comparison of mechanical properties in high temperature and thermal treatment granite. Trans. Nonferrous Met. Soc. China 2016, 26, 1926–1937. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Gao, F.; Xu, X.L. Experimental study of temperature effect of mechanical properties of granite. Rock Soil Mech. 2011, 32, 2346–2352. [Google Scholar] [CrossRef]
- Guo, P.Y.; Zhang, P.; Bu, M.H.; Wang, J.M.; Zheng, X.; He, M.C. Microcracking behavior and damage mechanism of granite subjected to high temperature based on CT-GBM numerical simulation. Comput. Geotech. 2023, 159, 105385. [Google Scholar] [CrossRef]
- Zhao, Z.H. Thermal influence on mechanical properties of granite: A microcracking perspective. Rock Mech. Rock Eng. 2016, 49, 747–762. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, Y.T.; Wu, S.C.; Yan, Q.; Sun, H. An equivalent crystal model for mesoscopic behaviour of rock. Chin. J. Rock Mech. Eng. 2015, 34, 511–519. [Google Scholar] [CrossRef]
- Chen, P.Y. Loading rate effect analysis on rock particle flow model under uniaxial compression. Chin. J. Undergr. Space Eng. 2018, 14, 635–642. [Google Scholar]
- Liu, P.; Liu, J.X.; Liu, Y.T. Particle flow simulation of crack extension in granite. Sichuan Build. Sci. 2016, 42, 100–103. [Google Scholar] [CrossRef]
- Wu, Z.J.; Li, M.Y.; Li, W. Thermal-stress-aperture coupled model for analyzing the thermal failure of fractured rock mass. Int. J. Geomech. 2020, 20, 04020176. [Google Scholar] [CrossRef]
- Kranz, R.L. Crack-crack and crack-pore interactions in stressed granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 37–47. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, K.; Shao, S.S.; Ranjith, P.G. Numerical investigation on the mechanical properties of Australian Strathbogie granite under different temperatures using Discrete Element Method. Rock Mech. Rock Eng. 2019, 52, 3719–3735. [Google Scholar] [CrossRef]
- Yang, S.Q.; Ranjith, P.G.; Jing, H.W.; Tian, W.L.; Ju, Y. An experimental investigation on thermal damage and failure mechanical behavior of granite after exposure to different high temperature treatments. Geothermics 2017, 65, 180–197. [Google Scholar] [CrossRef]
- Gao, F.Q.; Kang, H.P.; Wu, Y.Z. Experimental and numerical study on the effect of calcite on the mechanical behaviour of coal. Int. J. Coal Geol. 2016, 158, 119–128. [Google Scholar] [CrossRef]
- Rutter, E.H.; Brodie, K.H. Mechanistic interactions between deformation and metamorphism. Geol. J. 1995, 30, 227–240. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, F.; Meng, F.Z.; Hu, D.W.; Tan, X.F. Effect of real-time high temperature and loading rate on mode I fracture toughness of granite. Geotherm. Energy 2022, 10, 14. [Google Scholar] [CrossRef]
- Xu, X.L.; Kang, Z.X.; Ji, M.; Ge, W.X.; Chen, J. Research of microcosmic mechanism of brittle-plastic transition for granite under high temperature. Procedia Earth Planet. Sci. 2009, 1, 432–437. [Google Scholar] [CrossRef]
- Su, H.; Dang, C.H.; Li, Y.J. Study of numerical simulation of acoustic emission in rock of inhomogeneity. Rock Soil Mech. 2011, 32, 1886–1890. [Google Scholar] [CrossRef]
- Xu, X.L.; Gao, F.; Zhou, Q.; Chen, J. Energy analysis of rock deformation and failure process after high temperature. J. Wuhan Univ. Technol. 2011, 33, 104–107, 124. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).