Synergizing Transfer Learning and Multi-Agent Systems for Thermal Parametrization in Induction Traction Motors
Abstract
1. Introduction and Related Work
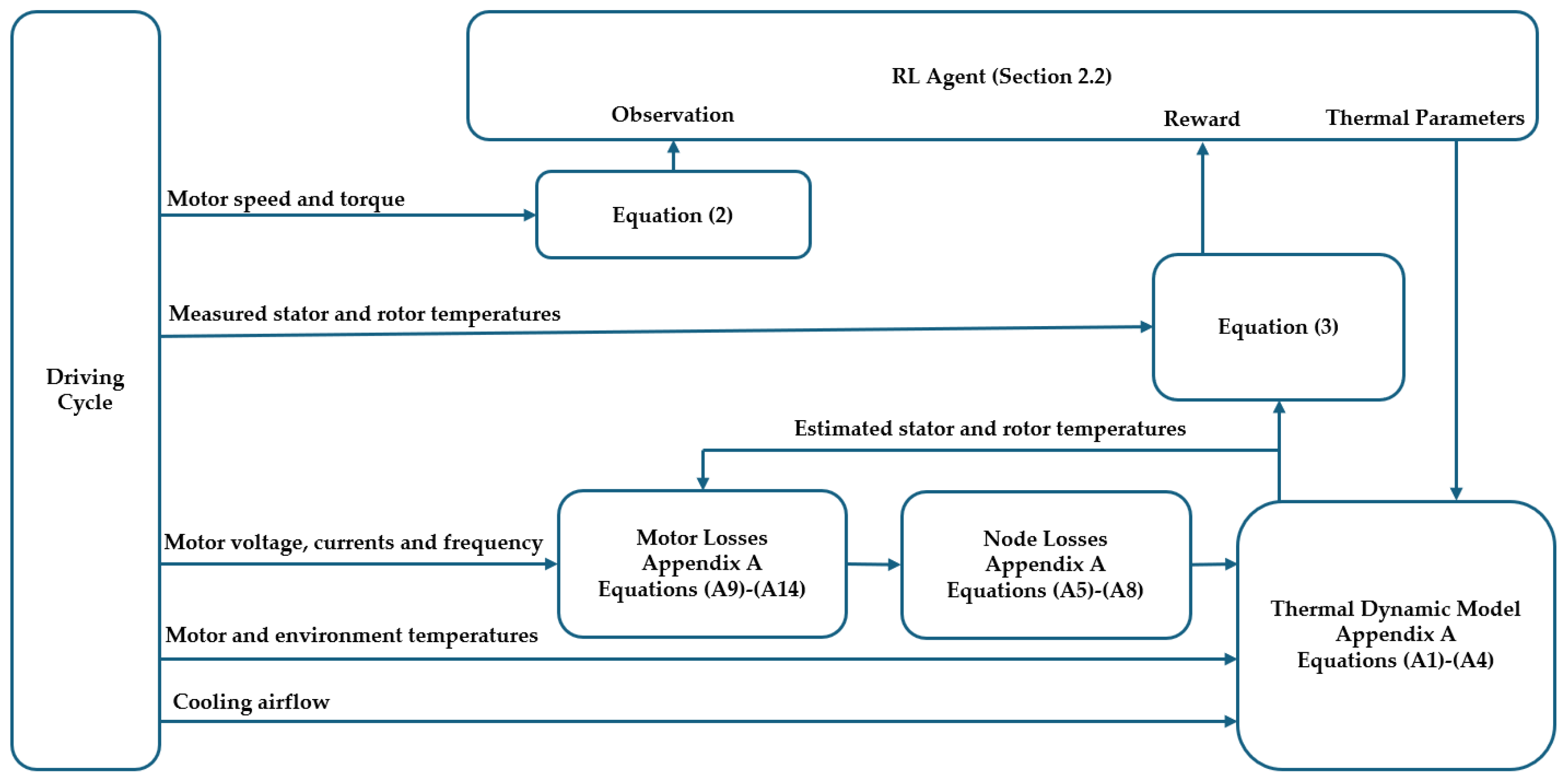
2. Multi-Agent Reinforcement Learning Framework and Transfer Learning Approach
2.1. The Reinforcement Learning Framework
2.2. RL Multiple Agents Composition
2.2.1. Twin-Delayed Deep Deterministic Policy Gradient (TD3) Structure
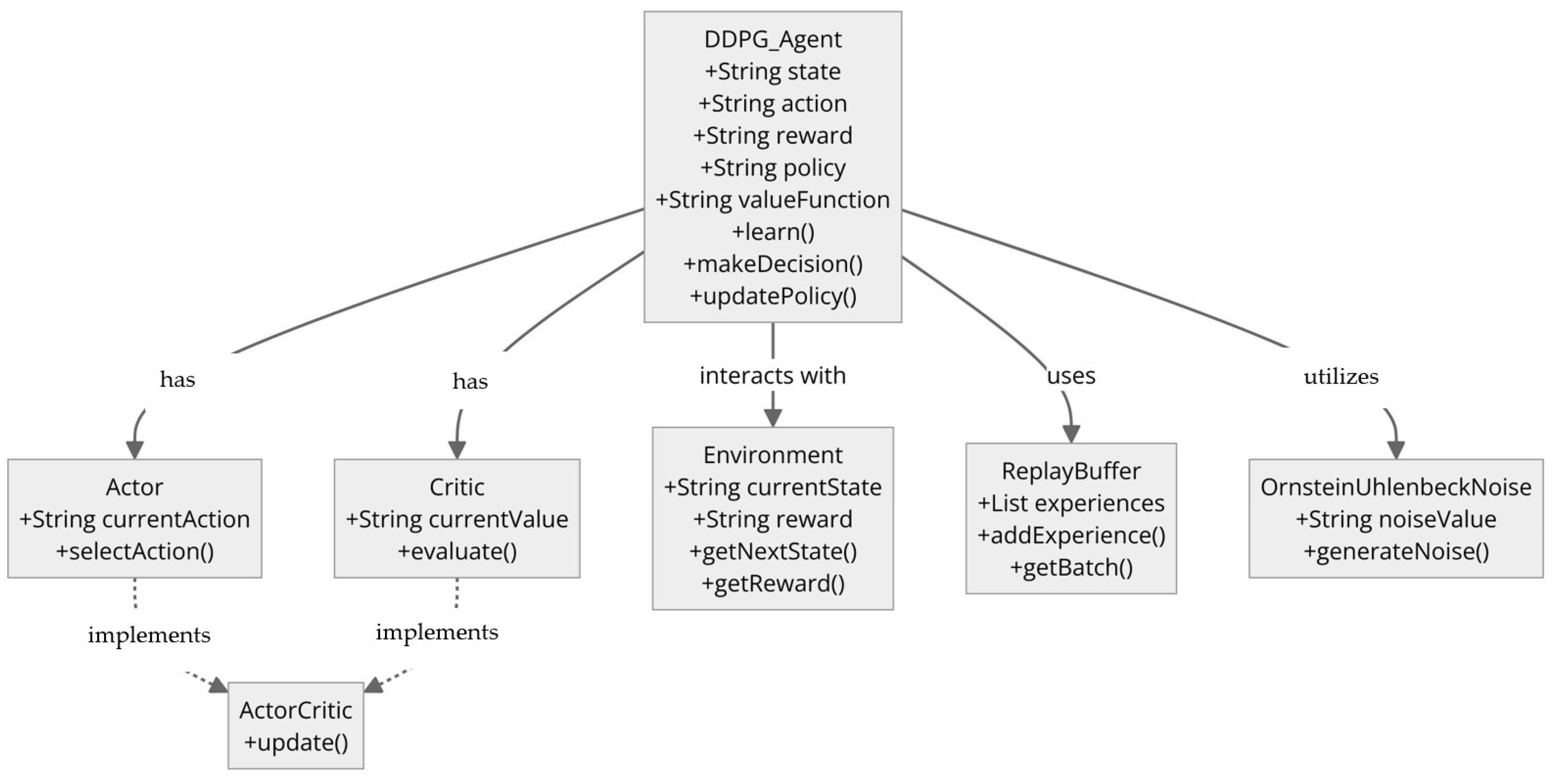
2.2.2. Deep Deterministic Policy Gradient (DDPG) Agent Structure
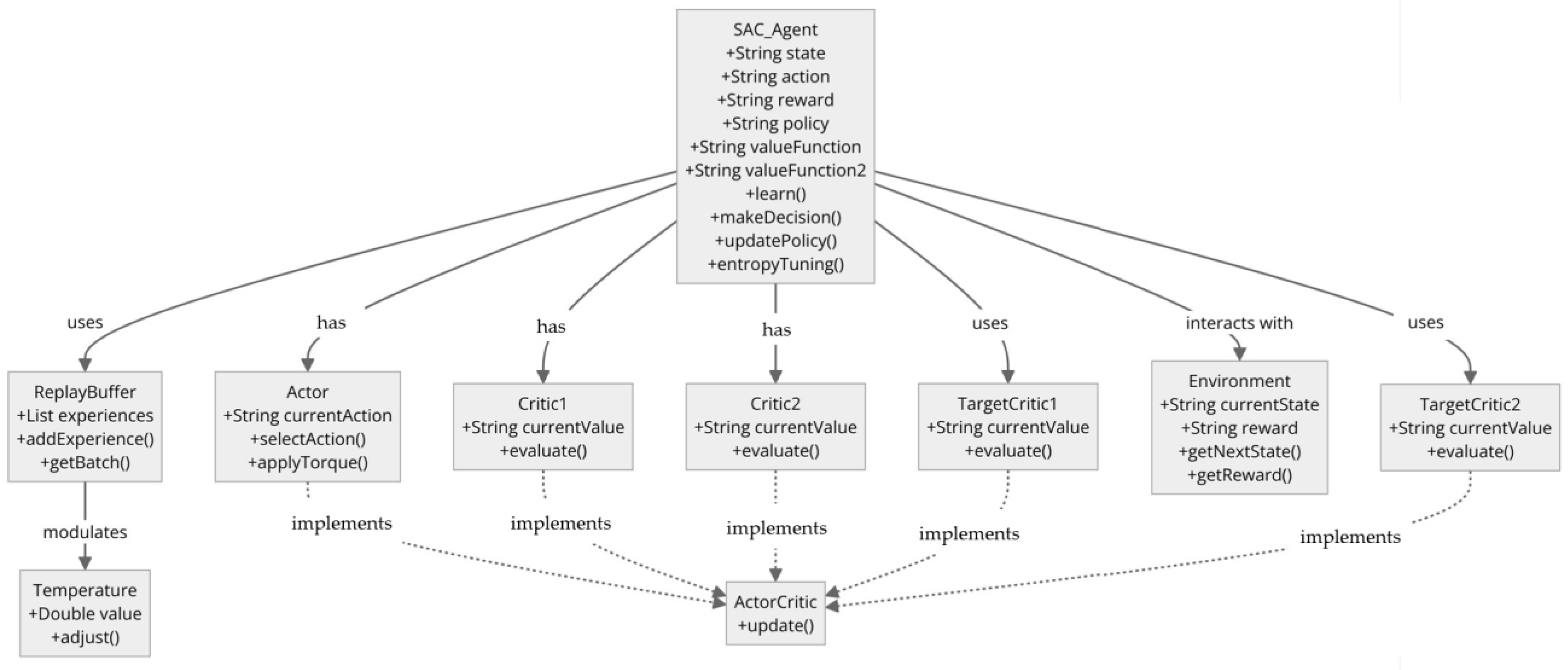
2.2.3. Soft Actor-Critic (SAC) Agent Structure
2.3. RL Agent Training Process
2.3.1. Pre-Processing of Dataset
2.3.2. The Training Process
2.3.3. Transfer Learning from Pre-Trained RL Models
3. Results & Discussion
3.1. Preprocessing the Dataset
3.2. Training the RL Agents
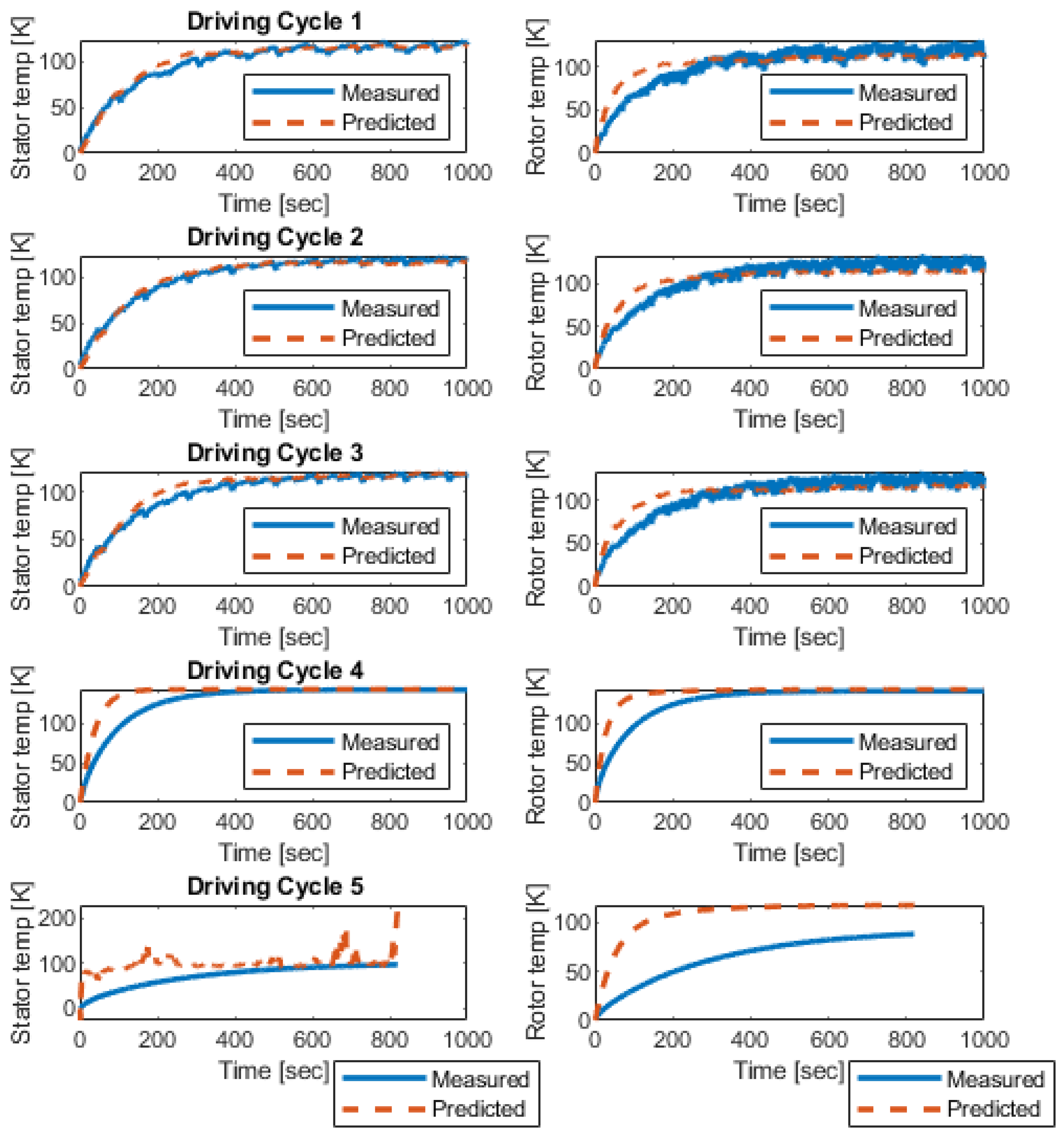
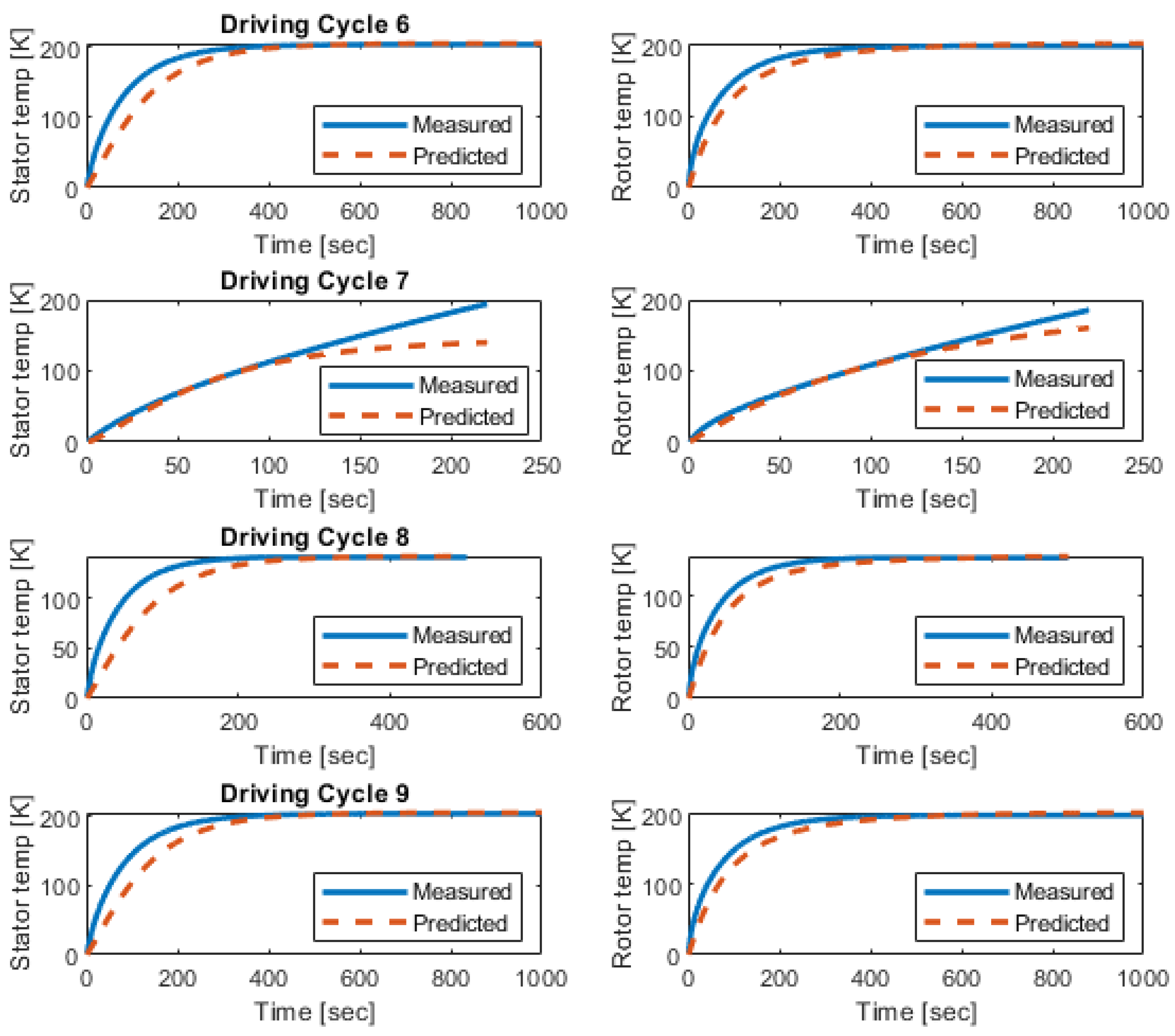
3.3. Validating the Trained Agents
4. Contrasting the Proposed Technique with the Prior One
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Parametrizing the Thermal Model
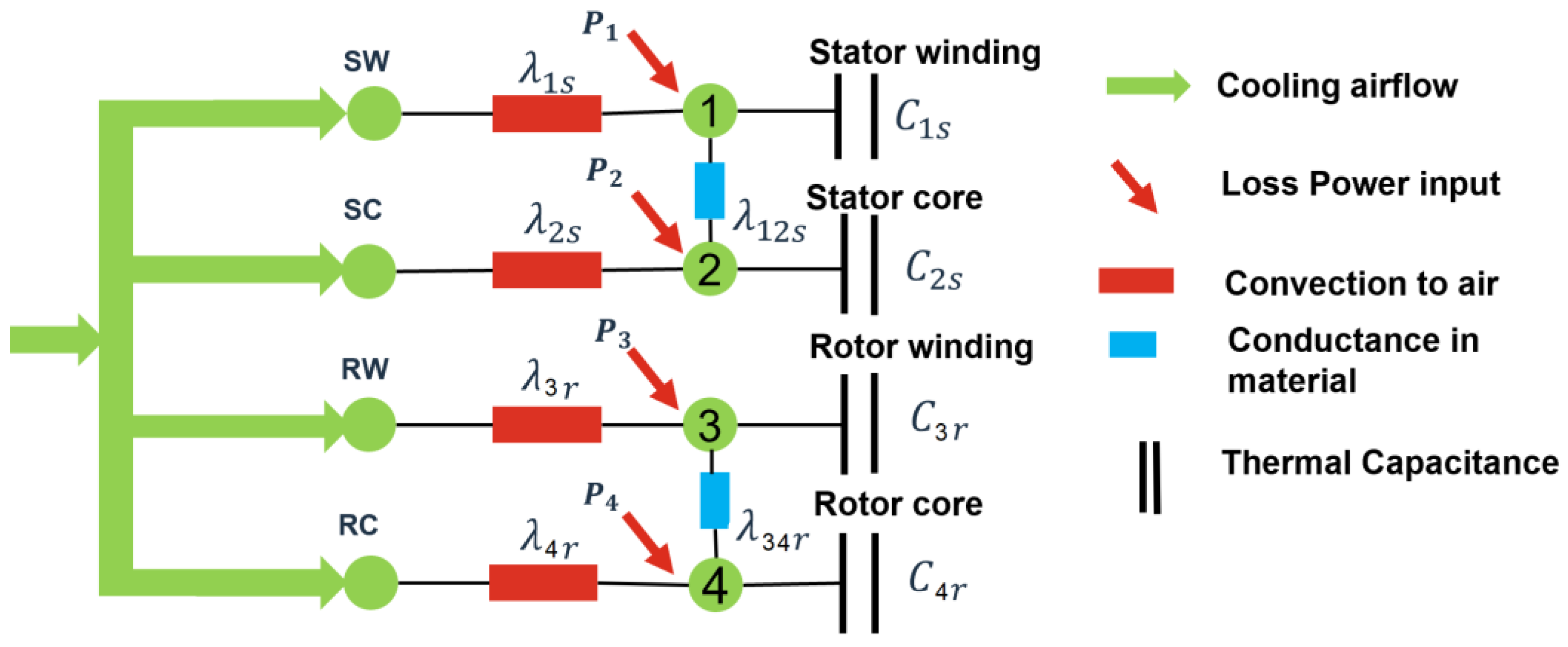
| Node | Winding Losses | Stray Losses | Harmonic Losses | Iron Losses |
|---|---|---|---|---|
| 1 | x | x | x | |
| 2 | x | |||
| 3 | x | x | x | |
| 4 | x |
References
- Fathy Abouzeid, A.; Guerrero, J.M.; Endemaño, A.; Muniategui, I.; Ortega, D.; Larrazabal, I.; Briz, F. Control strategies for induction motors in railway traction applications. Energies 2020, 13, 700. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ali, J.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2018, 81, 1611–1626. [Google Scholar] [CrossRef]
- Lemmens, J.; Vanassche, P.; Driesen, J. Optimal control of traction motor drives under electrothermal constraints. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 249–263. [Google Scholar] [CrossRef]
- Dorrell, D.G. Combined thermal and electromagnetic analysis of permanent-magnet and induction machines to aid calculation. IEEE Trans. Ind. Electron. 2008, 55, 3566–3574. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Islam, R.; Islam, M.; Sebastian, T. Real time estimation of parameters for controlling and monitoring permanent magnet synchronous motors. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1194–1199. [Google Scholar]
- Wilson, S.D.; Stewart, P.; Taylor, B.P. Methods of resistance estimation in permanent magnet synchronous motors for real-time thermal management. IEEE Trans. Energy Convers. 2010, 25, 698–707. [Google Scholar] [CrossRef]
- Wallscheid, O. Thermal monitoring of electric motors: State-of-the-art review and future challenges. IEEE Open J. Ind. Appl. 2021, 2, 204–223. [Google Scholar] [CrossRef]
- Kral, C.; Haumer, A.; Lee, S.B. A practical thermal model for the estimation of permanent magnet and stator winding temperatures. IEEE Trans. Power Electron. 2013, 29, 455–464. [Google Scholar] [CrossRef]
- Sciascera, C.; Giangrande, P.; Papini, L.; Gerada, C.; Galea, M. Analytical thermal model for fast stator winding temperature prediction. IEEE Trans. Ind. Electron. 2017, 64, 6116–6126. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiao, M.; Lu, K.; Wu, Z.; Tao, B. A simplified thermal model and online temperature estimation method of permanent magnet synchronous motors. Appl. Sci. 2019, 9, 3158. [Google Scholar] [CrossRef]
- Guemo, G.G.; Chantrenne, P.; Jac, J. Parameter identification of a lumped parameter thermal model for a permanent magnet synchronous machine. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1316–1320. [Google Scholar]
- Huber, T.; Peters, W.; Böcker, J. Monitoring critical temperatures in permanent magnet synchronous motors using low-order thermal models. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Gedlu, E.G.; Wallscheid, O.; Böcker, J. Permanent magnet synchronous machine temperature estimation using low-order lumped-parameter thermal network with extended iron loss model. In Proceedings of the 10th International Conference on Power Electronics, Machines and Drives (PEMD 2020), Online Conference, 15–17 December 2020; IET: London, UK, 2020. [Google Scholar]
- Wallscheid, O.; Böcker, J. Global identification of a low-order lumped-parameter thermal network for permanent magnet synchronous motors. IEEE Trans. Energy Convers. 2015, 31, 354–365. [Google Scholar] [CrossRef]
- Xiao, S.; Griffo, A. Online thermal parameter identification for permanent magnet synchronous machines. IET Electr. Power Appl. 2020, 14, 2340–2347. [Google Scholar] [CrossRef]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Data-driven permanent magnet temperature estimation in synchronous motors with supervised machine learning: A benchmark. IEEE Trans. Energy Convers. 2021, 36, 2059–2067. [Google Scholar] [CrossRef]
- Zhang, S.; Wallscheid, O.; Porrmann, M. Machine learning for the control and monitoring of electric machine drives: Advances and trends. IEEE Open J. Ind. Appl. 2023, 4, 188–214. [Google Scholar] [CrossRef]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Empirical evaluation of exponentially weighted moving averages for simple linear thermal modeling of permanent magnet synchronous machines. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 318–323. [Google Scholar]
- Nogay, H.S. Prediction of internal temperature in stator winding of three-phase induction motors with ann. Eur. Trans. Electr. Power 2011, 21, 120–128. [Google Scholar] [CrossRef]
- Wallscheid, O.; Kirchgässner, W.; Böcker, J. Investigation of long short-term memory networks to temperature prediction for permanent magnet synchronous motors. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1940–1947. [Google Scholar]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Deep residual convolutional and recurrent neural networks for temperature estimation in permanent magnet synchronous motors. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Thermal neural networks: Lumped-parameter thermal modeling with state-space machine learning. Eng. Appl. Artif. Intell. 2023, 117, 105537. [Google Scholar] [CrossRef]
- Wlas, M.; Krzeminski, Z.; Toliyat, H.A. Neural-network-based parameter estimations of induction motors. IEEE Trans. Ind. Electron. 2008, 55, 1783–1794. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Jung, J.W. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range. IEEE Trans. Ind. Inform. 2019, 16, 4747–4758. [Google Scholar] [CrossRef]
- Harashima, F.; Demizu, Y.; Kondo, S.; Hashimoto, H. Application of neutral networks to power converter control. In Proceedings of the Conference Record of the IEEE Industry Applications Society Annual Meeting, San Diego, CA, USA, 1–5 October 1989; IEEE: Piscataway, NJ, USA, 1989; pp. 1086–1091. [Google Scholar]
- Wishart, M.T.; Harley, R.G. Identification and control of induction machines using artificial neural networks. IEEE Trans. Ind. Appl. 1995, 31, 612–619. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hoque, M.A. On-line adaptive artificial neural network based vector control of permanent magnet synchronous motors. IEEE Trans. Energy Convers. 1998, 13, 311–318. [Google Scholar]
- Yi, Y.; Vilathgamuwa, D.M.; Rahman, M.A. Implementation of an artificial-neural-network-based real-time adaptive controller for an interior permanent-magnet motor drive. IEEE Trans. Ind. Appl. 2003, 39, 96–104. [Google Scholar]
- Zhang, Q.; Zeng, W.; Lin, Q.; Chng, C.B.; Chui, C.K.; Lee, P.S. Deep reinforcement learning towards real-world dynamic thermal management of data centers. Appl. Energy 2023, 333, 120561. [Google Scholar] [CrossRef]
- Egan, D.; Zhu, Q.; Prucka, R. A Review of Reinforcement Learning-Based Powertrain Controllers: Effects of Agent Selection for Mixed-Continuity Control and Reward Formulation. Energies 2023, 16, 3450. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, J.; He, L.; Zhao, D.; Zhao, Y. Reinforcement learning-based control for the thermal management of the battery and occupant compartments of electric vehicles. Sustain. Energy Fuels 2024, 8, 588–603. [Google Scholar] [CrossRef]
- Book, G.; Traue, A.; Balakrishna, P.; Brosch, A.; Schenke, M.; Hanke, S.; Kirchgässner, W.; Wallscheid, O. Transferring online reinforcement learning for electric motor control from simulation to real-world experiments. IEEE Open J. Power Electron. 2021, 2, 187–201. [Google Scholar] [CrossRef]
- Traue, A.; Book, G.; Kirchgässner, W.; Wallscheid, O. Toward a reinforcement learning environment toolbox for intelligent electric motor control. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 919–928. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Halder, S.; Balamurali, A.; Towhidi, M.; Iyer, L.V.; Kar, N.C. An advanced policy gradient based vector control of PMSM for EV application. In Proceedings of the 2020 10th International Electric Drives Production Conference (EDPC), Ludwigsburg, Germany, 8–9 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Fattouh, A.; Sahoo, S. Data-driven reinforcement learning-based parametrization of a thermal model in induction traction motors. In Proceedings of the 64th International Conference of Scandinavian Simulation Society, SIMS 2023, Västerås, Sweden, 25–28 September 2023; pp. 310–317. [Google Scholar]
- Wöckinger, D.; Bramerdorfer, G.; Drexler, S.; Vaschetto, S.; Cavagnino, A.; Tenconi, A.; Amrhein, W.; Jeske, F. Measurement-based optimization of thermal networks for temperature monitoring of outer rotor PM machines. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4261–4268. [Google Scholar]
- Filizadeh, S. Electric Machines and Drives: Principles, Control, Modeling, and Simulation; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Maroteaux, A. Study of Analytical Models for Harmonic Losses Calculations in Traction Induction Motors; KTH, School of Electrical Engineering (EES): Stockholm, Sweden, 2016. [Google Scholar]
- Roshandel, E.; Mahmoudi, A.; Kahourzade, S.; Yazdani, A.; Shafiullah, G. Losses in efficiency maps of electric vehicles: An overview. Energies 2021, 14, 7805. [Google Scholar] [CrossRef]





| Property | Value |
|---|---|
| max episodes | 10 |
| max steps per episodes | 600 |
| average window length | 500 |
| stop training value | −10 |
| agent sample time | 0.1 s |
| Property | Value (DC4, DC6, DC7) | Value (DC9) |
|---|---|---|
| max episodes | 1000 | 1000 |
| max steps per episodes | 600 | 20 |
| average window length | 500 | 20 |
| stop training value | −10 | −740 |
| agent sample time | 0.1 s | 0.1 s |
| Property | Value (Rotor) | Value (Stator) |
|---|---|---|
| max episodes | 1000 | 1000 |
| max steps per episodes | 600 | 20 |
| average window length | 500 | 50 |
| stop training value | −10 | −740 |
| agent sample time | 0.1 s | 0.1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehboob, F.; Fattouh, A.; Sahoo, S. Synergizing Transfer Learning and Multi-Agent Systems for Thermal Parametrization in Induction Traction Motors. Appl. Sci. 2024, 14, 4455. https://doi.org/10.3390/app14114455
Mehboob F, Fattouh A, Sahoo S. Synergizing Transfer Learning and Multi-Agent Systems for Thermal Parametrization in Induction Traction Motors. Applied Sciences. 2024; 14(11):4455. https://doi.org/10.3390/app14114455
Chicago/Turabian StyleMehboob, Fozia, Anas Fattouh, and Smruti Sahoo. 2024. "Synergizing Transfer Learning and Multi-Agent Systems for Thermal Parametrization in Induction Traction Motors" Applied Sciences 14, no. 11: 4455. https://doi.org/10.3390/app14114455
APA StyleMehboob, F., Fattouh, A., & Sahoo, S. (2024). Synergizing Transfer Learning and Multi-Agent Systems for Thermal Parametrization in Induction Traction Motors. Applied Sciences, 14(11), 4455. https://doi.org/10.3390/app14114455






