Next Article in Journal
Stability and Distribution of Rock Slope under Asymmetric Excavation
Next Article in Special Issue
Numerical Analysis of the Breakdown Process of CF3I at Low Pressure
Previous Article in Journal
The Evaluation of Pipeline Protection Influenced by Causeway Embankment Using the Finite Element Method (FEM)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 14
Issue 11
10.3390/app14114381
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

X-ray Line-Intensity Ratios in Neon-like Xenon: Significantly Reducing the Discrepancy between Measurements and Simulations

by
Shihan Huang
1,
Zhiming Tang
1,
Yang Yang
1,*,
Hongming Zhang
2,
Ziqiang Tian
1,
Shaokun Ma
1,
Jinyu Li
1,
Chao Zeng
2,
Huajian Ji
2,
Ke Yao
1 and
Yaming Zou
1
1
Shanghai EBIT Laboratory, Key Laboratory of Nuclear Physics and Ion-Beam Application (MOE), Institute of Modern Physics, Fudan University, Shanghai 200433, China
2
Institute of Plasma Physics, HFIPS, Chinese Academy of Sciences, Hefei 230031, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2024, 14(11), 4381; https://doi.org/10.3390/app14114381
Submission received: 22 April 2024 / Revised: 10 May 2024 / Accepted: 13 May 2024 / Published: 22 May 2024
(This article belongs to the Special Issue Plasma Physics: Theory, Methods and Applications)
Browse Figures
Versions Notes

Abstract

The X-ray spectra of L-shell transitions in Neon-like Xenon ion (Xe44+) have been precisely measured at the Shanghai Electron-Beam Ion Trap using a high-resolution crystal spectrometer. Focusing on the line-intensity ratio of the 3F {2p6-(2p51/23s1/2)J=1} and 3D {2p6-(2p53/23d5/2)J=1} lines (3F/3D), our measurements have achieved remarkable precision improvements over the previous studies. These spectra have been simulated using the collisional-radiative model (CRM) within the Flexible Atomic Code, showing good agreement with the measurements. The previously reported discrepancies, approximately ranging from 10% to 20%, have been significantly reduced in this work to below 1.4% for electron-beam energies exceeding 6 keV and to around 7% for lower energies. Furthermore, our analysis of population fluxes of the involved levels reveals a very high sensitivity of the 3F line to radiation cascades. This suggests that the current CRM, which conventionally excludes interionic population transfer processes, may underestimate the population of the upper level of the 3F line and the cascade-related higher levels, thus explaining the remaining discrepancies. These findings provide a solid foundation for further minimizing these discrepancies and are crucial for understanding the atomic structure and plasma model of these ions.

1. Introduction

In crystal imaging systems of ITER [1,2,3] and CFETR [4], Xenon (Xe) is chosen as an externally injected diagnostic probe impurity for the diagnosis of ion temperature and toroidal plasma velocity [5]. The Ne-like Xe44+ exhibits high concentrations across a wide range of electron temperatures. Its strong 3D {2p6-(2p53/23d5/2)J=1, 2.7203 Å [6]} line serves as a valuable diagnostic tool in the core plasma [7]. Consequently, this ion has attracted considerable research attention, leading to extensive measurements in various experiments, including tokamaks [6,8,9,10], EBITs [11,12,13,14,15,16,17], laser plasmas [18,19,20], and low-inductance spark devices [21]. Beyond the limitations of current diagnostic capabilities, the Ne-like Xe44+ holds promise for an even broader diagnostic potential [22,23,24], thereby asking for more precise atomic parameters and sophisticated plasma models to refine spectral emission mechanisms.
Ne-like ions, with their fully filled L-shell ground state, exhibit stability across a wide range of plasma temperatures and can emit exceptionally bright X-ray radiation that is easily observable. Consequently, the X-ray spectra emitted by these ions have been exploited for plasma diagnostics in high-temperature plasma, including magnetic confinement fusion [25,26,27,28], inertial confinement fusion [29,30,31], and astrophysical plasma [32,33,34]. For instance, the brightest 3C and 3D lines emitted by the Ne-like Fe ion in the Sun and other stellar coronal spectra offer great potential for diagnosing density and temperature [35,36,37]. Nevertheless, the discrepancy between experimental and theoretical 3C/3D oscillator-strength ratios poses significant obstacles to their diagnostic application [38,39,40,41,42]. These inconsistencies raised concerns about the accuracy of the emission intensities from Ne-like ions, prompting extensive research efforts to resolve this problem [43,44,45]. Recently, Kühn et al. [46] conducted measurements with high resolving power and an exceptionally high signal-to-noise ratio, coupled with Voigt fitting to distinguish Lorentzian wings, leading to the determination of the oscillator-strength ratio and achieved excellent agreement with high-precision theoretical calculations. This study finally resolves the long-standing mystery surrounding oscillator strengths in the Ne-like Fe ion and provides valuable implications for improving the accuracy of experimental line-intensity ratio measurements.
The variation of the 3C/3D oscillator strengths across the Ne-like isoelectronic sequence with respect to the atomic number Z provides an avenue to investigate various effects that contribute to the experimental-theoretical deviations, such as electron-correlation effects [47,48,49,50,51], population corrections [48,52,53,54], and polarization [55,56]. Recently, Yang et al. [14] demonstrated that there is an apparent change in the 3C/3D line-intensity ratio at approximately Z = 54, attributed to the suppressed collision strength for the upper level of the 3D line due to strong configuration mixing with the upper level of the adjacent 3F {2p6-(2p51/23s1/2)J=1, 2.7288 Å [6]} line. That strong mixing is associated with level crossing, which arises from the diminishing importance of Coulomb potential relative to relativistic and quantum electrodynamical (QED) effects with increasing atomic number. This also usually implies a transition from LS to jj coupling schemes and brings about a significant rearrangement of atomic structures. [57]. In the present case, Ne-like Xe44+ (Z = 54) is in the vicinity of level crossing between the upper levels of the 3F and 3D lines. As the atomic number over Z = 55, the upper level of the 3F line surpasses that of the 3D line. As a result, repelling and strong configuration mixing occurs between the upper levels of the 3D and 3F lines [12], resulting in anomalous behavior in relevant atomic parameters, including transition rates and collision strengths, along the isoelectronic sequences near Z = 54 [14,58,59,60]. Kato et al. [15] demonstrated that the strong configuration mixing between the upper levels of the 3D and 3F lines at Z = 54 can lead to a strong enhancement of the 3F/3D line-intensity ratio. This enhancement is a result of the redistribution of collision strengths and level populations. Their findings indicate that conducting precise measurements of the 3F/3D line-intensity ratio in the Ne-like Xe44+ can offer a valuable tool for exploring the effects of level crossings and configuration interaction and for testing the reliability of theoretical models for simulating the spectra of the Ne-like ions near the level crossing point. It is worth noting that a subsequent study conducted by Kato et al. [16] has revealed a substantial discrepancy between the experimental values of the 3F/3D line-intensity ratio and those obtained from HULLAC synthetic calculations across various electron-beam energies. These notable discrepancies actually highlight the limitations of the existing theoretical models and the inaccuracies in atomic parameters for plasma diagnostics. Therefore, there is a pressing need for further advancements in both the experimental measurements and spectral simulations of the Ne-like Xe44+ to enhance their reliability and accuracy.
In this work, we have conducted precise measurements of the 3D and 3F lines in Ne-like Xe ion, along with accompanying satellites and the two-electron-one-photon-transition (TEOPT) lines from neighboring charged states, at the Shanghai Electron Beam Ion Trap (Shanghai-EBIT) using a high-resolution crystal spectrometer. Specifically, we have conducted a comprehensive analysis of the line-intensity ratio of 3F/3D in the experimental spectra. The emission intensities of the spectral lines have been simulated using the collisional-radiative model (CRM) within the Flexible Atomic Code (FAC), providing the dependence of line-intensity ratios on electron-beam energies. Our results have achieved a significant improvement in the agreement between measurements and simulations of the 3F/3D line-intensity ratios across various ranges of the electron-beam energy, significantly reducing the discrepancy reported in previous studies. In particular, at the energies above 6 keV, the present experimental and simulated results exhibited a very high agreement, whereas small discrepancies still persist in the low-energy region. To address the remaining discrepancies, we delved into the population equilibrium of the involved levels within the present CRM. Based on these analyses, we have proposed potential approaches to further minimize these discrepancies, ultimately establishing the 3F/3D line-intensity ratio as a reliable tool for plasma diagnostics.

2. Experimental Setup

Using the Shanghai-EBIT [61,62], the measurements were conducted in a Xenon-dominated plasma environment with negligible Doppler shifts. In a vacuum environment better than 10−10 torr, a quasi-monoenergetic electron-beam, accelerated by an electric field and compressed by a magnetic field, undergoes continuous collisional ionization and excitation with externally injected Xenon in the trap region. The highly charged Xenon ions were produced and confined in the trap region by the axial electric potential, a magnetic field, and the space charge effect of the electron-beam, forming a high-temperature plasma light source along with the incident electrons.
In these experiments, the electron-beam energies were set between 5.5 keV and 7.6 keV, exceeding the ionization energy to produce Ne-like Xe at 3.33 keV [63] but slightly lower than that of F-like Xe at 7.66 keV [64], resulting in a charged state distribution dominated by Ne-like Xe. The electron-beam energy conditions were chosen based on the level structure of Ne-like Xe [65] to activate different cascade transition channels at each condition, leading to significant variation in emission intensity. The electron-beam energy was determined by the potential difference between the emission cathode and the drift tube, which is modified by the space charge effect in reference to previous studies [66,67,68]. During the experiments, the beam-current was maintained between 42 mA and 48 mA. Table 1 presents the main operating parameters of the Shanghai-EBIT in these experiments. The width of electron-beam in the trap region was measured by a slit imaging system [69], allowing the inference of the electron density in the trap plasma. Typical beam width and electron density values in these experiments are 73 µm and 1.6 × 1012 cm−3, respectively.
Spectra of xenon were obtained using a high precision flat crystal spectrometer with a nominal resolving power of approximately 6500 [70], which is sufficient for resolving the lines of interest in our experiments. The oil-free rotatable feedthrough system in the crystal spectrometer creates a favorable vacuum environment, enabling direct coupling with the EBIT main chamber without the need for isolation film. This setup avoids any impact on line-intensity measurements caused by absorption from isolation film. The spectrometer was equipped with a 5.0 × 2.5 × 0.5 cm3 Si(111) crystal, with the lattice constant of 2d = 6.2712 Å. The Bragg angle was set to approximately 25.8° for measuring the wavelength region near 2.71~2.78 Å. The spectra were recorded by a CCD with 2048 × 2048 pixels (pixel size Δx = 13.5 µm). Due to the energy difference between the 3D and 3F transitions being within 0.3%, the impact of the crystal reflectivity and the CCD’s quantum efficiency on intensity measurements can be neglected. Data accumulation time ranging from 14 to 34 h were conducted at each energy condition.
To enhance the reliability of intensity measurements, the two-dimensional pixel count arrays obtained through CCD accumulation were reconstructed by photonization and filtered by count threshold using a data processing program. This program can significantly improve the signal-to-noise ratio of the spectra, thus it has been widely employed in X-ray spectroscopy measurements in our laboratory [71,72]. In the spectral processing for these experiments, count thresholds were set according to the principle of less intensity loss and baseline normalization. Figure 1b illustrates the processed X-ray spectrum obtained with the nominal electron-beam energy of 5.5 keV, which has the longest data accumulation time.
The spectra at different energies were calibrated using four strong lines with known wavelengths [6,16]: 3D, 3F, 3DNa, and 3DMg. The latter two lines are satellites of 3D, with the spectator electrons of 3s and 3s2, respectively. Voigt profile was employed for the fitting of stronger 3D and 3F lines, while Gaussian profile was used for the latter two satellites. A linear dispersive function was established between the central pixels of the four reference lines and their known wavelengths, yielding a large coefficient of determination (R2 > 0.9999). Consequently, the wavelengths of the other four weaker spectral lines are determined and presented in Table 2. The wavelength uncertainty is comprised by statistical error of pixel centroids, invalidation of the dispersive function, and the average uncertainty of the reference lines [73]. It is worth noting that a second polynomial was also attempted as the dispersive function in calibration, yielding wavelength and uncertainty results consistent with those of present linear function.

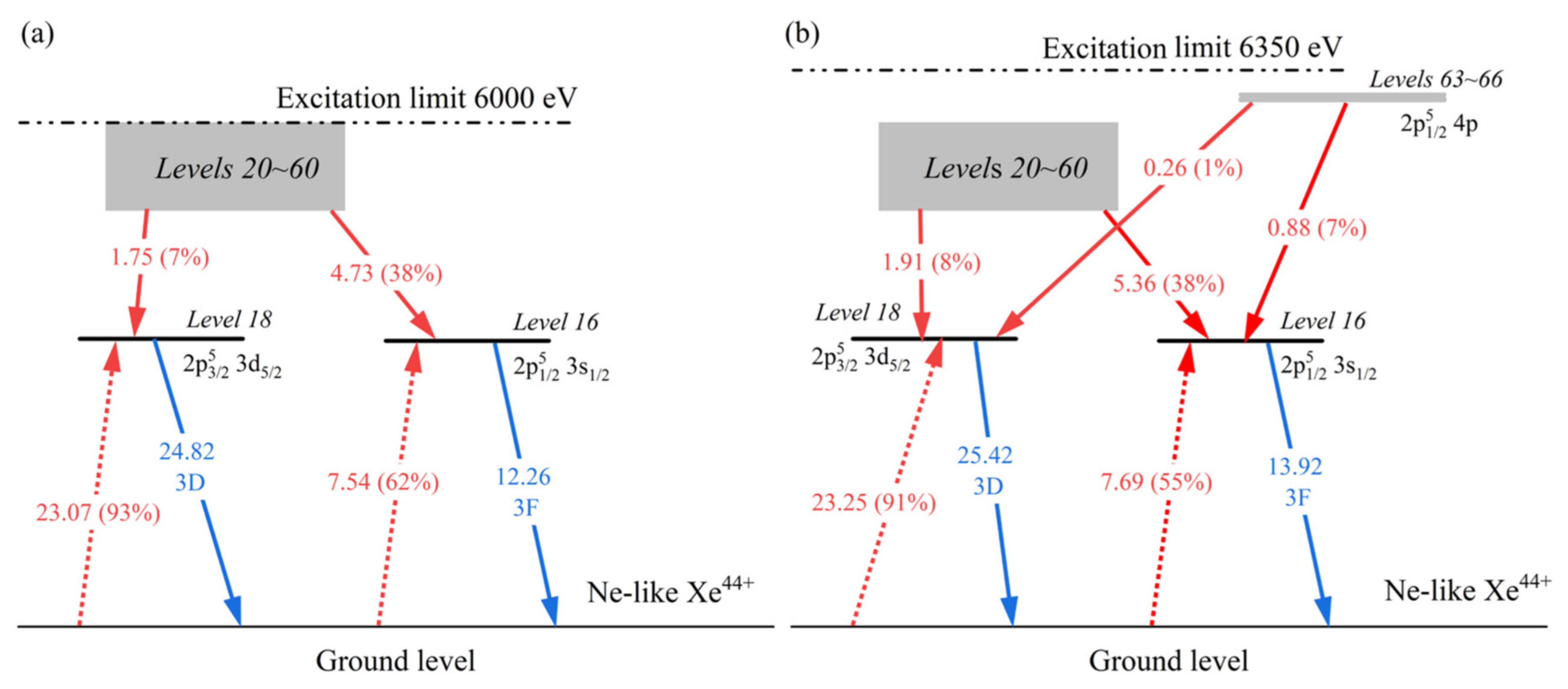
3. Calculations

We conducted atomic calculations and plasma spectroscopy simulations of highly charged Xenon using the Flexible Atomic Code (FAC) package developed by Gu [74,75,76]. Calculations about atomic levels and transitions in FAC were performed employing the Dirac-Coulomb-Breit Hamiltonian to adequately account for relativistic effects and treating electron-correlation effects within the framework of relativistic configuration interaction (RCI) approach. Additionally, FAC utilizes the distorted-wave (DW) approximation to compute collision cross-section and other parameters for electron-impact excitation (EIE), enabling us to perform simulations of electron-ion interaction in plasma.
In our calculations, for Ne-like Xe44+, a total of 293 energy levels were included, originating from the ground 1s22l8 and single-excitation configuration groups 1s22l73l (nmax = 7 and lmax = 4). The selection of configurations was guided by the discussions in Refs. [14,47] on the convergence with respect to principal quantum number n and the consideration of double excitations, while balancing computational efficiency and accuracy. Furthermore, xenon ions with near charge states were also included in the calculations. For Na-like Xe43+, a total of 1509 energy levels were included, originating from single-excitation configuration groups 1s22s22p6nl (n = 3–10 and lmax = 3) and double-excitation configuration groups 1s22l7n’l2 (n’ =3–7 and lmax = 3). For Mg-like Xe42+, a total of 3899 energy levels were included, originating from configuration groups 1s22s22p6nl2 (n = 3–5 and lmax = 2) and 1s22s22p53l2n’l1 (n’ = 3–4 and lmax = 2).
The collisional-radiative model (CRM) incorporated in FAC allows us to simulate spectra of above ions based on computed atomic parameters. CRM has been widely used in the simulation and interpretation of spectra observed from low-density, optically thin plasma, like EBIT [77,78], magnetic confinement fusion [79,80,81], astrophysical plasma [53,82], and so on. In the simulation, the processes inside EBIT plasma, which significantly influence the level populations, such as radiation transition, collisional excitation, and collisional de-excitation, are primarily considered [77]. Processes concerned about population transfers between different ions are neglected, such as radiative recombination, impact ionization, dielectronic recombination, and charge exchange. Under this assumption, the following rate equation can be used to describe the differential rate for the population of level i:
d N i d t = ∑ j > i A j i · N j + ∑ j < i C j i e · N j + ∑ j > i C j i d · N j − ∑ j < i A i j · N i − ∑ j > i C i j e · N i − ∑ j < i C i j d · N i ,
where N is the population for each level, and A, Ce, and Cd stand for the radiative transition rate, electron-impact excitation rate, and electron-impact deexcitation rate, respectively. The subscripts (i, j) represent the initial or the final levels, respectively. For EBIT plasma with monoenergetic electrons, electron-impact excitation rate Ce = neσv, where ne is electron density, v is impact electron velocity, σ is collision cross-section. The deexcitation rate Cd can be obtained from Ce by the detailed balance principle. These rate equations for all levels can be solved under the quasi-steady-state approximation dNi/dt = 0, and the normalized condition ΣiNi = 1. The line-intensity of transition can be calculated after the population of its upper level is determined.
Figure 1a illustrates the calculated spectra for Xe ions from 42+ to 44+. For comparison, plasma parameters in this simulation were set according to experimental conditions, with the electron-beam energy of 5.5 keV and the electron density of 1.6 × 1012 cm−3. The intensity results from each individual charge state were normalized to the brightest lines. In the simulated spectra, all transition lines were assumed to have the Gaussian profile with the linewidth of 0.8 mÅ, which corresponds to the experimental resolution. The theoretical wavelengths and emission intensities under the given plasma parameters are also presented in Table 2. The discrepancies between theoretical and experimental wavelengths for all lines in three ions are within 0.04%.

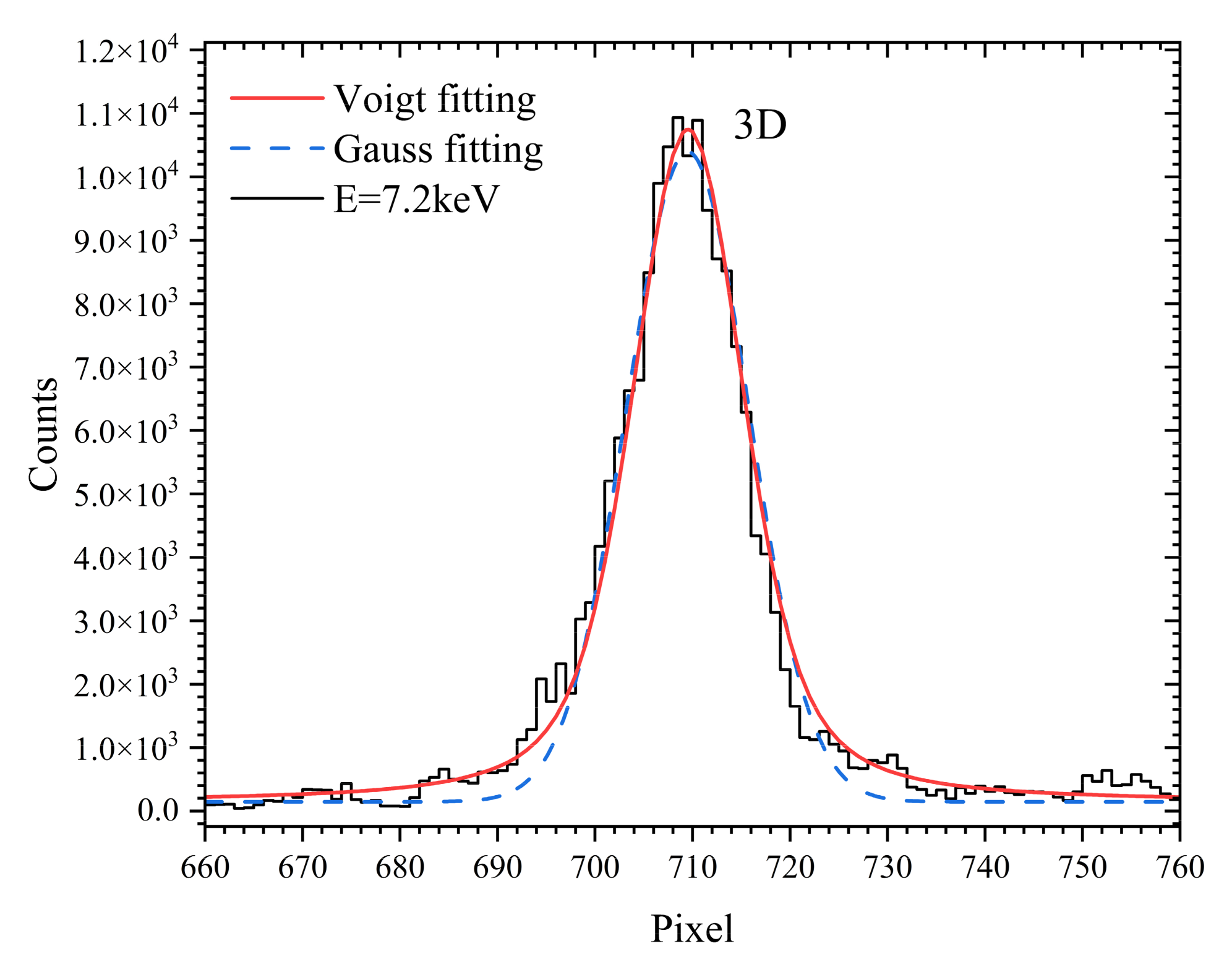
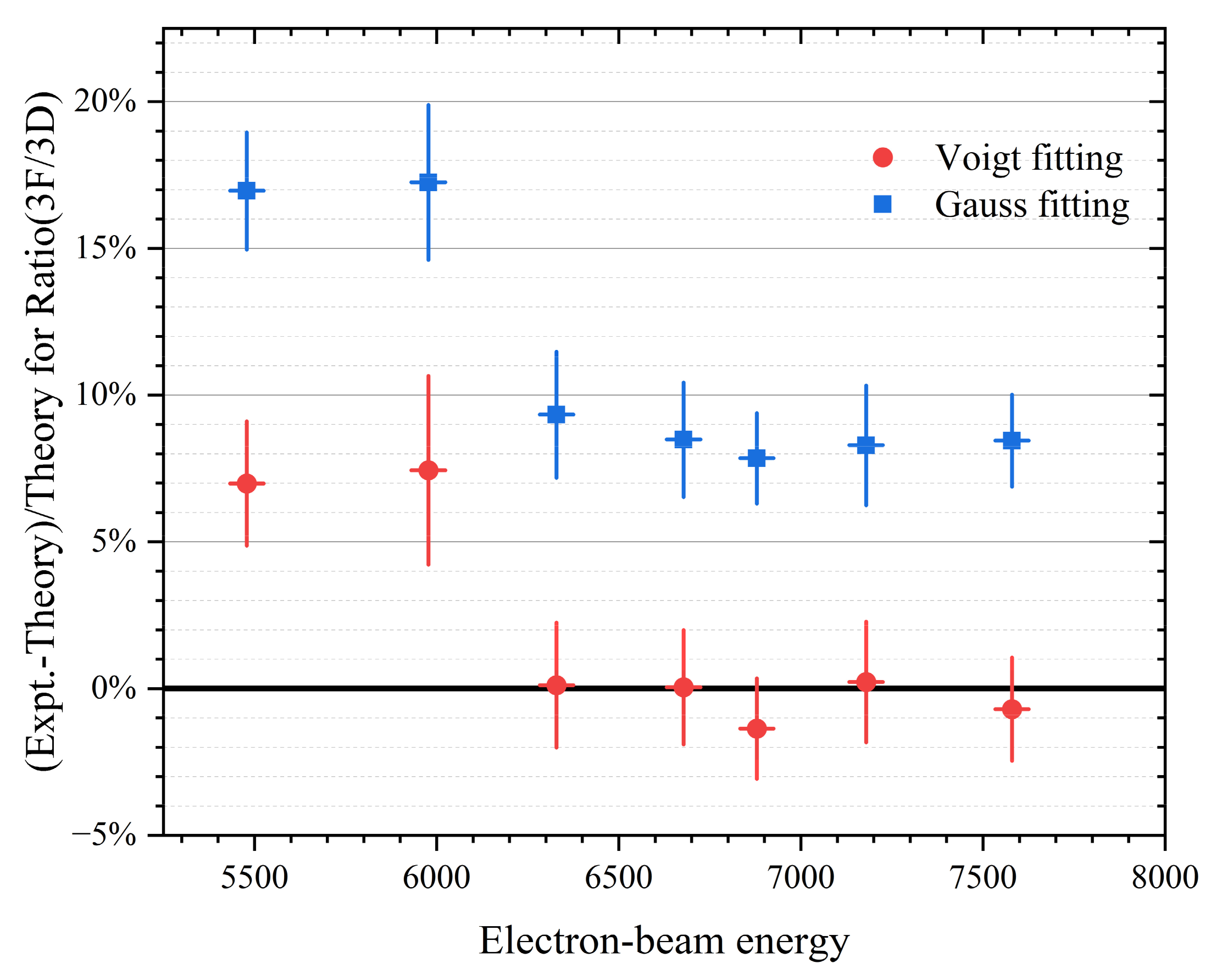
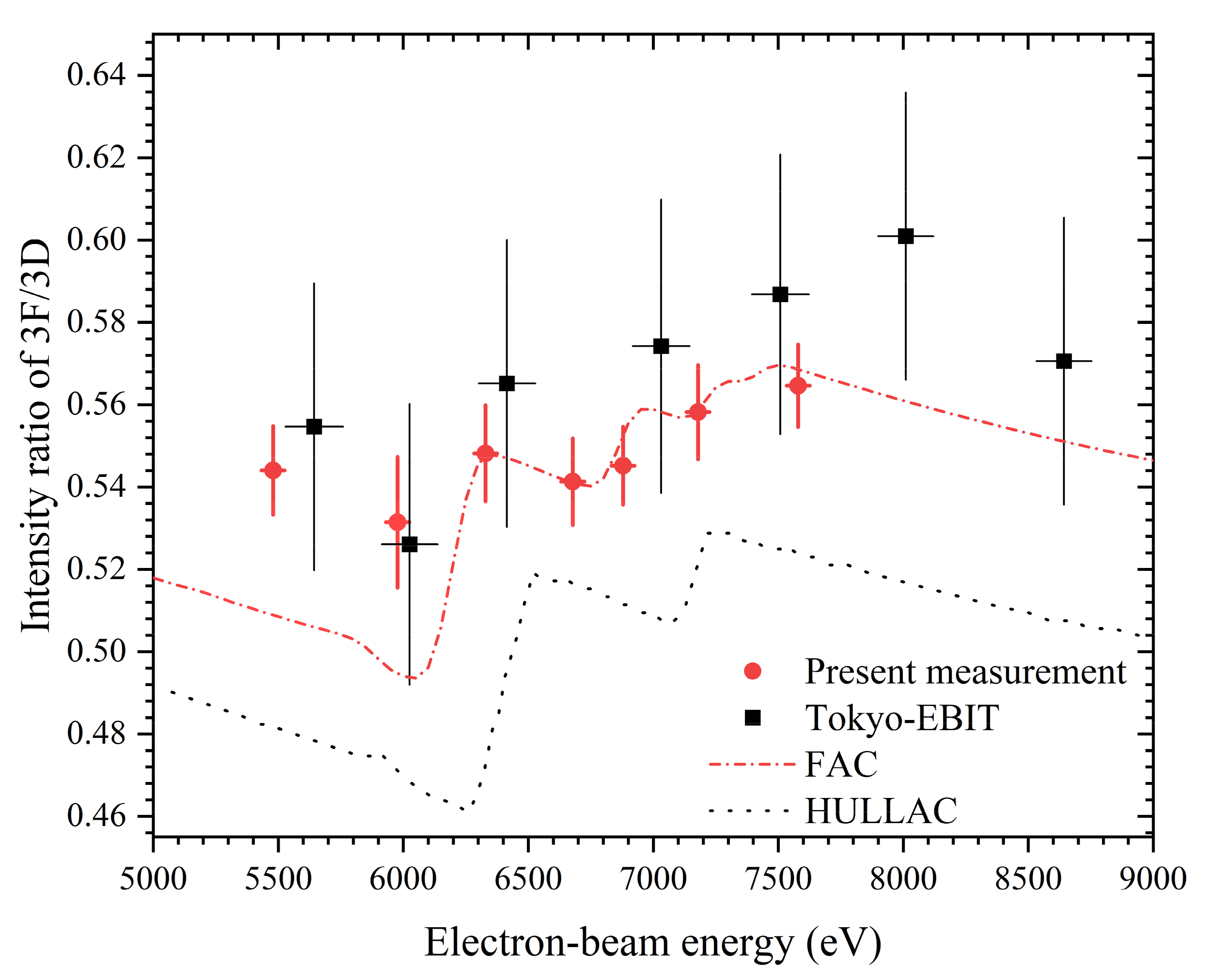
4. Results and Discussion

The identification of four weak lines was based on results from CRM simulations combined with previous measurements [9,16]. As shown in Figure 1, the experimental and theoretical spectra at 5.5 keV match well. Among the four weaker spectral lines, Na1 and Mg1 represent two-electron-one-photon transitions (TEOPT). TEOPT lines typically exhibit low intensity, attributed to their minimal transition probabilities induced by configuration interaction. Nevertheless, when a level in the TEOPT undergoes strong mixing with a correlated level that possesses the property for a strong one-electron electric-dipole transition channel, the transition probability of the TEOPT can be significantly enhanced, thus facilitating its observation. In the present case, the upper level of Mg1 (2p53/23s1/23p22)J=1 is mixed with the upper level of 3DMg (2p53/23s23d5/2)J=1, resulting in the line-intensity of Mg1 reaching 30% of the latter. The upper level of the Na1 (2p53/23p22)J=1/2 is mixed with (2p53/23s1/23d5/2)J=1/2, whose transition to the ground state has a line-intensity 1.45 times that of Na1 in the simulation. However, it cannot be observed due to blending with 3DNa in the spectrum. The Na1 line is very close to the 3D line used for ion temperature diagnostic in tokamaks (within 3.7 mÅ), making it indistinguishable in the spectrometer with insufficient resolution. This is disadvantageous for ion temperature diagnostics [24], especially at low electron temperatures. In our measurement, the Na1 line is only prominent at an electron-beam energy of 5.5 keV. The transition Na2 {(2p63p1/2)J=1/2 − (2p53/23p1/23d5/2)J=1/2}, observed for the first time, is another satellite of 3D but with 3p as the spectator electron, unlike 3DNa with 3s as the spectator electron. Its emission intensity is only 10.8% of the latter due to the absence of collisional pumping from its lower level and ground level. Thus, Na2 is almost blended with the background in the spectrum but can still be identified through careful comparison with the theoretical spectrum. In Maxwellian plasma, it may be enhanced due to resonant excitation through dielectronic capture, potentially serving as a means for electron temperature diagnostics. That is similar to well-known dielectronic satellites k (1s22p-1s2p2) in Li-like ions with 2p as the spectator electron [83,84].
Voigt profile is employed in the fitting of 3D and 3F lines at various electron-beam energies, which is crucial for line-intensity measurement according to Ref. [46]. In EBIT spectroscopy, Doppler broadening due to ion temperature and instrumental broadening typically exhibit Gaussian profiles. Additionally, excited levels have the energy distributions characterized by Lorentzian profile, with a natural width Γ related to the level lifetime τ according to the Heisenberg’s uncertainty principle [85]. Decoupling the broadening of the Voigt profile shape arising from the convolution of Lorentzian and Gaussian profile is a method for measuring level lifetimes [86]. According to calculations by Vilkas et al. [65], the lifetimes of the upper levels of 3D and 3F are 2.10 fs and 5.44 fs, respectively, corresponding to natural widths of 0.187 mÅ and 0.073 mÅ in terms of wavelength. In the fitting of 3D and 3F, these values are considered as fixed Lorentzian broadening within the Voigt function. Figure 2 illustrates the Voigt fitting curve for the 3D line at the spectrum under the electron-beam energy of 7.2 keV compared with the Gaussian one. It can be observed that the Voigt fitting curve closely follows the Lorentzian wings on both sides of the spectral peak, which is more consistent with the trend of the experimental data. By contrast, the peak area of the 3D line under Gaussian fitting profile is approximately reduced by 13.05%; while for 3F, it is reduced by 5.75%. This discrepancy in peak area loss can introduce a systematic overestimation in ratio 3F/3D if using Gaussian profile. As shown in Figure 3, relative deviations from calculations in line-intensity ratios 3F/3D under Gaussian fitting are uniformly 9.1% higher compared to Voigt fitting. This may explain the discrepancy between experimental ratios of 3F/3D and synthetic calculations reported in Ref. [16], although the fitting profile used for line-intensity ratio measurements in their work has not been described.
Figure 4 illustrates the variation of the experimental 3F/3D line-intensity ratio with electron-beam energy for all conditions, accompanied by corresponding error bars, with an average relative uncertainty of 2.1%. Total uncertainty contains statistical errors from fitting profile and reproducibility at the same energy conditions, and systematic error from threshold selection. Figure 4 also shows the theoretical curves obtained from CRM simulations based on FAC, which depicts the variation of 3F/3D line-intensity ratio with electron energy in the range 5000–8000 eV. The electron density was fixed at 1.6 × 1012 cm−3, because the impact of various electron density on the line-intensity ratios can be neglected according to another simulation with different density. The theoretical predictions of 3F/3D intensity ratio exhibit good agreement with the experimental results for electron-beam energy higher than approximately 6000 eV. Not only do they share the same trend, but the theoretical ratios also fall within the experimental error bars, with relative deviations less than 1.4%. For the results at about 6.0 keV and 5.5 keV, theoretical ratios are still lower than experimental measurements, with relative deviations of 7.0% and 7.4%, respectively. In previous study from Ref. [16], there is a larger significant discrepancy (≈13.7%) of 3F/3D between measured spectrum from Tokyo-EBIT and theoretical predictions calculated by the HULLAC code. These results are also presented in Figure 4. Our measured ratios fall within the error bars of their measured values and exhibit significantly better agreement with our calculated values, even for the results in the low-energy region. Their theoretical curves from HULLAC exhibit similar jagged changing patterns as the FAC results but differ in positions of peaks and valleys, averaging about 5% lower overall. This reflects the differences between these two theoretical methods in describing atomic structure and population equilibrium.
As previously mentioned and clearly illustrated in Figure 3, there persist notable discrepancies between experimental and theoretical results in the low electron-beam energy region. Notably, the deviations at different electron-beam energies exhibit remarkable similarity, specifically 7.0% and 7.4% for energies at 5.5 keV and 6.0 keV, respectively. This indicates that the remaining discrepancies are likely attributed to systematic shortcomings in the current CRM simulation. In the theoretical curves shown in Figure 4, there is a significant surge in the line-intensity ratio from 6000 eV to 6350 eV, whereas experimentally, the magnitude of this surge is much smaller. To explain this surge and discrepancy, we analyzed the feeding and decay fluxes in population equilibriums of the upper levels of 3F and 3D at 6000 eV and 6350 eV, as shown in Figure 5. Here the population flux refers to the rate of change in the population of a specific energy level due to electron impact excitation (EIE) and/or radiative transitions (flux = population × rate, given in cm−3·s−1). Due to the lower density in EBIT plasma, all collisional coupling processes among excited levels can be neglected, which is called corona approximation [87]. For the upper levels of 3D and 3F, the branching ratio of rapid transition to ground level is almost 100%, implying that cascade transitions to lower levels can be ignored in the decay path. Thus, the complex CRM for a certain level can be simplified to a balance among several main processes: EIE from the ground level and cascade transitions from higher levels and radiative transition, as shown in Figure 5. Particularly for feeding paths, branching ratios of EIE and cascade channel are also shown.
It can be observed from Figure 5 that for level 18 of 3D, EIE from ground level dominates the feeding path (>90%). However, for level 16 of 3F, radiative cascades from higher levels 20–60 are significant, accounting for 38% of the branching ratio at 6000 eV. As the electron-beam energy increases, the activation of new cascade channels becomes the primary factor leading to the growth of 3F intensity, as collision cross-sections exhibit less drastic changes with increasing incident electron energy. While the energy increases from 6000 eV to 6350 eV, EIE contributes only 9% to the total growth in feeding path, while cascades from new excited levels originating from 2p51/24p (levels 63–66, averaging 6170 eV above ground level) contribute 53% through rapid 4p-3s cascade channel. The rest of the growth comes from secondary cascades mediated by levels 20–60. It is noteworthy that level 64 (2p51/24p1/2)J=0 contributes the most to the growth, as its transitions back to the ground state are strictly forbidden. This indicates that the intensity of 3F is highly sensitive to changes in radiative cascade channel, unlike the idealized low-density limit where the radiative cascade is usually ignored [14,48]. In contrast, 3D is primarily influenced by the EIE from ground. Each rising edge in the theoretical curves in Figure 4 reflects the growth in cascade channels, while the declining edges reflect that the collision cross-section of the upper level of 3D rises more than that of 3F, resulting in the entire theoretical curve showing a jagged pattern.
Unlike the actual EBIT plasma environment, the current CRM discussed above only involves the population equilibrium among the levels in the single Xe44+. Further reduction of the discrepancy in the low-energy region may be achieved by considering the population transfer processes in neighboring charged states of Xenon ions, such as radiative recombination, resonance excitation and inner-shell impact ionization, as seen in the Refs. [53,88,89] for population correction in Neon-like iron. The high-sensitivity of 3F to the radiative cascade suggests that the interionic population transfer process described above can readily improve the population of the upper level of 3F by enhancing the 4p-3s or the other cascade channel. Therefore, it can be inferred that the CRM containing only a single Xe44+ underestimates the emission intensity of 3F, due to the omission of the unknown cascade channel across charged states. Our results suggest the existence of this unknown process, which is likely to be associated with low-charged ions such as Xe43+, Xe42+ or lower. This is because the experimental theoretical discrepancy is apparent only at low-energy region, where the concentration of low-charged Xenon ions is higher.
In tokamak plasma, Ne-like Xe reaches high concentration with an electron-temperature 4–10 keV [7,9]. According to our CRM simulation, in the ideal Maxwellian plasma where the EIE rates are calculated by convoluting σv (rate coefficient) with Maxwellian energy distribution function, the line-intensity ratio of 3F/3D remains constant at 0.526 ± 0.002 within this wide temperature range. This result theoretically indicates that the 3F/3D line-intensity ratio is insensitive to electron temperature, but it is inconsistent with the X-ray spectra for Ne-like Xe in EAST [9] and C-Mod tokamak [8]. The experimental 3F/3D ratios are clearly higher than above-mentioned theoretical value, especially at low electron temperature [8]. This trend implies that the unknown process described in the previous paragraph, which is also more significant at low-energy region, may have caused the discrepancy between the predicted ratios and the experimental results in tokamak.

5. Summary

At the Shanghai-EBIT, we have measured the X-ray spectra of L-shell transitions of Ne-like Xe in the range of 2.71–2.77 Å using a high-resolution crystal spectrometer. The experimental spectra contain the 3D, 3F, and 3E lines, including satellites and TEOPT lines of Na-like and Mg-like Xe. These spectra are simulated by CRM based on FAC, and are in good agreement with the experimental results. The Na2 satellite with 3p as the spectator electron is first observed, which may be relevant to temperature diagnostics in tokamak.
Our work focuses on the 3F/3D line-intensity ratios at different electron-beam energies. We use Voigt fitting profile with natural linewidth correction instead of conventional Gaussian profile during the fitting process. It is found that Voigt profile is crucial to reduce the intensity loss, and thus can obtain reasonable experimental line-intensity ratios. The discrepancies between theoretical and experimental results, previously reported approximately ranging from 10% to 20%, have been significantly reduced in this work to below 1.4% for electron-beam energies exceeding 6 keV and to around 7% for lower energies. We confirm the sensitivity of 3F intensity to higher-level radiative cascades and highlight the potential significant enhancement of the 4p-3s cascade transition channel for 3F. This suggests that the remaining discrepancies may originate from the undervaluation of the populations of cascade-related levels or the 3F upper level itself. The omission of indirect population transfer processes across charge states in the current CRM may lead to that. These findings provide a solid foundation for further minimizing these discrepancies and are crucial for understanding the atomic structure and plasma model of these ions. Similar discrepancy also exists in Tokamak spectra, which suggests that the unknown process enhancing 3F could be a new diagnostic method in fusion plasma. We leave the detailed analysis about this unaccounted process for future investigation.

Author Contributions

Conceptualization, Y.Y. and S.H.; methodology, Y.Y. and K.Y.; software, Y.Y. and S.H.; validation, S.H., Y.Y. and Z.T. (Zhiming Tang); formal analysis, S.H., C.Z., H.J., Z.T. (Ziqiang Tian) and Y.Y.; investigation, S.H., Z.T. (Ziqiang Tian) and Y.Y.; resources, Y.Y., H.Z., K.Y. and Y.Z.; data curation, S.H.; writing—original draft preparation, S.H. and Z.T. (Zhiming Tang); writing—review and editing, S.H., Z.T. (Zhiming Tang), Z.T. (Ziqiang Tian), S.M., J.L. and Y.Y.; visualization, S.H., Z.T. (Zhiming Tang) and Y.Y.; supervision, Y.Y. and H.Z.; project administration, Y.Y., H.Z. and K.Y.; funding acquisition, Y.Y., H.Z., K.Y. and Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by National Natural Science Foundation of China (Grants 11704076, 11911530229, U1732140, Grants 2021AMF01002, 1916321TS00103201, Nos. U23A2077, 12205072), the National Key Research and Development Project of PRC (approved No. 2020YFB1902100, 2022YFA1602500), the National Magnetic Confinement Fusion Science Program of China (Nos. 2019YFE0304002) and the IDP of CAS (approved No. YJKYYQ20180013).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hill, K.W.; Bitter, M.; Delgado-Aparicio, L.; Johnson, D.; Feder, R.; Beiersdorfer, P.; Dunn, J.; Morris, K.; Wang, E.; Reinke, M.; et al. Development of a spatially resolving x-ray crystal spectrometer for measurement of ion-temperature (Ti) and rotation-velocity (v) profiles in ITER. Rev. Sci. Instrum. 2010, 81, 10E322. [Google Scholar] [CrossRef] [PubMed]
  2. Beiersdorfer, P.; Clementson, J.; Dunn, J.; Gu, M.F.; Morris, K.; Podpaly, Y.; Wang, E.; Bitter, M.; Feder, R.; Hill, K.W.; et al. The ITER core imaging x-ray spectrometer. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 144008. [Google Scholar] [CrossRef]
  3. Cheng, Z.; Bader, A.; De Bock, M.; Barnsley, R.; Lorriere, P.; Pablant, N.; Costa, F.; Soeiro, J.; Bola, I.; O’Mullane, M.; et al. Novel dual-reflection design applied for ITER core x-ray spectrometer. Rev. Sci. Instrum. 2022, 93, 073502. [Google Scholar] [CrossRef] [PubMed]
  4. Lu, D.; Chen, J.; Wang, F.; Delgado-Aparicio, L.F.; Fu, J.; Zhang, H.; Bin, B.; He, L.; Shen, J.; Wang, Q.; et al. Design consideration of an x-ray imaging crystal spectrometer for China Fusion Engineering Test Reactor. Rev. Sci. Instrum. 2021, 92, 043544. [Google Scholar] [CrossRef] [PubMed]
  5. Delgado-Aparicio, L.F. Xe option for Ti and vt measurements in ITER. In Proceedings of the 32nd Meeting of ITPA Topical Group on Diagnostics, Chengdu, China, 9–12 May 2017. [Google Scholar]
  6. Beiersdorfer, P.; von Goeler, S.; Bitter, M.; Hinnov, E.; Bell, R.; Bernabei, S.; Felt, J.; Hill, K.W.; Hulse, R.; Stevens, J.; et al. X-ray transitions in highly charged neonlike ions. Phys. Rev. A 1988, 37, 4153–4162. [Google Scholar] [CrossRef]
  7. Hu, R.J.; Chen, J.; Delgado-Aparicio, L.F.; Wang, Q.P.; Du, X.W.; Shen, J.; Yang, X.S.; Wang, F.D.; Fu, J.; Li, Y.Y.; et al. Upgrade of X-ray crystal spectrometer for high temperature measurement using neon-like xenon lines on EAST. Rev. Sci. Instrum. 2018, 89, 10F110. [Google Scholar] [CrossRef]
  8. Rice, J.E.; Fournier, K.B.; Kemp, G.E.; Bitter, M.; Cao, N.; Delgado-Aparicio, L.; Hill, K.; Hubbard, A.E.; Hughes, J.W.; Reinke, M.L. X-ray observations of Ne-like Xe and satellites from C-Mod tokamak plasmas. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 055701. [Google Scholar] [CrossRef]
  9. Lu, D.; Wang, F.; Delgado-Aparicio, L.F.; Yang, Y.; Hill, K.; Bae, C.; Bitter, M.; Fu, J.; Zhang, H.; Shen, Y.; et al. Observations of xenon spectra on the EAST x-ray crystal spectrometer for high-temperature plasma diagnostics. Nucl. Fusion 2023, 63, 056002. [Google Scholar] [CrossRef]
  10. Liu, H.; Wang, F.; Fu, J.; Jin, Y.; He, L.; Lu, D.; Bae, C.; Zhang, H.; Fu, S.; Ji, H.; et al. Upgrade of poloidal and tangential x-ray imaging crystal spectrometers on EAST tokamak. In Proceedings of the 5th Optics Young Scientist Summit (OYSS 2022), Fuzhou, China, 16–19 September 2022; Lu, C.-Y., Chen, F., Li, Z., Cai, Y., Eds.; SPIE: Fuzhou, China, 2022; p. 96. [Google Scholar]
  11. Werner, T.; Zschornack, G.; Großmann, F.; Ovsyannikov, V.P.; Ullmann, E. X-ray Spectroscopy of Neon-like Xenon at the Dresden EBIT. Phys. Scr. 2001, T92, 241–243. [Google Scholar] [CrossRef]
  12. Nakamura, N.; Kato, D.; Ohtani, S. Evidence for strong configuration mixing in n=3 excited levels in neonlike ions. Phys. Rev. A 2000, 61, 052510. [Google Scholar] [CrossRef]
  13. Kentsch, U.; Zschornack, G.; Grossmann, F.; Ovsyannikov, V.P.; Ullmann, F.; Fritzsche, S. L x-ray transitions in F-like to Na-like xenon ions determined at a room temperature electron beam ion trap. X-Ray Spectrom. 2006, 35, 71–78. [Google Scholar] [CrossRef]
  14. Yang, Z.; He, Z.; Xiong, G.; Yao, K.; Yang, Y.; Wei, B.; Zou, Y.; Wu, Z.; Tian, Z.; Ma, Y.; et al. Apparent change of the 3C/3D line intensity ratio in neonlike ions. Opt. Express 2022, 30, 25326. [Google Scholar] [CrossRef] [PubMed]
  15. Kato, D.; Nakamura, N.; Ohtani, S.; Ohtani, S.; Sasaki, A. Z-Dependence of Photo-Emission Spectra for Highly Charged Neonlike Ions. Phys. Scr. 2001, T92, 126–129. [Google Scholar] [CrossRef]
  16. Kato, D.; Nakamura, N.; Shunsuke, O. X-Ray Spectral Analysis on Electron Interaction with Highly-Charged Ions in Tokyo-EBIT. J. Plasma Fusion Res. 2006, 7, 190–194. [Google Scholar]
  17. Beiersdorfer, P. Spectroscopy with trapped highly charged ions. Phys. Scr. 2009, T134, 014010. [Google Scholar] [CrossRef]
  18. Keane, C.J.; Lee, R.W.; Hammel, B.A.; Osterheld, A.L.; Suter, L.J.; Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B. Line broadening of Ne-like xenon as a diagnostic for high-density implosion experiments. Rev. Sci. Instrum. 1990, 61, 2780–2782. [Google Scholar] [CrossRef]
  19. Conturie, Y.; Yaakobi, B.; Feldman, U.; Doschek, G.A.; Cowan, R.D. Observation of new lines of Xe xliv, xlv, xlvi, and xlvii in the range 2.5–3.0 Å from laser-imploded targets. J. Opt. Soc. Am. 1981, 71, 1309–1314. [Google Scholar] [CrossRef]
  20. Keane, C.J.; Hammel, B.A.; Kania, D.R.; Kilkenny, J.D.; Lee, R.W.; Osterheld, A.L.; Suter, L.J.; Mancini, R.C.; Hooper, C.F.; Delamater, N.D. X-ray spectroscopy of high-energy density inertial confinement fusion plasmas. Phys. Fluids B Plasma Phys. 1993, 5, 3328–3336. [Google Scholar] [CrossRef]
  21. Aglitskii, E.V.; Ivanova, E.P.; Panin, S.A.; Safronova, U.I.; Ulityn, S.I.; Vainshtein, L.A.; Wyart, J.-F. Investigation of the spectra of dipole 2–3 transitions in Ne-like ions ( Z = 36–92). Phys. Scr. 1989, 40, 601–609. [Google Scholar] [CrossRef]
  22. Hu, L.Q.; Liu, Y. Progress of engineering design of CFETR diagnostics. Fusion Eng. Des. 2020, 155, 111731. [Google Scholar] [CrossRef]
  23. Hutton, R.; Zou, Y.; Andersson, M.; Brage, T.; Martinson, I. Some historic and current aspects of plasma diagnostics using atomic spectroscopy. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 144026. [Google Scholar] [CrossRef]
  24. Beiersdorfer, P. Highly charged ions in magnetic fusion plasmas: Research opportunities and diagnostic necessities. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 144017. [Google Scholar] [CrossRef]
  25. Rice, J.E.; Fournier, K.B.; Goetz, J.A.; Marmar, E.S.; Terry, J.L. X-ray observations of 2l-nl’ transitions and configuration-interaction effects from Kr, Mo, Nb and Zr in near neon-like charge states from tokamak plasmas. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 5435–5462. [Google Scholar] [CrossRef]
  26. Beiersdorfer, P.; Lepson, J.K.; Schneider, M.B.; Bode, M.P. L -shell x-ray emission from neonlike W64+. Phys. Rev. A 2012, 86, 012509. [Google Scholar] [CrossRef]
  27. Li, J.; Grumer, J.; Li, W.; Andersson, M.; Brage, T.; Hutton, R.; Jönsson, P.; Yang, Y.; Zou, Y. Theoretical investigation of magnetic-field-induced 2p53s 3P0,2–2p6 1S0transitions in Ne-like ions without nuclear spin. Phys. Rev. A 2013, 88, 013416. [Google Scholar] [CrossRef]
  28. Syrocki, Ł.; Słabkowska, K.; Węder, E.; Polasik, M.; Rzadkiewicz, J. Theoretical Modeling of High-Resolution X-ray Spectra Emitted by Tungsten and Molybdenum Ions from Tokamak Plasmas. J. Fusion Energy 2020, 39, 194–201. [Google Scholar] [CrossRef]
  29. Young, B.K.F.; Osterheld, A.L.; Walling, R.S.; Goldstein, W.H.; Phillips, T.W.; Stewart, R.E.; Charatis, G.; Busch, G.E. Measurement of density-sensitive electric quadrupole transitions in neonlike laser-produced plasmas. Phys. Rev. Lett. 1989, 62, 1266–1269. [Google Scholar] [CrossRef] [PubMed]
  30. Keane, C.J.; Hammel, B.A.; Osterheld, A.L.; Kania, D.R. Density and temperature sensitive features in high temperature plasma L-shell xenon emission spectra. Phys. Rev. Lett. 1994, 72, 3029–3032. [Google Scholar] [CrossRef]
  31. Shevelko, A.P.; Yakushev, O.F.; Vainshtein, L.A.; Andreev, S.N.; Tolstikhina, I.Y. X-ray spectroscopy comparison methods for diagnostics of high-temperature molybdenum plasmas. Phys. Plasmas 2018, 25, 073306. [Google Scholar] [CrossRef]
  32. Träbert, E.; Beiersdorfer, P.; López-Urrutia, J.R.C. Atomic lifetime measurements of Ne-like Fe ions in a magnetic field. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 408, 107–109. [Google Scholar] [CrossRef]
  33. Beiersdorfer, P.; López-Urrutia, J.R.C.; Träbert, E. Measurement of the radiative decay rate and energy of the metastable level in Fe xvii. Astrophys. J. 2016, 817, 67. [Google Scholar] [CrossRef]
  34. Paerels, F.B.S.; Kahn, S.M. High-Resolution X-Ray Spectroscopy with Chandra and XMM-Newton. Annu. Rev. Astron. Astrophys. 2003, 41, 291–342. [Google Scholar] [CrossRef]
  35. Behar, E.; Cottam, J.; Kahn, S.M. The Chandra Iron-L X-Ray Line Spectrum of Capella. Astrophys. J. 2001, 548, 966–975. [Google Scholar] [CrossRef]
  36. Brown, G.V.; Beiersdorfer, P.; Chen, H.; Chen, M.H.; Reed, K.J. Diagnostic utility of the relative intensity of 3C to 3D IN Fe xvii. Astrophys. J. 2001, 557, L75. [Google Scholar] [CrossRef]
  37. Schmelz, J.T.; Saba, J.L.R.; Chauvin, J.C.; Strong, K.T. Investigating the Effect of Opacity in Soft X-Ray Spectral Lines Emitted by Solar Coronal Active Regions. Astrophys. J. 1997, 477, 509–515. [Google Scholar] [CrossRef]
  38. Beiersdorfer, P.; Von Goeler, S.; Bitter, M.; Thorn, D.B. Measurement of the 3d → 2p resonance to intercombination line-intensity ratio in neonlike Fe XVII, Ge XXIII, and Se XXV. Phys. Rev. A 2001, 64, 032705. [Google Scholar] [CrossRef]
  39. Brown, G.V.; Beiersdorfer, P.; Chen, H.; Scofield, J.H.; Boyce, K.R.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S.; Gu, M.F.; Kahn, S.M.; et al. Energy-Dependent Excitation Cross Section Measurements of the Diagnostic Lines of Fe XVII. Phys. Rev. Lett. 2006, 96, 253201. [Google Scholar] [CrossRef] [PubMed]
  40. Nikulin, V.K.; Trzhaskovskaya, M.B. Comment on “Energy-Dependent Excitation Cross Section Measurements of the Diagnostic Lines of Fe XVII. ” Phys. Rev. Lett. 2012, 108, 139301. [Google Scholar] [CrossRef] [PubMed]
  41. Bernitt, S.; Brown, G.V.; Rudolph, J.K.; Steinbrügge, R.; Graf, A.; Leutenegger, M.; Epp, S.W.; Eberle, S.; Kubiček, K.; Mäckel, V.; et al. An unexpectedly low oscillator strength as the origin of the Fe xvii emission problem. Nature 2012, 492, 225–228. [Google Scholar] [CrossRef]
  42. Kühn, S.; Shah, C.; López-Urrutia, J.R.C.; Fujii, K.; Steinbrügge, R.; Stierhof, J.; Togawa, M.; Harman, Z.; Oreshkina, N.S.; Cheung, C.; et al. High Resolution Photoexcitation Measurements Exacerbate the Long-Standing Fe XVII Oscillator Strength Problem. Phys. Rev. Lett. 2020, 124, 225001. [Google Scholar] [CrossRef]
  43. Mendoza, C.; Bautista, M.A. Theoretical Confirmation of the Low Experimental 3C/3D f -Value Ratio in Fe xvii. Phys. Rev. Lett. 2017, 118, 163002. [Google Scholar] [CrossRef] [PubMed]
  44. Oreshkina, N.S.; Cavaletto, S.M.; Keitel, C.H.; Harman, Z. Astrophysical Line Diagnosis Requires Nonlinear Dynamical Atomic Modeling. Phys. Rev. Lett. 2014, 113, 143001. [Google Scholar] [CrossRef] [PubMed]
  45. Brown, G.V. A brief review of the intensity of lines 3C and 3D in neon-like Fe XVII. Can. J. Phys. 2008, 86, 199–208. [Google Scholar] [CrossRef]
  46. Kühn, S.; Cheung, C.; Oreshkina, N.S.; Steinbrügge, R.; Togawa, M.; Bernitt, S.; Berger, L.; Buck, J.; Hoesch, M.; Seltmann, J.; et al. New Measurement Resolves Key Astrophysical Fe XVII Oscillator Strength Problem. Phys. Rev. Lett. 2022, 129, 245001. [Google Scholar] [CrossRef] [PubMed]
  47. Santana, J.A.; Lepson, J.K.; Träbert, E.; Beiersdorfer, P. Electron-correlation effects on the 3C to 3D line-intensity ratio in the Ne-like ions Ar8+ to Kr26+. Phys. Rev. A 2015, 91, 012502. [Google Scholar] [CrossRef]
  48. Fournier, K.B.; Hansen, S.B. Resolution of the long-standing overprediction of the resonance to intercombination line-intensity ratio in mid-Z neonlike ions. Phys. Rev. A 2005, 71, 012717. [Google Scholar] [CrossRef]
  49. Chen, G.-X. Converged Dirac R-matrix calculation of electron impact excitation of Fe XVII. Phys. Rev. A 2007, 76, 062708. [Google Scholar] [CrossRef]
  50. Gu, M.F.; Beiersdorfer, P.; Brown, G.V.; Chen, H.; Boyce, K.R.; Kelley, R.L.; Kilbourne, C.A.; Porter, F.S.; Kahn, S.M. Laboratory Measurements of 3 → 2 X-Ray Emission Lines of Ne-like Ni xix. Astrophys. J. 2004, 607, L143–L146. [Google Scholar] [CrossRef]
  51. Panchenko, D.; Beiersdorfer, P.; Hell, N.; Brown, G.V.; Kelley, R.; Kilbourne, C.A.; Porter, F.S. Resonance-to-intercombination-line ratios of neonlike ions in the relativistic regime. Phys. Rev. A 2017, 95, 062503. [Google Scholar] [CrossRef]
  52. Wu, C.; Gao, X. Change of the relative line strengths due to the resonance induced population transfer between Fe XVII and FeXVI ions. Sci. Rep. 2019, 9, 7463. [Google Scholar] [CrossRef]
  53. Chen, G.X. X-ray line ratio 3C/3D in Fe xvii. Mon. Not. R. Astron. Soc. Lett. 2008, 386, L62–L66. [Google Scholar] [CrossRef]
  54. Loch, S.D.; Ballance, C.P.; Li, Y.; Fogle, M.; Fontes, C.J. Non-equilibrium modeling of the fe xvii 3C/3D line ratio in an intense x-ray free-electron laser excited plasma. Astrophys. J. 2015, 801, L13. [Google Scholar] [CrossRef]
  55. Wu, Z.W.; Tian, Z.Q.; An, Y.H.; Dong, C.Z. Angular Distribution and Polarization of the 3C and 3D Lines Following Electron-impact Excitation of Fe16+ Ions. Astrophys. J. 2021, 910, 142. [Google Scholar] [CrossRef]
  56. Petkov, E.E.; Safronova, A.S.; Kantsyrev, V.L.; Stafford, A.; Safronova, U.I.; Shlyaptseva, V.V.; Beiersdorfer, P.; Hell, N.; Brown, G.V. Polarization measurements of Ne-like Mo32+ x-ray lines excited by an electron beam. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 195002. [Google Scholar] [CrossRef]
  57. Beiersdorfer, P.; Scofield, J.H.; Brown, G.V.; Chen, M.H.; Hell, N.; Osterheld, A.L.; Vogel, D.A.; Wong, K.L. Avoided level crossings in very highly charged ions. Phys. Rev. A 2016, 93, 051403. [Google Scholar] [CrossRef]
  58. Beiersdorfer, P.; Obst, M.; Safronova, U.I. Radiative decay probabilities of the ( 2s22p51/23s1/2) J=0 level in neonlike ions. Phys. Rev. A 2011, 83, 012514. [Google Scholar] [CrossRef]
  59. Safronova, U.I.; Cowan, T.E.; Safronova, M.S. Relativistic many-body calculations of electric-dipole lifetimes, transition rates and oscillator strengths for 2l−1 3l′ states in Ne-like ions. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2741–2763. [Google Scholar] [CrossRef]
  60. Yang, Z.; Chen, G.; Zhong, Y.; Zhang, C.; Tu, H.; Luo, T.; He, Z.; Hu, Z. Effect of the configuration mixing on the polarization and angular distribution of x-ray line emissions following electron-impact excitation of Ne-like ions. Opt. Express 2024, 32, 9877. [Google Scholar] [CrossRef] [PubMed]
  61. Lu, D.; Yang, Y.; Xiao, J.; Shen, Y.; Fu, Y.; Wei, B.; Yao, K.; Hutton, R.; Zou, Y. Upgrade of the electron beam ion trap in Shanghai. Rev. Sci. Instrum. 2014, 85, 093301. [Google Scholar] [CrossRef]
  62. Zhu, X.; Liu, Y.; Wang, X.; Liu, Y.; Guo, P.; Lu, D.; Zhang, X.; Hu, W.; He, M.; Liljeby, L.; et al. Status of the Shanghai EBIT. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2005, 235, 509–513. [Google Scholar] [CrossRef]
  63. Theodosiou, C.E.; Curtis, L.J. Accurate calculations of 3p and 3d lifetimes in the Na sequence. Phys. Rev. A 1988, 38, 4435–4445. [Google Scholar] [CrossRef] [PubMed]
  64. Rodrigues, G.C.; Indelicato, P.; Santos, J.P.; Patté, P.; Parente, F. Systematic calculation of total atomic energies of ground state configurations. At. Data Nucl. Data Tables 2004, 86, 117–233. [Google Scholar] [CrossRef]
  65. Vilkas, M.J.; López-Encarnación, J.M.; Ishikawa, Y. Relativistic multireference Møller–Plesset perturbation theory calculations of the energy levels and transition probabilities in Ne-like xenon, tungsten, and uranium ions. At. Data Nucl. Data Tables 2008, 94, 50–70. [Google Scholar] [CrossRef]
  66. Lu, Q.; He, J.; Tian, H.; Li, M.; Yang, Y.; Yao, K.; Chen, C.; Xiao, J.; Li, J.G.; Tu, B.; et al. Observation of indirect ionization of W7+ in an electron-beam ion-trap plasma. Phys. Rev. A 2019, 99, 042510. [Google Scholar] [CrossRef]
  67. Liang, G.Y.; Crespo López-Urrutia, J.R.; Baumann, T.M.; Epp, S.W.; Gonchar, A.; Lapierre, A.; Mokler, P.H.; Simon, M.C.; Tawara, H.; Mäckel, V.; et al. Experimental investigations of ion charge distributions, effective electron densities, and electron-ion cloud overlap in electron beam ion trap plasma using extreme-ultraviolet spectroscopy. Astrophys. J. 2009, 702, 838–850. [Google Scholar] [CrossRef]
  68. Tu, B.; Lu, Q.F.; Cheng, T.; Li, M.C.; Yang, Y.; Yao, K.; Shen, Y.; Lu, D.; Xiao, J.; Hutton, R.; et al. Characteristics of the Shanghai high-temperature superconducting electron-beam ion trap and studies of the space-charge effect under ultralow-energy operating conditions. Phys. Plasmas 2017, 24, 103507. [Google Scholar] [CrossRef]
  69. Yang, Y.; Lu, D.; Fu, Y.-Q.; Yao, K.; Chen, W.-D.; Xiao, J.; Geng, Z.-X.; Zou, Y.-M. Electron beam density study using a portable slit imaging system at the Shanghai Electron Beam Ion Trap. Chin. Phys. B 2011, 20, 080701. [Google Scholar] [CrossRef]
  70. Yang, Y.; Xiao, J.; Lu, D.; Shen, Y.; Yao, K.; Chen, C.; Hutton, R.; Zou, Y. A high precision flat crystal spectrometer compatible for ultra-high vacuum light source. Rev. Sci. Instrum. 2017, 88, 113108. [Google Scholar] [CrossRef] [PubMed]
  71. Xiao, J.; Gao, Y.; Zhang, X.; Lu, D.; Hu, W.; Gao, M.; Chen, W.; Zou, Y. High resolution flat crystal spectrometer for the Shanghai EBIT. Rev. Sci. Instrum. 2008, 79, 093101. [Google Scholar] [CrossRef]
  72. Rzadkiewicz, J.; Yang, Y.; Kozioł, K.; O’Mullane, M.G.; Patel, A.; Xiao, J.; Yao, K.; Shen, Y.; Lu, D.; Hutton, R.; et al. High-resolution tungsten spectroscopy relevant to the diagnostic of high-temperature tokamak plasmas. Phys. Rev. A 2018, 97, 052501. [Google Scholar] [CrossRef]
  73. Li, Y.; Wang, Y.; Fan, J.; Si, R.; Li, J.; Zhang, M.; Huang, L.; Xiao, J.; Zou, Y.; Wei, B.; et al. Precise wavelength determination of the 4s24p 2P3/2–2P1/2 transition in Mo11+ and Ru13+ ions. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 235001. [Google Scholar] [CrossRef]
  74. Gu, M.F. The Flexible Atomic Code. In Proceedings of the AIP Conference Proceedings; AIP: Santa Fe, NM, USA, 2004; Volume 730, pp. 127–136. [Google Scholar]
  75. Gu, M.F. Electron-impact excitation of Fe XXII: Comparative study of relativistic R -matrix and distorted-wave approaches. Phys. Rev. A 2004, 70, 062704. [Google Scholar] [CrossRef]
  76. Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
  77. Ding, X.; Zhang, F.; Yang, Y.; Zhang, L.; Koike, F.; Murakami, I.; Kato, D.; Sakaue, H.A.; Nakamura, N.; Dong, C. Collisional-radiative modeling of the 5 p−5 s spectrum of W xiv–W xvi ions. Phys. Rev. A 2020, 101, 042509. [Google Scholar] [CrossRef]
  78. Ding, X.; Yang, J.; Zhu, L.; Koike, F.; Murakami, I.; Kato, D.; Sakaue, H.A.; Nakamura, N.; Dong, C. Collisional radiative model for the M1 transition spectrum of the highly-charged W 54+ ions. Phys. Lett. A 2018, 382, 2321–2325. [Google Scholar] [CrossRef]
  79. Słabkowska, K.; Polasik, M.; Syrocki, Ł.; Szymańska, E.; Rzadkiewicz, J.; Pereira, N.R. Modeling of the M X-ray line structures for tungsten and L X-ray line structures for molybdenum. J. Phys. Conf. Ser. 2015, 583, 012036. [Google Scholar] [CrossRef]
  80. Kozioł, K.; Brosławski, A.; Patel, A.; Weisen, H.; Rzadkiewicz, J. Ion temperature spectroscopic measurements in high rotation discharges by means of X-ray diagnostic at JET. J. Instrum. 2022, 17, C07008. [Google Scholar] [CrossRef]
  81. Xie Hui-Qiao; Tan Yi; Liu Yang-Qing; Wang Wen-Hao; Gao Zhe; Department of Engineering Physics, Tsinghua University, Beijing 100084, China A collisional-radiative model for the helium plasma in the sino-united spherical tokamak and its application to the line intensity ratio diagnostic. Acta Phys. Sin. 2014, 63, 125203. [CrossRef]
  82. Liang, G.Y.; Zhao, G.; Zeng, J.L.; Shi, J.R. Identification and analysis of soft X-ray lines of Ar xiii-Ar xvi in laboratory and astrophysical plasmas. Mon. Not. R. Astron. Soc. 2004, 350, 298–306. [Google Scholar] [CrossRef]
  83. Biedermann, C.; Radtke, R.; Fournier, K.B. Spectroscopy of heliumlike argon resonance and satellite lines for plasma temperature diagnostics. Phys. Rev. E 2002, 66, 066404. [Google Scholar] [CrossRef]
  84. Widmann, K.; Beiersdorfer, P.; Decaux, V.; Elliott, S.R.; Knapp, D.; Osterheld, A.; Bitter, M.; Smith, A. Studies of He-like krypton for use in determining electron and ion temperatures in very-high-temperature plasmas. Rev. Sci. Instrum. 1995, 66, 761–763. [Google Scholar] [CrossRef]
  85. Lewis, G.N.; Mayer, J.E. The quantum laws and the uncertainty principle of heisenberg. Proc. Natl. Acad. Sci. USA 1929, 15, 127–139. [Google Scholar] [CrossRef] [PubMed]
  86. Beiersdorfer, P.; Osterheld, A.L.; Decaux, V.; Widmann, K. Observation of Lifetime-Limited X-Ray Linewidths in Cold Highly Charged Ions. Phys. Rev. Lett. 1996, 77, 5353–5356. [Google Scholar] [CrossRef] [PubMed]
  87. Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 56, ISBN 978-3-642-02232-6. [Google Scholar]
  88. Doron, R.; Behar, E. The X-Ray Spectrum of Fe 16+ Revisited with a Multi-Ion Model. Astrophys. J. 2002, 574, 518–526. [Google Scholar] [CrossRef]
  89. Gu, M.F. Indirect X-Ray Line-Formation Processes in Iron L-Shell Ions. Astrophys. J. 2003, 582, 1241–1250. [Google Scholar] [CrossRef]
Applsci 14 04381 g001
Figure 1. A comparison between calculated (a) and observed (b) X-ray spectra of L-shell transitions from Ne-like Xe and near charge states. The observed spectrum was measured by a crystal spectrometer installed in the Shanghai-EBIT, utilizing a nominal electron-beam of 5.5 keV. The calculated spectrum was generated by CRM based on FAC package with the electron energy of 5.5 keV and electron density of 1.6 × 1012 cm−3. The results from each individual charge state are normalized to the brightest lines.
Figure 1. A comparison between calculated (a) and observed (b) X-ray spectra of L-shell transitions from Ne-like Xe and near charge states. The observed spectrum was measured by a crystal spectrometer installed in the Shanghai-EBIT, utilizing a nominal electron-beam of 5.5 keV. The calculated spectrum was generated by CRM based on FAC package with the electron energy of 5.5 keV and electron density of 1.6 × 1012 cm−3. The results from each individual charge state are normalized to the brightest lines.
Applsci 14 04381 g001
Applsci 14 04381 g002
Figure 2. The 3D peak from Ne-like Xe fitted with Gaussian (blue dash) and Voigt (red solid) profiles at an electron-beam energy of 7.2 keV. Voigt fitting was conducted with a fixed Lorentz width of 0.187 mÅ, as inferred from Ref. [65].
Figure 2. The 3D peak from Ne-like Xe fitted with Gaussian (blue dash) and Voigt (red solid) profiles at an electron-beam energy of 7.2 keV. Voigt fitting was conducted with a fixed Lorentz width of 0.187 mÅ, as inferred from Ref. [65].
Applsci 14 04381 g002
Applsci 14 04381 g003
Figure 3. Relative differences between experimental and theoretical line-intensity ratios of 3F/3D fitted with Gaussian (blue square) and Voigt (red circle) profiles.
Figure 3. Relative differences between experimental and theoretical line-intensity ratios of 3F/3D fitted with Gaussian (blue square) and Voigt (red circle) profiles.
Applsci 14 04381 g003
Applsci 14 04381 g004
Figure 4. The measured and calculated intensity ratio of 3F/3D as a function of electron-beam energy. The measured ratios (red circle) with errors are derived from Voigt fitting results of peaks in the spectra obtained from Shanghai-EBIT. The theoretical ratios (red short dash dot) are calculated using CRM based on the FAC package, with a fixed electron density of 1.6 × 1012 cm−3. Both experimental measurements (black square) by Tokyo-EBIT and theoretical predictions (black short dot) by the HULLAC code for the line-intensity ratios are from Ref. [16].
Figure 4. The measured and calculated intensity ratio of 3F/3D as a function of electron-beam energy. The measured ratios (red circle) with errors are derived from Voigt fitting results of peaks in the spectra obtained from Shanghai-EBIT. The theoretical ratios (red short dash dot) are calculated using CRM based on the FAC package, with a fixed electron density of 1.6 × 1012 cm−3. Both experimental measurements (black square) by Tokyo-EBIT and theoretical predictions (black short dot) by the HULLAC code for the line-intensity ratios are from Ref. [16].
Applsci 14 04381 g004
Applsci 14 04381 g005
Figure 5. Grotrian diagram of the main levels concerned about 3D and 3F transitions in Ne-like Xe44+. The italic numbers are the indexes of levels in FAC calculations, especially level 16 for 3F and level 18 for 3D. The gray rectangle refers to a series of energy levels 20–60 below 6000 eV. Levels 63–66 are from configuration 2p51/24p. The fluxes (in cm−3·s−1) of feeding paths (red arrows) and radiative decay paths (blue arrows) are shown in the electron-beam energy of 6000 eV (a) and 6350 eV (b), with the excitation limit on it respectively. The branching ratios of feeding paths for level 18 and level 16 are shown in parentheses behind the flux values, including electron-impact excitation (EIE, short dot arrows) and cascade transition (solid arrows).
Figure 5. Grotrian diagram of the main levels concerned about 3D and 3F transitions in Ne-like Xe44+. The italic numbers are the indexes of levels in FAC calculations, especially level 16 for 3F and level 18 for 3D. The gray rectangle refers to a series of energy levels 20–60 below 6000 eV. Levels 63–66 are from configuration 2p51/24p. The fluxes (in cm−3·s−1) of feeding paths (red arrows) and radiative decay paths (blue arrows) are shown in the electron-beam energy of 6000 eV (a) and 6350 eV (b), with the excitation limit on it respectively. The branching ratios of feeding paths for level 18 and level 16 are shown in parentheses behind the flux values, including electron-impact excitation (EIE, short dot arrows) and cascade transition (solid arrows).
Applsci 14 04381 g005
Table 1. EBIT operation parameters (electron-beam energy, current, and accumulation time).
Table 1. EBIT operation parameters (electron-beam energy, current, and accumulation time).
Ee (keV)Ie (mA)Time (h)
5.5042.334
6.0047.818
6.3545.022
6.7048.528
6.9047.020
7.2048.314
7.6048.022
Table 2. Summary of measured L-shell transition lines from highly charged Xenon and comparison with theoretical values calculated by FAC. All wavelengths are in Å. The line-intensity, given in photons/(ion·s), was calculated using CRM based on FAC at an electron-beam energy of 5.5 keV and an electron density of 1.6 × 1012 cm−3. Δ is the relative difference between present EBIT measured and calculated wavelength, where Δ = (λFAC − λmeasured)/λmeasured.
Table 2. Summary of measured L-shell transition lines from highly charged Xenon and comparison with theoretical values calculated by FAC. All wavelengths are in Å. The line-intensity, given in photons/(ion·s), was calculated using CRM based on FAC at an electron-beam energy of 5.5 keV and an electron density of 1.6 × 1012 cm−3. Δ is the relative difference between present EBIT measured and calculated wavelength, where Δ = (λFAC − λmeasured)/λmeasured.
ExperimentTheory
ChargeLabelUpper LevelLower LevelλmeasuredλotherλFACΔIntensity
443D(2p53/23d5/2)J=1(2p6)J=02.7203 (1)2.7203 (1) a,b2.720570.010%23.98
43Na1(2p53/23p22)J=1/2(2p63s)J=1/22.7240 (2)2.7240 d2.72385−0.006%2.96
443F(2p51/2 3s1/2)J=1(2p6)J=02.7288 (1)2.7288 (1) a,b2.729450.023%12.20
433DNa(2p53/23s1/23d5/2)J=3/2(2p63s)J=1/22.7358 (2)2.7358 (2) a,c2.735950.006%18.41
43Na2(2p53/23p1/23d5/2)J=1/2(2p63p1/2)J=1/22.7408 (2) 2.741030.009%1.99
423DMg(2p53/23s23d5/2)J=1(2p63s2)J=02.7460 (2)2.7460 (2) a,c2.74505−0.035%11.94
443E(2p53/23d3/2)J=1(2p6)J=02.7534 (2)2.7535 (2) c2.754250.030%1.33
42Mg1 (2p53/23s1/23p22)J=1(2p63s2)J=02.7595 (2)2.7596 (2) c2.759750.010%3.62
a Reference lines used in calibration; b Beiersdorfer et al., Ref. [6]; c Kato et al., Ref. [16]; d Lu et al., Ref. [9].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Huang, S.; Tang, Z.; Yang, Y.; Zhang, H.; Tian, Z.; Ma, S.; Li, J.; Zeng, C.; Ji, H.; Yao, K.; et al. X-ray Line-Intensity Ratios in Neon-like Xenon: Significantly Reducing the Discrepancy between Measurements and Simulations. Appl. Sci. 2024, 14, 4381. https://doi.org/10.3390/app14114381

AMA Style

Huang S, Tang Z, Yang Y, Zhang H, Tian Z, Ma S, Li J, Zeng C, Ji H, Yao K, et al. X-ray Line-Intensity Ratios in Neon-like Xenon: Significantly Reducing the Discrepancy between Measurements and Simulations. Applied Sciences. 2024; 14(11):4381. https://doi.org/10.3390/app14114381

Chicago/Turabian Style

Huang, Shihan, Zhiming Tang, Yang Yang, Hongming Zhang, Ziqiang Tian, Shaokun Ma, Jinyu Li, Chao Zeng, Huajian Ji, Ke Yao, and et al. 2024. "X-ray Line-Intensity Ratios in Neon-like Xenon: Significantly Reducing the Discrepancy between Measurements and Simulations" Applied Sciences 14, no. 11: 4381. https://doi.org/10.3390/app14114381

APA Style

Huang, S., Tang, Z., Yang, Y., Zhang, H., Tian, Z., Ma, S., Li, J., Zeng, C., Ji, H., Yao, K., & Zou, Y. (2024). X-ray Line-Intensity Ratios in Neon-like Xenon: Significantly Reducing the Discrepancy between Measurements and Simulations. Applied Sciences, 14(11), 4381. https://doi.org/10.3390/app14114381

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop