1. Introduction
Today, Permanent Magnet Synchronous Motors (PMSMs) are increasingly used in more applications in industry due to their high efficiency, high power density, dynamic performance, and control capabilities. However, condition monitoring (CM) is necessary to avoid anomalies and fault conditions. Different faults may appear during PMSM operation and can be related to the rotor [
1], bearings [
2], magnets [
3], or stator windings [
4]. Continuous and online condition monitoring of the system offers the possibility for early fault detection and thus better maintenance planning [
5], avoidance of catastrophic faults, and reduction in downtime [
6]. Various tools are used for motor health assessment, such as vibration analysis, acoustic emission analysis, temperature monitoring, or Motor Current Signature Analysis. Based on the requirements for continuous monitoring of the system, without interruptions, along with integrating possibilities into the existing system, Motor Current Signature Analysis (MCSA) is one of the prevailing options. Indeed, it has been shown that different possible faults can be detected through MCSA [
7,
8].
However, to automate fault diagnosis processes and enhance their capabilities, various AI and machine learning approaches must be utilized. In recent years, various approaches have been proposed for PMSM fault diagnosis. In [
9], MCSA and Wavelets were used to extract eccentricity-related features and then Principal Component Analysis (PCA), k-NN, and Support Vector Machine (SVM) were used for feature reduction, eccentricity type identification, and eccentricity degree estimation, respectively. In [
10], a similar approach is used to detect open circuits. FFT was used to extract frequency domain features from the measured signals, PCA was used to reduce dimensionality of the data, and then Bayesian Network (BN) was employed for open circuit fault diagnosis. Moreover, in [
11], interturn short-circuit fault diagnosis is addressed through Recurrent Neural Networks (RNNs). In that work, negative sequence and positive sequence currents are extracted from three-phase current measurements and fed into an Attention-Based RNN along with the PMSM’s operating speed. The authors achieve the evaluation of the severity of the fault under various operating conditions. In [
12], raw current signals from the PMSM are fed directly to a Convolutional Neural Network (CNN) to avoid the features extraction and signal processing stage. The proposed method achieves the identification of damages in permanent magnets of a PMSM. An extensive overview of PMSM fault diagnosis, including artificial intelligence and machine learning applications, can also be found in [
6,
7,
8].
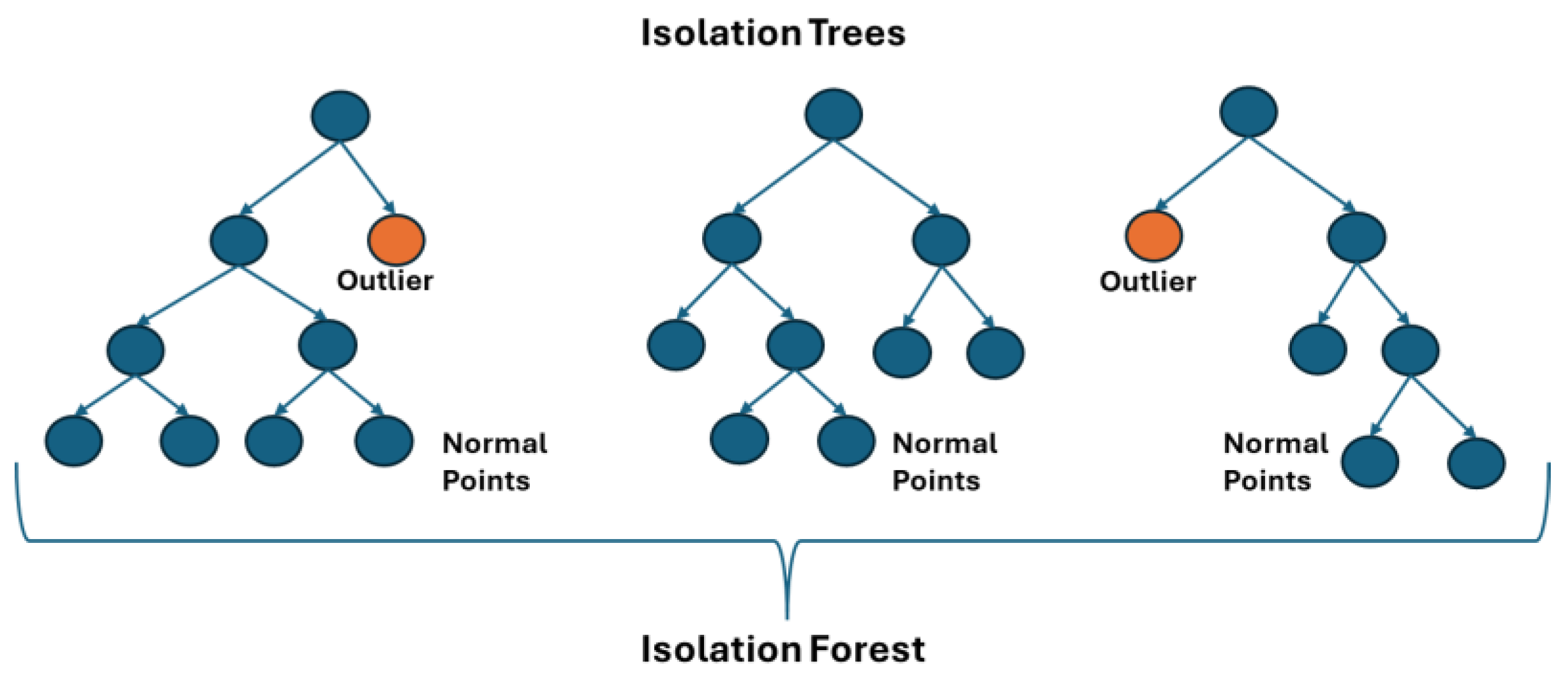
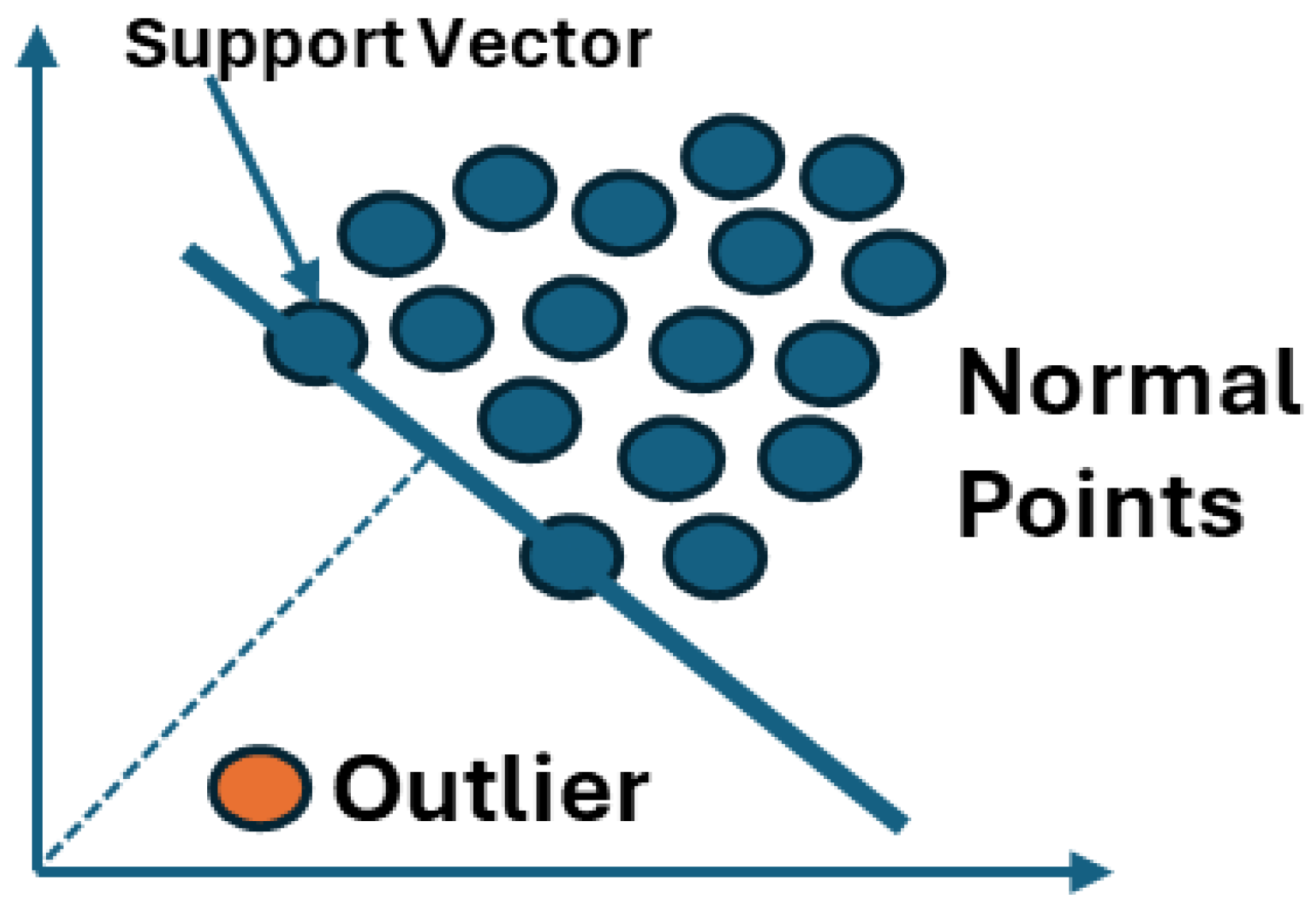
In outlier detection, the goal is to identify and isolate outliers in the data. Outliers can be categorized into Point Outliers and Collective Outliers [
13]. In the first category, a single point in a dataset deviates from the rest, while in the second one, there is a collection of points that deviate from the rest of the dataset. For fault detection and severity estimation of a PMSM, the Collective Outlier case is considered, as with the occurrence of a fault, samples that deviate from the normal operation will appear, especially with increasing severity. Three different widely used methods for outlier detection are investigated in this work. The first one is Isolation Forest, proposed by Liu et al. in [
14]. The second one is One Class Support Vector Machine (SVM) [
15] and the last one is Robust Covariance Ellipse [
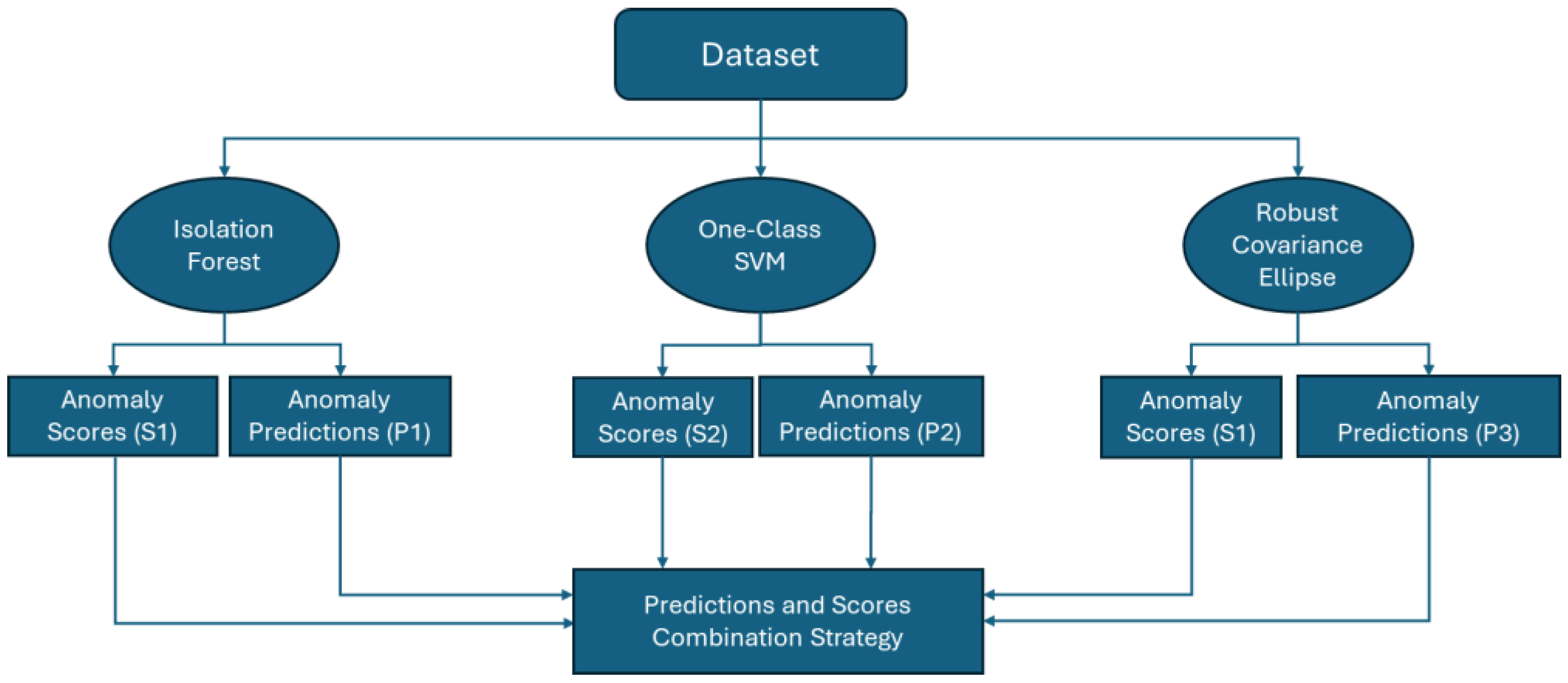
16]. The three methods are investigated separately and then an ensemble approach is proposed to address the methods’ limitations and further PMSM fault diagnosis challenges.
Several challenges exist in the integration of AI and machine learning for outlier detection and fault diagnosis of electrical machines, and particularly for PMSM. A key challenge is related to the Signal Processing and Feature Extraction stage [
17]. The features to be used by the diagnostic model must reflect as close as possible the existence of faults. In addition, they must be as independent as possible of load and speed operating conditions. For this reason, this paper proposes the utilization of the Park transform and the transformation of currents in the d-q rotational reference system. The presence of a fault in the motor leads to the distortion of d-q current signals in both time and frequency domains, so statistical indicators are used to describe these changes. An additional challenge in diagnosing PMSM faults has to do with the estimation of the severity of the fault. Other than the prediction of a fault, the diagnostic system should also give an estimate of how serious it is for the appropriate action to be taken. For this reason, the so-called Anomaly or Outlier Scores extracted by the selected methods are exploited. Moreover, for a specific diagnostic task, many models may fit and perform well, so a combination of them may yield to better results, improving the overall performance of the diagnostic system. For this reason, simple ensemble approaches, like Majority Voting and Mean Ensemble [
18], which combine independently the predictions and scores from the used models, are employed.
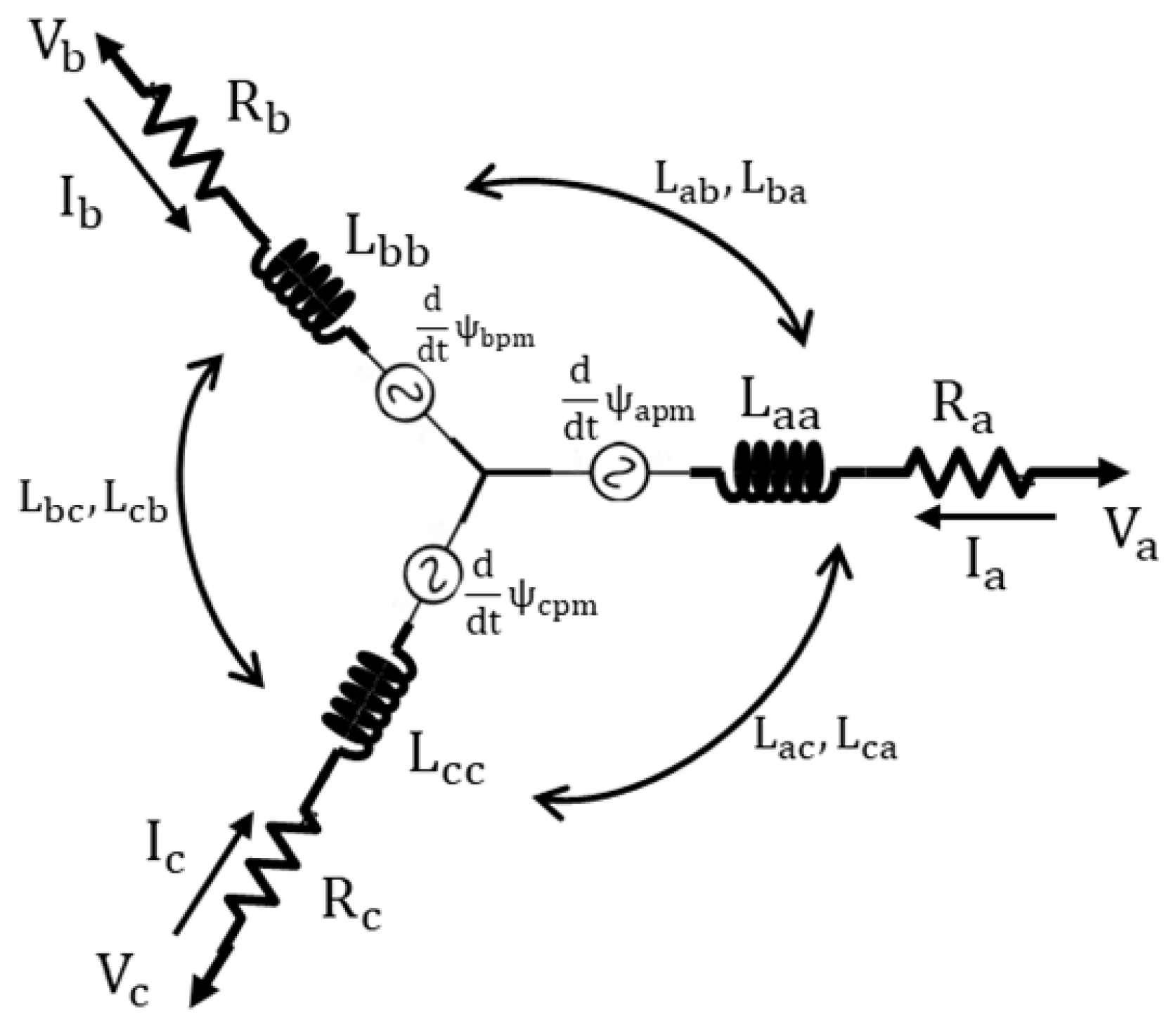
2. PMSM Mathematical Model
The voltage equations of the PMSM in the
abc reference system are the following:
where
is the stator’s winding resistance,
,
are the stator’s phase currents, and
are the stator’s flux linkages, which are given by the following equations:
where
is the self-inductance of the x phase,
is the mutual inductance of the
x and
y phases, and
,
are the flux linkages associated to the windings abc and the permanent magnets. A schematic representation of the PMSM model is shown in
Figure 1.
To simplify the above equations, the Park transform is used, where the Park matrix is obtained as:
with respect to an arbitrary reference frame with reference angle
θ and
q-axis alignment. By selecting
, where
is the rotational reference angle, the simplified voltage equations are the following:
where
p is the number of pole pairs,
,
are the d-q reference frame inductances,
is the flux linkage associated with permanent magnets. The zero sequence
Vo is neglected here.
3. Motor d-q Current Signature Analysis
Motor Current Signature Analysis (MCSA) relies on examining a motor’s stator current to find specific patterns associated with faults. The stator’s current is analyzed in the frequency domain in the interest of extracting specific frequencies associated with motor’s faults. For a healthy motor, the form of stator currents is as follows:
Using the Park transform matrix in the synchronous rotational reference system (
:
With the presence of a fault in the motor, additional harmonics appear in the current’s spectrum. The frequency patterns for MCSA related to eccentricity, demagnetization, and bearings faults are presented in
Table 1.
Currents under faulty PMSM state can be expressed as follows:
The above-mentioned quantities are expressed in the synchronous rotational reference system as:
From the above equations, we can observe that currents in the d-q rotating system contain two quantities, the dc quantities , , which refer to the healthy operational state, and the oscillating quantities which refer to additional harmonics associated with the fault. By analyzing the above quantities in the frequency domain, the frequencies that occur beyond dc can be used to detect and identify PMSM faults.
6. Experimental Procedure and Results
The test bench that was used for the experimental procedure is shown in
Figure 6. The test rig consists of a Nidec’s (Sycracuse, NY, USA) PMSM and DC Generator, a resistive load, an Inverter, a Current Measurement Unit, a Data Acquisition Unit, and a PC. The PMSM is coupled to the DC Generator through a flexible coupling. The DC Generator with the resistive load is used as a load for the PMSM. The PMSM parameters are shown in
Table 3.
The acquisition of current measurements is performed with a sampling frequency of 5 kHz using an NI Daq and LABVIEW. The fault considered in this case is a misalignment between PMSM and the DC Generator, causing eccentricity effects in the PMSM’s shaft. It was achieved by placing metal shims in the support base of the motor. Two levels of fault severity were considered by different shim widths.
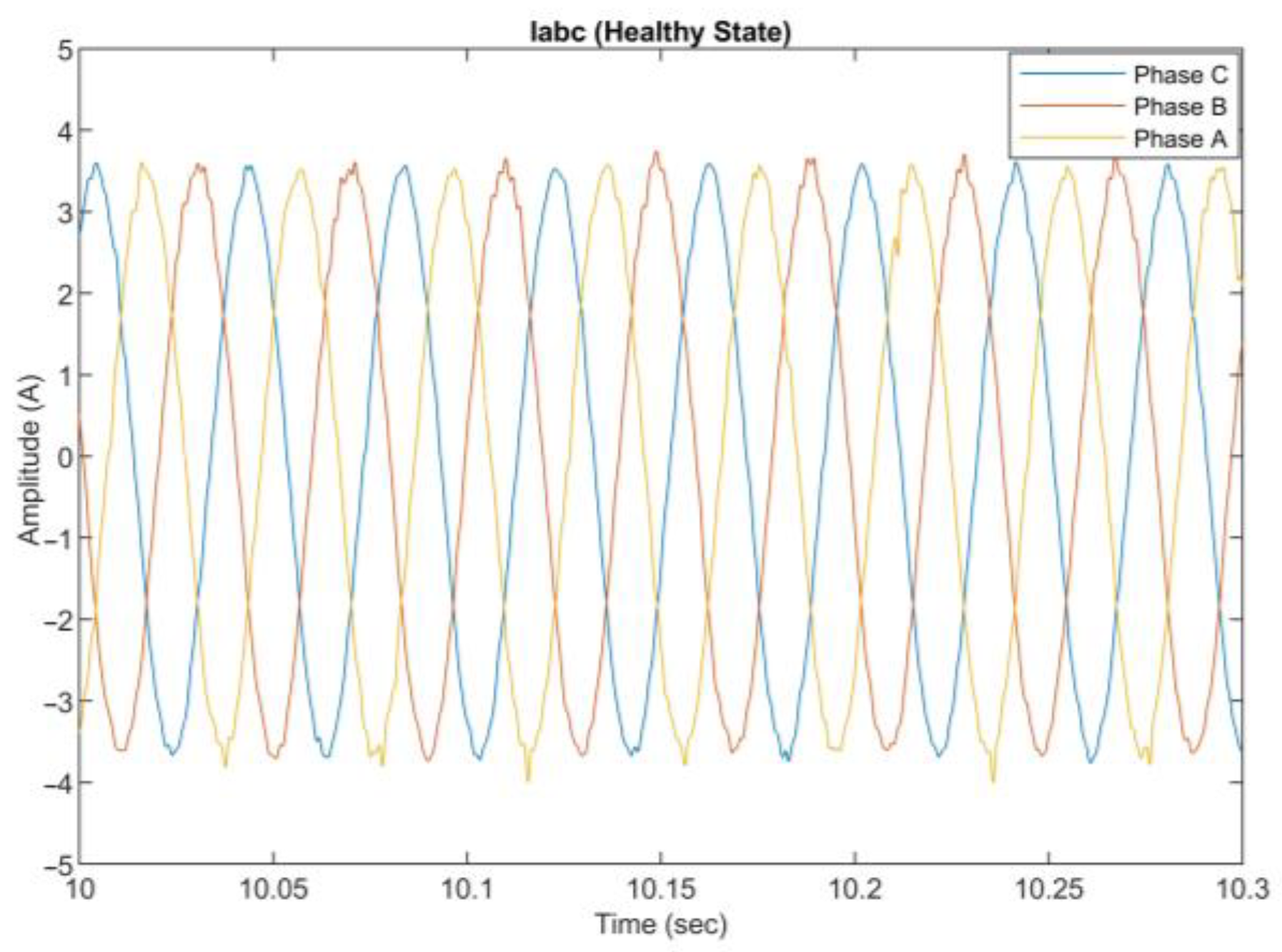
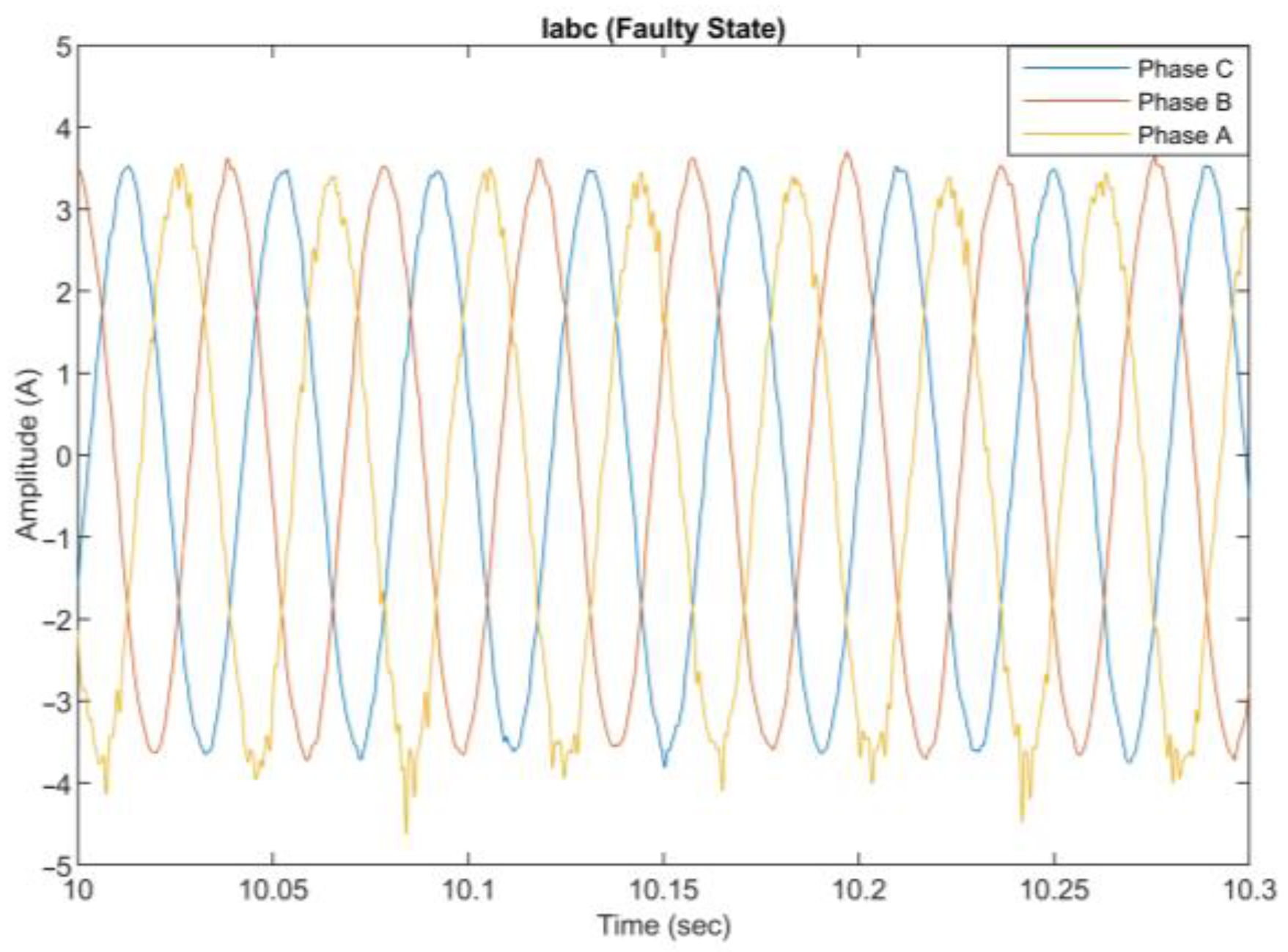
The collected data consist of three-phase current measurements for healthy and faulty operating conditions with increasing severity. In
Figure 7 and
Figure 8, abc current time waveforms for healthy and faulty operating conditions are presented, respectively. The operating speed of the PMSM is 1400 rpm, with a load of 6 Nm. We can notice the deformation of the waveform’s envelope in the faulty state due to the misalignment. To extract useful features of the faulty conditions, such as time and frequency domain features, d-q transformation and FFT analysis are employed. In
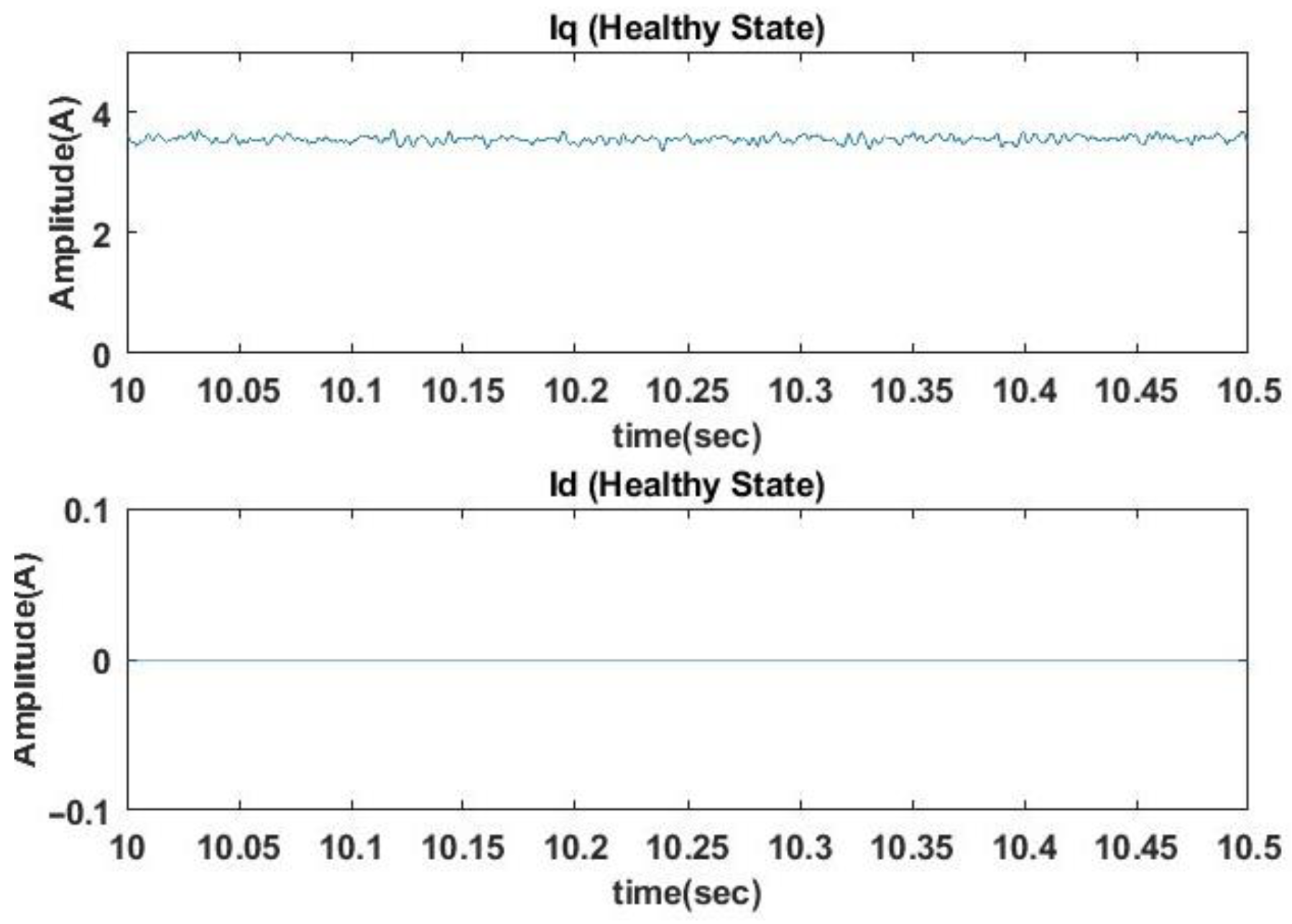
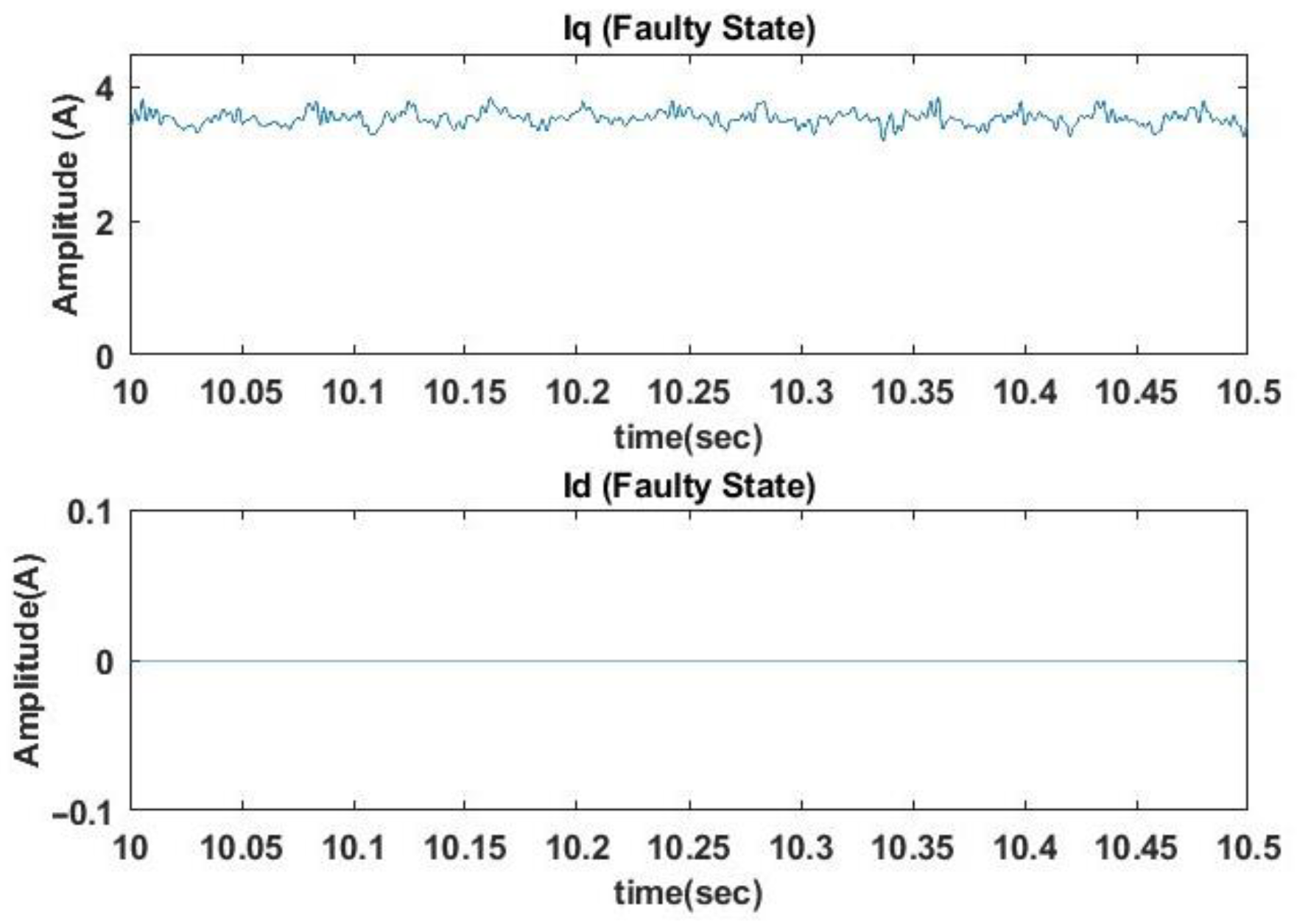
Figure 9 and
Figure 10, the corresponding waveforms for q and d axis current in a rotating reference frame are presented. The d current waveform remains at zero, as Field Oriented Control (FOC) is used to drive the PMSM. We observe an increased ripple and distortion in q current signal over time, due to the additional harmonics caused by the misalignment condition.
To derive the frequency characteristics of the fault, analysis of the current in the frequency domain is required. For this reason, in
Figure 11 and
Figure 12, Power Spectral Density is calculated. In
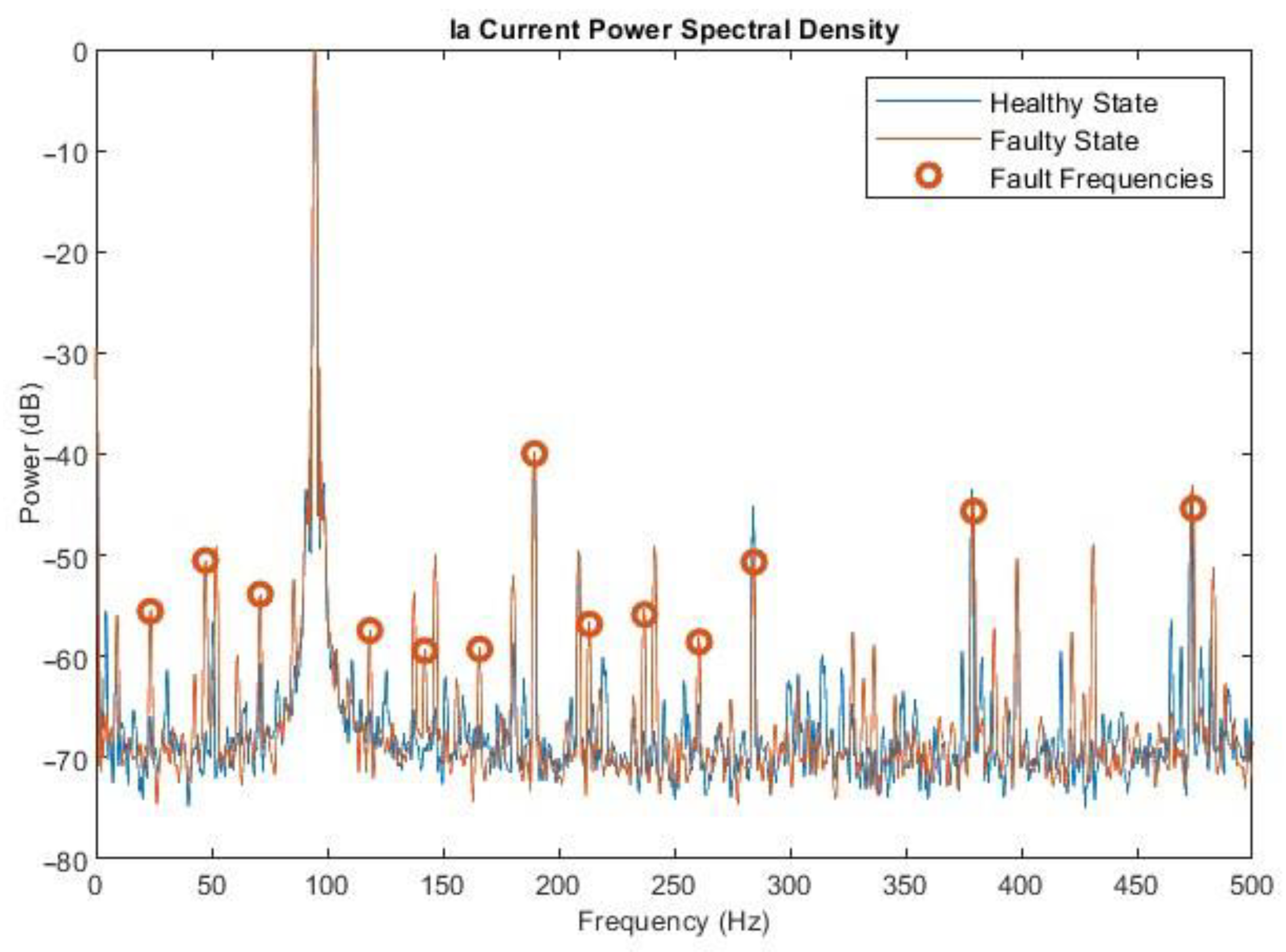
Figure 11, the spectrum of the healthy state (blue color) and faulty state (red color) are placed together. The specific eccentricity-related fault harmonics are indicated with red circles. In
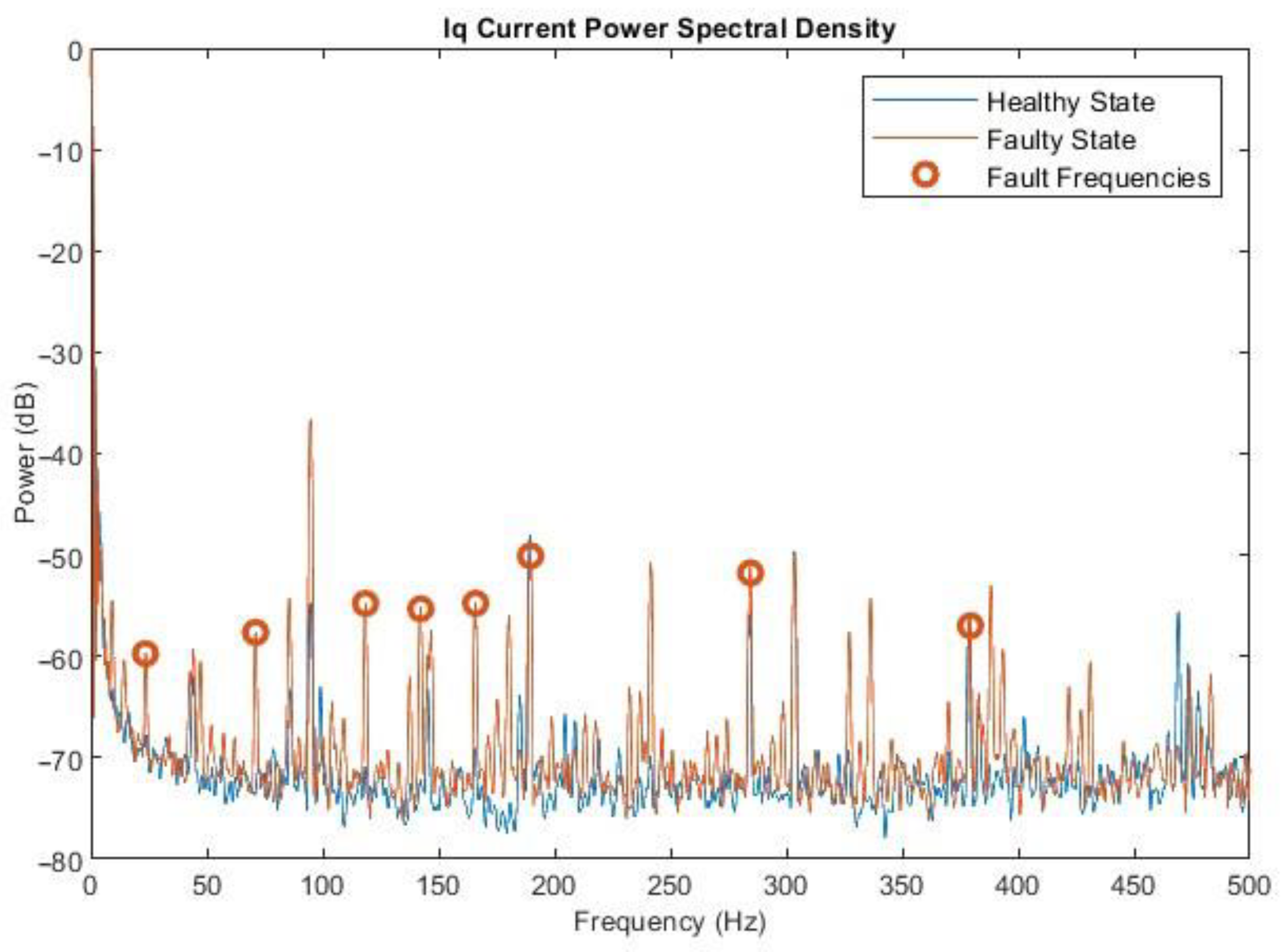
Figure 11, the q-axis Power Spectral Density is shown for the same conditions. Due to design and operation parameters of the PMSM test bench, some harmonics that follow the eccentricity-related pattern are also evident in the healthy state.
From the waveform of the current over time, the statistical features of standard deviation, variance, skewness, and kurtosis are calculated, and from the signal’s power spectrum, spectral density, spectral centroid, spectral spread, spectral skewness, and spectral kurtosis indices are calculated. The above characteristics are calculated for four different speeds and four different load levels under a healthy and faulty (misalignment) condition. The overall dataset consists of the above features for different operating modes and with an increasing severity of the fault.
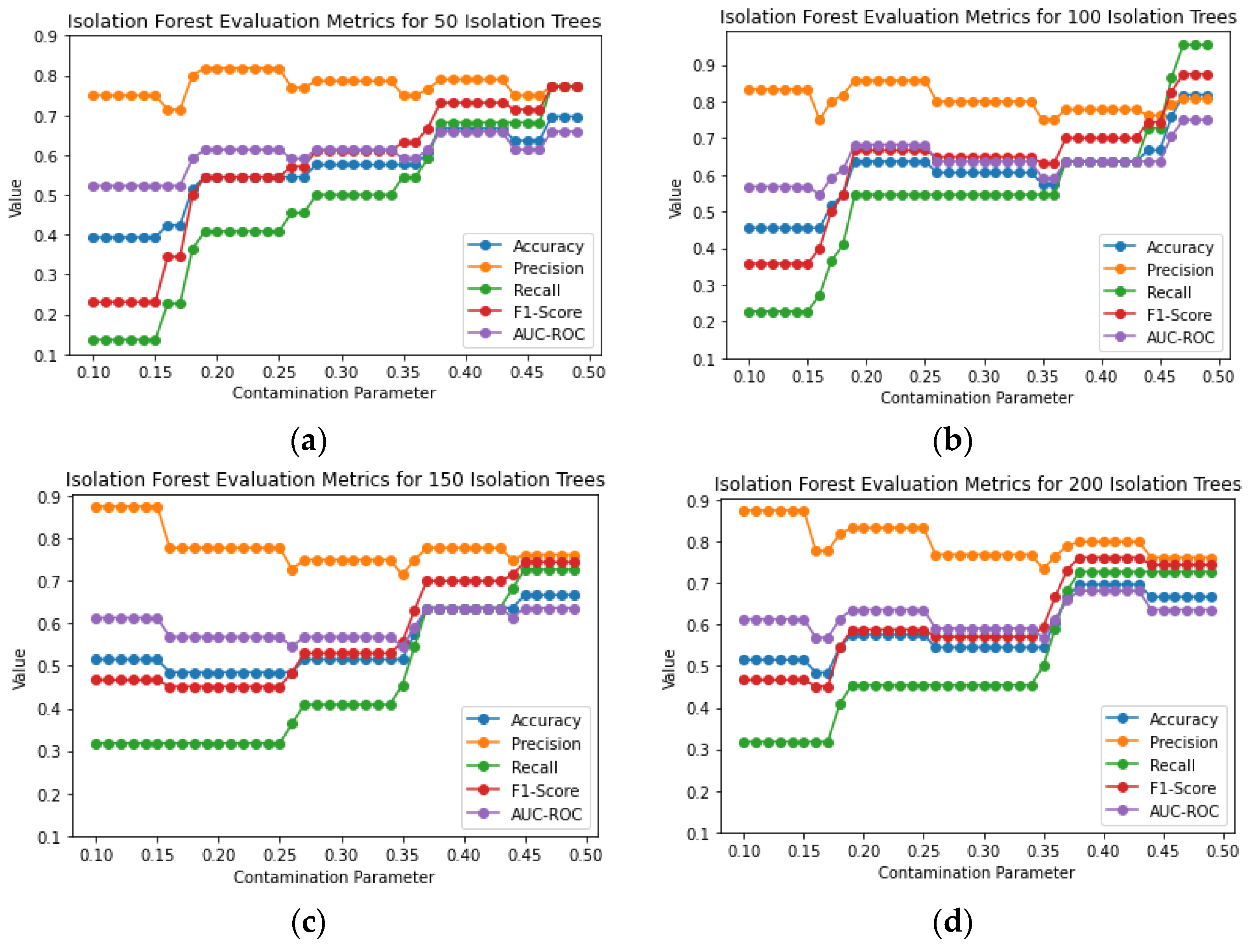
Initially, we investigate the three different methods separately and compare them. The implementation of all methods is performed using Python and Scikit-learn. First, the Isolation Forest is investigated. The training of the model is performed with healthy data, while the test is performed with a dataset of healthy data and faulty data with increasing severity of the misalignment fault. The model’s performance is investigated for different contamination parameter values and number of trees. As the number of samples and features is small in this dataset, the number of maximum features and maximum samples that can be adjusted as parameters are kept to the default values. However, it is important to note that in larger datasets and features, the above two parameters are important, as they can reduce computational complexity and indicate redundant features. Below, in
Figure 13 are the evaluation metrics for different values of the contamination parameter and different number of trees. We observe that in all cases (50, 100, 150, 200 iTrees), better evaluation metric values appear in the range of 0.4–0.5 for the contamination parameter. The best evaluation metric values for 100 Isolation Trees and contamination parameter in the range of 0.4–0.5 are shown in
Table 4.
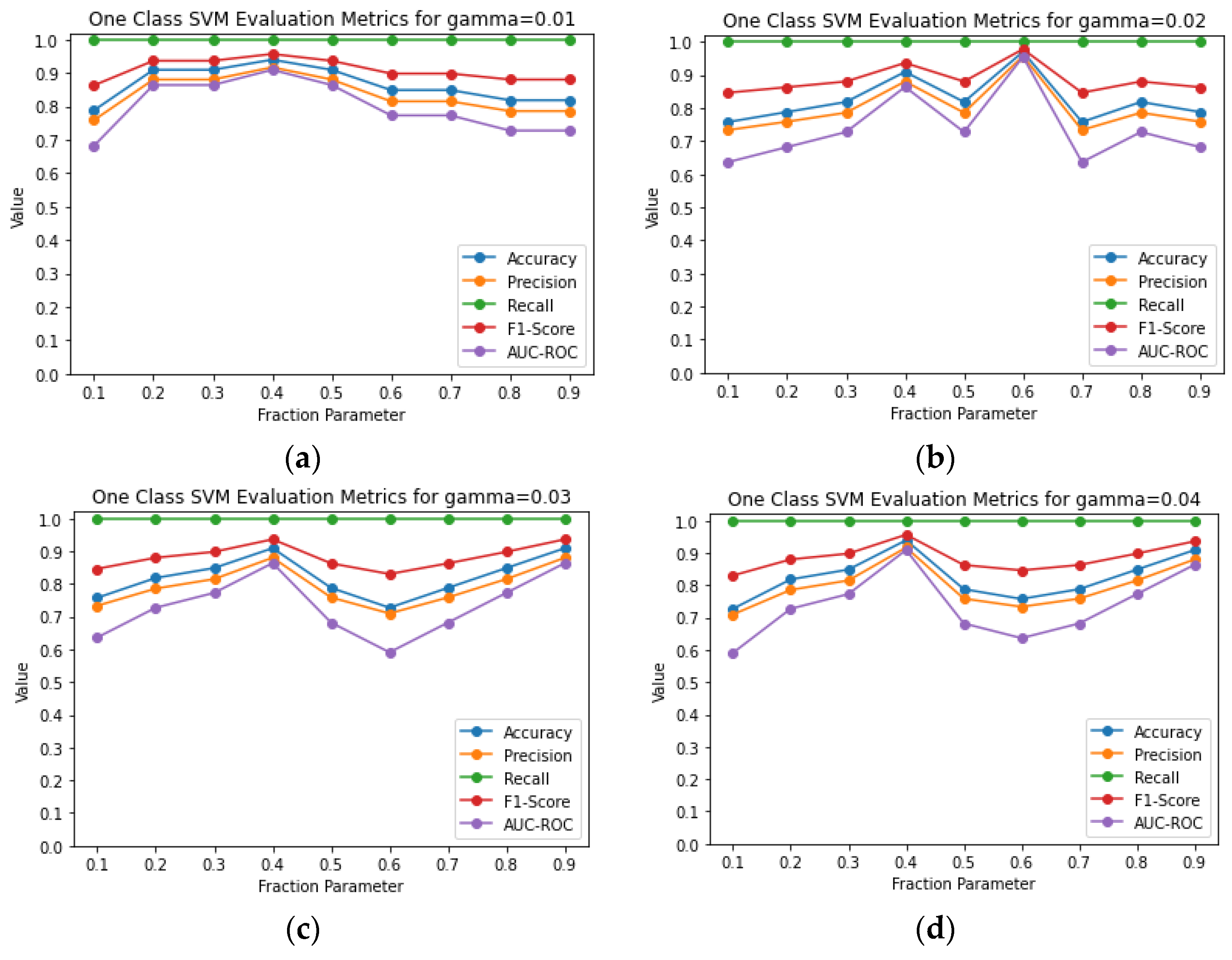
Subsequently, One Class SVM is investigated. Like iForest, only healthy data were used to train the model and then tested with a dataset of healthy and faulty states with increasing severity. One Class SVM was tested for the Radial Basis Function kernel for different gamma and fraction parameter values. The gamma range of the test is between 0.005 and 0.04, as there are no further improvements in the performance of the model above 0.04. This can be seen in the corresponding figures for gamma = 0.02, 0.03, and 0.04, in
Figure 14. The best values of evaluation metrics appear for gamma = 0.2 and fraction parameter = 0.6. For these cases, the evaluation metrics are shown in
Table 5.
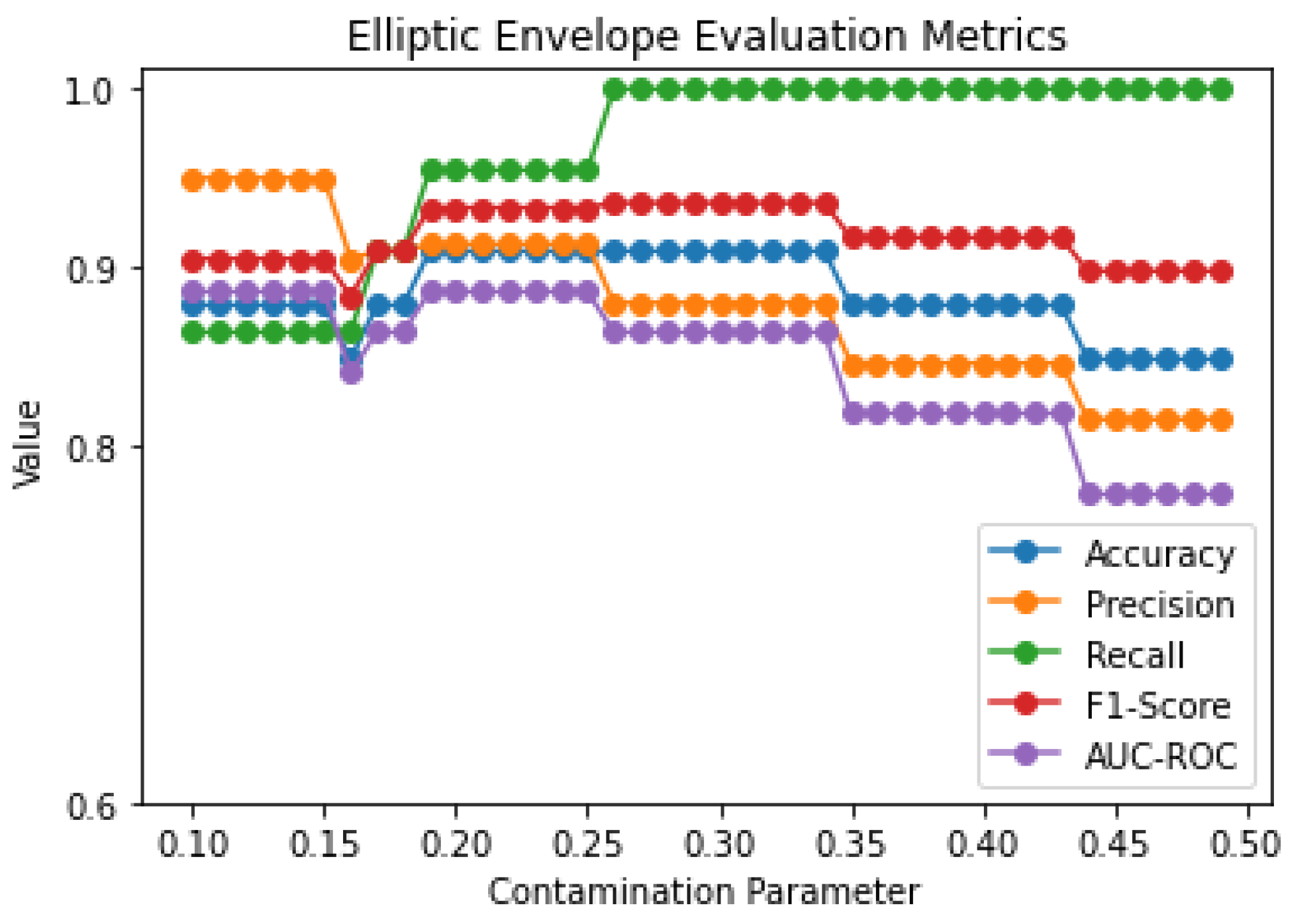
Lastly, Robust Covariance Elliptic Envelope was assessed for the same dataset. The influence of different contamination parameters is shown in
Figure 15. We can observe that the best values of the evaluation metrics arise for a contamination parameter equal to 0.2 or 0.3. The evaluation metrics for the above parameters are shown in
Table 6. The main difference lies in the decrease in precision and ROC AUC and the increase in Recall and F1-score for contamination parameter equal to 0.2 and 0.3, respectively.
The above models can be combined through different ensemble techniques, as discussed in
Section 5. More specifically, Majority Voting Ensemble can be used, where the majority of predictions are selected, and the Average Ensemble, where the average of the predicted values is calculated. Note that in the case of Averaging, rounding of the predicted values is required. The evaluation metrics for the above cases are shown in
Table 7.
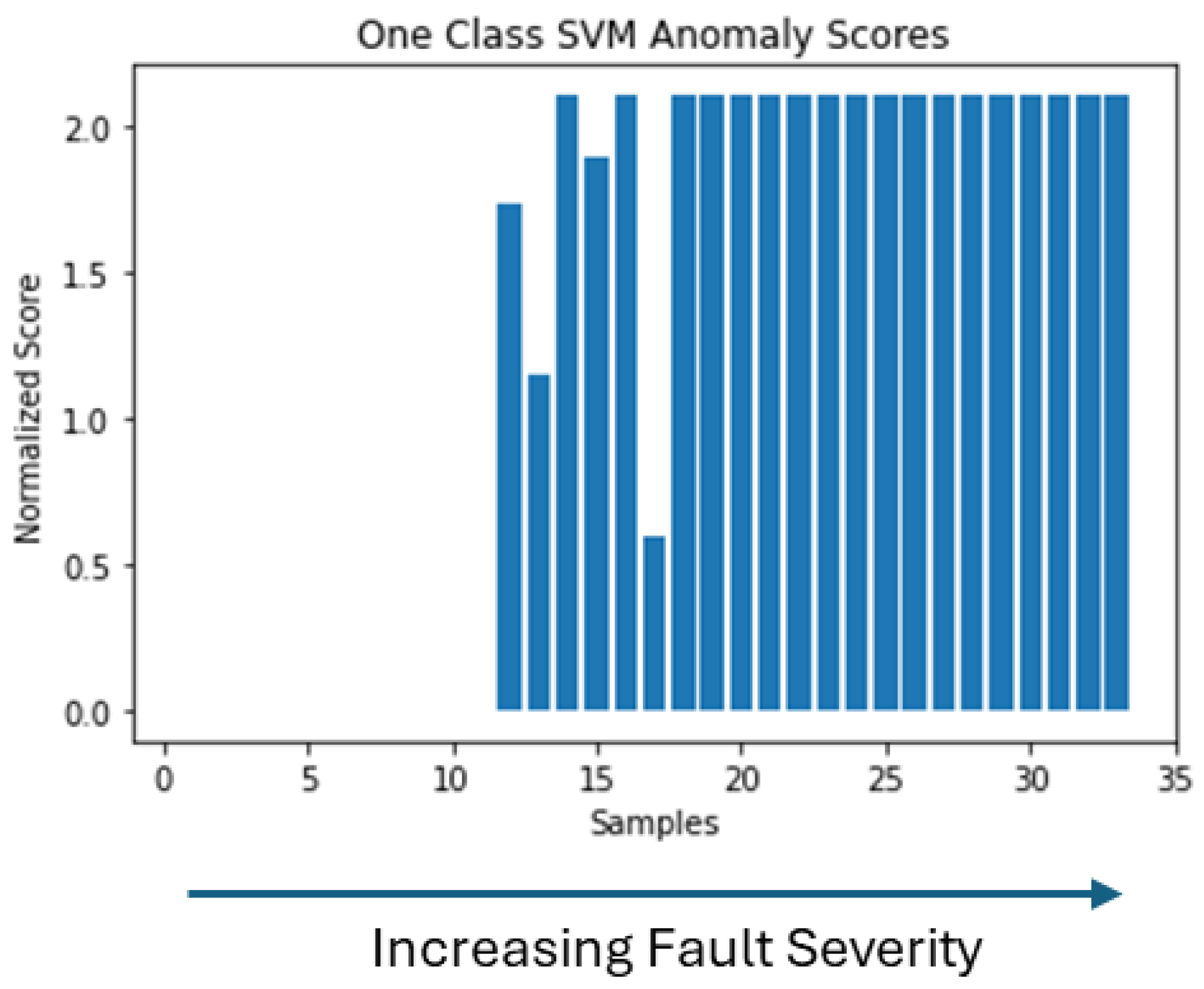
To estimate the severity of the fault, the anomaly scores generated by each model are employed. Based on how anomaly scores are generated, each of the above methods generates a different range of values. For this reason, the values are normalized. Higher anomaly scores indicate faulty operating conditions in the PMSM. In the test dataset, the first 11 samples respond to a healthy working state, while the following 11 respond to a faulty state with a low fault severity, and then the last 11 respond to an increased fault severity. In the case of the One Class SVM, in
Figure 16, we can see that healthy samples are distinguished from faulty samples, and especially the latest samples of increased severity. However, the difference between each sample for the latest samples and the increased severity is not clear. In the case of the Isolation Forest, in
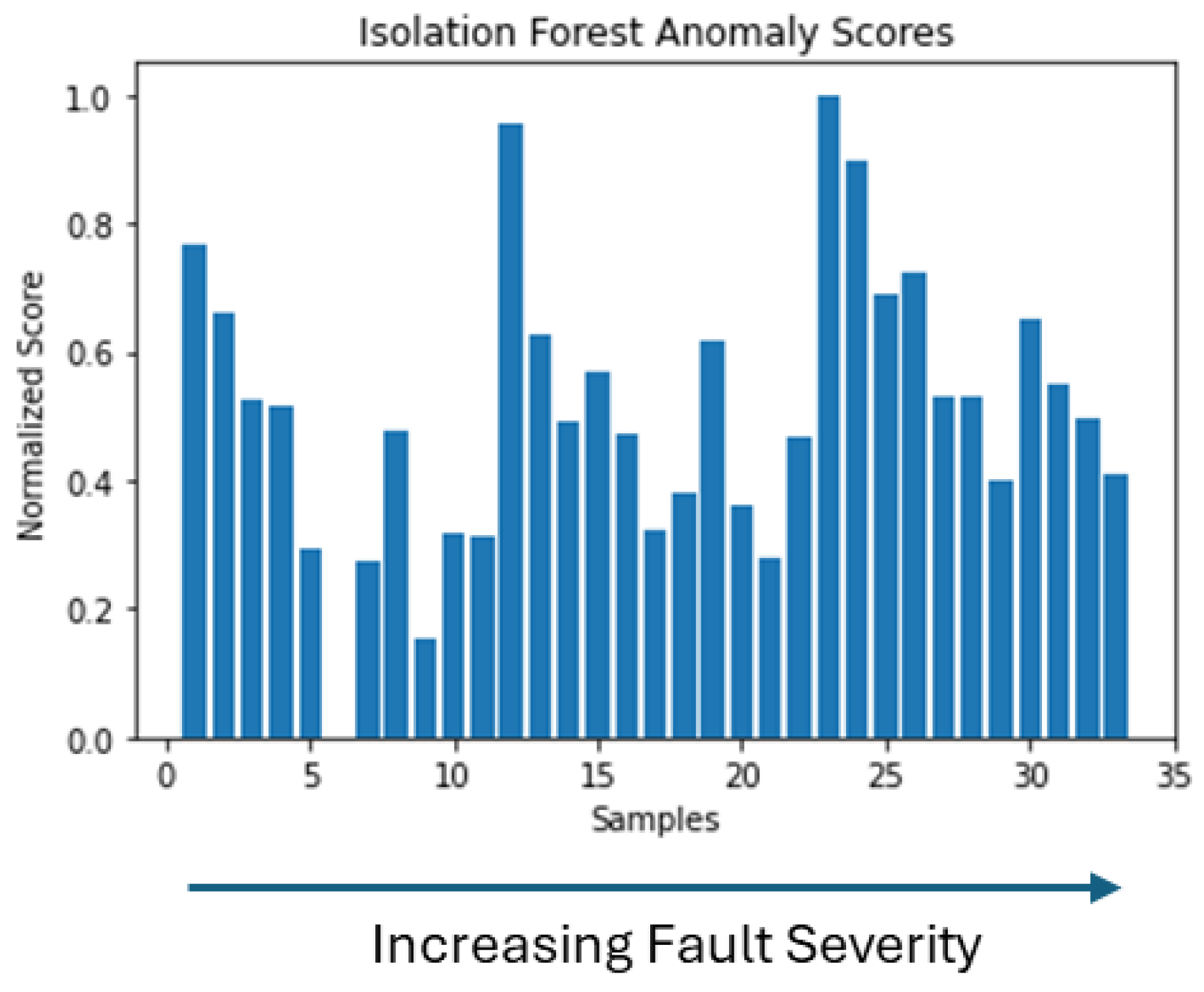
Figure 17, we see that we have increased anomaly scores for faulty cases that can be used as indicators of fault occurrence and increase in severity. In the case of the Elliptic Envelope, in
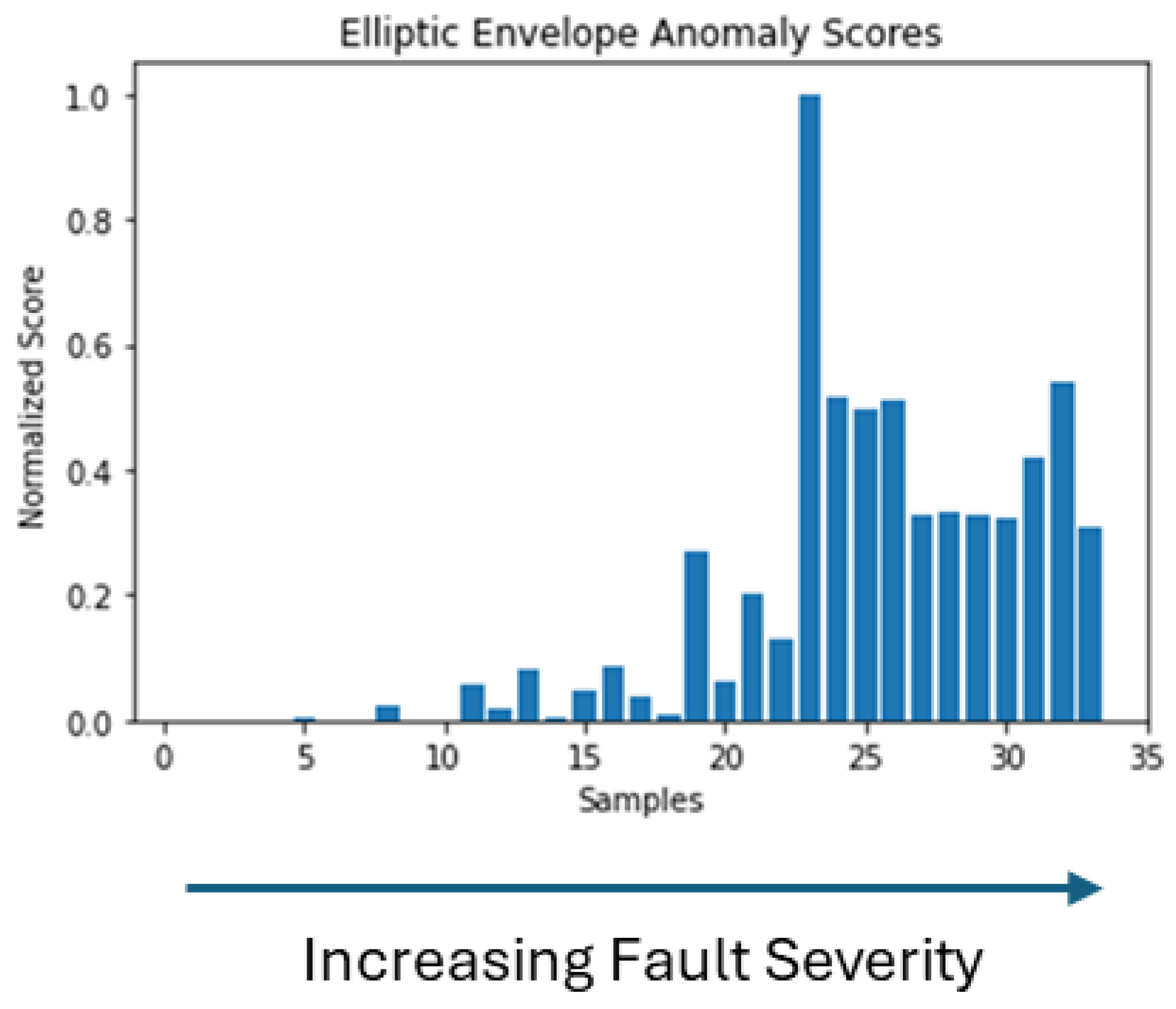
Figure 18, we have the clearest picture, as we observe that anomaly scores are low for healthy samples while increasing with the appearance of the fault and especially at higher severity.
Ensemble techniques can be employed to utilize the scores generated from the models and improve severity estimation. For each sample of the three models, the average values are calculated. This results in the mean anomaly scores, shown in
Figure 19. The evaluation metrics extracted in the previous section can be used to introduce weights to each anomaly score produced by each model, respectively. However, in this case, there was no notable change from the mean ensemble, so it was not examined further. Other than Mean Ensemble, Max Ensemble can be employed, where the max values from each model are used. The corresponding anomaly scores are shown in
Figure 20.
An additional important piece of information from the generated anomaly scores is related to the detection of conditions where the fault is more intense or detectable. It is known [
4,
6] that the operating conditions of motor speed and load affect the occurrence and detectability of the fault. By using anomaly scores, we can see in which operating condition the highest anomaly score is displayed, as well as compare each operating condition with the corresponding one with a fault.
7. Conclusions
The proposed methodology utilizes PMSM’s three-phase currents and speed measurements for online, non-invasive, and cost-effective condition monitoring of the PMSM. To extract fault-related features from the measurements, d-q transform was used. Distortions in time waveforms and several eccentricity-related frequencies in the power spectral density were observed for different speed and load conditions of the PMSM. Then, to extract useful indicators of fault conditions, statistical measures in time and frequency domain were used. The extracted statistical features were used for outlier detection by means of fault detection and severity estimation through Isolation Forest, One Class Support Vector Machine (SVM), and Robust Covariance Ellipse.
First, Isolation Forest was investigated for different isolation trees and contamination parameters. The best evaluation metrics were extracted for 100 Isolation Trees and a contamination parameter in the range of 0.4–0.5. The accuracy of Isolation Forest reached 0.82. One Class SVM was employed for the same task. Radial Basis Function was selected as the kernel and different gamma and fraction parameters were investigated. The best evaluation metrics were extracted for gamma equal to 0.2 and fraction parameter equal to 0.6. The accuracy reached 0.97. Lastly, Robust Covariance Ellipse fitting was tested. The highest accuracy achieved was 0.91 for gamma and contamination parameters equal to 0.2 and 0.3, respectively. One Class SVM was the best candidate in terms of Accuracy, Recall, Precision, F1-Score, and ROC AUC. For Severity Estimation, the extracted Outlier Anomaly Scores from the above methods were used. Comparing the three methods, increasing fault severity was better observed in Outlier Scores generated by Robust Covariance Ellipse fitting, then Isolation Forest, and lastly, One Class SVM. To combine the predictions and outlier scores, and so the advantages of each method, Independent Ensemble approaches are proposed. Majority Voting and Averaging Ensemble of the predictions led to Accuracy equal to 0,94 and 0,97, respectively. Max and Mean Ensemble of the Outlier Scores led to better observability of the increasing severity by each sample of the tested dataset.