Abstract
To improve the workshop production efficiency of textile enterprises and balance the total operating time of all machines in each operation, this paper proposes a modified algorithm based on the combination of the ant colony optimization (ACO) algorithm and production products, which we call the product ant colony optimization (PACO) algorithm. The local pheromone update rule in the ACO algorithm is modified through the close relationship between textile machinery and production products in the textile workshop; the pheromone is then introduced into production products based on the constraints of the textile machine. A heuristic function is designed to improve the utilization rate of textile machines to increase the heuristic value of machines that are less frequently used in the algorithm iteration process. In addition, this paper combines the convergence speed and the global search ability of the algorithm with a designed variable pheromone evaporate parameter. The comparison among the initially designed PACO algorithm, the separately modified PACO algorithm, and the integratively modified PACO algorithm demonstrates that the proposed enhancement effectively addresses scheduling issues in textile flexible workshops and various workshops with similar constraint conditions.
1. Introduction
Over the past few decades, most textile enterprises have been slowly upgrading and transforming from traditional manufacturing enterprises to intelligent enterprises and have made great efforts to develop, apply, and promote related common and key technologies, including product design informatization, production equipment intelligence, and production process intelligence [1]. However, most of the textile enterprises in the intelligent transformation [2,3] did not pay attention to the job-shop scheduling problems within the enterprise. Textile job-shop scheduling is an important part of the production process in the textile industry and is mainly involved in the allocation of production resources, production schedule, and other aspects [4]. Therefore, providing a good textile job-shop scheduling solutions can improve production efficiency, reduce production costs, ensure product quality, and enhance enterprise competitiveness.
Job-shop scheduling aims to scientifically allocate the operation sequence of processing workshops based on the reasonable demand of product manufacturing, so as to achieve effective utilization of product manufacturing resources and further enhance the economic benefits of enterprises. The flexible job-shop scheduling problem (FJSP) is a complex job-shop scheduling problem (JSP), which consists of two sub-problems: machine assignment and job ordering [5]. In the FJSP system, each job requires several operations that need to be transferred to different machines for processing [6]. JSP is distributed across various manufacturing industries, with a large number of researchers currently studying and solving JSP and FJSP in various fields. To address the issue of machine energy consumption in job-shop systems, Renna [7] proposed a switching strategy utilizing the workload control method based on JSP. Pan et al. [8] proposed learning-based multi-population evolutionary optimization (LMEO) to deal with the flexible job-shop scheduling problem with finite transportation resources (FJSP-Ts). Fatemi-Anaraki et al. [9] devised a mixed-integer linear programming (MILP) model, integrating three acceleration constraints to solve the no-wait JSP involving material exchanges among multiple robots. Gaiardelli et al. [10] introduced a randomized heuristic approach and considered dynamic job arrivals to design a fully rescheduling strategy. Kong and Wang [11] proposed an improved discrete particle swarm algorithm based on Pareto optimization to solve the multi-objective FJSP, which includes setup time, processing time, and handling time. Wang and Zhu [12] combined an improved optimal foraging algorithm (OFA) and Pythagorean fuzzy set (PFS) to solve multiobjective FJSP. Liang et al. [13], Ning and Cao [14], and Zhang et al. [15] used a modified genetic algorithm to deal with the related FJSP.
The ant colony optimization (ACO) algorithm [16] is a heuristic global optimization algorithm; the ants update the search strategy by learning from each other, which provides good collaboration and parallelism. The heuristic algorithm has the characteristics of randomness and a wide search range and can find the optimal solution faster and more flexibly. It can be used to deal with the FJSP problem, the problems of robot path planning and vehicle route planning, etc. Xu et al. [17] proposed an improved ACO algorithm to solve the FJSP in the early stage and provide the corresponding solution formulas. Anitha and Karpagam [18] improved the basic ACO algorithm by using a pheromone updating strategy to solve instances of job-shop problems. Wang et al. [19] proposed an improved ACO algorithm to optimize the makespan of FJSP to overcome low computational efficiency and the local optimal. Zhang et al. [20] studied the production scheduling problem in a flexible manufacturing system with two adjacent working areas. Miao et al. [21] and Yang et al. [22] solved the problems related to the path planning of mobile robots with an improved adaptive ACO algorithm. Jia et al. [23] proposed a novel bilevel ACO algorithm to deal with the vehicle routing problem.
In traditional textile workshops, during a certain period, machines in a particular operation only produce one type of textile, resulting in some machines in other operations being underutilized due to differences in operating time between operations. This leads to overall low production efficiency in the workshop. To improve production efficiency in the textile workshop, adopting the strategy of FJSP is essential. This allows the workshop to alternate between producing different types of textiles during a single period, thereby fully utilizing idle textile machines by selecting the optimal sequence for processing textile products.
This paper aims to discuss the textile-flexible job-shop scheduling problem (T-FJSP) by solving the problem of reasonable allocation of machines according to the operating time in textile workshops. In this paper, the traditional single ant colony is improved to multiple ant colonies, and multiple ant colonies search together to obtain the reasonable allocation of textile products on the machine. The local pheromone update rule is different from the independent update rule of the single ant colony, but it is updated in the form of the joint action of all the ant colonies. In order to solve the problem that the original ACO algorithm converges slowly and easily into the local optimum, the pheromone evaporates parameter in the algorithm is improved to make it variable, so as to synthesize the convergence speed and global search ability of the algorithm.
The rest of this paper is organized as follows. Section 2 describes the constraint conditions between textile operations, textile machines, and textile products, as well as the establishment of the T-FJSP model. Section 3 elaborates on the product ant colony optimization (PACO) algorithm designed in this paper, detailing the improvements made to this algorithm. Section 4 tests the PACO algorithm through simulation experiments by simulating the operation of textile workshops. Finally, Section 5 concludes the paper and outlines future research plans.
2. Textile Flexible Job-Shop Scheduling Problem
In this section, constraints concerning the interplay among processes, machines, and products of the textile workshop in T-FJSP research are presented. A T-FJSP model is constructed based on these constraints, and a comprehensive description of the model is provided through a combination of equations and textual exposition.
2.1. Problem Description
In a textile workshop, each textile undergoes a series of fixed production operations from initial cotton processing to the final product. The various types of textile correspond to essentially the same production operations. In the textile workshop, each textile, from the initial cotton to the final product, needs to go through fixed production operations; different textile design types corresponding to the production operations are basically the same. Considering the characteristics of the textile industry, the T-FJSP can be described as follows: The workshop produces n jobs (textile products) on m machines, in which m machines correspond to x different operations, and n jobs (textile products) correspond to y different textile categories. The constraints of the T-FJSP are as follows [24]:
- (1)
- The sequences of operations for all jobs are prespecified, and the processing time of product is fixed for the machines in each operation;
- (2)
- Each job must comply with the fixed operation, processing from the first operation to the last operation in sequence, and the processing sequence cannot be skipped or exchanged;
- (3)
- Each job is processed only once in one of the machines corresponding to each operation;
- (4)
- Once an operation starts on a machine, it cannot be interrupted;
- (5)
- Each machine can only process one job at any time;
- (6)
- The same job can only be processed on one machine at the same time.
The relevant symbols involved in the T-FJSP are as shown in Table 1.

Table 1.
T-FJSP symbols and their meanings.
2.2. Model Building
Each machine only corresponds to one production operation in the T-FJSP, which is different from other FJSPs, where each machine can correspond to one or more operations.
Based on the symbols provided above, the mathematical model of the T-FJSP is as follows [25]:
- (1)
- Select function , which represents the selection relationship between operations and jobs:
- (2)
- Indicator function represents the priority of work on the same machine:
- (3)
- When operation h of job j selects machine i:
- (4)
- The completion time of the previous operation must be smaller than the start time of the next operation:
- (5)
- The completion time of each workpiece cannot exceed the total completion time:
- (6)
- When precedes , select the start : if the current is greater than the current , the on machine i is the current ; otherwise, the on machine i is the current :
- (7)
- The machine constraint [26] specifies that each operation can only be processed by one machine at a time, and can be selected by only one machine i at the same time to make the value of 1, the rest are all 0:
- (8)
- The processing constraint between adjacent operations of the same job states that after the processing of is completed on machine i, the next operation, , can be carried out on machine e:
- (9)
- The constraint to be satisfied by the operations of different jobs competing for the same machine states that if is processed on machine i with priority over , then can be processed on machine i only after is completed on machine i:
- (10)
- The total machine operating time of machine i, that is, the total operating time of each job on machine i from the beginning of the first job run to the end of the last job run. The corresponding operating time of jobs that select machine i () is :
- (11)
- The total production time of the textile product (job), that is, the sum of the time experienced by the product from the beginning of each operation to the beginning of the next operation (when the adjacent operation selects the machine, there will be a pause time in the middle, and the pause time belongs to the experience time between operations). The operation number of job j is :
- (12)
- The total completion time of the workshop, that is, the sum of the maximum total machine operating time for each operation corresponding to all machines when all jobs are completed. The job j has machines, and the textile workshop has operations:
2.3. Objective Function
In actual production scheduling, the optimization objective of shop scheduling can be either single objective or multi-objective optimization. The improvement of a certain index in the textile workshop can bring huge economic benefits. In addition, considering the complexity of multi-objectives, this paper chooses a single objective when solving the textile FJSP. The objective function is to minimize the total completion time of the workshop:
where is the optimal total completion time of the workshop, represents the total completion time of the workshop at the k-th iteration, and is the maximum number of iterations initially designed for the algorithm.
3. Product Ant Colony Optimization Algorithm
In this section, we introduce an innovative ant colony optimization (PACO) algorithm, designed specifically for scheduling problems in textile workshops based on the original ACO algorithm. We dissect the core principles of this algorithm in detail and explain the mathematical formulas upon which each step of the algorithm relies. Finally, we present the algorithm run steps along with an algorithm flowchart to clarify the logic and process of the algorithm.
3.1. Original ACO Algorithm Description
The ACO algorithm is an intelligent optimization algorithm proposed by the Italian scholar Dorigo [27] based on the ant foraging principle. Ants release a substance called “pheromones” during their movement [28], and ant colonies communicate and cooperate through pheromones. Ants tend to follow paths with high pheromone concentrations, leaving behind pheromones on the path between the starting point of the path and the location of the food when foraging. A shorter path will have a larger number of ants passing through, corresponding to the concentration of its pheromone being high, which will prompt subsequent ants to favor the path to obtain the shortest path.
Ants randomly select routes based on the roulette wheel selection strategy. The probability calculation formula for ant k from node i to node j is given by Equation (14) [29].
where represents all target nodes that ant k can travel through from node i, corresponds to the pheromone value accumulated by ant k traveling from node i to node j, corresponds to the heuristic value for ant k from node i to node j, and and tune the relative importance in probability of the amount of the pheromone versus the heuristic distance. When is larger, the influence of the pheromone will be greater, and the algorithm’s search space will be larger. The larger is, the greater the influence of the heuristic function, and the more precise the algorithm’s search.
The heuristic function influences the ant search process. The larger its value, the more likely the ants are to choose a path with a higher heuristic value, resulting in a more fixed direction for the algorithm’s evolution. The heuristic function is typically inversely related to the distance:
where is the heuristic value of ants traveling from node i to node j and is the distance traveled by ants from node i to node j.
The algorithm locally updates all the path pheromones based on the pheromones left along the pathway routes as the ants move. The local pheromone update rules are shown in Equations (16) and (17). Equation (16) represents the pheromones accumulated by all ants in a certain iteration, while Equation (17) represents the pheromones accumulated by ant k during its search:
where is the pheromone accumulated by ants traveling from node i to node j during their searching, Z is the number of searching ants set by the algorithm, is the pheromone accumulated by ant k from node i to node j, Q is the pheromone enhancement parameter, and is the distance traveled by ant k from node i to node j.
The pheromone will be globally updated before the algorithm moves to the next iteration, and it will evaporate over time. The global pheromone update rule is shown as Equation (18):
where x represents the current number of iterations, is the updated total pheromone value, and is the pheromone evaporate parameter.
3.2. Modified Ant Colony Optimization Algorithm
In this paper, the ACO algorithm is introduced as the workshop scheduling algorithm for the reasonable configuration of textile production operations in a textile workshop. In the original ACO algorithm, there is only one group of ant colonies in each iteration of the algorithm, and the colony sets a reasonable number of ants to run the algorithm, finally selecting the best ant in each iteration by comparison. However, each ant in the single ant colony algorithm is in an independent state during the path search, making it difficult to consider the influence of multiple products on each other in the production of the entire workshop. Therefore, to solve the T-FJSP, this paper modifies the traditional single ant colony into multiple ant colonies. The number of ants in each ant colony corresponds to the number of textiles currently planned to be produced in the workshop. The algorithm is named product ant colony optimization (PACO) in this paper. According to the actual situation of the textile workshop, the number of textile products to be produced and the corresponding number of operations can be arbitrarily set. In order to better understand the work situation of each ant in a group of products and the relationship between them, it is assumed that a certain textile workshop produces four textile products and goes through three operations. The schematic diagram of the process of generating a solution in PACO is shown in Figure 1.
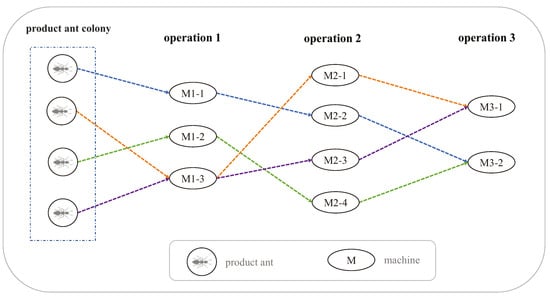
Figure 1.
Process of generating a solution in PACO.
Figure 1 depicts the workshop operation search of a group of product ants, where each ant in the ant colony represents a textile product to be produced. Each ant must complete all operations and can only select one machine at each operation. Different ants in the same operation can choose the same machine. Therefore, ants need to compete for machines using a combined heuristic function and pheromone information. During the selection of a machine at each operation, each ant is subject to influence from other ants within the product ant colony. If an ant is not the first selector of a machine, it must consider the usage time and completion time of all ants that have previously selected that machine, thus calculating its own start time of using this machine. The total usage time of each machine is also influenced by the product ant colony, and the ants in the product ant colony interact with one another. The total usage time of a machine is the sum of the usage times of all ants accessing that machine in the product ant colony when the algorithm iteration is completed. Since different ants represent different textile products, the types of textile products may not be the same. Therefore, the different sequencing of ants accessing the same machine will change the usage time of the machine during the algorithm run, thus affecting the next ant’s access to the machine and consequently affecting the overall algorithm.
In Figure 1, the workshop produces four textile products, so a product ant colony dispatches four ants to explore. If the workshop produces two textile products or seven textile products, the corresponding number of ants for each product ant colony is two or seven, respectively. Each ant in Figure 1 explores three operations and selects the machine for the next operation randomly using the roulette wheel selection rule based on the heuristic value and pheromone of all machines in the next operation. Adding or reducing an operation in the workshop will not affect the ants’ machine selection for that operation, so the number of operations explored by the ants is variable.
In the PACO algorithm, we use multiple product ant colonies for searching, and finally select the best ant colony and its allocation scheme by comparing the optimization objective results. Assuming four product ant colonies are used, the PACO algorithm schematic diagram is shown in Figure 2.
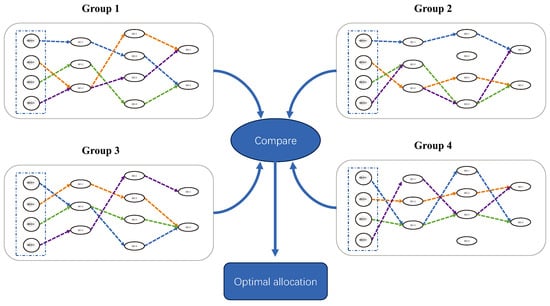
Figure 2.
Multi product ant colonies search for optimization.
3.3. Heuristic Function
In the original ACO algorithm, the heuristic function is the inverse of the distance. In research on the T-FJSP, with the goal of minimizing the total workshop completion time, the machine operating time is a key component in the calculation of the total workshop completion time, which is determined by ants when they access a machine. When an ant moves from one operation to the next operation, it selects a machine from among all machines corresponding to the next operation, with the machine’s current operating time being the primary consideration. To meet optimization requirements, the reciprocal of the machine’s current operating time is chosen as the heuristic function. In this case, the greater the current operating time of a machine, the smaller the probability of its being selected, which not only ensures ants in the product ant colony are more evenly distributed among the machines of the same operation, but also achieves algorithmic goal optimization. During machine selection, priority is given to unused machines to ensure the full utilization of all machines in the workshop and improve overall production efficiency. Thus, the heuristic value of unused machines is set to a relatively large value, making the next ant more inclined to choose an unused machine when selecting a machine in an operation. The formula is shown in Equation (19).
where is the heuristic function value for the ant to choose machine j from machine i, is the number of times machine j has been selected when the ant chooses, and is the current total operating time of machine j.
3.4. Multi-Pheromone of Product Ant Colony
In the original ACO algorithm, ants search for paths based on a single pheromone between route nodes. For the PACO proposed by the T-FJSP explored in this paper, having a single pheromone makes it difficult to satisfy the release of pheromones when different ants in the colony visit each route. Therefore, this paper adopts multi-pheromone combined with PACO. Each ant has a pheromone, and the number of pheromones corresponds to the number of ants in the product ant colony, that is, the number of pheromones corresponds to the number of textiles to be produced in the textile workshop.
Each pheromone corresponds to the paths between all accessible machine nodes of the ant, where the pheromone between machines belonging to the same operation and non-adjacent operations is 0. The expression of any pheromone is a square matrix:
Each row of the pheromone matrix corresponds to a machine. In the matrix, represents the pheromone deposited by an ant in the product ant colony when accessing a machine and m denotes the rank of the square matrix, representing the number of machines in the textile workshop. In each row, only the nodes of all the machines in the adjacent operation corresponding to the machine in that row are not 0, while the remaining corresponding pheromones are all set to 0.
Based on the multi-pheromone matrix designed for the product ant colony and the total completion time of the workshop, the PACO algorithm is formulated by improving the local pheromone update rule of the original ACO algorithm. When the algorithm iterates once, the total workshop completion time for that iteration is calculated. To minimize the total workshop completion time trend of the algorithm, the next iteration’s pheromone should be inversely proportional to the total completion time of the workshop. Therefore, the local pheromone update rule is expressed as Equation (21).
where is the pheromone accumulated by the k-th group of product ant colonies from machine i to machine j, Q is the pheromone enhancement parameter, and T represents the total completion time of the workshop for the current iteration of the algorithm.
Assuming the algorithm has Z groups of product ant colonies, the global pheromone update rule of the PACO algorithm, shown in Equation (22), is derived according to Equation (18).
where represents the global pheromone for the ant colony to move from machine i to machine j during the x-th iteration and represents the accumulated local pheromone of the k-th group of product ant colonies.
3.5. Variable Pheromone Evaporate Parameter
The pheromone evaporate parameter, , is directly related to the global search ability and convergence speed of the ACO algorithm [30]. If the is small, the convergence speed will be fast, but the algorithm will fall into local optimal. When the is large, the pheromone on the path evaporates quickly, which reduces the search efficiency of the algorithm and easily excludes some good paths.
This paper proposes a variable by comprehensively improving the global search ability and convergence speed of the ACO algorithm. The is updated according to the number of iterations of the algorithm. As shown in Equation (23), in the early stage, the is set to a smaller value to speed up the convergence of the algorithm. Since is small in the early stage, the algorithm easily falls into the local optimal value. To better search for the global optimum, the is set to a higher value in the later stage.
where and represent the initially set maximum and minimum values of , respectively, K is the total number of iterations of the algorithm, and k is the current number of iterations.
The algorithm initially gives the values of , . According to Equation (23), the effect diagram of 100 iterations is shown in Figure 3. It can be seen that the initial effect of the expression meets the improvement requirements.
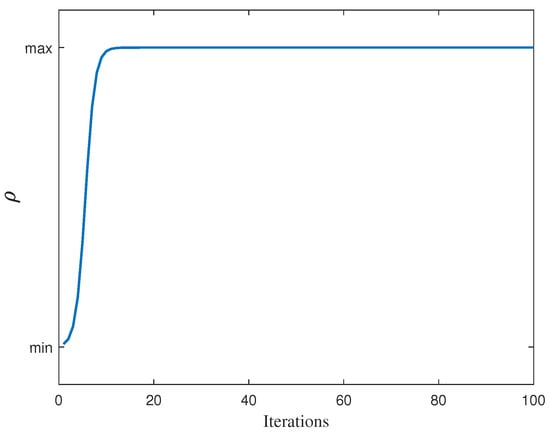
Figure 3.
The iterative effect of .
3.6. Modified Local Pheromone Update Rule
This paper improves the local pheromone update rule during iteration based on the multi-pheromone product ant colony. In the original ACO algorithm, the local pheromone update rule is based on the search performed by a group of ant colonies, with each ant acting independently. In the PACO algorithm, multiple groups of product ant colonies conduct path searches, where individual ants within a product ant colony influence each other, while the ant colonies themselves are independent of each other. Therefore, analogous to the original ACO algorithm, the overall product ant colony is introduced into the local pheromone update rule. To better eliminate ant colonies with a longer and retain those with a shorter , a local pheromone update rule is designed, as shown in Equation (24). At the end of each iteration, we extract the two groups of ant colonies with the maximum and minimum from all groups of ant colonies, using them as the basis for calculating the pheromone levels in that iteration. Then, we reduce the pheromone levels of ant colonies with a longer , based on a comparison of their values of [31].
where is the pheromone value accumulated by the k-th group of product ant colonies, Q is the pheromone enhancement factor, is the of the k-th group of product ant colonies, is the largest of the ant colony in this iteration, is the smallest of the ant colony in this iteration, and is the weight coefficient of the k-th group of product ant colonies.
In order to facilitate the elimination of ant colonies with a longer , the weight coefficients in Equation (24), whose values range from 0 to 1, are set to variable values. Specifically, the weight coefficient for ant colonies with a longer is set to a larger value, while the weight coefficient for ant colonies with a shorter is set to a smaller value. Utilizing an exponential function, the local pheromone of ant colonies with a longer is decreased, whereas that of ant colonies with a shorter is increased. Subsequently, due to the evaporation of global pheromones after several iterations, ant colonies with a longer are gradually eliminated, while those with a shorter are continuously updated by the algorithm. Additionally, throughout the algorithmic iterations, ant colonies with a longer are consistently eliminated. The expression for the weight coefficient is given in Equation (25). By sorting all product ant colonies’ values of in ascending order, the weight coefficient is set larger for colonies with a longer , ultimately updating the local pheromone values of the ant colonies accordingly.
where is the weight coefficient of the k-th group of product ant colonies and represents the weight coefficient factor. If this is set too high it may prematurely eliminate ant colonies with a longer , leaving only a few optimal ant colonies for exploration, which can easily lead to falling into local optima. Conversely, if it is set too low there may be little difference in the local pheromone levels generated by all ant colonies, making it difficult to eliminate ant colonies with a longer . To achieve better results, the value of should be within the range of 0 to 1; is the sorting of the k-th group of product ant colonies in ascending order of the among all groups of ant colonies in this iteration.
3.7. Algorithm Flow
This paper proposes the PACO algorithm to solve the T-FJSP; the PACO algorithm implementation process is as follows:
- Step 1:
- Initialize parameters of all operation machines and products (jobs). Initialize the number of product ant colonies and the maximum iteration number of the algorithm;
- Step 2:
- The algorithm begins to iterate, and the first group of product ant colonies performs a machine search between each operation. The number of ants in each group of ant colonies corresponds to the number of textile products (jobs) to be produced in the workshop, and the corresponding number of pheromones is initialized accordingly;
- Step 3:
- Each ant in the ant colony calculates the heuristic values of each machine and the pheromone between machines to choose a route from the machine corresponding to one operation to the machine corresponding to the next operation;
- Step 4:
- The next colony begins its search. After all product ant colonies complete the search, the ant colony with the minimum is selected as the best ant colony and is compared with the optimal value of the last iteration, thereby updating the global optimal ant colony global multi-pheromone;
- Step 5:
- After the algorithm reaches the set maximum number of iterations, The of the algorithm is obtained.
The PACO algorithm flow chart is shown in Figure 4.
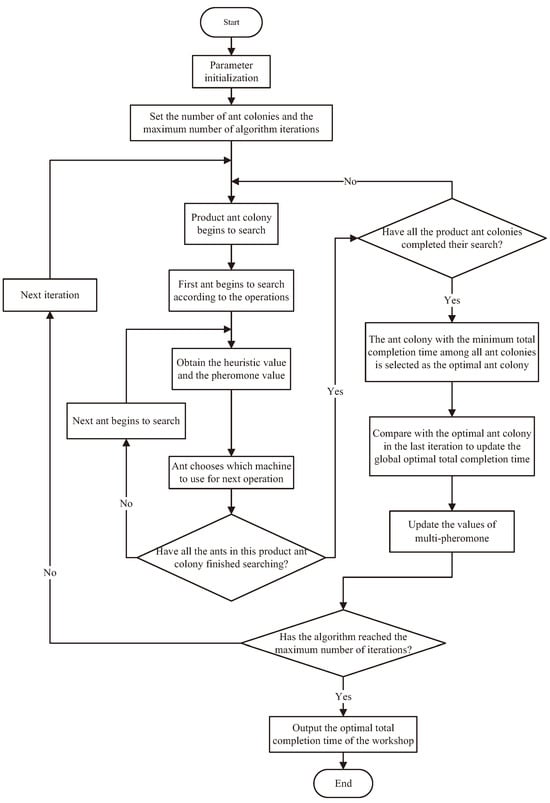
Figure 4.
The algorithm flow chart of PACO.
In the algorithm flowchart depicted in Figure 4, there are two loops. In the inner loop, each group of product ant colonies conducts a search path, where ants obtain heuristic values based on Equation (19) and pheromone values using Equations (20)–(22) for selecting machines. Ants then use the roulette wheel method based on the heuristic values and pheromones of all machines corresponding to the next operation to determine which machine to use for the next operation.
In the outer loop, the current iteration’s global optimum and the pheromone values of all ants in all groups of product ant colonies are updated. Local pheromones for ants are computed using Equation (21) or Equations (24) and (25). Equations (24) and (25) yield the local pheromones of the entire group of ant colonies, which are then used as the local pheromones for all ants in that group of ant colonies. Equation (23) is introduced into Equation (22) for global pheromone updates to obtain the pheromone values for all ants in the next iteration of the algorithm.
4. Results and Analysis
To validate the PACO algorithm designed in this paper for solving the T-FJSP, this section designs simulation experiments based on the constraints among operations, machines, and textile products in the textile workshop, as well as the fundamental conditions of the workshop. Additionally, multiple sets of experiments are established to verify that the modified algorithms based on the PACO algorithm can strengthen the algorithm’s global search capability and convergence speed. Furthermore, multiple sets of experiments are set up based on different numbers of operations and product types to demonstrate that the algorithm not only operates under the basic conditions of the textile workshop but can also solve workshop scheduling problems under similar workshop constraint conditions.
4.1. Simulation Model
This paper takes the actual textile workshop production process as a reference, assuming that all textiles in the experiment are six operations corresponding to the basic textile weaving operations (yarn hanging, beam warping, warp sizing, looming, weaving, packaging). In Section 2 and Section 3, this paper presents the PACO algorithm by delving into the constraints of the textile workshop and the T-FJSP model. To verify whether the PACO algorithm can accomplish scheduling tasks in the textile workshop, a set of experimental conditions is established: there are 27 machines available, and there are 8 textile products corresponding to 3 different types of textiles. The basic experimental conditions are shown in Table 2 and Table 3.

Table 2.
Parameters of machine.

Table 3.
The operating time (hours) and quantity of corresponding operations for textile products.
Based on the original ACO algorithm, the PACO algorithm is configured with the following parameters: the number of product ant colonies is set to 15, with each colony containing 8 ants corresponding to the total number of textile products; the algorithm iterates 100 times; setting and ensures that the heuristic value weight is greater than the pheromone weight, ensuring that ants fully utilize all machines during the path search; according to the empirical experience of the original ACO algorithm, a reasonable range for parameter is between 0.2 and 0.5—here, is set to 0.3; the value of Q in the heuristic function is set to a large value—here, Q is set to 10.
The PACO algorithm is executed based on the experimental conditions of the textile workshop, as described in Table 2 and Table 3, along with the basic algorithm parameters. The optimal allocation results of the experiment are shown in Figure 5 and Figure 6. Figure 5 illustrates the Gantt chart of the optimal machine allocation of textile products obtained by the algorithm. In the figure, different operations are separated by blue dashed lines, allowing for a clear visualization of the complete processing of all eight textile products by each operation. Almost every machine is assigned textile products for processing, fully utilizing the machines across workshop operations. Figure 6 depicts the Gantt chart of the optimal allocation of textile products to machines for each operation. In this chart, the same textile product is consecutively processed between consecutive operations, with no overlap in the total machine operating time, reflecting the actual production scenario in textile workshops. The algorithm achieves the expected performance.
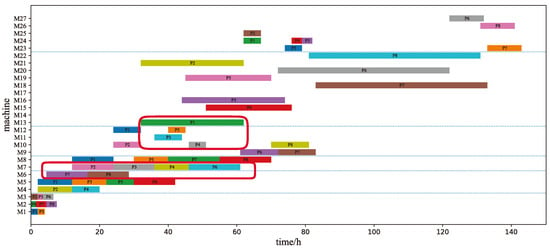
Figure 5.
The Gantt chart of task allocation of workshop machines of the PACO algorithm.
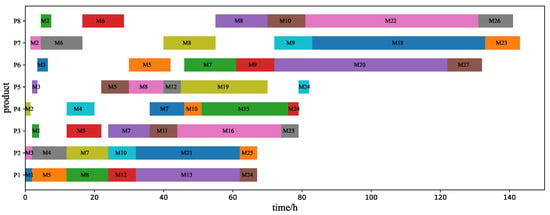
Figure 6.
The Gantt chart of task allocation of workshop products of the PACO algorithm.
Figure 7 illustrates the curve of the objective function during the algorithm’s iteration process, indicating that the algorithm successfully steers the objective function towards optimization. It achieves a relatively good optimization result in the early stages of the run, and the objective function continues to change throughout the entire iteration process, aligning with the expected behavior of the algorithm. Meanwhile, Figure 8 presents the optimization results of the objective function during the iteration process. It includes the initially obtained suboptimal results, the subsequent suboptimal results obtained during the iteration process, and the final optimal result. The figure clearly represents the machine in each operation, with the maximum total operating time corresponding to each optimization result. In both the initially obtained suboptimal result and the final optimal result, machine M23 has the maximum total usage time for the last operation. However, it is evident that the machine total operating times of machine M23 are different. This disparity is due to the fact that the number or type of processed textile products assigned to machine M23 differs between these two optimization results, resulting in different operating times for machine M23 and ultimately unequal total usage times for machines.
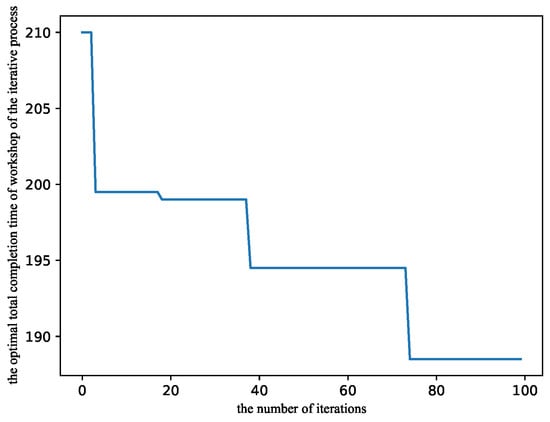
Figure 7.
The iterative process of workshop scheduling optimization of the PACO algorithm.
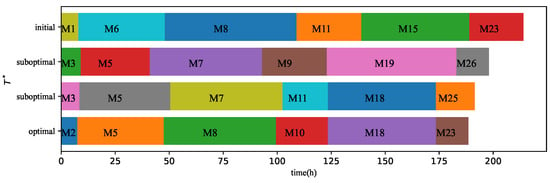
Figure 8.
The Gantt chart of the total completion time of the workshop of the PACO algorithm.
The final completion time in Figure 5 and Figure 6 is approximately 145 h, while the optimized result in Figure 8 has a final time of approximately 180 h. The reason for this difference is as follows: In Figure 5, the dashed lines separate different operations, and when multiple textile products are being produced the machines in each operation and those in adjacent operations can run simultaneously. As a result, there is overlap in the total operating time of machines between adjacent operations. After six operations, this overlap in machine operating time leads to a significant difference between the result obtained by the algorithm and the actual workshop completion time shown in Figure 5 and Figure 6. The red solid box in Figure 5 represents the effect of machine operating time overlap.
4.2. Modified PACO Algorithm Comparison
The PACO algorithm has essentially addressed the scheduling problem in textile workshops based on the constraints and the T-FJSP model. However, the final optimization results and the iterative effectiveness of the algorithm are still suboptimal. In order to enhance the performance of the PACO algorithm, we propose improvements to parameter and the local pheromone update rules. Four sets of simulation experiments are conducted to compare and verify the effectiveness of these improvements: the first set employs the PACO algorithm; the second set involves a modification solely to parameter , referred to as the MPACO 1 algorithm; the third set focuses solely on enhancing the local pheromone update rules, referred to as the MPACO 2 algorithm; the fourth set integrates the MPACO 1 and MPACO 2 algorithms, referred to as the IPACO algorithm. Each algorithm undergoes 100 iterations in the experiments, with 15 groups of product ant colonies and 8 ants per group. Other parameters for each algorithm are shown in Table 4.

Table 4.
The basic parameters of each algorithm.
Due to the potential randomness of running an algorithm once, in order to make the results of each algorithm more generalizable, each algorithm is executed 20 times under identical conditions in the experiments. The optimal total completion time achieved for the workshop and the iteration count when the optimal total completion time is first reached for each run are recorded. The results of 20 runs for each algorithm are presented in Table 5.

Table 5.
The results of 20 runs for each algorithm.
4.3. Comparative Analysis of Algorithms
A more intuitive line graph of the results of the four algorithms’ runs is plotted based on Table 5, as shown in Figure 9. The results of 20 runs for each algorithm are averaged, and the average optimal total completion time and the average optimal number of iterations are shown in Figure 10a,b. The effect of the iterative process on the optimal total completion time of each algorithm during 20 runs is taken for comprehensive comparison. The best results of the four algorithms are achieved in the 11th run of the PACO algorithm, the 18th run of the MACO 1 algorithm, the 5th run of the MACO 2 algorithm, and the 11th run of the IPACO algorithm. The comparative effect of the iterative process is shown in Figure 11.
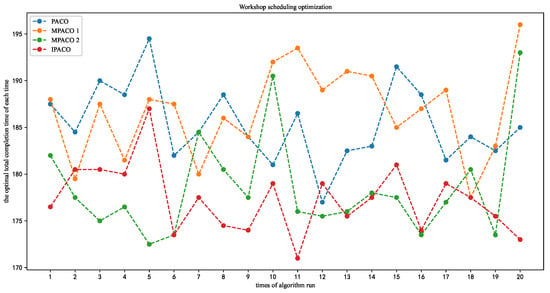
Figure 9.
The intuitive comparison of the four algorithms.
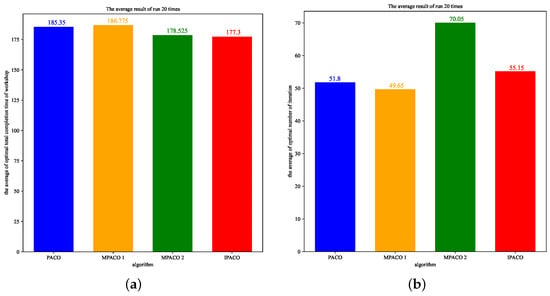
Figure 10.
The comparison of the average effect of algorithms. (a) The optimal completion time of the workshop; (b) The optimal number of iterations.
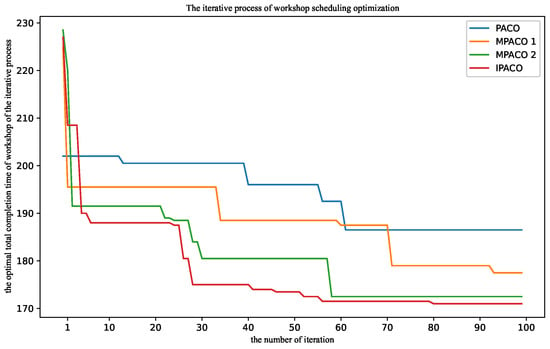
Figure 11.
The comparative effect of the iterative process.
By comparing the MACO 1 algorithm with the PACO algorithm, it can be seen that in the MACO 1 algorithm the overall convergence speed of the algorithm is accelerated, and it can reach the optimal state earlier and faster. The average effect is shown in Figure 10. We can conclude that the average of the two algorithms is almost the same, and the average optimal number of iterations of the MACO 1 algorithm is nearly 20 times lower than the PACO algorithm. According to Figure 9, it can be seen that the results of multiple runs of the MACO 1 algorithm are better than the results of the PACO algorithm. The MACO 1 algorithm has multiple times where the value of is lower than 180 h.
By comparing the MACO 2 algorithm with the PACO algorithm and the MACO 1 algorithm, according to Figure 9 and Figure 10, the MACO 2 algorithm is approximately 10 h lower than the two algorithms, but the convergence speed is significantly lower. The MACO 2 algorithm has multiple times where the value of in the workshop is less than 175 h, so the overall optimization effect of the MACO 2 algorithm is still better than the two algorithms.
The IPACO algorithm combines convergence speed and optimization effect. As shown in Figure 10, compared with the PACO algorithm the IPACO algorithm can achieve a more optimal state of optimization goal, and its convergence speed is approximately 15 times lower than the MACO 2 algorithm. According to Figure 11, the IPACO algorithm uses a modified to accelerate the initial iteration speed and quickly obtain a good optimization value. During the initial to later iteration process, the IPACO algorithm searches for optimization while the three algorithms compared in the later stage basically converge to the best effect and remain unchanged. The process of running the algorithm from 40 to 80 times shows that, in the later stage, the IPACO algorithm has been searching globally and not falling into the local optimum, so that the optimal result has been slightly changing to make the objective value better.
In Figure 11, comparing the final optimization results indicated on the y-axis, the optimization results obtained from the MPACO 1 algorithm, MPACO 2 algorithm, and IPACO algorithm are all lower than those of the PACO algorithm. Furthermore, the IPACO algorithm, which comprehensively incorporates modifications from both aspects, achieves the best performance, which is significantly better than that of the PACO algorithm.
The optimal task allocation of workshop machines obtained by executing the IPACO algorithm is shown in Figure 12. The optimal task allocation of workshop products is shown in Figure 13.
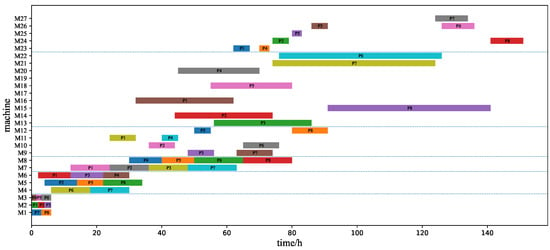
Figure 12.
The Gantt chart of task allocation of workshop machines of the IPACO algorithm.
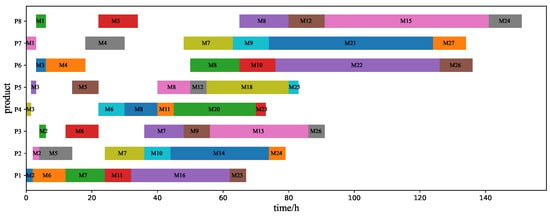
Figure 13.
The Gantt chart of task allocation of workshop products of the IPACO algorithm.
Figure 14 shows the Gantt chart of the optimal total completion time for the IPACO algorithm, and Table 6 presents the specific optimization results of the IPACO algorithm, including the scheduling results for each machine and the total machine operating time. According to Table 6, the maximum total operating time in operation 1 is 6 h, corresponding to , , and ; operation 2 is 30 h, corresponding to ; operation 3 is 51 h, corresponding to ; operation 4 is 19 h, corresponding to and ; operation 5 is 50 h, corresponding to and ; operation 6 is 15 h, corresponding to and . We can then calculate that the optimal objective of the 11-th PACO algorithm run is the sum of the maximum operating time of machines in each operation: .
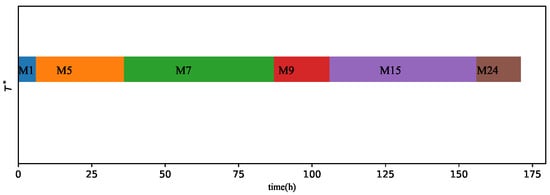
Figure 14.
The Gantt chart of the optimal total completion time of the workshop of the IPACO algorithm.

Table 6.
The best optimization result of PACO algorithm.
4.4. Verification of Algorithms under Different Conditions
In Section 4.2, an experiment was conducted to demonstrate the ability of the PACO algorithm to solve the T-FJSP. In Section 4.3, four series of experiments were conducted to evaluate the effectiveness of the IPACO algorithm, which incorporates two distinct improvements over the PACO algorithm. The results of these experiments demonstrated the superior efficiency of the IPACO algorithm relative to the PACO algorithm.
In Section 4.2 and Section 4.3, the experiments were based on the same condition: 27 textile machines across 6 processes, producing 3 types of textile products. To verify the applicability of the PACO algorithm to various workshops similar to textile manufacturing, four additional sets of experiments have been designed. These experiments involve different operations, varying numbers of textile machines, and different types and quantities of textile products, as illustrated in Table 7 and Table 8.

Table 7.
The corresponding parameters of machines and operations in each experimental group.

Table 8.
The operating time (hours) and the quantity of products corresponding to each experimental group of operations.
Experimental group 1 maintains the same number of operations and product types as the experiment in Section 4.2, but the number of machines in the operations and the number of products are changed to further validate the feasibility of the PACO algorithm. To ascertain the PACO algorithm’s capability in handling different numbers of operations, four sets of experiments are conducted with reduced and increased operations compared to the experiment in Section 4.2: Experimental groups 2 and 3 involve experiments with decreased operations, while experimental groups 4 and 5 involve experiments with increased operations. Similarly, to validate the PACO algorithm’s ability to handle different numbers of product types, the number of product types in the aforementioned four groups of experiments is varied: experimental groups 2 and 5 involve experiments with decreased product types, while experimental groups 3 and 4 involve experiments with increased product types.
To validate the effectiveness of the further improvements proposed in this paper on the initial PACO algorithm, five sets of experiments were conducted using the PACO algorithm, MPACO 1 algorithm, MPACO 2 algorithm, and IPACO algorithm. The basic parameters of the algorithms are set consistent with those in Section 4.2, and the results are presented in Figure 15 and Figure 16. Figure 15 provides a visual comparison of the results obtained from 20 runs of each algorithm across different groups, while Figure 16 illustrates the optimization process of the best-performing runs among the 20 runs for each algorithm.
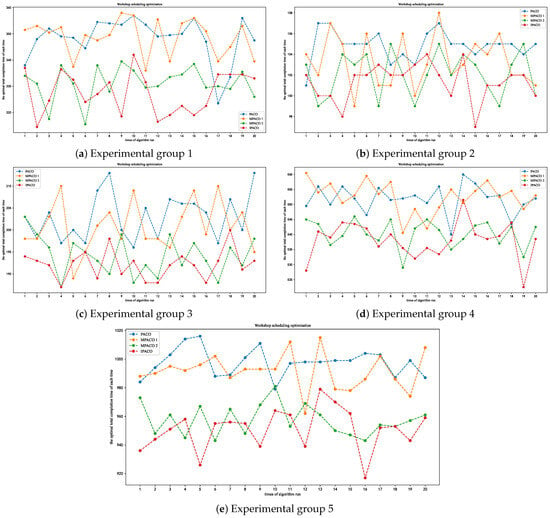
Figure 15.
The visual comparison chart of the results from 20 runs of each algorithm across different experimental groups.
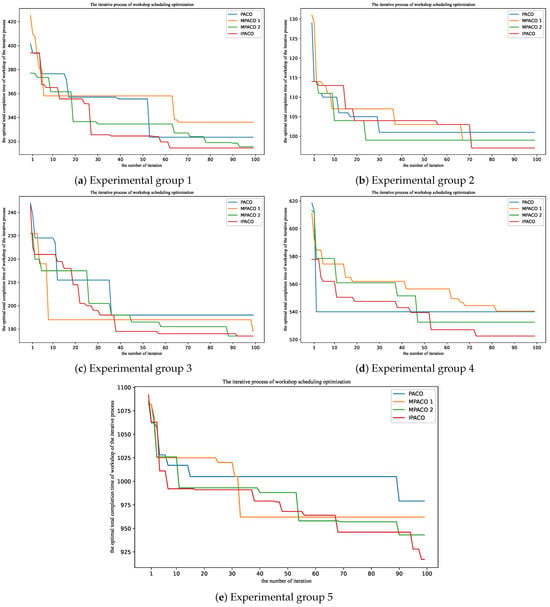
Figure 16.
The comparative visualization of the iteration process for the best optimal results achieved by each algorithm across different experimental groups.
Based on Figure 15 and Figure 16, it is evident that the PACO algorithm can effectively address workshop scheduling problems with varying numbers of operations and product types. Figure 15 clearly illustrates that the IPACO algorithm consistently produces significantly lower overall results across 20 runs in all five experimental groups compared to the PACO algorithm. While the MPACO 2 algorithm exhibits a trend similar to that of the IPACO algorithm, the IPACO algorithm consistently achieves the lowest optimization results among the 20 algorithm runs. Furthermore, comparing with Figure 16, which depicts the iterative optimization process, reveals that the early convergence and overall iterative search of the MPACO 2 algorithm are inferior to those of the IPACO algorithm. In all five experimental groups, the optimization curve of the IPACO algorithm continuously fluctuates from the initial stage to the end of the algorithm, resulting in superior outcomes, even if the changes are sometimes slight.
To compare the superiority of the IPACO algorithm over the PACO algorithm, MACO 1 algorithm, and MACO 2 algorithm, we recorded the average value of the objective function for 20 runs of each algorithm in five experimental groups, as well as the minimum obtained for each algorithm in the 20 runs. We then compared the average value of for each algorithm with the average value of obtained by the IPACO algorithm, and the optimal value of for each algorithm with the optimal value of obtained by the IPACO algorithm. We refer to this comparison as the relative percentage error (RPE) [32]. The RPE is defined by Equation (26).
where is the parameter obtained based on the average value of , represents the average value of obtained from 20 runs of each algorithm, represents the average value of obtained from 20 runs of the IPACO algorithm, is the parameter obtained based on , represents the minimum value of obtained from comparing 20 runs of each algorithm, and represents the minimum value of obtained from comparing 20 runs of the IPACO algorithm.
The results of each algorithm in the five experimental groups are presented in Table 9. As the parameter takes the value of the IPACO algorithm as the reference parameter, all values for the IPACO algorithm in the table are 0. By comparing the and values in Table 9, it can be observed that the IPACO algorithm significantly outperforms the PACO algorithm and the MPACO 1 algorithm in multiple experimental groups. While the indicator for the MACO 2 algorithm ranges from 0.4% to 1%, showing little difference compared to the IPACO algorithm, according to the indicator there is a difference of approximately 3% between them, indicating that the random optimality of the MACO 2 algorithm still falls short of the IPACO algorithm.

Table 9.
The values of each algorithm in the experimental groups.
5. Conclusions
This paper introduces the concept of product ant colony optimization (PACO) for the textile-flexible job-shop scheduling problem (T-FJSP), focusing on the internal processes of textile workshops and the constraints between textile machines and products. By constructing a simulation model of textile workshops, the effectiveness of the PACO algorithm in addressing the T-FJSP is validated. To further enhance the performance of the PACO algorithm in handling the T-FJSP, two improvements are proposed: the transformation of the invariant parameter in the PACO algorithm into a variable parameter , and the enhancement of the local pheromone update rule from single ant colony pheromones to the combination of multiple ant colony pheromones. Additionally, three sets of experiments are conducted to compare the results of the PACO algorithm with those of the improved algorithms: MPACO 1 algorithm, MPACO 2 algorithm, and IPACO algorithm. Through the comparison of results and the visualization of Gantt charts and iterative optimization processes, the superiority of the IPACO algorithm is demonstrated. It not only improves the convergence speed and global search capability of the algorithm but also achieves better optimization results for the objective function.
To verify that the PACO algorithm is not limited to textile workshops, this paper designs five sets of experiments to validate its applicability across varying numbers of operations and product types. The final experimental results demonstrate that the PACO algorithm can effectively solve workshop scheduling problems under constraints similar to those in textile workshops, even with varying numbers of operations and product types. Furthermore, through experiments conducted with modified algorithms in the five sets, the results and RPE indicators indicate that the proposed enhancements to the initial PACO algorithm are highly effective.
In this paper, the machine load generated during the machine run is not considered. In reality, the machine load has a greater impact on workshop production. In the future, to better improve the economic benefits of textile workshops, minimizing machine load can be used as the objective function and combined with the objective of this paper to research multi-objective optimization of workshop scheduling.
Author Contributions
Methodology, F.C. and W.X.; software, F.C. and X.W.; validation, F.C., J.M. and W.X.; formal analysis, F.C., X.W., and W.X.; investigation, F.C., J.C, and W.X.; resources, X.W., J.M. and J.C.; data curation, F.C., J.C., J.M. and X.W.; writing—original draft preparation, F.C.; writing—review and editing, W.X., X.W., and J.C.; project administration, W.X., J.M. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (No. 2022YFB4700601), the National Key R&D Program of China (No. 2022YFB4700602), the Taishan Scholars (No. tsqn201909153), the Ministry of Education industry-university cooperative education project (No. 22086429092517), and the major scientific and technological innovation projects in Shandong Province (2018CXGC0905).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACO | Ant Colony Optimization |
| PACO | Product Ant Colony Optimization |
| JSP | Job-shop Scheduling Problem |
| FJSP | Flexible Job-shop Scheduling Problem |
| LMEO | Learning-based Multipopulation Evolutionary Optimization |
| FJSP-Ts | Flexible Job-shop Scheduling Problem with finite Transportation resources |
| MILP | Mixed-Integer Linear Programming |
| OFA | Optimal Foraging Algorithm |
| PFS | Pythagorean Fuzzy Set |
| T-FJSP | Textile Flexible Job-shop Scheduling Problem |
| MPACO | Modified Product Ant Colony Optimization |
| IPACO | Integrated Product Ant Colony Optimization of MPACO 1 and MPACO 2 |
References
- Pan, R.; Zhang, N.; Xiang, J. Analysis of key technology and application status of textile intelligent factory. Cotton Text. Technol. 2023, 51, 105–110. [Google Scholar]
- Mei, S.; Hu, G.; Wang, J.; Chen, Z.; Xu, Q. Analysis of some key technology basis for intelligent textile manufacturing and its equipment. J. Text. Res. 2017, 38, 166–171. [Google Scholar]
- Zhou, J. Discussion on Feasibility of Weaving Enterprise to Realize Intelligent Production. Cotton Text. Technol. 2021, 49, 68–71. [Google Scholar]
- Ji, X. Discussion on Production Mode of Intelligent Weaving Factory. Cotton Text. Technol. 2020, 48, 75–78. [Google Scholar]
- Brucker, P.; Schlie, R. Job-shop scheduling with multi-purpose machines. Computing 1991, 45, 369–375. [Google Scholar] [CrossRef]
- Pan, Z.; Lei, D.; Wang, L. A Bi-Population Evolutionary Algorithm with Feedback for Energy-Efficient Fuzzy Flexible Job Shop Scheduling. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5295–5307. [Google Scholar] [CrossRef]
- Renna, P. Switch-Off Policies in Job Shop Controlled by Workload Control Concept. Appl. Sci. 2023, 13, 5210. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, L.; Zheng, J.; Chen, J.F.; Wang, X. A Learning-Based Multipopulation Evolutionary Optimization for Flexible Job Shop Scheduling Problem with Finite Transportation Resources. IEEE Trans. Evol. Comput. 2023, 27, 1590–1603. [Google Scholar] [CrossRef]
- Fatemi-Anaraki, S.; Tavakkoli-Moghaddam, R.; Foumani, M.; Vahedi-Nouri, B. Scheduling of Multi-Robot Job Shop Systems in Dynamic Environments: Mixed-Integer Linear Programming and Constraint Programming Approaches. Omega 2023, 115, 102770. [Google Scholar] [CrossRef]
- Gaiardelli, S.; Carra, D.; Spellini, S.; Fummi, F. Dynamic Job and Conveyor-Based Transport Joint Scheduling in Flexible Manufacturing Systems. Appl. Sci. 2024, 14, 3026. [Google Scholar] [CrossRef]
- Kong, J.; Wang, Z. Research on Flexible Job Shop Scheduling Problem with Handling and Setup Time Based on Improved Discrete Particle Swarm Algorithm. Appl. Sci. 2024, 14, 2586. [Google Scholar] [CrossRef]
- Wang, H.J.; Zhu, G.Y. Multiobjective Optimization for FJSP Under Immediate Predecessor Constraints Based OFA and Pythagorean Fuzzy Set. IEEE Trans. Fuzzy Syst. 2023, 31, 3108–3120. [Google Scholar] [CrossRef]
- Liang, X.; Chen, J.; Gu, X.; Huang, M. Improved Adaptive Non-Dominated Sorting Genetic Algorithm with Elite Strategy for Solving Multi-Objective Flexible Job-Shop Scheduling Problem. IEEE Access 2021, 9, 106352–106362. [Google Scholar] [CrossRef]
- Ning, G.; Cao, D. Multi-step Genetic Algorithm for Solving Dynamic Flexible Job Shop Scheduling Problem. In Proceedings of the 2021 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 27–28 August 2021; pp. 23–28. [Google Scholar]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Evolving Scheduling Heuristics via Genetic Programming with Feature Selection in Dynamic Flexible Job-Shop Scheduling. IEEE Trans. Cybern. 2021, 51, 1797–1811. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Xu, D.S.; Ai, X.Y.; Xing, L.N. An Improved Ant Colony Optimization for Flexible Job Shop Scheduling Problems. In Proceedings of the International Joint Conference on Computational Sciences & Optimization, Sanya, China, 24–26 April 2009. [Google Scholar]
- Anitha, J.; Karpagam, M. Ant colony optimization using pheromone updating strategy to solve job shop scheduling. In Proceedings of the 2013 7th International Conference on Intelligent Systems and Control (ISCO), Tamil Nadu, India, 4–5 January 2013; pp. 367–372. [Google Scholar]
- Wang, L.; Cai, J.; Li, M.; Liu, Z. Flexible Job Shop Scheduling Problem Using an Improved Ant Colony Optimization. Sci. Program. 2017, 2017, 9016303. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zhang, B.; Wang, S. Multi-objective optimisation in flexible assembly job shop scheduling using a distributed ant colony system. Eur. J. Oper. Res. 2020, 283, 441–460. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Comput. Ind. Eng. 2021, 156, 107230. [Google Scholar] [CrossRef]
- Yang, X.; Xiong, N.; Xiang, Y.; Du, M.; Zhou, X.; Liu, Y. Path Planning of Mobile Robot Based on Adaptive Ant Colony Optimization. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–4. [Google Scholar]
- Jia, Y.H.; Mei, Y.; Zhang, M. A Bilevel Ant Colony Optimization Algorithm for Capacitated Electric Vehicle Routing Problem. IEEE Trans. Cybern. 2022, 52, 10855–10868. [Google Scholar] [CrossRef]
- Lei, D.; Li, M.; Wang, L. A Two-Phase Meta-Heuristic for Multiobjective Flexible Job Shop Scheduling Problem with Total Energy Consumption Threshold. IEEE Trans. Cybern. 2019, 49, 1097–1109. [Google Scholar] [CrossRef]
- Zhang, G. Research on Methods for Flexible Job Shop Scheduling Problems. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2011. [Google Scholar]
- Li, R.; Gong, W.; Lu, C.; Wang, L. A Learning-Based Memetic Algorithm for Energy-Efficient Flexible Job-Shop Scheduling with Type-2 Fuzzy Processing Time. IEEE Trans. Evol. Comput. 2023, 27, 610–620. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colonies for the travelling salesman problem. Biosystems 1997, 43, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Mavrovouniotis, M.; Müller, F.M.; Yang, S. Ant Colony Optimization with Local Search for Dynamic Traveling Salesman Problems. IEEE Trans. Cybern. 2017, 47, 1743–1756. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Deng, H.; Liu, D.; Song, C.; Han, R.; Hu, T. A Job Shop Scheduling Method Based on Ant Colony Algorithm. In Proceedings of the 2021 IEEE International Conference on Progress in Informatics and Computing (PIC), Shanghai, China, 17–19 December 2021; pp. 453–457. [Google Scholar]
- Mao, W.; Li, S.; Xie, X.; Yang, X.; Nie, J. Global path planning of mobile robot based on adaptive mechanism improved ant colony algorithm. Control. Decis. 2023, 38, 2520–2528. [Google Scholar]
- Wei, D.; Zhang, X.; Hu, M. Joint Task Allocation Method Based on Multi-pheromone Ant Colony Algorithm. J. China Acad. Electron. Inf. Technol. 2019, 14, 798–807+812. [Google Scholar]
- Zheng, P.; Zhang, P.; Wang, M.; Zhang, J. A Data-Driven Robust Scheduling Method Integrating Particle Swarm Optimization Algorithm with Kernel-Based Estimation. Appl. Sci. 2021, 11, 5333. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).