Towards the Analytical Generalization of the Transcendental Energy Equation, Group Velocity, and Effective Mass in One-Dimensional Periodic Potential Wells with a Computational Application to Common Coupled Potentials
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Model Background and Simulation Details
3. Results
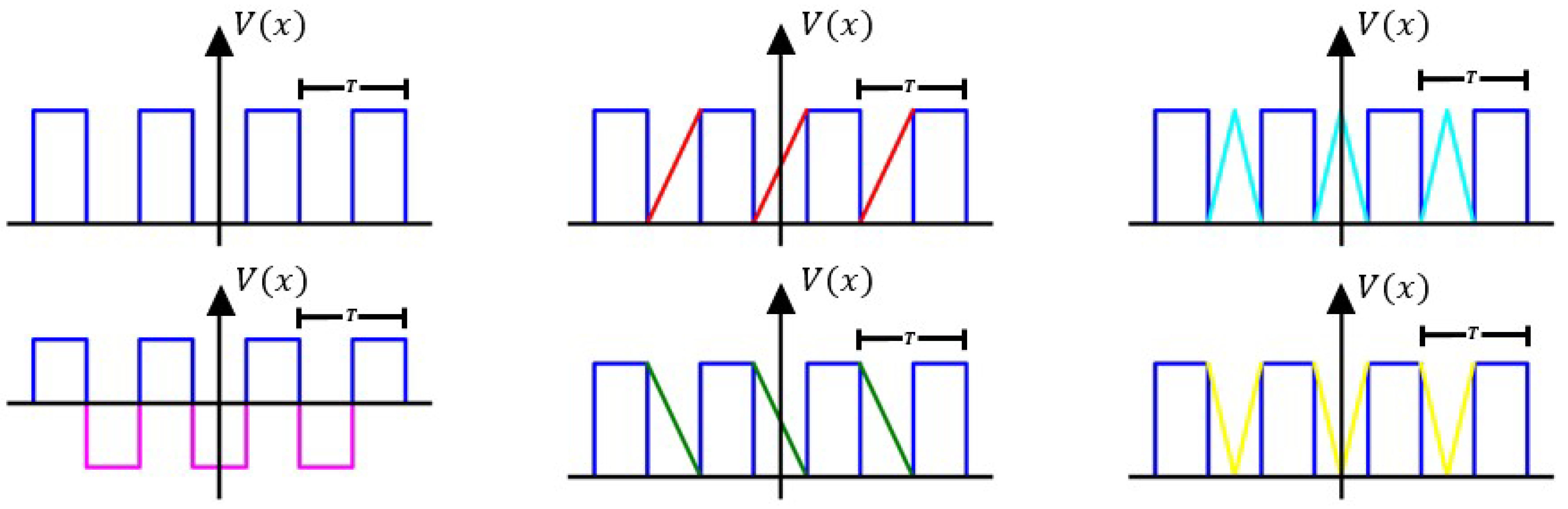
3.1. Periodic Potential of One Potential and a Rectangular-like Barrier
3.1.1. Rectangular-like Potential of Negative Intensity
3.1.2. Linear Potential with a Positive Slope
3.1.3. Linear Potential with a Negative Slope
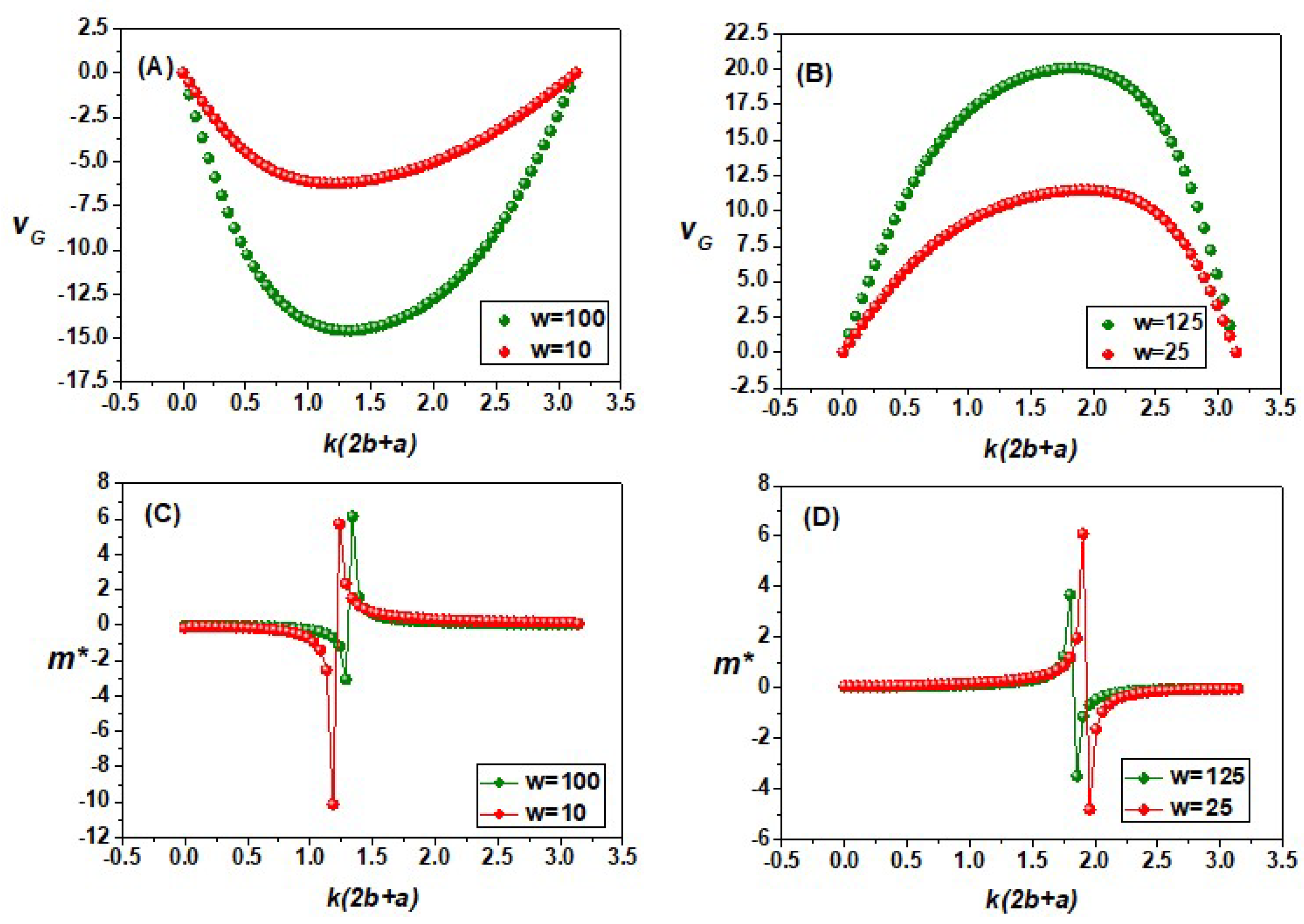
3.2. Group Velocity and Effective Mass for Rectangular-like Potentials of Negative Intensities
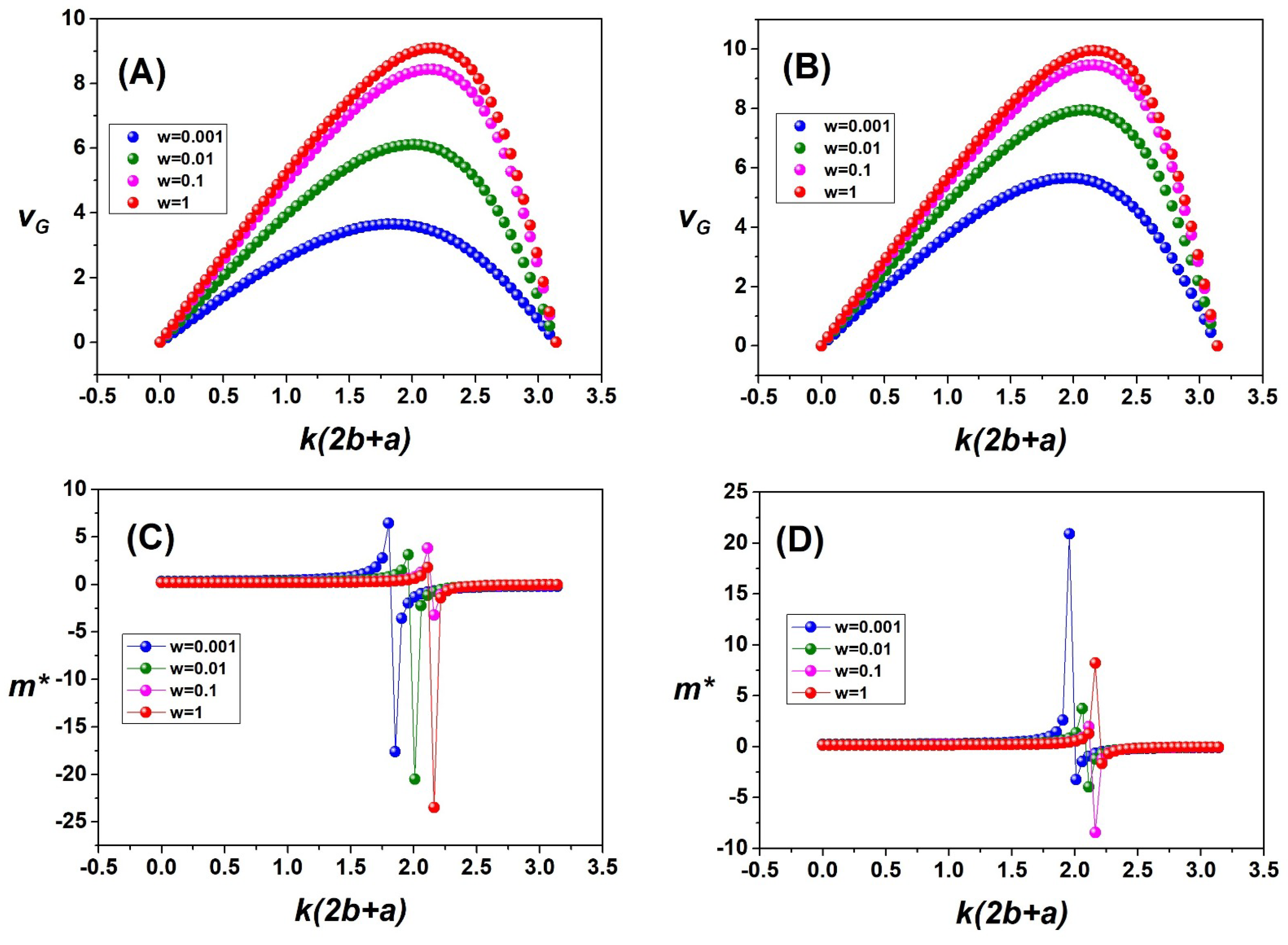
Group Velocity and Effective Mass for Linear Potentials
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
Appendix A.3
Appendix A.4
Appendix A.5
Appendix A.6
Appendix B
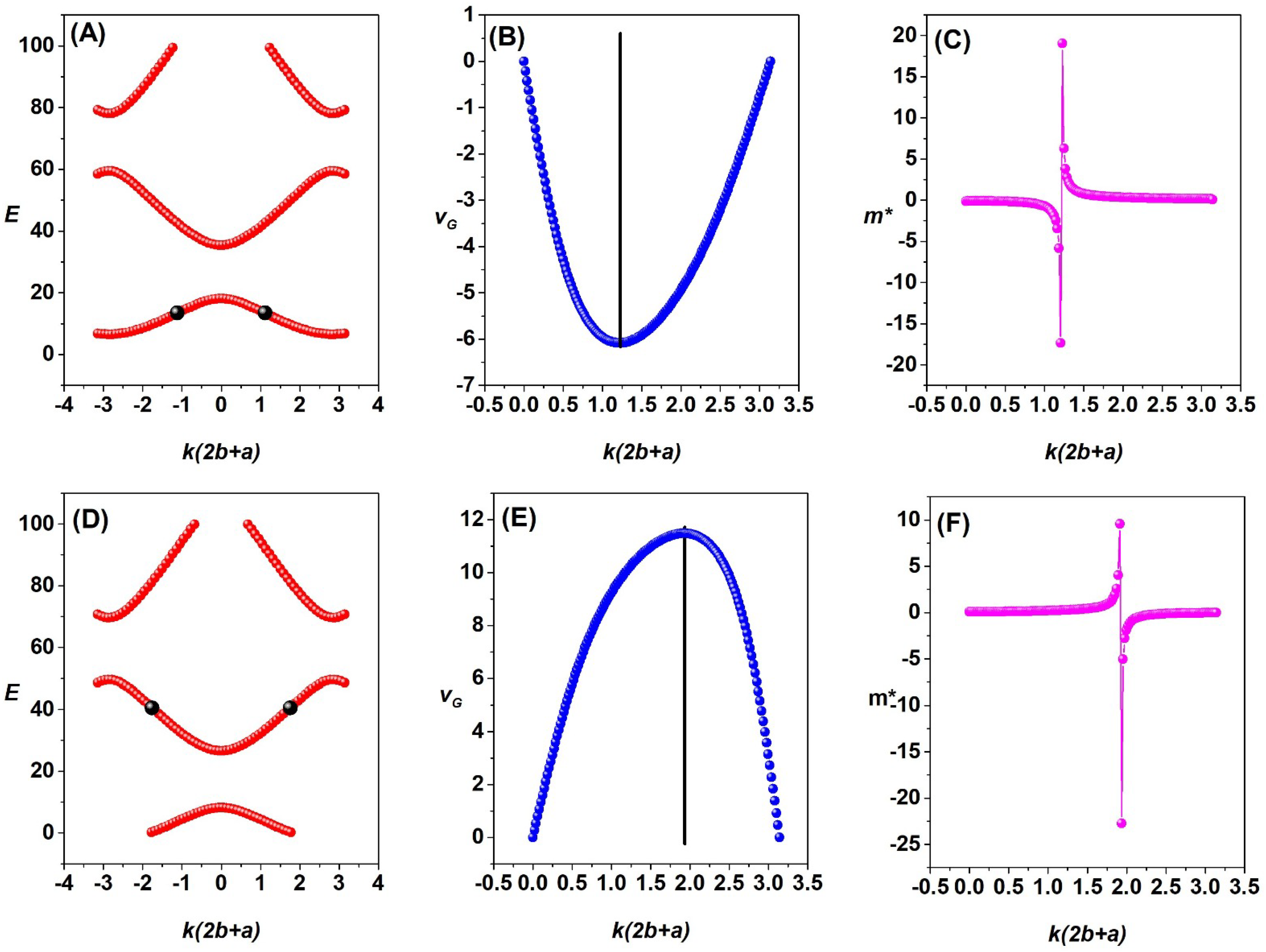
| Group Velocity | a | b | |||
|---|---|---|---|---|---|
| 100 | 1/10 | 1/2 | 1.23 | −6.08 | |
| 100 | 1/10 | 1/2 | 1.93 | 11.5 | |
| Effective Mass | |||||
| 100 | 1/10 | 1/2 | 1.22 | 13.5 | |
| 100 | 1/10 | 1/2 | 1.92 | 40.5 |
References
- Singh, S. Manifestation of Quantum Mechanics and Particle Physics in the Macroscopic World. J. Stud. Res. 2022, 11, 1–5. [Google Scholar] [CrossRef]
- Blount, E.I. Formalisms of band theory. Solid State Phys. 1962, 13, 305–373. [Google Scholar] [CrossRef]
- Vidal, V.E.B. Gas de Bosones en Una Serie Finita de Capas Delgadas Penetrables. Bachelor’s Thesis, Universidad Nacional Autónoma de México, Mexico City, Mexico, 2012. [Google Scholar]
- Vargas, J.H. Método Generalizado de la Matriz de Transferencia (Mgmt); Método de las Funciones de Green de Superficie (Mfgs), Relaciones y Aplicaciones en Sistemas Semiconductores Periódicos. Master’s Thesis, Universidad Nacional de Colombia, Bogota, Colombia, 2013. [Google Scholar]
- Fernández, F.M. Dimensionless equations in non-relativistic quantum mechanics. arXiv 2020, arXiv:2005.05377. [Google Scholar]
- Mommadi, O.; El Moussaouy, A.; El Hadi, M.; Chnafi, M.; Meziani, Y.M.; Duque, C.A. Stark shift and exciton binding energy in parabolic quantum dots: Hydrostatic pressure, temperature, and electric field effects. Philos. Mag. 2021, 101, 753–775. [Google Scholar] [CrossRef]
- Robinett, R.W. The Stark effect in linear potentials. Eur. J. Phys. 2009, 31, 1. [Google Scholar] [CrossRef]
- Keebaugh, C.; Marshman, E.; Singh, C. Improving student understanding of corrections to the energy spectrum of the hydrogen atom for the Zeeman effect. Phys. Rev. Phys. Educ. Res. 2019, 15, 010113. [Google Scholar] [CrossRef]
- Corona, G.P. Localización y Transporte en Medios Aleatorios en Una y Dos Dimensiones. Master’s Thesis, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, Mexico, 2017. [Google Scholar]
- Le Vot, F.; Meléndez, J.J.; Yuste, S.B. Numerical matrix method for quantum periodic potentials. Am. J. Phys. 2016, 84, 426–433. [Google Scholar] [CrossRef]
- Pavelich, R.L.; Marsiglio, F. The Kronig-Penney model extended to arbitrary potentials via numerical matrix mechanics. Am. J. Phys. 2015, 83, 773–781. [Google Scholar] [CrossRef]
- Grosso, G.; Parravicini, G.P. Solid State Physics; Academic Press: London, UK, 2013. [Google Scholar]
- Escudero, F.J. Conductores, aislantes y semiconductores. DYNA 1967, 42, 113–140. Available online: https://www.revistadyna.com/busqueda/conductores-aislantes-y-semiconductores (accessed on 31 January 2024).
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Cengage Learning: Boston, MA, USA, 1976. [Google Scholar]
- Moore, E.A.; Smart, L.E. Optical properties of solids. In Solid State Chemistry; CRC Press: Boca Raton, FL, USA, 2020; pp. 283–314. [Google Scholar]
- Merzbacher, E. The early history of quantum tunneling. Phys. Today 2002, 55, 44–50. [Google Scholar] [CrossRef]
- Gupta, R.; Singhal, T.; Verma, D. Quantum mechanical reflection and transmission coefficients for a particle through a one-dimensional vertical step potential. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 2882–2886. [Google Scholar] [CrossRef]
- de Oliveira, E.C.; Vaz, J. Tunneling in fractional quantum mechanics. J. Phys. A Math. Theor. 2011, 44, 185303. [Google Scholar] [CrossRef]
- Heim, D.M.; Schleich, W.P.; Alsing, P.M.; Dahl, J.P.; Varro, S. Tunneling of an energy eigenstate through a parabolic barrier viewed from Wigner phase space. Phys. Lett. A 2013, 377, 1822–1825. [Google Scholar] [CrossRef]
- Elabsy, A.; Attia, M. Quasi-resonant tunneling states in triangular double-barrier nanostructures. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Mendoza, J.A.; López, J.C.; Suárez, R.M. Análisis del comportamiento de un potencial lineal al solucionar la ecuación de Schrödinger. BISTUA Rev. Fac. Cienc. Básicas 2021, 18, 34–37. [Google Scholar]
- Yuce, C. Quantum inverted harmonic potential. Phys. Scr. 2021, 96, 105006. [Google Scholar] [CrossRef]
- Soto-Eguibar, F.; Moya-Cessa, H.M. Solution of the Schrödinger equation for a Linear potential using the extended Baker-Campbell-Hausdorff formula. Appl. Math. Inf. Sci. 2015, 9, 175. [Google Scholar] [CrossRef]
- Gil, A.; Segura, J.; Temme, N.M. Fast and accurate computation of the Weber parabolic cylinder function W (a, x). IMA J. Numer. Anal. 2011, 31, 1194–1216. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications: Mineola, NY, USA, 1965. [Google Scholar]
- Sun, G.H.; Chen, C.Y.; Taud, H.; Yáñez-Márquez, C.; Dong, S.H. Exact solutions of the 1D Schrödinger equation with the Mathieu potential. Phys. Lett. A 2020, 384, 126480. [Google Scholar] [CrossRef]
- Dong, S.H.; Dong, S.; Dong, Q.; Sun, G.H.; Femmam, S. Exact solutions of the Razavy cosine type potential. Adv. High Energy Phys. 2018, 2018, 5824271. [Google Scholar] [CrossRef]
- Chen, C.Y.; Lu, F.L.; Sun, G.H.; Wang, X.H.; You, Y.; Sun, D.S.; Dong, S.H. Exact solution of rigid planar rotor in external electric field. Results Phys. 2022, 34, 105330. [Google Scholar] [CrossRef]
- Chen, C.Y.; Wang, X.H.; You, Y.; Sun, D.S.; Lu, F.L.; Dong, S.H. Exact solutions to the angular Teukolsky equation with s≠0. Commun. Theor. Phys. 2022, 74, 115001. [Google Scholar] [CrossRef]
- Mendoza-Villa, F.; Ramos-Guivar, J.A.; Espinoza-Bernardo, R.M. Generalized One-Dimensional Periodic Potential Wells Tending to the Dirac Delta Potential. Physics 2024, 6, 75–93. [Google Scholar] [CrossRef]
- Carver, T.R. Mathieu’s functions and electrons in a periodic lattice. Am. J. Phys. 1971, 39, 1225–1230. [Google Scholar] [CrossRef]
- Yang, Z. Non-perturbative Breakdown of Bloch’s Theorem and Hermitian Skin Effects. arXiv 2020, arXiv:2012.03333. [Google Scholar] [CrossRef]
- Alvarez, L. Introduction of the concepts of hole and effective mass using an alternative to the Ek diagram. Rev. Mex. Fís. 2013, 59, 128–132. [Google Scholar]
- Náraigh, L.Ó.; O’Kiely, D. Homogenization theory for periodic potentials in the Schrödinger equation. Eur. J. Phys. 2012, 34, 19. [Google Scholar] [CrossRef]
- Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 2005, 1, 23–30. [Google Scholar] [CrossRef]
- Izquierdo, E.A. Funciones de Green Aplicadas a la Solución de Problemas de Contorno Basados en la Ecuacion Diferencial de Airy. Bachelor’s Thesis, Universidad de Narino, Pasto, Colombia, 2018. [Google Scholar]
- Gil, A.; Segura, J.; Temme, N.M. Numerical Evaluation of Airy-Type Integrals Arising in Uniform Asymptotic Analysis. J. Comput. Appl. Math. 2020, 371, 112717. [Google Scholar] [CrossRef]
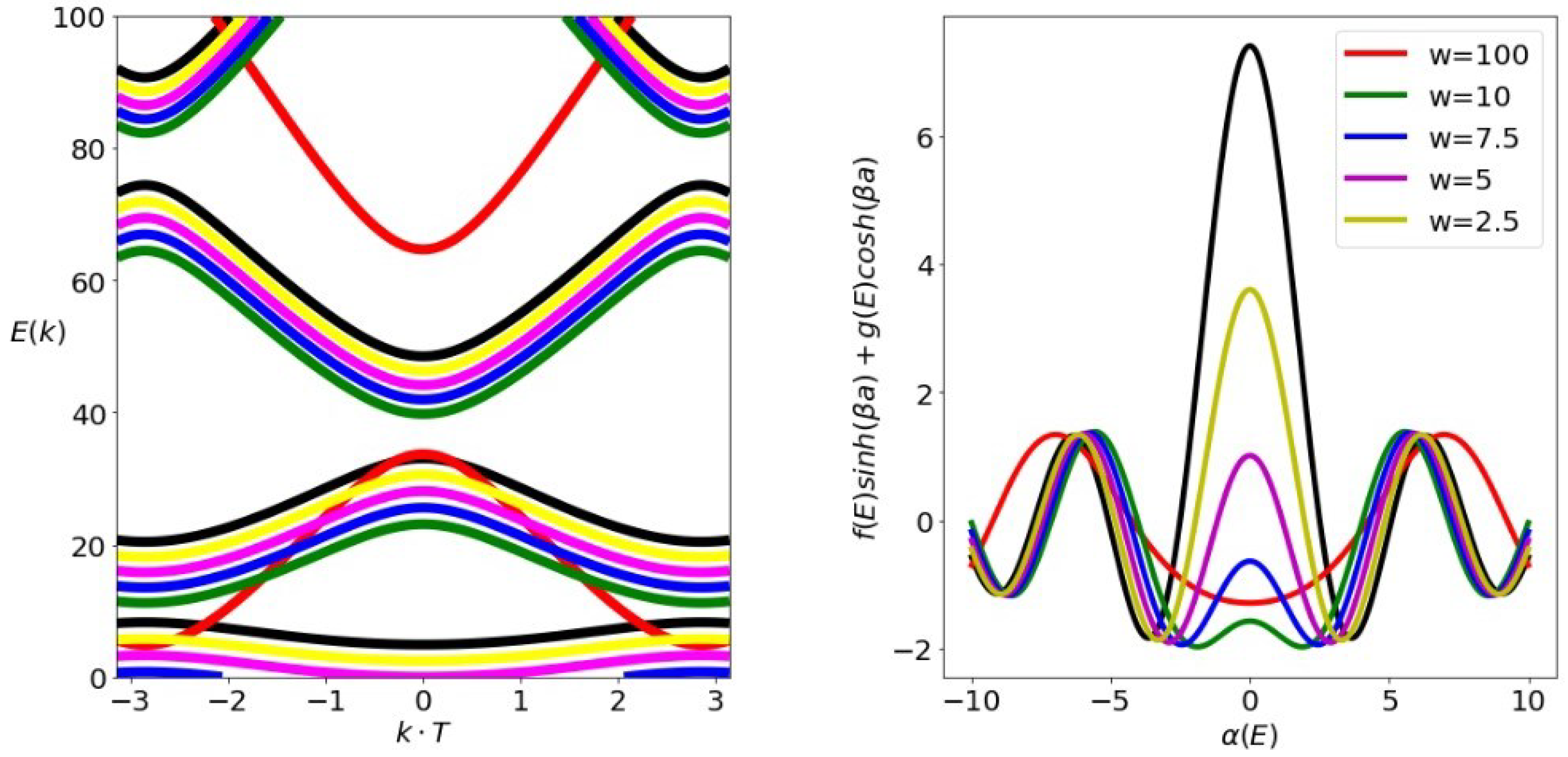
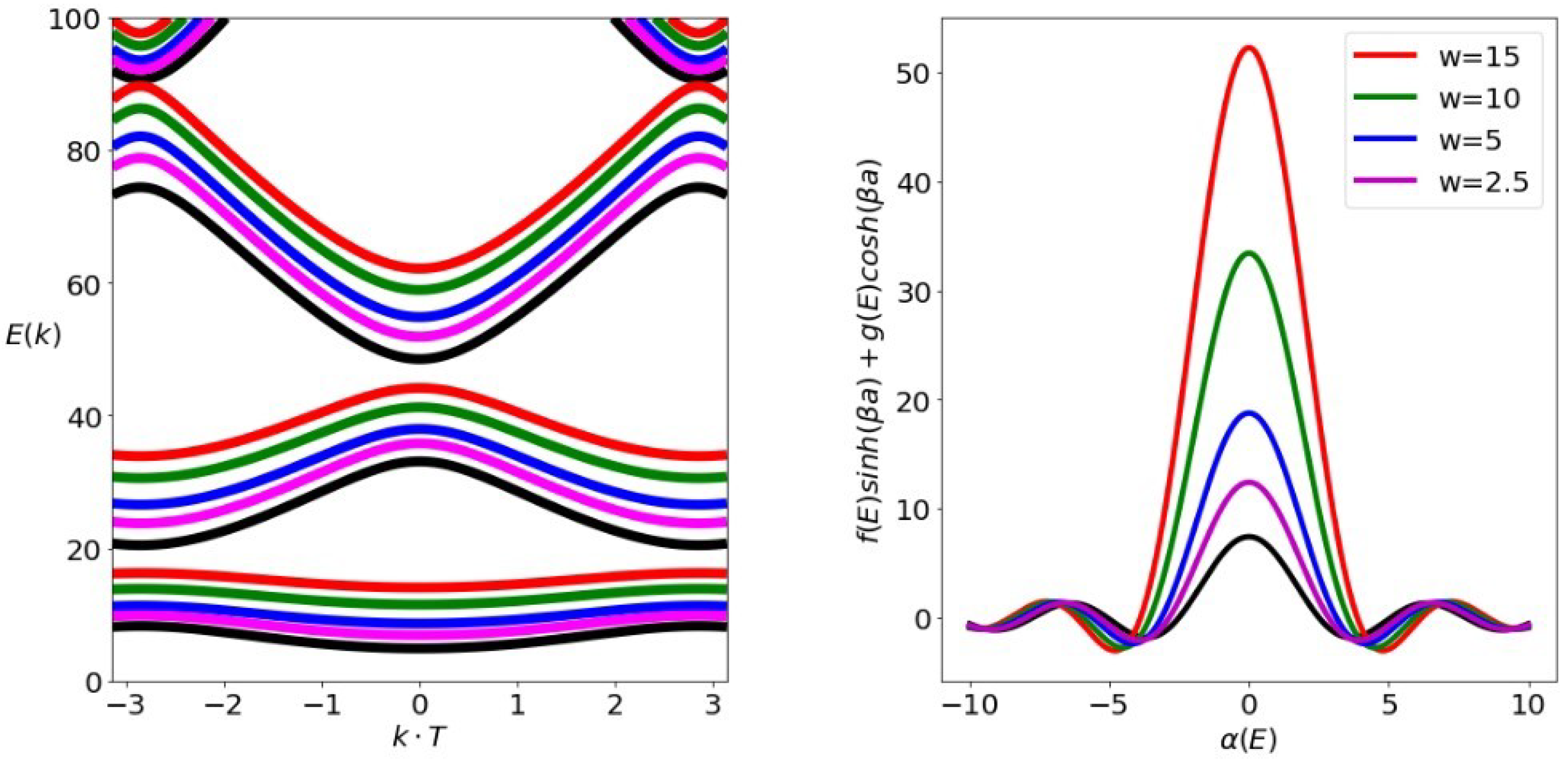

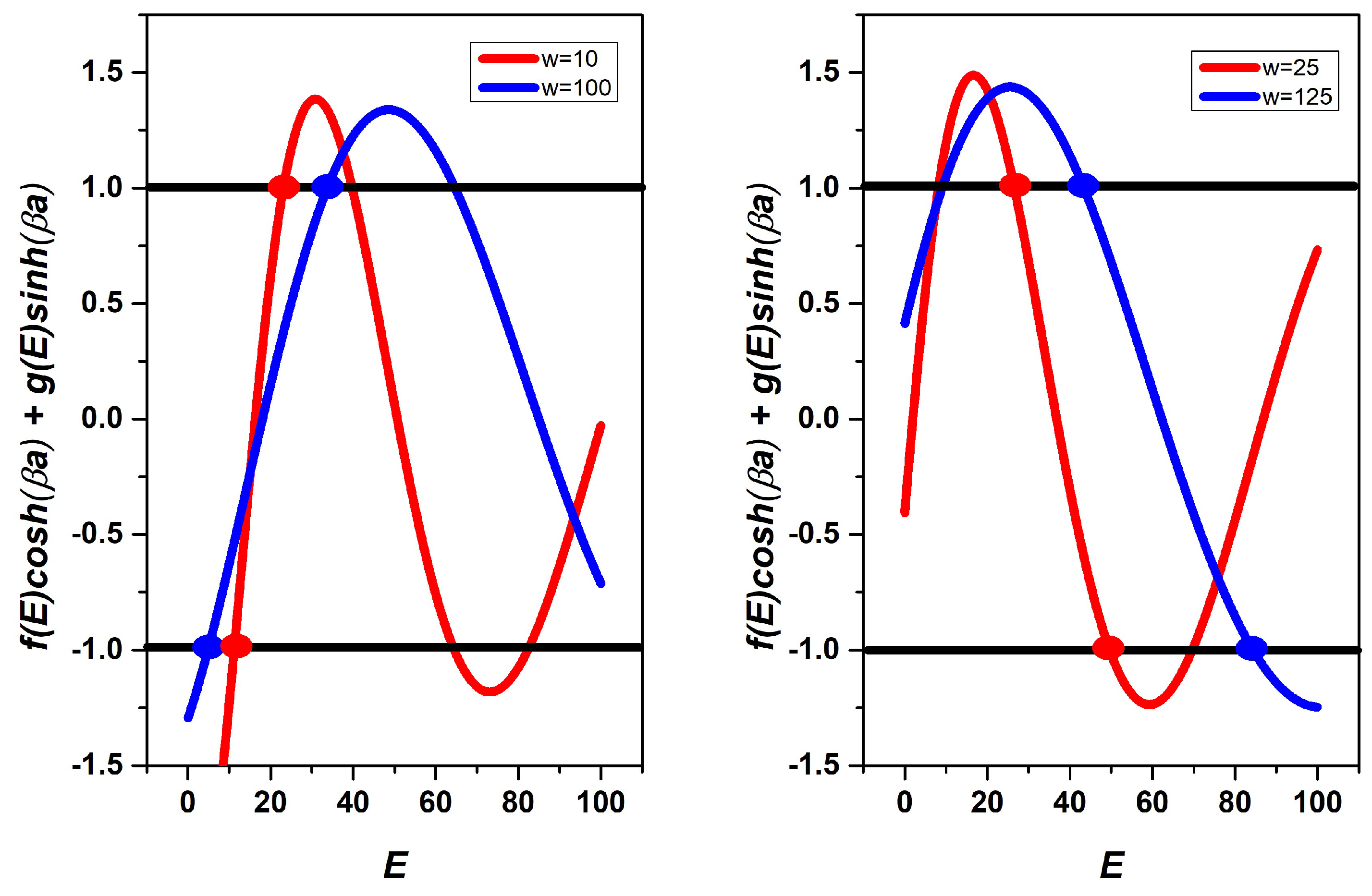


| First Energy Band | a | w | b | |
|---|---|---|---|---|
| positive | 100 | 1/10 | 125 | 1/2 |
| 100 | 1/10 | 25 | 1/2 | |
| 75 | 1/10 | 5 | 1/3 | |
| 75 | 1/10 | 5/2 | 1/3 | |
| 50 | 1/5 | 25 | 1/2 | |
| 50 | 1/5 | 150 | 1/2 | |
| 150 | 1/10 | 30 | 1/2 | |
| 150 | 1/10 | 150 | 1/2 | |
| 150 | 1/5 | 100 | 1/3 | |
| 150 | 1/5 | 120 | 1/3 | |
| negative | 100 | 1/10 | 100 | 1/2 |
| 100 | 1/10 | 10 | 1/2 | |
| 75 | 1/10 | 10 | 1/3 | |
| 75 | 1/10 | 25 | 1/3 | |
| 50 | 1/5 | 10 | 1/2 | |
| 50 | 1/5 | 100 | 1/2 | |
| 150 | 1/10 | 20 | 1/2 | |
| 150 | 1/10 | 100 | 1/2 | |
| 150 | 1/5 | 20 | 1/3 | |
| 150 | 1/5 | 30 | 1/3 |
| Group Velocity | w | ||
|---|---|---|---|
| Positive slope linear potential | 100 | 1.62 | 0.01550 |
| 75 | 1.62 | 0.00835 | |
| 50 | 1.62 | 0.00456 | |
| 25 | 1.62 | 0.00257 | |
| 10 | 1.62 | 0.00192 | |
| Negative slope linear potential | 100 | 1.62 | 0.003110 |
| 75 | 1.62 | 0.001920 | |
| 50 | 1.62 | 0.001160 | |
| 25 | 1.62 | 0.000701 | |
| 10 | 1.62 | 0.000544 |
| Effective Mass | w | E | |
|---|---|---|---|
| Positive slope linear potential | 100 | 1.57 | 62.2 |
| 75 | 1.57 | 52.5 | |
| 50 | 1.57 | 41.9 | |
| 25 | 1.57 | 30.2 | |
| 10 | 1.58 | 22.1 | |
| Negative slope linear potential | 100 | 1.57 | 59.4 |
| 75 | 1.57 | 49.9 | |
| 50 | 1.57 | 39.3 | |
| 25 | 1.57 | 27.6 | |
| 10 | 1.57 | 19.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendoza-Villa, F.; Manrique-Castillo, E.V.; Passamani, E.C.; Ramos-Guivar, J.A. Towards the Analytical Generalization of the Transcendental Energy Equation, Group Velocity, and Effective Mass in One-Dimensional Periodic Potential Wells with a Computational Application to Common Coupled Potentials. Appl. Sci. 2024, 14, 3987. https://doi.org/10.3390/app14103987
Mendoza-Villa F, Manrique-Castillo EV, Passamani EC, Ramos-Guivar JA. Towards the Analytical Generalization of the Transcendental Energy Equation, Group Velocity, and Effective Mass in One-Dimensional Periodic Potential Wells with a Computational Application to Common Coupled Potentials. Applied Sciences. 2024; 14(10):3987. https://doi.org/10.3390/app14103987
Chicago/Turabian StyleMendoza-Villa, F., Erich V. Manrique-Castillo, Edson C. Passamani, and Juan A. Ramos-Guivar. 2024. "Towards the Analytical Generalization of the Transcendental Energy Equation, Group Velocity, and Effective Mass in One-Dimensional Periodic Potential Wells with a Computational Application to Common Coupled Potentials" Applied Sciences 14, no. 10: 3987. https://doi.org/10.3390/app14103987
APA StyleMendoza-Villa, F., Manrique-Castillo, E. V., Passamani, E. C., & Ramos-Guivar, J. A. (2024). Towards the Analytical Generalization of the Transcendental Energy Equation, Group Velocity, and Effective Mass in One-Dimensional Periodic Potential Wells with a Computational Application to Common Coupled Potentials. Applied Sciences, 14(10), 3987. https://doi.org/10.3390/app14103987







