Abstract
This paper investigates the quantum Bayesian probability estimation of fault diagnosis based on Partially Observable Petri Nets (POPN) for a liquid-propellant rocket engine system. To solve the problem of a poor environment, a complex structure, and limited observable information in the liquid-propellant rocket engine system, a method of fault diagnosis based on POPN and quantum Bayesian probability estimation is proposed. According to the operating state and key actions of the system model, the places and transitions are set, and the unobservable key actions will become unobservable transitions. Combined with the trigger relationship of the transitions, a POPN model is established. All path estimation system states that satisfy the observable transition sequence information are traversed. If the diagnosis result is a possible failure, we establish a quantum Bayesian Petri net model corresponding to the failure transition, manually adjust the quantum parameters to calculate the quantum probability of the failure transition, and determine the system failure state. Finally, the model of the start-up process of the engine system based on the POPN is built to verify the effectiveness of the algorithm with the data in the simulation experiment.
1. Introduction
Reliable health monitoring is crucial for the safe operation of a discrete event dynamic system (DEDS). Highly constrained systems require minimal sensing and computing capacity, thus the prediction and diagnosis of the undetectable part of the fault are inevitable when only a part of the valid information is observed. The system behavior will highly change or may fail with the occurrence of some faults [1,2].
Due to the limitation of the number of sensors, to overcome the problem of incomplete observation of the information and meet the real-time requirements, the diagnosis system generally adopts the diagnosis method based on the qualitative model [3]. Petri nets were first applied to fault identification and diagnosis, power systems [4], communication systems [5], etc. Dimitri [5] proposed using Markov stochastic dynamics with the measured events and labeled sensors to represent the fault process and construct partially observable stochastic Petri nets. The probabilities of time and non-time marked trajectories consistent with the given time series are calculated systematically, and the diagnosis is based on the probability of failure. The authors of [6] proposed constructing a basis reachability graph, calculating the vector and the basis marker, identifying the fault class alarm level by introducing two kinds of fuzzy operators, and using bidirectional reasoning strategies (i.e., forward reverse reasoning) to determine the factor value of the diagnosis results. The problem of fault prediction for stochastic discrete event systems was studied, and an incremental algorithm was proposed. From the set of current possible states and their probabilities, the probability of consistent trajectories was evaluated based on the measured data, and the state estimation was obtained as a result. The probability model proposed the use of a method for evaluating future fault probability [7]. Bayesian network machine learning methods are widely used in fault prediction and diagnosis. Guo et al. [8] used the Grover quantum search algorithm to quickly search for the transformer fault, symptom type, and other target data. AHP deleted indicators with little impact on fault diagnosis and analyzed and determined the error classification rate of the variable precision rough set to obtain the minimum fault decision table to construct the Bayesian network fault reasoning model. It completed the diagnosis of transformer faults.
The current research mainly regards traditional probability estimation plus Bayesian statistical methods, and the accuracy of probability estimation needs to be improved [9,10,11,12,13]. In this paper, we first propose a fault diagnosis method based on quantum Bayesian estimation for partially observable discrete event dynamic systems [14,15,16,17,18,19,20]. When the uncertainty level of the network is very high, the uncertain elements in the network cause uncertain paths. Quantum Bayesian inference is introduced, and then the interference term is added to the Bayesian formula via the quantum superposition principle, which brings the probability estimation closer to the real probability. Compared with traditional fault diagnosis methods, the quantum Bayesian estimation method can greatly improve the accuracy of fault diagnosis. The quantum parameters are manually selected to calculate the firing probability of fault transitions and judge the fault state of the system by establishing the quantum Bayesian network model of unobservable fault transition by using the firing relationship of observable transitions and the firing probability of unobservable transitions [21,22,23,24,25,26,27].
This paper is structured as follows: Section 2 presents a description of the quantum Bayesian fault diagnosis problem in partially observable Petri nets [28,29,30,31]. Section 3 proposes a quantum Bayesian fault diagnosis method for Partially Observable Petri Nets. Section 4 illustrates the method with a case study and compares the proposed algorithm with the previous algorithm. Finally, Section 5 draws conclusions and provides some perspectives for future studies.
2. The Problem of Quantum Bayesian Fault Diagnosis for Partially Observable Petri Nets
2.1. Partially Observable Petri Nets
Definition 1.
A Partially Observable Petri Net (POPN) is defined as a sextuple: and . is a set of m places, is a set of n transitions, is a set of observable transitions, and is a set of unobservable transitions. and are the forward arc matrix and backward arc matrix of transition, respectively. The matrix is defined as the incidence matrix of the POPN, and is a set of non-negative integers. is the initial marking of the POPN.
Let the marking of the place p be , then the necessary and sufficient condition of the logical enablement of transition at marking is:
For any , . is prepositive set of , .
Transition fires at the marking , which is marked as . If after was fired, it is abbreviated as . It is called the equation of state of the POPN, and is the incidence matrix of the transition that is fired.
2.2. The Observation Sequence
The transition probability sequence (TPS) with the length is defined as:
The corresponding marking is or , and . is the transition fired last. Transition corresponds to the transition firing probability . is a range of probability values. However, it is clear that when , the observable transition probability sequence TPS does not occur. We denote as the logic sequence of transitions associated with neglecting the firing probability that they have been fired.
Definition 2.
The label POPN (LPOPN) is defined as . The label function allocates a label or an empty sequence label for transition . The observable transition set and the unobservable transition set .
For the label function, we extend the labeling function to define the recursively as follows:
- If, , then .
- If , then .
- If , then .
- Moreover, is an empty sequence.
- When , the label function is extended to:
Definition 3.
The observable label probability sequence (OLPS) is composed of the set of observable transition and its corresponding firing probability :
is the probability corresponding to the transition fired at the end of sequence . At least one TPS corresponding to .
2.3. Problem of Fault Diagnosis
In this paper, the main function of the fault diagnosis algorithm based on quantum Bayes and Petri nets is to judge whether the transitions of the unobservable part of Petri nets produces faults. The conditions of the fault diagnosis algorithm present the following assumptions:
Assumption 1.
The network and the identification of the initial marketing create the system.
Assumption 2.
The labels associated with the transition are observable.
Assumption 3.
There is no cyclic firing on the unobservable part of POPN, and it is acyclic.
Assumptions 1 and 2 show the knowledge level of the system. Assumption 3 is the common assumption in the field of fault detection based on PN model: That forbid the unobservable cycle.
Definition 4.
In the POPN, given a transition and its corresponding probability of firing conditions, the transition probability pair is . Its corresponding quantum probability amplitude is determined by Equation (1):
The introduction of an interference term resulted in a probability estimation value greater than 1, so this value need to be standardized by adding a normalization factor. The quantum probability table of all transitions in the POPN is .
Definition 5.
Given a OLPS , its corresponding probability transition sequence set is:
is the quantum firing probability of the probability transition sequence as the initial marking at the point of unobservable transition . Marking can make it enabled under the condition that the transition is observable and the firing probability is .
Definition 6.
Given an OLPS , its corresponding marking set is
Definition 7.
Given an OLPS , its corresponding state set is
In the formula, .
Theorem 1.
Given a OLPS , probability tables of transitions, fault class and system fault threshold . A fault function is defined:
is the fault class and belongs to the unobservable transition set. The fault classes may be actuator fault, improper system structure maintenance, environmental interference, etc. corresponds to specific transitions caused by the fault.
- When fault transition does not exist in all TPS, the system state is faultless.
- When the fault transition may exist in TPS, the system is in uncertain diagnosis and the fault incidence needs to be further determined. The fault probability of the system isif the system state is fault, else the system state is faultless.
- When the fault transition exists in all TPS, the system state is fault.
Proof of Theorem 1:
- If , satisfying
So the fault cannot be fired, and any TPS does not contain fault transitions.
- 2.
- If , satisfying
So fault transitions may or may not be fired, and there are TPS sequences that contain fault transitions and TPS sequence that do not contain fault transitions. The fault probability of the system is:
- 3.
- If , satisfying
So fault is fired and any TPS sequence contains fault transitions.
The fault diagnosis for the unobservable part of the POPN model needs to design a state diagnostor, and establish quantum Bayesian Petri nets with possible fault transitions, then estimate the fault probability of the POPN system with transition sequence and quantum Bayesian probability. Finally, judge the system’s state. □
3. A Quantum Bayesian Fault Diagnosis Method for Partially Observable Petri Nets
3.1. Quantum Bayesian Probability Estimation
The Bayesian network consists of a directed acyclic graph of nodes and the conditional probability table of each node [7,8]. Domain is the node variable of . denotes the conditional probability of the variable set in the node and the parent node . The joint probability distribution of all variables in the Bayesian network is as follows:
In Bayesian networks, let e be the observable variable and Y be the unobservable variable. Then, for the variable :
For the random variables , the number of basic events is m, and normalization factor .
In quantum Bayesian networks, quantum probability amplitude is used to replace the real probability quantity:
Application of the Born rule to Equation (3):
By expanding Equation (5), we obtain the quantum interference formula:
and where
When and , the quantum Bayesian network is transformed into the classical Bayesian network.
Using the backward reasoning of Bayesian estimation, the posterior probabilities of can be calculated from the Equations (4) and (6):
From the view of quantum mechanics, the quantum parameters generated by the interference effect are the displacement of the energy wave. From the perspective of quantum cognition, they can be interpreted as the association between events and the shared semantic relationship between them.
Definition 8.
The reliability of the fault set in the PN is called confidence [9] and it is denoted by . Given the probability sequence set corresponding to the fault transition is , then
Definition 9.
Quantum Bayesian Petri nets (QBPN) are defined as a seven tuple: . In QBPN, is the observable transition set, is the unobservable transition set. , and is quantum probability table of .
3.2. Quantum Bayesian Probabilistic Fault Diagnosis for Partially Observable Petri Nets
We build the QBPN model of fault transition to diagnose the fault state of the system. According to quantum Bayesian estimation, the prior probability can be calculated by the corresponding observable transitions in the fault transitions pre-set, then the firing order of observable transitions in the post-set can provide us the posterior probability of fault transitions. See Algorithm 1.
| Algorithm 1: Fault Diagnosis Based on QBPN |
| INPUT: The POPN model, quantum Bayesian probability table and possible fault transition |
| OUTPUT: System’s fault probability |
| 1 Initialization |
| 2 for do |
| While |
| do |
| Copy all transitions , place p and arcs between and to QBPN, , |
| While |
| do |
| Copy all transitions , place p and arcs between and to QBPN, , 3 if , cannot be fired then |
| Delete and its input and output arcs |
| 4 for do |
| According to the quantum probability table , set quantum probability amplitude . |
| 5 for do |
| According to the observable transition state of the forward path, calculate . |
| 6 for do |
| According to the firing order of the post-set of observable transitions, calculate |
| 7 Choose the maximum probability of the fault transitions as the fault probability of the system |
| 8 if then |
| else |
| 9 return |
Aiming at the unobservable fault transition in the POPN model, according to the firing relationship between the parent node and the child node, the parent node first traverses forward, stops searching when the observable transition is encountered. Transforms the transitions, places and arcs in the traversal process into quantum Bayesian node elements, and continues to traverse other parent node branches until the parent node collection is traversed. Then, the sub-nodes start to traverse backward, and stop searching when they encounter observable transitions. The transitions in the process of traversal, transform the transitions, places and arcs in the traversal process into the quantum Bayesian node element, and other sub-nodes continue to traverse until the collection of sub-nodes is traversed. Remove the transition elements causing the dead state to simplify the QBPN model structure. According to the quantum interference caused by the uncertain path, recalibrate the conditional probability table of the transition to obtain the quantum probability amplitude table. According to the pre-set of fault transition and quantum Bayesian reasoning, calculate the firing prior probability of the transition, and then the posterior probability is modified by the observable transition in the post-set. Estimate the state of the system by the maximum posteriori probability. When the fault transition is not unique, the fault with the maximum probability is selected as the fault source.
3.3. Algorithm Complexity Analysis
Starting from each fault transition, the algorithm traverses the transition sequence forward and backward, respectively, until the first observable transition occurs. In the worst case, the algorithm has to traverse transitions each time, and the complexity is . Then, remove irrelevant transitions, and the number of calculations is . Moreover, set the transition firing probability and mark the quantum probability amplitude. Calculate the probability of fault, and the complexity is . Suppose the number of fault transitions is , the complexity of the algorithm is .
4. Case Analysis and Verification
The working principle of the liquid-propellant rocket engine in the start-up stage:
High pressure helium flows into the propellant tank and squeezes the propellant into the downstream combustion chamber to produce thrust. In Figure 1, we establish a Petri net model to simulate the start-up phase of the engine with the key nodes as the places and the key actions as the transitions. Table 1 and Table 2 show the meanings of all places and transitions, respectively.
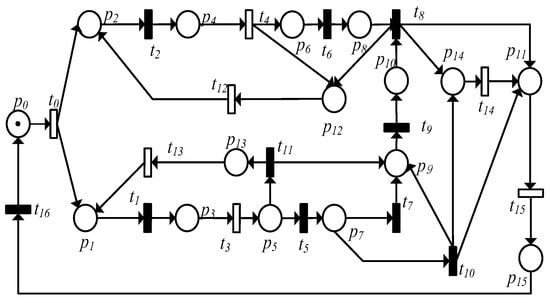
Figure 1.
The Petri nets model of DEDS.

Table 1.
The implication of each place.

Table 2.
Implication and observability of each transition.
The initial marking of the system model is , observable transition set , and unobservable transition set . Transition simulates fault and transition simulates fault .
4.1. Quantum Bayesian Petri Nets of Transition
The fault transitions are and so that the system fault state is possible fault. Estimate the system fault probability by the QBPN fault diagnosis method. Firstly, we structure the QBPN models of the fault transition and the fault transition respectively. Then, calculate the firing probability of fault transitions. Finally, choose the maximum probability as the system fault probability.
In the partially observable Petri nets model, given the fault transition. Search the pre-set in all its paths forward, and search the post-set in all its paths backwards. Stop searching when an observable transition occurs. For fault transition , Its path includes , , , . Observable transitions are , and unobservable transitions are . Then, establish the QBPN model corresponding to the (leakage fault of fuel filling valve), and the subnet is shown in Figure 2.
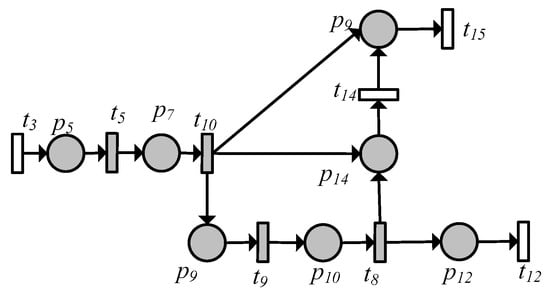
Figure 2.
The QBPN model of fault transition .
4.2. Convert the Conditional Probability Table to Quantum Probability Amplitude Table
In the POPN model, there are unobservable transitions. When the observed transition sequence is given and the transition sequence is uncertain, we obtain the quantum probability amplitude table by Equations (1) and (6). In Figure 3, the uncertain path of firing is , and . And it is caused by the unobservable transition.
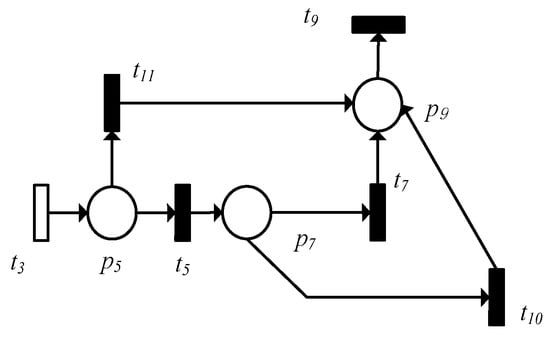
Figure 3.
The transition of the influence of quantum interference.
In Figure 4, the uncertain path of firing is , and . Through the path superposition principle, the uncertainty of and leads to the uncertainty of transition firing.
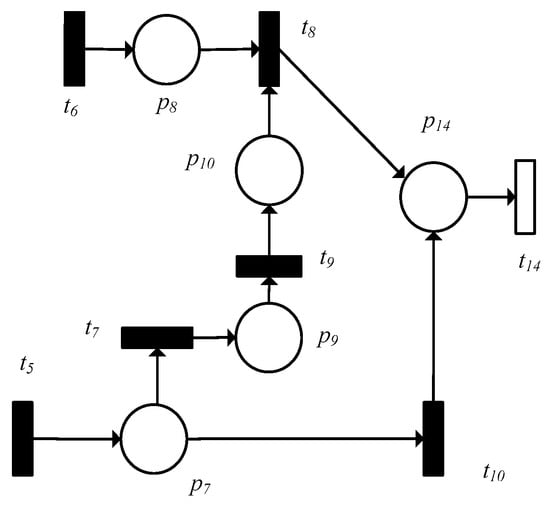
Figure 4.
The transition of the influence of quantum interference.
In Figure 5, the uncertain path of firing is , , and. . The source of uncertainty is the unobservable transition , and the observable transition . When the observable transition is fired, the number of the uncertain paths is 2, and the reduction of path uncertainty leads to the reduction in the interference effect.
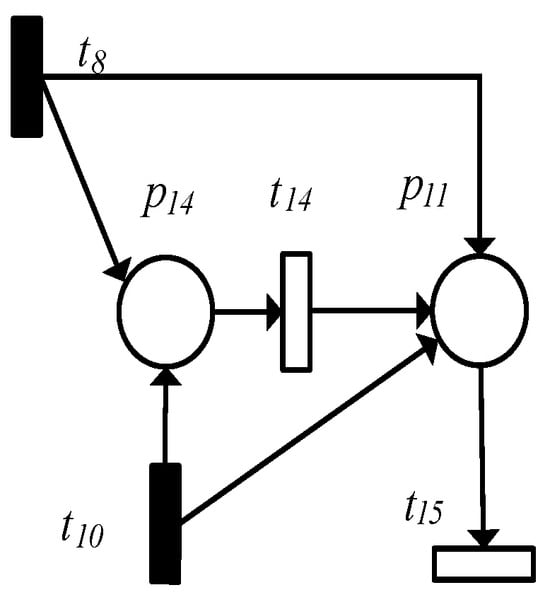
Figure 5.
The transition of the influence of quantum interference.
The modification of the transition firing probability is shown in Figure 6 as an example. When there is an uncertain path, in Table 1 the firing probability of is 0.81 under condition and quantum amplitude is . The firing probability of is 0.19 under condition and the quantum amplitude is . The firing probability of is 0.63 under condition and the quantum amplitude is . The firing probability of is 0.43 under condition and the quantum amplitude is . According to the probability information between transitions shown in Figure 6, the change curve of the probability value of quantum Bayes is obtained in Figure 7.
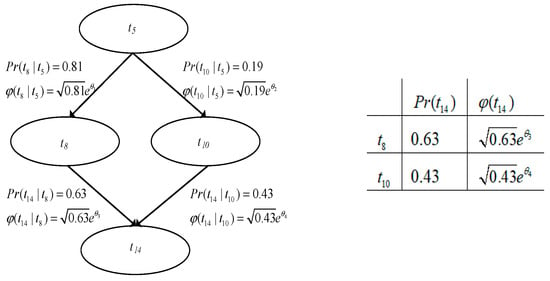
Figure 6.
Classical Bayesian probability and quantum Bayesian probability.
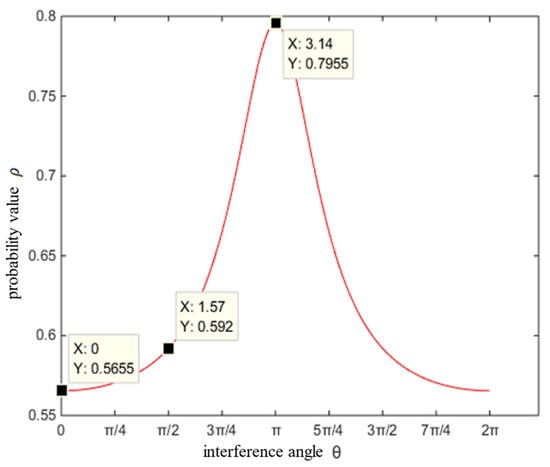
Figure 7.
The change in the quantum Bayesian probability value of under the condition of .
We obtain the following formula:
According to Equation (9), we obtain the probability results shown in Figure 7. The interference angle is on the interval , and the corresponding probability in the interval [0.5655, 0.7955] is an increasing function. Then, the firing probability of the total probability is 0.592, and the firing probability of by quantum Bayes theory is 0.7955. According to Equation (10), we obtain the probability results shown in Figure 8. The interference angle is on the interval , and the corresponding probability in the interval [0.4355, 0.2045] is a subtraction function. Then, the firing probability of by the total probability is 0.408, and obtain the firing probability of by quantum Bayes theory is 0.2045. From Figure 7 and Figure 8, the sum of the firing probability of and is 1 at the interference angle are the same, as shown in Table 3.
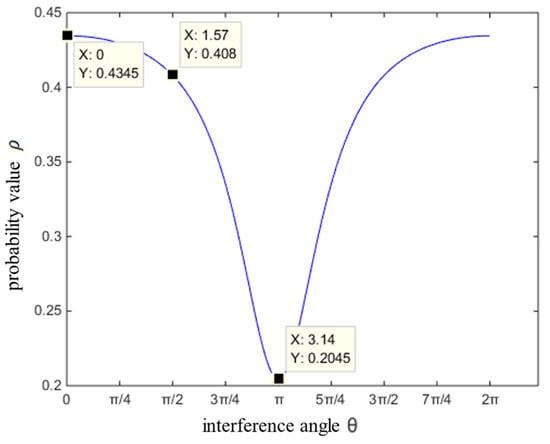
Figure 8.
The change in the quantum Bayesian probability value of under the condition of .

Table 3.
Comparison of probability estimates between the total probability and the quantum Bayesian.
In Figure 9, the more complicated case, firing probability under condition . At this time, we adjust multiple interference angles to meet the demand.
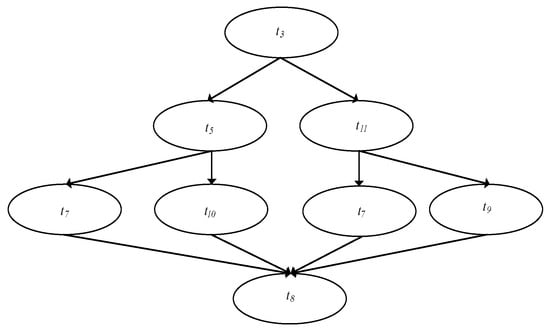
Figure 9.
The uncertain path from transition to .
Possible paths: , , and . Two of the different paths produce a superposition effect, and produce five interference angles . Fixing , we obtain the relation between the firing probability of under condition and the interference angle . In Figure 10, the probability transformation range is [0.83–0.88]. When , we obtain the maximum, and when , we obtain the minimum.
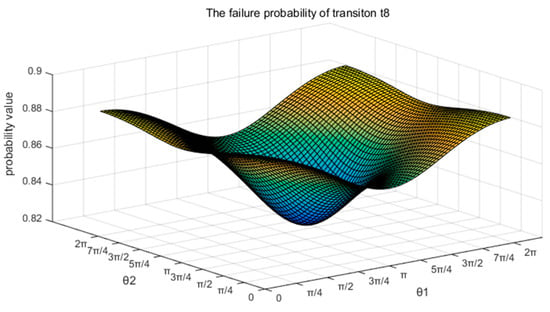
Figure 10.
Interference angle causes the change in the firing probability of under the condition of .
Fixing , we obtain the relation between the firing probability of under condition and the interference angle . In Figure 11, the probability transformation range is [0.81–0.93]. When , we obtain the maximum, and when , we obtain the minimum.
Figure 11.
Interference angle causes the change in the firing probability of under the condition of .
Quantum interference can be constructive or destructive, be selected according to needs. In Figure 10 and Figure 11, interference angle is the most constructive interference at , and interference angle is the most destructive interference at . Analyze the uncertainty of all transitions in the POPN model and correct the conditional probability.
4.3. Fault Diagnosis Results Based on QBPN
The application of the quantum Bayesian inference in the QBPN model is essential to the fault probability of unobservable fault transitions calculation, which reflects the uncertainty of fault occurrence and the conditions of the quantum interference effect.
Based on the POPN system model with an uncertain state, for the fault probability of the system estimation, the use of the QBPN fault diagnosis algorithm is vital. Table 4 shows the diagnosis results of the QBPN algorithm.

Table 4.
Fault diagnosis results of the quantum Bayesian fault algorithm based on POPN.
In the test, we diagnose the fault transition and fault transition . The observable transitions in the QBPN model are . When the observable label probability transition sequence , the transition is not in the probability transition set. The fault firing probability of is 0. Its confidence is 0 and the fault state of the system is 0. So the system state is faultless.
When , by observable transitions , the fault probability of is . According to the firing state of observable transition and Equation (7), we calculate the QB function of and the modified fault probability is . Similarly, for the analysis of fault transition , the fault firing probability is . So the fault probability of the system is 0.0076 and the confidence is 0.4. So the fault state of the system is faultless.
When . Firstly, calculate the firing probability of fault transition . According to Equation (6), the conditional probability of fault transition is . According to the firing state of observable transition and Equation (7), calculate the QB function. The modified firing probability of fault transition is . Adding transition , the modified firing probability of fault transition is . Continue to add the observable transition , and the modified firing probability of fault transition is . Similarly, the modified firing probability of fault transition is . The system fault probability is 0.9668. The system state is fault, and the confidence is 0.6.
When , the transition is in all probability transition set. Then, the fault probability of is 1. The fault probability of the system is fault, and the confidence is 1.
4.4. Algorithm Comparison
We use the BPN algorithm and the QBPN algorithm, respectively, to diagnose the same system state. After 100 simulations, we obtain the comparison diagram of the BPN algorithm and the QBPN algorithm, as shown in Figure 12. In Figure 13, the probability distribution interval of the BPN algorithm is [0.9425, 0.975], which is 0.961 after the curve fitting. In Figure 14, the probability distribution interval of the QBPN algorithm is [0.9525, 0.980], which is 0.966 after the curve fitting.
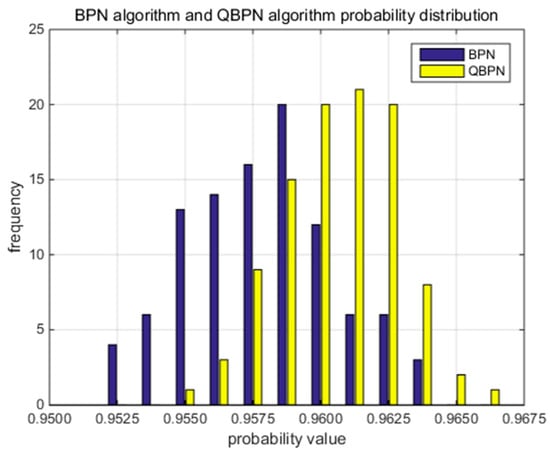
Figure 12.
Comparison of fault diagnosis probability between the BPN algorithm and the QBPN algorithm.
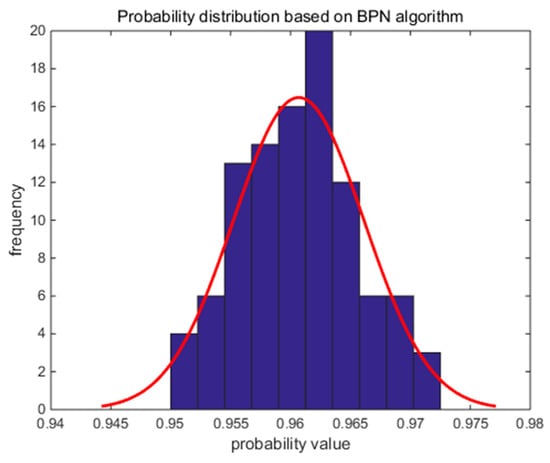
Figure 13.
Probability distribution based on the BPN algorithm.
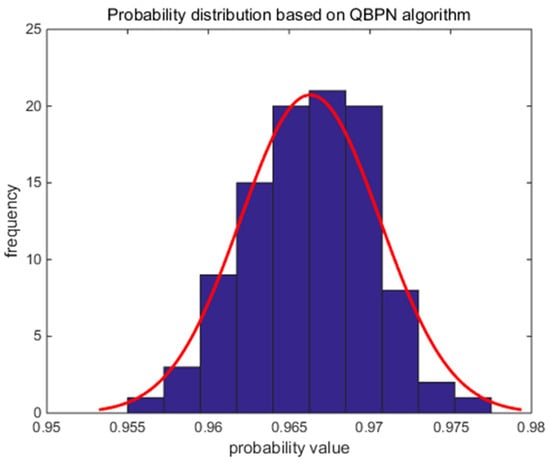
Figure 14.
Probability distribution based on the QBPN algorithm.
It can be concluded from Figure 12 that the QBPN algorithm can obtain better probability estimation after quantum interference correction.
In Table 5, we compare the performance of the BPN algorithm and the QBPN algorithm in this paper. On the basis of the case model, we diagnose the observable fault transitions by using the BPN algorithm. For the most complex OLPS considerable label probability sequence: after many tests, the average response time of the BPN algorithm is 300 ms. By applying the QBPN algorithm in this paper, the average response time of fault diagnosis based on the subnet model established for fault transitions is 230 ms. It is proved that the QBPN algorithm reduces the computational complexity and improves the efficiency. Meanwhile, in 5000 simulation experiments, the number of correct diagnoses the BPN algorithm is 4685. The accuracy of diagnosis is 93.70%. The QBPN algorithm modifies the fault probability by adjusting the quantum interference term. The number of correct diagnoses is 4937, and the accuracy of diagnosis is 98.74%. So the QBPN algorithm has higher fault diagnosis capability.

Table 5.
Comparison of diagnostic algorithms.
5. Conclusions
- In this paper, the POPN model proposed a QBPN fault diagnosis method. We combine the intuitive analytical description method of Petri nets with the characteristics of quantum Bayesian processing uncertainty knowledge expression and inference, calculate the probability of the firing of observable transitions according to the state and the quantum interference angle, then diagnose the fault of observable transitions in the system model.
- The QBPN model corresponding to the fault transition is established to simplify the model and reduce the complexity of the algorithm. The subnet model containing partial information has better fault-tolerance ability and better adaptability to topology changes.
- Based on the POPN fault diagnosis model, the QBPN model is simulated and verified through the simulation platform, which verifies the reliability of the QBPN algorithm and can reduce the complexity of the algorithm.
The complexity of the QBPN algorithm based on the POPN model depends on the number of possible fault transitions, and needed plenty of time to analyze the probabilistic data in the QBPN subnet. We studied the POPN model of transition generalized constraint conditions to reduce the search path of the fault transition set to achieve the purpose of optimizing the algorithm rate. In this paper, we executed the parameter selection of the quantum Bayesian interference term manually without randomness. In the following part, we will study the influence on the parameter selection of the quantum interference term, and attempt to obtain a more realistic transition probability distribution through the MCMC random sampling algorithm to further improve the accuracy of the fault probability of the system.
Author Contributions
Conceptualization, J.L. and E.S.B.M.; methodology, J.L.; software, J.L.; validation, J.L., X.Z. and A.D.; formal analysis, X.Z.; investigation, A.D.; resources, A.D.; data curation, J.L.; writing—original draft preparation, J.L.; writing—review and editing, X.Z.; visualization, E.S.B.M.; supervision, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The research has been partially supported by the National Natural Science Funds (61473144).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Henry, D.; Le Peuvédic, C.; Strippoli, L.; Ankersen, F. Robust Model-Based Fault Diagnosis of Thruster Faults in Spacecraft. IFAC-PapersOnLine 2015, 48, 1078–1083. [Google Scholar] [CrossRef]
- Djebko, K.; Puppe, F.; Kayal, H. Model-Based Fault Detection and Diagnosis for Spacecraft with an Application for the SONATE Triple Cube Nano-Satellite. Aerospace 2019, 6, 105. [Google Scholar] [CrossRef]
- Jiang, L.; Li, H.; Yang, G.; Yang, Q.; Huang, H. Research progress of Spacecraft Autonomous Fault Diagnosis Technology. Acta Astronaut. Sin. 2009, 30, 28–34. [Google Scholar]
- Xu, B.; Yin, X.; Yin, X.; Wang, Y.; Pang, S. Fault Diagnosis of Power Systems Based on Temporal Constrained Fuzzy Petri Nets. IEEE Access 2019, 7, 101895–101904. [Google Scholar] [CrossRef]
- Lefebvre, D. Fault diagnosis and prognosis with partially observed stochastic Petri nets. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 382–396. [Google Scholar] [CrossRef]
- An, R.; Liang, W. Unobservable Fuzzy Petri Net Diagnosis Technique. Aircr. Eng. Aerosp. Technol. 2013, 85, 215–221. [Google Scholar] [CrossRef]
- Ammour, R.; Leclercq, E.; Sanlaville, E.; Lefebvre, D. Faults prognosis using partially observed stochastic Petri-nets: An incremental approach. Discret. Event Dyn. Syst. 2018, 28, 247–267. [Google Scholar] [CrossRef]
- Guo, D.; Xiong, W.; Xu, Z.; Xu, J.; Han, J.; Li, Z. Research on Transformer Fault Diagnosis Based on Variable Precision Rough Set and Quantum Bayesian Network. Comput. Appl. Softw. 2017, 34, 93–99+105. [Google Scholar]
- Liu, J.; Zhang, Z.; Zhen, R.; Liu, H.; Yang, Z.; Wang, Z. Fault diagnosis of bipropellant propulsion system using partially observed time Petri nets. Syst. Eng. Electron. 2018, 40, 1337–1344. [Google Scholar]
- Lemm, J.C. Bayesian approach to inverse time-dependent quantum mechanics. Phys. Lett. A 2000, 276, 19–24. [Google Scholar] [CrossRef]
- Moreira, C.; Wichert, A. Andreas Exploring the relations between Quantum-Like Bayesian Networks and decision-making tasks with regard to face stimuli. J. Math. Psychol. 2017, 78, 86–95. [Google Scholar] [CrossRef]
- Yi, Y. Fault Diagnosis Based on Bayesian Petri Nets. Sens. Transducers 2014, 179, 114–120. [Google Scholar]
- Cabasino, M.P.; Giua, A.; Seatzu, C. Diagnosability of discrete event systems using labeled Petri nets. IEEE Trans. Autom. Sci. Eng. 2014, 11, 144–153. [Google Scholar] [CrossRef]
- Declerck, P.; Bonhomme, P. State estimation of timed labeled Petri nets with unobservable transitions. IEEE Trans. Autom. Sci. Eng. 2014, 11, 103–110. [Google Scholar] [CrossRef]
- Basile, F.; Cordone, R.; Piroddi, L. A branch and bound approach for the design of decentralized supervisors in Petri net models. Automatica 2015, 52, 322–333. [Google Scholar] [CrossRef]
- Shen, Q.; Qiu, J.; Liu, G.; Lv, K. Intermittent fault’s parameter framework and stochastic petri net based formalization model. Eksploat. I Niezawodn.-Maint. Reliab. 2016, 18, 210–217. [Google Scholar] [CrossRef]
- Galagedarage Don, M.; Khan, F. Dynamic process fault detection and diagnosis based on a combined approach of hidden Markov and Bayesian network model. Chem. Eng. Sci. 2019, 201, 82–96. [Google Scholar] [CrossRef]
- Sahu, A.R.; Palei, S.K. Real-time fault diagnosis of HEMM using Bayesian Network: A case study on drag system of dragline. Eng. Fail. Anal. 2020, 118, 104917. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Q.; Gao, Z.; Niu, L.; Zhao, Y.; Ma, Z.; Wu, D. Knowledge representation and general Petri net models for power grid fault diagnosis. IET Gener. Transm. Distrib. 2015, 9, 866–873. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, J.; Pan, F. Fault detection and diagnosis for data incomplete industrial systems with new Bayesian network approach. J. Syst. Eng. Electron. 2013, 24, 500–511. [Google Scholar] [CrossRef]
- Pensar, J.; Nyman, H.; Lintusaari, J.; Corander, J. The role of local partial independence in learning of Bayesian networks. Int. J. Approx. Reason. 2016, 69, 91–105. [Google Scholar] [CrossRef]
- Yoon, S. In-situ sensor calibration in an operational air-handling unit coupling autoencoder and Bayesian inference. Energy Build. 2020, 221, 110026. [Google Scholar] [CrossRef]
- Omoregbee, H.O.; Heyns, P.S. Fault detection in roller bearing operating at low speed and varying loads using Bayesian robust new hidden Markov model. J. Mech. Sci. Technol. 2018, 32, 4025–4036. [Google Scholar] [CrossRef]
- Lu, F.; Huang, J.; Lv, Y.; Qiu, X. Aircraft engine gas-path components health diagnosis based on nonlinear adaptive filters. Acta Aeronaut. Astronaut. Sin. 2013, 34, 2529–2538. [Google Scholar]
- Chen, J.; Zhai, G.; Wang, S.; Liu, Y.; Wang, H. Factors affecting characteristics of acoustic signals in particle impact noise detection for aerospace devices. Syst. Eng. Electron. 2013, 35, 889–894. [Google Scholar]
- Sharda, B.; Banerjee, A. Robust manufacturing system design using multi objective genetic algorithms, Petri nets and Bayesian uncertainty representation. J. Manuf. Syst. 2013, 32, 315–324. [Google Scholar] [CrossRef]
- Zhu, M.; Han, G.; Guo, Y. Optimized fault diagnosis based on FMEA-style CBR and BN for embedded software system. Int. J. Adv. Manuf. Technol. 2018, 94, 3441–3453. [Google Scholar]
- Rath, Y.; Glielmo, A.; Booth, G.H. A Bayesian inference framework for compression and prediction of quantum states. J. Chem. Phys. 2020, 153, 124108. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, L.; Jiang, W. Uncertainty measurement with belief entropy on the interference effect in the quantum-like Bayesian Networks. Appl. Math. Comput. 2019, 347, 417–428. [Google Scholar] [CrossRef]
- Pienaar, J. Quantum causal models via quantum Bayesianism. Phys. Rev. A 2020, 101, 012104. [Google Scholar] [CrossRef]
- Al-Ajeli, A.; Parker, D. Fault diagnosis in labelled Petri nets: A Fourier–Motzkin based approach. Automatica 2021, 132, 109831–109837. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).