Abstract
An anti-slide pile is a common landslide control measure. Compared with the full-length pile whose top extends to the ground, the buried pile is more optimal in internal force distribution, saves material and has remarkable economic benefits. At present, there is a lack of in-depth theoretical analysis on the pile length of the load section of double-row buried piles. In order to establish the design calculation method of pile length in the load section of double row buried piles, this paper is based on the failure mode of overtopping. The design equation of load section pile length is obtained by using the transfer coefficient and limit equilibrium method. Taking a landslide in Yan’an City, Shaanxi Province, China, as an example, the reliability and economics of double-row buried piles are verified by comparing the treatment effects of single-row, double-row and double-row buried piles, and the engineering design is completed. The results show that the landslide control project using the design calculation method can meet the requirements of slope stability and at the same time save a quarter of the material compared with the double row of full-length piles. The engineering example proves the rationality and practicability of the design method and provides engineering reference value for the use of the double-row buried anti-slide pile structure in large-scale landslide treatment.
1. Introduction
Landslides are common geological disasters across the globe. For example, a total of 4761 geological disasters occurred in China in 2021, of which 2335 were landslides, reaching half of the total number of geological disasters [1]. Figure 1 shows the statistical chart of the number of landslide occurrences, casualties and direct economic losses from 2010 to 2021, with data from the National Bureau of Statistics (the lower limit of the scale of geological disasters calculated in this paper is three people died and disappeared or caused direct economic losses of CNY 1 million) [1]. It can be seen that the number of landslide occurrences shows a decreasing trend. However, in terms of quantity, the number of landslides is still huge. Moreover, it has become one of the most important geological disasters affecting people’s lives, production and safety, contributing major threats and hazards to local human settlements and urban construction safety. The urban growth and population increase generate increasing risk as more people are exposed to such hazards. Therefore, landslide prevention and control has become a hot issue in geotechnical disaster prevention and mitigation [2,3].
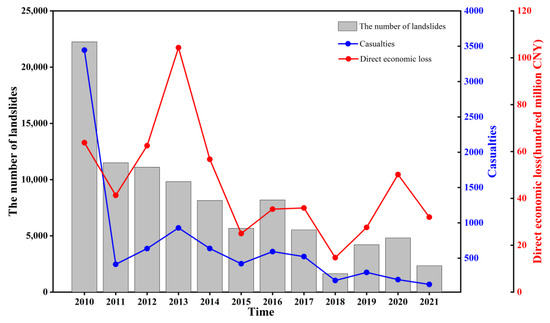
Figure 1.
Statistics on the number of and damage caused by landslides from 2010 to 2021 (data originate from National Bureau of Statistics).
An anti-slide pile is a common landslide treatment measure, which refers to the pile that penetrates through the slide body and goes deep into the slide bed to support the sliding force of the slide body and play the role of stabilizing the slope. The thrust of the sliding body is balanced by the resistance of stable ground below the sliding surface of the anti-slide pile, and the stability of the slope is increased. Anti-slip piles have been widely used in landslide treatment because of their advantages, such as flexible pile burial, strong anti-slip ability, obvious reinforcement effect and convenient construction [4,5]. For some accumulative landslides, when the pile body is damaged, the deformation of the pile body is “S”-shaped, and the deformation area is mainly concentrated near the sliding surface. The bending deformation area of a single-row pile body is about a quarter of the total length of the pile body, and the deformation area of the double-row pile group structure is about three tenths the total length of the pile body, and the deformation near the slope is relatively small [6,7]. When the ordinary fully buried anti-slide pile is selected, the resistance is mainly borne by the pile body near the sliding surface. The middle and upper part of the load section cannot give full play to the anti-slide function, resulting in the waste of the upper part of the pile material, which makes the project investment increase. According to the survey and design specifications of various industries in China, the engineering requirements can be achieved as long as the landslide reinforcement achieves a certain stability. Therefore, the length of anti-slide piles can be reduced under the premise of meeting the design requirements so as to reduce the engineering cost and save overall costs, which requires in-depth research regarding the structural form of anti-slide piles.
A buried anti-slide pile refers to an anti-slide pile with the whole pile body buried inside the slope body and a certain distance between the pile top and the slope surface [8]. The buried pile is mainly arranged near the sliding surface of the pile body. At this time, the pile body only bears part of the landslide thrust, and the remaining thrust over the top of the pile is resisted by the rock–soil body itself, so the internal force of the pile body will be much smaller than that of the full-length pile. Studies have shown that this pile structure can effectively overcome the shortcomings of full-length piles [9,10]. Compared with full-length piles, buried piles have shorter force section length, lower maximum bending moment of pile body, and lower material usage, which can reduce costs when treating landslides with larger sliding body thickness, and they have been applied to some extent in landslide treatment in recent years [11].
The second section will be devoted to the research results of single-row piles. At present, the research on buried piles mainly includes three aspects: theoretical analysis, model experiment and numerical simulation. Zeng Shiren et al. [12] proposed a simplified calculation method for embedding anti-slide piles in the horizontal and inclined sections of landslides and demonstrated the significant economic benefits of submerged piles in landslide treatment projects with engineering examples. GB 50843-2013 [13] Technical Code for Construction Slope Engineering, edited by Chongqing Urban and Rural Construction Commission and approved by the Ministry of Housing and Urban-Rural Development of the People’s Republic of China, mentioned that the top elevation of buried anti-slide piles should be controlled to avoid the sliding of rock and soil from the top of piles [13]. It is mentioned in GB/T38509-2020 [14] “Landslide Prevention and Control Design Code” that the design safety factor of buried anti-slide pile length should not be less than 1.25 (the design safety factor is the safety factor that the design should meet according to the grade of landslide control engineering and other factors. The safety factor is the coefficient of the anti-sliding stability of a landslide and is the ratio of anti-sliding force and sliding force along the sliding surface of a landslide). For a soil landslide, the cantilever length of the buried anti-slide pile should not be less than 0.55 times the thickness of the slide body, and it is stipulated that the landslide thrust should be verified by the limit balance method [14]. Xiao [9] used the limit equilibrium theory and the transfer coefficient method to obtain the calculation method of the buried depth of the rear pile. Moreover, he established the relationship between the buried depth of the pile top and the stability coefficient of the slope and draws the conclusion that the stability coefficient of the slope after reinforcement decreases with the increase in the buried depth, and the internal force of the pile is also decreasing. Yan [15] et al. derived the analytical solution of the buried depth of the top of the pile based on the possible failure mode of the buried-pile-reinforced landslide, combined with the transfer coefficient method and the variational method under the framework of the limit equilibrium theory, and analyzed the thrust of the sliding body in the buried section and the loaded section with the help of the rigid body limit equilibrium theory. Xiong [16] conducted a simple model test and numerical simulation for the buried pile, preliminarily discussed the thrust distribution rule of the pile, the buried depth and feasibility and concluded that the buried pile was more economical and optimal than the full-length pile. Zheng Yingren’s team [17,18,19,20] conducted a series of studies on buried piles. Using the finite element strength reduction method and large-scale physical model tests, they analyzed the magnitude and distribution mode of the thrust force of the pile body and pile top and obtained the relationship between the buried depth and the stability coefficient of the reinforced slope. They obtained the conclusion that the landslide thrust after the pile is negatively correlated with the buried depth, and the pile topsoil thrust is positively correlated with the buried depth.
The current research on single-row buried piles has been relatively mature. However, in large-scale landslides or important landslide control projects, because of the large sliding force, it is difficult to ensure the stability of slope or control the further deformation development of side slope. Therefore, in large-scale landslides or important landslide control projects, more of them are treated with double-row piles. In landslide control, if the buried pile is arranged in multiple rows, it can not only provide greater anti-sliding resistance but also solve the problem of waste of pile length in the load section, and the construction safety is greatly improved. The following part will discuss the research results of double-row piles. In the study of double-row buried piles, Wang Xu [21] used the finite element method to study the pile–soil interaction of double-row buried anti-slide piles with connected beams and obtained the variation trend in internal forces of front and back piles with row distance. Lu Meijun [22] theoretically analyzed the structure and force characteristics of double-row buried anti-slide piles with connected beams and, combined with engineering examples, studied the distribution of landslide thrust of buried double-row anti-slide piles. Li Junfei [23] theoretically derived the landslide thrust distribution model of the front and back rows of double-row buried anti-slide piles, analyzed the force and deformation characteristics of the front and back rows of piles with different row spacing by using the finite element method and put forward design suggestions for row spacing, pile spacing and layout. Yan Yuping [24] used the variational method under the framework of limit equilibrium theory to calculate the buried depth of the rear pile and proposed a method for calculating the thrust of the rear pile based on the strain softening effect of the sliding strip.
To sum up, the research on double-row buried piles is in its infancy; the design mainly relies on numerical simulation and engineering experience, and the design calculation model is still unclear. The main problems are unclear understanding of the internal force transfer mechanism of the soil in the top of the pile under the failure mode of overtopping and unclear theoretical design and calculation method of optimal pile length of double-row buried piles because most of the failure forms of anti-slide piles in engineering cases are overtop failure and overtop failure occurs easily because of the short pile length in the load section of the buried piles. Therefore, in this paper, the pile length of the load section of anti-slide piles under the failure mode of overtopping is studied, the theoretical design calculation is carried out for the first time and the reliability of the design method is verified by practical cases.
This paper first explains the anti-sliding mechanism of double-row buried piles under overtopping failure and at the same time deduces the design and calculation of the optimal pile length. By using the limit equilibrium theory and the transfer coefficient method, the calculation method of the optimal pile length of the load section of double-row buried piles is obtained. It is helpful to popularize the application of double-row buried piles in engineering.
2. Analytical Model
In Figure 2, the slip surface is the interface during the sliding process of the sliding body. The front anti-sliding pile represents the pile in the double row that is relatively close to the landslide front. The rear anti-sliding pile represents the pile in the double row of piles relative to the rear edge of the landslide. The potential slip surface refers to the new sliding surface generated when the overtop failure occurs after setting the buried pile. Line OA is the initial horizontal sliding surface, and line segments OB and BD are the potential sliding surface over the top. The angle between OB and the horizontal line is called the initial rupture angle. The extended line segment OB intersects at point Q at the front pile, and the angle formed by the line BD and BQ is called the secondary fracture angle. Line segment AB represents the load-bearing section length of the rear pile, and line segment CD represents the load-bearing section length of the front pile.
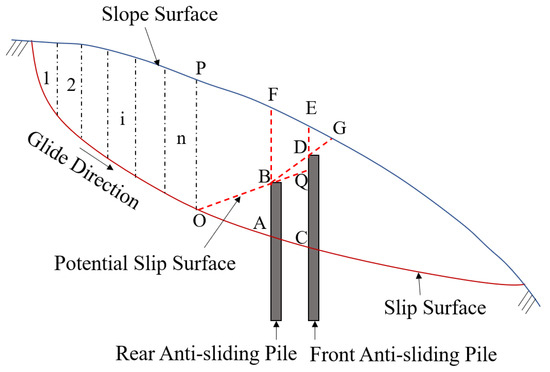
Figure 2.
Schematic diagram of landslide reinforcement by double rows of submerged piles.
In previous literature [9], a simplified calculation method for load section length of single-row submerged anti-slide piles was derived. On this basis, this paper proposes a simplified calculation model for strengthening the slope with double rows of buried piles, as shown in Figure 2. When overtopping failure occurs, a new potentially dangerous sliding surface is generated in the local sliding body above the sliding surface, which is generally shorter than the original potential sliding surface. If only a single row of buried piles is installed, the topsoil of the piles will slide along the OB fracture surface, and, when the sliding body is thicker, a larger landslide thrust will be generated, and the possibility of overtopping failure is greater. If double rows of buried piles are set and the load sections at the front and back are equal in length, the soil at the top of the pile will still follow the OB sliding surface of the fracture plane when the top failure occurs, and the anti-sliding effect is the same as that of single rows of buried piles, which cannot strengthen the anti-sliding effect. If double rows of buried piles are set and the load section length of the front row is slightly higher than that of the back row, a kick point (point B) will be generated on the fracture surface, forming an OB–BD fracture surface. Compared with the top failure mode of single rows of buried piles, the double rows of buried piles have stronger anti-sliding ability. Therefore, the analysis model of this paper is the double-row buried pile with load section in front slightly longer than that in back.
When the top failure occurs, only part of the sliding force of the back sliding body OAB is applied to the pile body because the back pile body AB prevents the deformation from the top of the pile to the sliding surface. The soil POBF at the top of the pile slides forward along the fracture plane OB, and the fracture angle is the angle between OB and the horizontal plane. In this case, since the deformation of the soil mass at the top of the back pile is not constrained, the soil pressure at the top of the pile is transmitted along the fracture plane OB to the soil mass at the top of the front pile and the soil mass between the rows. Moreover, the soil pressure at this part of the soil mass continues to be transmitted along the fracture plane BD, at which time a new angle of rupture ∠DBQ will be generated, and the overtop failure will eventually occur.
3. Calculation Method
3.1. Fundamental Assumption
The main control condition for determining the optimal pile length of the load section of the double-row buried pile is that no potential sliding surface over the top can be generated in the sliding body. To simplify the analysis, the following assumptions occur:
(1) The pile body has sufficient length and stiffness to prevent it from being destroyed; the initial slip surface of the slope is known and can be determined by geotechnical engineering or geological investigation.
(2) When double-row submerged anti-slide piles are used for governance, the front piles should first be set at the front edge of the sliding body as far as possible, and then the back piles should be set so that the back piles can play the anti-slide effect when the optimal row spacing is used.
(3) The initial sliding surface OAC between the OBD and the loading section of the pile is in the limit equilibrium state and meets the Coulomb strength criterion.
(4) Both OBFP and BDEF of wedge are rigid bodies, and the initial fracture angle of OBFP of wedge is β(β = 45° − ϕ/2). The secondary fracture angle of BDEF of wedge is β1, and β1 is the angle between BD of pile top and the extension line of initial fracture angle of OB.
3.2. Establishment of Calculation Method
3.2.1. Calculation When the Sliding Surface Is Horizontal
Figure 3 shows the simplified calculation diagram of double rows of buried piles when the sliding surface is horizontal. Figure 3a shows the general analysis model; line OA is the initial horizontal sliding surface, and line segments OB and BD are the potential sliding surface over the top. The angle β formed by line segments OA and OB is called the initial rupture angle (β = 45° − ϕ/2). The extended line segment OB intersects at point Q at the front pile, and the angle β1 formed by the line BD and BQ is called the secondary fracture angle. H1 represents the length of the rear pile above the sliding plane, h2 represents the length of the front pile above the sliding plane, H is the thickness of the sliding body, L is the distance between point O and point A, a is the distance between the front and back piles and b is the width of the pile, c as the cohesion coefficient and ϕ as the friction angle. Figure 3b shows the loading model of mass POBF, where E0 is the landslide thrust at line OP, E1 is the soil resistance generated by mass FBDE (direction parallel to line OB), W1 is the dead weight of mass POBF and N1 is the supporting force of mass OAB (direction perpendicular to line OB). Figure 3c shows the loading model of mass FBDE. E1’ is the landslide thrust transferred by mass POBF to the FB surface (equal in magnitude and opposite in direction to E1), W2 is the dead weight of mass FBDE and N2 is the supporting force on the BD surface (direction perpendicular to line BD).
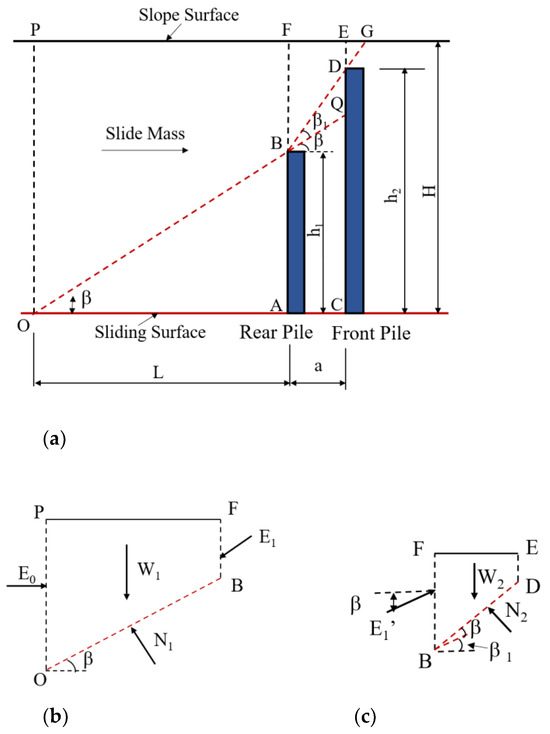
Figure 3.
Simplified calculation diagram of the row of buried piles (when the sliding surface is horizontal) (a). General analysis model; (b). loading model of mass POBF; (c). loading model of mass FBDE.
(1) h1 calculation when the sliding body does not slide along the passive earth pressure rupture surface OB.
Force analysis is carried out on the overtop slider OBFP. The soil body weight of the wedge OBFP is W1, the landslide thrust on the OP interface is E0, the resistance generated by the wedge BDEF is E1 (direction parallel to OB), the supporting force of the soil OAB is N1 (direction perpendicular to OB fracture plane) and the friction force is N1 tanϕ. The cohesion is .
Given the design safety factor, the landslide thrust E0 acting on the OP surface can be easily solved using the transfer coefficient method [21], and the relevant solving process is shown in Equations (1) and (2):
In Equations (1) and (2), Ei represents the remaining sliding force of bar i. Ei−1 represents the remaining sliding force of bar i − 1. Ψi represents the sliding plane inclination of bar i. θi−1 represents the sliding plane inclination of bar i − 1. Wi represents the dead weight of bar i. li represents the sliding plane length of bar i, and ci represents the cohesive force of bar i. ψi is the residual sliding force transfer coefficient between bars i − 1 and i. Fs is the design safety factor.
It should be noted that other classical limit equilibrium methods can also be used to solve the sliding force, such as Morgenstern–Price method [25], Spencer method [26], Janbu method [27], etc. The Morgenstern–Price method assumes that there is a proportional relationship between tangential force and normal force between bars. Moreover, the position of the force point between the bars changes with the inclination of the sliding surface. Spencer method assumes the ratio of horizontal and vertical forces between strips is constant, so the calculation is simple. Janbu method assumes that the position of the point of force between strips is 1/3 of the sliding surface, so the calculation may be difficult to converge.
The thrust force along OB under E0 is .
The thrust perpendicular to OB under E0 is
Therefore,
The equilibrium equation can be derived from the limit equilibrium condition of the force:
(2) h2 calculation when the sliding body does not slide along the passive earth pressure rupture surface BD.
Force analysis was carried out on the overtop slider BDEF (in order to make the design results biased to safety, only the force analysis was carried on the wedge BDEF, without considering the gravity of the wedge EDG). It was assumed that the body weight of the wedge BDEF soil mass was W2, and the landslide thrust on the BD interface was E1’ (E1’ and E1 were equal in size and opposite in direction).
The thrust force along BD under E1 is .
The thrust perpendicular to BD under E1 is
The equilibrium equation can be derived from the limit equilibrium condition of the force:
Simultaneously, (2) and (4) can be obtained,
Let
Therefore,
As can be seen from the position relationship in Figure 3,
When the sliding surface is horizontal, Equations (8) and (9) must be satisfied to ensure that the soil behind the pile does not slide along the OBD plane. When the initial sliding surface of slope body is known and soil parameters are determined, the optimal pile length of h1 and h2 can be obtained by Equation (8), and the optimal pile spacing of double row piles can be obtained by using the fracture angle . It is mentioned in GB/T38509-2020 “Landslide Control design Code” that the cantilever length of the buried anti-slide pile is not less than 0.55 times the thickness of the slide body, that is, h1 ≥ 0.55 H. Therefore, the optimal range of pile length of h2 can be determined when the row spacing is provided, and the obtained h1 and h2 are the minimum values when the stability conditions are met.
3.2.2. Calculation When the Sliding Surface Is Tilted
As shown in Figure 4, when the pile section is inclined, the wedge shape OBFP can be simplified to OBFH, and the calculation model when the sliding surface is inclined can be simplified to that when the sliding surface is horizontal. The optimal range of pile length of can be determined by using the equation ≥ 0.55 H. The slope angle of the sliding surface is set to θ, and the other conditions are the same as when the pile position is horizontal.
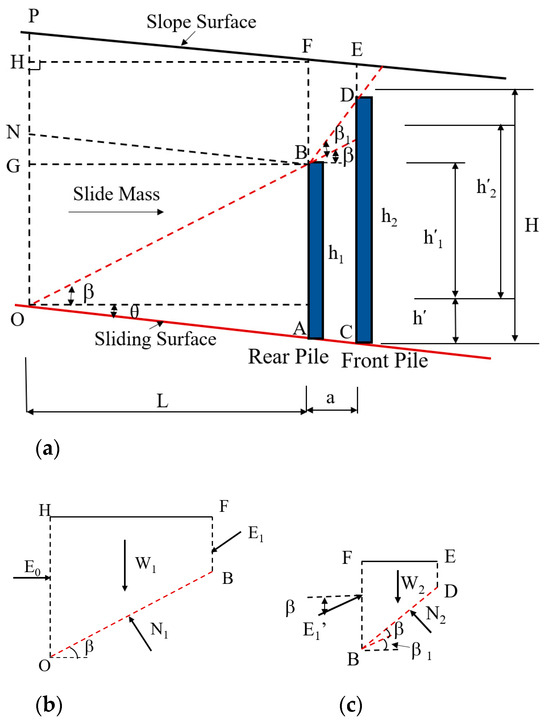
Figure 4.
Simplified calculation diagram of double row of buried piles (when the sliding surface tilts) (a). General analysis model; (b). loading model of mass HOBF; (c). loading model of mass FBDE.
So, when the pile site is inclined,
Then, according to Equation (9), the relationship between h1, h2 and β1 can be obtained when the pile section is inclined, namely,
In other words, when the pile position is inclined, Equation (11) must be satisfied to ensure that the soil behind the pile does not slide along the OBD surface. The above solution process provides a strict solution to the optimal pile length in the load section of the sunk pile in the failure mode over the top, and the solution process can be completed with the help of MATLAB.
4. Instance Analysis
4.1. Project Profile
A landslide was located in Yan’an City, Shaanxi Province. According to the relevant data combined with the comprehensive analysis of field investigation and drilling sampling, the longitudinal length of the landslide is about 556.9 m, the transverse width is 290.01 m, the landslide area is about 450.6 × 104 m2, the average thickness of the landslide body is 17.86–27.9 m and the highest point of the ground is located at the rear wall of the landslide. The ground elevation is 1048.01 m, the lowest ground is located at the shear exit of the landslide front and the ground elevation is 920.0 m, among which the ground elevation of the landslide body is 913.88–1010.83 m, and the height difference is about 97 m. Secondary scarp developed on the slope, the overall slope was 15–25°, the north side was slower and the south side was steeper. The geographical location of the landslide area is shown in Figure 5.
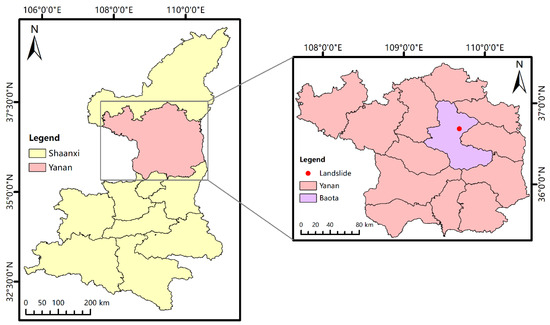
Figure 5.
Geographical location of the landslide area.
According to the field investigation, engineering geological mapping and landslide exploration, the structural characteristics of the landslide are summarized as follows: the landslide is a typical old landslide (old landslides are those that have occurred since the Holocene to 100 years ago or have not been experienced by living locals, and the rock and soil mass after the landslide is dense), and the slope has been reclaimed by the villagers into artificial terraces. In the middle and upper part of the slope, the ground slope is small, and the transverse fluctuation is not large. The ground elevation is 977.91 m–1014.45 m, and the slope is 3–4°. The stratigraphic structure is mainly composed of Upper Pleistocene loess (Q3eol), paleosol (Q3el), Middle Pleistocene loess (Q2eol), paleosol (Q2el) and Holocene landslide deposit loess soil. Figure 6 shows the panoramic satellite image of the landslide.
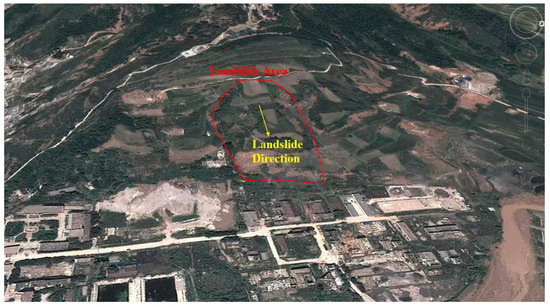
Figure 6.
Panoramic satellite image of landslide (according to Google Earth).
The central part of the platform is a wide platform with gully development at the front. There are two large gullies in the middle of the landslide, which are in the same direction as the landslide. The surface strata of the slope body are mainly loess soil accumulated in the Quaternary Holocene Series. The ground surface of the middle and lower part of the slide body presents an alternate geomorphic form of steep ridges and platforms. The height difference of the steep ridges is about 10 m to 20 m, and the slope is about 70 to 80°. From the bottom of the steep ridges to the front of the slide body, the terrain is relatively gentle, and the ground slope is 8° to 10°. The surface strata are mainly loess soil accumulated by the Quaternary Holocene landslide, and the terrain is connected by steep ridges of about 1 to 2 m. The upper part is planted with various crops. The landslide plan and the position of displacement monitoring points are shown in Figure 7.
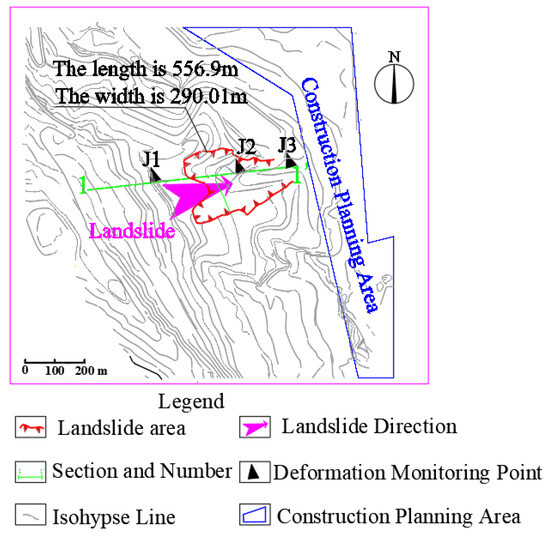
Figure 7.
Landslide plane topographic map and displacement monitoring point layout.
4.2. Stability Analysis
In order to obtain the mechanical properties of the sliding body soil layer, a certain number of undisturbed soil samples were taken from different boreholes on the sliding body for natural and saturated fast shear tests and natural and saturated shear tests. In order to facilitate the statistics of the physical and mechanical properties of the slip body, the strata of the slide body revealed in the exploration area were re-stratified and divided into:
- (1)
- Malan Loess (Q3eol): It is light yellow; the soil is mainly silty soil, low density and humidity. It contains a small amount of calcium nodules and calcium streaks, and its layer thickness is 0.80–19.80 m.
- (2)
- Paleosol (Q3el): It is brown, the soil is mainly silty clay and the humidity and density are moderate. White calcareous streaks and a few calcareous nodules are seen. Its layer thickness is 1.30–13.80 m.
- (3)
- Lishi loess (Q2eol): The soil is yellowish-yellow and mainly silt. Contains small amounts of calcareous nodules and ferromanganese streaks, containing mica. The soil layer is 1.70–36.40 m thick.
- (4)
- Paleosol (Q2el): The soil is yellowish-brown, mainly silty clay. There are a few white stripes and iron and manganese stripes, and the bottom contains a small amount of calcium nodules. The soil layer is 3.30–13.00 m thick.
- (5)
- Lishi loess (Q2eol): The soil is yellowish-yellow, mainly silty soil. Inside can be seen wormhole, pinhole development, iron and manganese spots. The soil layer is 3.20–15.60 m thick.
On the basis of stratification of the sliding body, according to the requirements of Code for Investigation of Geotechnical Engineering, the indoor soil test data of each layer in the sliding body are analyzed by mathematical statistics after individual discrete data are deleted. The statistical results of the shear strength index of each layer of the sliding body are presented in Table 1.

Table 1.
List of experimental results and index parameters of each soil layer of landslide.
The stability calculation equation is calculated using the equation in GB/T38509-2020 Design Code for Landslide Prevention and Control [14], and two working conditions are selected for this calculation. Condition 1: natural state, that is, the limit equilibrium state of the slope under natural conditions. This condition is used to evaluate the stability of the current slope and calculate the physical and mechanical parameters of the slide surface. Condition 2: saturated state, which is the most unfavorable case for continuous heavy rainfall. Under this condition, the slope body gained weight and the strength of the sliding surface decreased obviously, and the slope body was most likely to slide again under this condition.
Since the landslide threat object is the resident gathering area at the foot of the slope and contains the power project, the importance level of the facilities threatened by landslide is important. According to DZ/T0219-2006 “Technical Code for Design and Construction of Landslide prevention and control engineering”, the landslide control and control engineering should be grade I, and the safety factor under the natural condition is 1.3; the safety factor under the saturated condition is 1.15. The transfer coefficient method is used to calculate and analyze the stability and safety of the landslide after excavation, and the results are shown in Table 2.

Table 2.
Stability calculation results.
As can be seen from Table 2, the stability coefficient of the slope under natural conditions is 1.387, which is greater than the design safety factor 1.3 stipulated in the Technical Code for Design and Construction of Landslide Prevention Engineering. However, the stability coefficient of the slope under saturation conditions is 1.089, which is less than the specified value of 1.15. According to the results of slope stability analysis, its stability level is poor, and it is in urgent need of engineering treatment. Considering the relatively small annual rainfall in the survey area and the good natural drainage conditions around the slope, it is difficult to achieve full saturation of the slope. Therefore, the parameters representing the natural state are used for engineering design.
4.3. Construction Design
In landslide geological disaster control measures, anti-slide pile is widely used in landslide control because of its strong anti-slide ability, wide application conditions and good control effect. Therefore, according to the engineering examples in this paper, single-row full-length, double-row full-length and double-row buried anti-slide piles are selected, respectively, for landslide design, and the safety factor and engineering quantity after treatment are calculated to select the optimal treatment scheme.
(1) Single row of full-length anti-slide piles.
When a single row of full-length anti-slide piles is used for landslide treatment, the round-section mechanically drilled anti-slide piles are adopted. In order to meet the strength requirements, the pile diameter should be 4.0 m, the pile spacing between two adjacent piles is 8.0 m and the pile length of the load section of the pile body is the same as the thickness of the slide body, which is 26.0 m. The pile bottom is buried 8.0 m below the bedrock surface, the total length of anti-slide piles is 34.0 m and a total of 36 piles are arranged.
At this time, the transfer coefficient method recommended in the Technical Code for Design and Construction of Landslide Prevention Engineering, that is, Formulas (1) and (2), can be used to calculate the stability coefficient when a single row of full-length anti-slide piles is set, and the calculation process can be realized by normal rock and soil software. The calculated stability coefficient is 1.2 (less than the specified design safety factor 1.3), and engineering quantity of landslide control is 15,373 m3. It can be seen that the cost is high, the retaining effect is not ideal and the reinforcement does not meet the structural requirements because of the large section of the single-row full-length anti-slide pile. Therefore, the use of double-row full-length anti-slide piles is considered.
(2) Double row of full-length anti-slide piles.
If double rows of full-length anti-slide piles are used for treatment, the anti-slide piles used in this treatment project are circular anti-slide piles with a diameter of 2.5 m according to the principle of structural design, and the spacing between two adjacent piles is 5.0 m, and the spacing between rows is 5.0 m. The length of load section and anchorage section of pile body is the same as that of single row, and the tops of front and back anti-slide piles are level with the ground, and the number of anti-slide piles is 72. Under this design condition, the stability coefficient is 1.3 (it is equal to the safety factor value 1.3 stipulated in the Technical Code for Design and Construction of Landslide Control Engineering) and the engineering quantity is 12,717 m3. It can be seen that the strength of a double-row full-length anti-slide pile meets the requirements, but the engineering quantity is large, resulting in high cost.
(3) Double row of buried anti-slide piles.
It can be seen from the above that a landslide in Yan’an City, Shaanxi Province, has a large scale, large thickness of sliding body and large residual sliding force. If a row of anti-slide piles is set up with a large section, the cost is high and the retaining effect is not ideal. If double rows of anti-slide piles are set up, the materials used are also more, and, due to the needs of upper engineering construction, no structures can be set up at a certain position away from the slope, so double rows of submerged anti-slide piles are considered for treatment. In order to reduce the construction period, the anti-slide pile with circular section is mechanically drilled, the pile diameter is 2.5 m and the distance between two adjacent piles is 5.0 m, which is arranged according to a rectangle.
According to GB/T38509-2020 “Design Code for Landslide Prevention and Control”, the cantilever length of the buried anti-slide pile is not less than 0.55 times the thickness of the slide body, and, because the slope angle of the slide body is 8°, it can be determined that the length h1 of the load section of the rear pile should not be less than 18 m. It has been concluded in previous literature that the optimal row spacing of double-row anti-slide piles should be 2–4d (d is pile diameter) [23]. Therefore, based on the above optimal row spacing, this paper uses Equation (11) to analyze and discuss, and determines the minimum pile length of the load-bearing section of the front pile and the corresponding secondary rupture angle by changing the row spacing and the length of the load-bearing section of the back pile. The calculation results are shown in Table 3.

Table 3.
Calculation results of load section length of pile under different working conditions.
As can be seen from Table 3, when the row spacing increases, the minimum load-bearing section length of the corresponding front pile gradually increases. As can be seen from Table 3, in each case, the secondary fracture angle is smaller than the initial fracture angle, indicating that the scenario set in this paper where the front pile is larger than the back pile reduces the possibility of overtopping failure. At this time, both h1 and h2 obtained are the minimum values when no topping failure occurs; that is, the stability coefficient is 1.
As stipulated in the Design Code for Landslide Prevention and Control, the safety factor of the design stability of the buried anti-slide pile length should not be less than 1.25, and, because the prevention and control project of the landslide treatment should be grade I, the safety factor in the natural state is 1.3, so the safety factor of the design is 1.3. Therefore, the load-bearing section length of the back pile is 18 m and the load-bearing section length of the front pile is 22 m. By using the unbalanced thrust transfer coefficient method, the stability coefficient of the design condition is 1.305 > 1.3, which meets the stability requirements. The anchoring section length is 1/4 of the total pile length; that is, the anchoring section length of the back pile is 6 m, the anchoring section length of the front pile is 8 m and the row spacing is 5 m. At this time, the engineering quantity is about 9537 m3, and, compared with the double row of full-length piles, the material is saved about 1/4 and the economy of the project management is improved. Therefore, double-row buried piles are selected for engineering treatment, and the design diagram of slope reinforcement by double-row buried piles is shown in Figure 8.
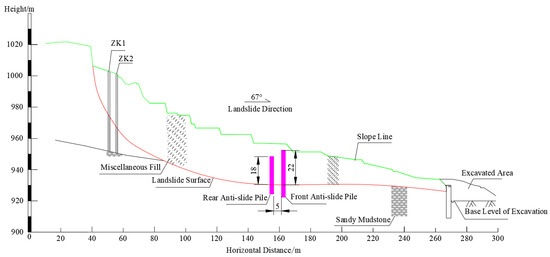
Figure 8.
1-1’ section view of landslide construction reinforced by double rows of buried piles.
In Figure 8, the sandy mudstone is light gray or dark gray, with an argillaceous structure and horizontal bedding. The mixed fill is grey and black, mainly consisting of cinder, brick and silty clay deposits. ZK1 and ZK2 represent the location of the borehole. As shown in Figure 8, the load-bearing section length of the front and back anti-slide piles is 22 m and 18 m, respectively, the anchoring section length is 8 m and 6 m, respectively, and the row spacing is 5 m. The landslide design was completed in 2017, and three displacement monitoring points, J1, J2 and J3, were set. The cumulative horizontal displacement monitoring data are shown in Figure 9.
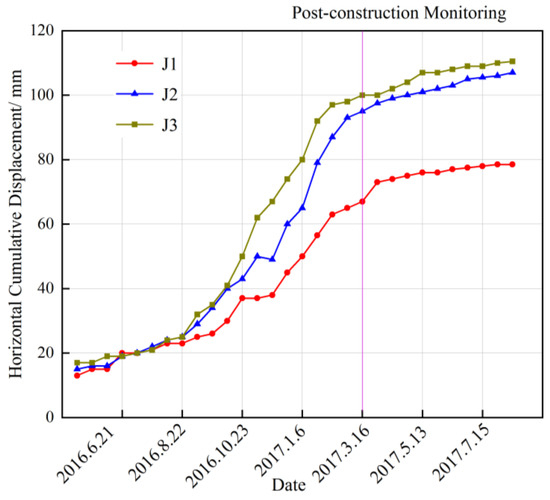
Figure 9.
J1, J2, J3 surface monitoring horizontal displacement diagram.
As can be seen in Figure 9, the cumulative horizontal displacements at J1, J2 and J3 gradually increase before landslide treatment. The increment of horizontal displacement decreases gradually after the double-row pile engineering is applied to the landslide. This shows that the landslide control is successful, and it is optimal to use the calculation equation of the pile length of the double-row buried pile derived in this paper. The engineering example proves the rationality and practicability of the design method and provides engineering reference value for the use of the double-row buried anti-slide pile structure in similar large-scale landslide treatments.
5. Results and Discussion
In this paper, based on the potential failure mode of overtopping, the mechanism of soil internal force transfer at the top of double-row buried piles is described, and the design calculation method of pile length at the load section of a double-row buried pile is proposed.
(1) Based on the simplified calculation model of the pile length of the loading section of the single-row buried pile, a theoretical analysis model of the double-row buried pile is established. The soil mechanical transfer mechanism of the double-row buried pile in the case of overtopping failure is expounded. In order to achieve a better anti-sliding effect, the pile length of the load section of the front pile should be slightly higher than that of the back pile. When overtopping failure occurs, a new rupture angle will be generated when the soil thrust acts on the front pile.
(2) Based on the established theoretical analysis model of double-row buried piles, the transfer coefficient method and rigid body limit equilibrium theory are used to analyze the force on the potential sliding surface over the top and the sliding body surrounding the slope. Moreover, the design calculation equation of the pile length at the load section is obtained when the pile position is horizontal and inclined.
(3) Taking a landslide project in Yan’an City, Shaanxi Province, China, as an example, the landslide control effects of single row length, double row length and double row sinking are compared. Compared with double-row full-length pile, the double-row buried pile saves about a quarter of the material and improves the economy of engineering treatment under the condition that the strength meets the requirement.
(4) The pile length design and calculation of the load section of the double-row buried pile in the landslide control project have been completed. The engineering feasibility of the proposed design calculation method is verified by practical application, which can provide engineering reference value for the use of the double-row buried anti-slide pile structure in similar large-scale landslide treatment.
(5) The design method of pile length at the load section of the double-row buried pile derived in this paper is suitable for landslides with a thick sliding body. When the sliding body is thick, it will produce a large landslide thrust if the use of double row of full-length pile treatment cost is greater and the construction difficulty is greater. At this time, double rows of buried piles can be used for treatment, which can avoid material waste and save costs under the premise that the strength meets the requirements.
(6) In order to facilitate calculation, the soil in front of the pile is assumed to be a rigid body in the analytical model in this paper, but the soil is actually an elastic material, so the equation derived in this paper has certain errors. The design method is used to analyze the strength of a landslide project in Yan’an, and the reliability of the calculation method is verified. It is hoped that future research will address these limitations and provide further insights.
Author Contributions
Conceptualization, X.L.; methodology, X.L.; software, M.W.; validation, M.W. and X.L.; formal analysis, M.W.; investigation, M.W.; resources, W.Y.; data curation, R.X.; writing—original draft preparation, M.W.; writing—review and editing, M.W.; visualization, W.Y.; supervision, R.X. and X.P.; project administration, X.P. All authors have read and agreed to the published version of the manuscript.
Funding
Natural Science Basic Research Program of Shaanxi (Program No. 2022JM-280).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used during the study appear in the submitted article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- National Bureau of Statistics. Available online: https://www.stats.gov.cn/ (accessed on 1 December 2023).
- Zhenwei, P.; Tingkai, N.; Hao, W.; Yanjun, Z.; Chaofeng, Z.; Rui, W. Research progress of landslide geological disaster emergency management technology. J. Disaster Prev. Mitig. Eng. 2021, 41, 1382–1394. [Google Scholar] [CrossRef]
- Derly, G.F.E.G.; Edier, A. Spatial and temporal landslide distributions using global and open landslide databases. Nat. Hazards 2023, 117, 25–55. [Google Scholar] [CrossRef]
- Tao, L.; Gang, C. Analysis of factors influencing anti-slip pile support in tunnel landslide systems for tunnels with different burial depths. Transp. Geotech. 2023, 42, 101079. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Kai, L. Research on Physical Model Test of Anti-Sliding Micro Pile. Ph.D. Thesis, Chang’an University, Xi’an, China, 2022. [Google Scholar] [CrossRef]
- Fengwu, G.; Chen, L.; Wenjuan, G.; Chenguang, L.; Zhanying, F.; Yinbo, Z. Geological Brigade of Hebei Geology and Mineral Exploration Bureau; Improvement of Stiffness calculation and displacement analysis of Double row pile and double beam combined support. Hydrogeol. Eng. Geol. 2022, 49, 109–116. [Google Scholar] [CrossRef]
- Yong, L.; Yingren, Z.; Keqin, C. Discussion on the concept of “skid-resistant short pile” and its mechanical influence. J. Undergr. Space Eng. 2009, 5, 608–615. [Google Scholar]
- Shiguo, X. A simplified approach for stability analysis of slopes reinforced with one row of buried stabilizing piles. Bull. Eng. Geol. Environ. 2017, 76, 1371–1382. [Google Scholar] [CrossRef]
- Yuping, Y.; Shiguo, X. A calculation method for the buried depth of stabilizing piles in reinforced slopes. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1077–1092. [Google Scholar] [CrossRef]
- Wenfeng, L.; Zhijun, Z. Application of buried double-row piles in soil landslide control engineering. J. South China Univ. 2018, 32, 37–43. [Google Scholar] [CrossRef]
- Shiren, Z. Design of Sinking anti-slide pile. Chongqing Archit. 2003, 1, 22–24. [Google Scholar]
- GB 50843-2013; Technical Specifications for Construction Slope Engineering. China Architecture & Building Press: Beijing, China, 2013.
- GB/T38509-2020; Design Code for Landslide Control. China Architecture & Building Press: Beijing, China, 2020.
- Yuping, Y. Thrust algorithm of load section and buried section of sinking pile in overtopping failure mode. Hydrogeol. Eng. Geol. 2023, 50, 76–84. [Google Scholar] [CrossRef]
- Zhiwen, X. Force distribution of deep-buried anti-slide pile. China Railw. Sci. 2000, 01, 50–58. [Google Scholar]
- Wenjie, L. Research on Finite Element Design Method and Large-Scale Physical Model Test of Landslide Reinforced by Pile Sinking. Ph.D. Thesis, Wuhan Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, China, 2006. [Google Scholar]
- Wenjie, L.; Yingren, Z.; Xiating, F. Discussion on finite element design method of buried pile. Chin. J. Rock Mech. Eng. 2006, S1, 2924–2929. [Google Scholar]
- Yakun, S.; Yingren, Z.; Wenjie, L. Numerical analysis of mechanical model test of submerged anti-slide pile. Rock Soil Mech. 2007, 28, 63–68. [Google Scholar] [CrossRef]
- Guiyong, A.O.; Yufang, Z.; Shangyi, Z.; Yingren, Z.; Yongfu, W. Analysis of landslide thrust borne by buried anti-slide pile. Eng. Mech. 2020, 37, 187–192. [Google Scholar]
- Xu, W.; Echuan, Y.; Meijun, L. Simulation of internal force distribution between piles in buried double-row pile-soil system. Coal Geol. Explor. 2006, 04, 57–60. [Google Scholar]
- Meijun, L.; Echuan, Y. Research on Landslide thrust distribution of embedded Double-row anti-slide piles. In Proceedings of the 9th National Conference on Rock Dynamics, Zhengzhou, China, 21 October 2005. [Google Scholar]
- Junfei, L. Analysis and Research on Working Mechanism of Double-Row Buried Anti-Slide Pile. Ph.D. Thesis, Chongqing University, Chongqing, China, 2009. [Google Scholar]
- Yuping, Y. Research on Mechanism and Calculation Method of Landslide Reinforcement with Full-Length Combined Anti-Slide Piles with Sunken Back and Front Rows. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2022. [Google Scholar] [CrossRef]
- Weihang, O.; Si-Wei, L.; Yi, Y. An improved morgenstern-price method using gaussian quadrature. Comput. Geotech. 2022, 148, 104754. [Google Scholar] [CrossRef]
- Krisnasiwi, I.F.; Sundari, W. Analysis of slope stability based in the spencer method on the ring road section, Sikumana. Kupang City. J. Phys. Conf. Ser. 2021, 2017, 012017. [Google Scholar] [CrossRef]
- Boxiang, L. Comprehensive Ground Penetrating Radar (GPR) Method and Janbu Method Study of Road Slope Geological Disaster. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).