An Interpretable Deep Learning Method for Identifying Extreme Events under Faulty Data Interference
Abstract
1. Introduction
- (a)
- The seismic responses of a cable-stayed long-span bridge are successfully identified under the interference of the multi-class monitoring system’s faulty data.
- (b)
- Transfer learning technique is utilized for efficient learning of monitoring data, especially the small-sample patterns.
- (c)
- An interpretation algorithm, termed Grad-CAM, is embedded into the DNN, enabling the model to provide interpretable visual evidence while outputting classification results.
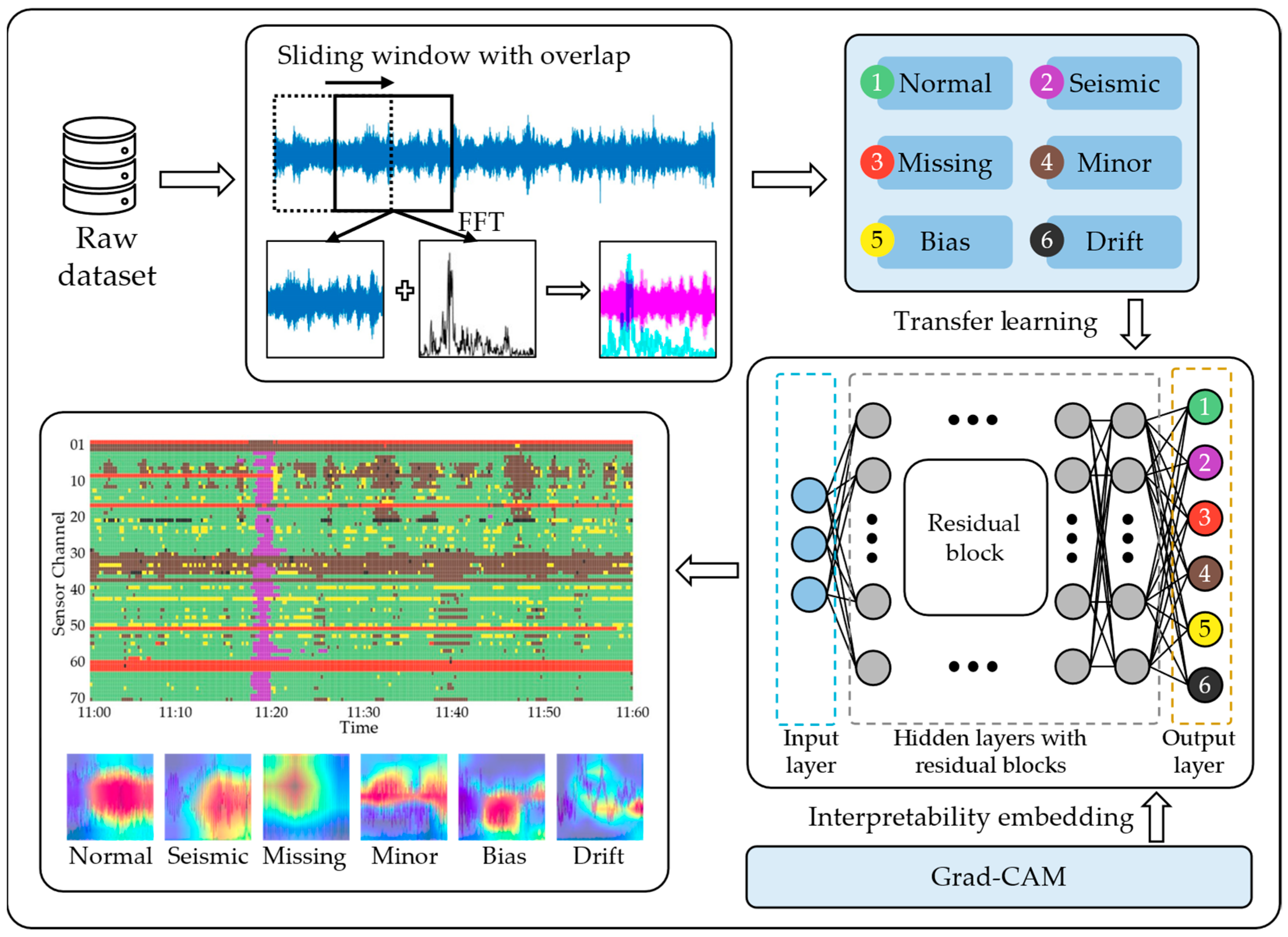
2. Methods
2.1. Data Representation Space
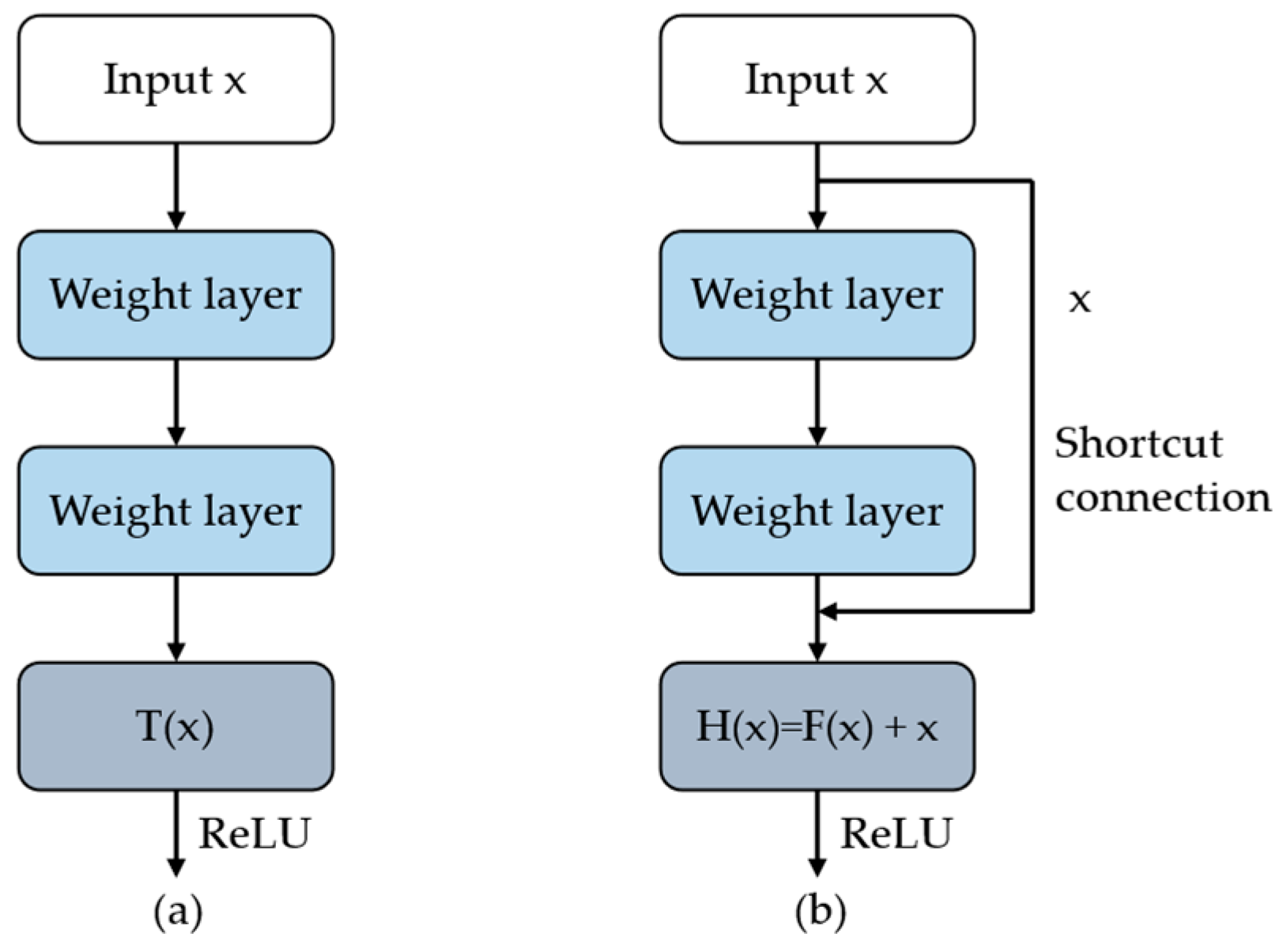
2.2. ResNet34 as the Feature Extractor
2.2.1. ResNet34 Architecture
2.2.2. Transfer Learning
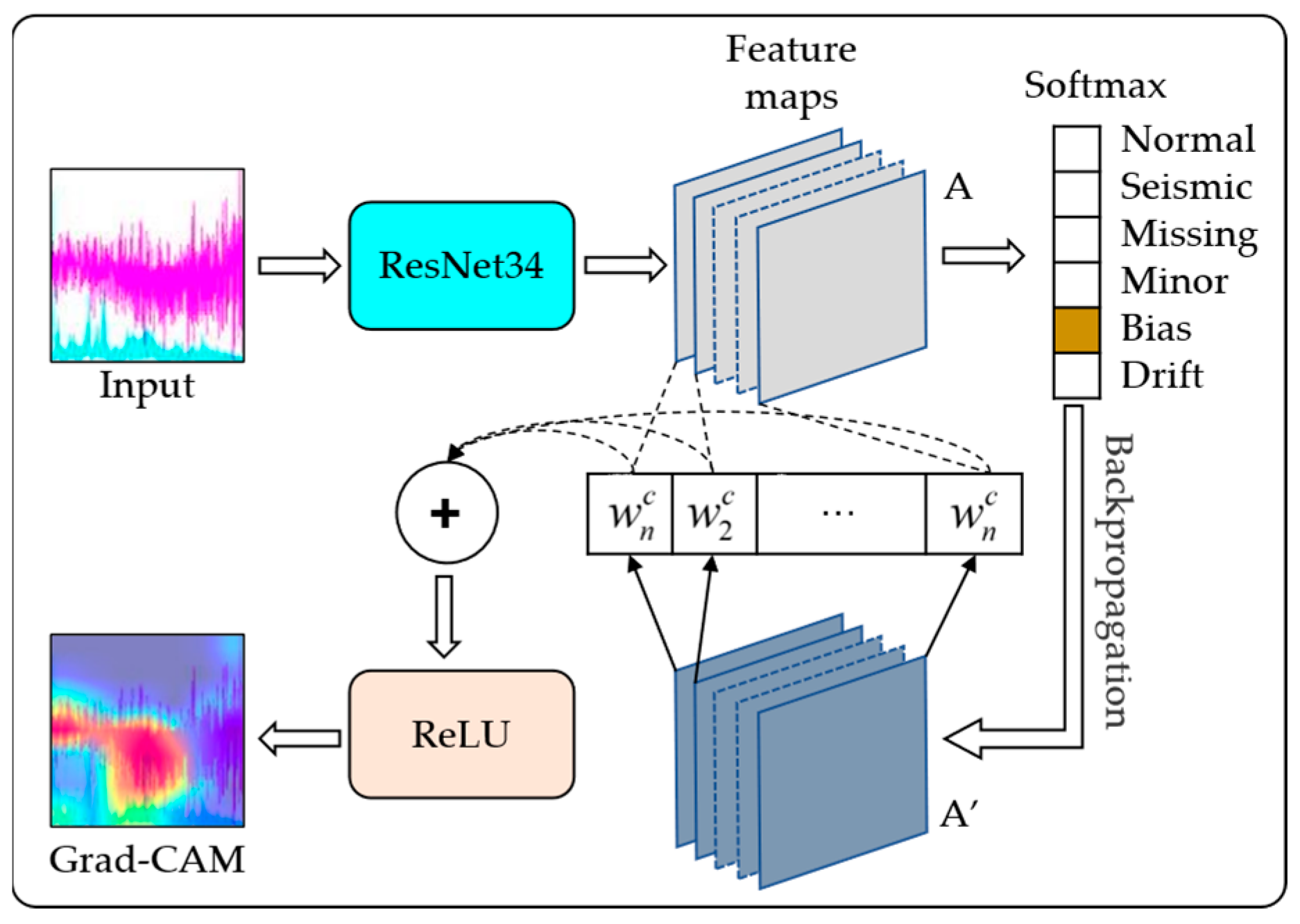
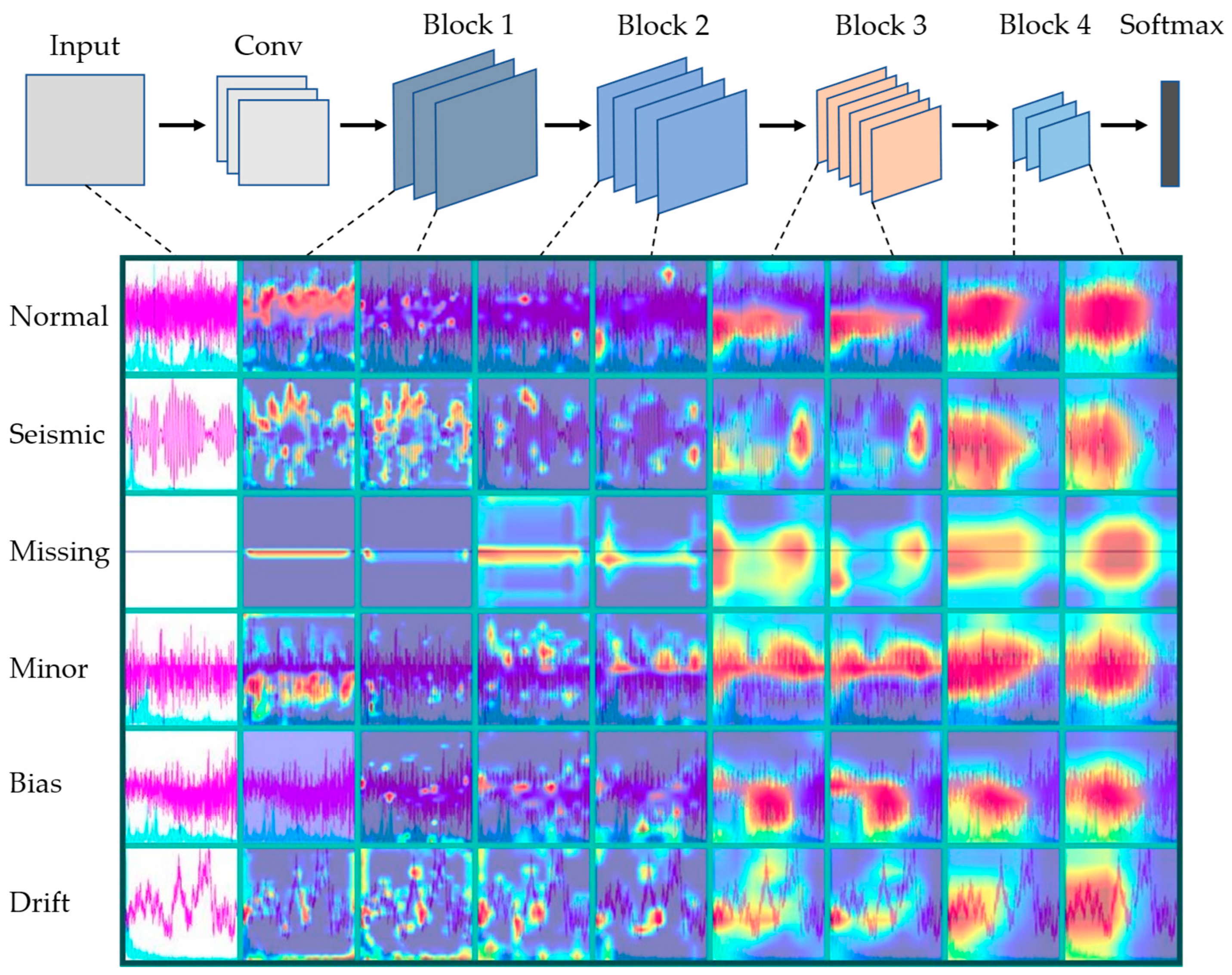
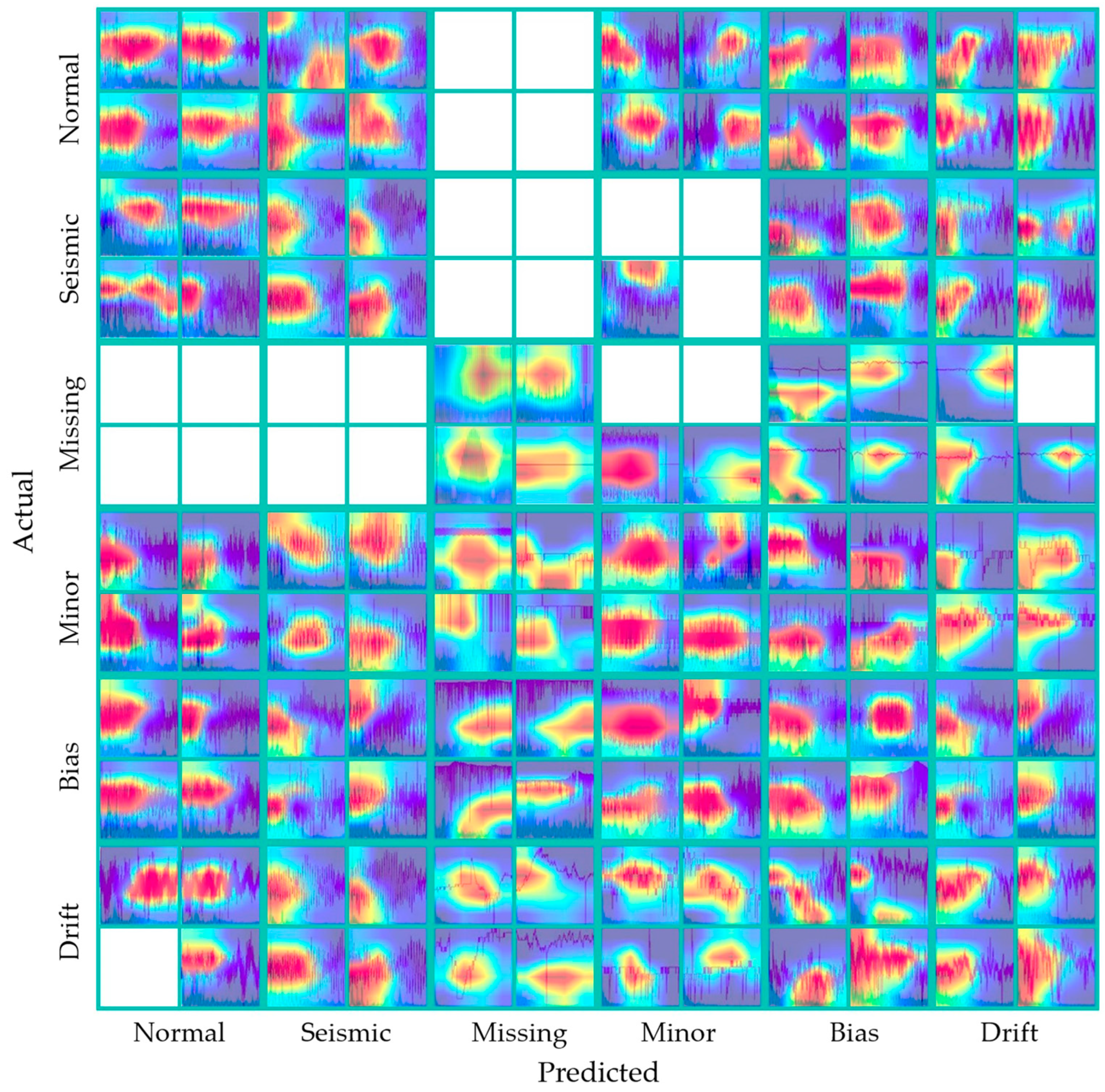
2.3. Grad-CAM
3. Example
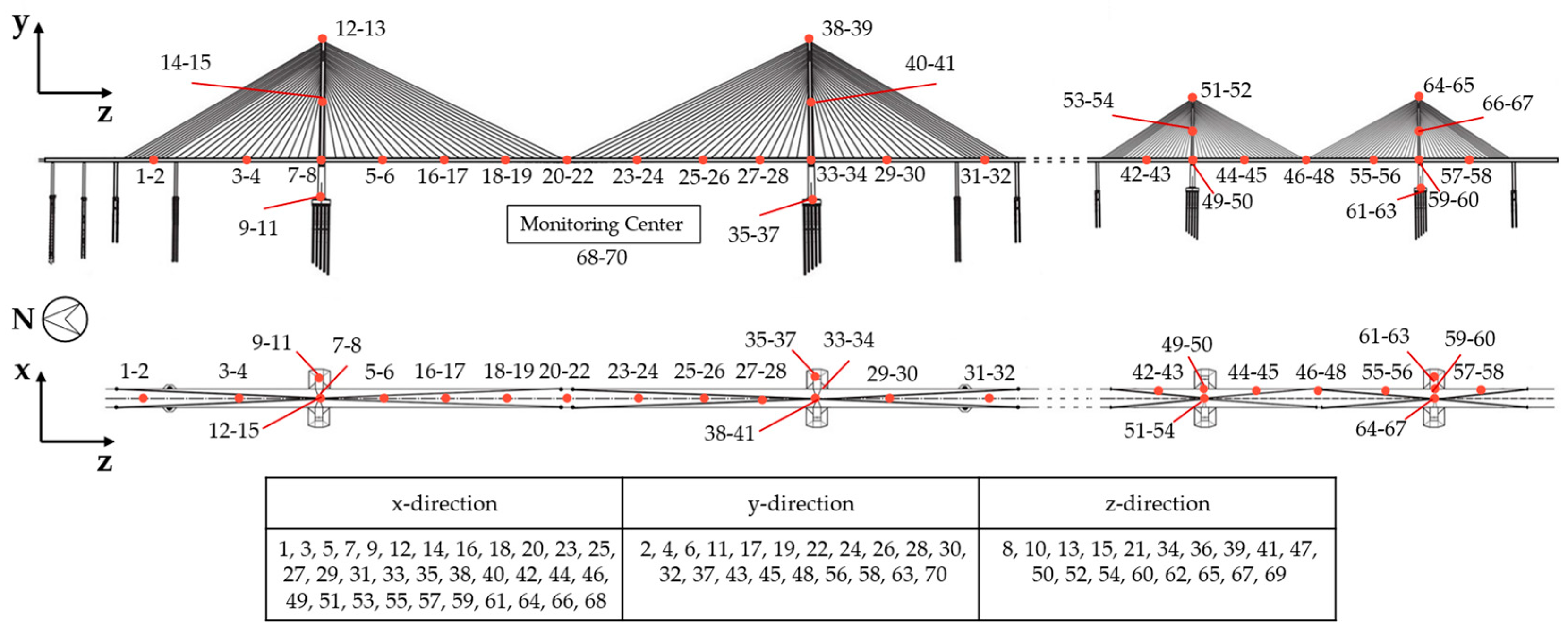
3.1. Data Collection and Dataset Generation
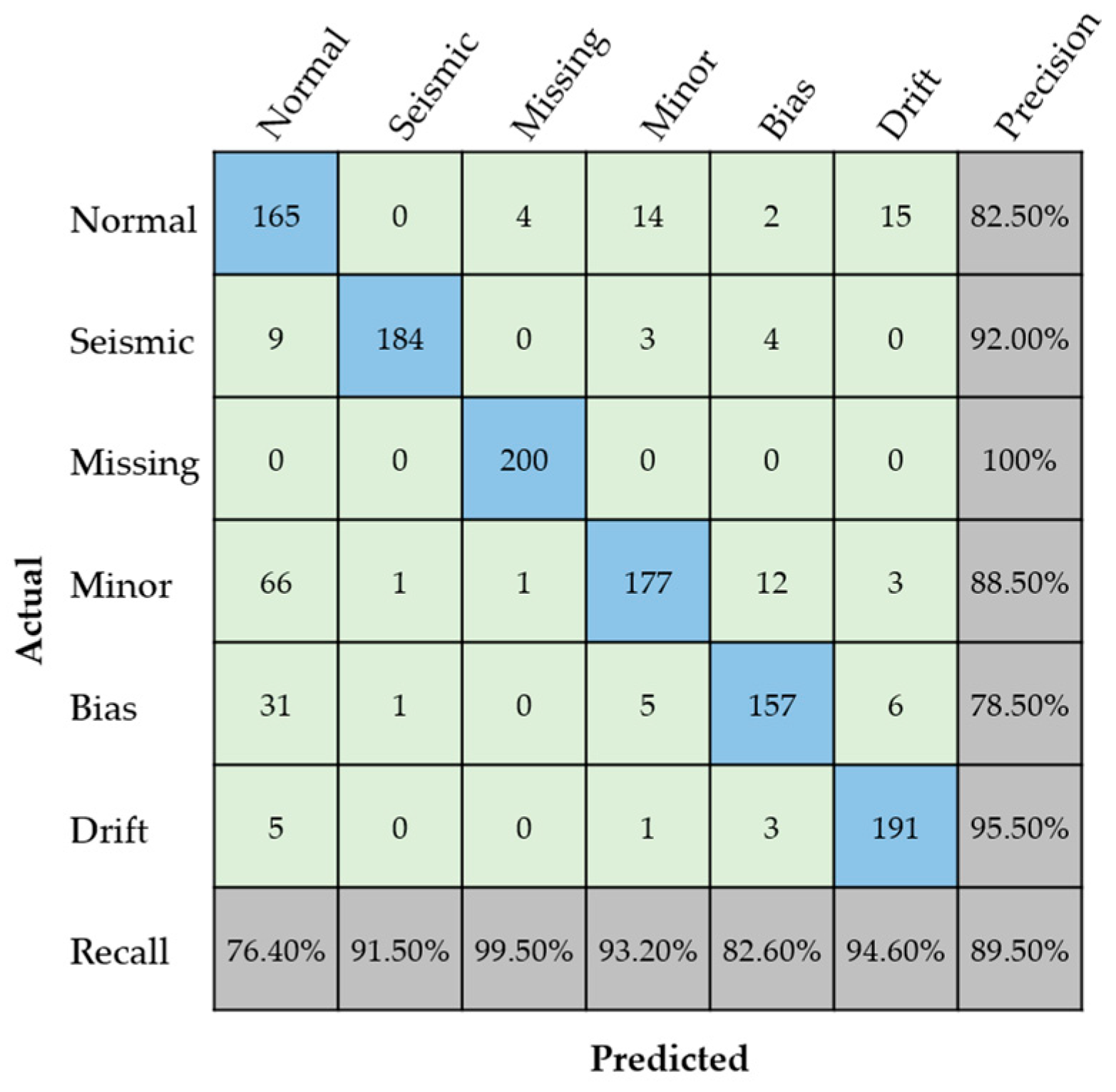
3.2. Neural Network Training and Validation
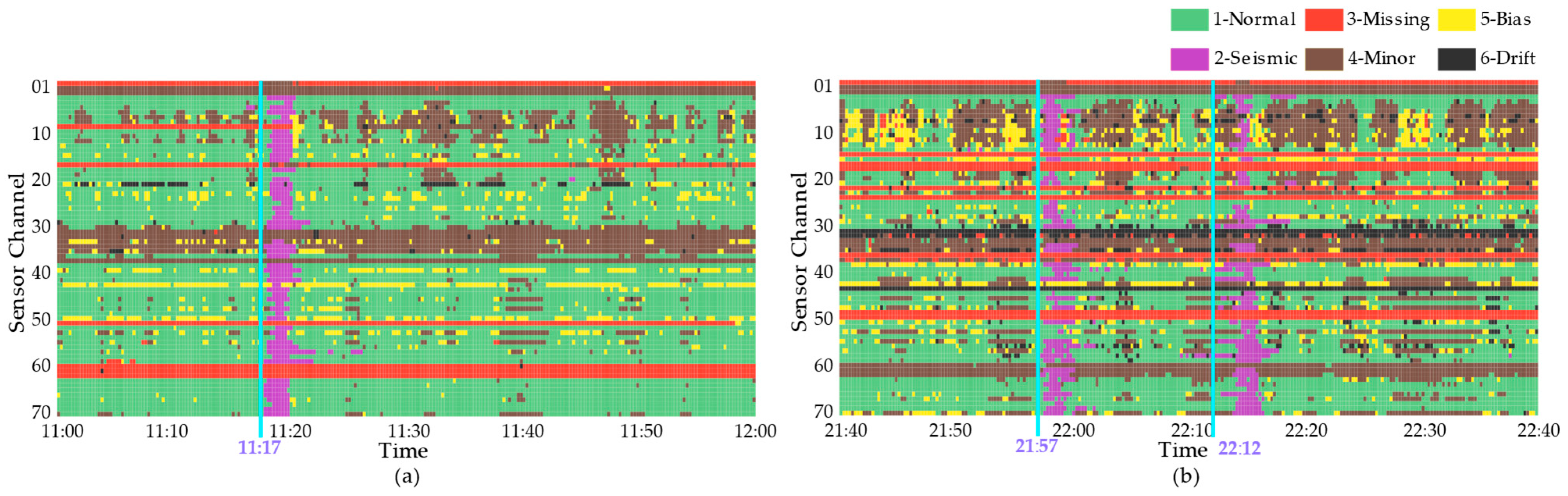
3.3. Test Using Real-World Seismic Events
4. Discussions
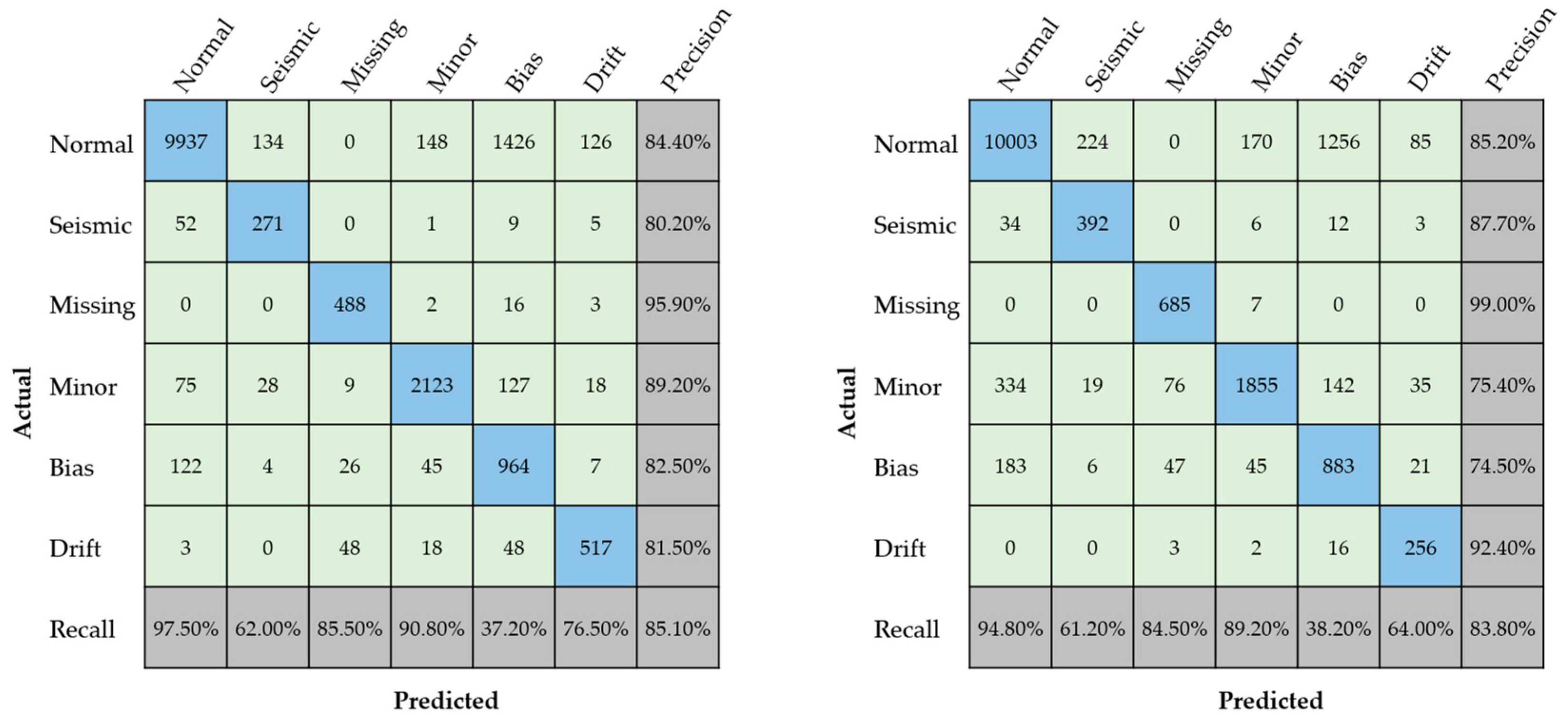
4.1. Panorama of Data Distribution
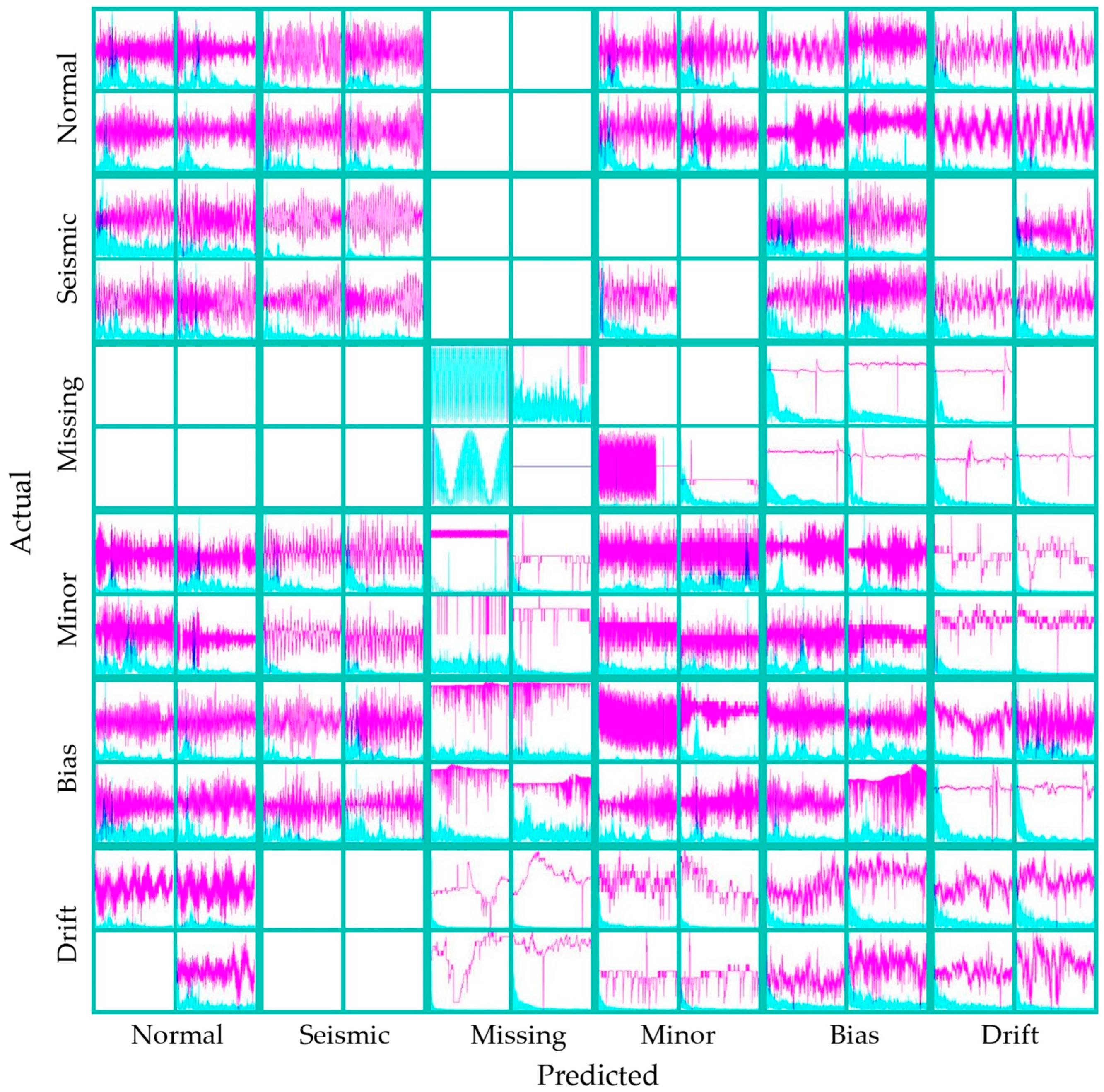
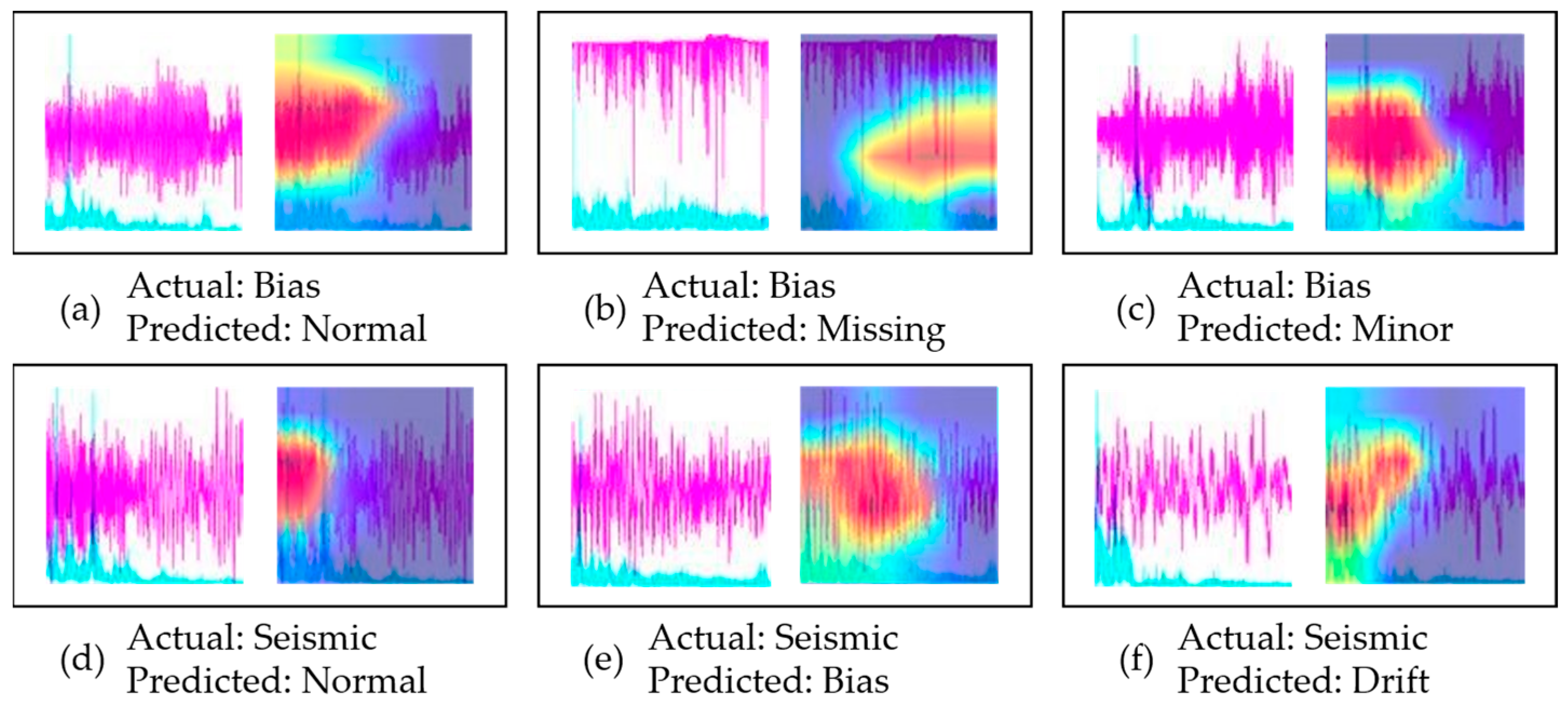
4.2. Misclassification Cases
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sony, S.; Laventure, S.; Sadhu, A. A Literature Review of Next-generation Smart Sensing Technology in Structural Health Monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Abdulkarem, M.; Samsudin, K.; Rokhani, F.Z.; Rasid, M.F.A. Wireless Sensor Network for Structural Health Monitoring: A Contemporary Review of Technologies, Challenges, and Future Direction. Struct. Health Monit. 2020, 19, 693–735. [Google Scholar] [CrossRef]
- Mei, H.; Haider, M.; Joseph, R.; Migot, A.; Giurgiutiu, V. Recent Advances in Piezoelectric Wafer Active Sensors for Structural Health Monitoring Applications. Sensors 2019, 19, 383. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Chen, Z.; Wei, S.; Xu, Y.; Tang, Z.; Li, H. The State of the Art of Data Science and Engineering in Structural Health Monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Balaban, E.; Saxena, A.; Bansal, P.; Goebel, K.F.; Curran, S. Modeling, Detection, and Disambiguation of Sensor Faults for Aerospace Applications. IEEE Sens. J. 2009, 9, 1907–1917. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer Vision and Deep Learning–Based Data Anomaly Detection Method for Structural Health Monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Z.; Bao, Y.; Li, H. Convolutional Neural Network-Based Data Anomaly Detection Method Using Multiple Information for Structural Health Monitoring. Struct. Control Health Monit. 2019, 26, e2296.1–e2296.22. [Google Scholar] [CrossRef]
- Saeed, U.; Jan, S.U.; Lee, Y.-D.; Koo, I. Fault Diagnosis Based on Extremely Randomized Trees in Wireless Sensor Networks. Reliab. Eng. Syst. Saf. 2021, 205, 107284. [Google Scholar] [CrossRef]
- Smarsly, K.; Law, K.H. Decentralized Fault Detection and Isolation in Wireless Structural Health Monitoring Systems Using Analytical Redundancy. Adv. Eng. Softw. 2014, 73, 1–10. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.D.; Koo, I.S. A Distributed Sensor-Fault Detection and Diagnosis Framework Using Machine Learning. Inf. Sci. 2021, 547, 777–796. [Google Scholar] [CrossRef]
- Li, S.; Wei, S.; Bao, Y.; Li, H. Condition Assessment of Cables by Pattern Recognition of Vehicle-Induced Cable Tension Ratio. Eng. Struct. 2018, 155, 1–15. [Google Scholar] [CrossRef]
- Mao, J.; Wang, H.; Spencer, B.F. Toward Data Anomaly Detection for Automated Structural Health Monitoring: Exploiting Generative Adversarial Nets and Autoencoders. Struct. Health Monit. 2021, 20, 1609–1626. [Google Scholar] [CrossRef]
- Sun, Z.; Zou, Z.; Zhang, Y. Utilization of Structural Health Monitoring in Long-Span Bridges: Case Studies. Struct. Control Health Monit. 2017, 24, e1979. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, P.; Li, M.; Chen, L.; Mou, J. A Data-Driven Approach for Ship-Bridge Collision Candidate Detection in Bridge Waterway. Ocean Eng. 2022, 266, 113137. [Google Scholar] [CrossRef]
- Lim, J.-Y.; Kim, S.; Kim, H.-K.; Kim, Y.-K. Long Short-Term Memory (LSTM)-Based Wind Speed Prediction during a Typhoon for Bridge Traffic Control. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104788. [Google Scholar] [CrossRef]
- Gentili, S.; Michelini, A. Automatic Picking of P and S Phases Using a Neural Tree. J. Seismol. 2006, 10, 39–63. [Google Scholar] [CrossRef]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional Neural Network for Earthquake Detection and Location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef]
- Ross, Z.E.; Meier, M.-A.; Hauksson, E.; Heaton, T.H. Generalized Seismic Phase Detection with Deep Learning. Bull. Seismol. Soc. Am. 2018, 108, 2894–2901. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Ding, Z.; Du, Y.; Xia, Y. Anomaly Detection of Sensor Faults and Extreme Events Based on Support Vector Data Description. Struct. Control Health Monit. 2022, 29, e3047. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Asteris, P.G. Structural Damage Identification Using Ensemble Deep Convolutional Neural Network Models. Comput. Model. Eng. Sci. 2023, 134, 835–855. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Barkhordari, M.M.; Armaghani, D.J.; Rashid, A.S.A.; Ulrikh, D.V. Hybrid Wavelet Scattering Network-Based Model for Failure Identification of Reinforced Concrete Members. Sustainability 2022, 14, 12041. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI. Inf. Fusion 2019, 58, 82–115. [Google Scholar] [CrossRef]
- Xu, K.; Liu, S.; Zhang, G.; Sun, M.; Zhao, P.; Fan, Q.; Gan, C.; Lin, X. Interpreting Adversarial Examples by Activation Promotion and Suppression. arXiv 2019, arXiv:1904.02057. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Brox, T. Inverting Visual Representations with Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 4829–4837. [Google Scholar]
- Panwar, H.; Gupta, P.K.; Siddiqui, M.K.; Morales-Menendez, R.; Bhardwaj, P.; Singh, V. A Deep Learning and Grad-CAM Based Color Visualization Approach for Fast Detection of COVID-19 Cases Using Chest X-Ray and CT-Scan Images. Chaos Solitons Fractals 2020, 140, 110190. [Google Scholar] [CrossRef]
- Xiao, G. FCSNet: A Quantitative Explanation Method for Surface Scratch Defects during Belt Grinding Based on Deep Learning. Comput. Ind. 2023, 144, 103793. [Google Scholar] [CrossRef]
- Zhang, Y.; Miyamori, Y.; Mikami, S.; Saito, T. Vibration-based Structural State Identification by a 1-dimensional Convolutional Neural Network. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 822–839. [Google Scholar] [CrossRef]
- Yang, R.; Singh, S.K.; Tavakkoli, M.; Amiri, N.; Yang, Y.; Karami, M.A.; Rai, R. CNN-LSTM Deep Learning Architecture for Computer Vision-Based Modal Frequency Detection. Mech. Syst. Signal Process. 2020, 144, 106885. [Google Scholar] [CrossRef]
- Canizo, M.; Triguero, I.; Conde, A.; Onieva, E. Multi-Head CNN–RNN for Multi-Time Series Anomaly Detection: An Industrial Case Study. Neurocomputing 2019, 363, 246–260. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; IEEE: Santiago, Chile, 2015; pp. 1026–1034. [Google Scholar]
- Liu, L.; Liu, X.; Gao, J.; Chen, W.; Han, J. Understanding the Difficulty of Training Transformers. arXiv 2020, arXiv:2004.08249. [Google Scholar]
- Basodi, S.; Ji, C.; Zhang, H.; Pan, Y. Gradient Amplification: An Efficient Way to Train Deep Neural Networks. Big Data Min. Anal. 2020, 3, 196–207. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 770–778. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. arXiv 2020, arXiv:1911.02685. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Xu, Y.; Bao, Y.; Zhang, Y.; Li, H. Attribute-Based Structural Damage Identification by Few-Shot Meta Learning with Inter-Class Knowledge Transfer. Struct. Health Monit. 2021, 20, 1494–1517. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Jung, T.-P. Improving EEG-Based Emotion Classification Using Conditional Transfer Learning. Front. Hum. Neurosci. 2017, 11, 334. [Google Scholar] [CrossRef]
- Du, Y.; Li, L.; Hou, R.; Wang, X.; Tian, W.; Xia, Y. Convolutional Neural Network-Based Data Anomaly Detection Considering Class Imbalance with Limited Data. Smart Struct. Syst. 2022, 29, 63–75. [Google Scholar]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional Neural Networks for Medical Image Analysis: Full Training or Fine Tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 2921–2929. [Google Scholar]
- Siringoringo, D.M.; Fujino, Y.; Namikawa, K. Seismic Response Analyses of the Yokohama Bay Cable-Stayed Bridge in the 2011 Great East Japan Earthquake. J. Bridge Eng. 2014, 19, A4014006. [Google Scholar] [CrossRef]


| No. | Data Period | Mainshock Time | Mainshock Magnitude | Epicenter |
|---|---|---|---|---|
| 1 | 11:00 to 12:00, 12 May 2016 | 11:17 | 6.2 | Yilan County, Taiwan |
| 2 | 21:40 to 22:40, 4 February 2018 | 21:56 | 6.4 | Hualien County, Taiwan |
| 3 | 09:40 to 10:40, 3 April 2019 | 9:52 | 5.9 | Taitung County, Taiwan |
| 4 | 12:50 to 13:50, 18 April 2019 | 13:01 | 6.7 | Hualien County, Taiwan |
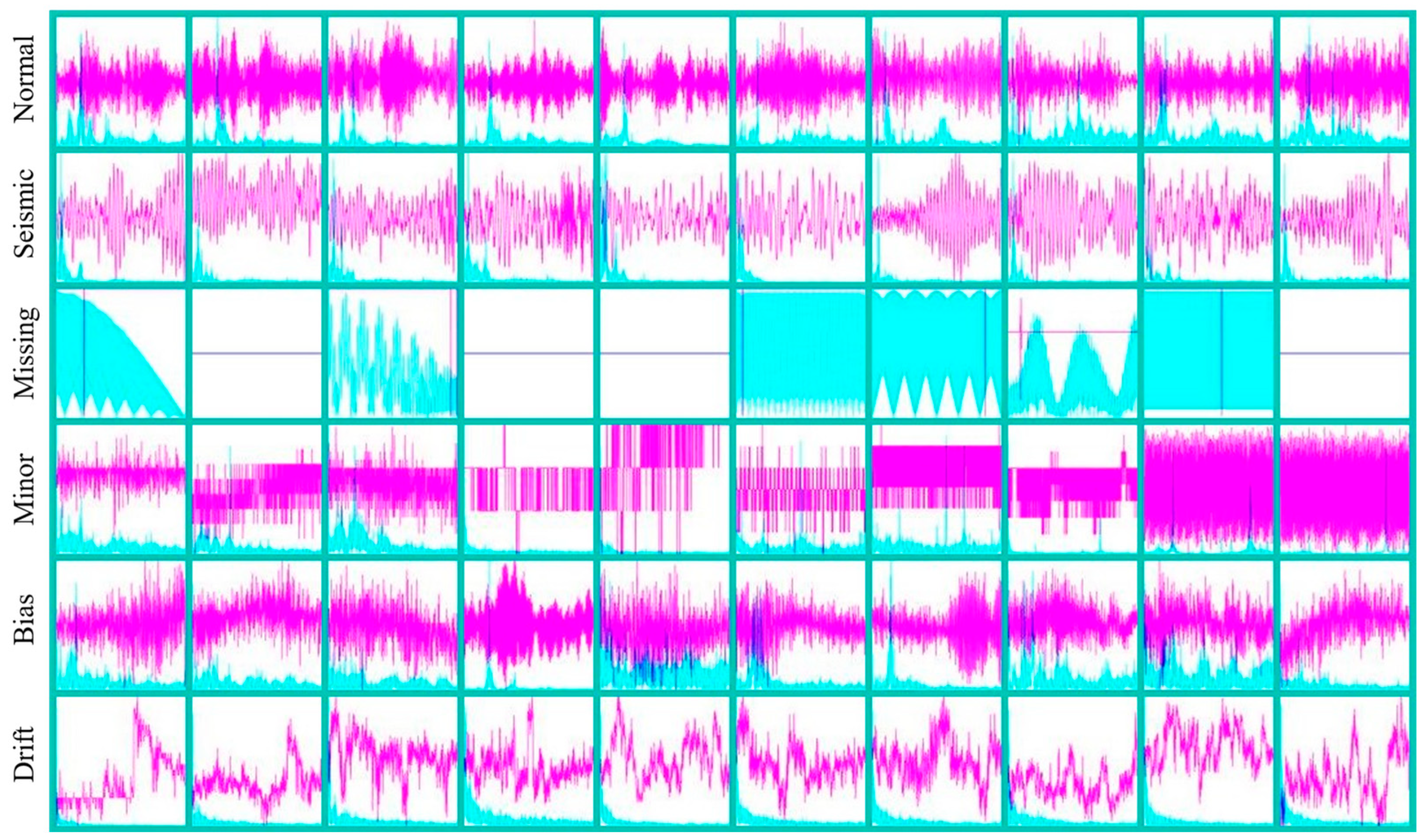
| No. | Anomaly Patterns | Description |
|---|---|---|
| 1 | Normal | The time series is symmetrical, the vibration amplitude is relatively steady, and the frequency response is concentrated in the mid-frequency band. |
| 2 | Seismic | The time series shows sparse long period features. Additionally, the frequency response is concentrated in the low frequency band. |
| 3 | Missing | Most/all of the time series is missing or meaningless values, and the frequency response is correspondingly zero or meaningless disorder. |
| 4 | Minor | The time series appears sawtooth-shaped, and the vibration amplitude is very small in the time domain. |
| 5 | Bias | Relative to the pattern Normal, the time history is Bias towards one side. |
| 6 | Drift | The time series is nonstationary, with random drift, and the frequency response is concentrated in the low frequency band. |
| Item | Normal | Seismic | Missing | Minor | Bias | Drift | Total |
|---|---|---|---|---|---|---|---|
| No.1 | 10,447 | 458 | 1487 | 3172 | 1117 | 119 | 16,800 |
| No.2 | 6750 | 773 | 2259 | 4468 | 1448 | 1102 | 16,800 |
| No.3 | 11,771 | 338 | 509 | 2380 | 1168 | 634 | 16,800 |
| No.4 | 11,738 | 447 | 692 | 2461 | 1185 | 277 | 16,800 |
| Total | 40,706 | 2016 | 4947 | 12,481 | 4918 | 2132 | 67,200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Tang, Z.; Zhang, C.; Xu, W.; Wu, Y. An Interpretable Deep Learning Method for Identifying Extreme Events under Faulty Data Interference. Appl. Sci. 2023, 13, 5659. https://doi.org/10.3390/app13095659
Guo J, Tang Z, Zhang C, Xu W, Wu Y. An Interpretable Deep Learning Method for Identifying Extreme Events under Faulty Data Interference. Applied Sciences. 2023; 13(9):5659. https://doi.org/10.3390/app13095659
Chicago/Turabian StyleGuo, Jiaxing, Zhiyi Tang, Changxing Zhang, Wei Xu, and Yonghong Wu. 2023. "An Interpretable Deep Learning Method for Identifying Extreme Events under Faulty Data Interference" Applied Sciences 13, no. 9: 5659. https://doi.org/10.3390/app13095659
APA StyleGuo, J., Tang, Z., Zhang, C., Xu, W., & Wu, Y. (2023). An Interpretable Deep Learning Method for Identifying Extreme Events under Faulty Data Interference. Applied Sciences, 13(9), 5659. https://doi.org/10.3390/app13095659






