Abstract
The integral equations technique has been successfully modified for studying the plane E-polarized electromagnetic wave scattering by multilevel coplanar systems of zero-thickness impedance strips. Reformulation of the scattering problem in the form of the second-kind regular integral equations has been realized on the base of the Carleman regularization technique. Two novel and original classes of specific Cantor functions have been presented and analyzed. Using new Cantor functions, it is easy to create a lot of non-classical orderings for specific multilevel coplanar strips systems. That sort of system can be useful for modeling irregular natural processes and zones in the future. Considerable attention was focused on the plane E-polarized electromagnetic wave scattering by sparsely filled coplanar systems of electrically narrow impedance strips. An explicit solution of the scattering problem has been obtained for such case of strips system.
1. Introduction
The theory of regular and singular integral equations is an important subject within applied mathematics to solve different physical problems [1,2,3]. The method of integral equations can be successfully used for the correct reducing of an outer three-dimensional physical model to a one-dimensional mathematical model. In particular, nanotechnologies are expensive, and therefore, the preceding modeling with the aid of trusted, accurate, and time-economic software becomes not only a desired but also a necessary element of research [4]. Systems of integral equations were successfully used as mathematical models for the plane electromagnetic wave scattering by flat gratings with a finite number of impedance zero-thickness strips presented in the articles [5,6,7]. The first-kind singular integral equations are usually classified as ill-conditioned [3]. It means that small changes in initial input data can lead to much larger changes in the output solution. So, a reformulation of the scattering problems in the form of the second-kind regular integral equations is important and useful to obtain correct and convenient mathematical models for the examination of these scattering problems.
The integral equations’ technique has been successfully modified for the studying of the plane electromagnetic wave scattering by the simplest coplanar systems of zero-thickness impedance strips in the proceeding papers [8,9]. In particular, in the last publication, some novel types of the specific Cantor function, corresponding to one-dimension self-similar fractal perfect sets with variable Hausdorff dimension, have been presented and analyzed. Using new Cantor functions, it is easy to create a lot of non-classical intervals sets for ordering of different and specific multilevel coplanar strips system for modeling of irregular or terrible natural processes and zones. The proceeding papers, mentioned above, deal with the plane H-polarized electromagnetic wave scattering by the simplest coplanar systems of impedance zero-thickness strips. The first-kind singular integral equations were obtained for modeling of the plane H-polarized electromagnetic wave scattering problem only. So, it is interesting to consider the plane E-polarized electromagnetic wave scattering problem as well. The case of E-polarization is essentially different, so, it needs a new approach to find the first-kind singular integral equations for correct modeling of that scattering process.
In the present article, such new approach to examine the plane E-polarized electromagnetic wave scattering problem starting from Maxwell’s equations will be presented for coplanar multilevel zero-thickness strips system. Then, the mathematical model will be improved by a reformulation of the scattering problems in the form of the second-kind regular integral equations. Zero-thickness electrically conducting strips of coplanar multilevel strips system can be ordered according to new specific, but correct mathematical laws. To have a lot of correct mathematical laws, novel classes of specific Cantor functions, corresponding to novel classes of one dimensional self-similar perfect sets with variable fractal dimension, will be presented. In the case of the E-polarized wave scattering by sparsely filled coplanar systems of electrically narrow impedance zero-thickness strips, asymptotical solutions of scattering problems in the closed form (for the main approximation) will be obtained.
2. The Plane E-Polarized EM Wave Scattering by a Coplanar Strip System
The initial general formulation of the plane electromagnetic (EM) wave scattering by zero-thickness electrically conducting strip system is well known, widely used, and a classical one [10]. In the case of flat strip grating, the plane E-polarized EM wave scattering problem was formulated and examined in the article [6]. Let us repeat the initial general formulation of that scattering problem for a coplanar multilevel system of finite number of impedance zero-thickness flat strips. Under a coplanar strips system, it is understood here to be the same as for 3D vectors: they are coplanar if they are parallel to the same plane.
2.1. Formulation of the Scattering Problem
This subsection deals with reformulation of the plane EM wave scattering problem starting from Maxwell’s equations in the vector differential equation form. Let a plane linearly polarized EM wave be incident upon a coplanar system, consisting of zero-thickness electrically conducting flat strips with parallel edges. The strips’ edges will be oriented to the ordinate axis of a Cartesian frame. The transverse cross-section of that coplanar strip system represents an appropriate number of segments or intervals, depending on type of mathematical law. In mathematics, a segment is a closed interval, but an interval (in short) means open interval. It is important for the construction of a pre-fractal set (where segments are used) or a stage of terrible Cantor function, where intervals are used (see Section 4.1). Those intervals have to be placed in the xOz plane upon parallel straight lines. In Figure 1, one can see the simplest coplanar system, which consists of two unequal zero-thickness electrically conducting flat strips, illuminated by the plane E-polarized EM wave. The transverse cross-section of that simplest coplanar system consists of two intervals placed in the xOz plane upon parallel straight lines z = const.
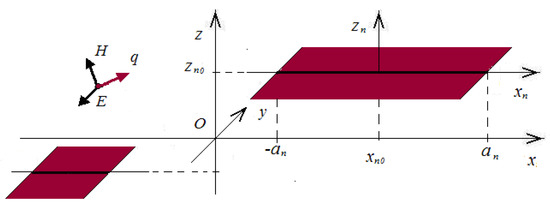
Figure 1.
System of parallel flat strips, illuminated by the plane E-polarized EM wave.
Starting from the first two basic Maxwell’s equations in the vector differential equation form, we obtain partial differential equation of the second order with respect to single second component of the electric field intensity vector :
Here the symbol denotes Laplacian operator and the letter k denotes the wave number. The magnetic field intensity will be of the form: , where the letter i denotes the imaginary unit and the variable χ is the wave resistance of a medium around the strips. The boundary conditions on the electrically conducting flat strips have the form: , here w is the surface strip impedance [2,6]. So, the impedance boundary condition on intervals will be in more simple and convenient form:
where the variable μ = w/χ is the dimensionless impedance parameter. Thus, we have the exterior mixed boundary-value problem for the Equation (1). This two-dimensional boundary-value problem has unique solution provided two types of conditions. The first one is the radiation condition at infinity:
The second type of conditions deal with conditions at the strip boundary points in the Meixner form [6].
Thus, the plane E-polarized EM wave scattering problem in three-dimensional space is correctly simplified to a two-dimensional boundary-value problem. It is a powerful aid to simplify and examine similar exterior boundary-value problems for elliptic partial equations of mathematical physics is a classical integral equations technique [2]. So, this technique modification will be used firstly for reformulation of that plane E-polarized EM wave scattering boundary-value problem.
2.2. The Integral Equations Technique
According to classical integral equations technique, the unknown function of the mixed plane wave scattering boundary-value problem will be represented in form of the sum: . The known function , where is the radius vector of the Cartesian coordinate system, the vector points the direction of exciting wave. The first addend presents the initial plane E-polarized EM wave. The second addend, dealing with scattering process of initial wave with coplanar system, has to be written in standard integral form (see, for example, [8]):
Here N is the number of strips, the function is the first kind Hankel function of order zero and the root of its argument (see Figure 1). New unknown functions of one variable and , determined in intervals, are expressed by the following formulas:
Using the boundary condition (2) in the interval , it is easy to obtain the relationship between these unknown functions . This important relationship will be helpful to simplify integrals under sum in (4) and that formula can be simplified to the form:
Due to the first kind Hankel function properties, the function satisfies both the Equation (1) and the radiation condition at infinity (3) [8]. The main step of integral equations technique’s realization will be reducing of the two-dimensional exterior boundary-value problem to a one-dimensional one. For this purpose we ought to use the boundary impedance condition (2) upon the interval :
Substitution into which of the expression (6) yields the system of coupled integral-differential equations:
To take the limits in kernel functions we ought to use the relationship:
It is true for . That relationship allows separate differential and integral parts of the coupled integral-differential equations’ system (8) as well. As an intermediate result, we arrive at the ordinary differential equations of the second order:
New unknown functions of one variable are represented by the sum of linear integral transformations:
The ordinary inhomogeneous differential Equation (9) can be examined similar to easier case of flat grating with finite electrically conducting strips, firstly presented in the article [6]. So, making use of the small parameter’s method with respect to measureless impedance parameter, we can find correct partial solution of the differential Equation (9):
It is easy to see that these relationships defined a system of the first-kind singular integral equations due to linear integral transformations (10).
Summarizing, we can say that an integral equations technique modification allows us to correctly reformulate the third exterior two-dimensional boundary-value problem as an intermediate one-dimensional mathematical model of the plane E-polarized wave scattering problem. That one-dimension mathematical model is presented by two Formulas (10) and (11) and will be improved by an analytical technique of regularization, first presented in the article [6].
3. The Analytic Technique of Carleman Regularization
The first-kind singular integral equations systems are usually ill-conditioned, and so they need to be improved for the correct usage of different direct numerical methods. Just obtained system is convenient for transformation to the second-kind integral equations’ set. Here, the Carleman inversion formula for the first-kind integral equation with simple logarithmic singularity can be used [1].
3.1. The Simplest Transformations of the First-Kind Singular Integral Equations
In any correct mathematical model, input and output variables have to be dimensionless. Firstly we normalize the input parameters of coplanar strips system , (n = 1, …, N) multiplying them by the wave number k (see Figure 1). So, starting from the intermediate one-dimensional mathematical model, presented by Formulas (10) and (11), we obtain new mathematical model in the form of the first-kind singular integral equations’ system:
Here, new unknown functions are defined by the formula: , new arguments of kernel functions and known constants of the right-hand side functions . In the case of diagonal kernel functions (n = m) the root and we can use the following series representation:
Here, the value of lnγ means the Euler constant, which is irrational number: lnγ = 0.557215664…. That series representation of diagonal kernel functions gives us possibility to separate logarithmic singularity in the simplest form. So, multiplying by a corresponding constant, we obtain the first-kind system of log-singular integral equations:
In that first-kind system new regular kernel’s functions are presented by the following expressions:
The new mathematical model is more correct, but has some deficiencies and needs to be improved further. To do this, we can transform it to the second-kind integral equations set by the Carleman regularization technique. That regularization technique is similar to the case of flat gratings with finite number of impedance zero-thickness strips, presented in the article [6].
3.2. The Carleman Regularization Technique
To realize the Carleman regularization technique, at first, the first-kind singular integral equations’ system (14) can be rewritten in the form of the simplest log-singular integral equation:
Where the right-hand part functions are determined by the formulas:
Secondly, the Carleman inversion formula for the simplest log-singular integral equation has to be used [1]. Due to it we have the expression:
Derivatives under the first integral are, with respect to the variable of integration and “p.v.”, before that integral means principal value of improper Cauchy integral. Then, we substitute expressions of the right-hand part functions, presented by the Formula (17) and change order of integration. Introducing new regular kernel functions and new right-hand part functions, we find a second-kind integral equations set of the form:
It will be noted that these regular kernel functions and right-hand part functions have expressions similar to the case of flat gratings with finite number of impedance strips [6]. Having that second-kind integral equations system with smoother kernel functions, it is easy to make correct and effective calculation algorithms.
To show productivity of that full-wave mathematical model, let us focus our attention on an asymptotical case. To realize that asymptotic mathematical model, two principal assumptions with respect to normalized input parameters have to be true. The first assumption deals with the grating’s strips: they have to be electrically narrow (). The second principal assumption deals with distances between the grating’s strips: they have to be sufficient greatly spaced. In the case that the plane E-polarized wave scattering from sparsely filled coplanar electrically conducting flat strips system, the second-kind integral equations system (19) has an explicit asymptotic solution. Let us prove that statement in the main approximation.
The main terms of regular kernel functions, presented by the expressions (15), do not dependent on variables t and τ and we have simple expressions: , , here . The last normalized input parameters deal with distances between intervals’ centers (see Figure 1). So, due to the second principal assumption for these normalized input parameters the relationships: have to be true. The main terms of right-hand part functions of the second-kind integral equations system (19) are simple as well. In the main approximation, they are presented by the expressions: . Thus, the Formulas (17)–(19) give us explicit asymptotic solutions of the following form: . The constants in the numerator are solutions of rather simple linear algebraic equations system:
Thus, the plane E-polarized electromagnetic wave scattering problem is completely solved for the sparsely filled coplanar system with finite number of electrically narrow impedance flat strips in the main approximation.
Let us present some numerical results for the simplest case of two strips’ grating (see Figure 1). In the linear algebraic equations system (20), we substitute normalized input parameters:, , , , . Easy calculation gives us a numerical result for the system’s solution:, . The direction vector and the dimensionless impedance parameter μ = (1 + i)/2. Due to the above presented assumptions, the calculation error is 0.01.
In general, situational disorder of coplanar electrically conducting flat strips systems is not easy to obtain and vary fine and useful formulas. So it is interesting and important to find correct, in the sense of strict mathematics, ordering of strips in a system. A lot of strip orderings in flat gratings deal with one-dimensional self-similar fractals—unique perfect sets [11]. Novel type of pre-fractal flat gratings has a potential of wide use in microwave devices in the future (see, for example, the article [5]). It is important that such flat gratings depend on two or three dimensionless geometrical parameters. For the case of coplanar multilevel electrically conducting flat strips systems, terrible Cantor functions can be used to obtain novel types of strict mathematical strips ordering [9].
4. Scattering by Coplanar Multilevel Ordered Strip System
There are huge sets of zero-thickness flat strips systems, ordered according to some one-dimensional fractal creation stages—pre-fractal flat strips gratings [7]. Such gratings have strong mathematical ordering and certain advantages over periodic diffraction gratings, widely applied in modern microwave and quasi-optic devises. For every fractal perfect set, it is possible to construct irregular or terrible Cantor function in the same manner as “classic” irregular Cantor function [11]. Sometimes its graph is called “Devil stairs” due to singularity of terrible Cantor function. Constructive stages of such Cantor functions can be used for original and strong ordering of zero-thickness coplanar multilevel strips system. Here a coplanar strips system means the same as for 3D vectors: they are coplanar if they are parallel to the same plane. The strips system consists of zero-thickness flat strips with parallel edges.
4.1. Some Novel Classes of Cantor Functions
In this subsection, we will consider novel types of irregular Cantor functions, which enable us to create new original and strong coplanar multilevel grating, consisting of flat strips with parallel edges. The transverse cross-section of such coplanar grating structure represents an appropriate number of collinear intervals in two-dimensional space, ordering in original and mathematical strong sense.
The basic fractal perfect set, the Smith–Cantor set, has numerous modifications to generalize a series of one-dimensional perfect sets with variable fractal dimension. The simplest modification uses triadic principle of fractal perfect set creation [5,12]. For that modification, a straight-line segment (the initiator) is divided into three specific parts: two equal sub-segments and an interval or gap between them. On that interval, the Cantor function is equal to zero and we have the main step (Figure 2a). On two gaps of the second construction stage for Cantor function values, we put ±0.5. So, new two equal steps are added to graph of Cantor function and so on.

Figure 2.
(a,b) The cross-sections of not classic strips systems.
Figure 2a shows a stage of the Cantor function creation procedure constructed on the base of the fourth stage of a triadic perfect set [7,13]. One can see seven intervals corresponding to eight segments of the fourth stage of the triadic perfect set. That Cantor function constructive procedure deals with Smith–Cantor perfect set, as the base for domain of that function definition. Due to the simplest generalization of the Smith–Cantor set, the class of triadic perfect sets with variable fractal dimensions can construct a lot of novel terrible Cantor functions.
The second generalization of basic Smith–Cantor set uses rather unwieldy principle of perfect set creation to obtain five-parts classes of perfect sets with variable fractal dimensions. For that class a straight-line segment (the initiator) is divided into five specific parts: three equal sub-segments and two intervals or gaps [9]. On these two intervals for Cantor function values we put ±d (Figure 2b). So, we have two basic equal steps (third and sixth in Figure 2b) for graph of Cantor function: x = ±b + at, z = ±d. One can see three geometrical parameters, which have to be multiplied by the wave number in correct modeling of scattering process. These parameters determine pre-fractal construction process and stages of Cantor function’s construction as well.
The lower part of Figure 2b shows the second stage of a perfect set creation: nine equal segments. Then we correctly defined Cantor function on six unequal gaps (intervals) of the second construction stage of perfect set creation. For instance, on the intervals number 4 and number 5 for Cantor function values, we put ±d/3 and so on. It will be noted that Cantor function’s “steps” are intervals, unlike stage of a perfect set’s creation is a set of segments. In Figure 2b, intervals (in general not equal) of domain of Cantor function’s definition are between nine equal segments of the second stage of a perfect set’s creation. Due to the generalization of the Smith–Cantor set, a five-part class of perfect sets with variable fractal dimensions can be constructed, as well as a lot of novel irregular Cantor functions. It is important that such Cantor functions depend on three or four dimensionless geometrical parameters.
In the next subsection, we will consider the simplest novel types of non-classical coplanar gratings, dealing with irregular Cantor functions, in order to obtain explicit solutions of the plane wave scattering problem.
4.2. Scattering by the Simplest System of Electrically Narrow Strips
Let us return to the mathematical modeling of the plane E-polarized electromagnetic wave scattering from non-classical coplanar systems of electrically conducting flat strips using the Carleman regularization technique. It is interesting to consider the asymptotic mathematical models of the plane wave scattering for the simplest, sparsely filled coplanar system with a finite number of electrically narrow impedance strips. Figure 3 presents such coplanar strips systems: the first strips system deals with the first stage of a five-part perfect set (see Figure 2b). Here, we have two equal electrically conducting flat strips (see Figure 3a). Normalized input parameters of corresponding E-polarized electromagnetic wave scattering problem have to be under the assumptions: .
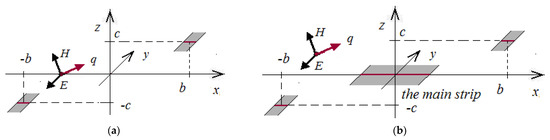
Figure 3.
(a,b) The simplest gratings dealing with irregular Cantor functions.
For that simple electrically conducting flat strips’ system determinant of linear algebraic equations set (20) of the second order (N = 2) is defined by the simplest formula:
Due to the simplest Cramer’s rule the main constants (which define output variables of that asymptotic mathematical model) are determined by the expressions:
Here, new constants are presented the formula: .
Thus, the plane E-polarized electromagnetic wave scattering problem is completely solved for the simplest sparsely filled coplanar system dealing with irregular Cantor functions in the main approximation. Those two levels of coplanar grating consists of two electrically narrow impedance strips.
The second coplanar strips system, presented in Figure 3b, deals with the second stage of a three-part perfect set and we have three unequal strips: the central strip is not equal to two others (see Figure 2a). In that more complicated case, we ought to consider three normalized input parameters. The first one deals with distances between strips, so, it will be under the same assumption (as for two levels previous coplanar gratings):. Two other normalized input parameters, dealing with electrically narrow strips, are under similar assumptions. For the main (central) strip, we have the same assumption: ; for two other equal strips, similar assumptions are true automatically due to the three-part perfect set’s construction [5,7]. So, two principal normalized parameters α and ρ determine input variables of geometric structure of grating.
For that, the simplest electrically conducting flat strips grating determinant of linear algebraic equations set (20) of the third order (N = 3) is defined by a rather unwieldy formula:
The constants (which define output variables of that asymptotic mathematical model) can be determined by the simplest Cramer’s rule as well.
Let us perform some computer simulation to show simplicity just presented asymptotic scattering model. The initial normalized parameters: α = 0.1, kb = 2, kc = 1. The direction vector and the dimensionless impedance parameter μ = (1 + i)/2. Easy calculation gives us numerical results: j = (0.14 − 2.4i, 2.34 + 0.36i, −0.36 + 1.68i). Due to above presented assumptions the calculation error is 0.01.
Thus, the plane E-polarized electromagnetic wave scattering problem is completely solved for sparsely filled coplanar system of three electrically narrow impedance zero-thickness strips for the main approximation.
Using just-obtained asymptotical solutions of two simple scattering problems in the closed form, it is easy to examine scattered electromagnetic fields in the far zone. Calculation algorithms can be developed for integral scattering characteristics of sparsely filled non-classical coplanar gratings and computer simulation can be performed like in the case of H-polarized wave scattering, presented in the publication [9].
5. Conclusions
Modifications of a well-known integral equations technique has been used for studying the plane of an E-polarized harmonic electromagnetic wave scattering by multilevel coplanar gratings of zero-thickness impedance strips. Reformulation of the scattering problem in the form of the second-kind regular integral equations has been realized to obtain correct and convenient mathematical models. It based on Carleman’s regularization technique to the plane E-polarized harmonic electromagnetic wave scattering by a flat system of impedance strips [6].
Two novel classes of irregular or specific Cantor functions, corresponding to novel classes of one dimensional self-similar perfect sets with a variable fractal dimension, have been presented and analyzed. Using new Cantor functions, it is possible to create a huge number of non-classical pre-fractal orderings for different and specific multilevel coplanar strips systems. That sort of systems can be useful for modeling irregular or terrible natural processes and zones [9]. Terrible classical and novel-specific Cantor functions can be used for mathematical modeling of irregular or terrible sons in rainfall and stream flows as well [14].
Considerable attention was focused on the plane E-polarized harmonic electromagnetic wave scattering by sparsely filled coplanar systems of electrically narrow impedance zero-thickness strips. Due to the Carleman regularization technique, simple asymptotical solutions of scattering problems in the closed form (for the main approximation) have been obtained. In particular, such explicit solutions are very important for validation of full-wave scattering models [15,16,17]. They can be applied to create algorithms for integral scattering characteristics of sparsely filled gratings and simulate some computer numeric experiments as well.
Author Contributions
All authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gakhov, F.D. Boundary-Value Problems; Pergamon Press: Oxford, UK, 1977; pp. 532–596. [Google Scholar]
- Colton, D.; Kress, R. Integral Equation Methods in Scattering Theory; John Wiley and Sons: New York, NY, USA, 1983; pp. 77–112, 123–163. [Google Scholar]
- Atkinson, K.E. The Numerical Solution of Integral Equations of the Second Kind; Cambridge University Press: Cambridge, UK, 1997; pp. 306–350. [Google Scholar]
- Lucido, M.; Balaban, M.V.; Nosich, A.I. Plane wave scattering from thin dielectric disk in free space: Generalized boundary conditions, regularizing Galerkin technique and whispering gallery mode resonances. IET Microw. Antennas Propag. 2021, 15, 121–133. [Google Scholar] [CrossRef]
- Koshovy, G.I. The plane H-polarized electromagnetic wave scattering by pre-fractal grating of impedance strips. Int. J. Microw. Wirel. Technol. 2020, 12, 269–275. [Google Scholar] [CrossRef]
- Koshovy, G.I.; Koshovy, A.G. The Carleman regularization technique in the modeling of the plane E-polarized electromagnetic wave scattering by a flat system of impedance strips. IET Microw. Antennas Propag. 2021, 15, 1218–1224. [Google Scholar] [CrossRef]
- Koshovy, G.I. The Cauchy method of analytical regularization in the modelling of plane wave scattering by a flat pre-fractal system of impedance strips. IET Microw. Antennas Propag. 2021, 15, 1310–1317. [Google Scholar] [CrossRef]
- Ahapova, O.O.; Koshovy, G.I. On EM Wave Scattering by Coplanar System of Flat Impedance Strips. In Proceedings of the IEEE 40th International Conference on Electronics and Nanotechnology, Kyiv, Ukraine, 20–22 April 2020; pp. 34–37. [Google Scholar]
- Koshovy, G.I.; Logvinov, Y.F.; Karpenko, V.I. The Plane Wave Scattering by Not Classic Multi Level Coplanar Systems of Flat Impedance Strips. In Proceedings of the IEEE 41th International Conference on Electronics and Nanotechnology, Kyiv, Ukraine, 10–14 October 2022; pp. 38–42. [Google Scholar]
- Eom, H.J. Electromagnetic Wave Theory for Boundary-Value Problems; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–45, 196–204. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983; pp. 112–126. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications; Wiley: Chichester, UK, 2003; pp. 3–125. [Google Scholar]
- Edgar, G.A. Measure, Topology and Fractal Geometry; Springer: New York, NY, USA, 2008; pp. 1–7, 117–122, 165–188. [Google Scholar]
- Maskey, M.; Puente, C.; Sivakumar, B. Temporal downscaling rainfall and stream flow records through a deterministic fractal geometric approach. J. Hydrol. 2019, 568, 447–461. [Google Scholar] [CrossRef]
- Gandel’, Y.V.; Dushkin, V.D. Mathematical Model of Scattering of Polarized Waves on Impedance Strips Located on a Screened` Dielectric Layer. J. Math. Sci. 2016, 212, 156–166. [Google Scholar]
- Kaliberda, M.E.; Lytvynenko, L.M.; Pogarsky, S.A. Modeling of graphene planar grating in the THz range by the method of singular integral equations. Frequenz 2018, 72, 277–284. [Google Scholar] [CrossRef]
- Fikioris, G. Regularised discretisations obtained from the first-kind Fredholm operator equations. IET Microw. Antennas Propag. 2021, 15, 1211–1217. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).