Finite Element Analysis (FEA) for a Different Type of Cono-in Dental Implant
Abstract
1. Introduction
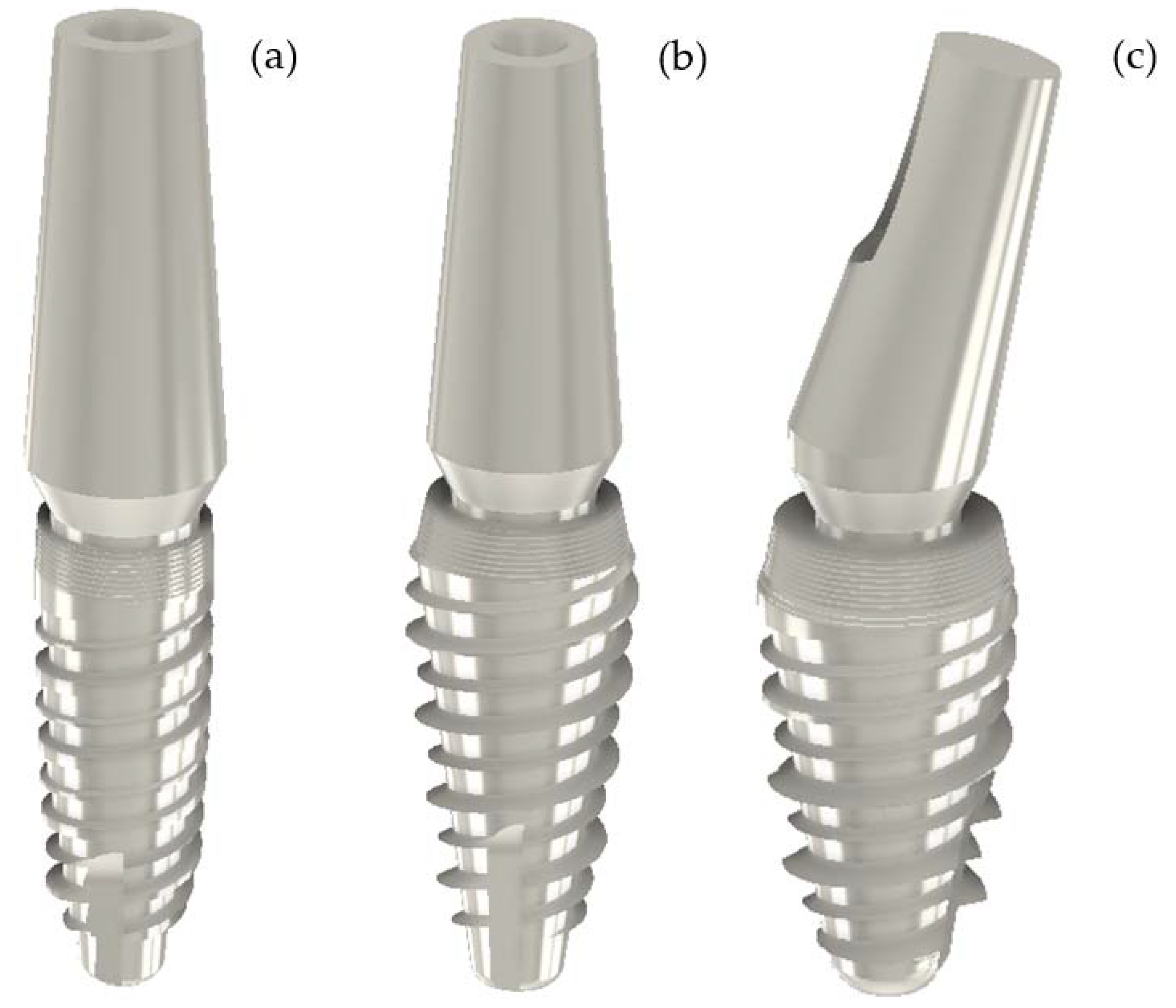
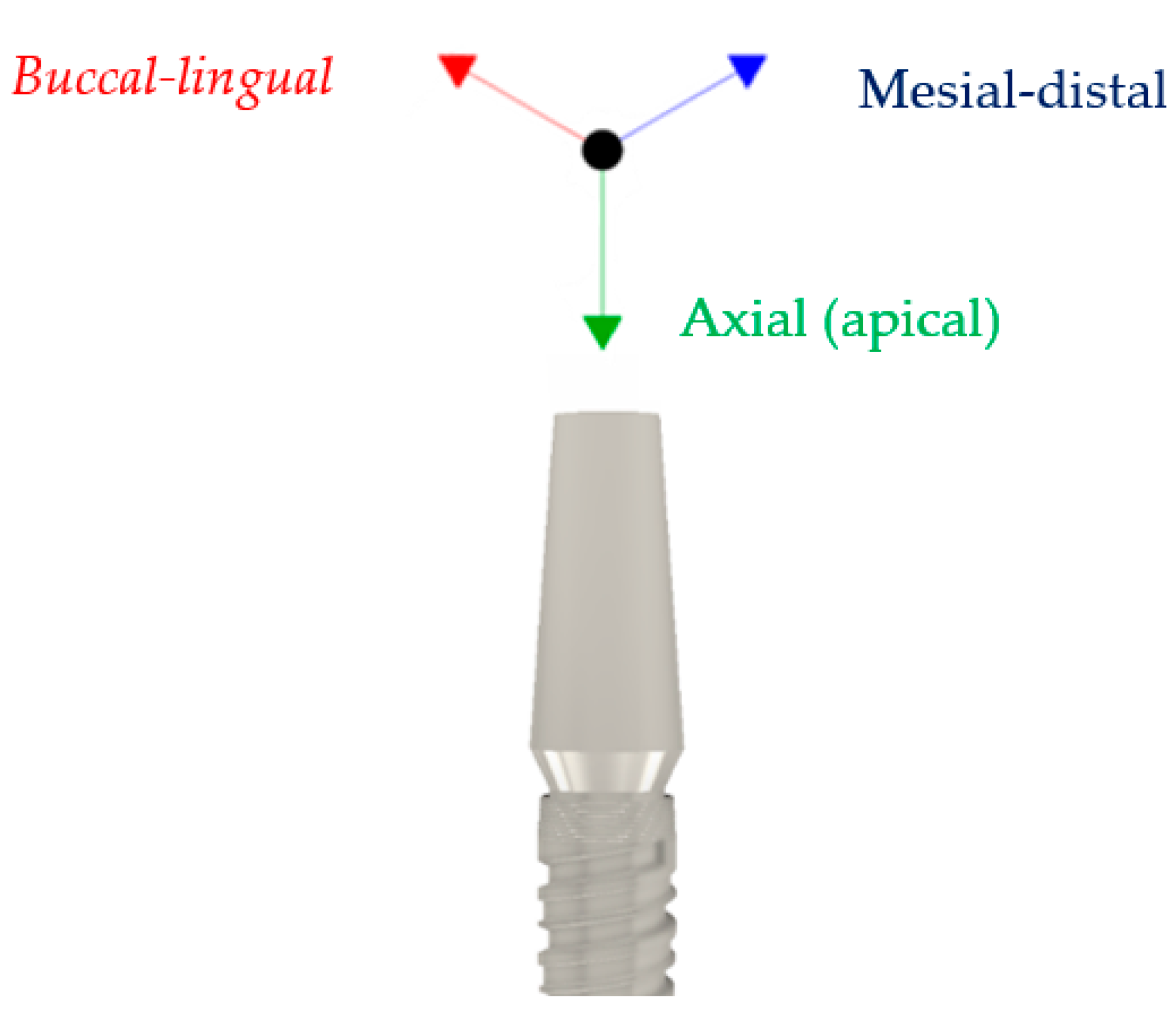
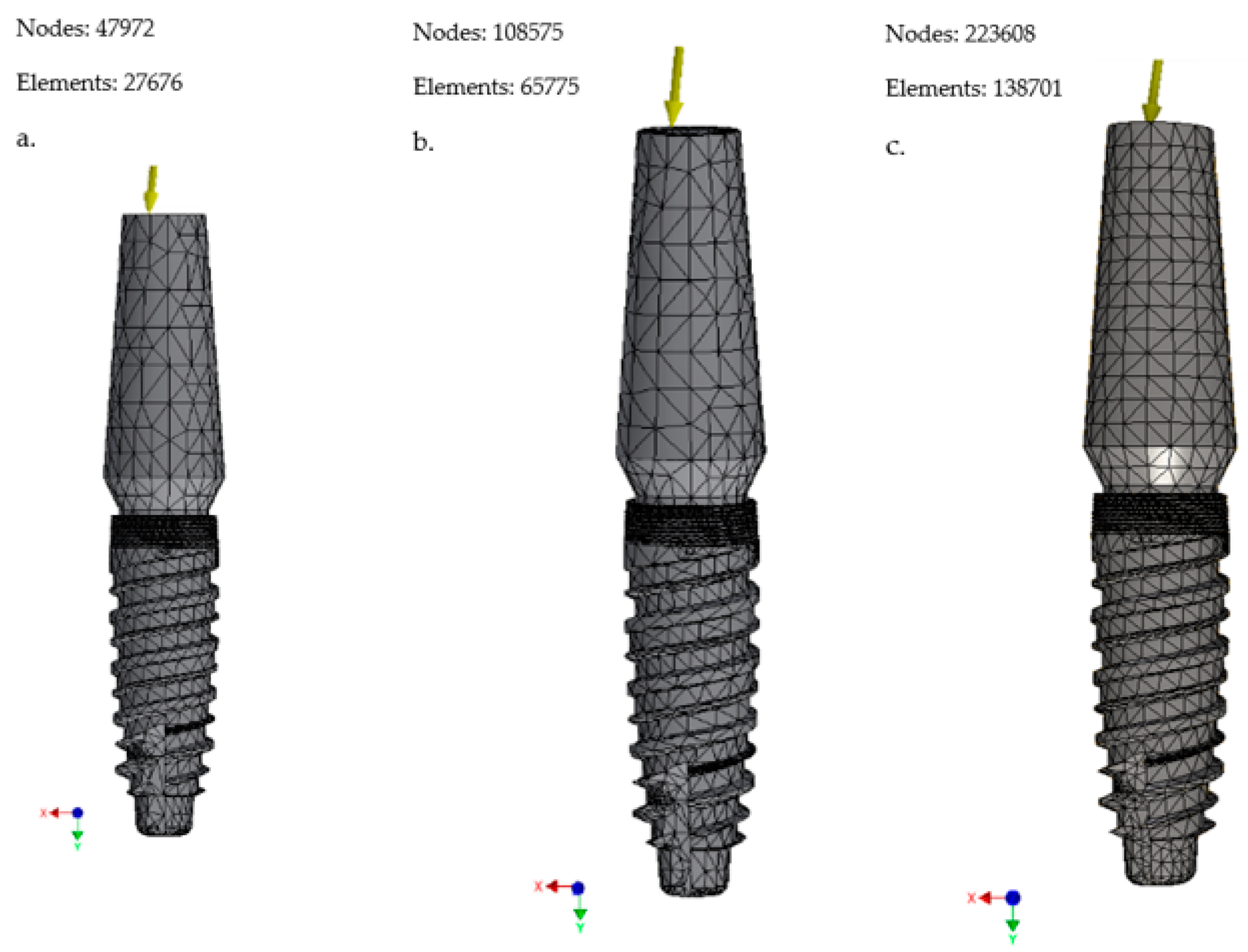
2. Materials and Methods
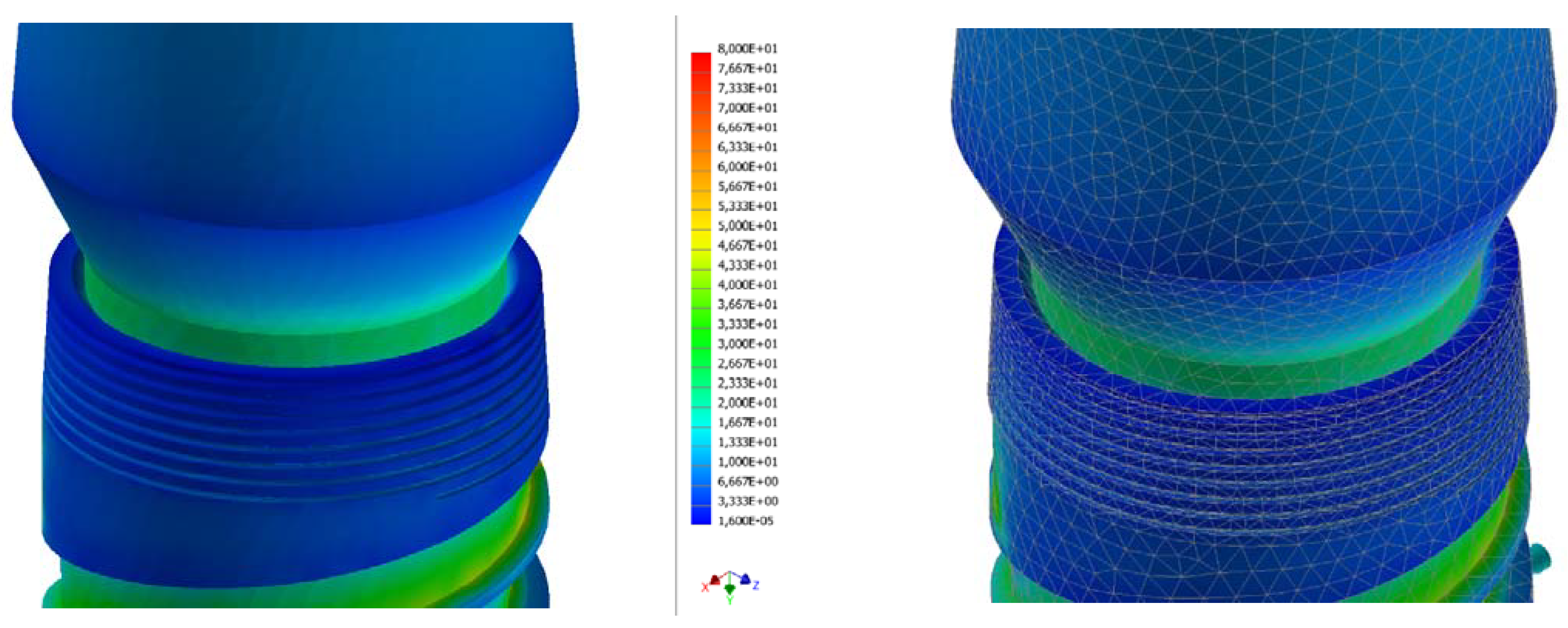
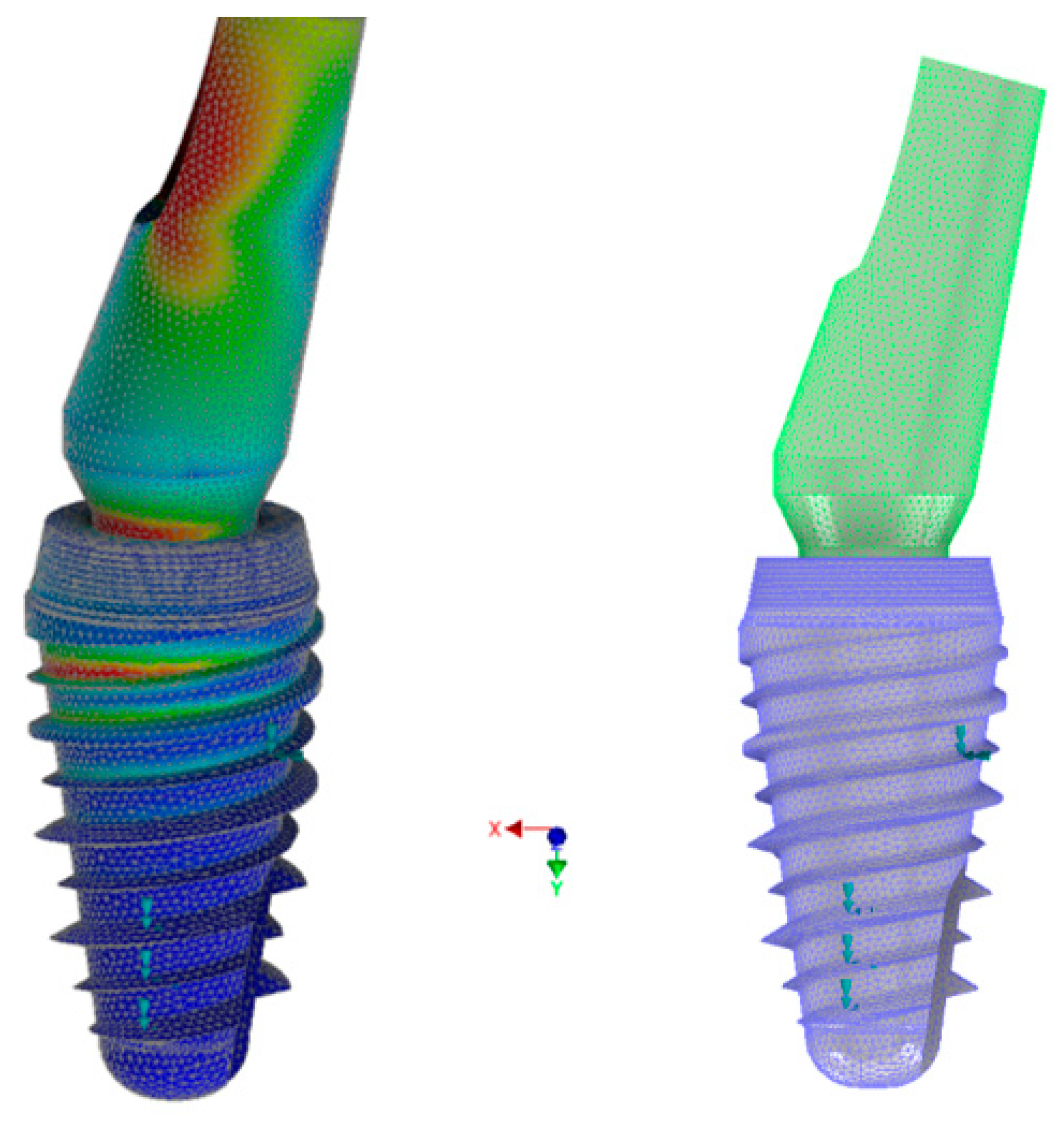
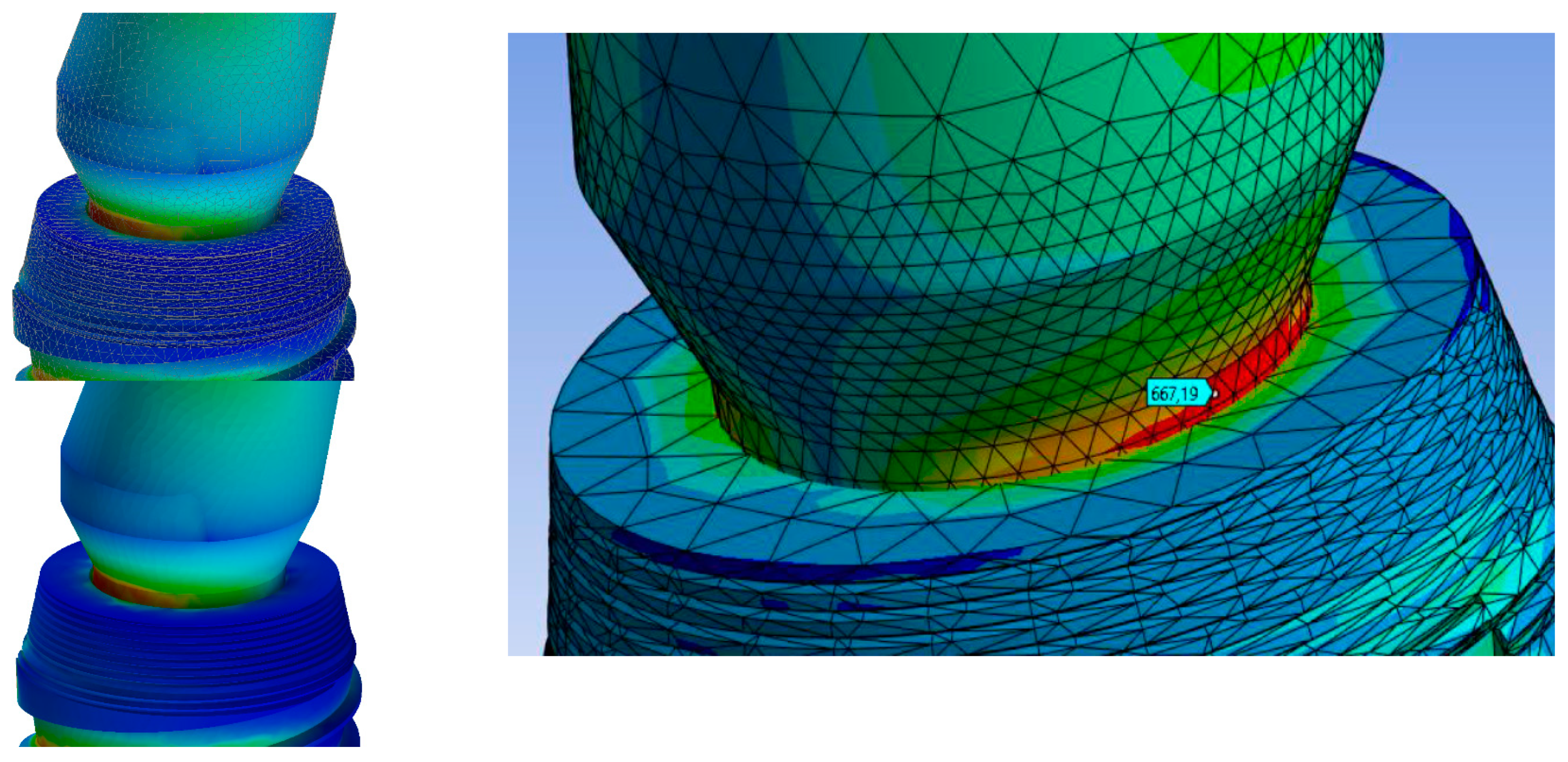
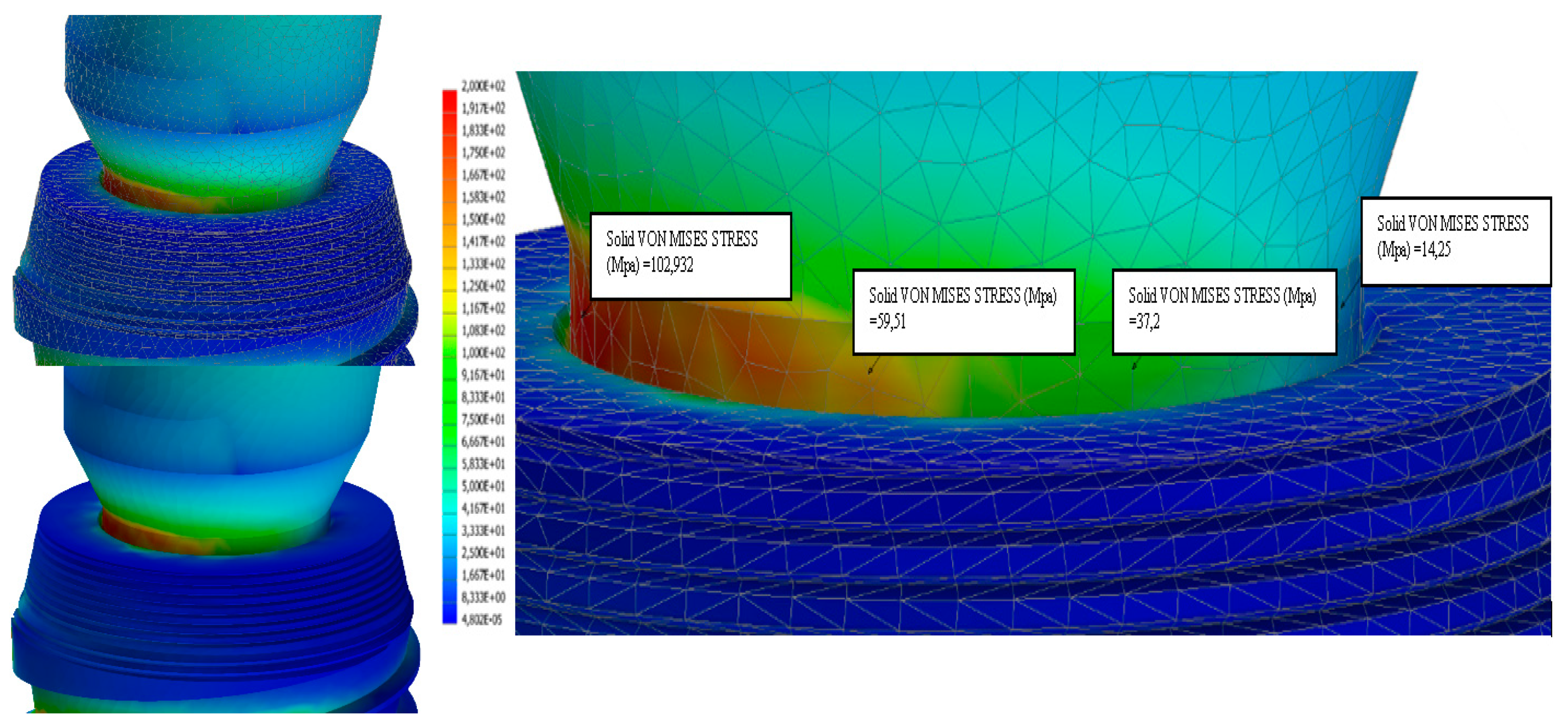
3. Results
4. Discussion
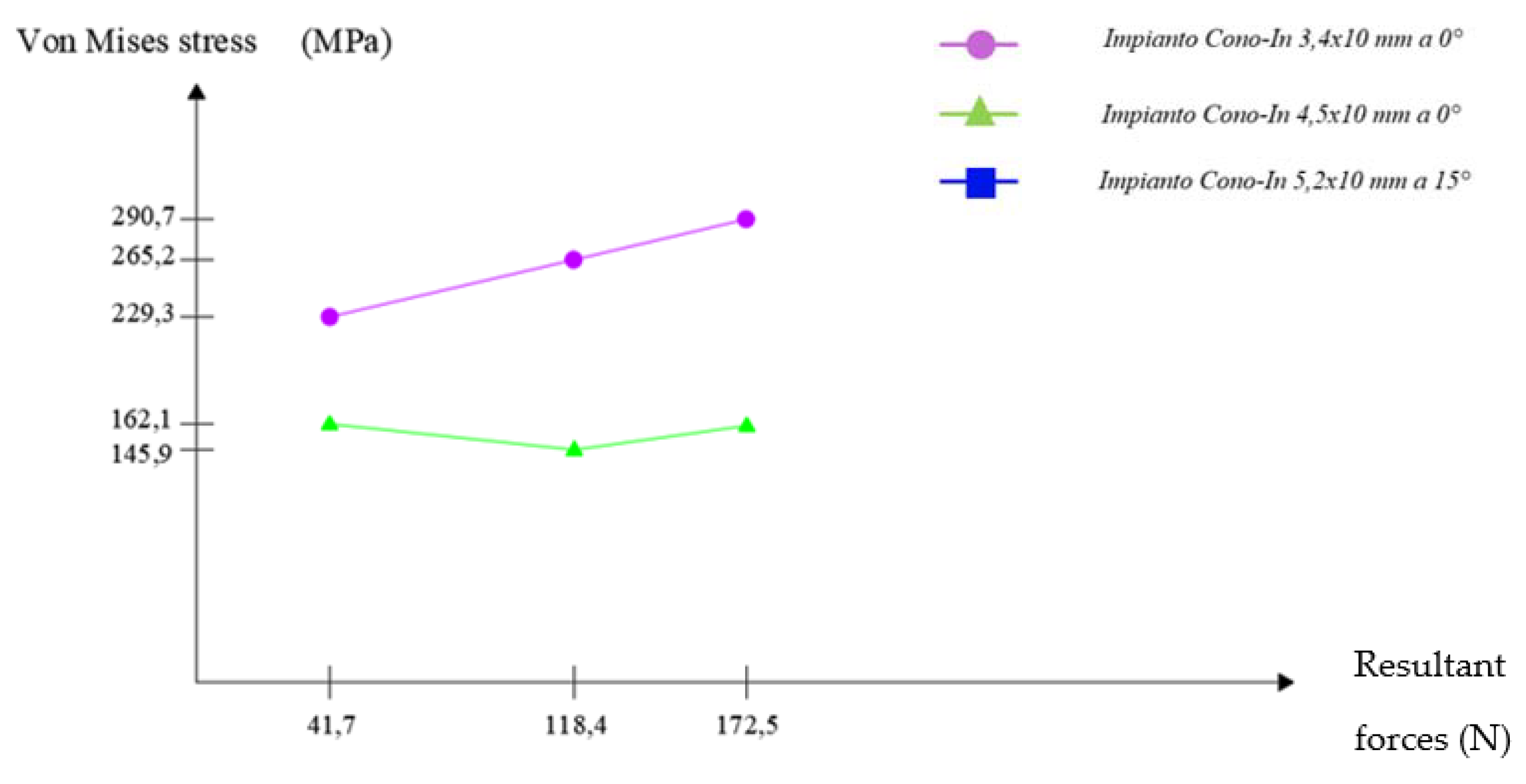
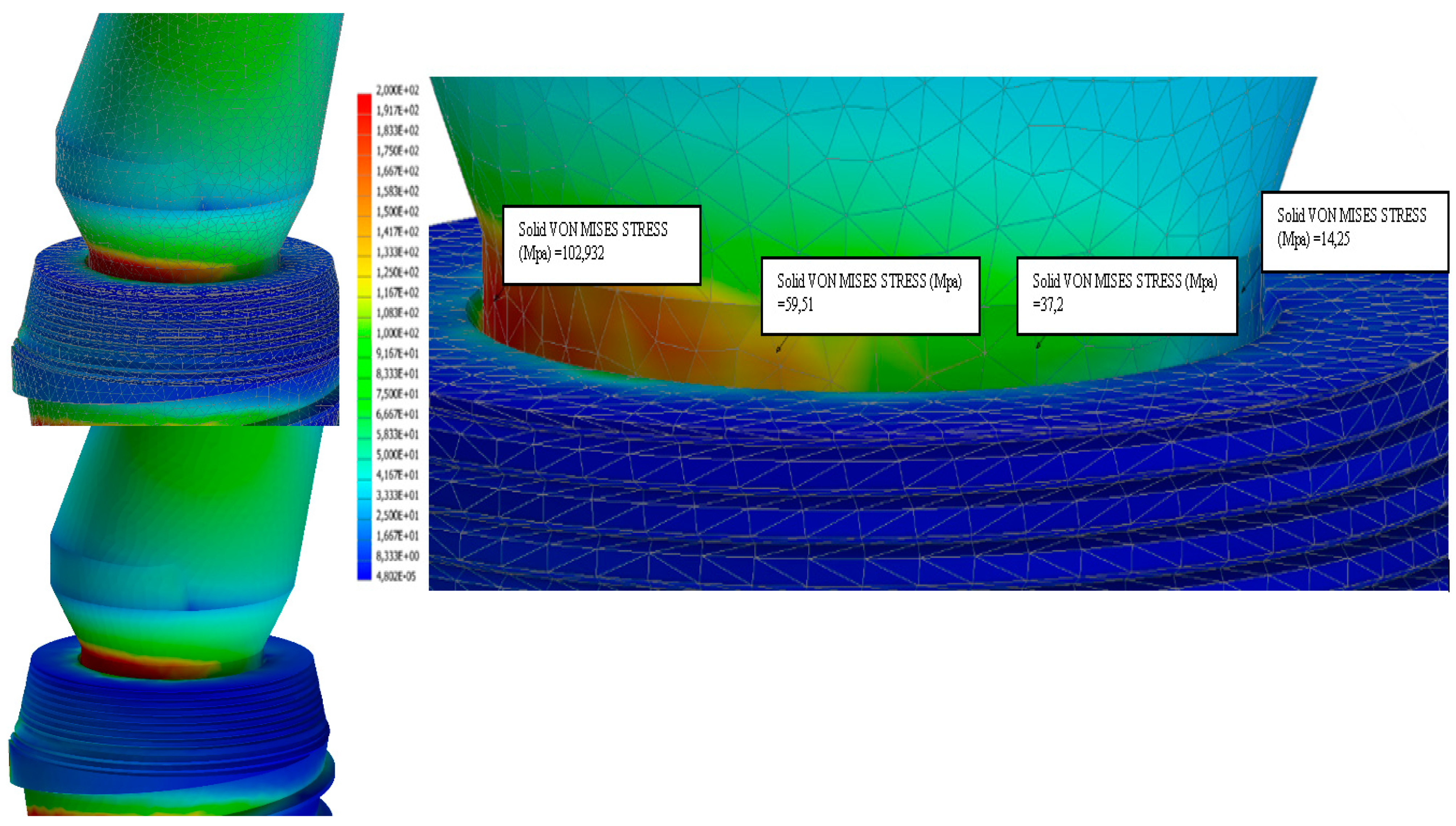
- For an occlusal force of 100 N stress → range in MPa (7, 46);
- For an occlusal force of 200 N → stress range in MPa (15, 103);
- For an occlusal force of 300 N → stress range in MPa (20, 150).
5. Conclusions
- The 3.4 mm Cono-in system was more stressed by large occlusal forces in the peri-crestal area with a much lower stress distribution;
- The 5.2 mm implant resisted higher occlusal loads than the first one thanks to its more consistent geometry; but, in the peri-crestal area, it had values and distributions of the most important stresses due to the inclination of the abutment, which needs more attention;
- An inclined load leads to an increase in stress in the abutment–implant connection area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quaresma, S.E.T.; Cury, P.R.; Sendyk, W.R.; Sendyk, C. A Finite Element Analysis of Two Different Dental Implants: Stress Distribution in the Prosthesis, Abutment, Implant, and Supporting Bone. J. Oral Implantol. 2008, 34, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Heo, S.-J.; Koak, J.-Y.; Kim, S.-K. Mechanical complications of implant-supported restorations with internal conical connection implants: A 14-year retrospective study. J. Prosthet. Dent. 2021. ahead-of-print. [Google Scholar] [CrossRef] [PubMed]
- Kunavisarut, C.; Lang, L.A.; Stoner, B.R.; Felton, D.A. Finite element analysis on dental implant-supported prostheses without passive fit. J. Prosthodont. 2002, 11, 30–40. [Google Scholar] [CrossRef] [PubMed]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall: Upper Saddle River, NJ, USA, 1996; Chapter 4; pp. 148–377. [Google Scholar]
- Gultekin, B.A.; Gultekin, P.; Yalcin, S. Finite Element Analysis—New Trends and Developments, 1st ed.; Sciyo: Rijeka, Croatia; IntechOpen: London, UK, 2012. [Google Scholar]
- Chen, L. Finite Element Analysis-New Trends and Developments; Ebrahimi, F., Ed.; IntechOpen Ltd.: London, UK, 2012; ISBN 978-953-51-0769-9. [Google Scholar]
- Danza, M.; Zollino, I.; Paracchini, L.; Riccardo, G.; Fanali, S.; Carinci, F. 3D finite element analysis to detect stress distribution: Spiral family implants. Maxillofac. Oral Surg. 2009, 8, 334–339. [Google Scholar] [CrossRef]
- Cho, S.Y.; Huh, Y.H.; Park, C.J.; Cho, L.R. Three-Dimensional Finite Element Analysis on stress distribution of internal Implant-Abutment engagement features. Int. J. Oral Maxillofac. Implants 2018, 33, 319–327. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, S.; Choi, H.; Woo, D.; Park, Y.B.; Shim, J.S.; Kim, H.S.; Lee, K.W. A three-dimensional Finite Element Analysis of short Dental Implants in the posterior maxilla. Int. J. Oral Maxillofac. Implants 2014, 29, e155–e164. [Google Scholar] [CrossRef]
- Kharsan, V.; Bandgar, V.; Mirza, A.; Jagtiani, K.; Dhariwal, N.; Kore, R. Comparative Evaluation of three abutment-implant interfeces on stress distribution in and around different implant systems: A Finite Element Analysis. Contemp. Clin. Dent. 2019, 10, 590–594. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Muraru, L.; Júnior, E.M.; Vaz, L.G.; Sloten, J.V.; Duyck, J.; Jaecques, S.V.N. Influence of Implant Connection Type on the Biomechanical Environment of Immediately Placed Implants—CT-Based Nonlinear, Three-Dimensional Finite Element Analysis. Clin. Implant Dent. Relat. Res. 2010, 12, 219–234. [Google Scholar] [CrossRef]
- Yalçin, M.; Kaya, B.; Laçin, N.; Ari, E. Three-Dimensional Finite element analysis of the effect of endosteal implants with different maco designs on stress distribution in different bone qualities. Int. J. Oral Maxillofac. Implants 2019, 34, 43–50. [Google Scholar] [CrossRef]
- Yenigun, S.; Ercal, P.; Ozden-Yenigun, E.; Katiboglu, A.B. Influence of Abutment design on stress distribution in narrow implants with marginal bone loss: A Finite Element Analysis. Int. J. Oral Maxillofac. Implants 2021, 36, 640–649. [Google Scholar] [CrossRef]
- Unsal, G.S. Three-Dimensional Finite Element Analysis of Different implant configurations in Enlarged first molar areas. Int. J. Oral. Maxillofac. Implants 2020, 35, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Doganay, O.; Kilic, E. Comparative Finite Element Analysis of short implants with different treatment approaches in the atrophic mandible. Int. J. Oral Maxillofac. Implants 2020, 35, e69–e76. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.C. Static and Dynamic Stress Analysis of Standard- and Narrow-Diameter Implants: A 3D Finite Element Analysis. Int. J. Oral Maxillofac. Implants 2020, 35, e58–e68. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, L.; Cicciù, M.; D’Amico, C.; Mauceri, R.; Oteri, G.; Cervino, G. Finite Element Method and Von Mises Investigation on Bone Response to Dynamic Stress with a Novel Conical Dental Implant Connection. Hindawi BioMed Res. Int. 2020, 2020, 2976067. [Google Scholar] [CrossRef]
- Akça, K.; Cehreli, M.C.; Iplikçioğlu, H. Evaluation of the mechanical characteristics of the implant-abutment complex of a reduced-diameter morse-taper implant, A nonlinear finite element stress analysis. Clin. Oral. Implants Res. 2003, 14, 444–454. [Google Scholar] [CrossRef]
- Formiga, M. Evaluation Using FEM on the Stress Distribution on the Implant, Prosthetic Components and Crown, with Cone Morse, External and Internal Hexagon Connections. Dent. Press Implantol. 2013, 7, 67–75. [Google Scholar]
- Cho, S.Y.; Huh, Y.H.; Park, C.J.; Cho, L.R. Three-Dimensional Finite Element Analysis of the stress distribution at the internal Implant-Abutment connection. Int. J. Periodontics Restor. Dent. 2016, 36, 49–58. [Google Scholar] [CrossRef]
- Maslucan, R.A.; Dominguez, J.A. A Finite Element Stress Analysis of a Conical Triangular Connection in Implants: A New Proposal. Materials 2022, 15, 3680. [Google Scholar] [CrossRef]
- Dantas de Moraes, S.L.; Verri, F.R.; Santiago Júnior, J.F.; Augusto de Faria Almeida, D.; Lemos, C.A.A.; Marcela de Luna Gomes, J.; Pellizzer, E.P. Three-dimensional Finite Element Analysis of varying diameter and connection type in implants with high crown-implant ratio. Braz. Dent. J. 2018, 29, 36–42. [Google Scholar] [CrossRef]
- Faria Almeida, D.A.; Pellizzer, E.P.; Verri, F.R.; Santiago, J.F., Jr.; Carvalho, P.S. Influence of tapered and external hexagon connections on bone stresses around tilted dental implants: Three-dimensional finite element method with statistical analysis. J. Periodontol. 2014, 85, 261–269. [Google Scholar] [CrossRef]
- Santiago Júnior, J.S.; Verri, F.R.; Almeida, D.A.; Souza Batista, V.E.; Lemos, C.A.; Pellizzer, E.P. Finite element analysis on influence of implant surface treatments, connection and bone types. Mater. Sci. Eng. C Mater. Biol. Appl. 2016, 63, 292–300. [Google Scholar] [CrossRef] [PubMed]
- Merz, B.R.; Hunenbart, S.; Belser, U.C. Mechanics of the implant-abutment connection: An 8-degree taper compared to a butt joint connection. Int. J. Oral Maxillofac. Implants 2000, 15, 519–526. [Google Scholar] [PubMed]
- Brunski, J.B. Biomechanical factors affecting the bone dental implant interface. Clin. Mater. 1992, 10, 153–201. [Google Scholar] [CrossRef] [PubMed]
- Geris, L.; Andreykiv, A.; Van Oosterwyck, H.; Vander Stolen, J.; van Keulen, F.; Duyck, J.; Naert, I. Numerical simulation of tissue differentiation around loaded titanium implants in a bone chamber. J. Biomech. 2004, 37, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Vandamme, K.; Naert, I.; Geris, L.; Vander Sloten, J.; Puers, R.; Duyck, J. The effect of micromotion on the tissue response Influence of Implant-Abutment Connection on the Biomechanical Behavior of Implants 233 around immediately loaded roughened titanium implants in the rabbit. Eur. J. Oral Sci. 2007, 115, 21–29. [Google Scholar] [CrossRef]
- Canay, S.; Akça, K. Biomechanical aspects of bone-level diameter shifting at implant-abutment interface. Implant Dent. 2009, 18, 239–248. [Google Scholar] [CrossRef]
- Albrektsson, T.; Zarb, G.; Worthington, P.; Eriksson, A.R. The long-term efficacy of currently used dental implants: A review and proposed criteria of success. Int. J. Oral Maxillofac. Implants 1986, 1, 11–25. [Google Scholar] [PubMed]
- Laster, Z.; Weissberg, I.; Kablan, F. Biomechanics and Peri-implantisis: The effect of a subcrestal wing-thread to decrease alveolar crestal bone strain. Theory, Finite Element Analysis, and Clinical Application. Int. J. Oral Maxillofac. Implants 2014, 29, e265–e271. [Google Scholar] [CrossRef]
- Li, T.; Kong, L.; Wang, Y.; Hu, K.; Song, L.; Liu, B.; Li, D.; Shao, J.; Ding, Y. Selection of optimal dental implant diameter and length in type IV bone: A three-dimensional finite element analysis. Int. J. Oral Maxillofac. Surg. 2009, 38, 1077–1083. [Google Scholar] [CrossRef]
- Brånemark, P.-I.; Adell, R.; Breine, U.; Hansson, B.O.; Lindström, J.; Ohlsson, Å. Laboratory ofLaboratory of Experimental Biology, Department of Anatomy, University of Gothenburg and the Department of Plastic Surgery, Sahlgrenska Sjukhuset, Gothenburg, Sweden Intra-osseous anchorage of dental prostheses. I. Experimental studies. Scand. J. Plast. Reconstr. Surg. 1969, 3, 81–100. [Google Scholar] [CrossRef]
- Schroeder, A.; Pohler, O.; Sutter, F. Tissue reaction to an implant of a titanium hollow cylinder with a titanium surface spray layer. SSO Scweiz. Monatsschr. Zahnheilkd. 1976, 8, 713–727. [Google Scholar]
- Cervino, G.; Romeo, U.; Lauritano, F.; Bramant, E.; Fiorillo, L.; D’Amico, C.; Milone, D.; Laino, L.; Campolongo, F.; Rapisarda, S.; et al. FEM and Von Mises Analysis of OSSTEM Dental Implant Structural Comoonents: Evalutation of Different Direction Dynamic Loads. Open Dent. J. 2018, 12, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Abuhussein, H.; Pagni, G.; Rebaudi, A.; Wang, H.L. The effect of thread pattern upon implant osseointegration. Clin. Oral Implants Res. 2010, 21, 129–136. [Google Scholar] [CrossRef] [PubMed]
- Roberts, W.E.; Viecilli, R.F.; Chang, C.; Katona, T.R.; Paydar, N.H. Biology of biomechanics: Finite element analysis of a statically determinate system to rotate the occlusal plane for correction of a skeletal Class III open-bite malocclusion. Am. J. Orthod. Dentofac. Orthop. 2015, 148, 943–955. [Google Scholar] [CrossRef] [PubMed]
- Ueda, N.; Takayama, Y.; Yokoyama, A. Minimization of dental implant diameter and length according to bone quality determined by finite element analysis and optimized calculation. J. Prosthodont. 2016, 379, 324–332. [Google Scholar] [CrossRef]
- Al-Zordk, W.; Ghazy, M.; El-Anwar, M. Stress Analysis Around Reduced-Diameter Zirconia and Titanium One-Piece Implants with and without microthreads in the neck: Experimental and Finite Element Analysis. Int. J. Oral Maxillofac. Implants 2020, 35, 305–312. [Google Scholar] [CrossRef]
- Duyck, J.; Ronald, H.J.; Van Oosterwyck, H.; Naert, I.; Vander Sloten, J.; Ellingsen, J.E. The influence of static an dynamic loading on marginal bone reactions around osseointegrated implants: An animal experimental study. Clin. Oral Implants Res. 2001, 12, 207–218. [Google Scholar] [CrossRef]
- Isidor, F. Loss of osseointegration caused by occlusal load of oral implants. A clinical and radiographic study in monkeys. Clin. Oral Implants Res. 1996, 7, 143–152. [Google Scholar] [CrossRef]
- Can Sivrikaya, E.C.; Omezli, M.M. The Effect of Tapered and Cylindrical Implants on Stress Distribution In Different Bone Qualities: A Finite Element Analysis. Int. J. Oral Maxillofac. Implants 2019, 34, e99–e105. [Google Scholar] [CrossRef]
- Roberts, W.E.; Smith, R.K.; Zilberman, Y.; Mozsary, P.G.; Smith, R.S. Osseous adaption to continuous loading of rigid endosseous implants. Am. J. Orthod. 1984, 86, 95–111. [Google Scholar] [CrossRef]



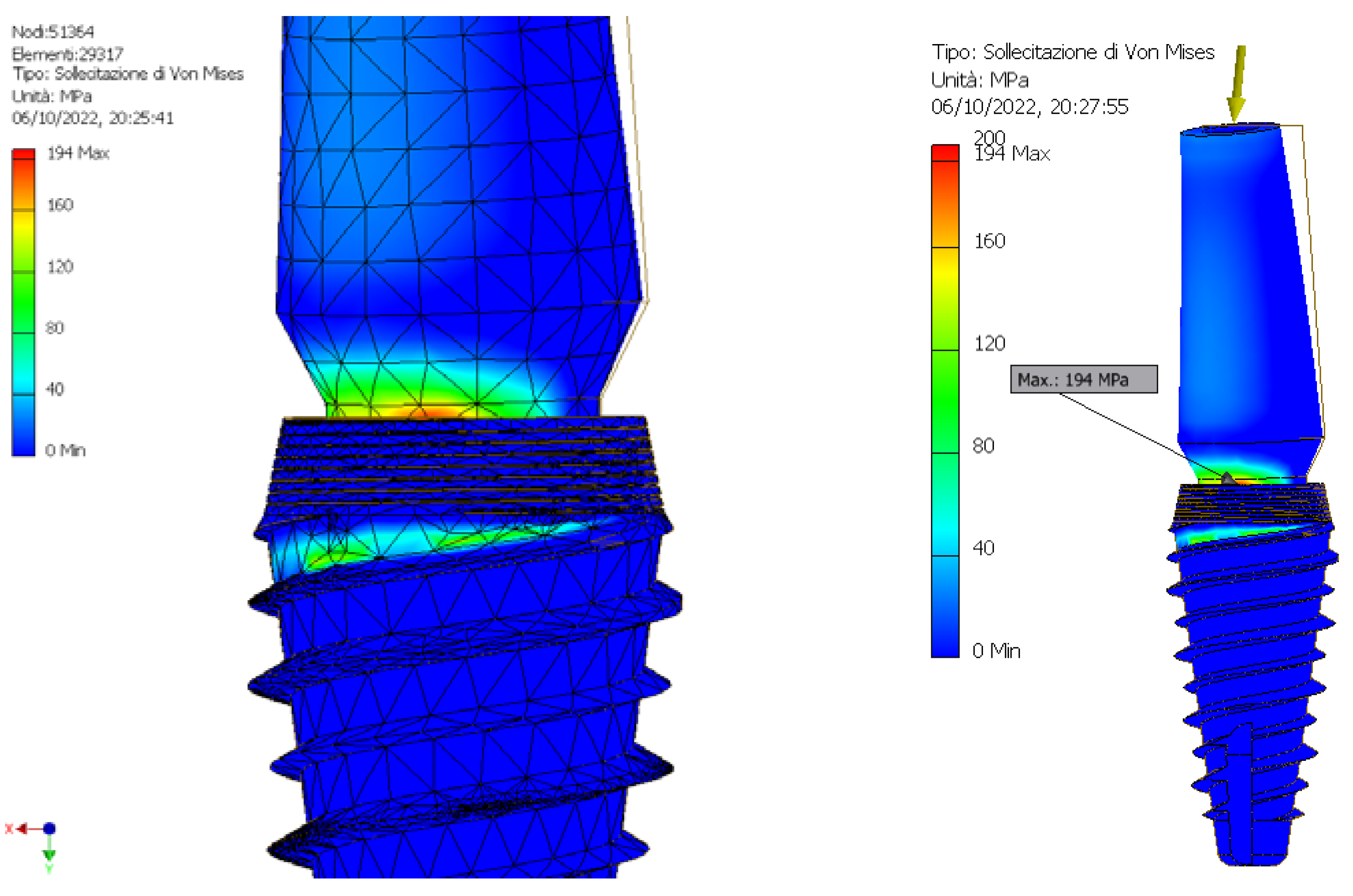
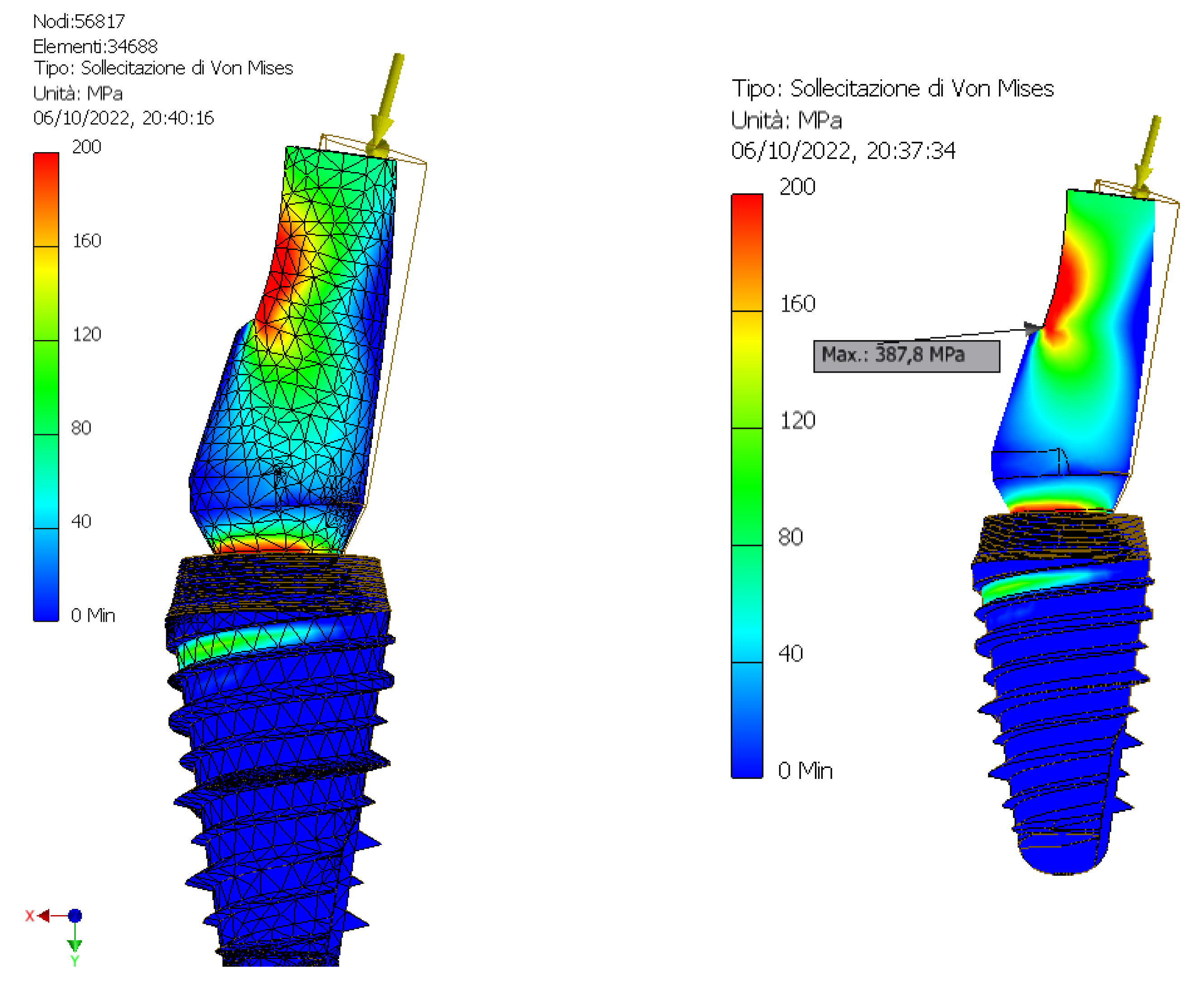
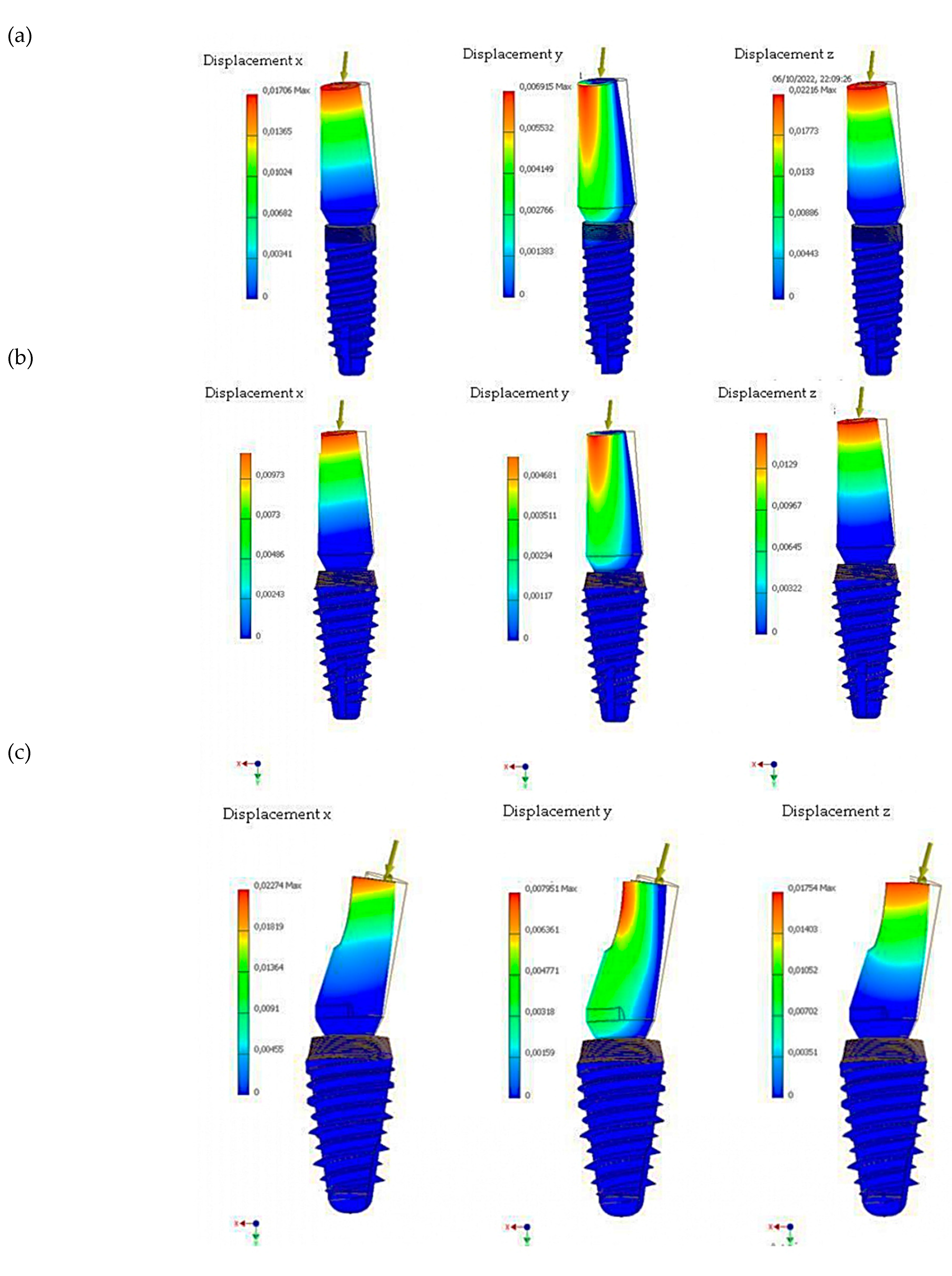




| Maximum Von Mises Stress (MPa) | ||||||||||
| Cono-In 3.4; abutment 0° | Cono-In 4.5; abutment 0° | Cono-In 5.2; abutment 15° | ||||||||
| Mesh 0.1 mm | Mesh 0.08 mm | Mesh 0.05 mm | Mesh 0.1 mm | Mesh 0.08 mm | Mesh 0.05 mm | Mesh 0.1 mm | Mesh 0.08 mm | Mesh 0.05 mm | ||
| Magnitude Strength (N) | 502.8 | 249.1 | 290.7 | 260.7 | 154.4 | 161 | 194 | 394 | 366.7 | 387.8 |
| 402.9 | 335.9 | 296.1 | 239.1 | |||||||
| 172.5 | 293 | 338.5 | 239.1 | |||||||
| 122.5 | ||||||||||
| 118.4 | 23.7 | 265.2 | 241.6 | 143.4 | 145.9 | 179.9 | ||||
| 41.7 | 202.8 | 229.3 | 206.5 | 131.6 | 162.1 | 158.1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Callea, C.; Ceddia, M.; Piattelli, A.; Specchiulli, A.; Trentadue, B. Finite Element Analysis (FEA) for a Different Type of Cono-in Dental Implant. Appl. Sci. 2023, 13, 5313. https://doi.org/10.3390/app13095313
Callea C, Ceddia M, Piattelli A, Specchiulli A, Trentadue B. Finite Element Analysis (FEA) for a Different Type of Cono-in Dental Implant. Applied Sciences. 2023; 13(9):5313. https://doi.org/10.3390/app13095313
Chicago/Turabian StyleCallea, Caterina, Mario Ceddia, Adriano Piattelli, Alessandro Specchiulli, and Bartolomeo Trentadue. 2023. "Finite Element Analysis (FEA) for a Different Type of Cono-in Dental Implant" Applied Sciences 13, no. 9: 5313. https://doi.org/10.3390/app13095313
APA StyleCallea, C., Ceddia, M., Piattelli, A., Specchiulli, A., & Trentadue, B. (2023). Finite Element Analysis (FEA) for a Different Type of Cono-in Dental Implant. Applied Sciences, 13(9), 5313. https://doi.org/10.3390/app13095313






