Experimental Investigation on Structural Performance Enhancement of Brick Masonry Member by Internal Reinforcement
Abstract
1. Introduction
2. Experimental Program
2.1. Material Properties
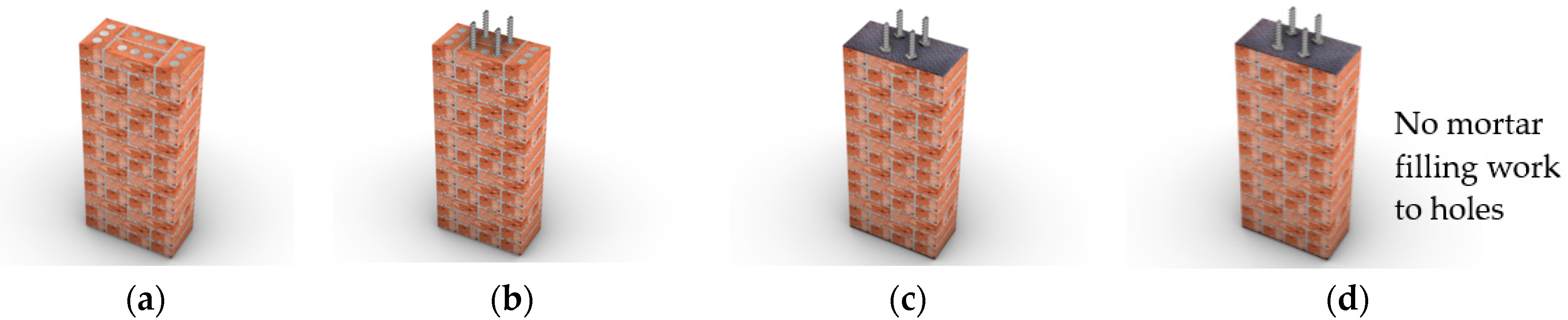
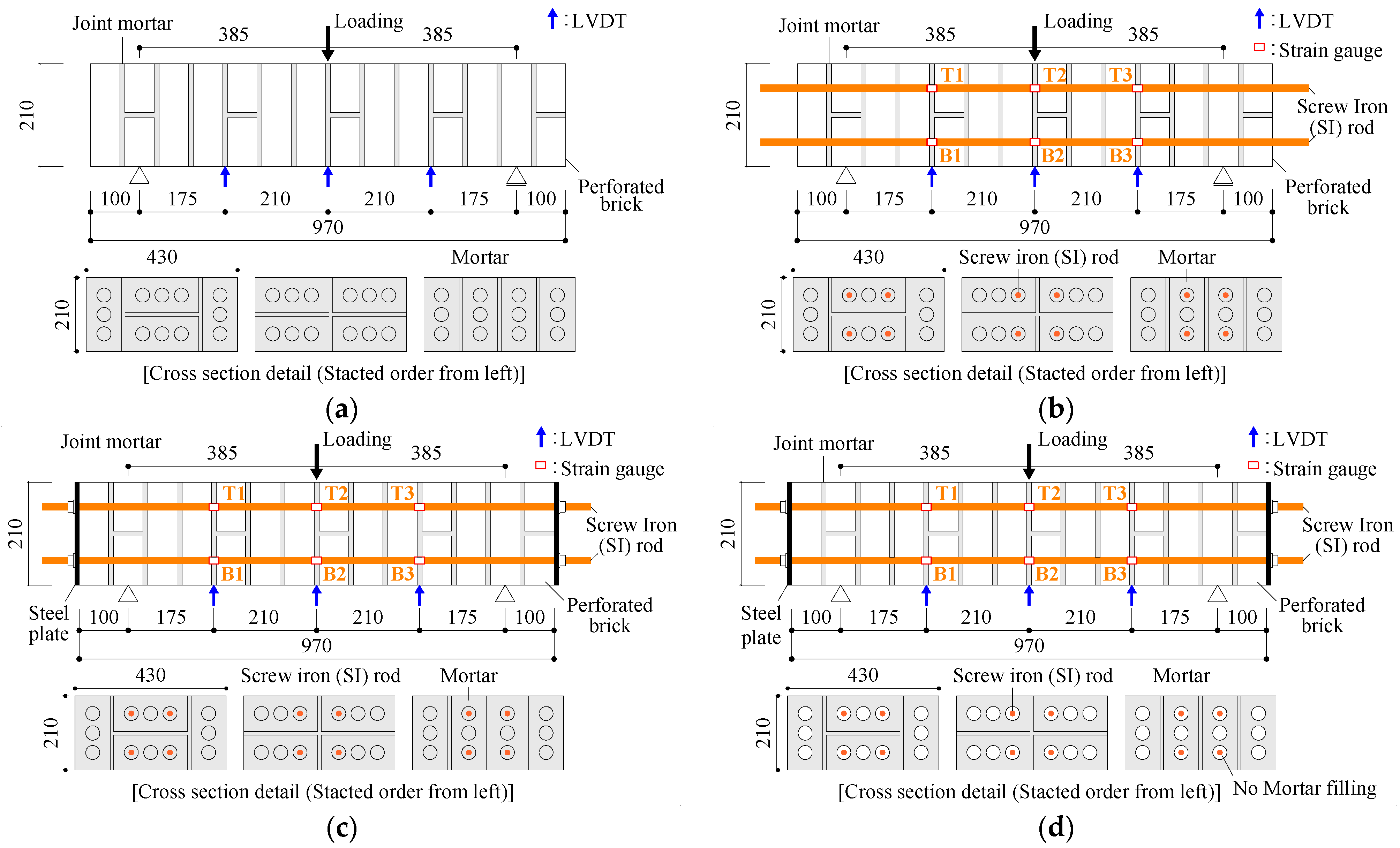
2.2. Specimen and Experiment Outline
3. Experiment Results
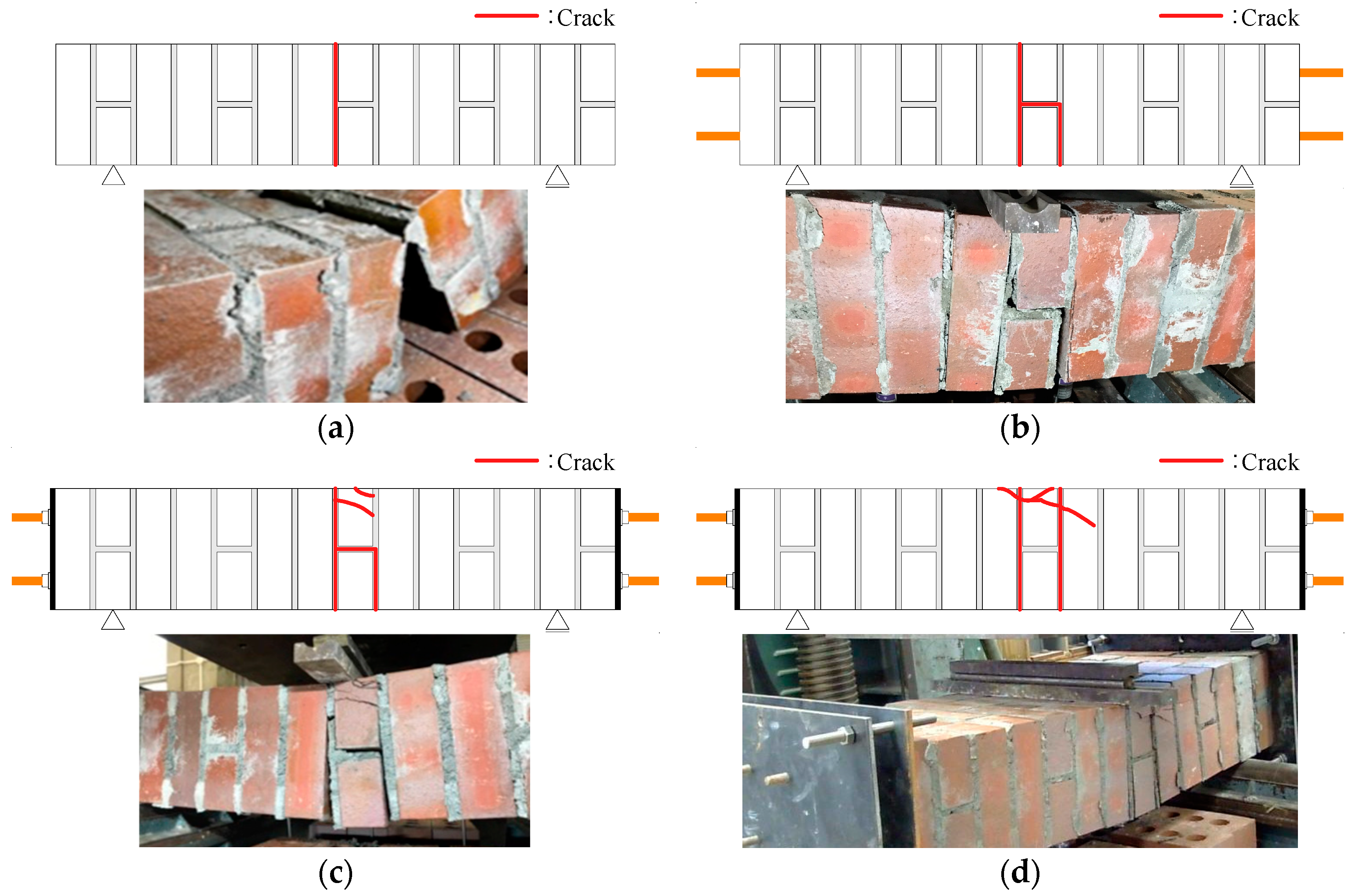
3.1. UBM (Unreinforced Brick Member)
3.2. IRBM (Internally Reinforced Brick Member)
3.3. IRBM—F (Internally Reinforced Brick Member Fixed by Nut)
3.4. IRBM—FNM (Internally Reinforced Brick Member Fixed by Nut with No Inside Mortar)
4. Discussion
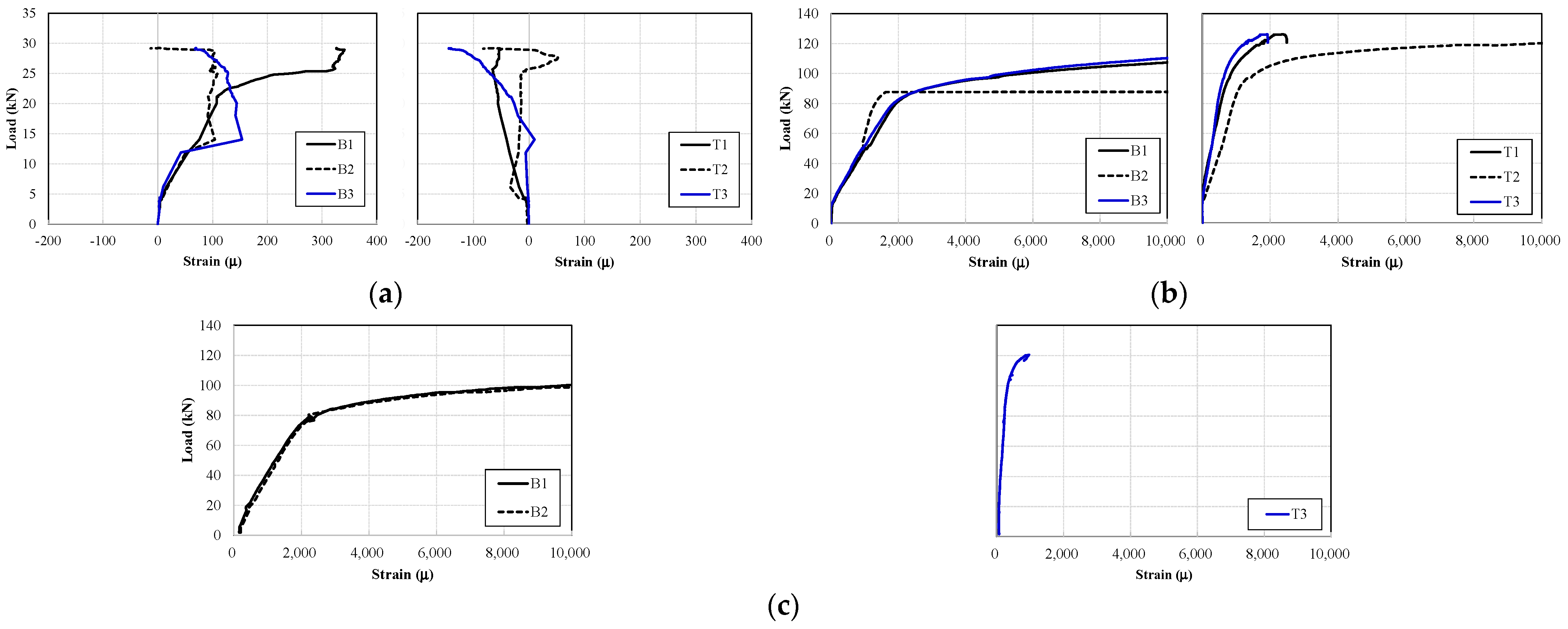
4.1. Bond Stress between Mortar and Reinforcing Rod
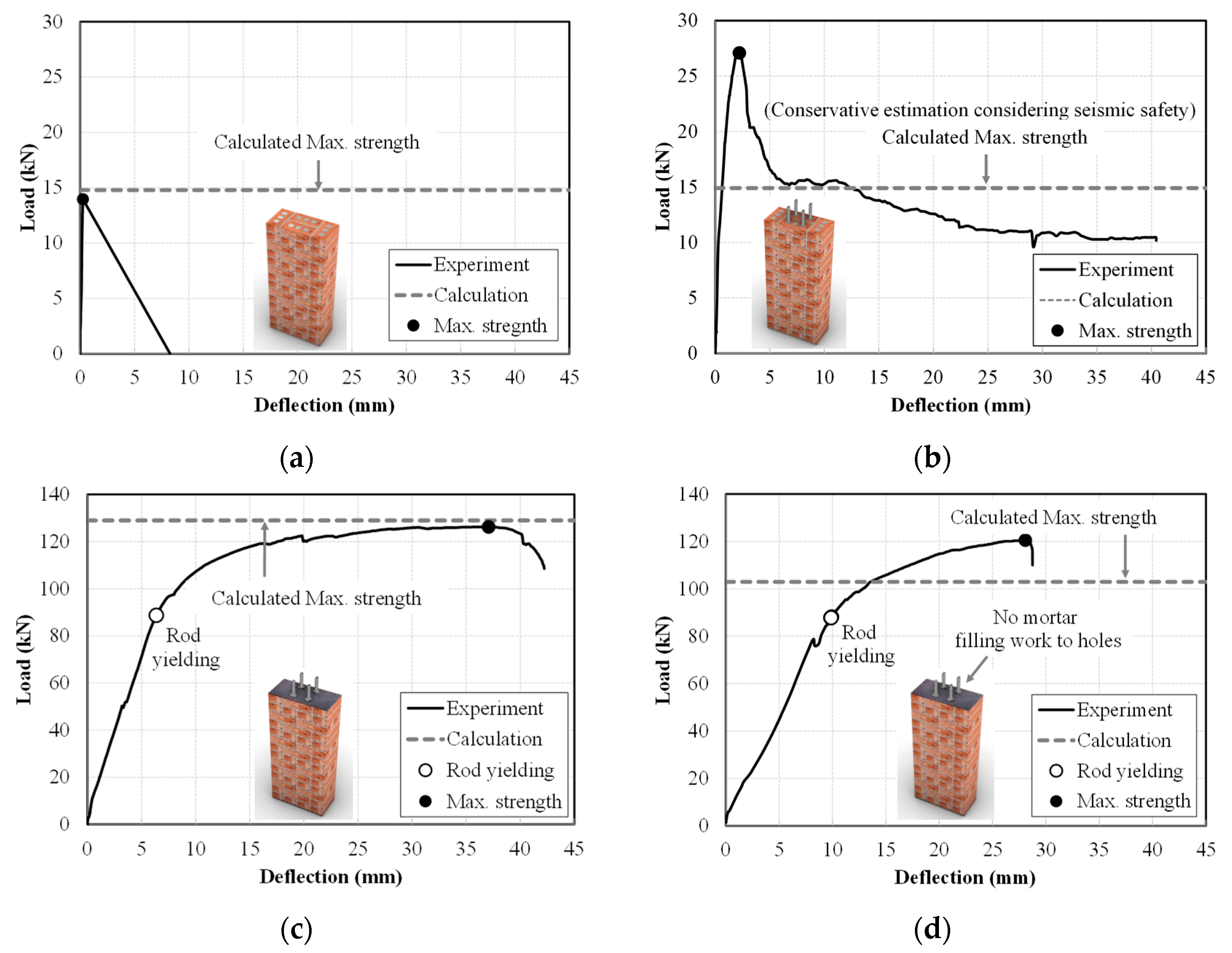
4.2. Maximum Strength Evaluation
4.2.1. UBM (Unreinforced Brick Member)
4.2.2. IRBM (Internally Reinforced Brick Member)
4.2.3. IRBM—F (Internally Reinforced Brick Member Fixed by Nut)
4.2.4. IRBM—FNM (Internally Reinforced Brick Member Fixed by Nut with No Filling Mortar)
5. Conclusions
- In UBM without any reinforcement, an abrupt strength decrease occurred right after a flexural crack development, showing a load–deflection relationship with a poor deformation capacity. The failure deflection angle was only 0.068%.
- In IRBM with SI rods, complete bonding deterioration occurred before the maximum strength and expected reinforcing effect could not be obtained. However, the maximum strength was two times that of UBM, and a stable residual strength could be maintained even after the maximum strength declined due to the bending resistances of the rods. SI rods not only increased the maximum strength but also provided better deformation capacities.
- In IRBM—F, the SI rods fixed by steel plates and nuts provided robust integrities with the brick members and greatly enhanced the structural performance. The maximum strength was demonstrated by more than nine times that of UBM and by more than four times that of IRBM. Moreover, the strength degradation did not occur by an extremely large deformation angle of 1/10. The SI rods were efficiently utilized, and the effectiveness of the proposed material and method was verified.
- In IRBM—FNM, the mortar filling work was eliminated for better workability as well as cost and material savings. Even in this case, the load–deformation curve was found to be almost the same as IRBM—F. Although sudden strength degradations occurred after the maximum strength, they were found at the large deformation angle of 1/15, and efficient use of the internal reinforcements was also achieved.
- A maximum strength evaluation was carried out, and the calculation results reasonably agreed with the experimental values. The ratios of the calculations to the experiments of maximum strength were between 0.85 and 1.03 in UBM, IRBM—F, and IRBM—FNM. The ratio was somewhat small in IRBM, but conservative estimation could be performed considering seismic safety.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meguro & Numada Lab of the University of Tokyo. Available online: http://risk-mg.iis.u-tokyo.ac.jp/index.html (accessed on 1 April 2023).
- Holmes, M. Steel frames with brickwork and concrete infilling. Proc. Inst. Civ. Eng. 1961, 19, 473–478. [Google Scholar] [CrossRef]
- Smith, S.B. Lateral stiffness of infilled frames. J. Struct. Div. 1962, 88, 183–199. [Google Scholar] [CrossRef]
- Smith, S.B. Behaviour of the square infilled frames. J. Struct. Div. 1966, 92, 381–403. [Google Scholar] [CrossRef]
- Smith, S.B.; Carter, C. A method of analysis for infill frames. Proc. Inst. Civ. Eng. 1969, 44, 31–48. [Google Scholar]
- Mainstone, R.J. On the stiffness and strength of infilled frames. Proc. Inst. Civ. Eng. 1971, 44, 57–90. [Google Scholar]
- Hendry, A.W. Structural Masonry; Macmillan: London, UK, 1998. [Google Scholar]
- Applied Technology Council (ATC). Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings; FEMA 306: Redwood City, CA, USA, 1998. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1992; pp. 584–592. [Google Scholar]
- Shing, P.B.; Mehrabi, A.B. Behaviour and analysis of masonry-infilled frames. Prog. Struct. Eng. Mater. 2002, 4, 320–331. [Google Scholar] [CrossRef]
- Cavaleri, L.; Trapani, F.D. Prediction of the additional shear action on frame memebers due to infills. Bull. Earthq. Eng. 2015, 13, 1425–1454. [Google Scholar] [CrossRef]
- Jin, K.; Choi, H.; Nakano, Y. Experimental Study on Lateral Strength Evaluation of Unreinforced Masonry-Infilled RC Frame. Earthq. Spectra 2016, 32, 1725–1747. [Google Scholar] [CrossRef]
- Mohammad, A.F.; Faggella, M.; Gigliotti, R.; Spacone, E. Seismic performance of older R/C frame structures accounting for infills-induced shear failure of columns. Eng. Struct. 2016, 122, 1–13. [Google Scholar] [CrossRef]
- Suzuki, T.; Choi, H.; Sanada, Y.; Nakano, Y.; Matsukawa, K.; Paul, D.; Gulkan, P.; Binici, B. Experimental evaluation of the in-plane behaviour of masonry wall infilled RC frames. Bull. Earthq. Eng. 2017, 15, 4245–4267. [Google Scholar] [CrossRef]
- Milanesi, R.R.; Morandi, P.; Magenes, G. Local effects on RC frames induced by AAC masonry infills through FEM simulation of in-plane tests. Bull. Earthq. Eng. 2018, 16, 4053–4080. [Google Scholar] [CrossRef]
- Alwashali, H.; Sen, D.; Jin, K.; Maeda, M. Experimental investigation of influences of several parameters on seismic capacity of masonry infilled reinforced concrete frame. Eng. Struct. 2019, 189, 11–24. [Google Scholar] [CrossRef]
- Applied Technology Council (ATC). Prestandard and Commentary for the Seismic Rehabilitation of Buildings; FEMA 356: Reston, VA, USA, 2000. [Google Scholar]
- American Society of Civil Engineers. Seismic Rehabilitation of Existing Buildings; ASCE Publications [ASCE/SEI 41-06]: New York, NY, USA, 2007. [Google Scholar]
- Stavridis, A.; Shing, B. Simplified modeling of masonry-infilled RC frames subjected to seismic loads. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Jin, K.; Choi, H. A simplified evaluation method of skeleton curve for RC frame with URM infill. Earthq. Struct. 2017, 13, 309–322. [Google Scholar]
- Alwashali, H.; Torihata, Y.; Jin, K.; Maeda, M. Experimental observations on the inplane behaviour of masonry wall infilled RC frames; focusing on deformation limits and backbone curve. Bull. Earthq. Eng. 2018, 16, 1373–1397. [Google Scholar] [CrossRef]
- Akhoundi, F.; Vasconcelos, G.; Lourenco, P.; Silva, L.C. Out-of-Plane Response of Masonry Infilled RC Frames: Effect of Workmanship and Opening. In Proceedings of the 16th International Brick and Block Masonry Conference, Padova, Italy, 26–30 June 2016. [Google Scholar]
- Dizhur, D.; Walsh, K.; Giongo, I.; Derakhshan, H.; Ingham, J. Out-of-Plane Proof Testing of Masonry Infill Walls. Structures 2018, 15, 244–258. [Google Scholar] [CrossRef]
- Petrone, C.; Magliulo, G.; Manfredi, G. Shake Table Tests for the Seismic Assessment of Hollow Brick Internal Partitions. Eng. Struct. 2014, 72, 203–214. [Google Scholar] [CrossRef]
- Yu, J.H.; Park, J.H. Investigation of Steel Fiber-Reinforced Mortar Overlay for Strengthening Masonry Walls by Prism Tests. Appl. Sci. 2020, 10, 6395. [Google Scholar] [CrossRef]
- Karalar, M.; Özkılıç, Y.O.; Aksoylu, C.; Sabri, M.M.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban, E.M. Flexural behavior of reinforced concrete beams using waste marble powder towards application of sustainable concrete. Front. Mater. 2022, 9, 1068791. [Google Scholar] [CrossRef]
- Gilstrap, J.M.; Dolan, C.W. Out-of-plane bending of FRP-reinforced masonry walls. Compos. Sci. Technol. 1998, 58, 1277–1284. [Google Scholar] [CrossRef]
- Sonia, M.; Elio, S. Modeling of reinforced masonry elements. Int. J. Solids Struct. 2001, 38, 4177–4198. [Google Scholar]
- ElGawady, M.; Lestuzzi, P.; Badoux, M. A review of conventional seismic retrofitting techniques for URM. In Proceedings of the 13th International Brick and Block Masonry Conference, Amsterdam, The Netherlands, 4–7 July 2004. [Google Scholar]
- Seki, M.; Popa, V.; Lozinca, E.; Dutu, A.; Papurcu, A. Experimental Study on Retrofit Technologies for Rc Frames with Infilled Brick Masonry Walls in Developing Countries. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Gattesco, N.; Boem, I. Out-of-Plane Behavior of Reinforced Masonry Walls: Experimental and Numerical Study. Compos. Part B Eng. 2017, 128, 39–52. [Google Scholar] [CrossRef]
- Alwashali, H.; Sen, D.; Maeda, M.; Seki, M. Advantages and limitations of retrofitting masonry infilled RC Frames by Ferro-cement based on experimental observations. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 26 September–2 October 2020. [Google Scholar]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Impact of the Textile Mesh on the Efficiency of TRM Strengthening Solutions to Improve the Infill Walls Out-of-Plane Behaviour. Appl. Sci. 2020, 10, 8745. [Google Scholar] [CrossRef]
- Scamardo, M.; Cattaneo, S.; Biolzi, L.; Vafa, N. Parametric Analyses of the Response of Masonry Walls with Reinforced Plaster. Appl. Sci. 2022, 12, 5090. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Bridgeman, D.O. Seismic Resistance of Brick Masonry Walls. Bull. New Zealand Natl. Soc. Earthq. Eng. 1974, 7, 167–187. [Google Scholar] [CrossRef]
- Mayrhofer, C. Reinforced masonry walls under blast loading. Int. J. Mech. Sci. 2002, 44, 1067–1080. [Google Scholar] [CrossRef]
- Haach, V.G.; Vasconcelos, G.; Lourenco, P.B. Study of the behaviour of reinforced masonry wallets subjected to diagonal compression through numerical modeling. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Haile, F.; Corradi, M.; Adkins, J. Titanium rods with high mechanical properies were embedded into the horizontal mortar bed joint. In Proceedings of the Conservation of Architectural Heritage (CAH)—6th Edition, Sicily, Italy, 25–27 May 2022. [Google Scholar]
- Triantafillou, T.C.; Fardis, M.N. Strengthening of historic masonry structures with composite materials. Mater. Struct. 1997, 30, 486–496. [Google Scholar] [CrossRef]
- Ma, R.; Jiang, L.; He, M.; Fang, C.; Liang, F. Experimental investigations on masonry structures using external prestressing techniques for improving seismic performance. Eng. Struct. 2012, 42, 297–307. [Google Scholar] [CrossRef]
- Hwang, S.H.; Kim, S.; Yang, K.H. In-plane seismic performance of masonry wall retrofitted with prestressed steel-bar truss. Earthq. Struct. 2020, 19, 459–469. [Google Scholar]
- Baqi, A.; Bhandari, N.M.; Trikha, D.N. Experimental study of prestressed masonry flexural elements. J. Struct. Eng. 1999, 125, 245–254. [Google Scholar] [CrossRef]
- Phipps, M.E. Prestressed masonry. Prog. Struct. Eng. Mater. 2000, 2, 304–310. [Google Scholar] [CrossRef]
- Foti, D.; Monaco, P. Post-tensioned masonry: State of the art. Prog. Struct. Eng. Mater. 2000, 2, 311–318. [Google Scholar] [CrossRef]
- Wight, G.D.; Ingham, J.M.; Kowalsky, M.J. Shaketable testing of rectangular post-tensioned concrete masonry walls. ACI Struct. J. 2006, 103, 587. [Google Scholar]
- Yang, K.H.; Mun, J.H.; Hwan, S.H. Cyclic shear behavior of masonry walls strengthened with prestressed steel bars and glass fiber grids. Compos. Struct. 2020, 238, 111961. [Google Scholar] [CrossRef]
- ACI 530-02/ASCE 5-02/TMS 402-02; Building Code Requirements for Masonry Structures. Masonry Standards Joint Committee, 2002. Available online: https://engineering.purdue.edu/~ramirez/CE479/FALL05/MasonryBuildingCode1-3-02.pdf (accessed on 3 April 2023).
- TEK 14-20A; Post-Tensioned Concrete Masonry Wall Design. National Concrete Masonry Association (NCMA): Herndon, VA, USA, 2001.
- Jin, K.; Masuda, T.; Habara, Y.; Tomizawa, T. Structural Performance of Reinforced Masonry Member for Stilt House in Southeast Asia (Part 1: 3-Point Bending Test for unreinforced and reinforced masonry specimens). In Summaries of Technical Papers of Annual Meeting; Architectural Institute of Japan (AIJ): Hokkaido, Japan, 2022. (In Japanese) [Google Scholar]
- Jin, K.; Song, S.; Kitayama, K.; Hao, L. Detailed evaluation of the ultimate flexural states of beams in unbonded precast prestressed concrete frames. Bull. Earthq. Eng. 2019, 17, 1495–1519. [Google Scholar] [CrossRef]
- Jin, K.; Hao, L.; Kitayama, K. Direct evaluation method for load-deformation curve of precast prestressed concrete frame with different tendon forces. Bull. Earthq. Eng. 2021, 19, 3597–3626. [Google Scholar] [CrossRef]
- Jin, K.; Ota, R.; Hao, L.; Kitayama, K. Evaluation Method for Ultimate Flexural State of Prestressed Precast Reinforced Concrete Beam–Column Connection with Debonded Partial Tendon. Appl. Sci. 2023, 13, 2843. [Google Scholar] [CrossRef]
- Jin, K.; Kitayama, K.; Song, S.; Kanemoto, K. Shear Capacity of Precast Prestressed Concrete Beam-Column Joint Assembled by Unbonded Tendon. ACI Struct. J. 2017, 114, 51–62. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. AIJ Standard for Structural Calculation of Reinforced Concrete Structures; Architectural Institute of Japan (AIJ): Tokyo, Japan, 2018. [Google Scholar]




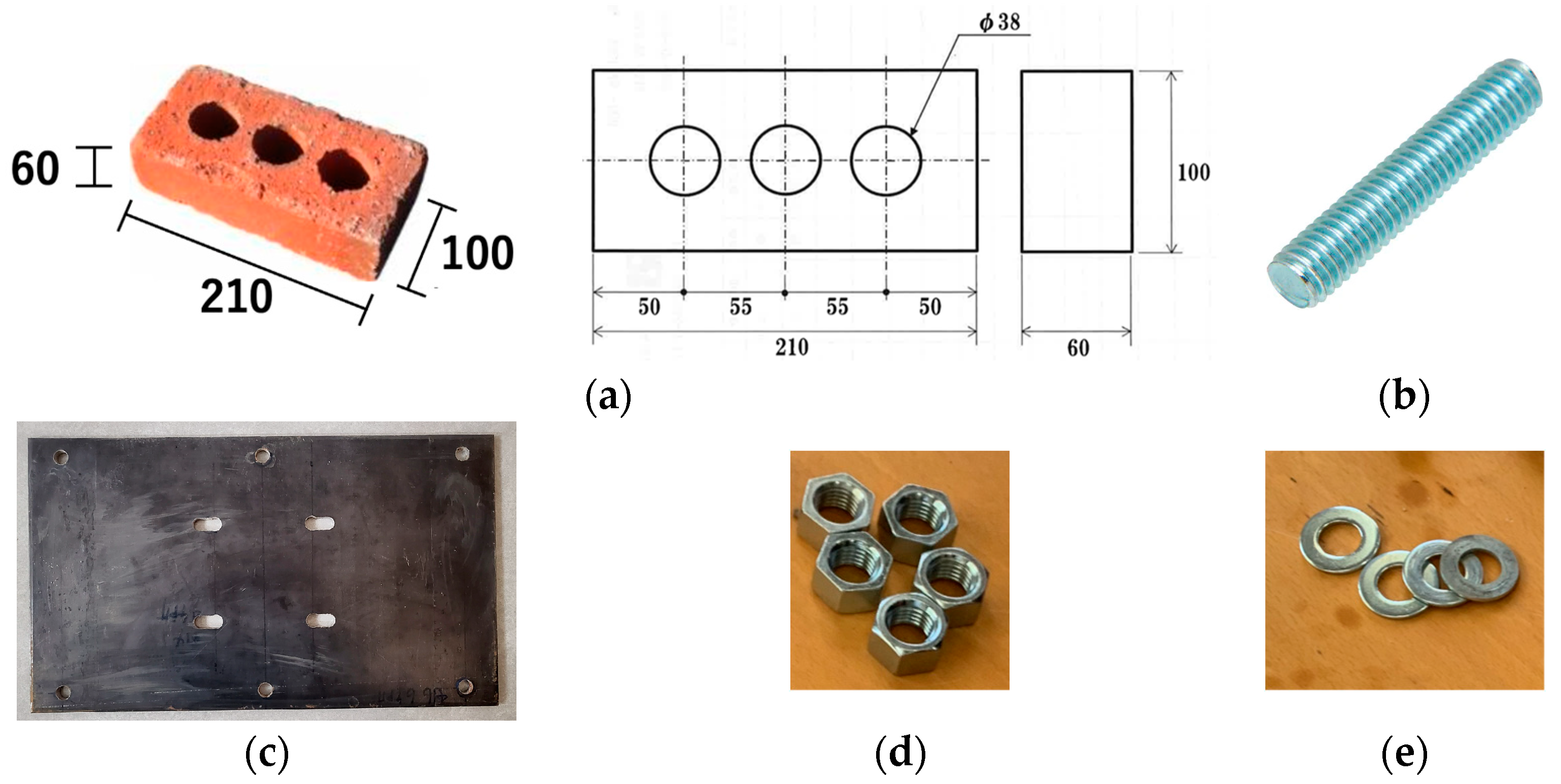



| Brick Unit | Mortar | |
|---|---|---|
| Compressive strength | 39.1 MPa | 15.1 MPa |
| Tensile strength σT | — | 0.9 MPa |
| Brick Prism without SI Rod | Brick Prism with SI Rod | |
|---|---|---|
| Compressive strength | 21.1 MPa | 23.0 MPa |
| Shear strength by push-out test | 0.7 MPa | 3.2 MPa |
| Yield Strength σy (MPa) *a | Yield Strain εy (μ) *a | Tensile Strength σt (MPa) |
|---|---|---|
| 446.9 MPa | 3833 μ | 537.4 MPa |
| Specimen | Qmax,cal (kN) | Qmax,exp (kN) | Qmax,cal /Qmax,exp |
|---|---|---|---|
| UBM | 14.84 | 13.96 | 1.06 |
| IRBM | 14.84 *a | 27.08 | 0.55 |
| IRBM—F | 129.43 | 126.20 | 1.03 |
| IRBM—FNM | 102.92 | 120.47 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, K.; Choi, H.; Quan, C. Experimental Investigation on Structural Performance Enhancement of Brick Masonry Member by Internal Reinforcement. Appl. Sci. 2023, 13, 5287. https://doi.org/10.3390/app13095287
Jin K, Choi H, Quan C. Experimental Investigation on Structural Performance Enhancement of Brick Masonry Member by Internal Reinforcement. Applied Sciences. 2023; 13(9):5287. https://doi.org/10.3390/app13095287
Chicago/Turabian StyleJin, Kiwoong, Ho Choi, and Chunri Quan. 2023. "Experimental Investigation on Structural Performance Enhancement of Brick Masonry Member by Internal Reinforcement" Applied Sciences 13, no. 9: 5287. https://doi.org/10.3390/app13095287
APA StyleJin, K., Choi, H., & Quan, C. (2023). Experimental Investigation on Structural Performance Enhancement of Brick Masonry Member by Internal Reinforcement. Applied Sciences, 13(9), 5287. https://doi.org/10.3390/app13095287







