Influence of Wheel-Rail Contact Algorithms on Running Safety Assessment of Trains under Earthquakes
Abstract
1. Introduction
2. Wheel-Rail Contact Model
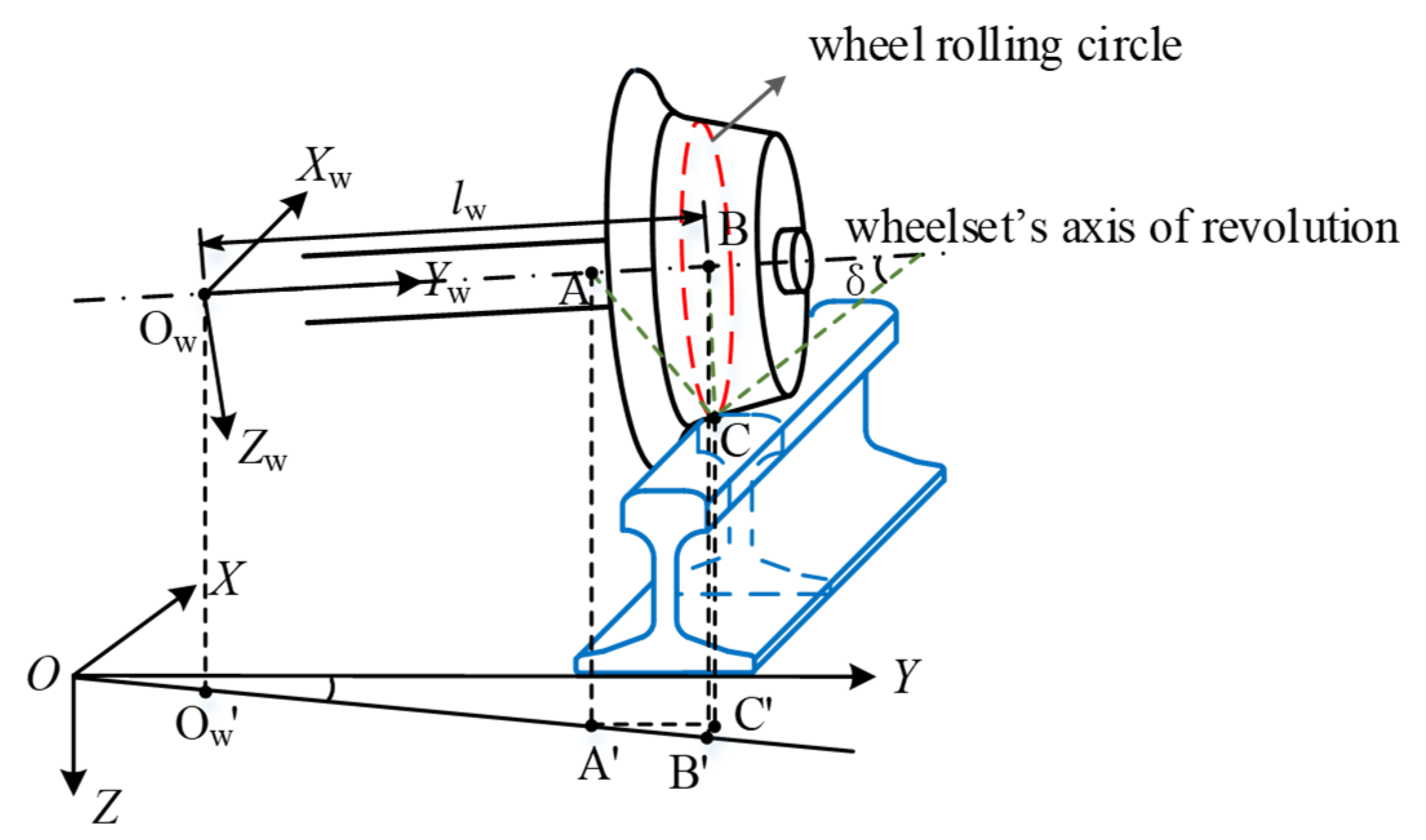
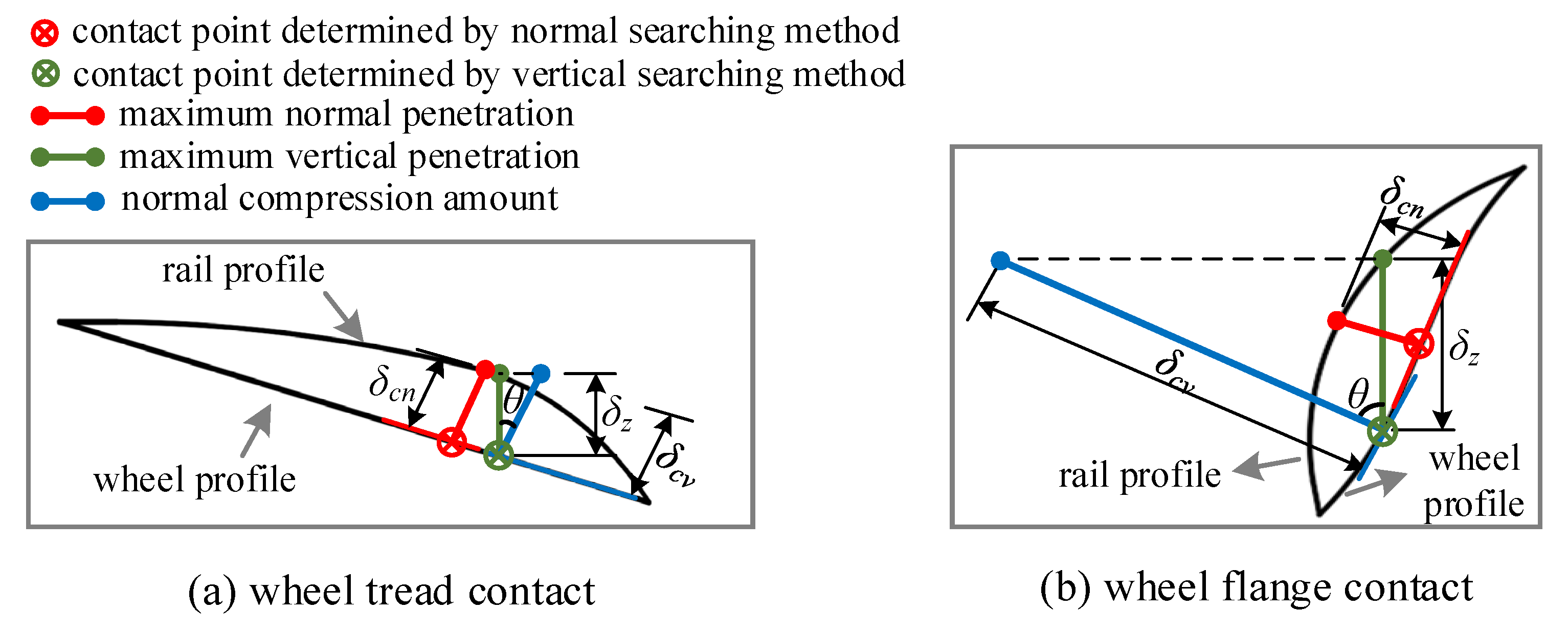
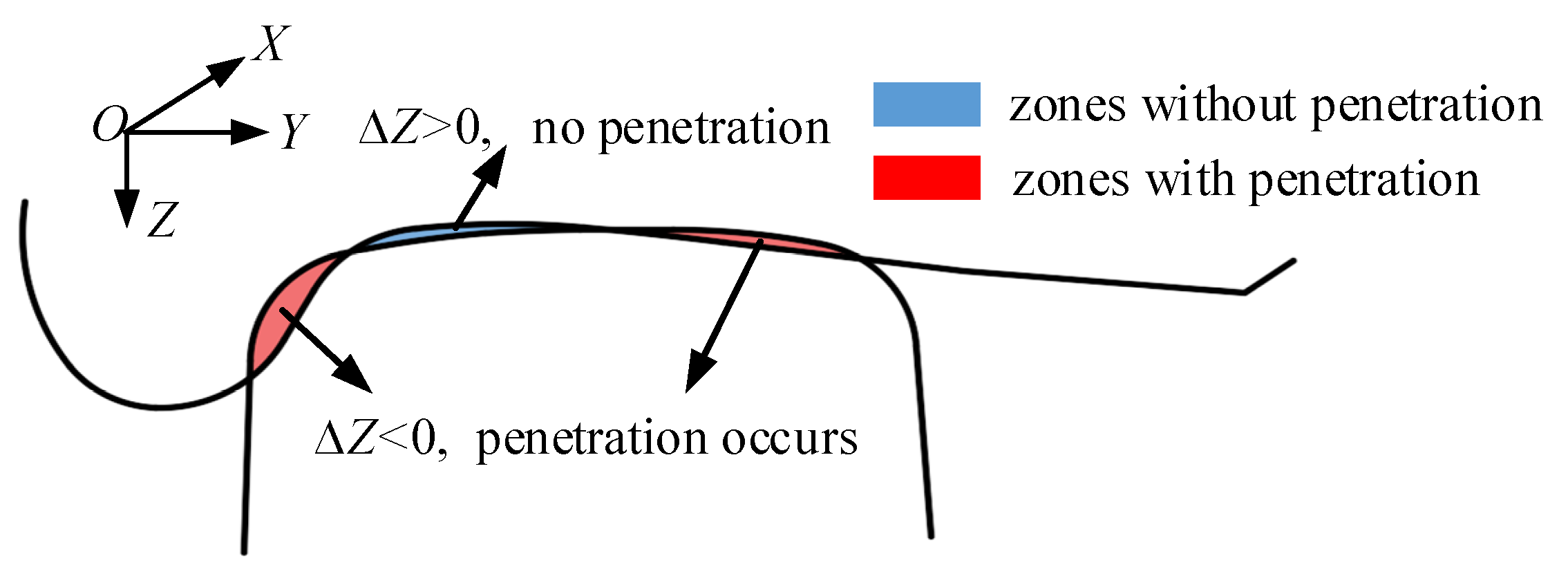
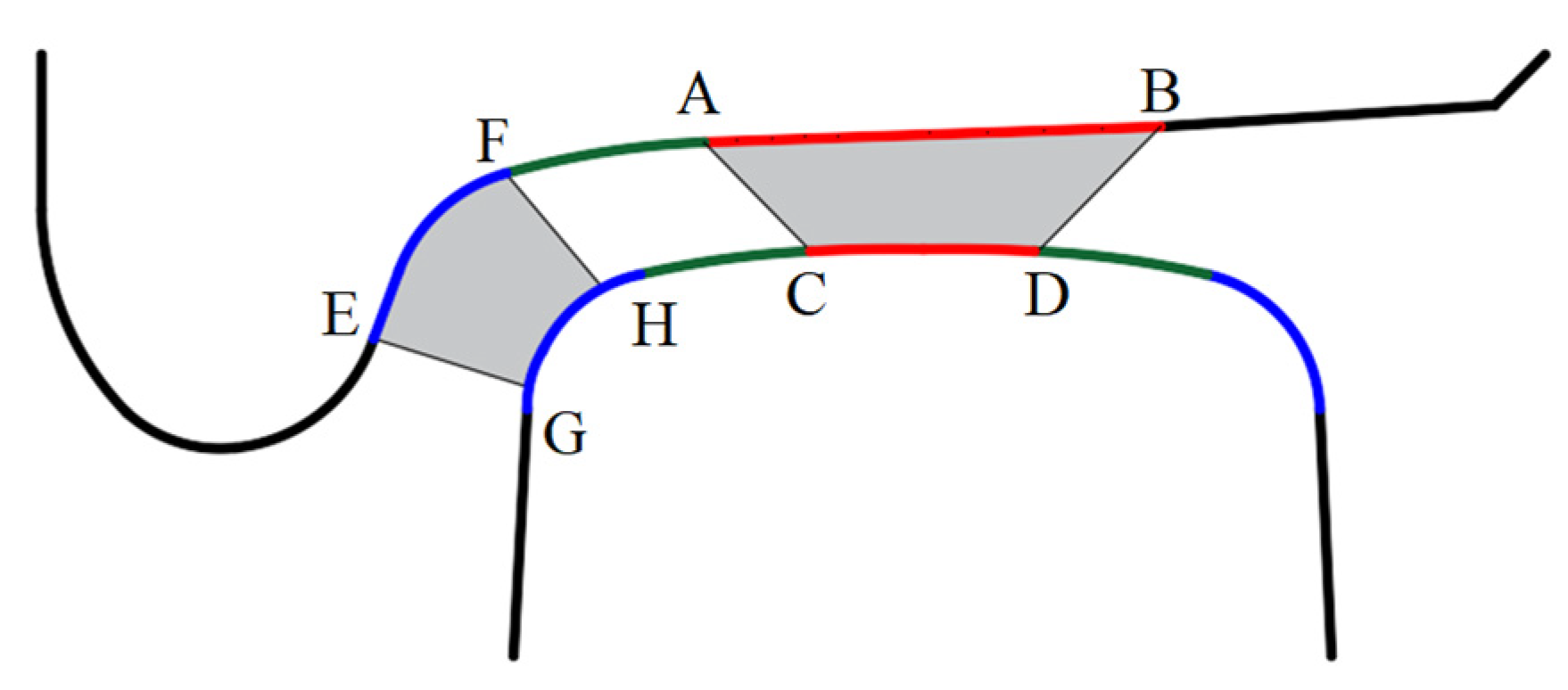
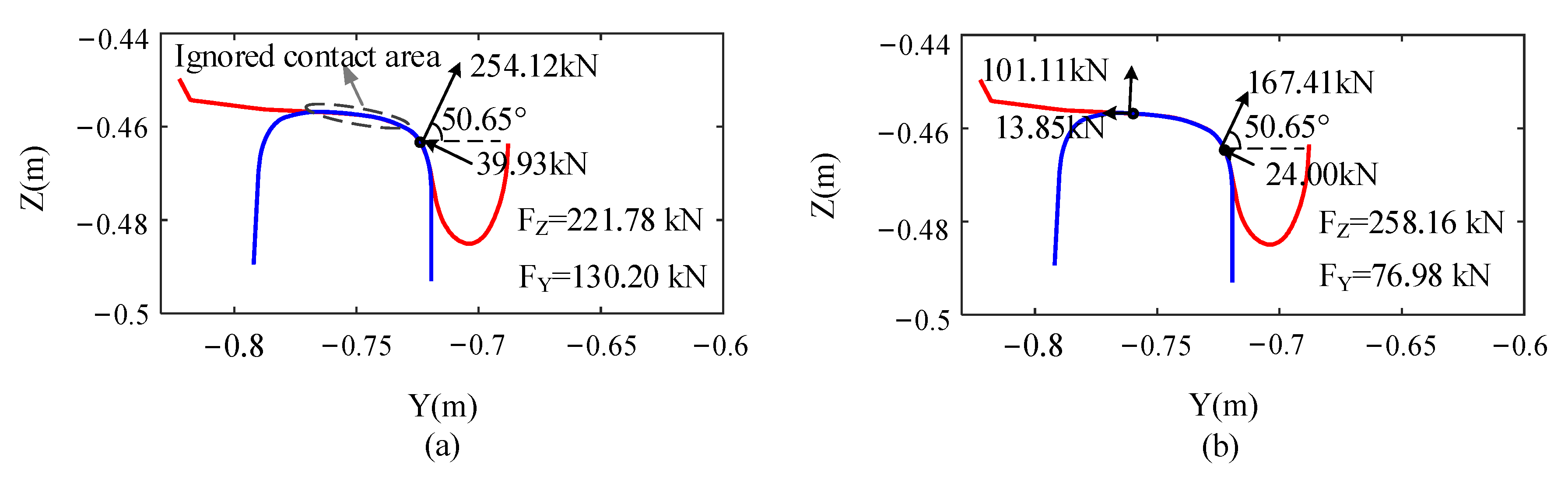
2.1. Wheel-Rail Contact Geometry Calculation
2.2. Wheel-Rail Contact Force Calculation

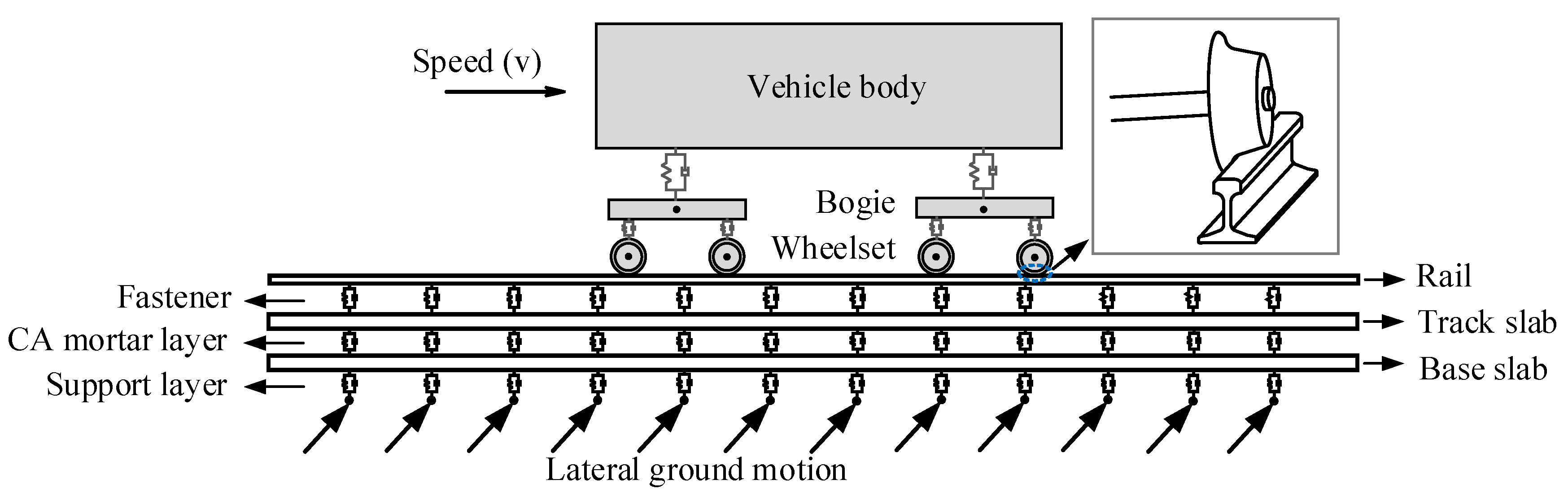
3. Dynamic Analysis Model of Train-Track Coupling System under Earthquakes
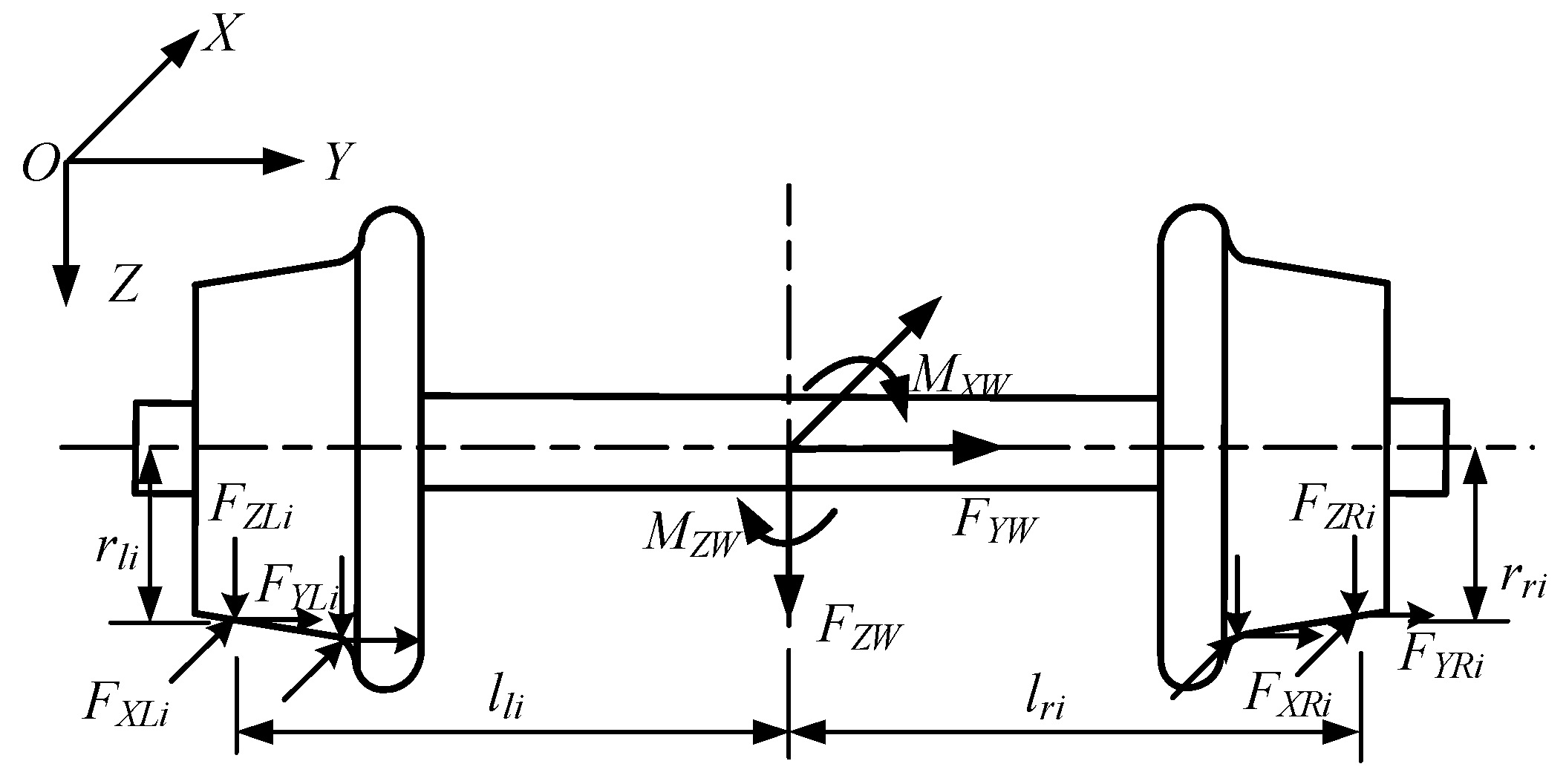
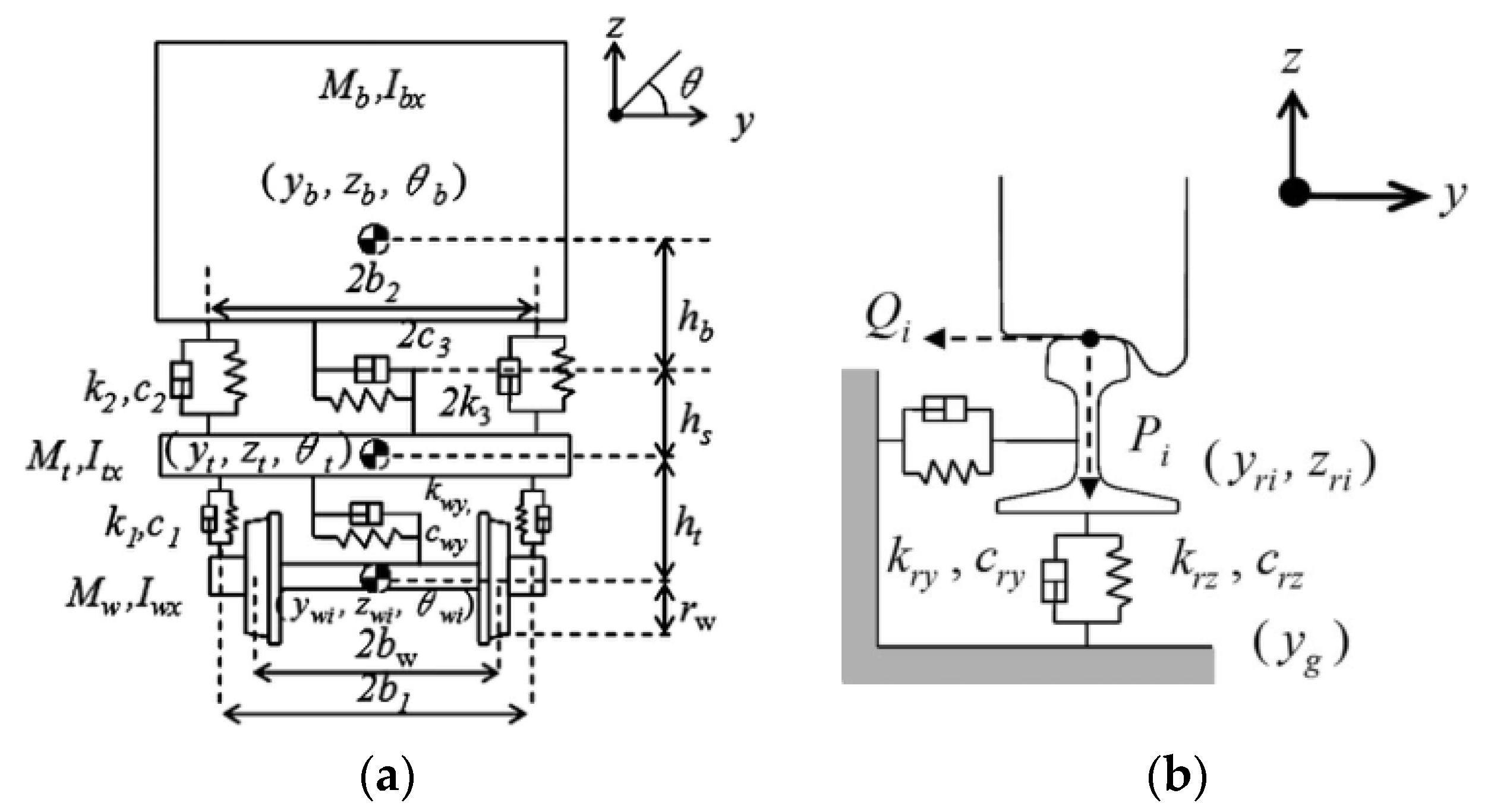
3.1. Train Subsystem
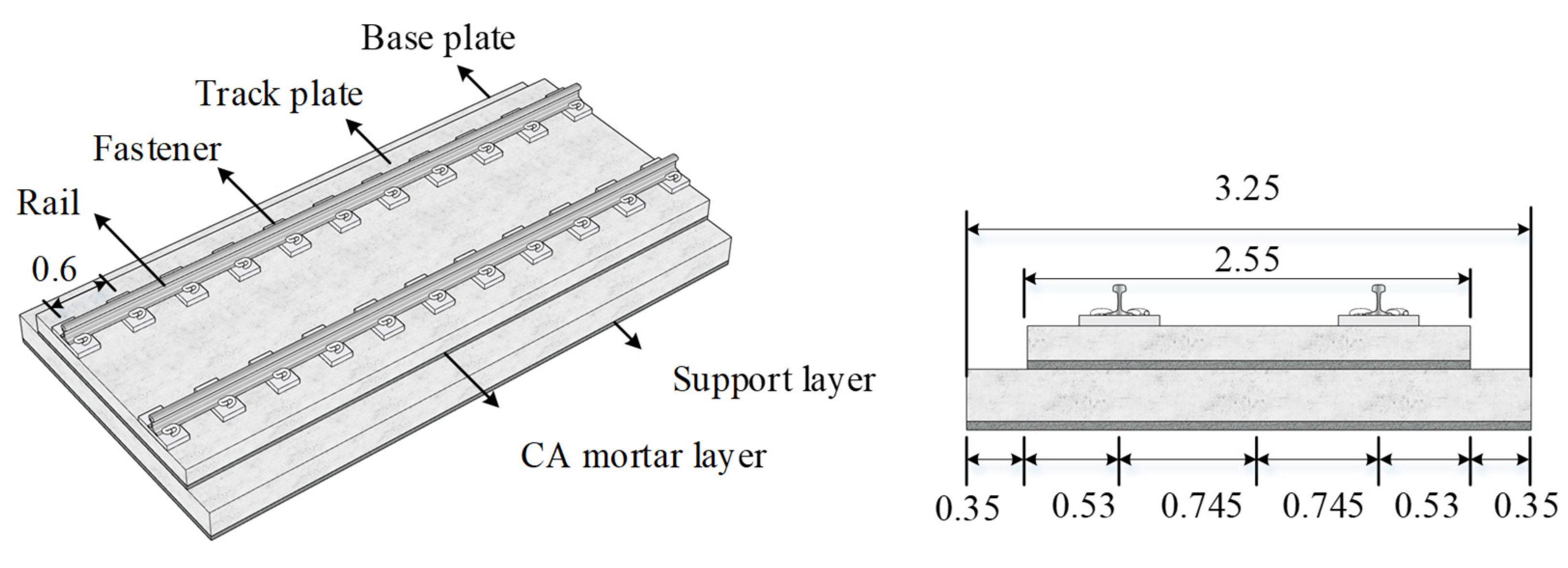
3.2. Track Subsystem
3.3. Train-Track Coupling
4. Comparison of Different Wheel-Rail Contact Models
4.1. Comparison under Ordinary Conditions
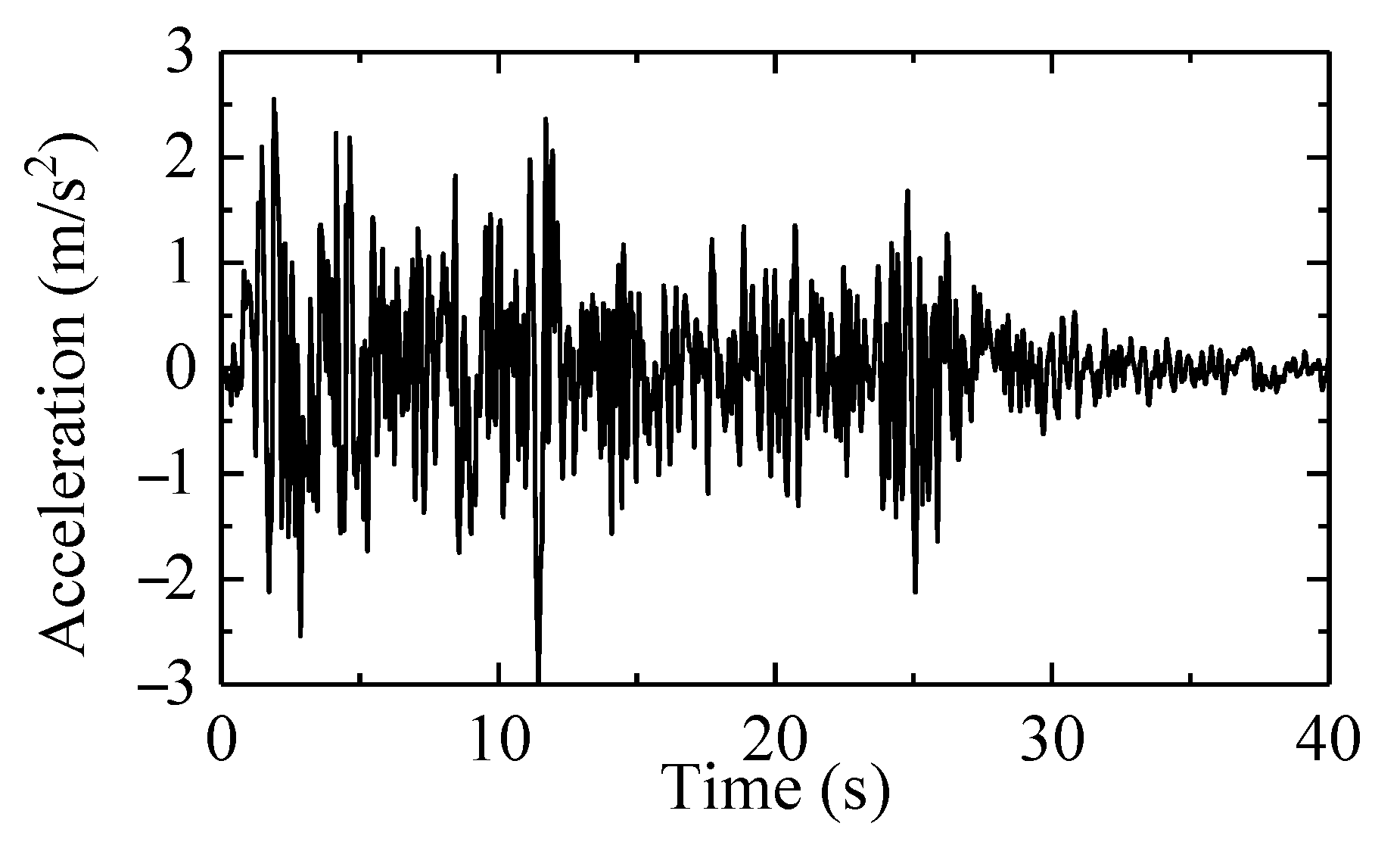
4.2. Comparison under Seismic Conditions
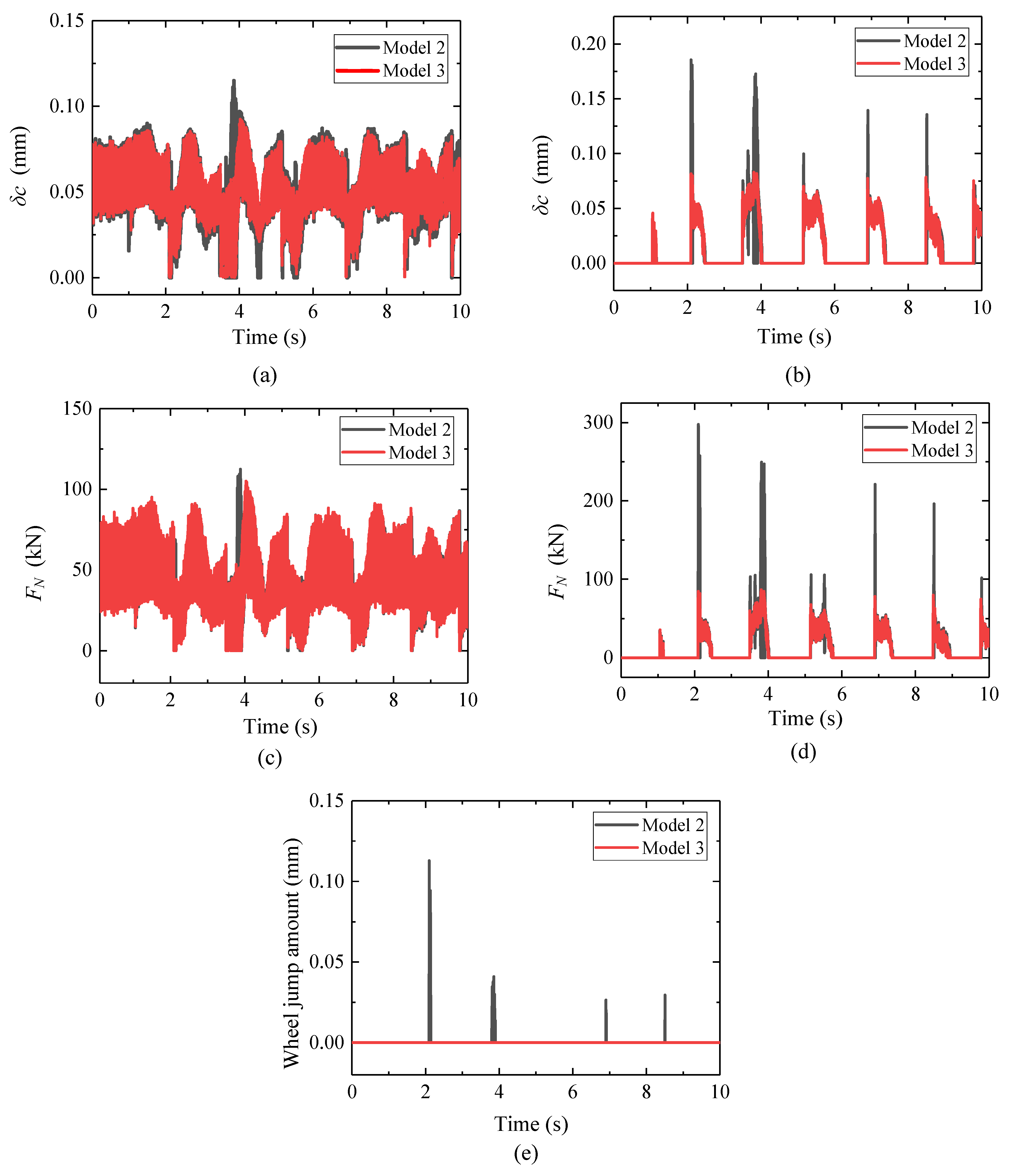
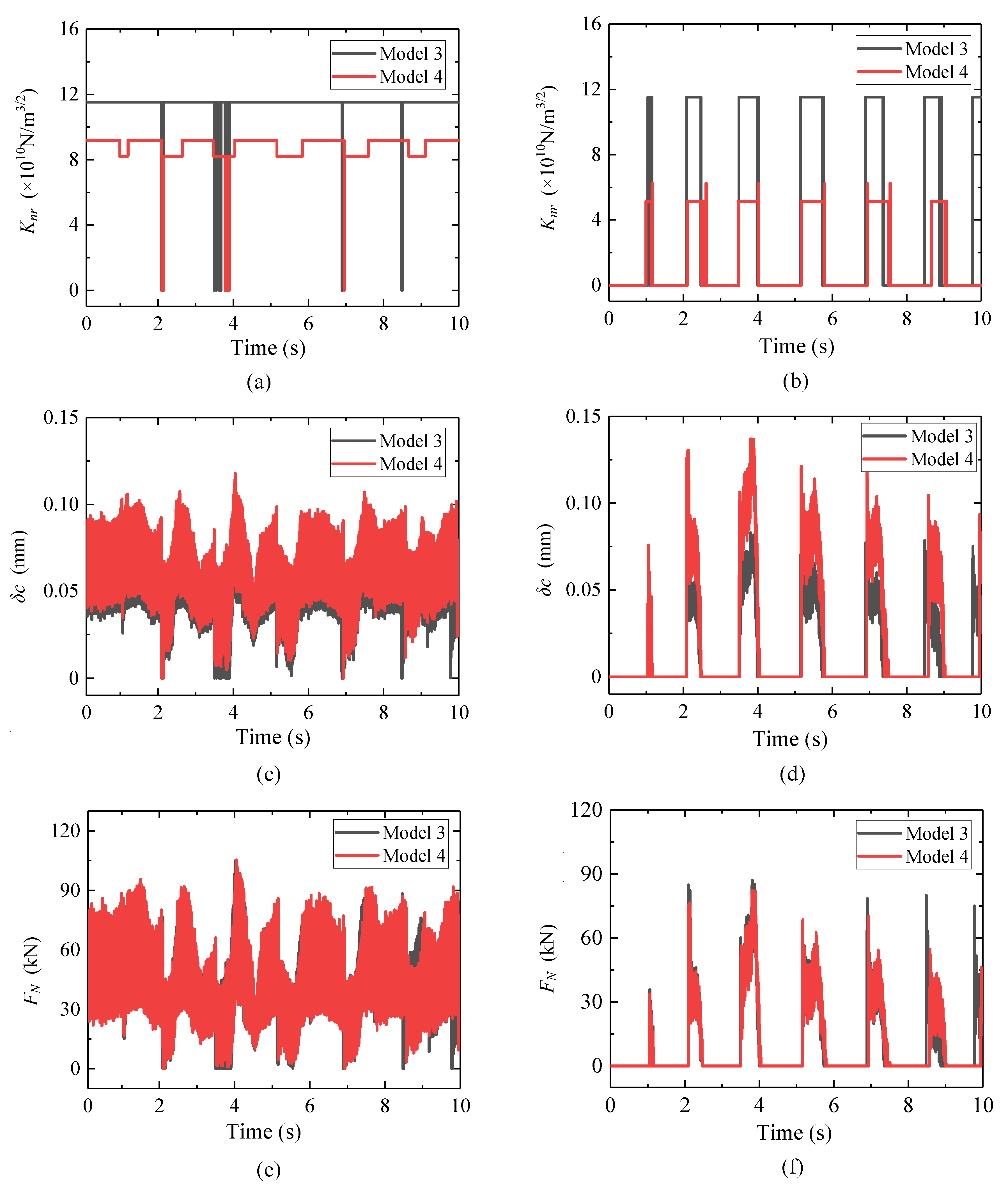
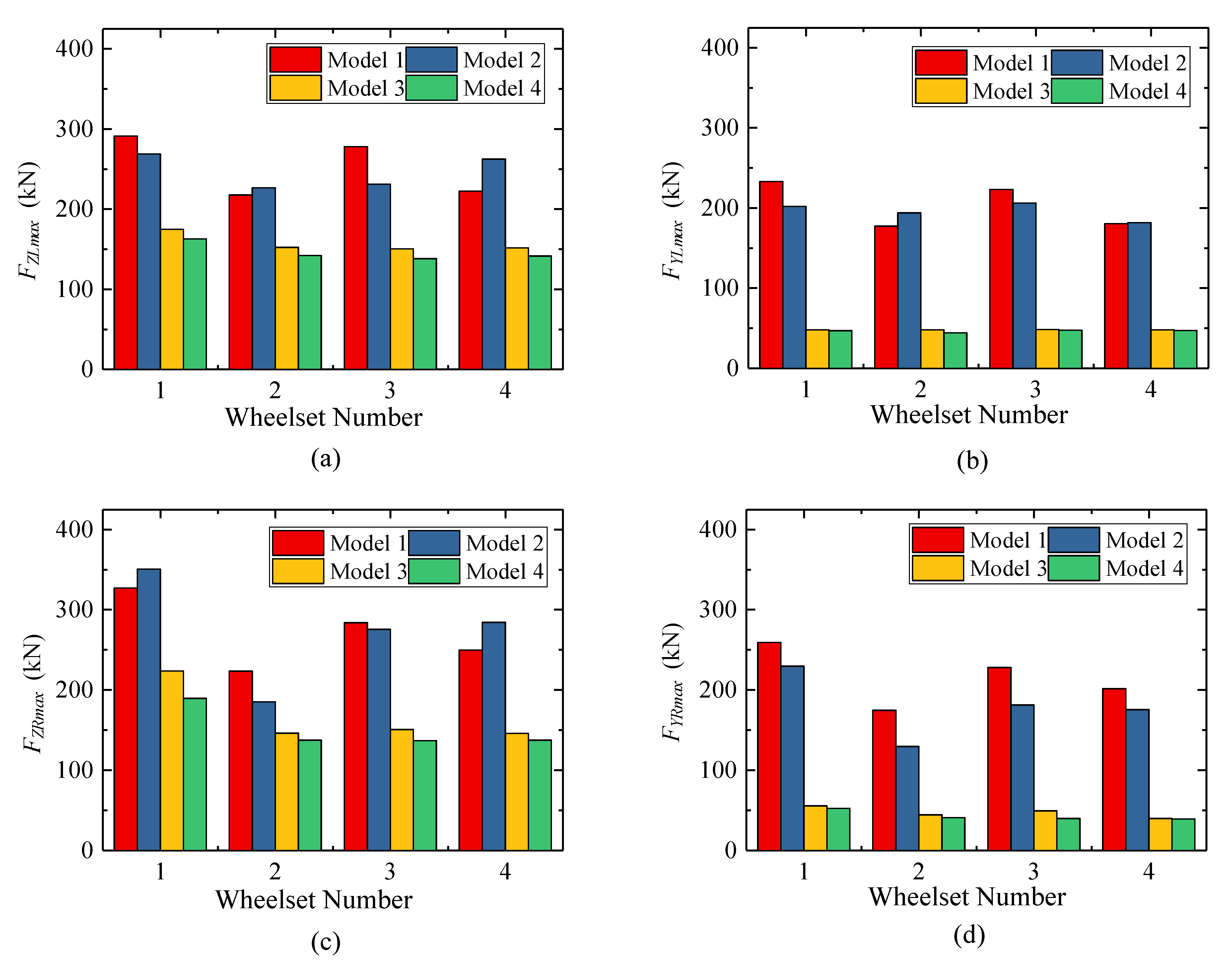
4.2.1. Wheel-Rail Contact Dynamics
4.2.2. Running Safety Assessment
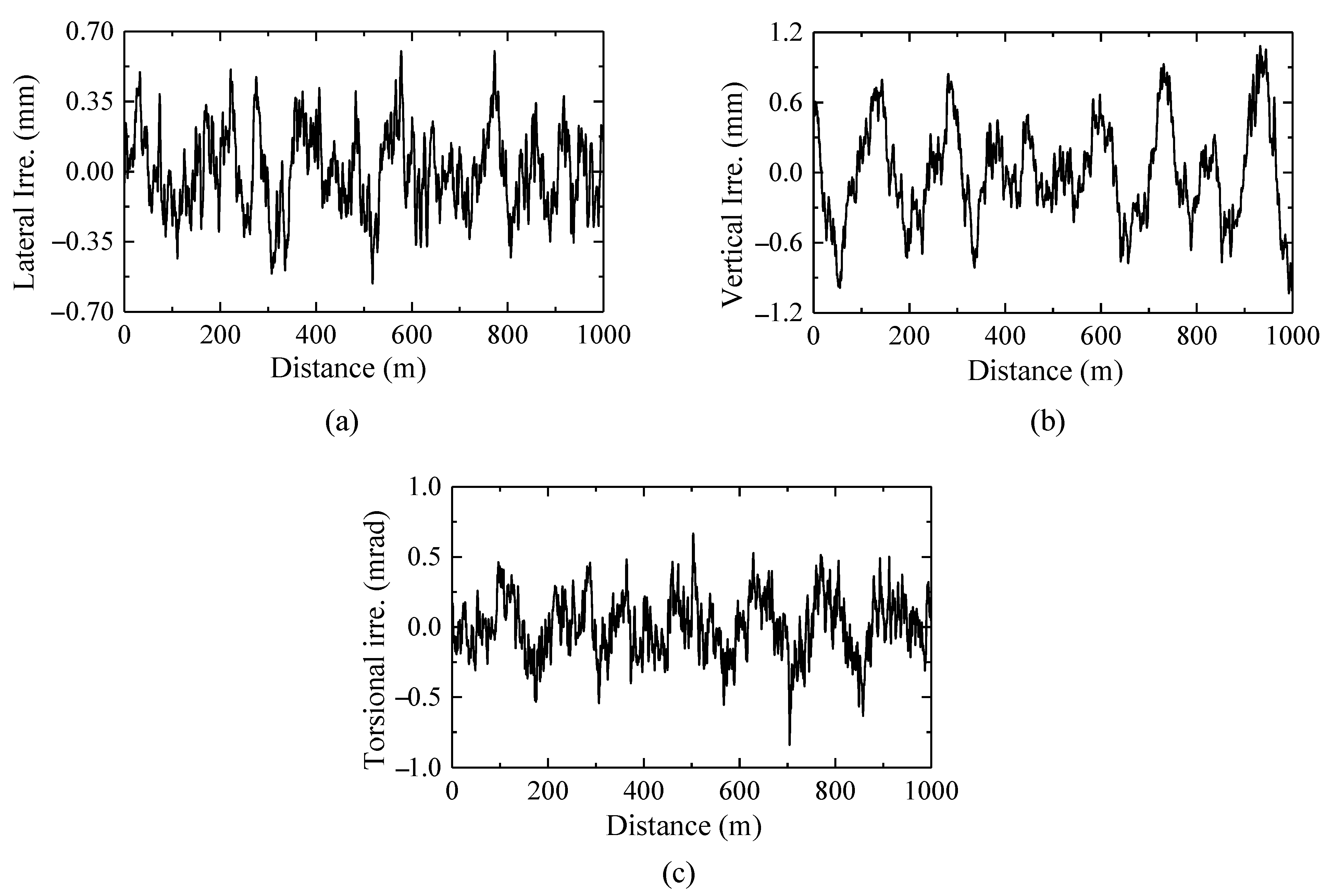
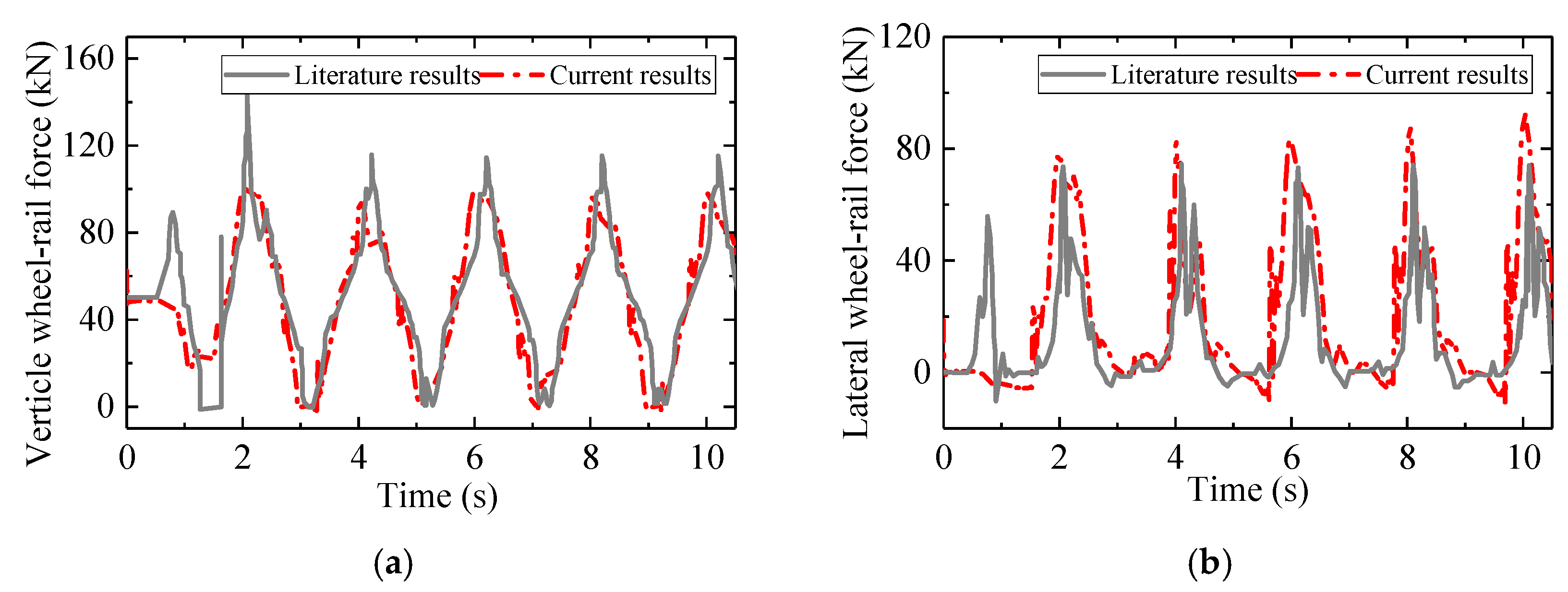
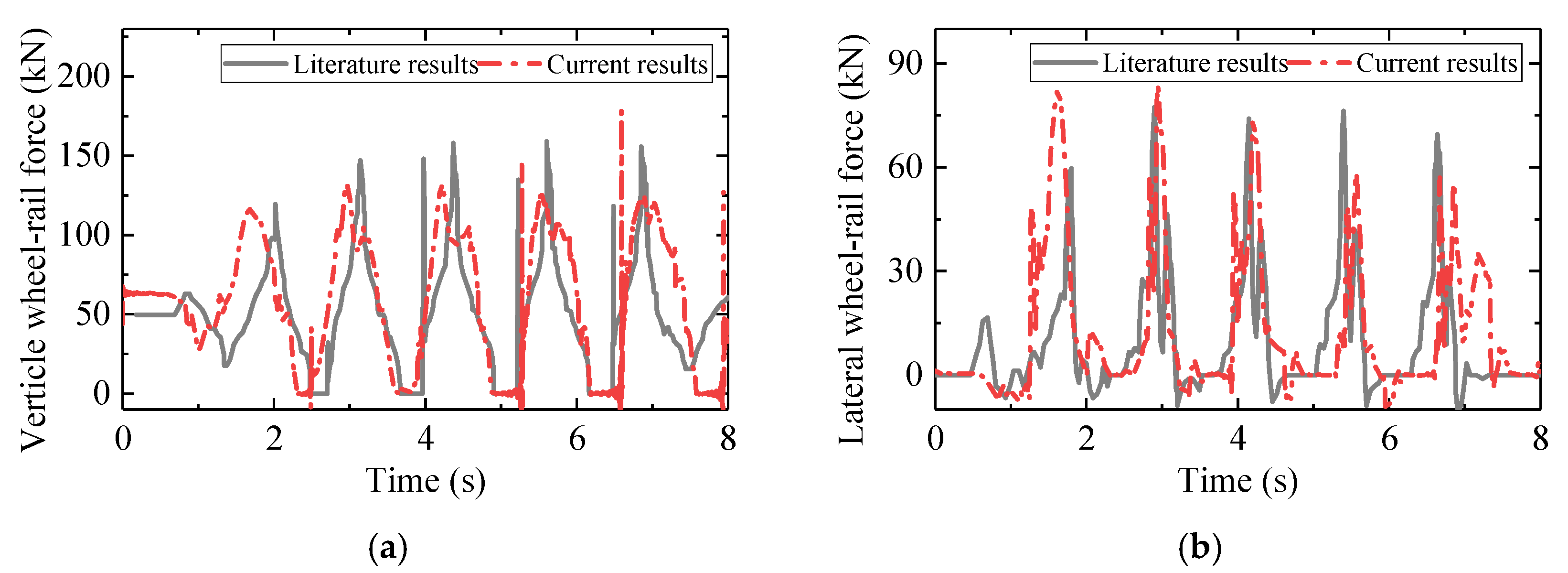
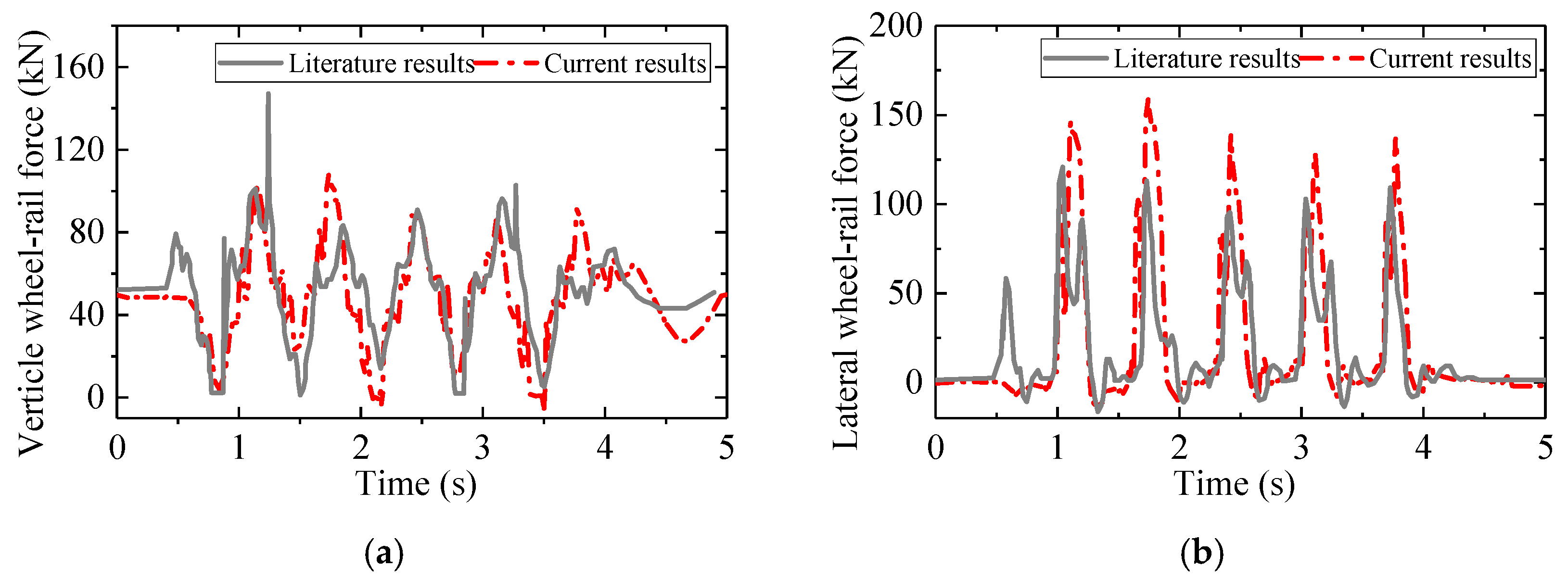
5. Model Validation
6. Conclusions
- Using different wheel-rail contact algorithms will significantly affect the calculation accuracy of wheel-rail force in the case of flange-root contact under earthquakes. The most significant influence is due to the normal compression algorithm. Using an algorithm based on vertical penetration can lead to a maximum relative error of 339.50% for the case considered in this study. The consideration of the number of wheel-rail contact points also has a notable impact, with a maximum relative error of 35.00% caused by only considering single point contact. The influence of the normal contact stiffness algorithm is the least significant, with a maximum relative calculation error of 23.55% caused by using the empirical formula.
- Using different wheel-rail contact algorithms will have a significant impact on the indices of running safety assessment under earthquakes. Using wheel-rail normal compression algorithm based on vertical penetration will significantly underestimating the train running safety margin, while only considering the wheel-rail single point contact will overestimate the train running safety margin, and using the wheel-rail normal contact empirical formula has little impact.
- To ensure the accuracy of running safety assessment of trains under earthquakes, it is recommended to use the normal compression algorithm based on normal penetration and consider multi-point contact in wheel-rail contact modelling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, L.C.; Yang, C.W.; Zhang, J.J. Derailment Behaviors of the Train-Ballasted Track-Subgrade System Subjected to Earthquake Using Shaking Table. KSCE J. Civ. Eng. 2020, 24, 2949–2960. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Vehicle-bridge interaction analysis modeling derailment during earthquakes. Nonlinear Dyn. 2018, 93, 2315–2337. [Google Scholar] [CrossRef]
- Meymand, S.Z.; Keylin, A.; Ahmadian, M. A survey of wheel-rail contact models for rail vehicles. Veh. Syst. Dyn. 2016, 54, 386–428. [Google Scholar] [CrossRef]
- Chen, H.Y.; Jiang, L.Z.; Li, C.Q.; Li, J.; Shao, P.; He, W.K.; Liu, L.L. A semi-online spatial wheel-rail contact detection method. Int. J. Rail Transp. 2021, 10, 730–748. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Hedrick, J.K.; Elkins, J.A. A comparison of alternative creep force models for rail vehicle dynamic analysis. Veh. Syst. Dyn. 1983, 12, 79–83. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, S.Y.; Zhai, W.M. An advanced train-slab track spatially coupled dynamics model: Theoretical methodologies and numerical applications. J. Sound Vib. 2021, 501, 116059, 1–30. [Google Scholar] [CrossRef]
- Zhai, W.M.; Han, Z.Y.; Chen, Z.W.; Ling, L.; Zhu, S.Y. Train-track-bridge dynamic interaction: A state-of-the-art review. Veh. Syst. Dyn. 2019, 57, 1–44. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W.M. Train-track coupled dynamics analysis: System spatial variation on geometry, physics and mechanics. Railw. Eng. Sci. 2020, 28, 36–53. [Google Scholar] [CrossRef]
- Liu, H.Y.; Yu, Z.W.; Guo, W.; Jiang, L.Z.; Kang, C.J. A novel method to search for the wheel-rail contact point. Int. J. Struct. Stab. Dyn. 2019, 19, 1950142, 1–21. [Google Scholar] [CrossRef]
- Xu, J.M.; Wang, P.; Ma, X.C.; Xiao, J.L.; Chen, R. Comparison of calculation methods for wheel-switch rail normal and tangential contact. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 231, 148–161. [Google Scholar] [CrossRef]
- Gong, W.; Zhu, Z.H.; Liu, Y.; Liu, R.T.; Tang, Y.J.; Jiang, L.Z. Running safety assessment of a train traversing a three-tower cable-stayed bridge under spatially varying ground motion. Railw. Eng. Sci. 2020, 28, 184–198. [Google Scholar] [CrossRef]
- Chen, L.K.; Kurtulus, A.; Dong, Y.F.; Taciroglu, E.; Jiang, L.Z. Velocity pulse effects of near-fault earthquakes on a high-speed railway vehicle-ballastless track-benchmark bridge system. Veh. Syst. Dyn. 2021, 60, 2963–2987. [Google Scholar] [CrossRef]
- Jin, Z.B.; Liu, W.Z. Fragility analysis for vehicle derailment on railway bridges under earthquakes. Railw. Eng. Sci. 2022, 30, 494–511. [Google Scholar] [CrossRef]
- Ling, L.; Xiao, X.B.; Wu, L.; Jin, X.S. Study on dynamic responses and running safety boundary of high-speed train under seismic motions. J. China Railw. Soc. 2012, 34, 16–22. (In Chinese) [Google Scholar]
- Zhao, H.; Wei, B.; Jiang, L.Z.; Xiang, P. Seismic running safety assessment for stochastic vibration of train-bridge coupled system. Arch. Civ. Mech. Eng. 2022, 22, 180, 1–24. [Google Scholar] [CrossRef]
- Yamashita, S.; Sugiyama, H. Numerical procedure for dynamic simulation of two-point wheel/rail contact and flange climb derailment of railroad vehicles. J. Comput. Nonlinear Dyn. 2012, 7, 041012, 1–7. [Google Scholar] [CrossRef]
- Ren, Z.S.; Iwnicki, S.D.; Xie, G. A new method for determining wheel-rail multi-point contact. Veh. Syst. Dyn. 2011, 49, 1533–1551. [Google Scholar] [CrossRef]
- Xiao, X.B.; Jin, X.S.; Wen, Z.F.; Zhu, M.H.; Zhang, W.H. Effect of tangent track buckle on vehicle derailment. Multibody Syst. Dyn. 2010, 25, 1–41. [Google Scholar] [CrossRef]
- Meli, E.; Ridolfi, A. An innovative wheel-rail contact model for railway vehicles under degraded adhesion conditions. Multibody Syst. Dyn. 2013, 33, 285–313. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Neves, S.G.M.; Calçada, R.; Tanabe, M.; Sogabe, M. Wheel-rail contact formulation for analyzing the lateral train-structure dynamic interaction. Comput. Struct. 2015, 152, 200–214. [Google Scholar] [CrossRef]
- Magalhaes, H.; Marques, F.; Antunes, P.; Flores, P.; Pombo, J. Wheel-rail contact models in the presence of switches and crossings. Veh. Syst. Dyn. 2022, 61, 838–870. [Google Scholar] [CrossRef]
- Shabana, A.A.; Zaazaa, K.E.; Escalona, J.L.; Sany, J.R. Development of elastic force model for wheel/rail contact problems. J. Sound Vib. 2004, 269, 295–325. [Google Scholar] [CrossRef]
- Ling, L.; Jin, X.S. A 3D model for coupling dynamics analysis of high−speed train/track system. J. Zhejiang Univ. Sci.-A 2014, 15, 964–983. [Google Scholar] [CrossRef]
- Guan, Q.H.; Zhao, X.; Wen, Z.F.; Jin, X.S. Calculation Method of Hertzian Normal Contact Stiffness. J. Southwest Jiaotong Univ. 2021, 56, 883–890. (In Chinese) [Google Scholar]
- Shabana, A.A.; Berzeri, M.; Sany, J.R. Numerical Procedure for the Simulation of Wheel/Rail Contact Dynamics. J. Dyn. Syst. Meas. Control. 2001, 123, 168–178. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J.; Silva, M. A new wheel–rail contact model for railway dynamics. Veh. Syst. Dyn. 2007, 45, 165–189. [Google Scholar] [CrossRef]
- Marques, F.; Magalhães, H.; Pombo, J.; Ambrósio, J.; Flores, P. A three-dimensional approach for contact detection between realistic wheel and rail surfaces for improved railway dynamic analysis. Mech. Mach. Theory 2020, 149, 1–28. [Google Scholar] [CrossRef]
- Zhai, W.M. Vehicle-Track Coupled Dynamics Theory and Applications; Springer: Singapore, 2019; pp. 56–122. [Google Scholar]
- Kalker, J.J. On the Rolling Contact of Two Elastic Bodies in the Presence of Dry Friction. Ph.D. Dissertation, Delft University of Technology, Delft, The Netherlands, 1967. [Google Scholar]
- Zhang, N.; Xia, H.; De Roeck, G. Dynamic analysis of a train-bridge system under multi-support seismic excitations. J. Mech. Sci. Technol. 2010, 24, 2181–2188. [Google Scholar] [CrossRef]
- Wu, X.W.; Chi, M.R.; Gao, H.; Ke, X.M.; Zeng, J.; Wu, P.B.; Zhu, M.H. Post-derailment dynamic behavior of railway vehicles travelling on a railway bridge during an earthquake. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 230, 418–439. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.X. Development of high-speed railway vehicle derailment simulation-Part I: A new wheel/rail contact method using the vehicle/rail coupled model. Eng. Fail. Anal. 2012, 24, 77–92. [Google Scholar] [CrossRef]
- Nishimura, K.; Terumichi, Y.; Morimura, T.; Sogabe, K. Development of Vehicle Dynamics Simulation for Safety Analyses of Rail Vehicles on Excited Tracks. J. Comput. Nonlinear Dyn. 2009, 4, 011001, 1–9. [Google Scholar] [CrossRef]
- Sun, L.; Chen, L.L.; Zelelew, H.H. Stress and Deflection Parametric Study of High-Speed Railway CRTS-II Ballastless Track Slab on Elevated Bridge Foundations. J. Transp. Eng. 2013, 139, 1224–1234. [Google Scholar] [CrossRef]
- Xu, Y.D.; Yan, D.B.; Zhu, W.J.; Zhou, Y. Study on the mechanical performance and interface damage of CRTS II slab track with debonding repairment. Constr. Build. Mater. 2020, 257, 119600. [Google Scholar] [CrossRef]
- Jin, Z.B.; Pei, S.L.; Li, X.Z.; Liu, H.Y.; Qiang, S.Z. Effect of vertical ground motion on earthquake-induced derailment of railway vehicles over simply-supported bridges. J. Sound Vib. 2016, 383, 277–294. [Google Scholar] [CrossRef]
- Jiang, L.Z.; Zhou, T.; Liu, X.; Xiang, P.; Zhang, Y.T. An Efficient Model for Train-Track-Bridge-Coupled System under Seismic Excitation. Shock. Vib. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Li, M.; Liu, J.W.; Zhang, G.C. Safety Analysis of the Running Train under Earthquake Dynamic Disturbance. Shock. Vib. 2021, 2021, 1–21. [Google Scholar] [CrossRef]
- Nishimura, K.; Terumichi, Y.; Morimura, T.; Adachi, M.; Morishita, Y.; Miwa, M. Using Full Scale Experiments to Verify a Simulation Used to Analyze the Safety of Rail Vehicles During Large Earthquakes. J. Comput. Nonlinear Dyn. 2015, 10, 031013, 1–9. [Google Scholar] [CrossRef]




| Wheel-Rail Contact Model | Consideration of Contact Point | Calculation Basis for Normal Compression Amount | Algorithm for Normal Contact Stiffness |
|---|---|---|---|
| Model 1 | Single-point contact | Vertical penetration | Empirical formula |
| Model 2 | Multipoint contact | Vertical penetration | Empirical formula |
| Model 3 | Multipoint contact | Normal penetration | Empirical formula |
| Model 4 | Multipoint contact | Normal penetration | Theoretical formula |
| Running Safety Indices | Q/P | ∆P/P | ∑Q (kN) |
|---|---|---|---|
| Limit | 0.8 | 0.8 | 55 |
| Running Safety Indices | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| Q/P | 0.83 | 0.87 | 0.78 | 0.78 |
| ∆P/P | 0.95 | 1.0 | 0.80 | 0.79 |
| ∑Q (kN) | 228.79 | 250.99 | 49.33 | 46.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, G.; Zhu, Z.; Gong, W.; Zhou, G.; Jiang, L.; Ye, B. Influence of Wheel-Rail Contact Algorithms on Running Safety Assessment of Trains under Earthquakes. Appl. Sci. 2023, 13, 5230. https://doi.org/10.3390/app13095230
Cai G, Zhu Z, Gong W, Zhou G, Jiang L, Ye B. Influence of Wheel-Rail Contact Algorithms on Running Safety Assessment of Trains under Earthquakes. Applied Sciences. 2023; 13(9):5230. https://doi.org/10.3390/app13095230
Chicago/Turabian StyleCai, Guanmian, Zhihui Zhu, Wei Gong, Gaoyang Zhou, Lizhong Jiang, and Bailong Ye. 2023. "Influence of Wheel-Rail Contact Algorithms on Running Safety Assessment of Trains under Earthquakes" Applied Sciences 13, no. 9: 5230. https://doi.org/10.3390/app13095230
APA StyleCai, G., Zhu, Z., Gong, W., Zhou, G., Jiang, L., & Ye, B. (2023). Influence of Wheel-Rail Contact Algorithms on Running Safety Assessment of Trains under Earthquakes. Applied Sciences, 13(9), 5230. https://doi.org/10.3390/app13095230







