Featured Application
The trajectory optimization scheme for multiple UAVs in this paper can be used for the coverage of 5G networks in cities and mountainous areas.
Abstract
In this paper, we study the three-dimensional (3D) trajectory optimization problems of unmanned aerial vehicles (UAV) with a solar energy supply, aiming to provide communication coverage for mobile users on the ground. In general, the higher UAVs fly, the more solar energy they collect, but the smaller the range of coverage they could achieve, and vice versa. How to plan optimal trajectories for UAVs so that more users can be encompassed, while allowing UAVs to collect enough solar energy, is a challenging issue. Moreover, we also consider how geographically fair coverage for each ground user can be achieved. To solve these problems, we designed a multiple solar-powered UAV (SP-UAV) energy consumption model and a fairness model, while designed an observation space, state space, action space, and reward function. Then, we proposed a multiple SP-UAV 3D trajectory optimization algorithm based on deep reinforcement learning (DRL). Our algorithm is able to balance the energy consumption of UAVs to extend the system’s lifetime, while avoiding both collisions and flying out of communication range. Finally, we trained our model through simulation experiments and conducted comparative experiments and analysis based on real network topology data. The results show that our algorithm is superior to the existing typical algorithms in coverage, fairness, and lifetime.
1. Introduction
With the rapid development of communication network technology, the demand for network by users is exploding. However, under certain special circumstances (such as ground base station failure) [1,2], existing communication facilities are not sufficient to satisfy the demands of users for communication networks. Due to traffic congestion and other reasons, it is difficult to deploy fixed base stations or emergency communication vehicles in a short period of time, which poses a huge challenge to traditional networks. The UAV-assisted wireless network, as an emerging technology, is being applied in the challenging scenarios mentioned above. For example, China Telecom has built UAV bases in multiple cities, such as Suzhou, Suqian, and Chongqing, to provide network coverage services. To combat the problem of the excessive energy consumption during flight and the short service duration of ordinary UAVs [3,4], this article uses mobile base stations deployed on multiple SP-UAVs to provide communication network coverage for users in the target area [5,6]. The SP-UAV is a drone equipped with solar cells, which is able to collect solar energy to power itself during flight. Although SP-UAVs could alleviate the problem of the high power consumption of traditional UAVs and has advantages such as high flexibility and ease of deployment [7,8,9], using SP-UAVs to provide network coverage also poses many problems.
Firstly, for SP-UAVs to collect enough solar energy requires increasing flight altitude, which leads to a decrease in the coverage range of the SP-UAV [10]. Moreover, providing network coverage to the target area often requires the use of multiple SP-UAVs, and since SP-UAVs are expensive, it is usually not possible to deploy enough of them. Therefore, it is necessary to plan a set of optimal 3D flight trajectories to prevent a single UAV from consuming too much energy and causing the entire system’s lifetime to end quickly, while simultaneously cover more users with limited SP-UAVs.
In addition, when multiple SP-UAVs are used to provide coverage to ground users, it is possible that the majority of users will receive long-term coverage while a few users will never be covered. This phenomenon is caused by the fact that the majority of users are densely distributed, while a few users may be located in remote areas. SP-UAVs are reluctant to fly to these users’ surroundings as they are designed to save flight energy. This results in geographical unfairness, even if the overall coverage rate is high. In scenarios such as earthquakes and tsunamis, however, we would like all users to be able to communicate equally. Therefore, we also consider the issue of multiple SP-UAVs providing geographically fair coverage to users.
To solve the above problems, we modeled the flight energy consumption and solar energy collection of SP-UAVs and introduced a fairness index in order to characterize the geographical fairness of UAVs providing coverage to ground users. The research object of this paper is defined as a multi-objective optimization problem, with constraints on UAV flight altitude, speed, and direction. To solve this problem, we proposed a DRL-based multiple SP-UAV 3D trajectory optimization algorithm, which aims to find a set of optimal flight trajectories that maximize coverage rates and fairness indexes and minimize energy consumption. The algorithm can also prevent a single UAV from consuming too much power and quickly running out of energy, thus extending the entire system’s lifetime. The contributions of our works are as follows:
- We establish a model that utilizes multiple SP-UAVs to provide communication coverage for ground users and characterize the research problem as a multi-objective joint optimization problem.
- We propose a new trajectory optimization algorithm based on DRL to study the multi-objective optimization problem in this paper, in which the state space, observation space, action space, and reward function are clearly defined.
- In order to evaluate the effectiveness of this algorithm, extensive simulation experiments were conducted in this research. Taking into account factors, such as lighting conditions and urban structure, we also selected a dataset from the urban area of Melbourne, Australia, for further experiments. The results show that compared to the existing technology, this scheme is able to significantly improve coverage and the fairness index while extending the lifetime of the system.
The rest of the paper is organized as follows. Section 2 reviews the relevant work related to our research and describes the differences in comparison with the work presented here. Section 3 introduces the system model and outlines problem statement. Section 4 provides a detailed introduction to our algorithm and conducts a complexity analysis. Section 5 presents our experimental content, which encompasses comparative experiments with several typical algorithms currently in use. Finally, Section 6 summarizes our research and provides prospects for future studies.
2. Recent Works
Recently, many researchers have conducted studies on the use of UAVs for network coverage. This paper is related to the coverage problem and fairness problem in UAV trajectory optimization. Therefore, in this section, we review recent related work and point out their differences to the research in this paper.
2.1. Coverage of UAV
In 2019, Yin S et al. [11] studied the problem of intelligently tracking ground users with UAVs without access to user-side information, such as user location. The authors established a reinforcement learning model and applied the deterministic policy gradient (DPG) algorithm to the model but ignored the relationship between the coverage range of UAVs and the width and height of antenna beams. Qureshi H N et al. [12] revealed and analyzed new trade-offs between UAV design space dimensions in different scenarios but did not consider the uplink link scenarios for the UAV coverage of disaster-affected areas. Shakhatreh H et al. [13] proposed a gradient projection-based algorithm to find the optimal position of UAVs, thus maximizing the duration of uplink transmission while covering users, but only considered the two-layer network structure between UAVs and users.
In 2020, Li X et al. [14] proposed a three-layer network system of satellites, UAVs, and ground to enhance network coverage and solved the problem using problem decomposition, continuous convex optimization, and bisection search tools. However, they did not consider that different ground users have different network quality requirements. Zeng F et al. [15] classified ground users with different network requirements and studied the UAV coverage problem in terms of maximizing energy efficiency and user experience quality but did not consider non-intentional interference from the ground on UAVs. Yuan X et al. [16] studied the problem of the uninterrupted coverage of UAVs in an environment that allows ground interference and evaluated the impact of external interference on the connectivity of UAV groups.
In 2021, Bhandarkar A B et al. [17] designed a greedy algorithm based on DRL to determine the optimal trajectory of UAVs in order to maximize the coverage of ground users for a higher coverage rate. Ghasemi Darehnaei Z et al. [18] introduced a SI-EDTL technique and used it to construct an accurate and tunable deep transfer learning model for multiple object detection by UAV.
In 2022, Ye Z et al. [19] studied the problem of UAV coverage under partially observable conditions and introduced a new network architecture based on deep recursive graphs in order to deal with information loss caused by partial observability.
2.2. Fairness Issues of UAV
From 2018 to 2019, Zhang X et al. [20] studied the problem of minimizing the maximum deployment delay and total deployment delay between UAVs, while considering fairness and coverage efficiency. However, this reference regarded UAVs as fixed and immobile aerial nodes without considering their movement. Xu J et al. [21] studied the problem of maximizing total energy and fairness in energy transmission when using movable UAVs to provide wireless power transfer services for ground devices. However, in this study, UAVs hover at a fixed location for a long time during charging. Hu Y et al. [22] optimized the hovering time of UAVs and studied the fairness issue in the power supply network of UAVs based on it but only optimized the one-dimensional trajectory of UAV flight. Dai H et al. [23] studied the fairness issue of UAVs providing wireless communication services for ground users, where UAVs fly in a two-dimensional plane at a fixed height and introduced the concept of α-fairness [24] to characterize fairness but did not consider the energy consumption of UAVs. Qin Z et al. [25] considered the fairness of energy consumption between communication, hovering, and motion energy consumption of UAVs used for reconnaissance tasks and used a heuristic algorithm to solve this problem.
From 2020 to 2021, Qi H et al. [26] proposed efficient and fair 3D UAV scheduling with energy replenishment. Under this model, UAVs can be charged while serving users. The author proposes a UAV control strategy based on a depth deterministic strategy gradient to ensure energy efficiency and fair coverage for each user in a large area, while simultaneously ensuring service durability. However, there is no research on energy efficiency fairness between different UAVs. Liu X et al. [27] formulated a fair energy-saving resource optimization problem, which maximizes the minimum energy efficiency of UAVs by optimizing the flight trajectory of multiple UAVs to achieve energy-saving fairness among UAVs.
In 2022, Liu Y et al. [28] introduced a new fairness index to ensure the fair distribution of service quality based on the coverage and service quality of UAVs. This study proposes an alternating algorithm based on proximal random gradient descent to optimize the position of unmanned aerial vehicles.
2.3. Our Research
Unlike the existing works described above, our research is based on a dynamic UAV scenario, taking into account the coverage of the UAVs and geographical fairness over the entire target area. In addition, this article considers the lifetime of the system, which is the total time from the release of all UAVs to the end of any UAV power outage, because in some harsh environments, the UAV fleet cannot meet the conditions required to return to the starting point for charging and then returning for service. This article also considers the issue of using solar energy to charge UAVs, which has an impact on the selection of appropriate flight trajectories for UAV groups. The joint optimization problems discussed in this paper are evidently unlike those studied in the related works introduced above.
3. System Model and Problem Statement
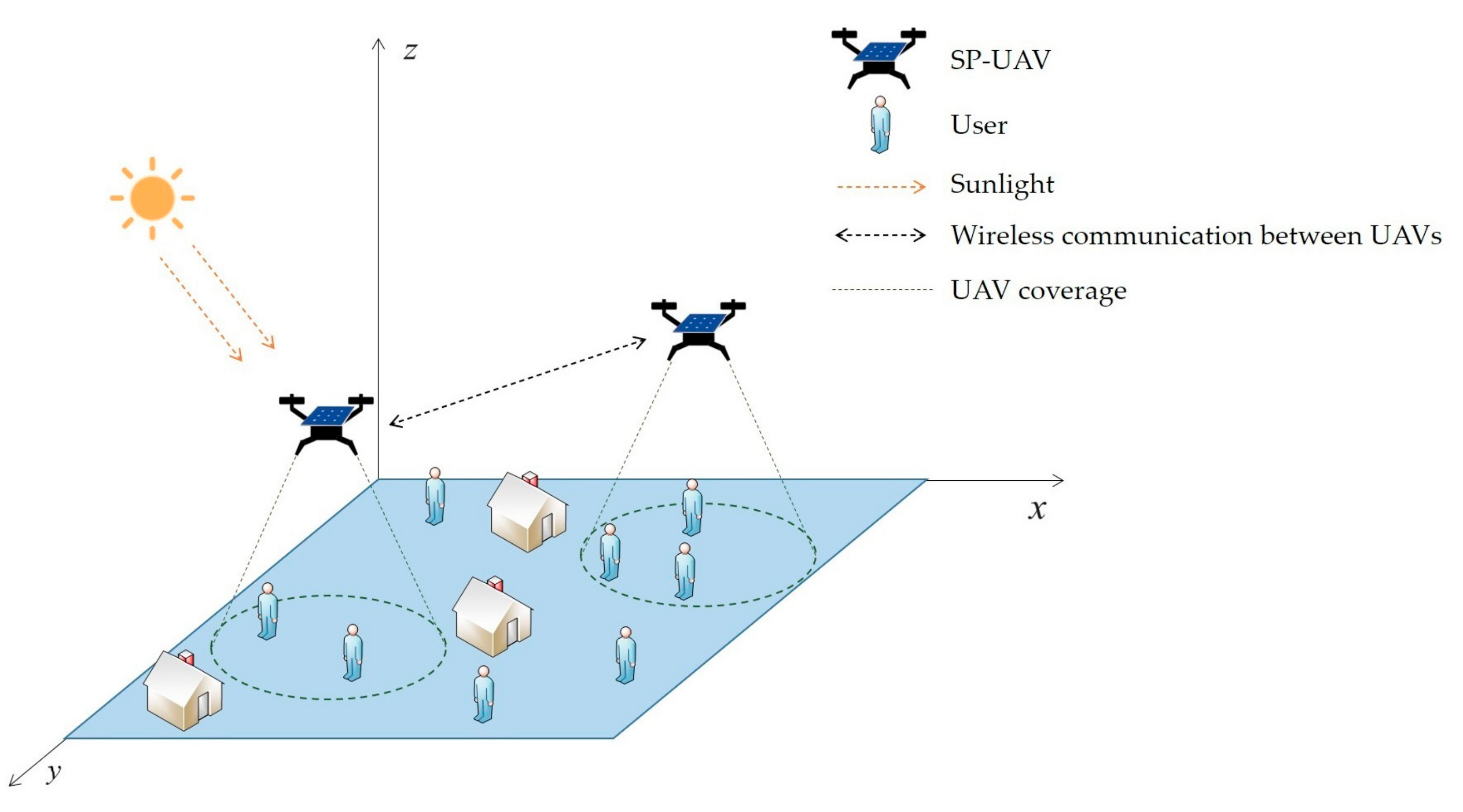
As shown in Figure 1, we consider a scenario where a group of UAVs equipped with solar panels take off from the same location and achieve fair coverage of the target area. The UAVs are represented by the set , and serve as height-adjustable aerial base stations to support ground users with coverage services in an A × A meter area. All UAVs are limited by a connectivity constraint and lose connection with the swarm of UAVs when there are no other UAVs within communication range. Since UAVs may move vertically, their coverage range changes with movement, where .
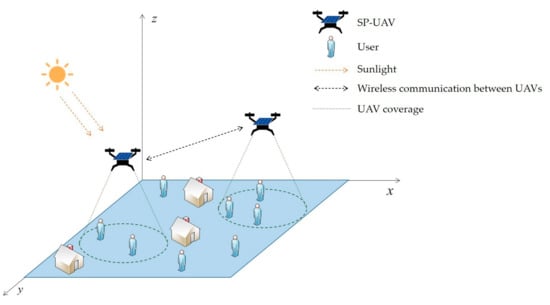
Figure 1.
The structure of our network model.
The flight cycle D is composed of M equally long time slots, denoted by . We set the time slot to meet . In this paper, is set to be small enough so that the position of the UAV can be considered as constant during each time slot. Multiple ground users are randomly distributed in the target area. In the current time slot, if a user is within the coverage range of an UAV, the swarm of UAVs is considered to be providing coverage for the user. Our task is for all UAVs to move around the target area and simultaneously provide network coverage services to ground users within the flight cycle D. The position of the UAV in time slot t is represented by the 3D Cartesian coordinate system [x[t], y[t], z[t]]T, where . x[t], y[t], and z[t], respectively, represent the horizontal x-coordinate, horizontal y-coordinate, and vertical z-coordinate of a UAV. Since the flight of UAVs in this paper is divided into horizontal flight and vertical flight, the horizontal coordinates of the UAV need to be separately represented as ω[t] = [x[t], y[t]]T, where . Users are represented by the set , and their positions are represented by horizontal coordinates q[k] = [x[k], y[k]]T, where .
3.1. Fairness Model
Our characterization of fairness consists of two important indicators. First, the overall situation of UAV coverage for each user is measured using the average coverage score. In any time slot t, if a user falls within the coverage area of a UAV, the user’s device is considered to be covered in the current time slot. Therefore, we obtain the coverage score for a single user as follows:
where is the number of time slots in which user k is covered during the flight cycle D, and . From this, we obtain the average coverage score for all users as:
In addition, in order to ensure fair service for each user, it is necessary to consider the issue of geographical fairness. If the UAVs are less inclined serve certain users (who may be in a remote location, for example) due to an increased consumption of flight resources, then even if the overall coverage score is high, it cannot be guaranteed that every user will receive relatively fair service, and some users may never receive service.
In order to ensure that every user is able to communicate, we refer to the Jain fairness index to characterize geographical fairness [29]. The Jain fairness index is a standard for measuring fairness in a network. It considers all users in the system, not just those who are assigned the least resources [30]. The value of the Jain fairness index is always between 0 and 1, where 1 represents absolute fairness. In this paper, the fairness index is defined as:
3.2. Energy Consumption Model
Due to the fact that communication energy consumption is very small compared to the total energy consumption of UAVs, we only consider the flight energy consumption of UAVs. The battery energy E of the UAV is used for flight (flying to the next coordinate in the 3D Cartesian coordinate system) or hovering (maintaining a certain coordinate in the air without movement). The flight power of the UAV during time slot t is modeled as follows [31]:
where represents the induction power of the UAV in hover state, represents the average speed of the UAV rotor, and represents the disturbance parameter of the UAV speed. and , respectively, represent the horizontal flight speed and vertical flight speed of the UAV during time slot t. and represent the horizontal flight power and vertical flight power of the UAV. Therefore, the flight energy consumption of the UAV during time slot t can be obtained as follows:
Therefore, the flight energy consumption of the UAV during the entire flight cycle D can be expressed as:
We ignore the impact of clouds on solar energy collection and model the power of a UAV collecting solar energy at height z[t] during time slot t as [10]:
where is the energy conversion efficiency, S is the area of the solar panel, is the average solar radiation, is the maximum atmospheric transmittance, is the atmospheric extinction coefficient, and is the average atmospheric height. As can be seen from the above equation, UAVs can collect more solar energy at a higher altitude within a time slot unit. Therefore, the solar energy collected in time slot t can be expressed as:
From this, it can be concluded that the solar energy collected by the UAV during the entire flight cycle is:
3.3. Problem Statement
Combining the fairness model and the energy consumption model, we define the problem under study as a multi-objective joint optimization problem and set a series of constraints as follows:
Equations (11) and (12) represent the constraints on the horizontal flight speed and vertical flight speed of the UAV. Equation (13) represents the range of the UAV flight direction . Equation (14) limits the maximum and minimum values of the current flight altitude of the UAV. Equation (15) requires that the minimum distance between any two UAVs is greater than the maximum safety distance in order to prevent UAV collisions. Equation (16) requires that the distance between each UAV and at least one other UAV is within the communication range to ensure that each UAV in the UAV swarm can maintain communication; where , , .
4. Proposed Solution
This section proposes a multiple SP-UAV trajectory control scheme based on DRL to supply long-term coverage for users in the target area. We characterize the problem as a partially observable Markov decision process and design the observation space, state space, action space, and reward function. Finally, an algorithm based on the deep deterministic policy gradient (DDPG) is proposed in order to solve this problem.
4.1. DRL
Deep reinforcement learning, as an emerging paradigm, is being used to solve decision problems in complex state spaces, is attracting widespread attention from industry and academia, and is being tested for the optimization of UAV trajectories.
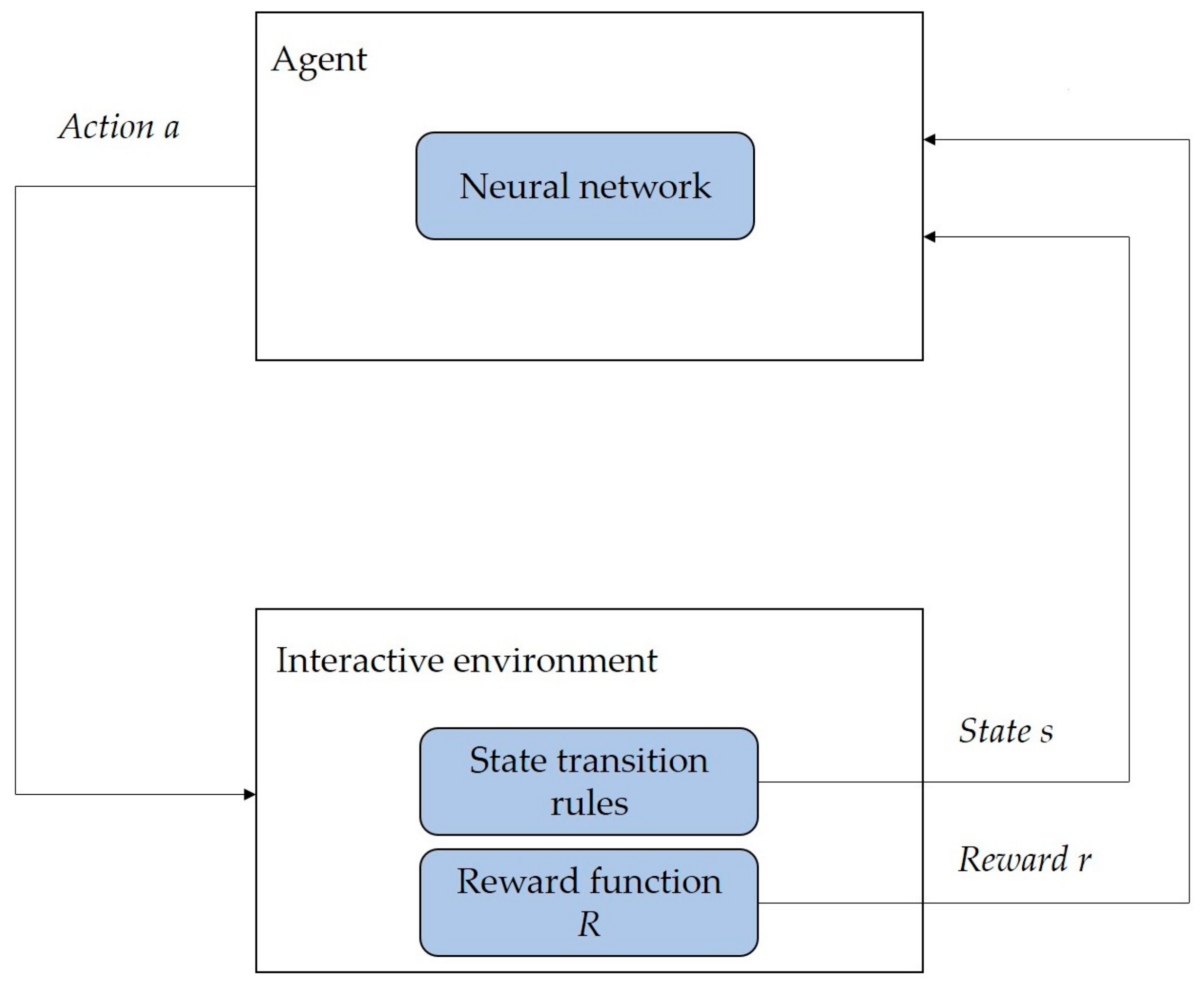
As shown in Figure 2, DRL usually consists of an agent and an interactive environment. The interactive environment includes reward function rules and state transition rules.
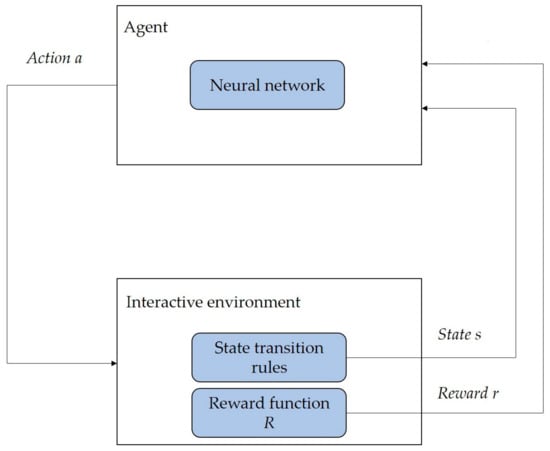
Figure 2.
Explanation of the basic principles of DRL.
The state–action–reward is a step in the training of DRL. The goal of DRL is to train the agent to take actions to maximize the reward. As shown in Figure 2, the agent obtains state s from the interactive environment and inputs action a to be executed to the interactive environment through a neural network. The interactive environment returns the obtained reward r on the basis of the reward function R and updates the state to the next state on the basis of the state transition rules.
DRL typically models a problem as a Markov decision process, which refers to the current state , action , reward , and the next state as an ancestor . Through the continuous cycle of state action reward steps, the agent is fully trained to explore the best strategy to maximize the cumulative reward R, that is, to explore the best strategy to achieve the set goal [32].
where represents the decay factor, which allows the cumulative reward R to converge to an upper bound and represents the decreasing influence of future rewards on R.
4.2. DDPG
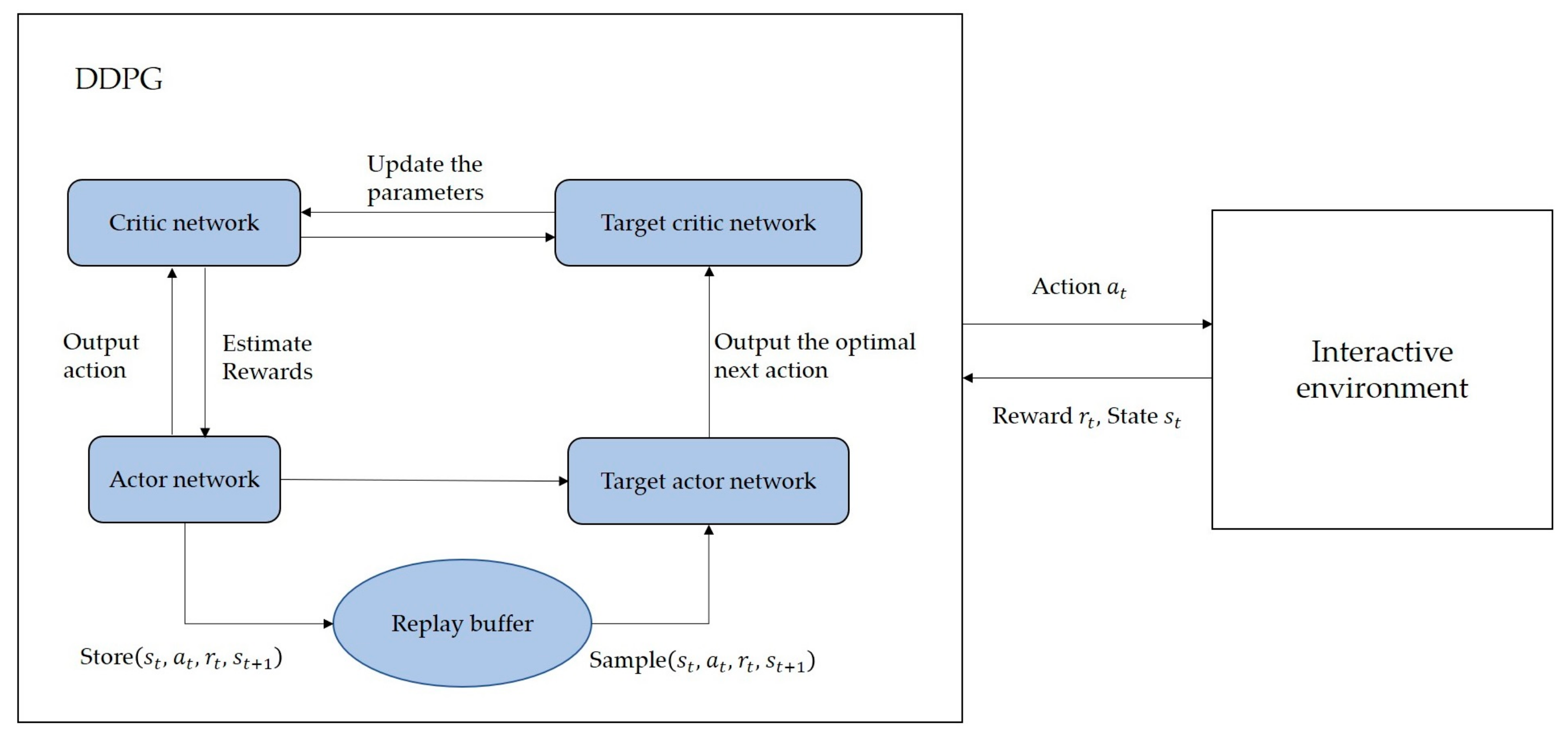
DDPG is a DRL algorithm used to solve continuous control problems and is highly suitable for the model in this article. As shown in Figure 3, the core of DDPG includes experience replay and target network, both of which function similarly to the agent in DRL.
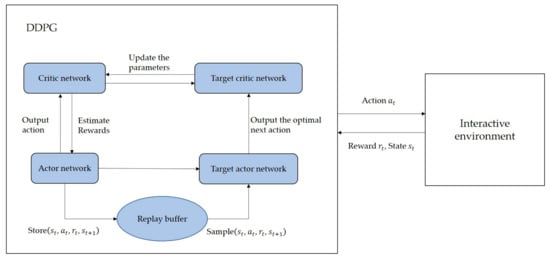
Figure 3.
Explanation of the basic principles of DDPG.
4.2.1. Experience Replay
Experience replay refers to the agent storing the training quadruple into an experience replay buffer and randomly selecting multiple sets of from the experience replay buffer during training. The existence of the experience replay buffer stabilizes the probability distribution of experiences, thereby improving the stability of the training.
4.2.2. Target Network
As shown in Figure 3, the network structure system of the DDPG algorithm consists of an actor network, a critic network, and their corresponding target actor network and target critic network. The actor network is used to output the action , the critic network estimates the reward obtained by the current action, the target actor network chooses the optimal next action according to the next state sampled from the experience replay buffer, and the target critic network updates the parameters in the critic network.
4.3. Trajectory Optimization Algorithm Based on DDPG
We designed an algorithm suitable for the model in this research based on DDPG. The optimization objective of the algorithm is to find the optimal policy that maximizes the cumulative reward R, which in this paper means finding the optimal flight trajectory that maximizes the optimization objective in problem P1.
This section designs the observation space , state space , action space 𝒜, and reward function R and provides a detailed introduction to the algorithm in this article, as well as complexity analysis.
4.3.1. Observation Space and State Space
For each UAV at time slot t, its observation space contains three elements: the UAV’s position, the remaining energy of the battery carried by the UAV, and the coverage of the user (referring to the total time slots covered by the user from the UAV’s launch to the current time slot). In the scenario set out in this paper, the environment is partially observable. The state space is the set of all possible states, which summarizes the current environment and is the basis for the agent’s decision-making. The state space includes the space observed by the UAV and the energy consumption of the UAV in the current time slot, as described in Table 1.

Table 1.
Explains the notations, explanations, and value ranges of each quantity in the state space.
Where represents the boundary of the maximum horizontal flight area of the UAV set in this article, represents the maximum power of the UAV battery, and represents the maximum operating time of the UAV set in this paper. Therefore, state space can be defined as:
4.3.2. Action Space 𝒜
Action space represents the set of all possible actions. For each UAV at time slot t, its action space consists of three parts, namely the direction of the UAV’s horizontal movement, the distance of the UAV’s horizontal movement, and the distance of the UAV’s vertical movement. The specific description is shown in Table 2.

Table 2.
Explains the notations, explanations, and value ranges of each quantity in the action space.
Therefore, action space can be defined as:
4.3.3. Reward Function
We assume that the UAV observes the state and takes action at the beginning of each time slot. Then, it transitions to state based on . represents the expected immediate reward received by the UAV after transitioning from state to by taking action . For each UAV, we take into account coverage and fairness and define the real-time coverage efficiency as follows:
The reward function in this article consists of three parts. The first part is coverage efficiency, which includes two indicators: coverage score and fairness index, where .
The second part defines the reward function that represents the relative energy consumption of the UAVs. Since SP-UAVs are used in the model of this paper, the relative energy consumption of the UAV swarm is made up of the energy consumed by the UAV’s flight and the energy supplemented by solar power. In this paper, relative energy consumption is defined as the ratio of collected solar energy to flight energy consumption. Here, we consider the overall relative energy consumption, because using the relative energy consumption of a single UAV instead of the overall relative energy consumption in the reward function may lead to a situation where one UAV has a high relative energy consumption while the relative energy consumptions of other UAVs are low. This will cause one UAV to quickly run out of power. Considering the overall relative energy consumption, however, will result in the remaining energy consumption of each UAV being more balanced, thereby extending the lifetimes of the UAVs.
The third part sets a penalty term , where when the UAV is flying within the target area. When the UAV flies out of the target area, will be equal to a constant V, and the reward obtained for this action will decrease accordingly, encouraging the UAV to avoid actions that will cause it to fly out of the target area insofar as possible. It is worth noting that we do not set penalty terms for UAV collisions or disconnections, because these two situations are not tolerable in the context of this paper. Once a UAV collides or loses connection, the flight cycle of the UAV swarm will immediately stop, and the lifetime will be limited to the current total number of time slots. Therefore, the obtained reward and penalty functions are as follows:
4.3.4. Basic Idea
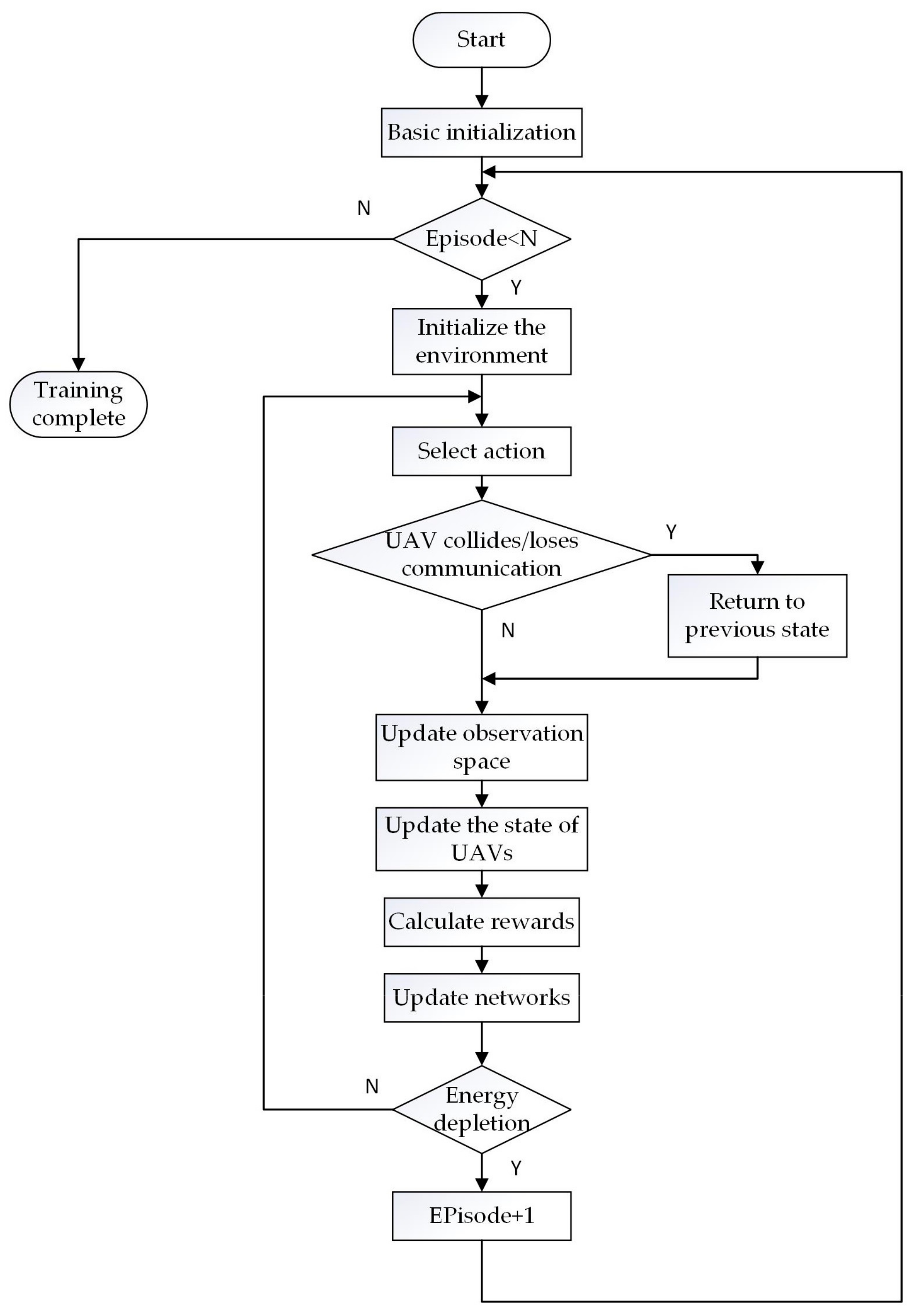
The flowchart of the trajectory optimization algorithm based on DDPG designed in this paper is shown in Figure 4. The algorithm is composed of two nested loops. The outer loop iterates N times to train the model proposed in this paper. As the number of iterations in the outer loop increases, we can determine whether the training has reached convergence based on the trend of reward changes. The inner loop represents a single training process in a specific scenario, which continues until the energy of a UAV in the system is depleted. In the inner loop process, the algorithm performs steps such as action selection, collision avoidance, communication control, and reward calculation and updates the state space and network.

Figure 4.
Explanation of the flow of our algorithm.
4.3.5. Overall Algorithm
The specific description of our algorithm is shown in Algorithm 1. Initially, in line 1, the experience replay buffer B is initialized. In lines 2–4, the actor and critic networks are randomly initialized.
The training loop of the algorithm is located in lines 5–27, and each iteration of the loop trains the DRL network model once. This algorithm sets N scenarios for training simulations. In line 6, the parameters of each scenario are initialized. In line 7, a parameter called ‘done’ is set to determine the termination condition for the current scenario’s training. Once a UAV runs out of energy, the training for that scenario is terminated. In lines 8–10, each UAV selects an action based on the exploration rate from either free movement or the deep learning network. In lines 11–13, we check whether there is any collision between UAVs and whether the communication between the UAV group is stable during this time slot. In line 14, we update the observation space for the user coverage, which indicates how many time slots each user has been covered from the beginning of the mission to the current time slot. In line 15, we use the newly obtained state to replace the current state of the UAV. In lines 16–17, we calculate the coverage score for each user, then obtain the overall coverage score and fairness index of the system, and finally, calculate the total reward for the current UAV group. In lines 18–20, we check whether there are any UAV power outages that would result in the end of the system’s flight cycle.
Finally, in lines 21–25, the parameters of the actor network, critic network, and target network are updated.
| Algorithm 1 3D trajectory optimization algorithm based on DDPG |
| 1: Initialize the experience replay buffer B 2: FOR UAV = 1, …, M DO 3: Randomly initialize actor network and critic network 4: END FOR 5: FOR episode = 1, …, N DO 6: Initialize the environment 7: WHILE done==FALSE 8: FOR UAV = 1, …, M DO 9: select an action 10: END FOR 11: IF D_m1_m2 < OR all the distances between any UAV and another > THEN 12: Return all UAVs to their previous state positions, and this action is invalidated 13: END IF 14: Update user coverage in the observation space 15: Update the current status of each UAV ← 16: Calculate coverage scores for all users, fairness index 17: Calculate overall rewards 18: IF any UAV runs out of energy THEN 19: done = TRUE 20: END IF 21: FOR UAV = 1, …, M DO 22: Update actor network 23: Update critic network 24: Update target actor network and target critic network 25: END FOR 26: END WHILE 27: END FOR |
4.3.6. Complexity Analysis
After sufficient training, the model proposed in this paper, including the networks, was used for testing. In each time slot, all UAV actions were generated by the actor network instead of being selected from random actions. In this article, the time complexity for the UAV to select actions from the actor network is . Where G is the number of network layers in the deep learning network, and g is the number of neurons in layer G. The time complexity of determining whether the UAV has collided and is within a reasonable communication distance is . The time complexity of updating user coverage in observation space is . Therefore, our algorithm’s time complexity is .
5. Performance Evaluation
In this section, in order to show the feasibility of the proposed solution and the superiority of our algorithm, we first trained our model on a smaller scale and conducted numerical simulation experiments. Afterwards, we expanded the size of the target range and conducted further experiments using a dataset from the Melbourne CBD, Australia. Considering the actual application situation, all UAVs are set to take off from the same location in the numerical simulation experiments. All users are randomly placed at the beginning of each training session and are distributed within a square area of 100 × 100 m2. Table 3 lists the important parameters used in this paper.

Table 3.
List of important parameters in this article.
Where parameters , , , , , , and related to UAV flight are taken from references [31,33] and fine-tuned according to the actual situation. and are taken from references [34,35] and fine-tuned according to the actual situation. Parameters , , , , , and related to solar charging are taken from reference [10].
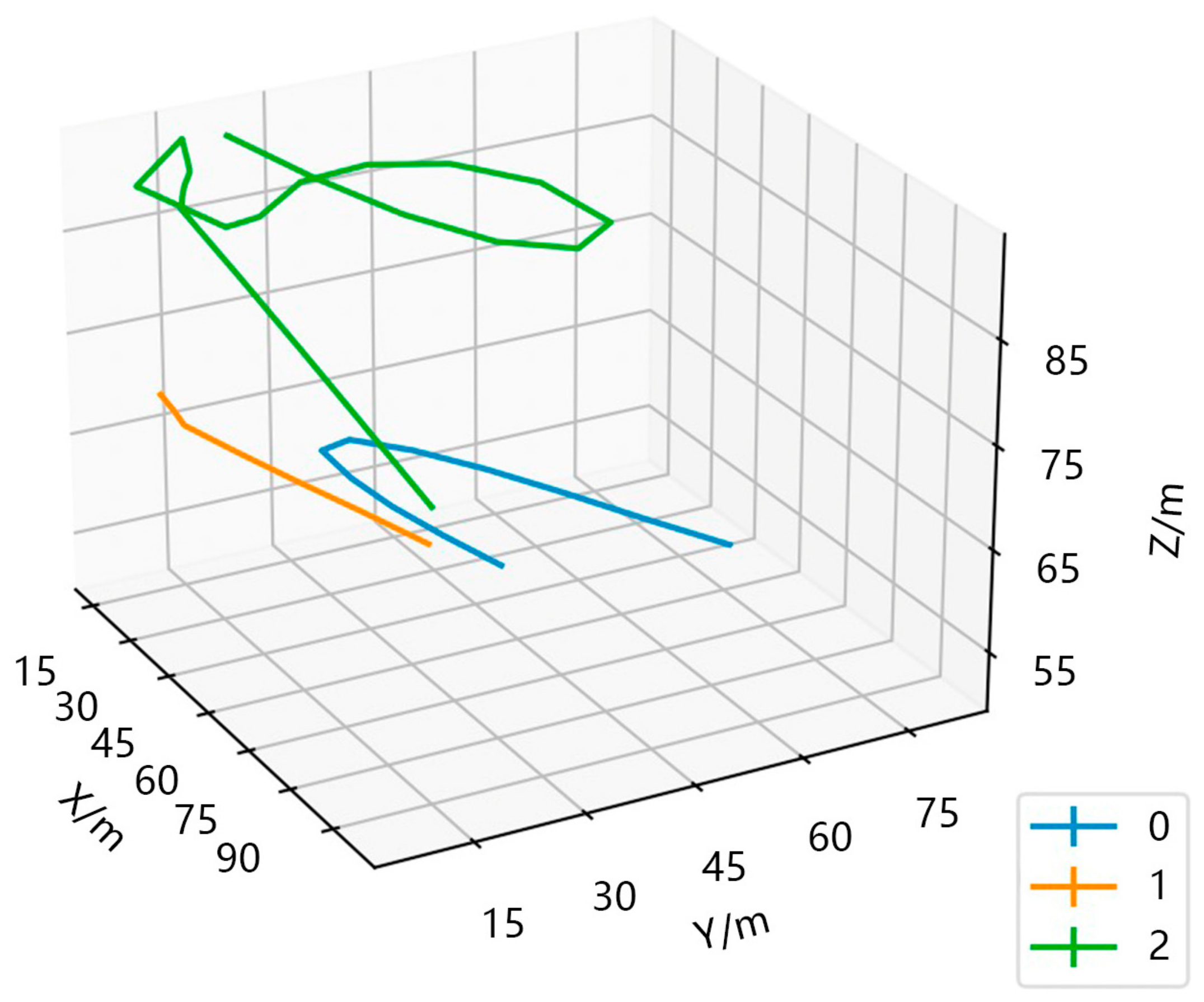
The initial flight height of all UAVs was set to 50 m, and the maximum and minimum flight heights were set to 100 m and 50 m, respectively. Within 400 time slots, a UAV at its maximum flight altitude received an additional 37.87 W of energy compared to a UAV at its lowest flight altitude. When the maximum flight altitude was extended to 500 m, the UAV at the maximum flight altitude gained an additional 333.19 W of energy compared to the UAV at the lowest flight altitude. Figure 5 shows a set of flight trajectories from our simulation experiment. Due to its long flight distance, the UAV 2 increased flight altitude to collect more solar energy. However, UAVs 0 and 1 had shorter flight distances and remained at lower altitudes to expand their coverage area.
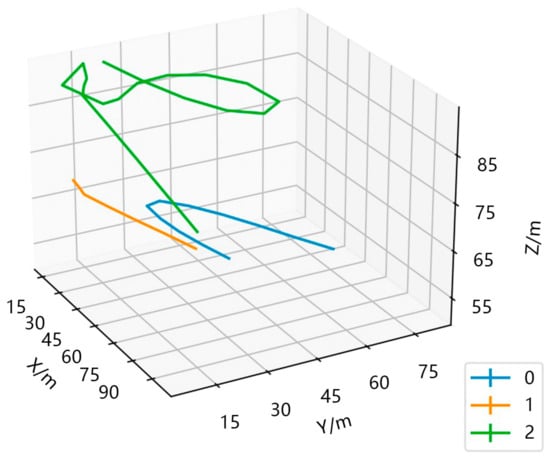
Figure 5.
A set of flight trajectories in our simulation experiment.
5.1. Neural Network Convergence
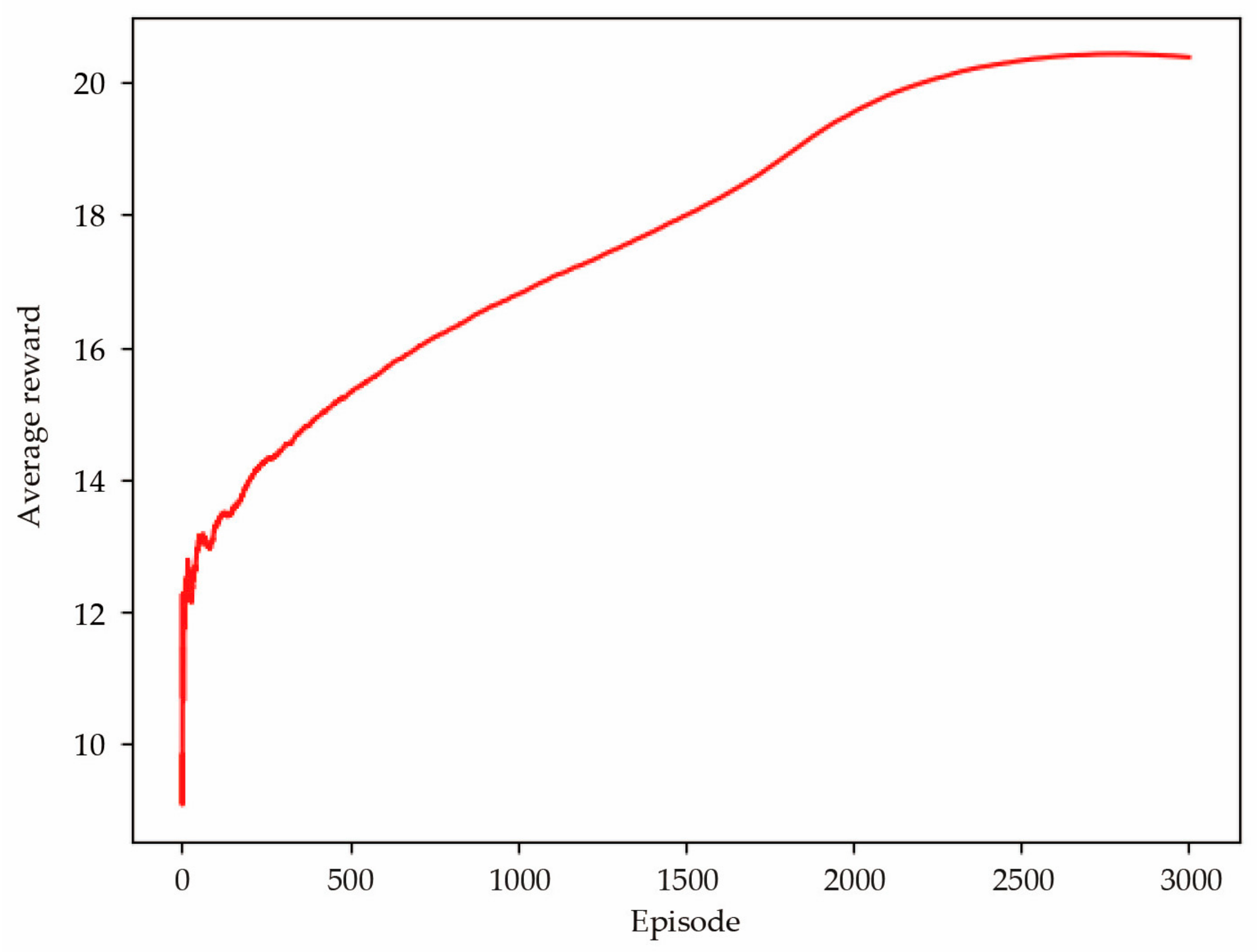
In this section, we first demonstrate the convergence of the proposed model, as shown in Figure 6. During the first 300 iterations, the average reward fluctuated and gradually increased. After 300 training sessions, it steadily increased and tended to stabilize. This is because at the beginning of each training session, all UAVs took off from a fixed location and users were randomly distributed. This uncertainty made the network unable to select appropriate actions for UAVs to provide high coverage and fairness to users during the early stages of training. As the number of training sessions increased, the model became more mature and UAVs selected appropriate actions through the network to complete tasks, resulting in a steady increase in rewards. The figure clearly shows that the average reward obtained no longer increases significantly after the number of training sessions reaches 2500 and the trained model converged.
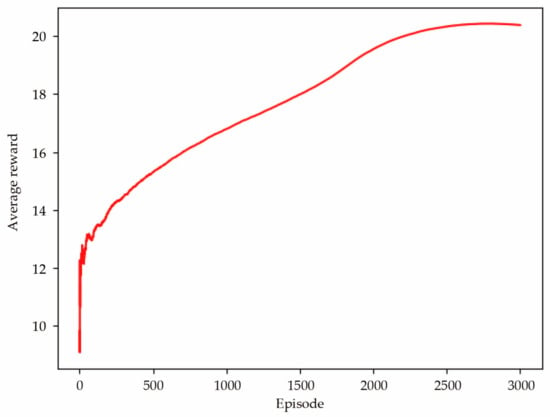
Figure 6.
The trend of average reward increasing with episode.
5.2. Comparative Experiment
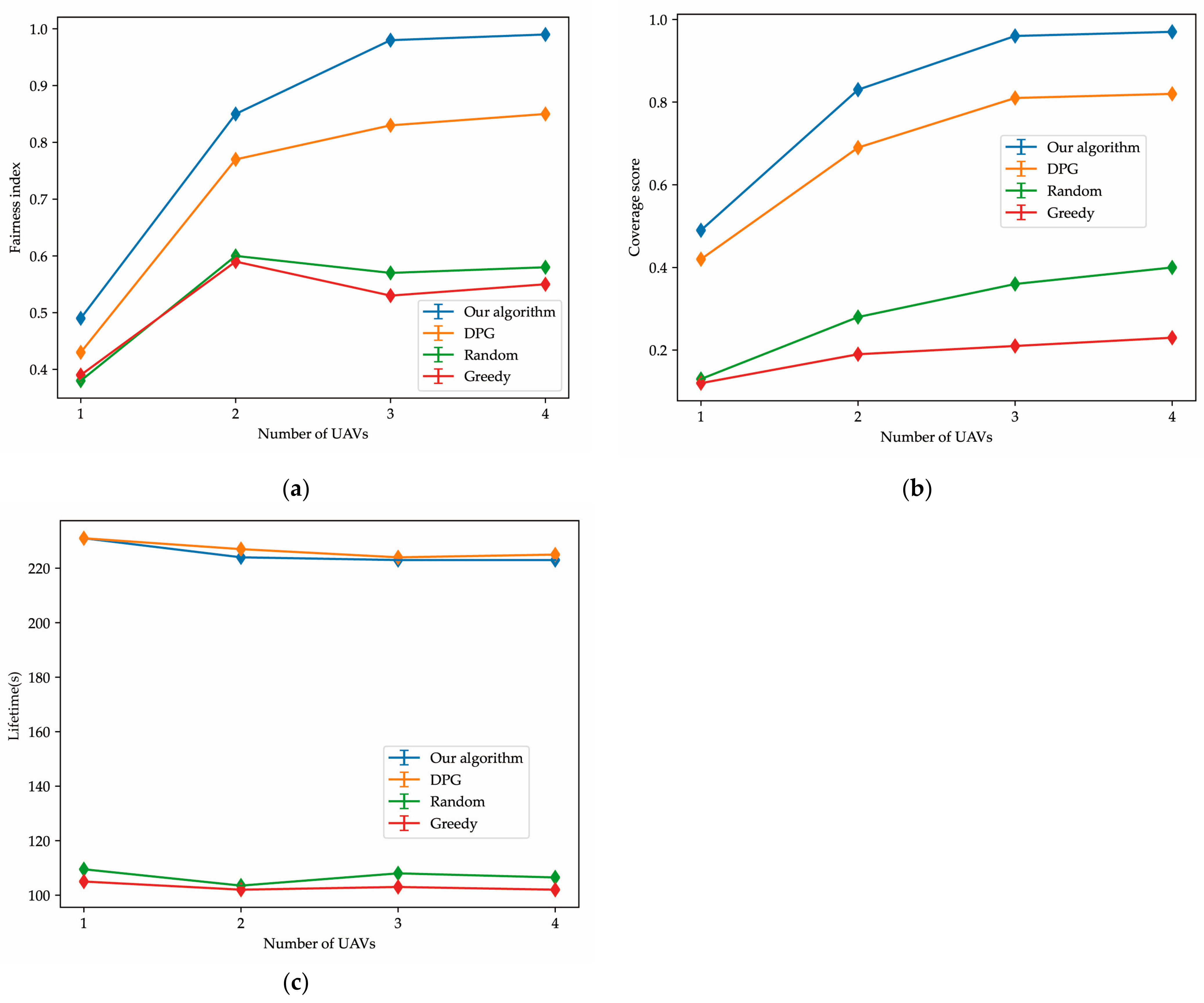
In this section, we compared our proposed approach with three typical solutions. As shown in Figure 7, we first studied the effect of the number of UAVs on the three important indicators of our problem. Figure 7a shows that as the number of UAVs increases from 1 to 4, our algorithm improves the fairness index to 0.49, 0.85, 0.98, and 0.99, respectively, which is better than the other algorithms. Figure 7b shows that our algorithm improves the coverage score to 0.49, 0.83, 0.96, and 0.97, which is better than the other three comparison algorithms. This indicates that as the number of UAVs increases, our algorithm performs better in overall coverage than the other three algorithms and can achieve the near-complete coverage of users in the target area when the number of UAVs reaches 3. Figure 7c also shows that the random exploration algorithm and the greedy algorithm have a significant disadvantage in terms of lifetime compared to our proposed algorithm and the DPG algorithm. This is because the selection of random exploration actions may cause UAVs to fly out of bounds, lose connection with other UAVs, and cause the overall network to end quickly, while the greedy algorithm may get trapped in local optima due to its excessive consideration of coverage score and fairness during the exploration process.
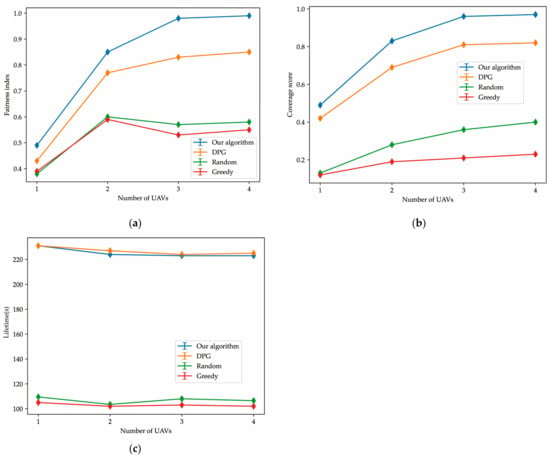
Figure 7.
(a) Fairness index trend changing with the number of UAVs changes; (b) coverage score trend changing with the number of UAVs changes; (c) lifetime trend changing with the number of UAVs changes.
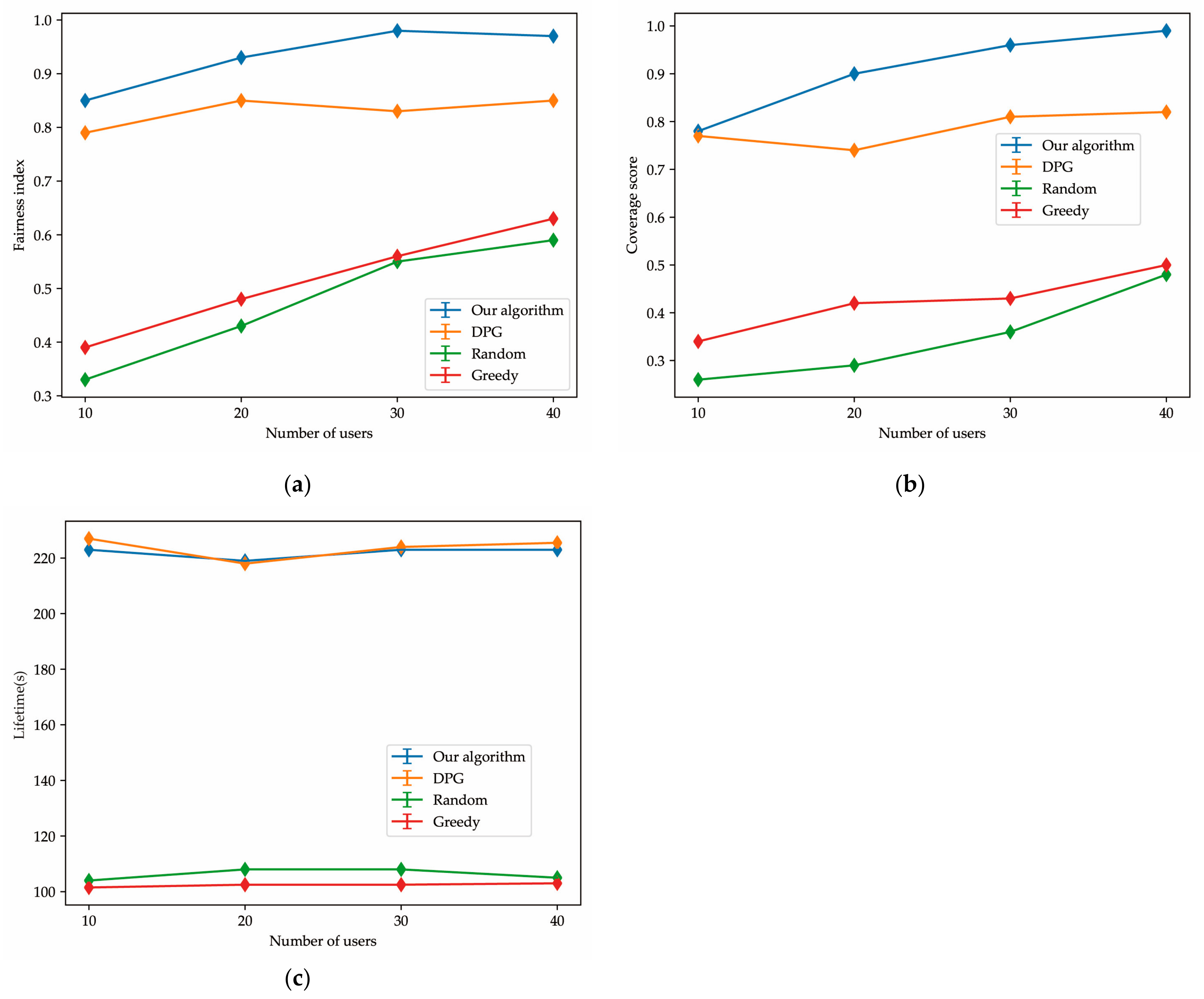
Figure 8a–c shows the effect of the increase in the number of users on the optimization problem in this article. We gradually increase the number of randomly distributed users from 10 to 40 to verify the superiority of our algorithm. Figure 8b shows that our algorithm is significantly superior to the other three algorithms in terms of coverage. As can be seen from Figure 8c, our algorithm is not significantly different from the deterministic strategy gradient algorithm in terms of lifetime, but both Figure 8a and Figure 8b show that the algorithm in this paper is superior to the deterministic strategy gradient algorithm in terms of coverage score and fairness index. By synthesizing Figure 7 and Figure 8, it can be proven that the algorithm in this paper has obvious advantages over the other three algorithms in the context of simulation experiments.
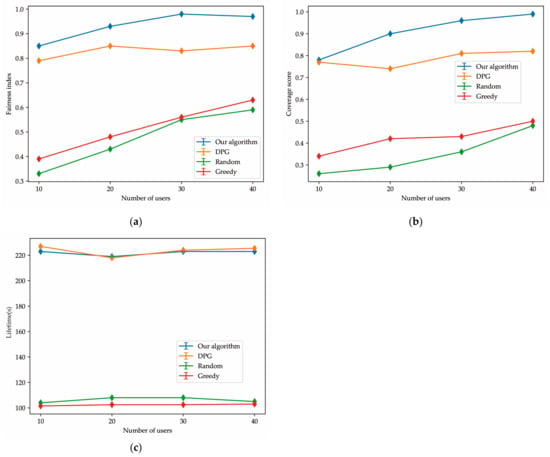
Figure 8.
(a) Fairness index trend changing with the number of users changes; (b) coverage score trend changing with the number of users changes; (c) lifetime trend changing with the number of users changes.
Based on the analysis of the above experimental results, we can conclude that the UAV actions designated by the random algorithm cannot effectively prevent a UAV from flying out of the target area or losing communication. Greedy algorithms are prone to falling into local optima, leading to the premature power outage of a UAV. Compared to the DPG algorithm, our algorithm adds two target networks, which can improve the stability and convergence of the actor network and the critic network. Meanwhile, compared to the DPG algorithm, our algorithm is more conducive to handling continuous action problems. So, our algorithm exhibits the best optimization results.
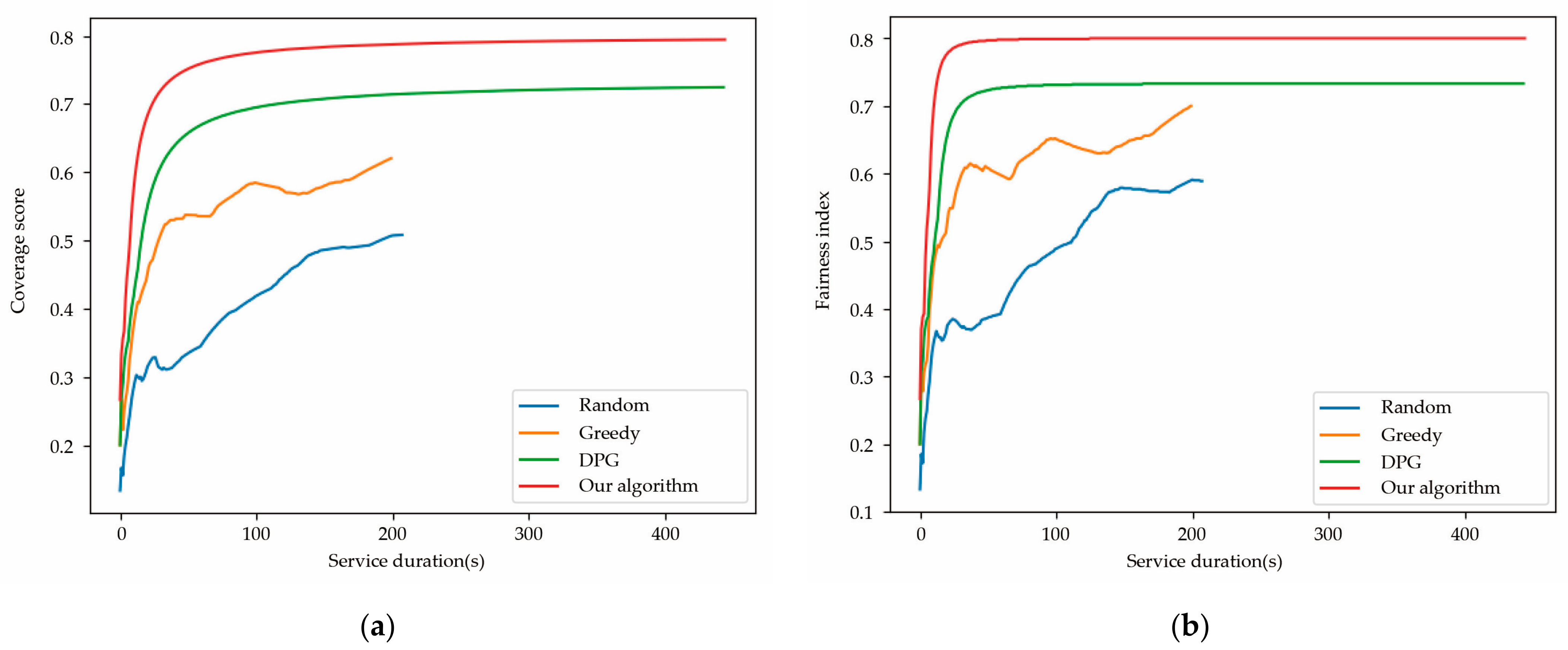
Without a loss of generality, we used a dataset from the Melbourne CBD area in Australia for further experiments to verify the feasibility of the model and algorithm in this paper. We selected a 1000 × 1000 m2 area, using 20 UAVs to provide coverage services to 312 users within the area. The UAVs were evenly divided into five groups, taking off from the four corners and center points of the target area. Figure 9a,b show that using the UAV flight trajectory provided by the greedy algorithm and the random exploration algorithm, the UAV swarm ended its work in the 198th and 207th time slots, respectively. This is because one of the UAVs in the swarm ran out of battery, which prevented the other UAVs from establishing a stable network connection. However, the DPG algorithm and our proposed algorithm have a significant advantage in terms of lifetime, and they both maintained a stable working state even after 400 time slots. In the environment of this dataset, our proposed algorithm achieves a coverage score and fairness index of over 0.8, while the DPG algorithm only achieves 0.7, indicating that our algorithm performs better in coverage than the DPG algorithm. In summary, our algorithm performs better in coverage and lifetime than the other three comparison algorithms and has good performance.
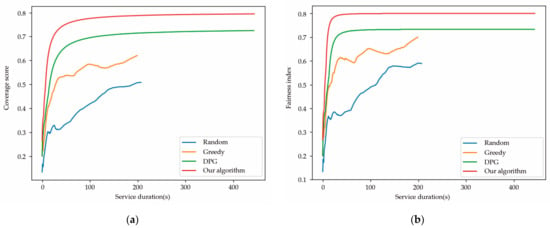
Figure 9.
(a) Coverage score trend changing with the number of service duration increases; (b) fairness index trend changing with the number of service duration increases.
6. Conclusions
In this paper, we considered the problem of flight trajectory optimization using multiple SP-UAV to achieve the network coverage of the target area. We established a mathematical model based on the actual environment and the actual parameters of the UAV. Considering the issues of coverage, coverage fairness, system lifetime, and UAV collision avoidance, we defined observation space, state space, action space, and reward functions and designed a trajectory optimization algorithm based on DDPG to solve this problem. We conducted a multitude of simulation experiments and verified the rationality of the algorithm in practical applications through specific urban datasets. Experimental results show that the trajectory optimization scheme in this paper has significant advantages.
In future work, our research will extend in two directions. The first direction is to consider user mobility and line of sight communication between UAVs and users based on current research. The second direction is to consider maximizing the number of rescue personnel and minimizing rescue time [36] in the context of UAV disaster relief.
Author Contributions
Conceptualization, S.C. and J.L.; methodology, S.C.; software, S.C.; validation, S.C.; formal analysis, S.C. and J.L.; investigation, S.C.; resources, S.C.; data curation, S.C.; writing—original draft preparation, S.C.; writing—review and editing, S.C. and J.L.; visualization, S.C.; supervision, S.C. and J.L.; project administration, S.C. and J.L.; funding acquisition, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-Dense Networks: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Qiu, Y.; Liang, J.; Leung, V.C.M.; Wu, X.; Deng, X. Online Reliability-Enhanced Virtual Network Services Provisioning in Fault-Prone Mobile Edge Cloud. IEEE Trans. Wirel. Commun. 2022, 21, 7299–7313. [Google Scholar] [CrossRef]
- Li, M.; Cheng, N.; Gao, J.; Wang, Y.; Zhao, L.; Shen, X. Energy-Efficient UAV-Assisted Mobile Edge Computing: Resource Allocation and Trajectory Optimization. IEEE Trans. Veh. Technol. 2020, 69, 3424–3438. [Google Scholar] [CrossRef]
- Zhao, M.; Li, W.; Bao, L.; Luo, J.; He, Z.; Liu, D. Fairness-Aware Task Scheduling and Resource Allocation in UAV-Enabled Mobile Edge Computing Networks. IEEE Trans. Cogn. Commun. Netw. 2021, 5, 2174–2187. [Google Scholar] [CrossRef]
- Moradi, M.; Sundaresan, K.; Chai, E.; Rangarajan, S.; Mao, Z.M. Skycore: Moving Core to the Edge for Untethered and Reliable UAV-Based LTE Networks. Mob. Comput. Commun. Rev. 2019, 23, 24–29. [Google Scholar] [CrossRef]
- Liu, C.H.; He, T.; Lee, K.W.; Leung, K.K.; Swami, A. Dynamic Control of Data Ferries under Partial Observations. In Proceedings of the Wireless Communications & Networking Conference, Sydney, NSW, Australia, 18–21 April 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Zhao, N.; Li, Y.; Zhang, S.; Chen, Y.; Lu, W.; Wang, J.; Wang, X. Security Enhancement for NOMA-UAV Networks. IEEE Trans. Veh. Technol. 2020, 69, 3994–4005. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Zhao, N.; Chen, Y.; Zhang, S.; Ding, Z.; Yu, F.R. Placement and Power Allocation for NOMA-UAV Networks. IEEE Wirel. Commun. Lett. 2019, 8, 965–968. [Google Scholar] [CrossRef]
- Liu, C.H.; Ma, X.; Gao, X.; Tang, J. Distributed Energy-Efficient Multi-UAV Navigation for Long-Term Communication Coverage by Deep Reinforcement Learning. IEEE Trans. Mob. Comput. 2020, 19, 1274–1285. [Google Scholar] [CrossRef]
- Fu, Y.; Mei, H.; Wang, K.; Yang, K. Joint Optimization of 3D Trajectory and Scheduling for Solar-Powered UAV Systems. IEEE Trans. Veh. Technol. 2021, 70, 3972–3977. [Google Scholar] [CrossRef]
- Yin, S.; Zhao, S.; Zhao, Y.; Yu, F.R. Intelligent Trajectory Design in UAV-Aided Communications with Reinforcement Learning. IEEE Trans. Veh. Technol. 2019, 68, 8227–8231. [Google Scholar] [CrossRef]
- Qureshi, H.N.; Imran, A. On the Tradeoffs Between Coverage Radius, Altitude, and Beamwidth for Practical UAV Deployments. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2805–2821. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Khreishah, A.; Ji, B. UAVs to the Rescue: Prolonging the Lifetime of Wireless Devices Under Disaster Situations. IEEE Trans. Green Commun. Netw. 2019, 3, 942–954. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Chen, Y.; Wang, C.-X.; Ge, N. Maritime Coverage Enhancement Using UAVs Coordinated with Hybrid Satellite-Terrestrial Networks. IEEE Trans. Commun. 2020, 68, 2355–2369. [Google Scholar] [CrossRef]
- Zeng, F.; Hu, Z.; Xiao, Z.; Jiang, H.; Zhou, S.; Liu, W.; Liu, D. Resource Allocation and Trajectory Optimization for QoE Provisioning in Energy-Efficient UAV-Enabled Wireless Networks. IEEE Trans. Veh. Technol. 2020, 69, 7634–7647. [Google Scholar] [CrossRef]
- Yuan, X.; Feng, Z.; Ni, W.; Wei, Z.; Liu, R.P.; Xu, C. Connectivity of UAV Swarms in 3D Spherical Spaces Under (Un)Intentional Ground Interference. IEEE Trans. Veh. Technol. 2020, 69, 8792–8804. [Google Scholar] [CrossRef]
- Bhandarkar, A.B.; Jayaweera, S.K. Optimal Trajectory Learning for UAV-Mounted Mobile Base Stations using RL and Greedy Algorithms. In Proceedings of the 2021 17th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Bologna, Italy, 11–13 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 13–18. [Google Scholar]
- Darehnaei, Z.G.; Shokouhifar, M.; Yazdanjouei, H.; Fatemi, S.M.J.R. SI-EDTL: Swarm intelligence ensemble deep transfer learning for multiple vehicle detection in UAV images. Concurr. Comput. Pract. Exp. 2022, 34, e6726. [Google Scholar]
- Ye, Z.; Wang, K.; Chen, Y.; Jiang, X.; Song, G. Multi-UAV Navigation for Partially Observable Communication Coverage by Graph Reinforcement Learning. IEEE Trans. Mob. Comput. 2021. early access. [Google Scholar]
- Zhang, X.; Duan, L. Fast Deployment of UAV Networks for Optimal Wireless Coverage. IEEE Trans. Mob. Comput. 2018, 18, 588–601. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, Y.; Zhang, R. UAV-Enabled Wireless Power Transfer: Trajectory Design and Energy Optimization. IEEE Trans. Wirel. Commun. 2018, 17, 5092–5106. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Xu, J.; Schmeink, A. Optimal 1D Trajectory Design for UAV-Enabled Multiuser Wireless Power Transfer. arXiv 2018, arXiv:1811.00471. [Google Scholar]
- Dai, H.; Zhang, H.; Hua, M.; Li, C.; Huang, Y.; Wang, B. How to Deploy Multiple UAVs for Providing Communication Service in an Unknown Region? Wirel. Commun. Lett. IEEE 2019, 8, 1276–1279. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K.-K. UAV-Assisted Emergency Networks in Disasters. IEEE Wirel. Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
- Qin, Z.; Dong, C.; Li, A.; Dai, H.; Wu, Q.; Xu, A. Trajectory Planning for Reconnaissance Mission Based on Fair-Energy UAVs Cooperation. IEEE Access 2019, 7, 91120–91133. [Google Scholar] [CrossRef]
- Qi, H.; Hu, Z.; Huang, H.; Wen, X.; Lu, Z. Energy Efficient 3-D UAV Control for Persistent Communication Service and Fairness: A Deep Reinforcement Learning Approach. IEEE Access 2020, 8, 53172–53184. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Zhou, M. Fair energy-efficient resource optimization for green Multi-NOMA-UAV assisted internet of things. IEEE Trans. Green Commun. Netw. 2021. early access. [Google Scholar]
- Liu, Y.; Huangfu, W.; Zhou, H.; Zhang, H.; Liu, J.; Long, K. Fair and Energy-efficient Coverage Optimization for UAV Placement. IEEE Trans. Commun. 2022, 70, 4222–4235. [Google Scholar]
- Sediq, A.B.; Gohary, R.H.; Schoenen, R.; Yanikomeroglu, H. Optimal Tradeoff Between Sum-Rate Efficiency and Jain\”s Fairness Index in Resource Allocation. IEEE Trans. Wirel. Commun. 2013, 12, 3496–3509. [Google Scholar] [CrossRef]
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness And Discrimination For Resource Allocation In Shared Computer Systems. arXiv 1998, arXiv:cs.ni/9809099. [Google Scholar]
- Lv, Z.; Hao, J.; Guo, Y. Energy minimization for MEC-enabled cellular-connected UAV: Trajectory optimization and resource scheduling. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 478–483. [Google Scholar]
- Huang, Z.; Zhang, J.; Tian, R.; Zhang, Y. End-to-end autonomous driving decision based on deep reinforcement learning. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 658–662. [Google Scholar]
- Dai, Z.; Liu, C.H.; Han, R.; Wang, G.; Leung, K.K.; Tang, J. Delay-sensitive energy-efficient uav crowdsensing by deep reinforcement learning. IEEE Trans. Mob. Comput. 2021, 22, 2038–2052. [Google Scholar] [CrossRef]
- Luo, Y.; Ding, W.; Zhang, B. Optimization of task scheduling and dynamic service strategy for multi-UAV-enabled mobile-edge computing system. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 970–984. [Google Scholar] [CrossRef]
- Wang, L.; Wang, K.; Pan, C.; Xu, W.; Aslam, N.; Hanzo, L. Multi-agent deep reinforcement learning-based trajectory planning for multi-UAV assisted mobile edge computing. IEEE Trans. Cogn. Commun. Netw. 2020, 7, 73–84. [Google Scholar] [CrossRef]
- Goli, A.; Malmir, B. A covering tour approach for disaster relief locating and routing with fuzzy demand. Int. J. Intell. Transp. Syst. Res. 2020, 18, 140–152. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).