Multi-Frequency Fringe Projection Profilometry: Phase Error Suppression Based on Cycle Count Adjustment
Abstract
1. Introduction
2. Principle of Heterodyne Phase Unwrapping
2.1. Solution of Phase Principal Value
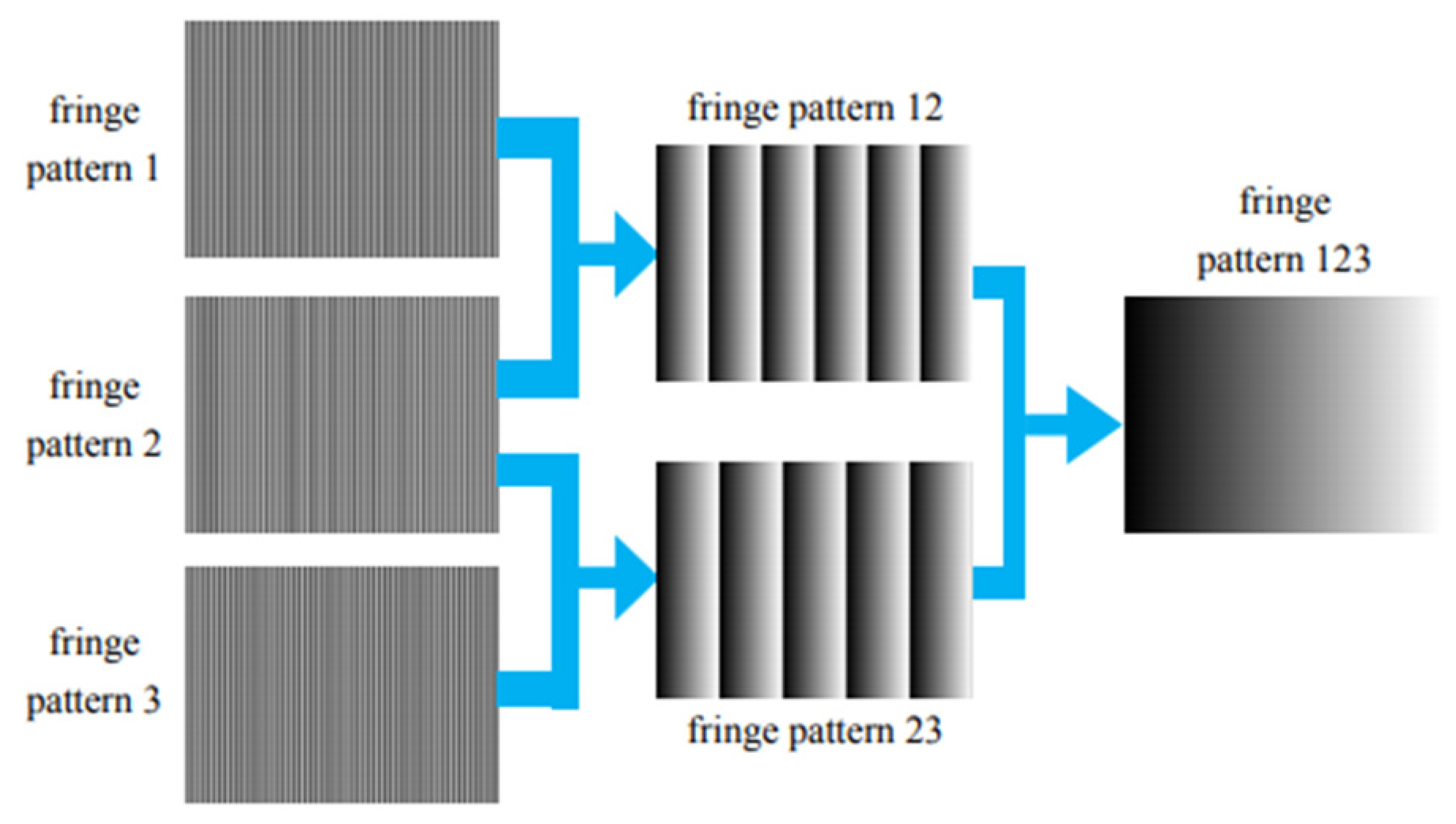
2.2. Principle of Heterodyne Phase Unwrapping
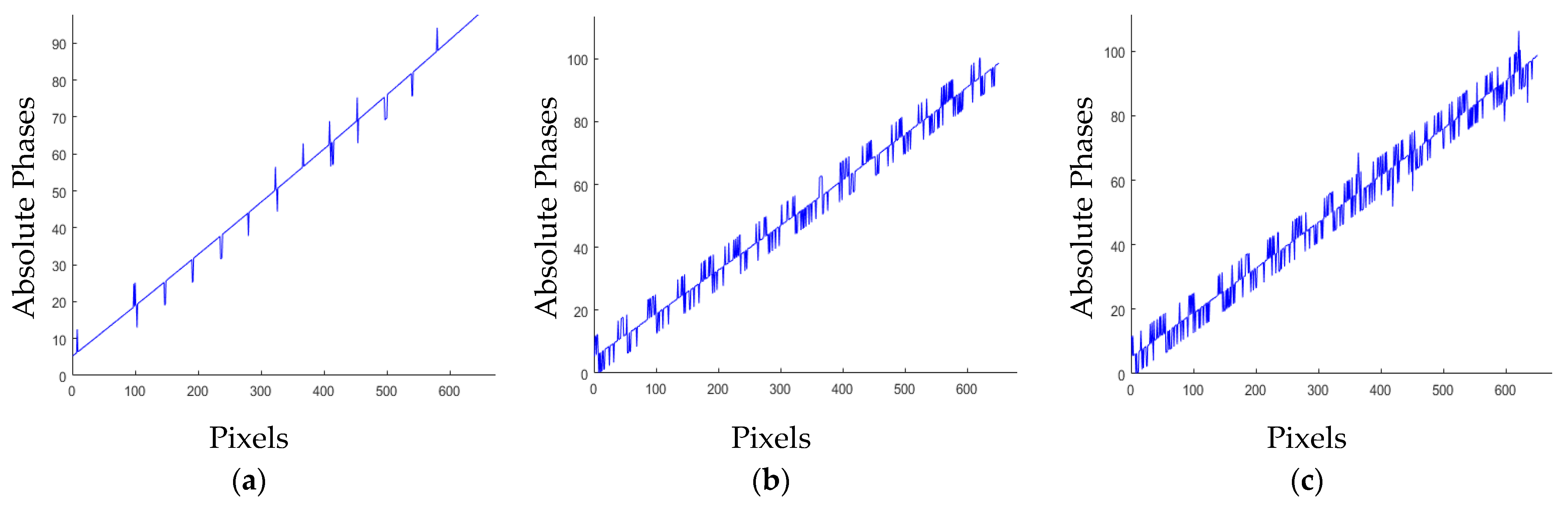
2.3. Error Analysis
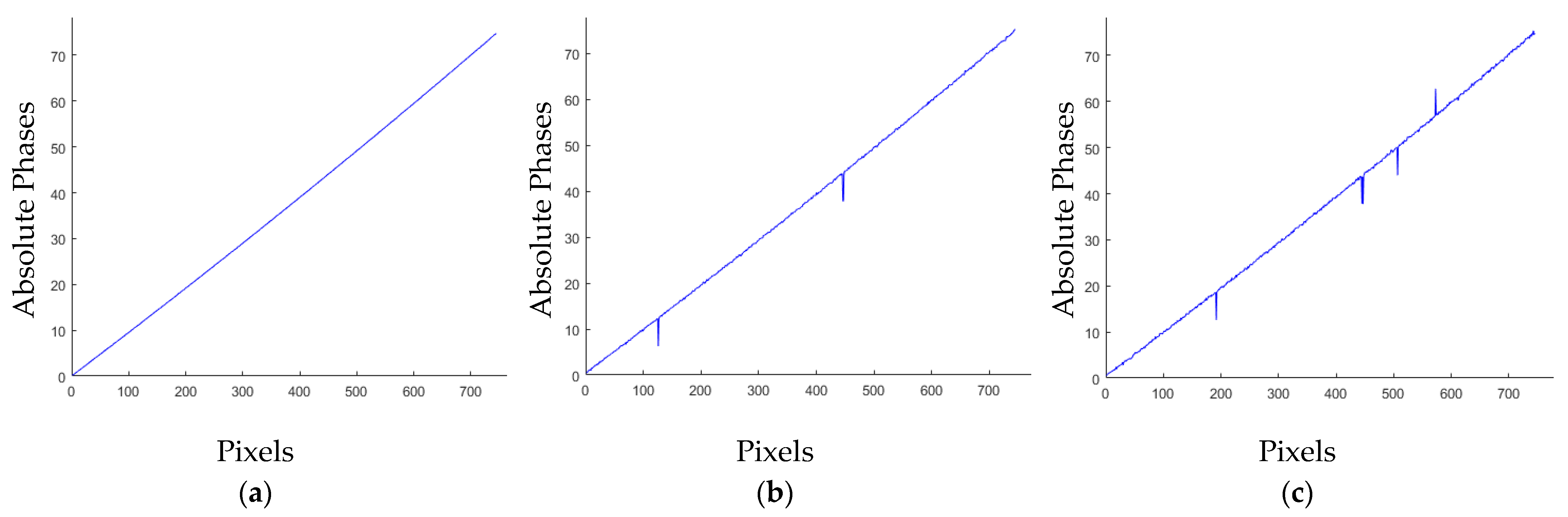
- If |Δn12r − Δn12t| < T, the cycle will jump accurately and no adjustment is needed.
- If |Δn12r − Δn12t| ≥ T and Δn12r − Δn12t > 0, the cycle will jump upward and the number of cycles will be minus one.
- If |Δn12r − Δn12t| ≥ T and Δn12r − Δn12t ≤ 0, the cycle will jump downward and the number of cycles will be plus one.
3. Experiments and Result Analysis
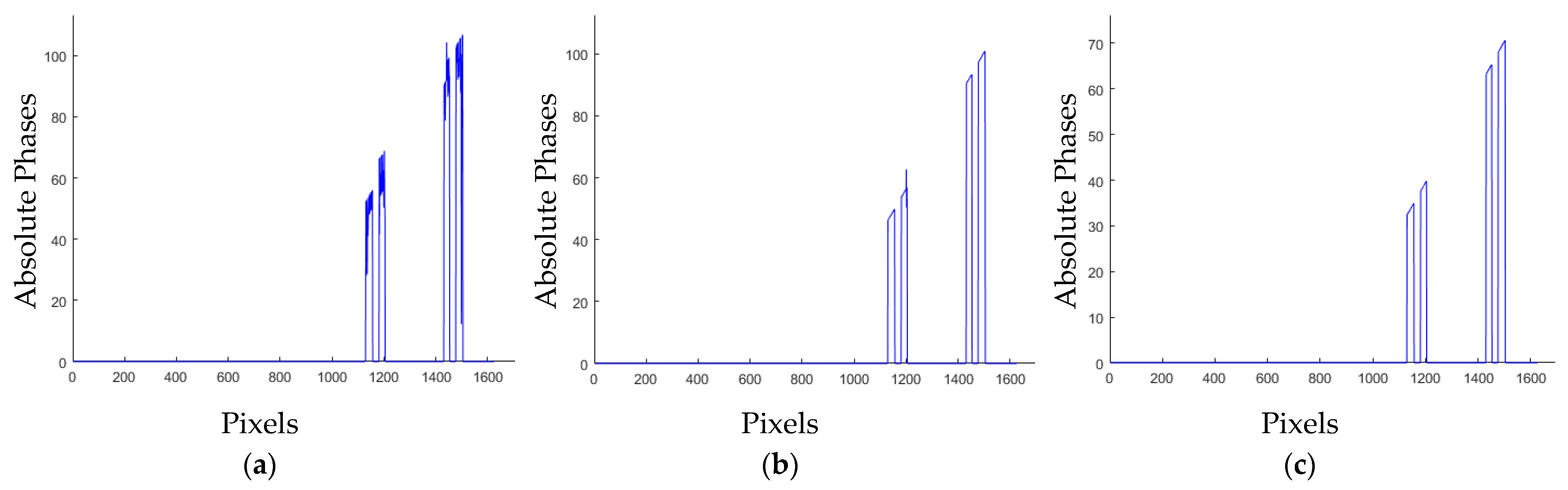
3.1. Simulation Experiments
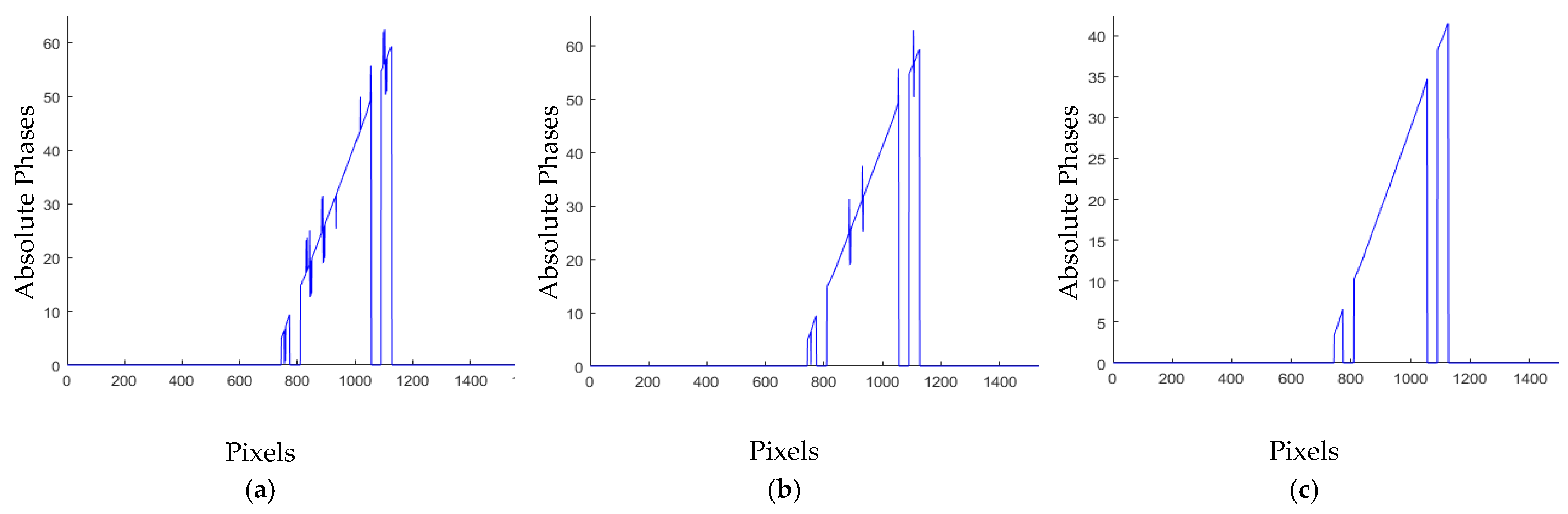
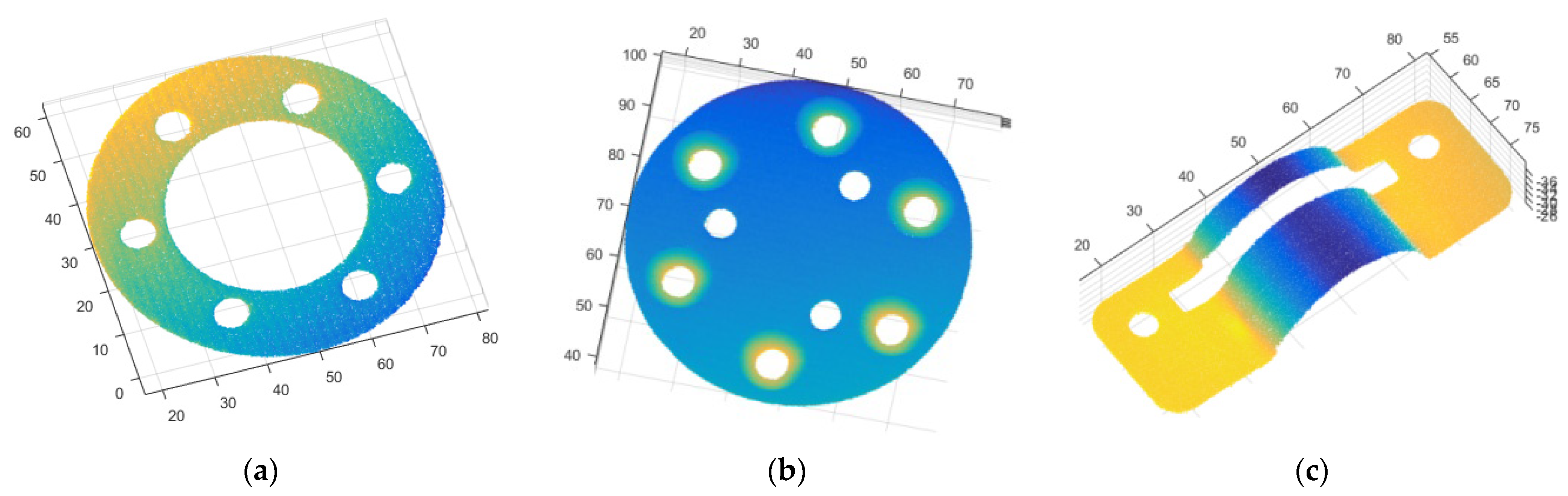
3.2. Real Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Guo, W.; Shen, J.; Wu, Z.; Zhang, Q. Motion-Induced Phase Error Compensation Using Three-Stream Neural Networks. Appl. Sci. 2022, 12, 8114. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Y.; Wu, J.; Jiang, G. Dual-frequency fringe Fourier transform profilometry based on defocusing. Opt. Commun. 2013, 295, 92–98. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Y.; Wan, Y.; Luo, L.; Peng, J. Single-Shot Multi-Frequency 3D Shape Measurement for Discontinuous Surface Object Based on Deep Learning. Micromachines 2023, 14, 328. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.Y. High Accuracy Surface Structured Light Projection Three Dimensional Measurement Research. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2015. [Google Scholar]
- Lei, Z.H.; Li, J.B. Full automatic phase unwrapping method based on projected double spatial frequency fring. Acta Opt. Sin. 2006, 26, 39–42. [Google Scholar]
- Hanqing, Z. The Research Based on Projected Various Fringes for Curved-Surface Measurement; Huazhong University of Science and Technology: Wuhan, China, 2006. [Google Scholar]
- Chen, S.L.; Zhao, J.B.; Xia, R.B. Improvement of phase unwrapping method based on multi frequency heterodyne principle. Acta Opt. Sin. 2016, 36, 155–165. [Google Scholar]
- Li, F.Q.; Chen, W.J. Phase Error Analysis and Correction for phase-shifting Profilometry Using Crossed Grating. Acta Opt. Sin. 2021, 41, 95–106. [Google Scholar]
- Cheng, N.J.; Su, W.H. Phase-Shifting Projected Fringe Profilometry Using Binary-Encoded Patterns. Photonics 2021, 8, 362. [Google Scholar] [CrossRef]
- Xu, Y.; Jia, S.; Luo, X.; Yang, J.; Zhang, Y. Multi-frequency projected fringe profilometry for measuring objects with large depth discontinuities. Opt. Commun. 2013, 288, 27–30. [Google Scholar] [CrossRef]
- Fu, G.; Cao, Y.; Wang, Y.; Wan, Y.; Wang, L.; Li, C. Dynamic Phase Measuring Profilometry Based on Tricolor Binary Fringe Encoding Combined Time-Division Multiplexing. Appl. Sci. 2019, 9, 813. [Google Scholar] [CrossRef]
- Yang, C.; Cao, Y.; Huang, X. Single-Shot Phase Measuring Profilometry Based on Quaternary Grating Projection. Appl. Sci. 2021, 11, 2536. [Google Scholar] [CrossRef]
- Mohammadi, F.; Kofman, J. Multi-wavelength digital-phase-shifting Moiré based on moiré wavelength. Appl. Sci. 2019, 9, 1917. [Google Scholar] [CrossRef]
- Luo, X.; Li, H.; Dong, Z.; Zhu, S. InSAR Phase Unwrapping Based on Square-Root Cubature Kalman Filter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4627–4641. [Google Scholar] [CrossRef]
- Lei, J.F.; Chen, Z.Q.; Zhang, M. Improvement of phase unwrapping method for dual-frequency projection fringe. Opt. Precis. Eng. 2021, 29, 1337–1345. [Google Scholar] [CrossRef]
- Wu, Y.; Dantanarayana, H.G.; Yue, H.; Huntley, J.M. Accurate characterisation of hole size and location by projected fringe profilometry. Meas. Sci. Technol. 2018, 29, 065010. [Google Scholar] [CrossRef]
- Dong, H.; Yang, C.; Ao, M.; Liu, Y. Heterodyne phase measurement in low signal-to-noise ratios using genetic algorithm. Opt. Commun. 2019, 434, 152–156. [Google Scholar] [CrossRef]
- Joo, K.I.; Kim, M.; Park, M.K.; Park, H.; Kim, B.; Hahn, J.; Kim, H.R. A 3D Optical Surface Profilometer Using a Dual-Frequency Liquid Crystal-Based Dynamic Fringe Pattern Generator. Sensors 2016, 16, 1794. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhang, Q.; Li, Q.; Wu, Z.; Chen, C.; Xu, J.; Xue, J. Research on Morphology Detection of Metal Additive Manufacturing Process Based on Fringe Projection and Binocular Vision. Appl. Sci. 2022, 12, 9232. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Optimizing the minimum cost flow algorithm for the phase unwrapping process in SAR radar. Bull. Pol. Acad. Sci. Technol. Sci. 2014, 62, 511–516. [Google Scholar] [CrossRef]
- Xue, J.; Zhang, Q.; Li, C.; Lang, W.; Wang, M.; Hu, Y. 3D Face Profilometry Based on Galvanometer Scanner with Infrared Fringe Projection in High Speed. Appl. Sci. 2019, 9, 1458. [Google Scholar] [CrossRef]
- Ding, M.J.; Niu, P.J.; Li, Y.T. Research on the Methods and Development Trend of Grating Projection 3D Profile Measurement. Ome Inf. 2008, 9, 31–36. [Google Scholar]


| Gaussian Noise | Jumping Point | Correction Rate/% | |||
|---|---|---|---|---|---|
| Mean Value | Variance | Traditional Method | Method of Literature [15] | Method of this Paper | |
| 0 | 0 | 40,339 | 1668 | 1305 | 96.8 |
| 0.01 | 0.002 | 112,654 | 2345 | 2249 | 98.0 |
| 0.03 | 0.004 | 142,195 | 3705 | 2762 | 98.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Lu, Z.; Li, Y.; Dai, Y. Multi-Frequency Fringe Projection Profilometry: Phase Error Suppression Based on Cycle Count Adjustment. Appl. Sci. 2023, 13, 5117. https://doi.org/10.3390/app13085117
Ma Z, Lu Z, Li Y, Dai Y. Multi-Frequency Fringe Projection Profilometry: Phase Error Suppression Based on Cycle Count Adjustment. Applied Sciences. 2023; 13(8):5117. https://doi.org/10.3390/app13085117
Chicago/Turabian StyleMa, Zuqi, Zongsheng Lu, Yongling Li, and Yuntong Dai. 2023. "Multi-Frequency Fringe Projection Profilometry: Phase Error Suppression Based on Cycle Count Adjustment" Applied Sciences 13, no. 8: 5117. https://doi.org/10.3390/app13085117
APA StyleMa, Z., Lu, Z., Li, Y., & Dai, Y. (2023). Multi-Frequency Fringe Projection Profilometry: Phase Error Suppression Based on Cycle Count Adjustment. Applied Sciences, 13(8), 5117. https://doi.org/10.3390/app13085117





